Theis不稳定潜水井流模型的改进
——具入渗补给
2021-11-20陈崇希唐仲华
陈崇希,唐仲华
(中国地质大学(武汉)环境学院,湖北 武汉 430074)
潜水含水层地下水的补给、排泄主要是垂向的地面入渗补给、蒸发排泄(蒸发可视为入渗的负值)及侧向的地表水补给、排泄。作为水文地质学最基本的问题之一—地下水可持续开釆量的评价准则,是补给增量与排泄减量之和。地下水的开采动态,也涉及补给量与排泄量的改变。因此地下水开采的预测模型必须包含上述两类的补排因素,否则不能满足要求。
地下水井流问题,是当今地下水动力学理论和应用最重要的课题之一。然而地下水井流的两个经典解析模型,即1863年的Dupuit 稳定井流模型[1]和1935年的Theis 不稳定井流模型[2](包括以影像井替代河流边界的作用),也只有地表水体的补排,而不涉及地面入渗补给和蒸发排泄。如此,这两个经典模型基本上只能在旱季用于地下水井流试验求取含水系统的参数,而不能够用于预测。
陈崇希[3]作为初次研究具有入渗补给和地表水补排的井流问题,是从经典的Dupuit 圆岛稳定井流模型的改进—具入渗补给开始,建立了相关的水位分布方程和流量方程。应当特别指出,Chen 等[4]提出一个新型的稳定井流模型,它有别于Dupuit 圆岛稳定井流模型,它不是圆岛,不是靠湖海水的补给增量形成稳定井流,而是依赖初始的地下水的蒸发与地面入渗补给的平衡,当抽水后潜水位下降导致蒸发量减少,且单位时间减少的蒸发量等于地下水抽水流量时,地下水流便转变为稳定流。就地下水可持续开采量评价准则而言,此稳定井流模型是由于地下水的(蒸发)排泄减少量等于抽水量而形成的稳定井流。
在完成对Dupuit 模型的改进—具入渗补给之后,本文着手对Theis 不稳定潜水井流模型的改进—具入渗补给的研究。
经典的无界含水层Theis 不稳定井流模型不能直接加以地面入渗补给,这种条件会出现地下水位无限上升的荒谬状态。因此,本文引入定水位的河流边界,当抽水井远离河流边界,或者说河流边界对抽水井漏斗区的作用还没有明显起作用时,这时的问题,就是Theis 不稳定井流加上地面入渗补给的模型,从而使得本问题得以顺利研究。当河流边界对井流发生明显作用时,此时的井流同时考虑了侧向地表水的补排和地面入渗、蒸发的补排作用。这就是我们所需要的模型。
首先基于质量守恒原理,假定渗流服从Darcy 定律并满足Dupuit 徦定,建立了地下水运动基本微分方程。然后,研究了两类自然界比较常见的区域,即两条平行定水位边界条件(所谓河间地区)和一条定水位边界平行另一条隔水边界构成的两类无限条形区域,建立了在均匀稳定入渗补给条件下的Theis 潜水井流问题。这是一个复杂的水文地质问题。其次,与用水头刻画的承压水流不同,这是一个非线性的潜水流问题,我们采用第二类线性化的势函数来刻画潜水流问题。此外,我们将一个含有入渗补给、抽水井作用以及初始条件(现有的井流问题的初始条件通常是h(t=0)为常数的关系)是一个未知待求的复杂水文地质问题(数学模型),分解成几个相对简单的水文地质问题(子模型),这些简单的子模型或者已有它的解,或者比较容易求解。之后再把它们合成,成为原复杂水文地质问题(数学模型)的解。此外,提出并采用“边界对边界的反映法”用以求解一条定水位边界平行另一条隔水边界构成的无限条形区域的同一问题,减少了许多推导过程。
上述导出的方程,可用来预测相应条件的地下水位分布特征与动态规律,以及为降雨入渗补给条件下抽水试验确定含水系统有关参数提供了理论基础。
此外,本文对上述获得的理论成果做了初步的应用,也是个重要的应用。即在河水水质不能满足要求的河流附近,有一口抽水井,建立了计算该抽水井在不汲取河水前提下的抽水井临界流量方程,获得具重要意义的、结构简洁的关系式。该方程也可以用于滨海区的抽水井,在不发生海水入侵前提下的临界抽水流量计算。它的意义,似乎更具普遍性。
本文给出了河间地区某典型条件下的地下水流网图。其流网与Theis 井流的不同,也与无入渗补给的承压均匀流中的井流不同。其特点是,区域上由两条河之间的地下分水岭向两侧水力坡度由小到大地分布。在这个背景下,一个定流量抽水井工作一定时间的流网图。它是不稳定流过程某时刻的流网。
Wilson[5]讨论了具入渗补给的井流问题,但是均属于稳定流范畴。本文讨论的基于Theis 不稳定井流模型加上地面入渗补给,两者是不同的。
与Theis 模型相同,本文仅讨论隔水底板水平的均质含水层,且为稳定均匀入渗的条件。
1 两平行定水位边界井流问题解析解
1.1 假设条件及数学模型
设某潜水含水层为均质、各向同性,隔水底板水平,两侧被两平行完整河流(间距为l)切割,且两河流水位相等(h1=h2)并保持不变;因此视为水位相等的定水位边界,初始条件是由均匀入渗条件下形成的稳定水位分布,随后保持初始的入渗强度不变;在距河1 为 λ处有一口定流量完整抽水井(图1)。

图1 具有入渗补给的河间地区潜水井流模型Fig.1 Model of inter rivers area with infiltration recharge
取坐标如图1 示,x轴垂直于河流,y轴位于河1 右岸水边线。设井流水位的基准面在潜水层之下隔水层顶面处。假定渗流服从Darcy 定律并满足Dupuit假定,根据质量守恒原理,则该问题的基本微分方程可以写成:
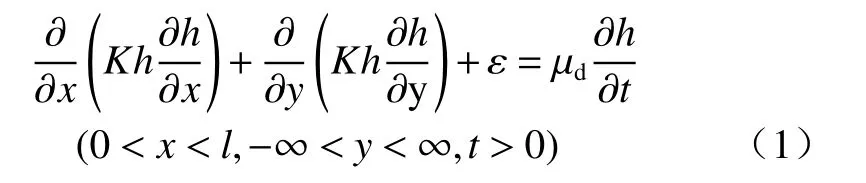
式中:K—渗透系数/(m·d−1);
h—潜水位,本文坐标系中即潜水层厚度/m;
ε—入渗强度/(m·d−1);
µd—重力给水度。
这就是潜水流问题基本微分方程,是非线性的。为求得其解析解,需将其线性化。采用第二类线性化的方法,即设

由于含水层为均质,于是用势表示的潜水流动方程为:

式中:a—水位传导系数或水力扩散系数/(m2·d−1)。

式中:hm—潜水层平均厚度/m。
如此,该问题的数学模型可以写成:

式中:φ0—初始势函数;
φ1φ2、—河1 和河2 的水位势;
Qw—抽水井流量(大于0 为抽水,小于0 为注水)/(m3·d−1);
r—极点位于井中心的极轴上某点的极径;
(xw,yw)—抽水井位置坐标/m;
a—潜水层水位传导系数/(m2·d−1)。
模型[I]中的初始势φ0(x,y)由子模型[II]确定。

设

即

由[I]和[II]及式(14)可得:

由此,模型[I]分解为子模型[II]和[III]。
1.2 模型的解析求解
对于子模型[II],采用积分方法可以求得初始势函数 φ0,即:

下面讨论子模型[III]—抽水势增量 ∆φ。
子模型[III]表述的是无入渗条件下两平行河流间的Theis 不稳定井流问题。对于这种条件,地下水动力学已经有解,即抽水井对边界进行无穷次反映(图2)。但由于井函数W随r的增大而减小,因此实用上有时只要取其有限个虚井即可近似表示。

图2 两条平行定水位边界内抽水井的无穷反映Fig.2 Infinite reflection of pumping wells in the area of two parallel boundaries with constant water level
已知无界含水层单井定流量抽水的Theis 方程,用势表示为:

(1)当边界对抽水漏斗区尚未明显起作用时
当虚井的作用与实际抽水井的作用相比,可以忽略不计时,即边界还没有明显起作用时,可近似认为只有一个实际抽水井在工作。
将式(20)和(21)代入式(13),得到此条件势的分布:

将无压势 φ的定义代入,得水位方程:
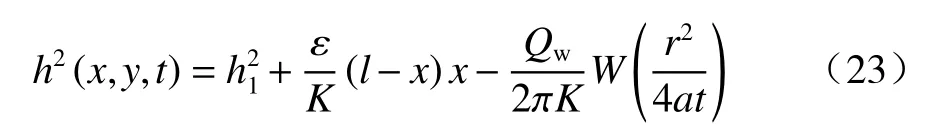
此时,当r=rw则h=hw,得抽水井水位方程:
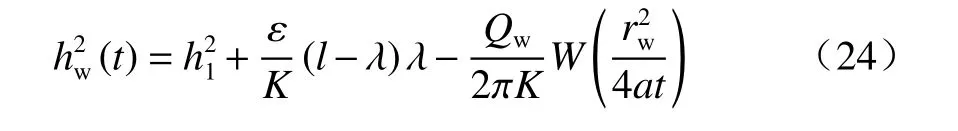
由式(23)得到流量方程:

该方程的应用,例如,某矿区有一个已经报废的老矿井,在它的附近计划建立一个新矿井,拟利用老矿井抽水以疏干新矿井的水位至某设计标高,达到安全采矿的目标。这时,根据新矿井要求的疏干水位及疏干时间,就可以利用该公式计算老矿井的排水量Qw。某些岩土工程中的疏干排水,也可能用到此方程。
当然,以上述方程为基础,可以讨论种种抽水试验方法,包括观测孔的部署,来建立求取含水系统的各种参数的方程。

上面为忽略边界作用,单一抽水井作用下势和水位分布等问题的讨论。
如此,作为本问题,剩下的仅仅是抽水井与边界的距离及抽水延续时间等,如何考虑边界的作用问题。
(2)抽水井靠近左侧(河1)定水位边界且抽水时间很不长(河1 起做用而河2 尚未明显起作用)
此类条件是经常遇到的。这时,图2 中河1(虚1 井)的作用必须考虑,而河2(虚2 井)的作用尚可忽略不计(图3)。此时相关的势函数 φ为:

图3 靠近左侧定水位边界抽水井的反映Fig.3 Reflection of a pumping well near the boundary of a constant water level

将无压势 φ的定义代入,得水位方程:

由此可得抽水井的水位hw方程:

由式(29)得到流量方程:


于是式(29)可以写成:
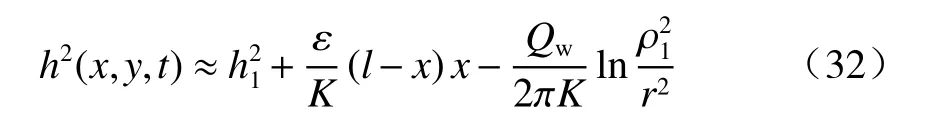
由此得到抽水井的水位hw方程:
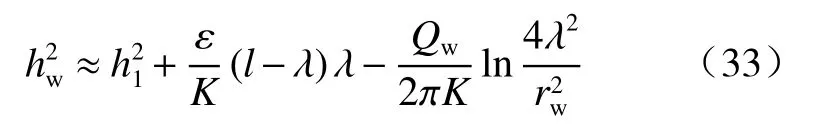
由式(32)得到流量方程:

在此范围内形成近似稳定流,可以开展具入渗补给条件下的近似稳定井流相应的应用。
(3)随抽水时间延续,或抽水井至两边界的距离差别不大,而抽水时间尚不很大时
此时,则需考虑1 个实井和2 个虚井的作用(图2中虚1 井和虚2 井),可以写出类似上述方程,不再赘述。
(4)当长时间抽水时
这时,两条边界都明显起作用,要考虑无穷反映,根据无穷反映原理,得:
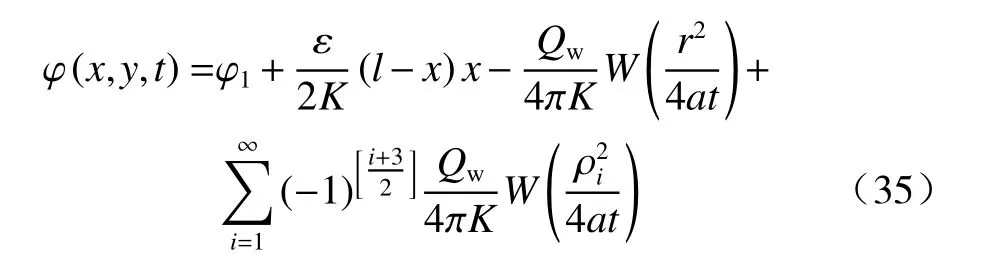
由于虚拟井i的横坐标为,纵坐标ywi=0,所以
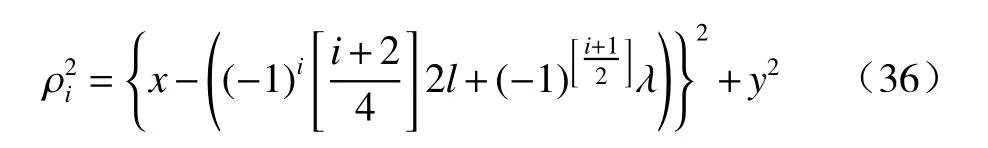
式(35)无穷级数方程中,序列号i是按照虚井到点p的距离 ρi的大小的顺序排列的,即ρi+1>ρi(图2)。只要实际抽水井和点p都在两河间分水岭的靠河1 一侧,此条件必定满足。这也是最需要讨论的实际问题。
将无压势 φ的定义代入,得水位方程:

此即具入渗补给的两条平行定水位边界区内井流的通用水位方程。求和项i(虚井)的取数,视边界的作用可否忽略不计或作用程度而定,此条件与井位、含水层参数及抽水延续时间等要素有关。
式(35)和(37)的特点:第一,各项是正负交错的无穷级数;第二,由于 λ小于l,故第i+1项的绝对值小于第i项的绝对值;第三,级数的通项趋于0。所以该无穷级数是收敛的。这个特点反映了相应的水文地质条件。
图4 是自然界的一个典型情景—具有入渗补给的河间地区存在一个抽水井形成的流网图。其模型参数是:l=10 000 m,K=10 m/d,µd=0.2,h1=h2=100 m,h0=100 m,ε=0.000 5 m/d,λ=3 000 m,(xw=3 000,yw=0),rw=0.1 m,Qw=5 000 m3/d,hm=102.8 m,t=600 d。

图4 Qw =5 000 m3/d 时抽水600 d 的流网图Fig.4 Fow network with long-term pumping of 600 d at Qw =5 000 m3/d
此图的一个特点,抽水前的地下水力坡度,由两河间地下分水岭处的零向两侧逐渐加大,体现了入渗补给作用。当抽水井工作后,将会在抽水井与河流1 之间形成一个地下水分水点,通过这个点做流线,存在一条地下水分流线。在分流线之内地下水流向抽水井,在分流线之外,地下水仍然保持流向河流1。这条分水线的意义很重要,如果这个范围内存在污染水体,它迟早会流入抽水井。再一个特点,原来的两河间的正中间有一条直线状地下水分水岭。当一侧抽水以后,地下分水岭就会呈喇叭口型向邻河推移。这在地下水资源评价原则上有其重要意义。地下分水岭的推移使得原来入渗补给到相邻河流的,转化为流向抽水一侧来了,它成为抽水一侧(水源地)的补给增量。对这个水源地来说,它是一个补给增量。这在水均衡计算上以及地下水开采动态上都会有所反应。
(5)长时间抽水形成稳定井流
如果t足够大时可形成稳定井流,俄罗斯学者鲍契维尔在1963年[6]曾对相同侧边界条件下的无入渗/无越流承压水层稳定井流导出相应的公式(也可参考文献[7])。他认为当时,可近似计算。我们将其用于承压含水层水头降深s表示的方程,改为用势φ表示的方程(以便转化为用于潜水含水层的水位h方程的建立),即:

将无压势 φ的定义代入,得水位方程:
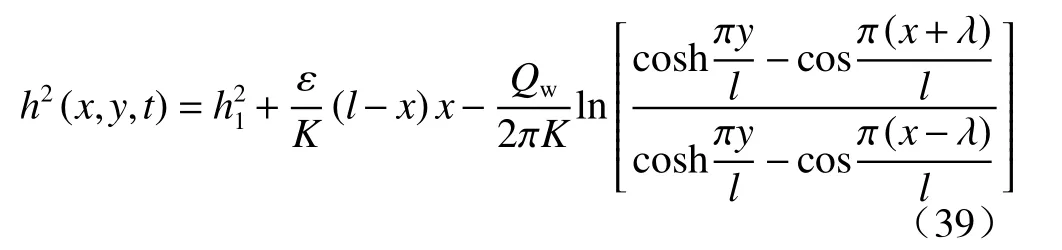
利用文献[6]的结果,可得到抽水井的水位hw方程:
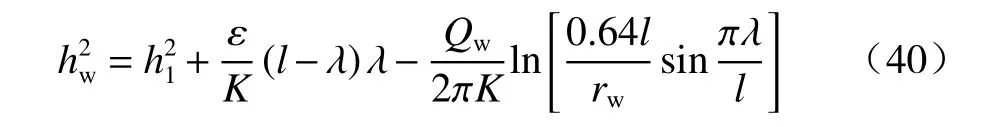
于是流量方程为:
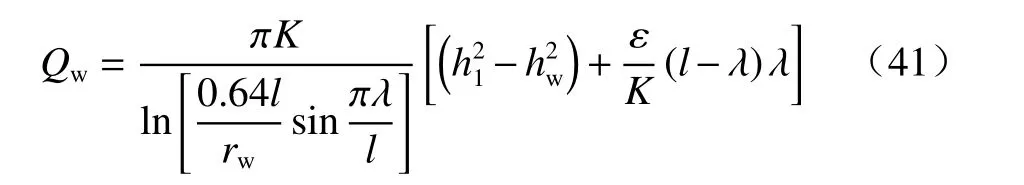
为了对形成稳定流的时间有一点概念,若取l=10 000 m,K=10 m/d,平均水位h=10 m,µd=0.2,则形成稳定流的时间t=100 000 d;若取l=1 000 m,其它参数不变,则形成稳定流的时间t=1 000 d。由此可见,地下水不稳定流的过程,是有必要讨论的。
上面讨论的是针对河间地区一个定流量抽水井所建立的方程。对于多个抽水井或者对于变流量的抽水井,均可按地下水动力学中的有关方法处理。
2 一条定水位边界和一条平行的隔水边界条件井流问题
2.1 假设条件
基本条件与第2 节相同,只是右侧定水位边界改为隔水边界。坐标如图5所示。

图5 具有入渗补给的一定水位边界平行一隔水边界条件潜水井流模型Fig.5 Model of a constant water level boundary parallel to an impermeable boundary with infiltration recharge
对此问题,可以按照上节的步骤来建立相关方程。但可以换一种思维方法考虑:边界附近的抽(注)水井可以通过反映法替代边界的作用,那么边界附近的边界是否也可以采用反映法替代一边界的作用呢?本文用此思路求解问题。
以右侧隔水边界为镜面(对称面),左侧定水位边界和抽水井一起反映过去,转变为间距为2l的,左右两侧为平行的、水位相等的定水位边界的区域,且有两个互相对称的抽水井的问题(图6)。显然,转换后的问题,其中心线是其地下水分水岭,这正是原问题隔水边界的基本性质。由此可见,上述边界如同抽水井一样,对附近边界作反映,可以替代(后者)边界的作用。

图6 由图5 问题通过边界反映获得的等效问题Fig.6 Equivalent problem obtained by the boundary reflection of the problem in Fig.5
请注意,如果以等水位线为对称面,将隔水边反映过去,获得的仍然是隔水边界,而不是等水位边界。
如此,本节的隔水边界平行定水位边界的井流问题,变换为两条平行的、水位相等的定水位边界问题。只要将两边界的距离l改为 2l,且抽水井增加一个对称的抽水井,就可按上节已建的方程来建立相应的方 程。如此,可省去了大量的推导过程。
2.2 问题的解析解
(1)抽水井远离边界且抽水时间不长
虽然本节与第2 节的边界条件不同,但由于“抽水时间不长”,两边界对抽水漏斗区尚未明显起作用,因此其水位方程,依式(23)并考虑定水位边界对隔水边界的反映,得:

由此得抽水井的水位hw方程:

由式(42)得流量方程:
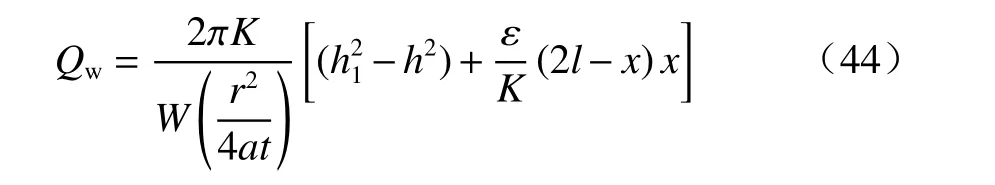
(2)抽水井靠近左侧定水位边界且抽水时间很不长(隔水边界尚未明显起作用)
此时,虚1 井的作用必须考虑,而虚2 井与虚3 井等的作用可忽略不计(图7)。

图7 一条定水位边界附近抽水井的反映法Fig.7 Reflection method of a pumping well near the boundary of a constant water level
该问题水位方程可类似式(29)并按边界对边界的反映,得:

水位hw方程为:

流量方程为:

(3)抽水井靠近隔水边界而远离左侧河流边界且抽水时间不很长
此条件(图8)只需考虑隔水边界的作用,即虚1 井的作用必须考虑,而虚2 井与虚3 井等的作用可忽略不计。根据图8,此时相关的 φ为:

图8 抽水井靠近隔水边界的镜像影射示意图Fig.8 Mirror image of the pumping well close to the impermeable boundary

该问题水位函数的解仿照式(45),注意抽水井对隔水边界反映为抽水井,并考虑定水位边界对隔水边界的反映,得:

其中,
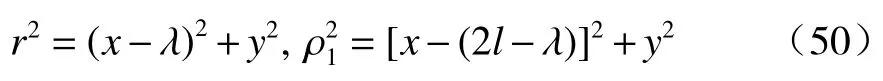
而抽水井水位hw方程 :
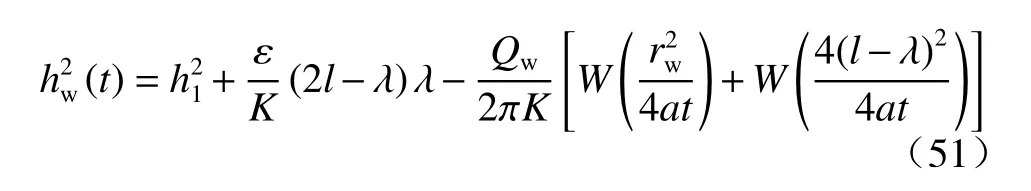
由式(49)得到流量方程:

(4)当较长时间抽水需考虑多个虚井时
此时,必须考虑多次反映。
1)实井靠近河流边界
根据无穷反映原理(图9),得:
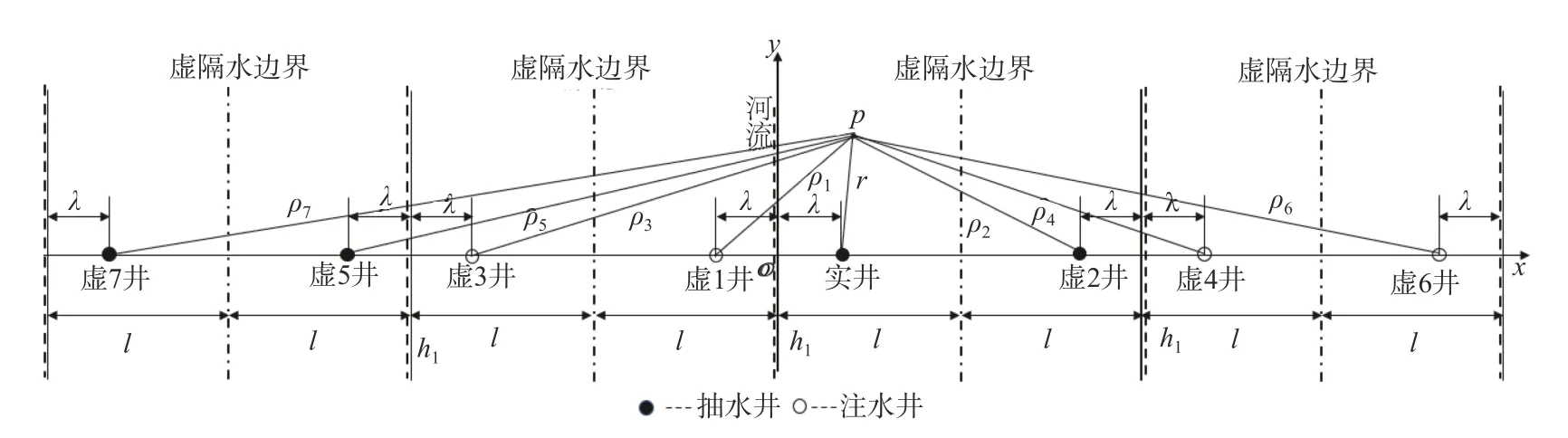
图9 一条定水位边界和一条平行隔水边界,实井靠近定水位边界的井流模型无穷反映示意图Fig.9 Diagram of infinite reflection of the well flow model with a boundary of constant water level and a parallel impermeable boundary and a pumping well close to the boundary of constant water level

将无压势 φ的定义代入,得水位方程:
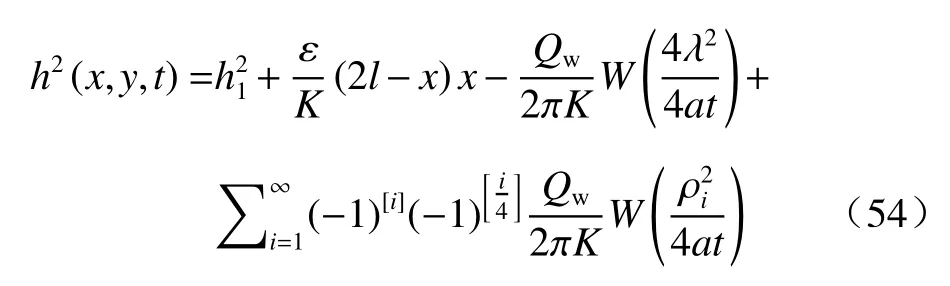
此即具入渗补给的一条定水位边界和一条平行隔水边界区内实井靠近定水位边界井流的通用水位方程。求和项i(虚井)的取数,视边界的作用可否忽略不计而定,此条件与井位、含水层参数及抽水延续时间等要素有关。
2)实井靠近隔水边界
根据无穷反映原理(图10),与图9 不同,图10 的1 号虚井为抽水井,且位于隔水边界的右侧。此条件的势函数为:
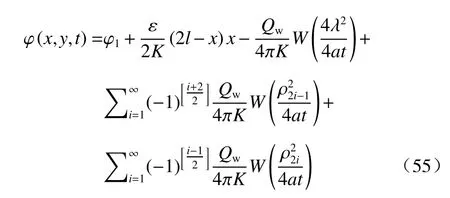
这里的 ρi如图10所示。由于虚井坐标为:
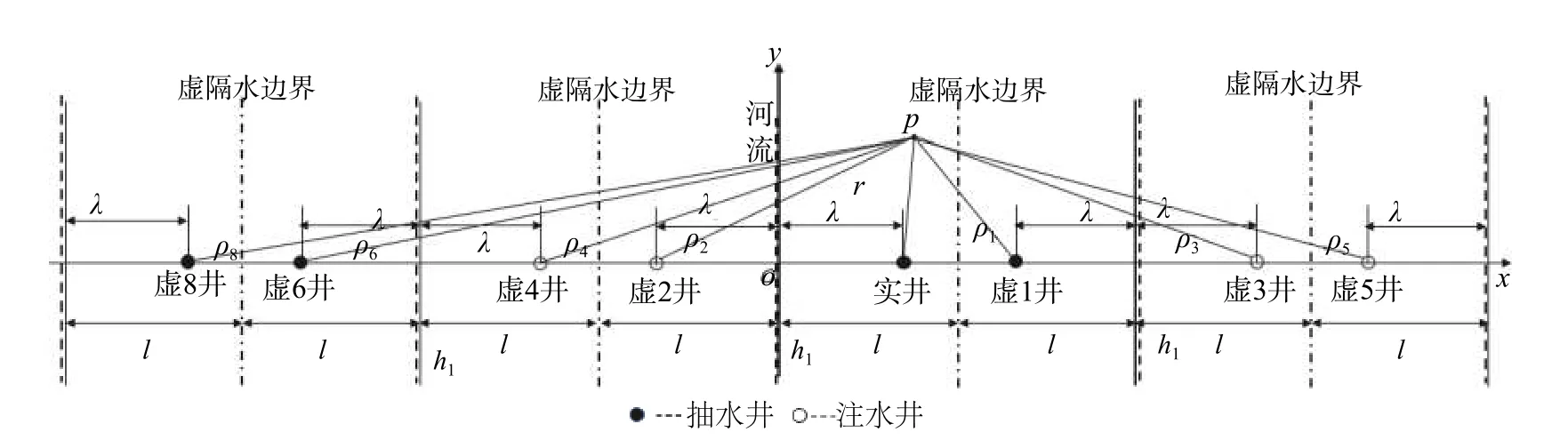
图10 一条定水位边界和一条平行隔水边界,实井靠近隔水边界的井流模型无穷反映示意图Fig.10 Diagram of infinite reflection of the well flow model with a boundary of constant water level and a parallel impermeable boundary and a pumping well close to the impermeable boundary

所以 ρi的表达式如下:

将无压势 φ的定义代入,得水位方程:
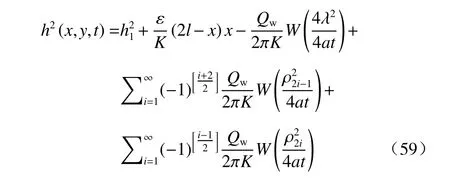
(5)长时间抽水形成稳定井流
若t足够大,则可形成稳定井流,俄罗斯学者鲍契维尔[6]曾对相同侧边界的无入渗/无越流承压水层稳定井流导出相应的公式,也可参考文献[7]。他认为当时,可近似式计算。我们将其用于承压含水层水头降深s表示的方程,改为用势 φ表示的方程(以便转化为潜水含水层的水位h方程),即:
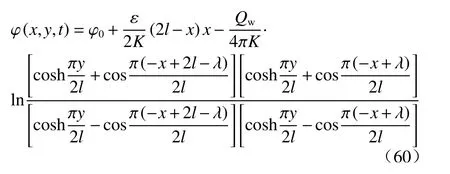
将无压势 φ的定义式代入上式,得水位方程:

利用文献[6]的结果,得到抽水井的水位hw方程:

其流量方程为:

3 傍河(海)抽水井临界抽水流量方程的建立
水质不符合要求的河水(暂称为“污染水”)的傍河抽水井,存在一个临界抽水流量。若超过该流量,则“污染水”会入侵抽水井。作为上述建立理论的一个初步应用,这里对前述两平行定水位边界井流情形进行分析。
海边界附近的潜水抽水井,同样会遇到其临界抽水流量问题。地下水可持续开采量评价中的排泄量减少诸要素中,截取地下水排泄入海以及地下水蒸发(也有称其为无效蒸发),是真正无代价、可以“白得”的两大要素。其他要素,往往是地下水与地表水互相转化的关系,地下水补给的增量或排泄减量,是要付出代价的。由此可见,滨海区抽水井临界流量的计算是极其重要的课题。
3.1 在河流1 附近抽水井的临界抽水流量
为建立抽水井的临界抽水流量方程,要求令xd等于零,显然,此时河流边界对抽水漏斗已经明显起作用。此时,要考虑左边界,即1 号虚拟注水井的作用。由已求得此情形的水位方程式(29),对此方程沿x轴(y=0)关于x求导,并令得此情形下地下水分水点xd满足下述方程:
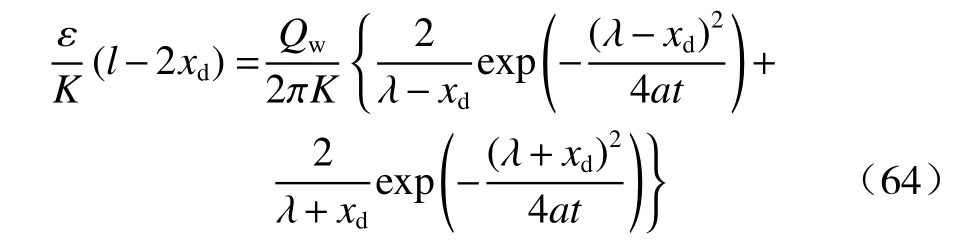
取xd=0,此时抽水井的流量为临界抽水流量Qc,即:

这就是傍河(海)抽水井(单井)的临界抽水流量公式,其结构十分简洁。该方程表明,临界抽水流量Qc是随抽水时间t的增大而减小,但它不会无限地减小,其极限值为:

其物理意义十分明确。记q为未抽水时,天然条件下地下水单(位)宽(度)流量,即:

在河1 边界上,即x=0 处,单宽流量为:

于是式(66)可改写为:

上式说明,傍河抽水井的临界抽水流量是河1 边界单宽流量乘以以 λ为半径的圆周长的1/2。这个临界抽水流量,就是抽水井截取这个宽度的地下水入渗补给的流量。
要注意,式(65)的应用是有前提的,也就是,右端(河流2)的定水位边界还没有明显起作用。而式(66)(69)却是式(65)的t趋于无限大的条件得到的。此时就意味着右边的定水位边界肯定起了明显的作用。但是,式(66)(69)可作为式(65)的近似估计应用(依此两式计算Qc无需参数水位传导系数,有其优点)。
据图2(抽水井与注水井的分布,及其 ρi的大小)可以预计到,若考虑右侧河流的作用,其Qc会稍微增大。
3.2 多个虚井起作用时抽水井的临界抽水流量
如前所述,当长时间抽水时,根据无穷反映原理,得到水位方程(37),对此方程沿x轴(y=0)关于x求导,并令得到此情形下,地下水分水点xd满足下述方程:
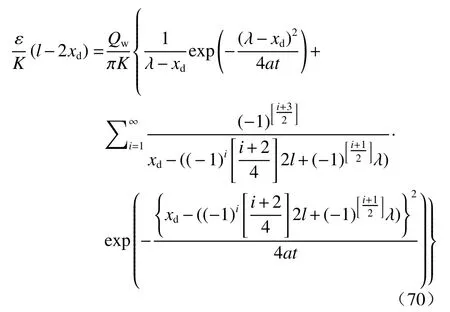
利用此式计算上述流网的算例(基础数据相同),虚井数i取15 项或16 项求和,计算得到xd≈2 404.23 m。
若上式中取xd=0,则Qw成为Qc,即:

由此得:
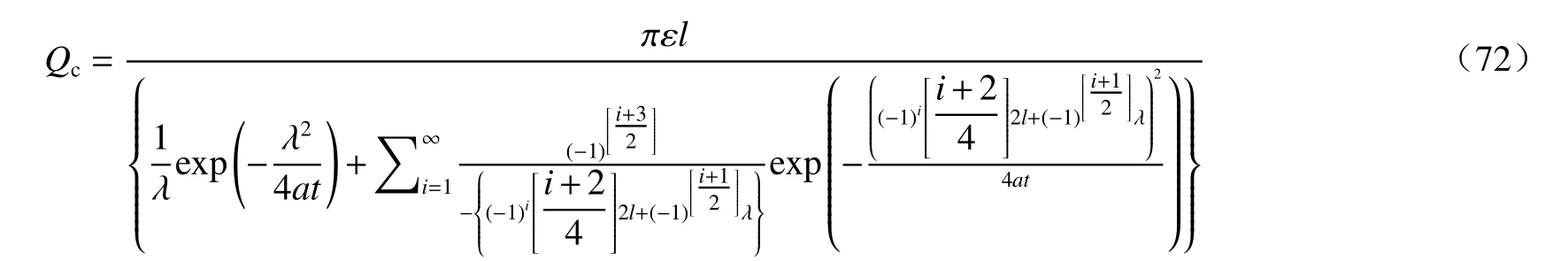
上式求和项若只取一项i=1,则得到前述3.1 节的结 果,即式(65)。
3.3 稳定流状态
如前所述,得到稳定流状态的水位方程式(39),对此方程沿x轴(y=0)关于x求导,并令得到地下水分水点xd所满足的方程:

当地下水分水点移到河流边界处,此时的流量为抽水井的临界抽水流量。即:
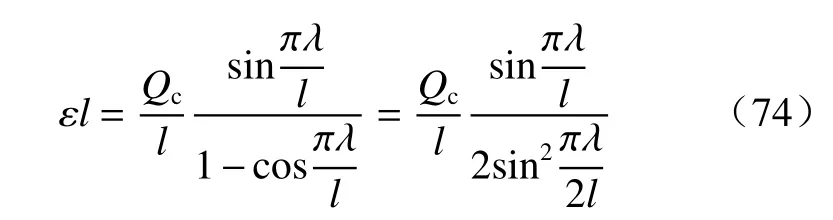
由此得:

这就是傍河稳定井流状态临界抽水流量公式。
4 结论
(1)对经典的Theis(1935)不稳定潜水井流模型做了改进—具入渗补给(蒸发示为其负值)。建立了考虑均匀稳定入渗补给条件下井流的解析模型,拓展了Theis 模型。
(2)研究涉及的是含入渗补给及抽水井的双重作用的复杂水文地质问题,我们将其分解为几个相对简单的子问题,而这些子问题,或者是比较容易求解,或者是已经有了解。然后再把它们合成,形成原问题的解。
(3)研究的问题是复杂的非线性潜水运动问题。我们采用第二类线性化的势函数来刻画。如此比较有利于模型的分解及合成。
(4)为了同时考虑潜水含水层垂向的地面入渗补给以及水平方向的地表水体的补排这两类补排关系,本文建立了以河流为代表的定水位边界和隔水边界所组成的两类典型地区的井流问题,建立有关潜水位方程和流量方程,前者包括无穷反映的通用水位方程及常用的傍河(隔水边界)抽水的水位方程等。使其不仅具理论意义而且有实用价值。如此,新的解析模型不仅可以进行可持续开采量的评价和地下水开采动态的预测。同时还可以为利用雨季抽水试验数据求取含水层有关参数提供基础。
(5)由于经典的Theis 模型区域是无限大,因此如果直接在Theis 模型(无定水位边界)上加以入渗补给,会出现地下水位无限上升,这有悖于物理意义。因此,本文引入定水位的河流边界,当抽水井远离河流边界,或者说河流边界对抽水井的漏斗区还没有明显起作用时,这时的问题,就是Theis 不稳定井流加上地面入渗补给的模型。从而使得本问题得以顺利研究。
(6)本文提出并采用“边界对边界的反映法”用以求解一河流平行一隔水边界条形区域的同一问题。减少了许多推导过程。
(7)本文根据所建立的理论方程,给出自然界的一个典型情景—具有入渗补给的河间地区存在一个抽水井形成的流网图,在抽水井与河流1 之间存在一条喇叭口型的地下水分流线。它在地下水资源评价和管理上有重要的意义。如果在分流线之内有污染的地下水,它会流入抽水井。抽水井下游的地下水稳定分水点,会随着抽水流量的增大而接近海/河边界。当分水点移到海/河边界,这时就是地下水临界抽水流量,即最大允许开采量。
(8)此外,本文对上述获得的理论成果做了初步的应用,也是个重要的应用。即在河水水质不能满足要求的河流附近,有一口抽水井,建立了计算该抽水井在不汲取河水前提下的抽水井临界流量方程,获得具重要意义的、结构简洁的关系式。该方程也可以用于滨海区的抽水井,在不发生海水入侵前提下的临界抽水流量的计算。它的意义,似乎更具普遍性。
(9)在建立解析方程的过程中,假设满足Dupuit假定。引入Dupuit 假定,对本问题解析研究可以降维(略去z变量)而使有关方程变得简单明了。然而实际上,在某些r断面上是可能出现偏离Dupuit 假定的,主要在地下水分水岭附近。这一点,Bear(1972)[8]有过相关的讨论。即使没有入渗补给的原始Theis 模型,如果潜水含水层厚度与两边界距离之比较大,且当抽水井水位降深与潜水含水层厚度之比较大时,在抽水井附近也会出现偏离Dupuit 假定。已知非完整抽水井附近的三维流,向外逐渐转变为二维流(忽略z分量),此径距r大约是含水层厚度的1.5 倍[7]。借助这一研究成果,估计Dupuit 假定(忽略z分量)不满足的地段,可能不会大于含水层厚度的1.5 倍。上述种种偏离Dupuit 假定对解析结果影响的定量分析,还需要作另一专题研究。
认识到Dupuit 假定在某些区段可能会有所偏离,那么在抽水试验求取含水层有关参数时,观测孔的部署要尽量回避这些区段。
(10)对于不稳定潜水井流问题,本身是非线的,本文釆用的是第二类线性化方法,其中将参数a(Khm/µd)视为常量。当然,如果水位降深相对于潜水层厚度是个很小的比值,则可以近似取潜水层厚度,如同承压含水层一样。否则将存在hm如何取值的问题。这个问题既使对于无入渗补给的经典Theis 模型也存在此类线性化带来的平均值取值问题。这也是一个待研究的专题问题。
