一种改进的地下水模型结构不确定性分析方法

孙晓卓，曾献奎，吴吉春，孙媛媛

（南京大学地球科学与工程学院/表生地球化学教育部重点实验室，江苏 南京 210023）

地下水数值模型能够定量刻画地下水流和污染物的时空分布特征，已被广泛应用于地下水资源的科学管理和保护[1−5]。由于实际地下水系统十分复杂，限于认知不足，通常需对其进行简化，这将导致建立的水文地质概念模型与实际水文地质条件之间存在差异，即模型存在结构误差，如含水层空间分布的刻画偏差、化学反应动力学模型存在偏差等。使用带有结构误差的模型进行预测时，即使进行参数识别，预测结果也可能存在偏差[6−8]。因此，为提高模拟结果的可靠性，需要定量刻画模型的结构误差，从而可为地下水资源管理和决策提供更可靠的依据。

近十年来，众多研究者开始注重对模型结构不确定性的研究[9−12]。贝叶斯模型平均（BMA）和基于数据驱动的结构误差统计学习方法是目前常用的处理方法。BMA 在贝叶斯框架下建立一组可行的概念模型，根据每个模型的表现赋予相应的权重，从而对这些模型的预测结果进行加权平均[13−18]。研究结果表明，对比于其他多模型方法或单一模型法，采用BMA方法能得到更准确和可靠的预测结果[19−20]。尽管如此，BMA 在实际应用过程中存在局限性，如模型空间（概念模型集合）的定义及先验权重具有主观性、模型间相关性未能准确量化等，从而影响BMA 的预测效果[20−21]。

数据驱动法（DDM）通过某种统计模型刻画模型结构误差，如支持向量机回归[22−23]、人工神经网络[24]、随机森林[25]、高斯过程回归[26−27]等机器学习方法。其中，高斯过程回归（GPR）是一种基于贝叶斯理论的监督学习算法，被广泛用于模型结构误差的学习。Xu等[26−27]利用GPR 刻画多个地下水流模型的结构误差，通过马尔科夫链蒙特卡洛模拟（MCMC）识别地下水模型参数（物理参数）和GPR 参数（超参）。结果表明，GPR 可以刻画模型结构误差的时空相关性，显著提高地下水模型的预测能力。Pan 等[28]通过GPR 刻画地下水中重质非水相液体（DNAPL）运移模型的结构误差，并进行针对地下水DNAPL 污染的人类健康风险评价。结果表明与不考虑模型结构误差相比，通过GPR 刻画DNAPL 运移模型结构误差，能够在关键区域获得更准确的人体健康风险评价。

尽管如此，当前基于GPR 进行模型结构误差刻画的研究中，通常假设物理参数和超参相互独立，且对这些参数进行联立识别。然而，在实际情况下物理参数和超参的独立性假设不够合理。同时，超参没有物理意义，进行物理参数和超参联立识别时，可能导致参数的过度识别，影响模型预测效果[29−30]。

本文提出两步识别DDM 方法进行参数识别和模型结构误差定量刻画，克服了传统联立识别DDM 方法中的过度拟合问题，并通过一个地下水溶质运移案例和一个地下水水流案例，对提出方法的可靠性和优越性进行了验证和分析。

1 研究方法

1.1 高斯过程回归（GPR）

地下水模型中观测值f可以表示为：

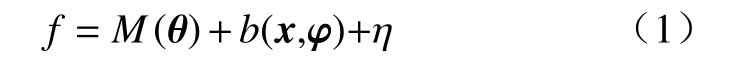
式中：M—地下水模型；

θ—地下水模型参数（物理参数）；

b—模型结构误差；

x—模型输入；

φ—超参；

η—随机测量误差。

在GPR 中，假定结构误差b（x,φ）在空间各点服从均值为μ，协方差矩阵为C的联合多元高斯分布[31−32]。本文均值函数μ为0，协方差矩阵C采用平方指数型：

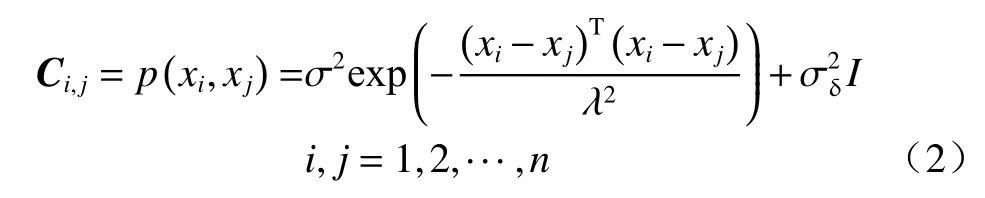
式中：λ—特征长度；

σ2—控制b（x,φ）的边缘方差；

n—观测数据的个数；

I—n×n阶的单位矩阵。

测量误差η的先验为独立同分布。物理参数θ和超参被认为是相互独立并服从先验分布p（θ,φ）=p（θ）p（φ）。根据贝叶斯原理，推导得到θ与φ的后验分布为：

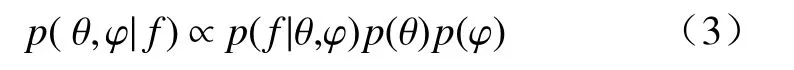
式中：p（θ）—θ的先验函数；

p（φ）—φ的先验函数。

1.2 基于联立识别的数据驱动方法

传统的数据驱动方法（DDM）中，通常假设物理参数θ和超参φ独立分布，通过MCMC 模拟对其进行联立识别[26,28]。本次研究中采用改进的差分进化自适应算法DREAMzs（DiffeRential Evolution Adaptive Metropolis）[33−34]进行MCMC 模拟，基于联立识别的DDM 基本步骤如下：

（1）定义物理参数θ和超参φ的先验分布；

（2）通过MCMC 模拟获得物理参数θ和超参φ的后验样本；

（3）对于新的模型输入x∗，输入模型获得输出M∗，根据式（2）计算协方差矩阵C、C∗、C∗∗；

（4）根据式（5）—（7），使用多元正态抽样生成b∗、η∗；

（5）通过式（8）计算预测值f*。

1.3 基于两步识别的数据驱动方法

假设物理参数θ和超参φ不独立，将其分开进行两步识别。首先，在φ的全部先验分布空间内识别θ。根据贝叶斯理论，物理参数θ后验概率p（θ|f,M）可以表示为：

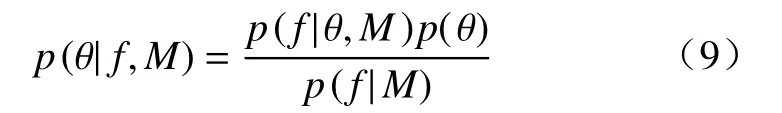
其中，p（f|θ,M）为模型M（θ）的边缘似然值，即M（θ）在φ的全部先验分布空间内似然函数的平均值。其表达式为：

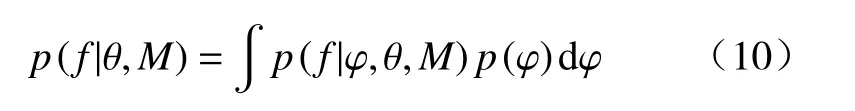
其中，p（f|φ,θ,M）为物理参数θ和超参φ的联合似然函数，p（φ）为φ的先验分布。

获得θ的后验概率p（θ|f,M）之后，超参后验概率p（φ|f,M）可以表示为：

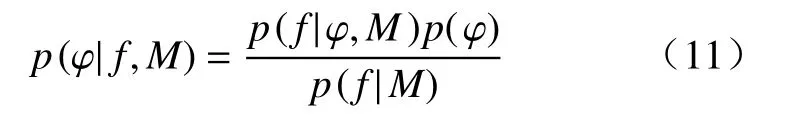
其中，p（f|φ,M）是模型M的边缘似然值，即M（φ）在θ的全部后验分布空间内似然函数的平均值。其表达式为：

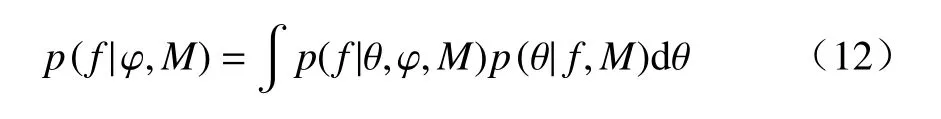
边缘似然值即式（10）（12）表示似然函数在高维参数概率分布空间内的积分，由于非线性似然函数的复杂性，边缘似然值的解析表达式难以获得。本文采用算术平均估计方法AME[35−36]计算式（10）（12），计算公式为：

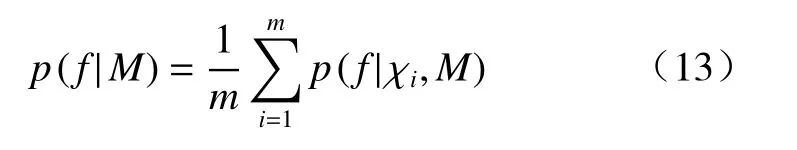
式中：χi—模型M参数概率分布空间内的一个样本；

m—χi的样本数量。

通过AME 计算边缘似然值通常需要大量的样本，m数值一般为几十万至几千万，一个样本代表运行物理模型一次。此外，通过MCMC 方法获得θ和φ后验分布（即式（9）（11））时需多次使用AME。因此，模型边缘似然值的计算具有严重的计算负荷。本文使用当前应用广泛的自适应稀疏网格（adaptive SG）技术[37−41]构建边缘似然值的替代模型，克服计算耗时困难。

通过式（9）—（13）获得θ和φ的后验分布之后，进行模型预测。两步识别DDM 法计算步骤为（图1）：

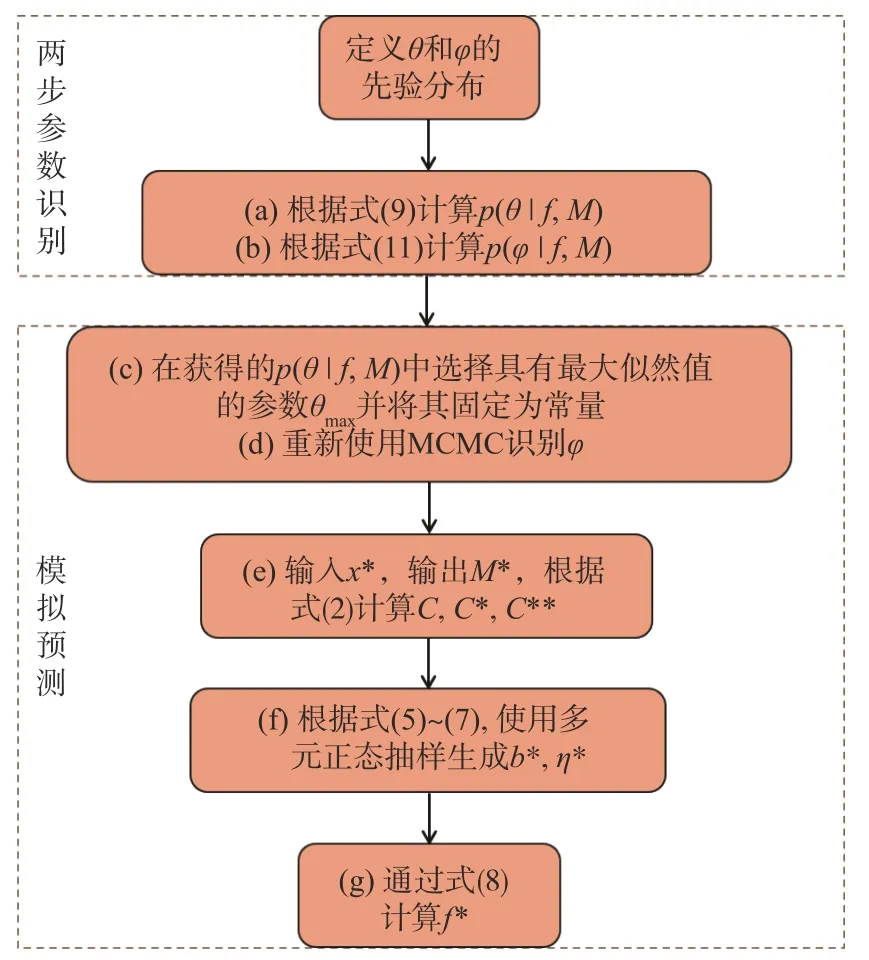
图1 两步识别DDM 法计算步骤图Fig.1 Flow chart of the two-stage based DDM method

（1）从θ的后验样本中，选择一组在整个超参空间内表现最优的参数θmax（即边缘似然值p（f|θ,M）最大），并在物理模型中将其固定为常量；

（2）重新使用MCMC 识别φ得到其后验分布；

（3）对于新的模型输入x∗,输入模型获得输出M∗，根据式（2）计算协方差矩阵C，C∗，C∗∗；

（4）根据式（5）—（7），使用多元正态抽样生成b∗，η∗；

（5）通过式（8）计算预测值f∗。

2 地下水溶质运移案例分析

假设真实情况下的溶质运移过程为非平衡等温吸附模型，实际使用线性平衡吸附模型，因此存在模型结构误差。分别在不考虑模型结构误差、考虑模型结构误差（联立识别DDM、两步识别DDM）进行参数识别及模型预测。

2.1 溶质运移案例概况

该案例描述的是在定浓度通量边界条件下，一维稳定流溶质运移模型。真实情况下的模型为非平衡等温吸附模型，解析表达式见式（14）—（17）。其中，输入浓度C0为50 mol/L，水流速度v为50 cm/d，弥散系数D为40 cm2/d，注入污染物的时间t0为5 d，系数γ为0，衰变常数μ为0.1，阻滞因数R为1.3，初始浓度Ci为0 mol/L。

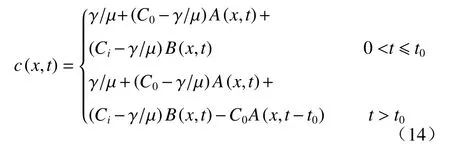
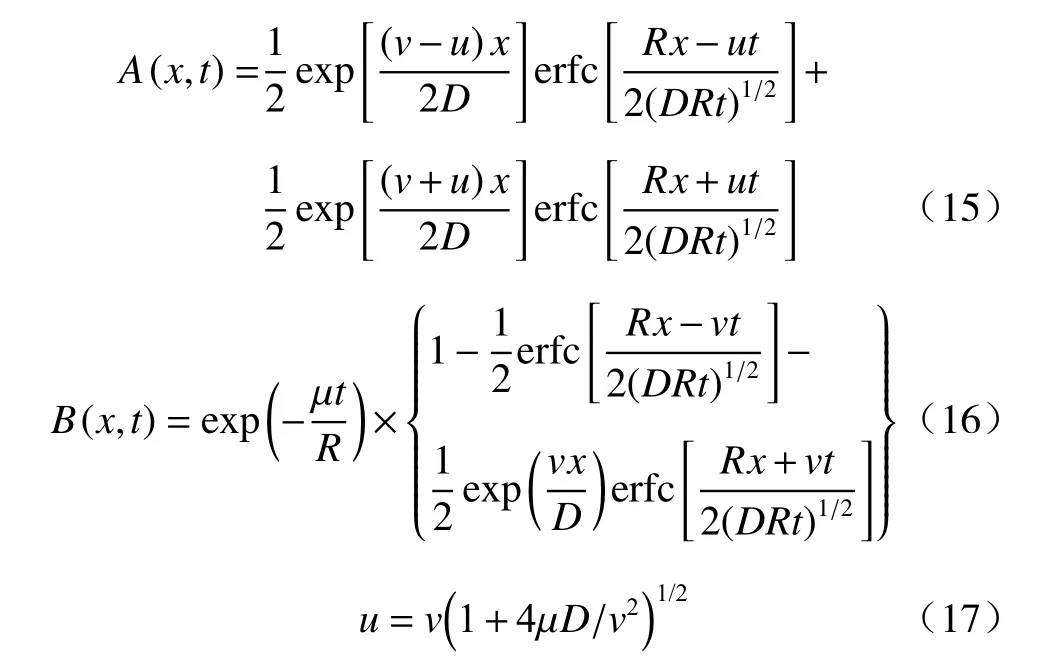
将真实模型运行后得到浓度观测值，同时考虑时间尺度（t:0～10 h）和空间尺度（x:0～250 cm），如图2所示，分别选取21 个和36 个观测数据用于模型识别和验证。

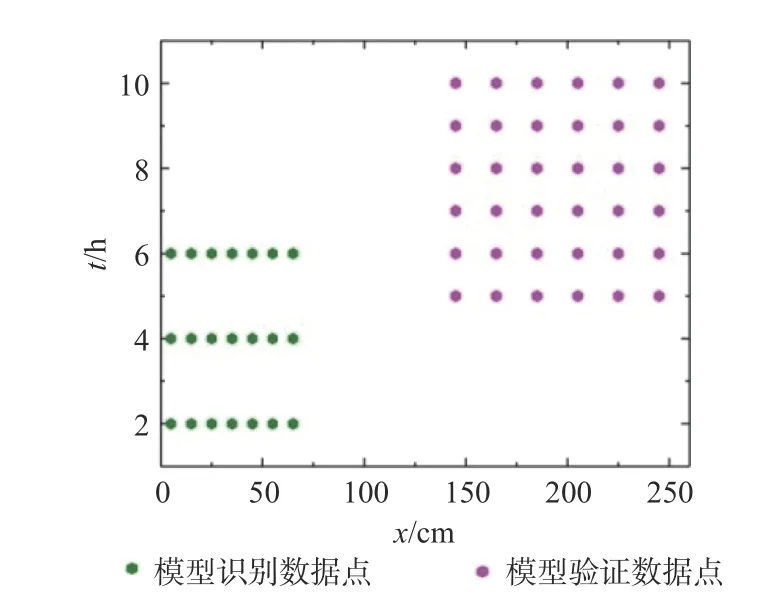
图2 模型识别和验证数据点的位置Fig.2 Location of model observation wells during calibration and validation periods

实际使用的模型为线性平衡吸附模型，解析表达式为：

基于该模型描述溶质运移过程时，污染物吸附模型的偏差会导致模拟结果受到模型结构不确定性的影响。

2.2 案例分析

基于线性平衡吸附模型，分别不考虑和考虑模型结构误差进行参数识别。假设输入浓度C0和水流速度v为随机变量，其余参数与真实模型相同。表1所示为物理参数与超参的先验分布。

表1 模型参数的先验分布Table 1 Prior distributions of model parameters

采用DREAMzs 算法进行参数识别，设置3 条平

行的马尔科夫链，每条链的预热长度为6 000，预热后迭代长度为6 000。对于不考虑和考虑模型结构误差情况下的参数识别，均选取收敛后的18 000 次样本统计边缘后验分布，结果见图3。

从图3 可知，3 种方法得到的物理参数后验分布差异明显，考虑模型结构误差的情况下，参数后验范围明显变小，呈正态分布的形式。对于参数C0和v，联立识别DDM 得到的参数后验分布范围均最小，联立识别DDM 和两步识别DDM 具有相近的后验均值。两种DDM 识别得到的超参边缘后验分布也存在显著差异。对比联立识别DDM，两步识别DDM 得到的超参后验分布范围均较大。对于λ，两步识别法得到的参数后验分布集中在0.4，联立识别法的后验分布集中在0.3。对于σ，两步识别法的后验分布趋势平缓，联立识别法后验分布集中于3.0。对于σδ，两种DDM得到的后验分布均集中在0.1，联立识别DDM 具有较大的峰值概率密度。因此，忽略模型结构偏差直接进行参数识别会导致参数补偿。基于DDM 考虑模型结构偏差时，物理参数和超参的独立性假设会影响参数识别结果。

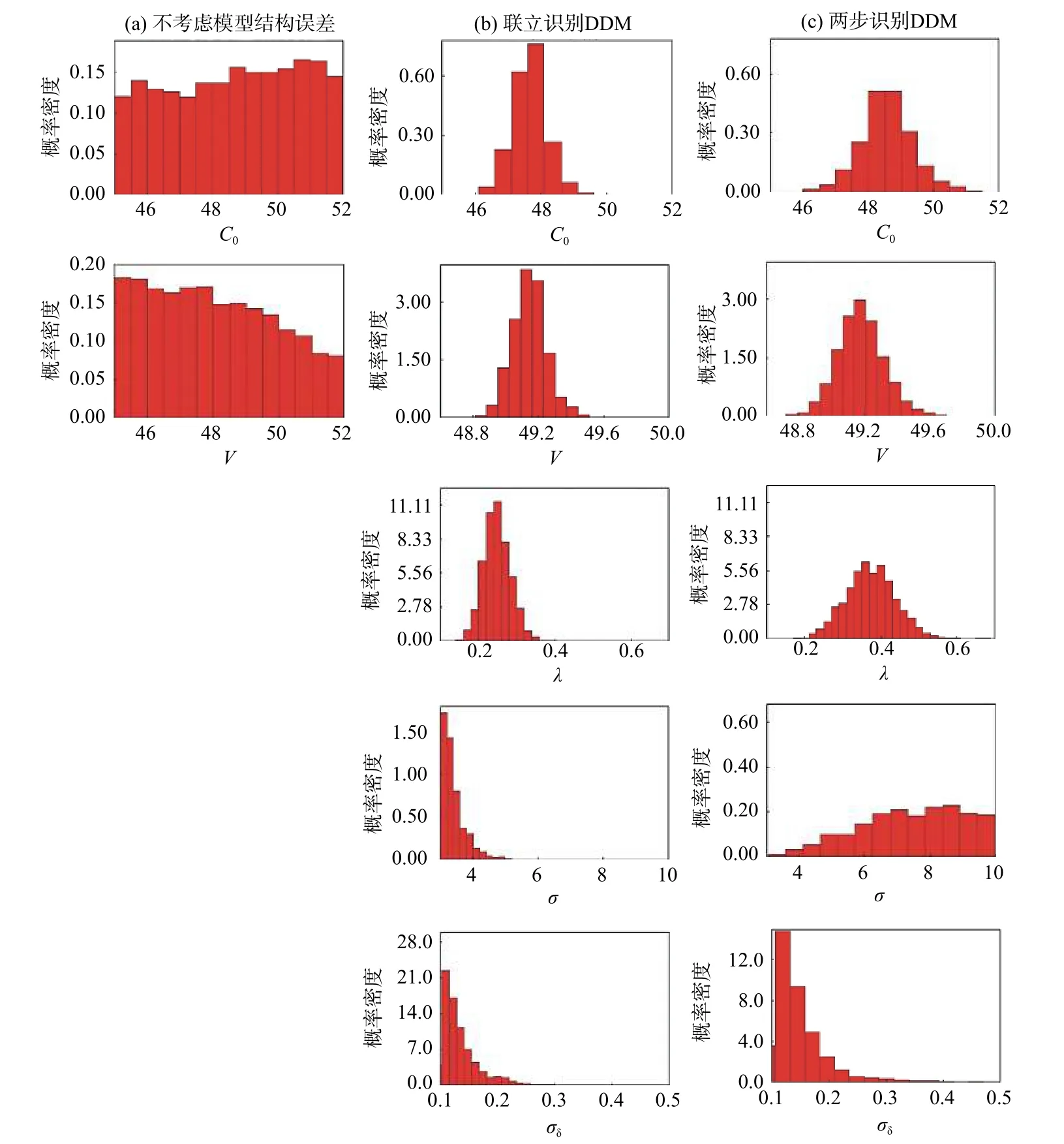
图3 识别得到的模型参数和超参边缘后验分布Fig.3 Identified marginal posterior distributions of model parameters and hyperparameters

基于识别得到的模型参数后验分布，获得模型在识别期和验证期的模拟值，通过频率统计获得模拟值的置信区间和平均值等信息。本次研究采用3 个指标评价模型在识别期和验证期的表现：均方根误差（RMSE）、预测误差均值（MAE）、相对误差的均值（MRE）。这3 个指标值越小，表明模拟值越接近观测值，模型预测性能越好，各指标统计结果见表2。

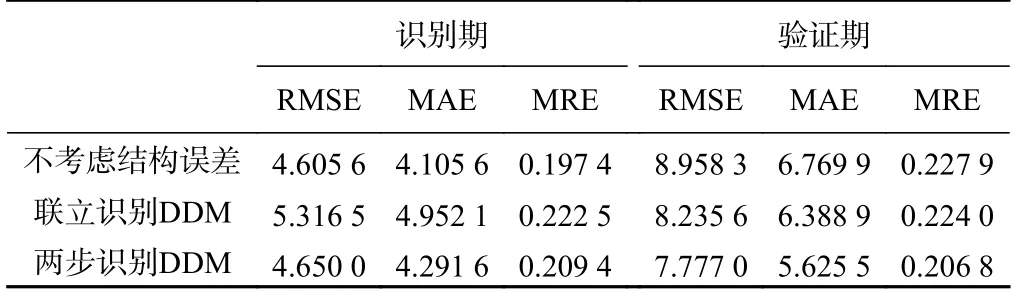
表2 模型预测性能指标统计结果Table 2 Statistics of model prediction performance

从表2 可以看出，在模型识别期，不考虑模型结构误差得到的RMSE 值、MAE 值、MRE 值均最低，识别效果最好；在模型验证期，不考虑模型结构误差得到的RMSE 值、MAE 值、MRE 值均最高，预测效果最差。结果证明，不考虑结构误差直接进行参数识别会产生参数补偿问题，即参数过度拟合补偿结构误差，从而影响模型预测效果。对于两种DDM，两步识别DDM 法在模型识别期和验证期均得到较低的RMSE、MAE、MRE。因此，通过两步识别DDM 法量化模型结构误差，能够减少物理参数和超参独立性假设导致的参数过度拟合，从而提高模型的预测效果。

3 地下水水流案例分析

假设真实情况下地下水流模型为有越流过程的定流量非完整井流模型，实际使用的模型没有考虑越流过程，因此存在模型结构误差。分别在不考虑和考虑模型结构误差（联立识别DDM、两步识别DDM）条件下进行参数识别及模型预测。

3.1 水流案例概况

该案例刻画了在第一类越流系统中，定流量非完整井流模型。真实情况下的模型为有越流过程的定流量非完整井流模型（图4）。抽水井以定流量Q=8 000 m3/d 向外抽水，过滤管位于深度z=d和z=l之间（d=4 m，l=8 m）。观测井水位表示含水层中（r,z）处的水头值，降深s的解析表达式见式（20）。其中，观测时刻t=8 d，承压含水层储水系数μ为0.003，垂向渗透系数Kzz为5 m/d。

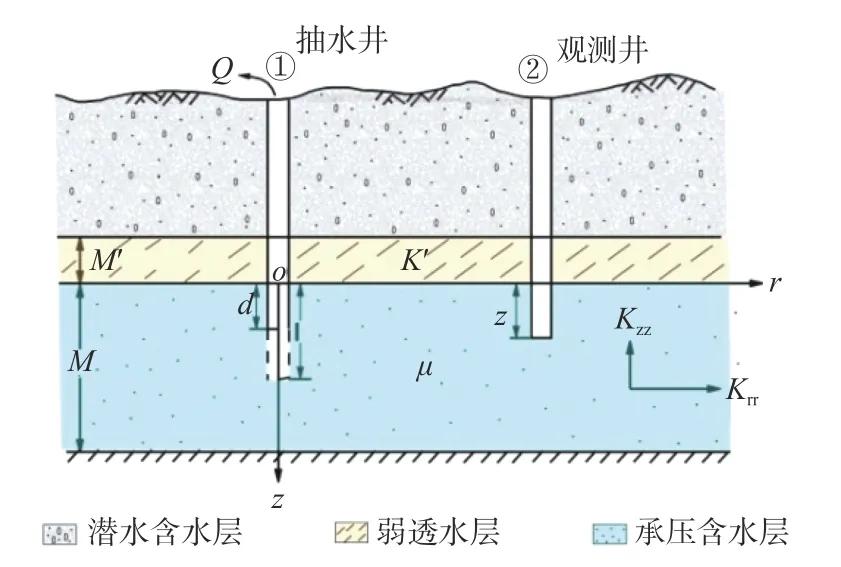
图4 定流量非完整井流模型示意图Fig.4 Diagrammatic representation of partially penetrating well pumping at a constant rate

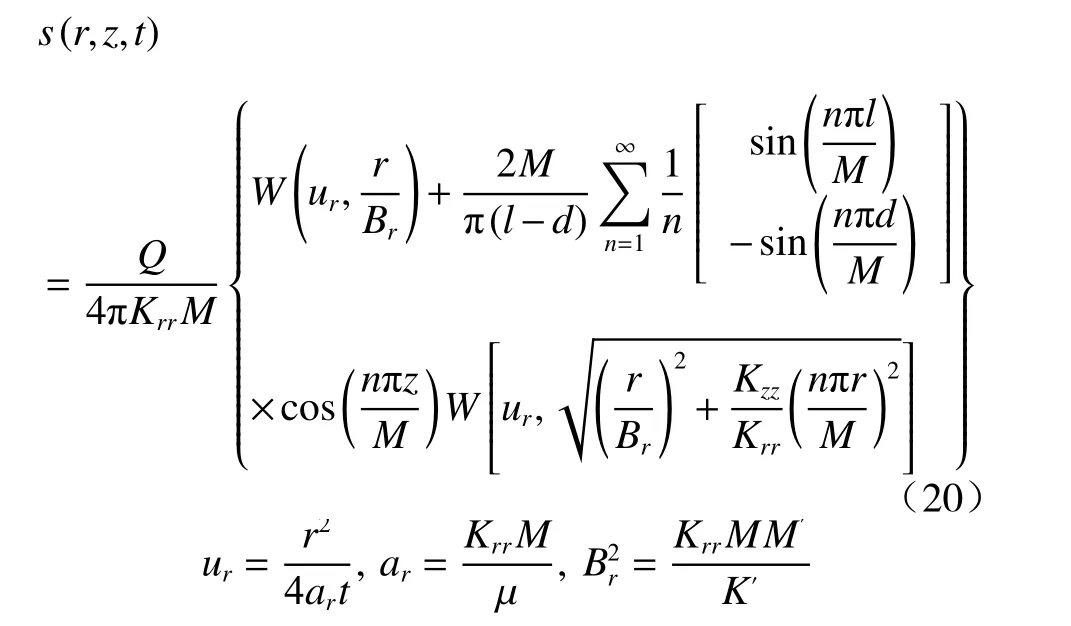
将真实模型运行后得到降深观测值（图5），考虑不同方向的空间尺度（r:0～20 m；z:0～20 m），时间固定在t=8 d，分别选取21，58 个观测数据用于模型识别和验证。

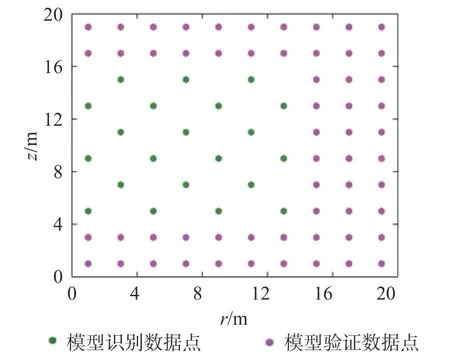
图5 模型识别和验证数据点的位置Fig.5 Location of model observation wells during calibration and validation periods

实际使用的模型没有考虑越流过程，即弱透水层的厚度M′为0 m，渗透系数K′不存在，其余参数设置和真实模型相同，解析表达式见式（20）。基于该模型描述定流量非完整井抽水引起的水位变化时，由于对越流过程刻画的差异，导致模型存在结构误差，预测结果受模型结构不确定性的影响。

3.2 案例分析

基于没有考虑越流过程的井流模型，分别不考虑和考虑模型结构误差进行参数识别。假设承压含水层水平渗透系数Krr和厚度M为随机变量，其余参数与真实模型相同。表3 为物理参数与超参的先验分布。

表3 模型参数的先验分布Table 3 Prior distributions of model parameters

采用DREAMzs 算法进行参数识别，设置3 条平行的马尔科夫链，每条链预热6 000 次，预热后迭代6 000 次。不考虑和考虑模型结构误差（联立识别DDM、两步识别DDM）的参数边缘后验分布均取收敛后的18 000 次样本，结果见图6。

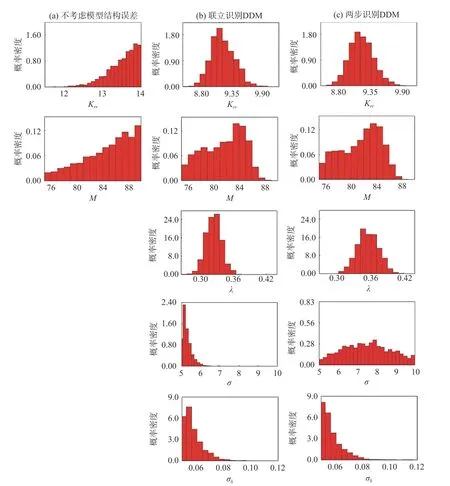
图6 识别得到的模型参数和超参边缘后验分布Fig.6 Identified marginal posterior distributions of model parameters and hyperparameters

从图6 可以看出，3 种方法得到的物理参数后验范围存在差异，且后验分布形态明显不同。考虑模型结构误差时，物理参数后验范围均较小，分布更集中。对于Krr，两种DDM 的参数后验分布均集中在9.2 附近，联立识别DDM 具有较大的峰值概率密度。对于M，两种DDM 的参数后验分布均集中在84 附近，两步识别DDM 具有较大的概率密度。此外，两种DDM 得到的超参边缘后验分布差异明显，两步识别DDM 得到的超参后验分布范围均较大。对于λ，两步识别法的后验分布集中在0.36，联立识别法的后验分布集中在0.33。对于σ，两步识别法的后验分布趋势平缓，联立识别法的后验分布集中于5.0。对于σδ，两种DDM 得到的后验分布均集中在0.05，联立识别DDM 具有较大的峰值概率密度。因此，基于DDM刻画模型结构偏差时，物理参数和超参的独立性假设会影响参数识别结果。

基于DREAMzs 算法得到模型在识别期和验证期的模拟值，通过频率统计获得模拟值的置信区间和平均值。模型预测性能指标统计见表4。

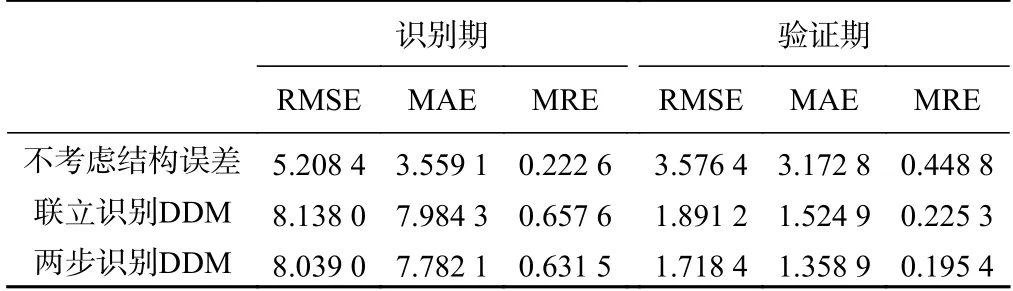
表4 模型预测性能指标统计结果Table 4 Statistics of model prediction performance

从表4 可以发现，与地下水溶质运移案例结果类似（表2），在模型识别期，不考虑模型结构误差得到的RMSE 值、MAE 值、MRE 值均最低，在模型验证期各指标值均最高。表明不考虑模型结构误差直接进行参数识别会影响模型预测效果。对于两种DDM，两步识别DDM 法在模型识别期和验证期均得到较低的RMSE、MAE、MRE。因此，两步识别DDM 能提高模型的预测精度。需要说明的是，本次研究提出的两步识别DDM 方法适用于任意形式的数学模型，包括解析模型和数值模型，因为对于实际复杂的水文地质条件，建立的地下水模型均存在结构偏差。

4 结论

（1）不考虑模型结构误差直接进行参数识别会产生参数补偿问题，即通过参数过度拟合补偿模型结构误差，从而影响模型的预测效果。

（2）基于DDM 刻画模型结构偏差时，物理参数和超参的独立性假设会影响参数识别结果。相对于联立识别DDM，两步识别DDM 得到模型预测的均方根误差（RMSE）、均值（MAE）、相对误差均值（MRE）均明显降低。通过两步识别DDM 法量化模型结构误差，能够减少物理参数和超参独立性假设而导致的参数过度拟合，从而能够更加准确地刻画结构误差，预测结果更加可靠。