杨辉三角在解决遗传学问题中的妙用

>>>辛 波

本文通过对杨辉三角和数量遗传的分析，找到了两者之间的数学逻辑关系，进而提出解决数量遗传题的新方法，为利用数学知识解决遗传学问题提供了新思路。

一、杨辉三角的特点

杨辉三角，是二项式系数在三角形中的一种几何排列，由我国南宋数学家杨辉于1261年在其所著的《详解九章算法》中首先提出。在人教版八年级数学上册中，我们已经接触过杨辉三角。下图即为杨辉三角：

图1 杨辉三角

杨辉三角的内容有很多，本文主要用到下面几点：

（1）每个数等于它上方两数之和。

（2）每行数字左右对称，由1 开始逐渐变大。

（3）第n 行的数字有n 项。

二、数量遗传的特点

杨辉三角与遗传学有什么关系呢？杨辉三角的数学特征与遗传学中的数量遗传有密切关系。高中生物课本中孟德尔遗传定律所提到的性状，例如豌豆的高茎和矮茎、圆粒和皱粒，在表现型上都显示出质的差别，所以叫质量性状。但是除了质量性状外，生物体中还广泛存在着另一类性状差别，这些性状的变异呈连续状态，界限不清楚，不容易区分，叫做数量性状。生物体的很多性状，如玉米穗的长度、作物的产量、小麦种子的颜色等，都属于数量性状。数量性状的遗传虽然复杂，但本质上仍然属于孟德尔遗传定律的范畴，可以用多基因理论来解释。数量遗传的多基因理论主要包括以下三点：

（1）数量性状受多对基因支配。

（2）这些基因对表现型影响小，相互独立，但以积累的方式影响相同的表现型。

（3）每对基因均表现为不完全显性，按孟德尔法则分离。

三、杨辉三角和数量遗传的逻辑关系

上面给大家介绍了杨辉三角和数量遗传的多基因理论，那么这两者之间到底存在着怎样的逻辑关系呢？下面通过一道例题来分析一下。

例1.小麦的粒色受两对基因R1和r1、R2和r2控制，且独立遗传。R1和R2决定红色，r1和r2决定白色，并有累加效应，所以麦粒的颜色随R的增加而逐渐加深。将红粒(R1R1R2R2)与白粒(r1r1r2r2)杂交得F1，F1自交得F2，则F2的表现型有 种，比例为 。

解析：根据题干中所给信息：R1和R2决定红色，r1和r2决定白色，并有累加效应，麦粒的颜色随R的增加而逐渐加深，这属于数量遗传。下面把F2的基因型和表现型详细展示出来。

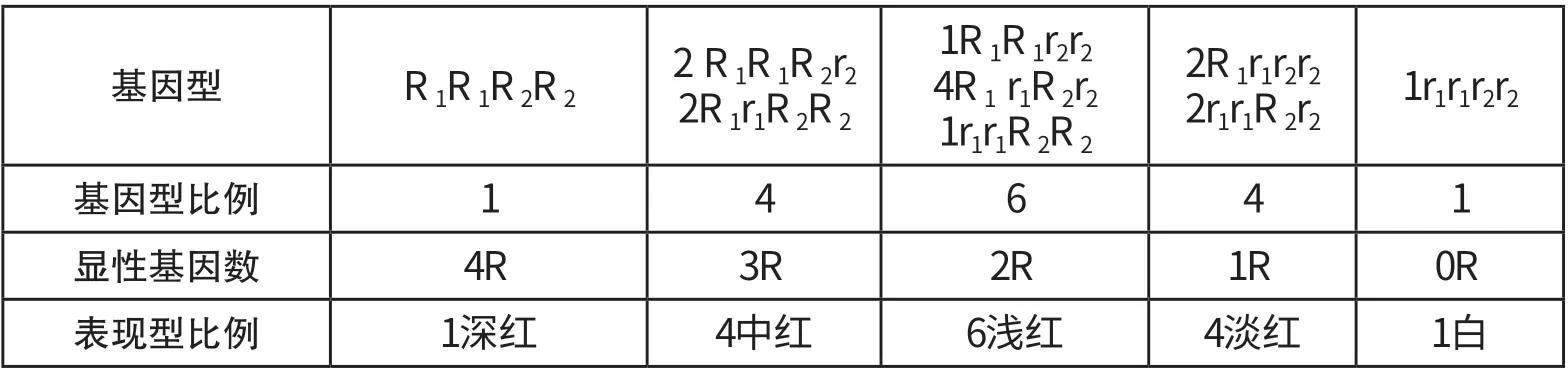
表1 两对基因决定的小麦粒色的遗传

从图表中可以看出表现型有5 种，比例为1:4:6:4:1。那么这组数字有什么规律呢？通过与杨辉三角比较发现，这组数字就出现在了杨辉三角中，也就是说，两对基因控制的数量遗传对应的数字是杨辉三角中的1:4:6:4:1。那么，如果是由三对基因控制的数量遗传与杨辉三角又有什么关系呢？我们继续假设小麦的粒色是由三对等位基因R1r1R2r2R3r3控制，那么F2中显性基因的数量和表现型的比例为：

表2 三对基因决定的小麦粒色的遗传

我们把这组数字和杨辉三角比较发现，1:6:15:20:15:6:1 再次出现在了杨辉三角中，而且和刚才的1:4:6:4:1 正好隔了一行。通过比较这两组数据可以发现这样的规律：数量遗传的数学特征是符合杨辉三角分布的，而且是取其单数行遗漏双数行得到的。两对基因控制的数量遗传对应第5行，三对基因控制的数量遗传对应第7 行，如果是四对基因控制的呢？答案是第9 行。其他以此类推。找到规律后，在解题中就可以直接使用了。

四、杨辉三角的应用

例2.(2014年上海生物卷，25题）某种植物果实重量由三对等位基因控制，这三对基因分别位于三对同源染色体上，对果实重量的增加效应相同且具叠加性。已知隐性纯合子和显性纯合子果实重量分别为150g和270g。现将三对基因均杂合的两植株杂交，F1中重量为190g的果实所占比例为（ ）。

A.3/64 B.5/64 C.12/64 D.15/64

解析1（传统方法）：由于显性纯合子AABBCC 和隐性纯合子aabbcc 果实重量分别为270g 和150g，所以每个显性基因增重为20g，AaBbCc 果实重量为210g。F1中重量为190g 的果实基因型中含有两个显性基因和四个隐性基因，共有六种基因型：AAbbcc、aaBBcc、aabbCC、AaBbcc、AabbCc、aaBbCc。AAbbcc所占比例为1/4×1/4×1/4=1/64，同理aaBBcc和aabbCC均为1/64；AaBbcc所占比例为2/4×2/4×1/4=4/64，同理AabbCc 和aaBbCc 均为4/64；所以1/64×3+4/64×3=15/64。

解析2（杨辉三角法）：通过对题干分析我们发现，果实重量是受三对基因控制的数量遗传，三对基因在杨辉三角中对应的数字是1:6:15:20:15:6:1，一共是64 份，190g 的个体含有两个显性基因，两个显性基因对应的数字是15，这样我们就得到15/64。

通过这两道例题我们展示了杨辉三角和数量遗传的逻辑关系，而这种逻辑关系巧妙地解决了数量遗传中的数学问题，提供了一种新的方法。利用杨辉三角来解决遗传问题，相对于传统方法而言计算量下降、准确度提高。数学中有很多知识可以用来解决生物问题，例如排列组合、二项式定理等。当然还有更多的数学知识等待大家去发掘，希望大家能多多研究，带来更精彩的内容。