基于分段高斯伪谱法的组合动力飞行器火箭挂飞轨迹规划

2021-11-19曲文慧张晗祺吴了泥尤延铖董一巍

航天控制 2021年4期

曲文慧张晗祺吴了泥尤延铖董一巍

厦门大学航空航天学院，厦门 361102

0 引言

宽速域水平起降飞行器是未来航空航天领域的发展方向，其设计制造是目前研究的热点问题。由于宽速域飞行器的速度需要从0至高马赫数，跨度很大，其使用的动力系统就对飞行器的性能有着至关重要的影响。通过目前的研究，涡轮基组合循环(Turbine-based Combined Cycle, TBCC)发动机是实现宽速域飞行的关键技术之一。

在组合动力发动机的研制过程中，需要进行高空飞行试验，验证其稳定和控制特性，获得地面试验无法获得的流动和气动数据。但是受当前技术水平限制，无法使用涡喷发动机使中小型试验飞行器直接从速度0加速至超音速。因此本文采用助推火箭将飞行器带至所需马赫数再进行分离的技术路线，不仅可以解决目前技术水平限制的问题，还可以通过这种方法使得飞行器达到所需的高度和速度，对飞行器进行高空高速试验，具有研究意义和工程应用价值。

采用可回收式助推火箭带飞后分离的方法涉及到两套系统的一体化轨迹优化问题。其中较为重要的是分离点的选取，若分离点高度选取过低，则飞行器气动阻力较大，同时，垂直发射的助推火箭在分离点仍有较大轨迹角，飞行器无法通过自身的机动快速拉平实现平飞，不利于试验段的加速。若选取的分离点过高，虽然气动阻力会减小，但是会造成涡喷发动机吸入气流不够，导致推力不足，甚至熄火等问题。同时该助推火箭和飞行器双系统的轨迹优化问题还受到飞行器结构、引射火箭与发动机性能等多约束条件的限制。因此，研究一种适应多种约束条件，适应助推火箭和飞行器双系统的轨迹优化方法，具有十分重要的意义。

轨迹优化问题是一个非线性的、受到各种约束的最优控制问题。求解最优控制问题目前大致分为间接法和直接法两大类[1]。其中间接法是将最优控制问题转换为Hamilton边值问题，该方法求解复杂的非线性问题非常困难。而直接法是通过离散化方法将连续系统的最优控制问题转化为非线性规划问题，再通过数值方法求解[2]。直接法中通过离散控制变量和状态变量的伪谱方法，由于在计算效率上的优势，逐渐成为最优控制问题求解方法的研究热点，同时在航空航天领域得到了广泛的应用[3-5]。目前常见的伪谱方法包括Legendre伪谱法、Radau伪谱法和Gauss伪谱法。Fahroo等[6]从近似精度、收敛速度和计算效率等方面比较了3种伪谱方法。其结果表明Gauss伪谱法在状态变量、控制变量和协调变量的近似精度以及收敛速度等方面优于Legendre伪谱法，且对协调变量边界值的估计精度高于Radau伪谱法。同时，Gauss伪谱法在处理含初始和终端约束的问题上具有优势[7]，因此本文选取Gauss伪谱法求解轨迹优化问题。

杨志红等[8]研究了在一定高度、速度和轨迹角的初始条件下投放高超声速飞行器，基于Gauss伪谱法以最末端轨迹角最小为性能指标进行的爬升端轨迹优化；杨希祥等[9]研究了基于Gauss伪谱法的多级固体运载火箭上升段的轨迹快速优化，并且提出了连接点的概念；王文虎[10]研究了基于Gauss伪谱法和向前拉道伪谱法的亚轨道飞行器返回轨迹快速优化，并比较了两种伪谱法在处理复杂问题时的能力；刘超越等[11]研究了Gauss伪谱法在多阶段二级助推战术火箭轨迹规划当中的应用。之前的研究，基本都是基于Gauss伪谱法针对单一系统的最优轨迹求解，而本文采用Gauss伪谱法，对两个不同系统的分离问题进行求解，得到多条件约束下的最优轨迹。

本文以某型助推火箭和高超声速飞行器双系统为研究对象，飞行任务分为5段：火箭助推段、火箭带飞段、姿态调整段、试验段和无动力返回段，如图1所示。

图1 飞行任务剖面图

每个阶段的具体描述为：

阶段1：火箭助推段。该阶段飞行器与火箭组合，由地面垂直发射，利用火箭推力加速爬升至一定高度和马赫数。

阶段2：火箭带飞段。该阶段火箭燃料耗尽，推力消失，但飞行器仍未与火箭分离，作为组合体继续爬高。

阶段3：姿态调整段。该阶段飞行器与火箭分离，飞行器在无动力的情况下调整姿态，以达到试验窗口要求。

阶段4：试验段。该阶段飞行器自身引射火箭工作，飞行器正加速，组合动力发动机点火，采集相关数据，完成试验任务。

阶段5：无动力返回段。该阶段飞行器无动力返回至起飞点。

为简化，火箭助推段轨迹已由经验设计程序攻角，形成弹道方案，本文在此基础上对火箭带飞段、姿态调整段轨迹进行研究。

本文按照试验段任务目标，结合引射火箭与无人机特性设计了试验窗口，通过建立飞行器运动学模型、过程约束、边界约束，利用分段式高斯伪谱法搭建轨迹优化模型，将助推火箭与高超声速飞行器分离的轨迹规划问题转化为以末端高度最高、速度最大、轨迹平滑为性能指标函数的最优控制问题。利用控制变量法研究单项性能指标的权重系数对分离点的影响，多次对比后选取最佳权重系数，得到符合任务要求的分离轨迹，为飞行器与运载器分离轨迹规划提供参考。

1 轨迹优化方法

1.1 高斯伪谱法

Gauss伪谱法的实质就是同时离散控制变量和状态变量的直接法，也可以被称作配点法或者被称作直接配点非线性规划DCNLP(Direct Collocation with Nonlinear Programming)。

Gauss伪谱法的解算步骤如下：将需要求解的最优控制问题的控制变量和状态变量在一系列Legendre-Gauss(LG)点上进行离散；通过离散点为节点构造的Lagrange插值对控制变量和状态变量进行逼近，通过全局插值多项式近似状态变量的导数，从而将系统从微分方程约束转化为代数方程约束。性能指标中的积分项由Gauss积分计算，终端状态由初始状态加上右函数在整个过程中的积分而得。最优控制问题因此转化为非线性规划问题而求解[12-13]。

1)一般非线性系统动力学方程

考虑一般形式的非线性系统动力学方程为：

(1)

式中：状态变量x(t)∈Rn，控制变量u(t)∈Rm，时间t∈[t0,tf]。

2)时域变换

假设最优控制问题的时间区间为[t0,tf]，而Gauss伪谱法的时间区间为[-1,1]，因此对时间t进行变换：

(2)

3)全局插值多项式近似状态变量与控制变量

(3)

(4)

(5)

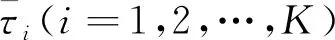
4)动力学方程约束转为代数约束

状态变量的导数可以通过对式(3)求导而得，从而将动力学方程约束转化为代数约束，再代入动力学方程可得状态变量在配点处应满足的代数方程：

(6)

5)边界条件及过程约束

边界条件约束满足：

φ(X0,t0,Xf,tf)=0

(7)

过程约束满足：

(8)

6)性能指标函数的近似

将最优控制问题的性能指标函数中的积分项用Gauss积分近似，得到：

J=Φ(X0,t0,Xf,tf)+

(9)

式(9)即为Gauss伪谱法中的性能指标函数。

根据上述的数学变换，Gauss伪谱法离散最优控制问题可以描述为：求离散状态变量Xi、控制变量Uk和终端时刻tf，使得在满足式(4)、式(6)～(8)的情况下，使得其性能指标函数J，即式(9)最小。从而将最优控制问题转化为一般非线性规划问题[14]。

1.2 分段高斯伪谱法

本文对火箭带飞段、姿态调整段轨迹分别运用Gauss伪谱法进行规划，通过在分段处设置连接点并加上一定的约束条件，对连接点进行约束[9,15]。

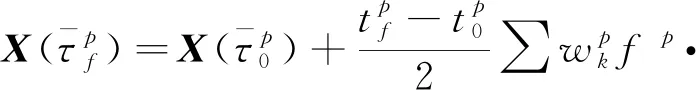
(10)

(11)

式中：k=1,2,…,K，p=1,2,…,N，Dki∈Rm为微分矩阵。

边界条件约束：

(12)

过程约束：

(13)

同时，为保证各阶段连接点的连续性，在连接点处应满足如下条件：

(14)

则分段Gauss伪谱法即是在满足式(10)-式(14)的情况下来对多段轨迹进行求解。

2 弹道优化模型

2.1 动力学模型

本文轨迹优化问题所采用的动力学模型如下：

(15)

式中：状态量[Vxhθ]T为速度、射程、飞行高度、轨迹角，控制量α为迎角，状态量与控制量对应2.1节中的状态变量x(t)和控制变量u(t)。m为系统总质量，需要根据不同阶段进行切换；g为重力加速度；L和D分别为升力、阻力：

(16)

式中：Sref为参考面积；升力系数CL和阻力系数CD由马赫数和攻角决定，通过气动参数表值得出；大气密度ρ可通过国际标准大气表查表得到。

2.2 约束条件和性能指标

考虑到试验段引射火箭和发动机工作的苛刻条件以及飞行器在结构和热防护的可靠性，飞行器需要满足诸多过程约束以及终端约束。本文选取动压、过载、迎角作为过程约束，末端高度、马赫数、弹道倾角作为边界条件约束[8]。结合第2章中式(7)～(9)及式(12)～(14)，在建模过程中需满足以下条件：

2.2.1 过程约束

1)动压约束：

为了满足飞行器结构设计以及控制效率的要求，需要对动压进行约束。

(17)

式中：q为动压，ρ为大气密度，V为飞行速度。

2)过载约束：

由于飞行器机体结构所能承受的过载有限，因此在全过程中对过载进行约束，其中nx为轴向过载，nz为法向过载。

nxmin≤nx≤nxmax
nzmin≤nz≤nzmax

(18)

3)迎角约束：

由于飞行器结构、引射火箭与发动机的限制，同时为了满足控制飞行器控制能力要求，需约束迎角。

αmin≤α≤αmax

(19)

式中：α为飞行器迎角。

2.2.2 边界条件约束

为了满足试验段引射火箭工作以及发动机点火的要求，需约束终端弹道倾角θf、高度hf及速度Vf。

θfmin≤θf≤θfmax

(20)

hfmin≤hf≤hfmax

(21)

Vfmin≤Vf≤Vfmax

(22)

2.2.3 性能指标

试验段需要以引射火箭作为动力使飞行器正加速，应尽量减小试验段阻力，选取末端高度最高为优化性能指标：

J1=-Hf

(23)

同时为了保证试验段引射火箭点火，选取末端的速度最大为优化性能指标：

J2=-Vf

(24)

兼顾轨迹的平滑性，将弹道倾角角速率的平方进行积分作为性能指标：

(25)

最终的性能指标为式(23)～(25)的加权和[16]：

J=w1J1+w2J2+w3J3

(26)

式中：w1，w2和w3为权重系数，通过调节权系数，使轨迹在速度最优、高度最优以及轨迹平滑性之间权衡，以规划出合理轨迹。

3 轨迹优化算例

基于某型高超声速无人机及某型小型运载火箭，分析并设计试验窗口并以此作为终端约束，利用Gauss伪谱法进行轨迹设计，并根据仿真结果，分析性能指标对分离点以及试验段的影响。

3.1 试验窗口

引射火箭点火的最低马赫数为2.5，引射火箭推力为8000N，为实现飞机正推力的要求，对比了轨迹角分别为-10°、-5°、0°、5°、10°情况下飞机加速度为0的马赫数-高度关系曲线，如图2所示。

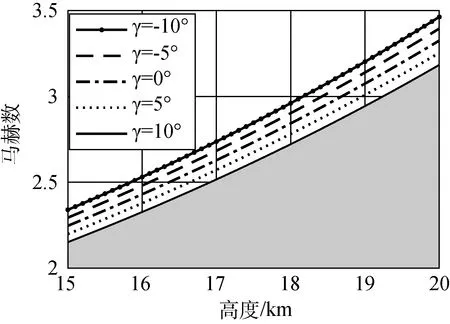
图2 试验窗口

各曲线右下方区域为加速度大于0的试验窗口，当高度一定时，随着轨迹角的增加，窗口最低马赫数减小；马赫数一定时，随着轨迹角的增加，窗口最低高度增加。综合考虑，设计试验窗口为:

(27)

3.2 轨迹优化

利用分段高斯伪谱法对火箭带飞段与姿态调整段进行设计，飞行器总重400kg，火箭与飞机总重1856kg。

轨迹初始条件与终端条件如表1：

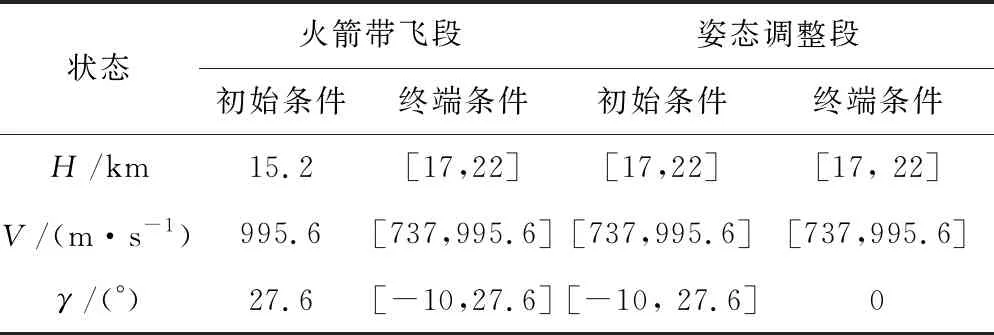
表1 约束条件

其中，括号中数值[min,max]分别对应状态量的上限与下限，无括号则表示状态量数值确定。

控制约束选取-20°≤α≤20°；过载约束选取-3g≤nx≤g，-6g≤nz≤g；动压约束选取20kPa≤q2≤100kPa。

性能指标按照2.2节中的式(26)选取，由于3种性能指标数值量级不同，首先将J1×10-3、J2×10-2、J3×103使得3种性能指标处于同一数量级，保证权系数的改变能对总性能指标产生明显影响。利用控制变量法研究3种权系数对规划轨迹的影响，选取参数1：w1=1,w2=1,w3=1；参数2：w1=1,w2=20,w3=1；参数3：w1=20,w2=1,w3=1三种参数进行仿真，仿真结果如图3所示。考虑引射火箭推力8000N,以规划结果的终端状态作为试验段初始状态时所对应的初始加速度见表2。

表2 试验段初始加速度

图3 规划结果

从图3中的规划结果可以看出，三种参数下规划轨迹除迎角外各状态量随时间变化平缓，而迎角突变点即为分离点，由于此时飞行器与火箭分离，参考模型发生变化，发生突变是合理的。

当弹道倾角权重w3不变时，增大速度权重w2会使分离点提前，末端速度增加，末端高度减小，使得末端阻力增加，初始加速度大幅度减小，不利于试验段加速；而增大高度权重w1会使分离点推迟，末端高度增加，但对末端速度影响较小，从而减小末端阻力，增大初始加速度，有利于试验段加速。

此方法能够按照飞行任务剖面设计轨迹，最大程度发挥飞行器与运载火箭的性能，同时可以通过改变约束条件与性能指标权重，更为精细地调整弹道。

经过多次对比后选取w1=1,w2=25,w3=1进行规划，并将结果与火箭助推段、试验窗口段、无动力返回段结合，最终飞行任务剖面如图4所示。

图4 飞行任务剖面

整个任务剖面与图1一致，飞行器与助推火箭结合，垂直发射，加速爬升至马赫数3.37、高度15.2km、轨迹角27.6°；之后助推火箭燃料耗尽，组合体减速爬升至马赫数2.6、高度18.17km；飞行器与助推火箭分离，飞行器拉平，缓慢减速爬升至马赫数2.54，高度18.2km，达到试验窗口；引射火箭点火，在12 s的工作时间内平飞加速至Ma2.7，整个轨迹状态量变化平缓，符合任务要求。