地球卫星动力学定轨中摄动模型的选取

张 峰 张香莎 高旭东

1.火箭军工程大学导弹工程学院，西安 710025

2.黄河交通学院汽车工程系，河南 焦作 454950

0 引言

航天领域的发展越来越成为世界各国综合国力的体现，而航天器的在轨运行情况无疑是航天领域中最为重要的环节之一。几十年来，世界各国科学家在航天器在轨运行方面付出了巨大努力，力求得到最逼近于实际情况下的航天器在轨运行状态[1-3]。

在动力学定轨中，卫星动力学模型的准确与否直接影响导航精度。卫星动力学模型中包含了最基本的二体模型以及各种摄动模型，但是各种摄动模型对于不同轨道卫星的影响量级不同。针对不同轨道及定轨精度要求，需要选取不同的摄动模型。特别是随着我国北斗卫星导航系统的全面组网运行，不少学者研究动力学定轨中的摄动模型[4-7]。

在动力学定轨的摄动模型研究中，文献[1]主要针对低轨卫星星座精度定轨及运行控制进行了综述；文献[2]针对太阳摄动的真实力学模型下地月系平动点的不稳定性进行研究；文献[3]主要验证了不同重力场的适用范围，从计算精度和效率两方面制定了优化的定轨策略；文献[4,6]主要考虑太阳光压对定轨影响；文献[5]设计的历书拟合模型主要适用于地球静止轨道和倾斜地球同步轨道卫星。目前，关于卫星定轨研究多是从某一方面建模分析，系统性的建模分析研究较少。

本文对地球轨道卫星动力学模型的地球非球形摄动、大气阻力摄动、太阳光压摄动和日月引力摄动等4个主要摄动因素进行了建模及仿真，计算了各种摄动模型下低轨和高轨卫星的星历，并由星历反求出其在二体模型下的轨道六根数，进而分析各摄动项对不同轨道高度卫星的影响；最后给出了三种轨道的摄动模型星历与其二体模型星历的最大标量误差[8-10]。

1 二体模型及轨道六根数

如图1所示，在讨论二体模型之前，先建立一个惯性坐标系，将在此坐标系下，对质量为m的卫星和质量为M的地球的运动状态进行分析[11-13]。

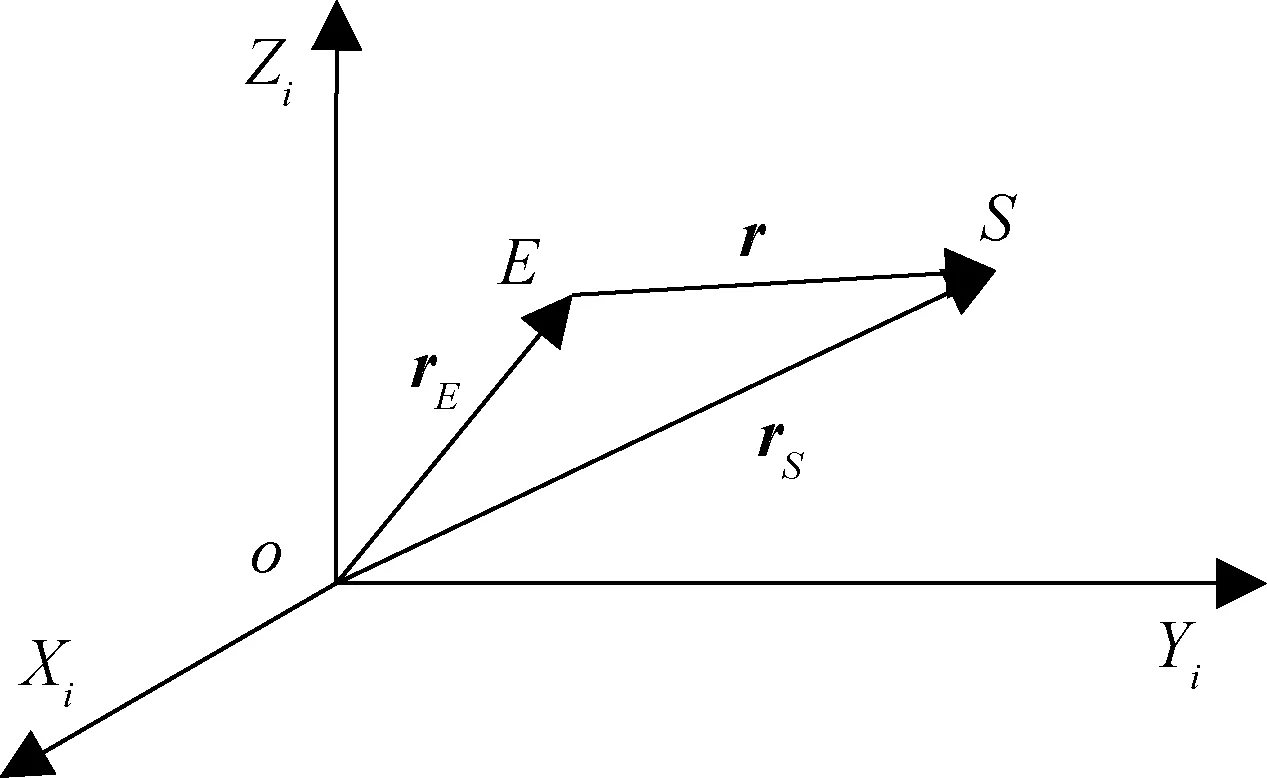
图1 二体模型

图中E表示地球，S表示卫星，rE是地球位置在O-XiYiZi坐标系中的矢量表示，rs是卫星位置的矢量表示，r是卫星相对于地球的位置。

在此坐标系中，以地球为中心天体，忽略卫星质量，对卫星进行受力分析，进而得到卫星相对于地球的运动方程：

(1)

其中，μ=GM是地球引力常数，e是由地球指向卫星的单位向量。对二体模型下卫星的运动方程求解，可以得到轨道六根数。

轨道六根数如图2所示，半长轴决定了卫星轨道的大小；偏心率决定了卫星轨道的形状；轨道倾角和升交点赤经Ω共同决定了卫星轨道平面相对与地球赤道平面的位置；近地点幅角ω决定了卫星在其轨道平面内轨道的走向；飞行器过近地点的时刻、初始时刻的真近点角以及初始时刻的平近点角则给出了卫星在轨道内的相对位置[14]。

图2 轨道六根数示意图

本文仿真使用的卫星轨道参数如表1所示。

表1 轨道参数

2 摄动模型对轨道参数影响分析

2.1 地球非球形摄动

地球非球形摄动主要影响卫星轨道平面倾角，使其逐渐减小，并使卫星轨道平面产生一种被称为轨道面进动的长期变化[15]。此外还会对卫星运动引起其它的摄动，这些摄动将会影响卫星轨道根数的变化，尤其对低轨卫星的影响较为显著。

在地固坐标系中，地球引力势和引力导致的加速度的表达式为：

(2)

(3)

式中：

(4)

将地固坐标系下的加速度通过转换矩阵转为地心惯性系下的加速度：

(5)

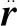
本文在20×20引力场模型(J20.20)下进行了卫星星历计算，并反求出卫星每个时刻星历所对应的二体模型下的六根数，仿真结果如图3～4所示。

可以看出，地球非球形摄动使低轨卫星轨道发生了旋转，如图3(a)所示，这种变化称之为轨道面进动；低轨卫星运动一天的时间内其轨道倾角随时间的变化最大可达1.2×10-2°，升交点赤经变化最大可达1°，如图3(b)、(c)所示。这些变化是导致卫星轨道面进动的直接原因。

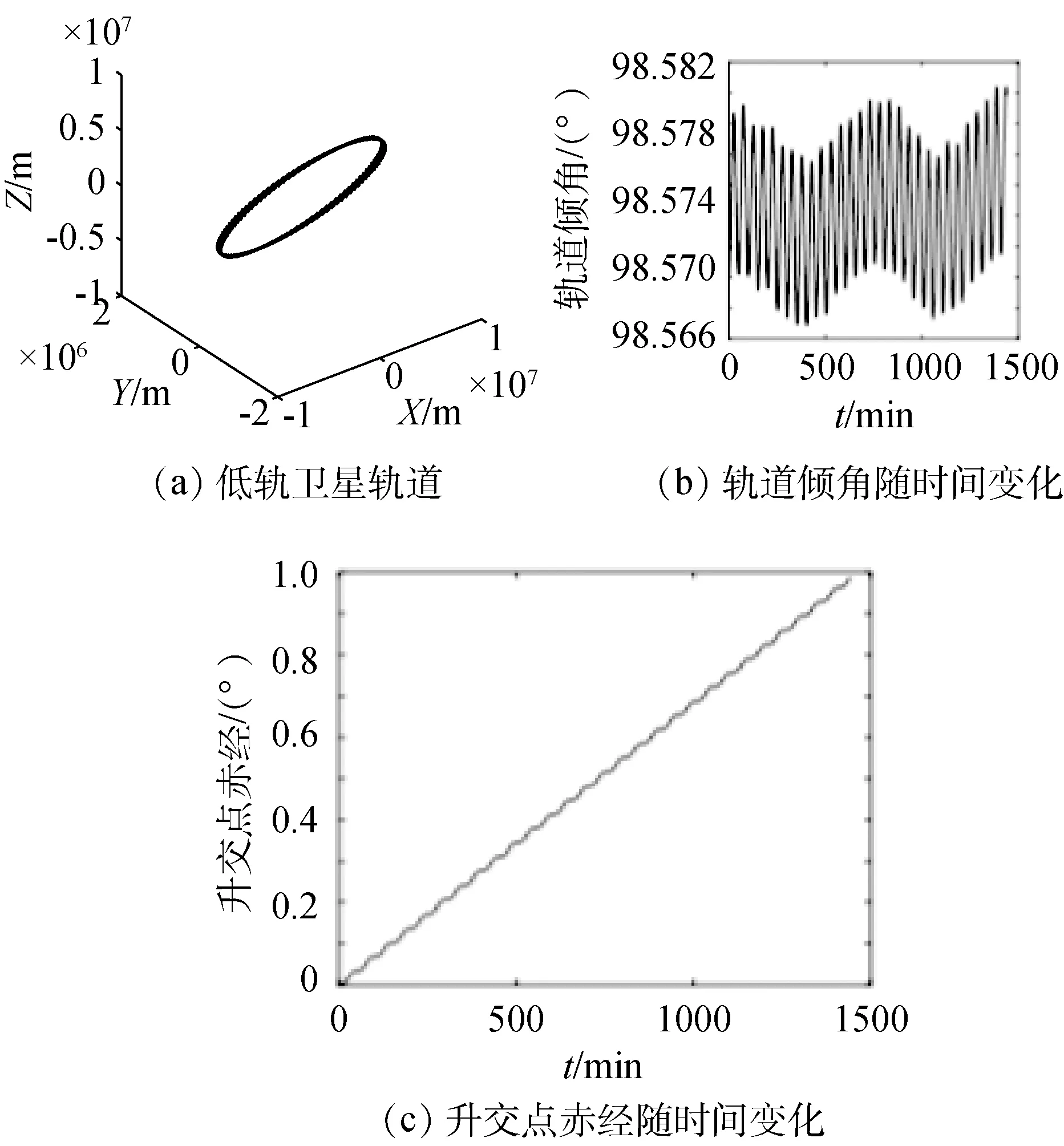
图3 地球非球形摄动下低轨卫星仿真结果

高轨卫星运动一天的时间内其轨道倾角随时间变化的最大值只有2.5×10-5°，升交点赤经变化最大值不到2×10-2°，如图4(b)、(c)所示。高轨卫星轨道如图4(a)所示，与图3(a)相比较，地球非球形摄动对高轨卫星的影响较小，这是由于引力与距离的二次方成反比关系，轨道越高，影响越小。

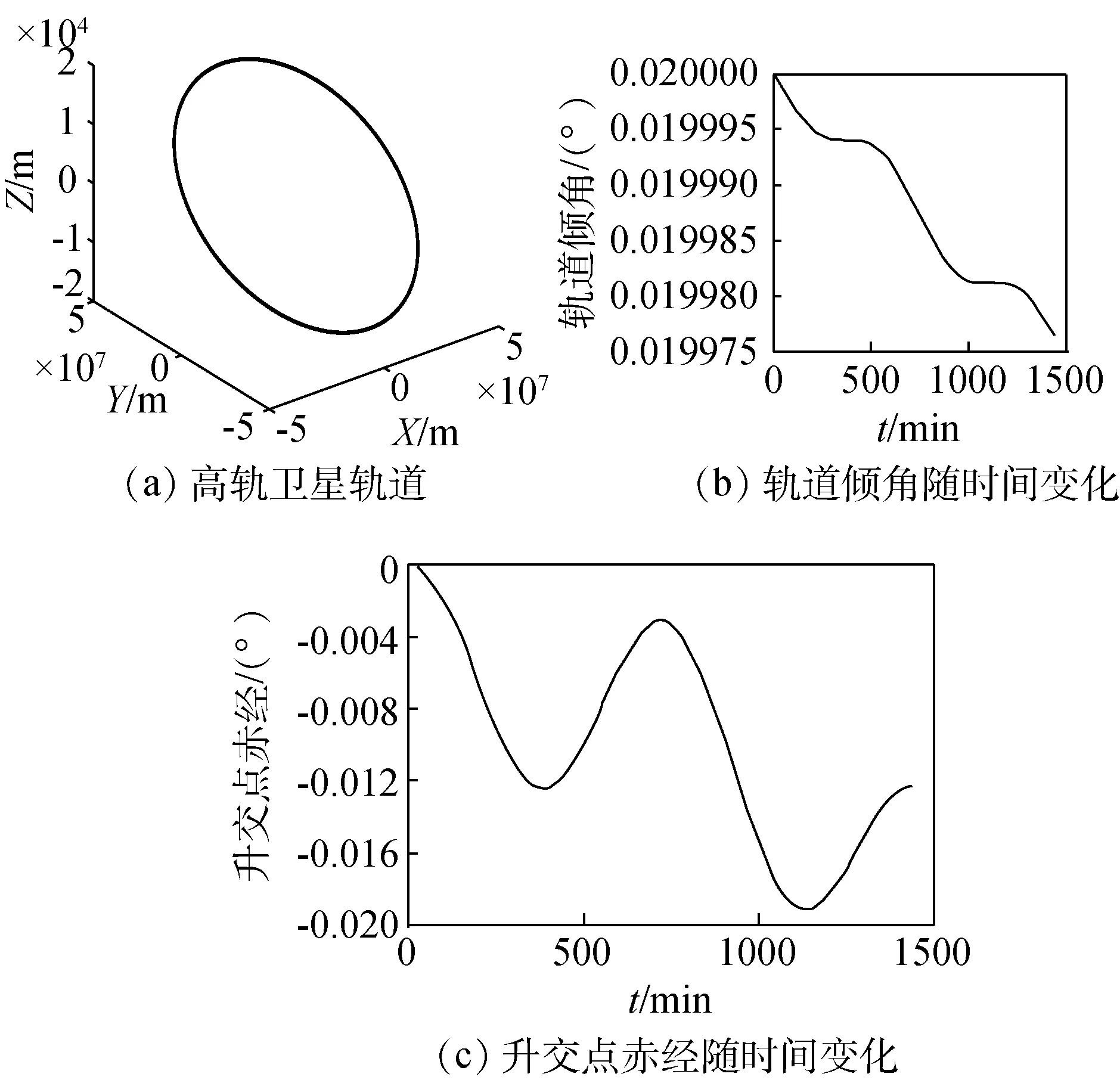
图4 地球非球形摄动下高轨卫星仿真结果

2.2 日、月引力摄动

如图5所示，卫星在轨运动时，不仅受到地球对其的引力，同时太阳和月球也会对其有引力作用，并且太阳和月球还会对地球有引力作用，二者作用力之差，便是日、月引力摄动。

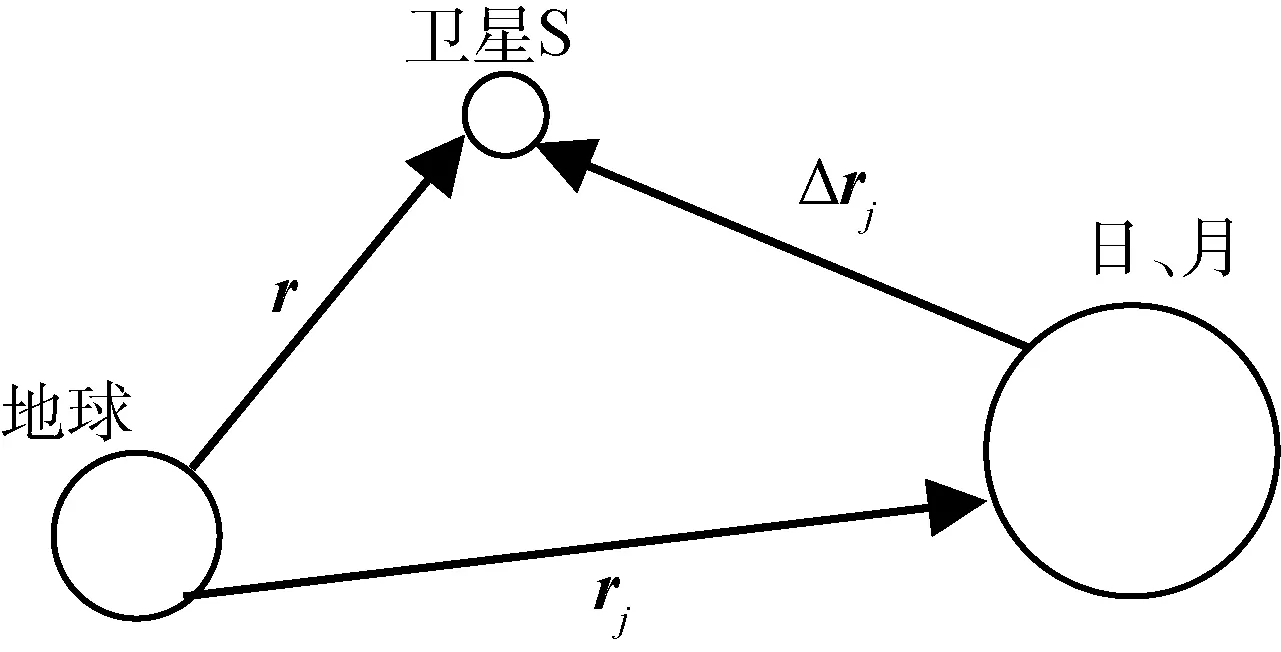
图5 三体模型

由卫星、地球、日月的几何关系对卫星进行受力分析，得到卫星的加速度表达式：

(6)

其中，S、M分别表示太阳和月球；MS,MM分别表示太阳和月球的质量；Δrj是摄动体到卫星的中心距离，Δrj=r-rj，r,rj是卫星和摄动体在地心惯性系中的位置矢量。

由式(6)可以看出，只要求出摄动体在地心惯性系中的位置矢量，便可以得到卫星的加速度。在实际应用中，由于日、月引力远小于地球对卫星的引力，因此在计算日、月摄动下的卫星加速度无需知道日、月的精确坐标。多数情况下，使用低精度的日、月坐标就可以使计算精度达到0.1%～1%[17]。

太阳引力摄动的仿真结果如图6和图7所示。在太阳引力摄动下，低轨卫星轨道的形状与二体轨道形状相似，都呈现出一个光滑的椭圆形，如图6(a)所示；低轨卫星轨道半长轴随时间变化的最大变化值仅有8×10-4，轨道倾角变化的最大值只有不到6×10-5°，如图6(b)、(c)所示。

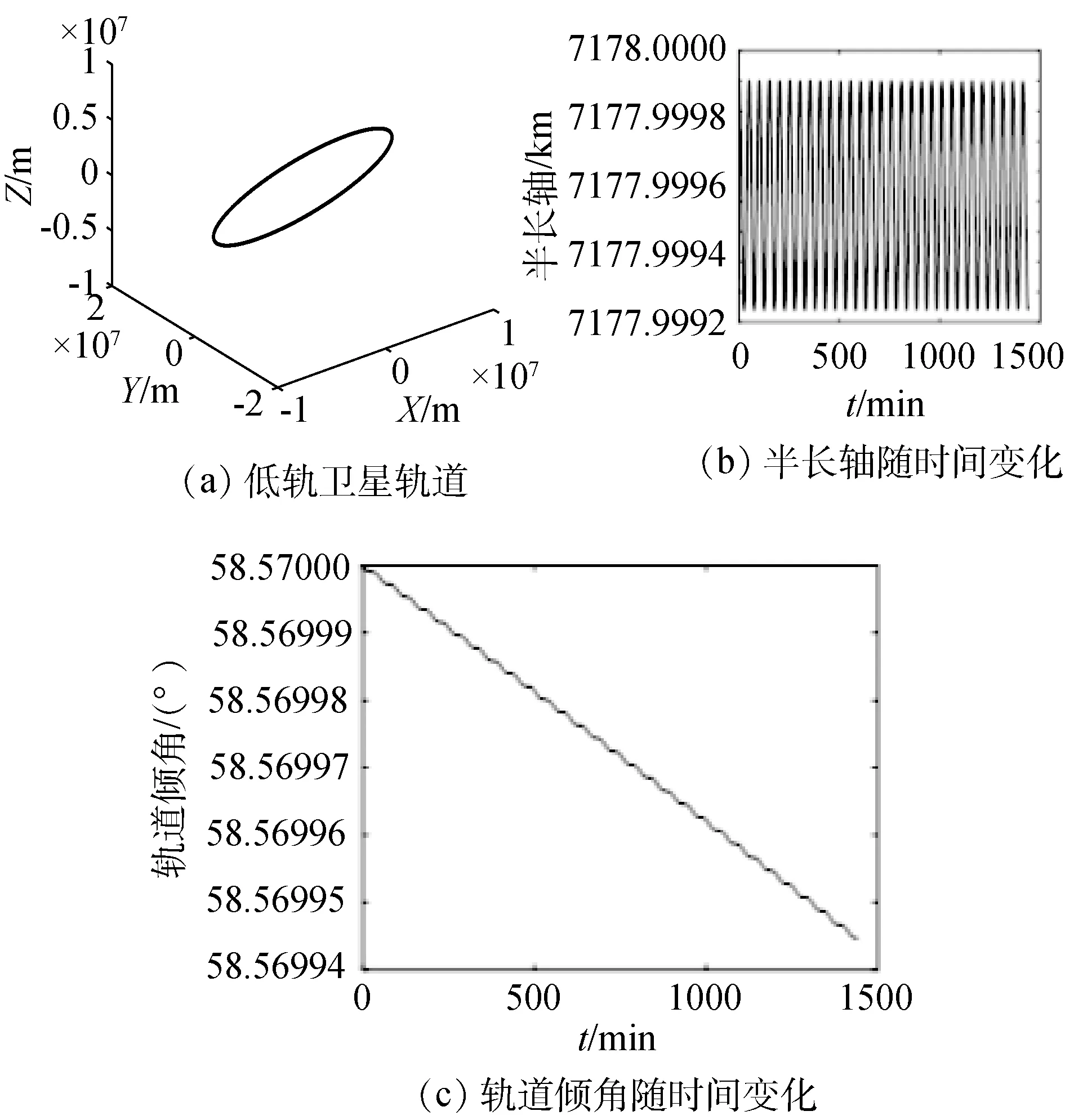
图6 太阳引力摄动下低轨卫星仿真结果

高轨卫星轨道的形状基本无变化，如图7(a)所示；同时从图7(b)、(c)中可以看出，太阳引力摄动下高轨卫星轨道半长轴随时间变化的值不超过1，轨道倾角变化最大不到3.5×10-4°。由上述分析可知，太阳引力摄动对高轨卫星和低轨卫星的影响都比较小，但是对高轨卫星的影响要大于低轨卫星，这是由于太阳引力与距离的二次方成反比，日地距离过远导致的。

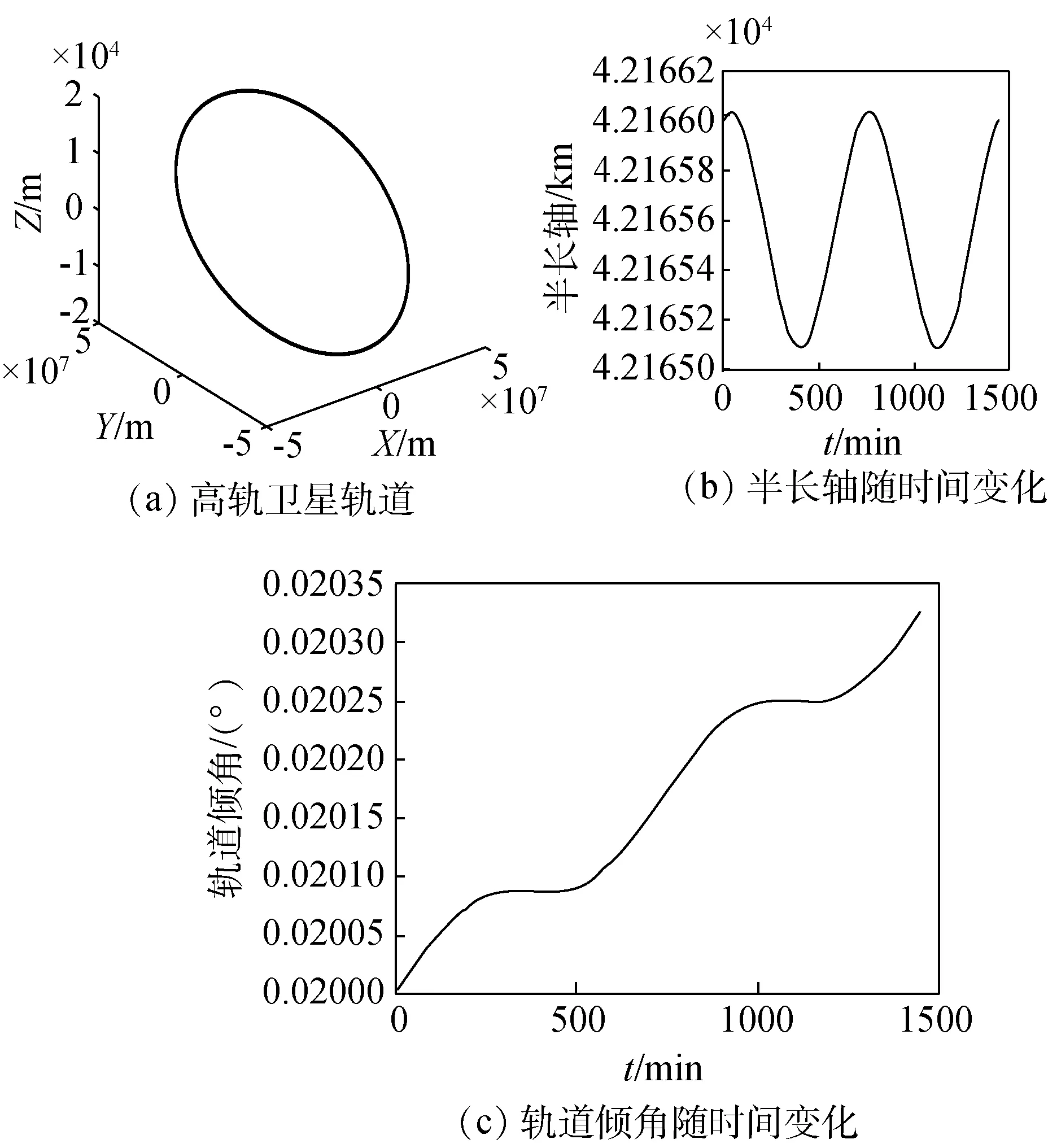
图7 太阳引力摄动下高轨卫星仿真结果

月球引力摄动的仿真结果如图8和图9所示。在月球引力摄动下，低轨卫星轨道的形状与二体轨道形状相似，如图8(a)所示；低轨卫星轨道半长轴随时间变化的量最大仅有大约1.6×10-3，轨道倾角变化的最大值不到3×10-4°，如图8(b)、(c)所示。

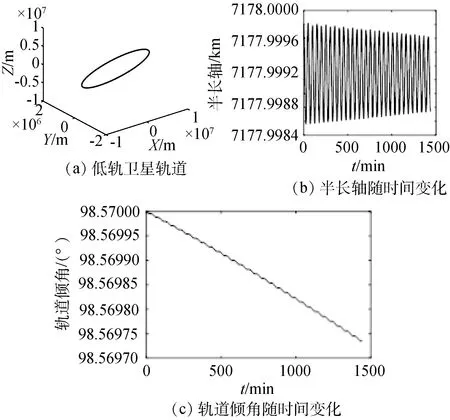
图8 月球引力摄动下低轨卫星仿真结果

月球引力摄动下，高轨卫星的轨道有明显的“折痕”，图9(a)所示；高轨卫星轨道半长轴随时间变化最大可达1左右，轨道倾角变化最大可达9×10-4°，如图9(b)、(c)所示。由上述分析可知，由于月球引力与距离的二次方成反比，月球引力摄动对高轨卫星的影响比较明显，对低轨卫星影响甚微。

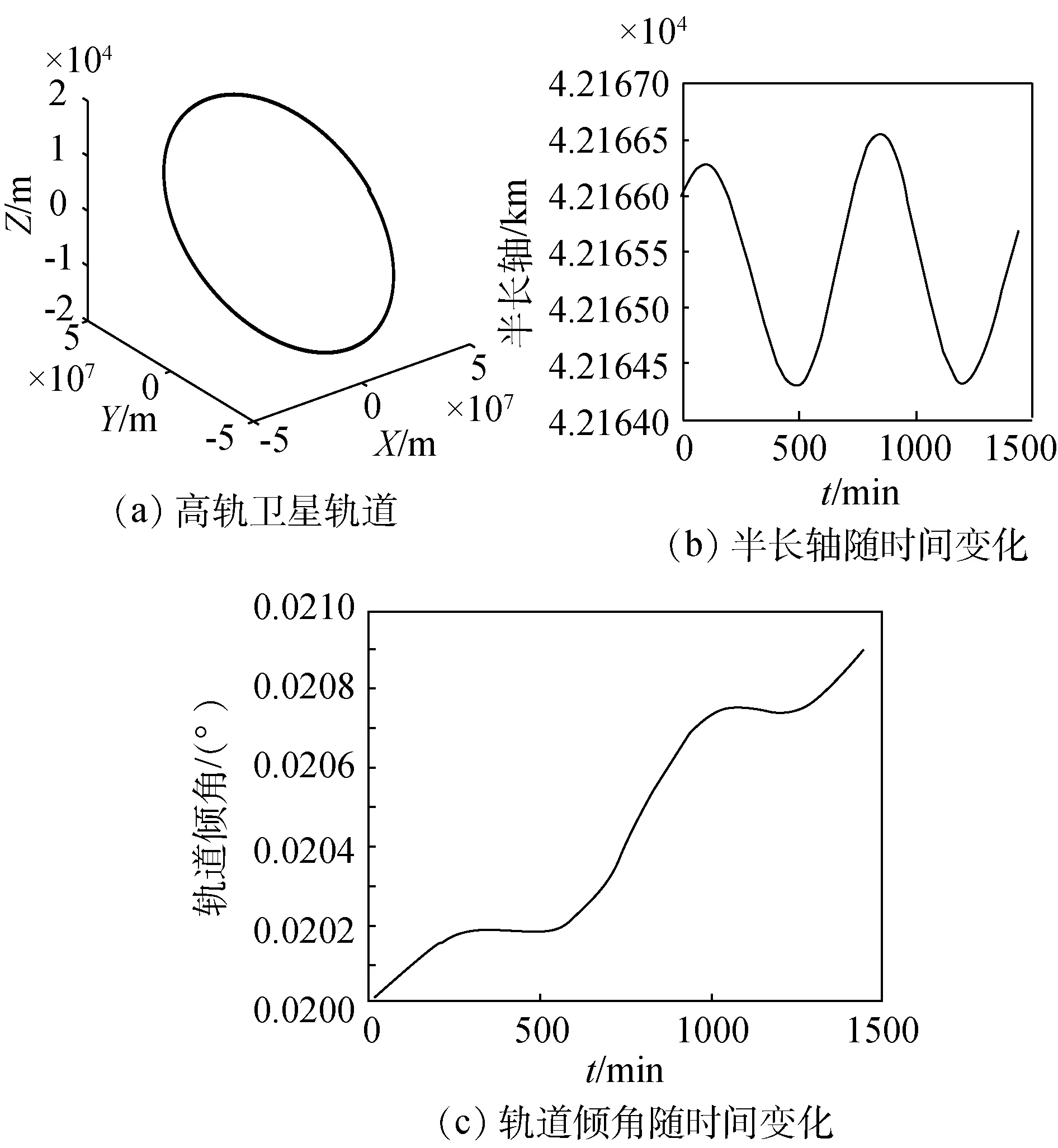
图9 月球引力摄动下高轨卫星仿真结果

2.3 太阳光压摄动

太阳光压是太阳光粒子流冲击卫星表面产生的压力，太阳光压摄动对于面质比较大、轨道高度较高的卫星影响较大。同时卫星运动时，太阳光会被地球或者月球遮挡，还有地球的反光等因素，所以太阳光压摄动情况相当复杂[18-19]。

首先已知在距离太阳1AU处，太阳流量为φ≈1367W·m-2，太阳辐射压P的大小则是由太阳流量大小来决定的：

(7)

其中，c是光速，假设所有撞击卫星表面的光子都垂直射入并全部被吸收。

考虑太阳光照射卫星表面有全反射、全吸收以及太阳光被遮挡等情况，引入太阳光压系数CR和阴影函数υ，给出太阳光压引起的卫星加速度：

(8)

r是卫星与太阳的距离，eΘ为由卫星指向太阳方向的单位矢量。对太阳光压摄动的仿真结果如图10～11所示。

太阳光压辐射模型下低轨卫星偏心率随时间变化的最大变化值仅有2.5×10-8左右，轨道倾角随时间变化的最大值仅有4×10-8°，如图10(b)、(c)所示。

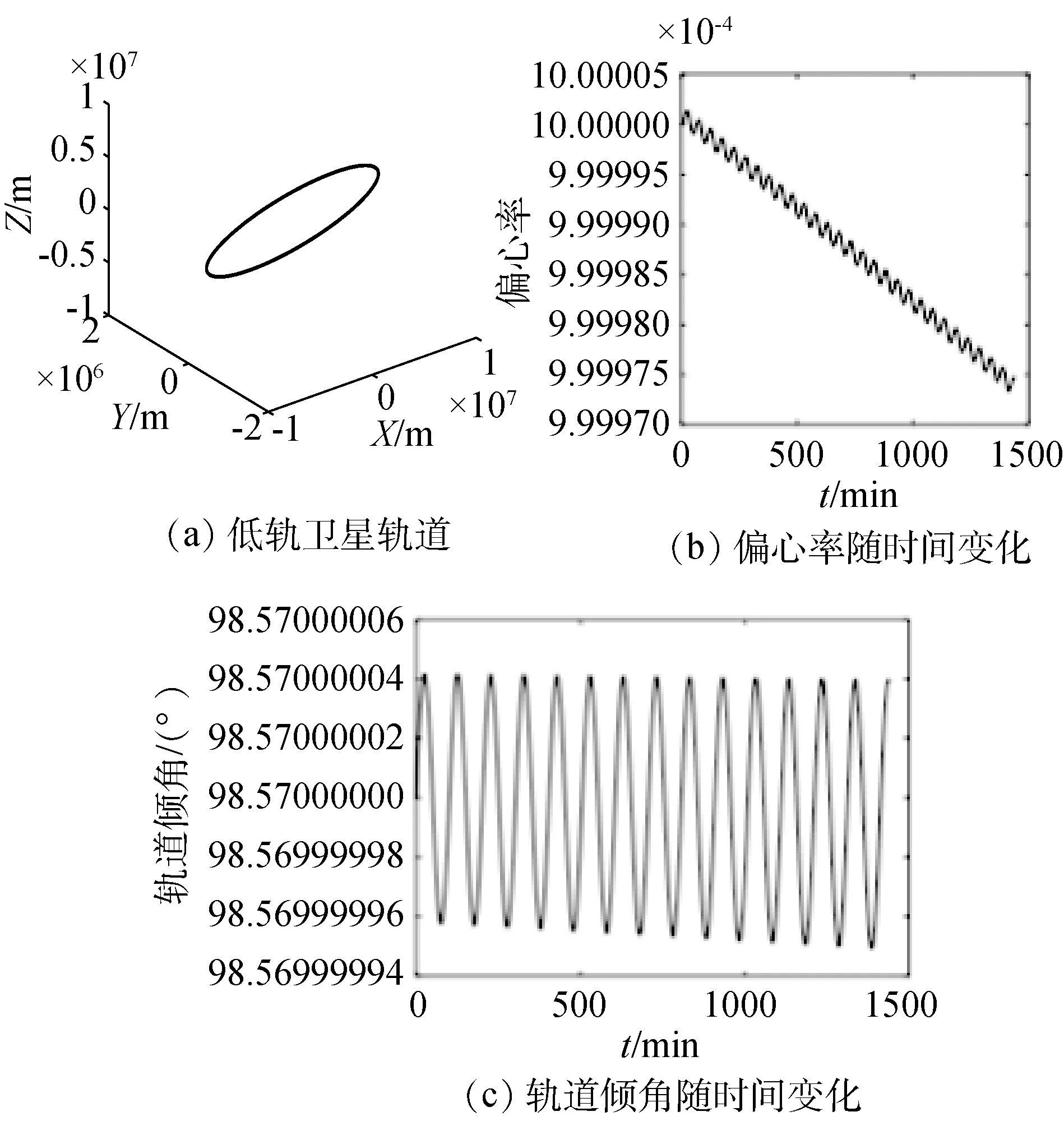
图10 太阳光压辐射摄动下低轨卫星仿真结果

太阳光压辐射模型下高轨卫星偏心率随时间变化最大可达2.5×10-7左右，轨道倾角随时间变化最大不到8×10-7°，如图11(b)、(c)所示。由上述分析可知，太阳光压辐射摄动主要影响高轨卫星的运动，对低轨卫星的影响比高轨卫星小一个量级，原因是太阳光到达地球附近时，其流量急剧减小。

图11 太阳光压辐射摄动下高轨卫星仿真结果

2.4 大气阻力摄动

大气阻力会不断消耗卫星动能，减小卫星速度，减小半长轴，降低偏心率，使卫星轨道逐渐变为圆形，最终使卫星在浓密的大气层中燃烧。但是由于大气阻力方向始终与卫星运动方向相反，所以大气阻力只影响卫星轨道的形状，对于轨道倾角，基本没有影响。

大气阻力摄动产生的卫星加速度为：

(9)

其中，CD是大气阻尼系数，描述了大气与卫星表面材料的相互作用，一般为1.5～2.3；m为卫星质量；ev是与相对速度方向相同的单位向量。

大气阻力摄动影响下的卫星运动仿真结果如图12～13所示。大气阻力使得低轨卫星的轨道半长轴和偏心率随时间变化不断减小，如图12(b)、(c)所示；但是由于大气阻力方向始终与卫星轨道在同一平面上，大气阻力摄动下低轨卫星轨道倾角随时间变化最大值仅有2.5×10-7°，如图12(d)所示，。

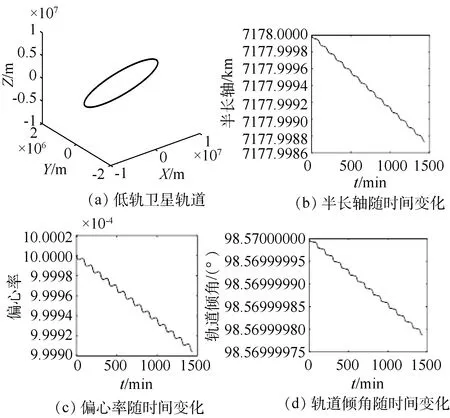
图12 大气阻力摄动下低轨卫星仿真结果

由于在4万公里高度处，地球大气极其稀薄几乎为0，大气阻力摄动下高轨卫星的各个参数均不随时间变化，如图13所示。由上述分析可知，大气阻力摄动只对低轨卫星有显著影响，不会影响高轨卫星的运动。

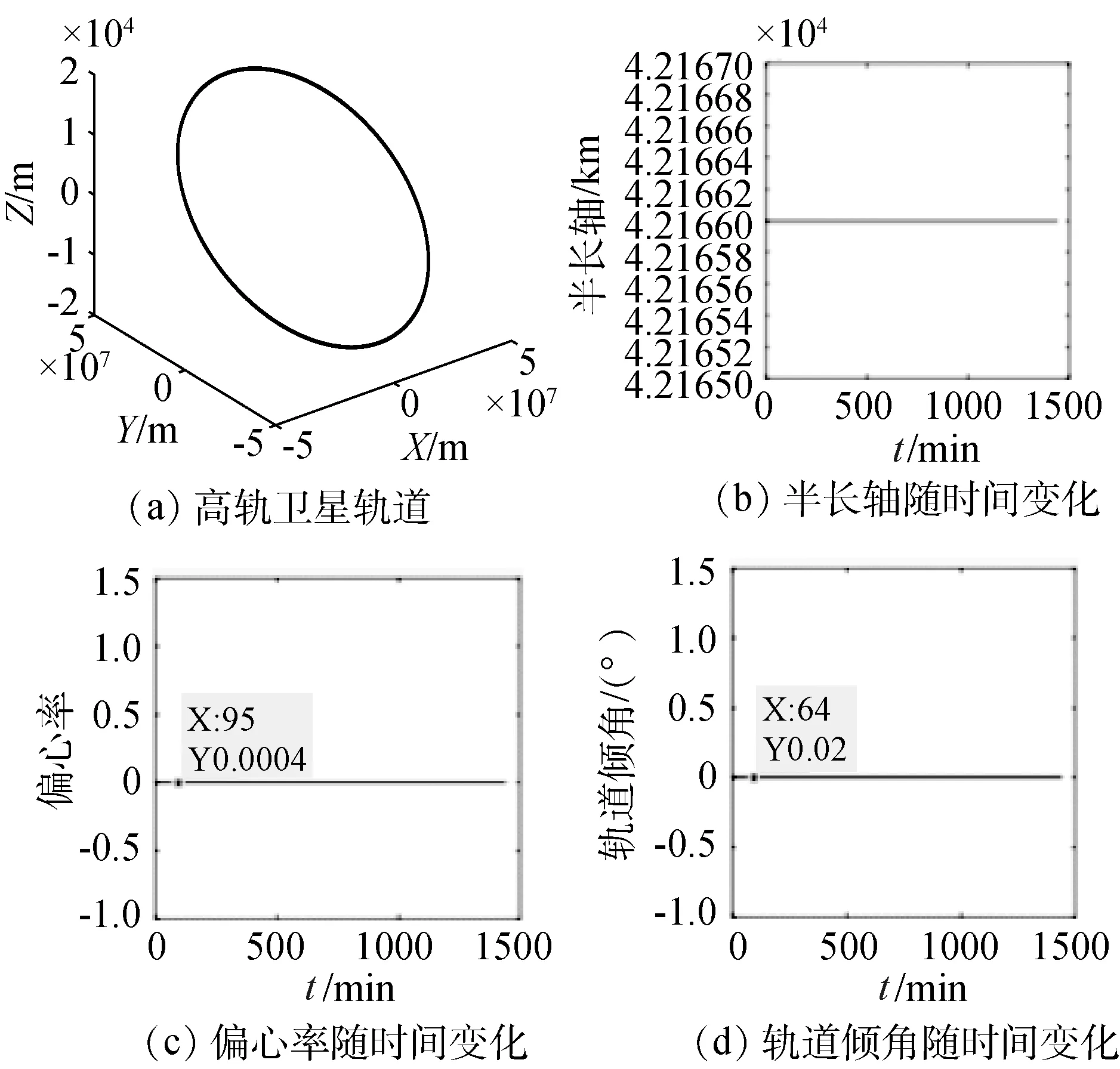
图13 大气阻力摄动下高轨卫星仿真结果

3 摄动模型综合影响分析

通过前面4个小节的建模与仿真，分析了不同轨道高度的卫星在不同摄动模型下的轨道六根数的变化。本节则计算一段时间内，近地轨道、中轨轨道和同步轨道卫星在不同摄动下的星历与其在二体模型下的星历之间的最大标量误差。并以此为依据，进一步说明不同摄动项对不同轨道高度卫星的影响，计算结果如表2所示。

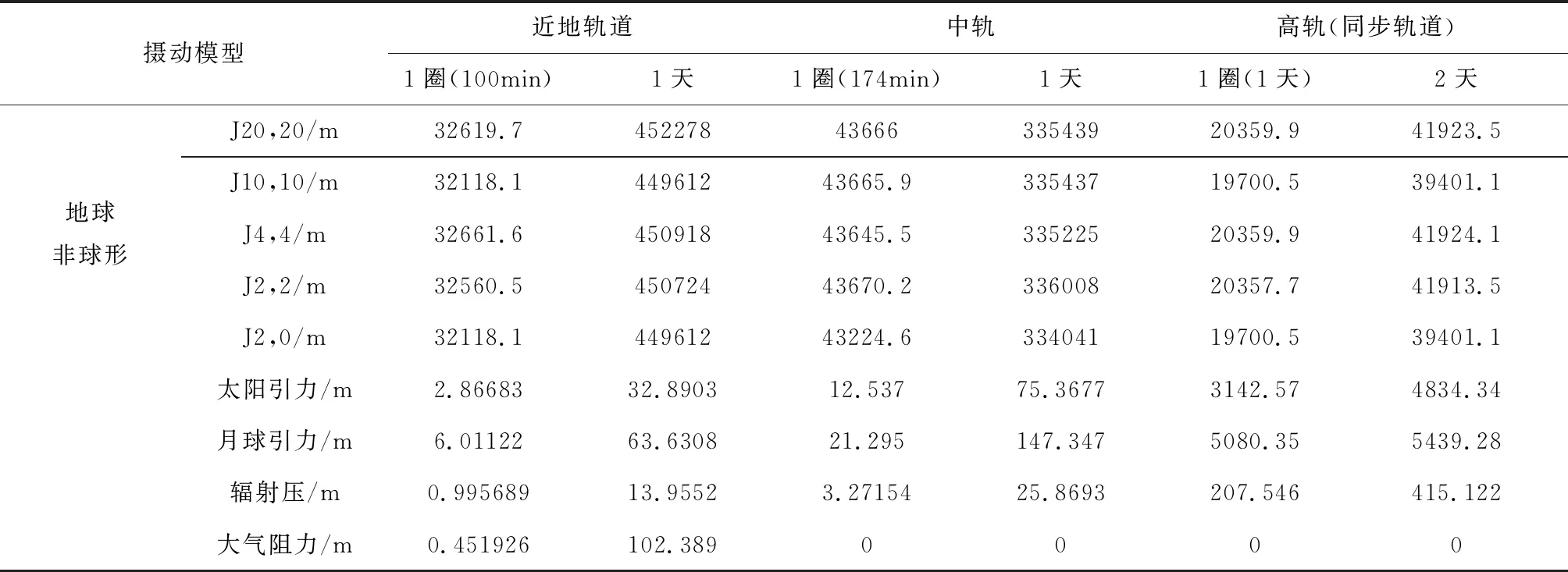
表2 一段时间内星历的最大标量误差

可以看出，在一天的时间内，地球非球形摄动对近地轨道、中轨轨道、同步轨道的卫星的影响是依次降低的，其量级分别为400km、300km和20km，因此，在卫星轨道计算中所使用的动力学模型不可忽略地球非球形摄动的影响。日月引力对高轨卫星的影响量级在千米以上，对低轨和中轨卫星的影响在百米左右，所以在计算高轨卫星轨道时其动力学模型中不可忽略日月引力摄动。太阳辐射压对于高轨卫星的影响量级在200m左右，对低轨和中轨卫星只有几十米。实际计算中，在精度要求不太高的情况下，可以忽略太阳辐射压的影响。大气阻力只对低轨卫星有影响，对于高轨和中轨卫星没有影响[20]。

4 总结

根据卫星精密定轨的需求，对二体模型和四种摄动模型进行了模型建立及仿真，分析了各种模型下对低轨和高轨卫星的轨道影响。

根据仿真分析可知，在计算卫星轨道的动力模型中，对低轨卫星必须考虑地球非球形摄动和大气阻力摄动，在精度要求不高的情况下可以忽略日月引力摄动和太阳辐射压摄动；对中轨卫星必须考虑地球非球形摄动，在精度要求不高的情况下，可以忽略其它摄动项；而对高轨卫星必须考虑地球非球形摄动和日月引力摄动，在精度要求不高的情况下可以忽略太阳辐射压摄动，大气阻力摄动对高轨卫星没有影响。