基于智能PID和扩张状态观测器的姿态控制方法*

李依彤 刘晓东 张惠平 王晓东

1.北京航天自动控制研究所，北京 100854

2.宇航智能控制技术国家级重点实验室，北京 100854

3.中国运载火箭技术研究院，北京 100076

0 引言

PID控制器以其结构简单易于实现的优点被广泛应用于各种实际工程中，飞行器姿态控制也不例外[1]。飞行器的控制参数设计通常是采用增益调度的方法：首先由设计人员针对不同的特征点设计出多组PID控制参数，然后再将这些参数装载于飞行器上，并按照一定的准则调度进行提取，实现控制参数的变化。这种方法对设计人员的经验能力有很高的要求，且设计繁琐，耗费资源。因此迫切需要能够自适应调整飞行器姿态控制的参数。

自适应控制被提出以来，各种控制方法层出不穷，而模型参考自适应是其中一个重要且发展较为成熟的分支[2]。模型参考自适应控制是以理想模型的输出状态为参照来调整自适应机构，进而使被控对象的输出跟踪理想模型输出。另外这种控制方法能够平缓系统过渡过程，降低系统响应超调量，降低控制量，在一定程度上减小了控制能量的浪费。近年来，得益于计算机技术的发展，模型参考自适应控制技术逐渐成熟，不仅能够与其他控制技术相结合[3]，在机械手臂控制[4-5]、电动汽车充电[6]和航空发动机[7]等领域都有相关研究和应用。

神经网络出现以来，就成为了各界学者的研究热点，主要是因为其能够通过学习逼近任意复杂的非线性关系，具有较强的容错性和鲁棒性，在某种程度上能够处理系统的不确定性。在控制领域，神经网络的出现更加促进了自适应控制的发展。文献[8]和文献[9]均是用神经网络实现了对被控对象不确定性和扰动部分的逼近，并与传统算法相结合。在飞行器姿态控制方向，虽然也有一些神经网络整定控制参数的相关研究[1,10]，但大多是针对某一特征点进行设计，未将研究对象扩展到整个飞行段。

本文提出了一种基于模型参考自适应控制框架的神经网络PID姿态控制方法。神经网络选用了结构简单的BP神经网络，网络输入选择能够表征助推段飞行状态的视速度和参考模型与被控对象输出之差，对PID控制参数增益进行整定。引入视速度后可以提高控制器的适用范围，从而实现全飞行包络的自适应控制。为保证系统抗干扰性，加入了两阶线性扩张状态观测器(Extended State Observer，ESO)，并对其进行了误差分析，从理论上证明两阶LESO能够较为准确的对系统状态进行估计。最后以某导弹主动飞行段俯仰通道为研究对象进行仿真验证，仿真结果表明本文的姿态控制方法能够较好地实现姿态控制指令的跟踪。

1 导弹运动模型建立

以某导弹主动飞行段俯仰通道为研究对象，该导弹俯仰与偏航通道采用摆动喷管进行姿态控制，滚转通道采用空气舵进行姿态控制，因此各通道可以独立设计，建立其俯仰通道的小偏差线性化数学模型为

(1)

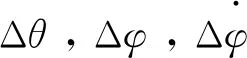
(2)

其中，Δθ为弹道倾角偏差，单位为rad；Δα为攻角偏差，单位为rad；Δφ为俯仰角偏差，单位为rad；Δδφ为俯仰通道姿控喷管摆角，单位为rad。c1f为俯仰通道与推力和升力有关的动力系数，单位为1/s；c2f为俯仰通道重力系数，单位为1/s；c3f为俯仰通道控制力系数，单位为1/s；b1f为俯仰通道气动阻尼力矩系数，单位为1/s；b2f为俯仰通道气动力矩系数，单位为1/s2；b3f为俯仰通道控制力矩系数，单位为1/s2。

(3)

2 基于BP神经网络的PID参数调节模型设计

在模型参考自适应控制框架的基础上，系统控制框图设计如图1所示。俯仰角程序指令φcx同时作用于参考模型和原俯仰通道闭环控制系统，输出分别为φm和φ，二者之差为φe。BP神经网络输入选择φe、视速度WX1以及偏置值1(未在框图中画出)。在此条件下，通过训练网络实现PID控制参数的自适应调节。

图1 模型参考自适应控制方案框图

2.1 BP神经网络基本框架

选用了三层BP神经网络，包含输入层I，隐含层H和输出层O，网络结构如图2所示。

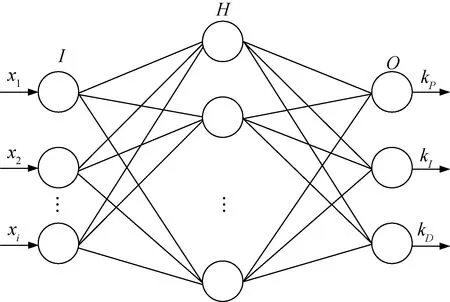
图2 BP神经网络结构

输入层I的神经元节点输入与输出相同，表示为：

(4)

式中：上标in和out分别指神经元的输入和输出，k指当前时刻，M为输入层神经元的个数。显然，本文中M取3。

隐含层H的输入、输出分别为：

(5)

(6)

式中：wih为输入层和隐含层之间的网络权重，N为隐含层神经元的个数；隐含层神经元的激活函数一般选用关于原点正负对称的Tan-Sigmoid函数：

(7)

输出层O的输入、输出分别为：

(8)

(9)

式中：who为隐含层和输出层之间的网络权重。神经网络输出为PID参数，也可以表示为：

(10)

(11)

(12)

PID参数的输出系数为2.5、0.01和0.25。由于PID参数不能为负数，因此输出层神经元的激活函数为非负的Log-Sigmoid函数：

(13)

2.2 BP神经网络权值更新率设计

选取性能指标函数为：

(14)

式中：yd(k)为期望输出，y(k)为实际输出，取二者之差的平方作为网络训练的性能指标，训练的最终目标是使J(k)收敛到最小值。采用最速下降法来对各层神经网络权重进行调制。训练时，沿着性能指标减小的方向，从输出层开始逐层向前进行修正。因此应计算J(k)对who的梯度，输出层和隐含层之间的网络权重的增量为：

(15)

式中：η3>0为学习速率，α3>0为动量因子，α3Δwho(k-1)为惯性项。上式表示网络权重系数的修正和2部分有关：1)当前时刻J(k)对who的梯度值；2)前一时刻权值更新的方向和幅度，这样一定程度上增加了权值更新的惯性，使网络训练具有了一定的抗震荡能力，同时也能加速网络的收敛。

然后根据链式求导法则和误差反向传播算法即可求出神经网络权值更新率，文献[2]中有详细原理推导，在此不再赘述，最终得到输出层和隐含层之间的权值更新率为：

(16)

(17)

隐含层到输入层之间的权值更新率为：

(18)

(19)

式中，η2>0为学习速率，α2>0为惯性系数。

3 线性扩张状态观测器设计

扩张状态观测器是自抗扰控制的核心组成部分，它将被控对象的输入量和输出量作为输入，能够将内部不确定性和外部扰动扩张为新的变量估计出来，并实现对控制量的补偿[11]。将非线性ESO简化为LESO，降低了需要调整的参数的数量，因此也被推广到实际工程应用中。图3为加入LESO后的模型参考自适应控制方案框图，图中的观测器为三阶，若为两阶观测器，则观测器输出为z1和z2，b的取值与系统特性有关，此时b=b3f。那么补偿后的控制量可以用式(20)表示：

图3 加入LESO后的模型参考自适应控制方案框图

δφ=uφ-ub

(20)

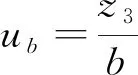
(21)

(22)

上式的扩张状态观测器可建立如下：

(23)

式中：z1和z2是LESO的输出，z1是被控对象俯仰角速度的估计值，y1是被控对象俯仰角速度输出值，z2是总干扰ξ的估计值。l1和l2是扩张状态观测器的增益值。

对式(23)进行拉式变换并整理可以分别得到由观测器输入u，y1到z1和z2的传递函数：

(24)

式中，特征方程为Δ=s2+l1s+l2。

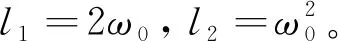
下面对LESO进行误差分析，首先定义估计误差为：

(25)

结合式(23)和(25)，可以得到：

(26)

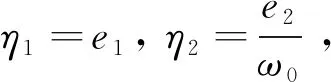
(27)

结合式(24)和(25)，可以得到:

(28)

显然观测器的输入u和y1必然是有界的，则可以得到观测器的稳态误差为：

(29)

从理论上可以证明两阶的线性扩张状态观测器能够较为准确的跟踪系统状态和干扰项。

4 仿真实验与分析

分别按照图1和3所示的控制方案，在MATLAB的Simulink工具箱中搭建控制系统框架进行仿真，仿真步长设置为5ms。参考模型选取如式(30)[2]：

(30)

BP神经网络选取3-10-3的结构，学习速率0.5，动量因子0.05，神经网络初值选取[-0.5,0.5]之间的随机数。在导弹飞行过程中，其弹体模型在不断变化，因此对式(3)中各个小偏差方程的系数按照时间做插值处理，即自变量为导弹飞行时间，因变量为各个小偏差系数，具体变化范围：b1f为0，b2f为[-0.439,-1.671]，b3f为[28.045,101.093]，b2f为负数说明导弹在此飞行过程中一直处于静不稳定状态。导弹二级主动段飞行时间为35s，姿控喷管最大摆角为4.2°。在本文设计的控制方案下，BP神经网络根据网络输入进行权值更新，经过多次前向计算和误差反向传播，最后获得一组收敛的权值。仿真时，将收敛后的网络权值送入网络，进行一次前向计算得到仿真结果。

4.1 姿态控制结果分析

图4和5中，导弹的俯仰角输出曲线和俯仰角指令具有良好的一致性，刚开始跟踪误差较大，但很快误差下降到0.5°以内，属于可接受范围。图6是俯仰通道姿控喷管摆角曲线，在最大限幅以内。图7是PID控制参数自适应调整曲线，其参数变化规律和实际工程较为相似，并且由图8的开环系统伯德图和表1中的裕度统计可以看出，此时控制系统的相位裕度均大于30°，幅值裕度均大于4dB，满足工程实际需求。

图4 俯仰角指令跟踪曲线

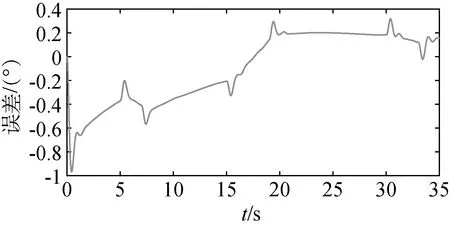
图5 俯仰角跟踪误差曲线

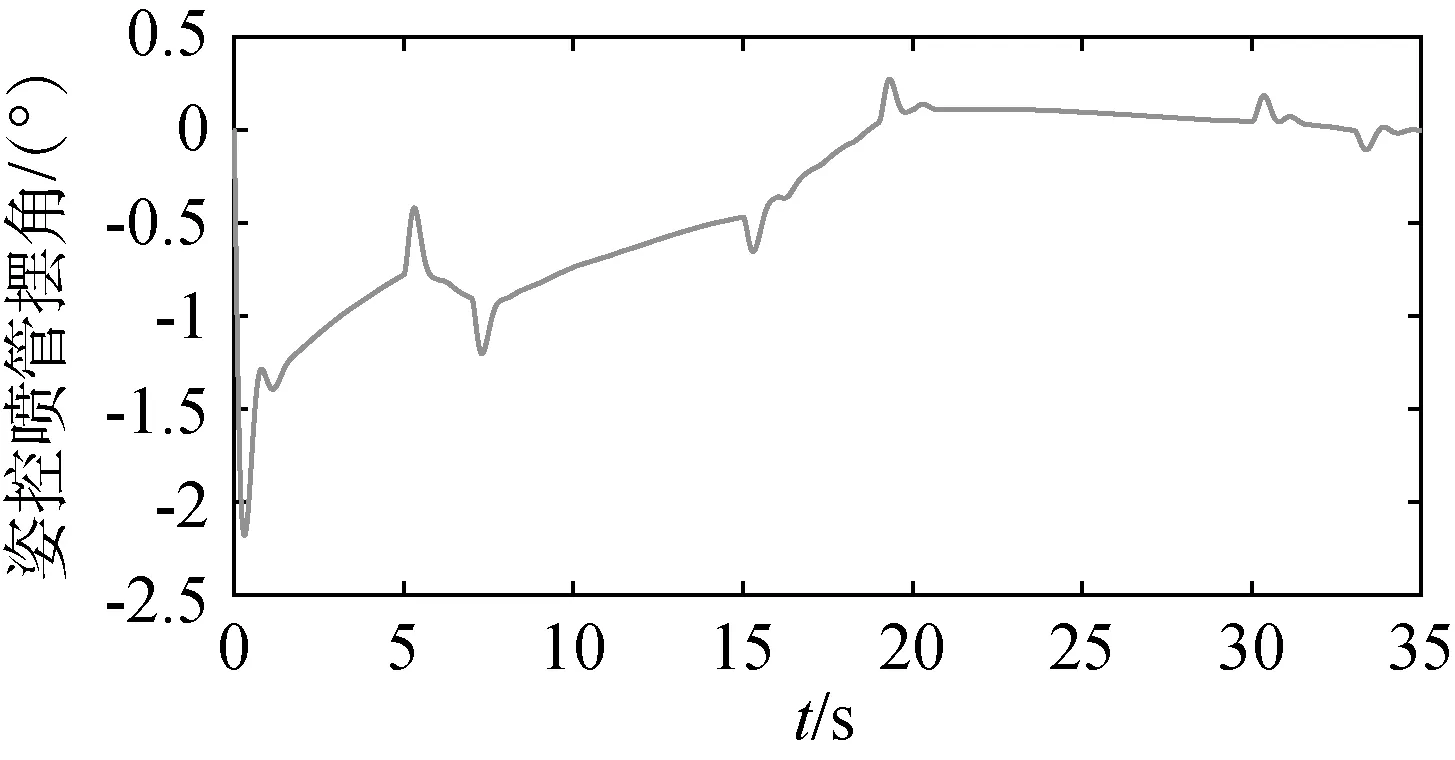
图6 喷管摆角曲线

图7 控制参数曲线

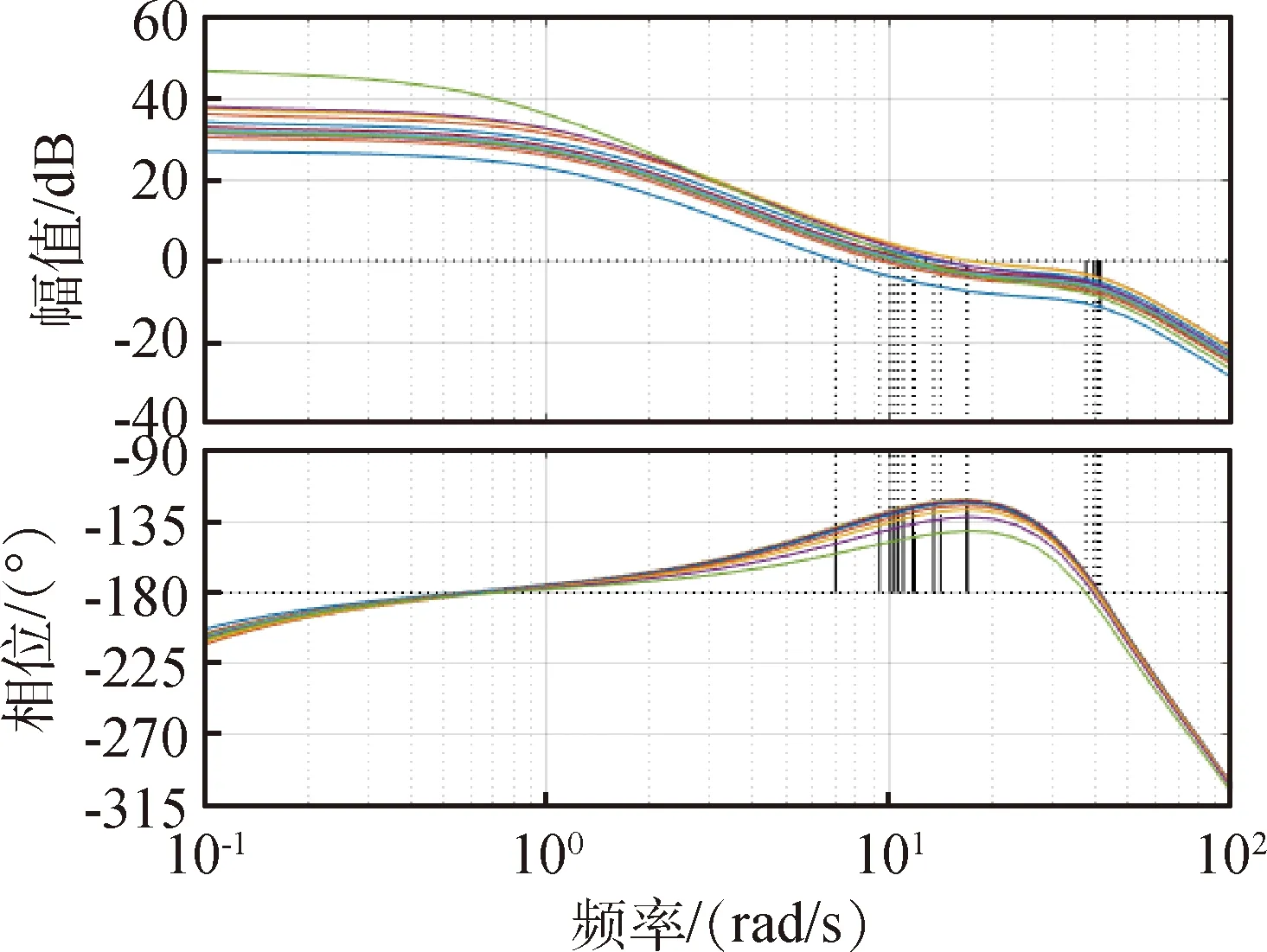
图8 开环系统伯德图

表1 裕度统计表

4.2 加入LESO后姿态控制结果分析

为了进一步提高姿控系统在干扰条件下的鲁棒性，按照式(23)搭建LESO，ω0取10rad/s，加入观测器后的仿真结果如下：

在运行1s时分别加入外部常值干扰fd=2/57.3×1(t)和正弦变化干扰fd=2/57.3sin(0.2t)，图9是在加入干扰后不同情况下俯仰角误差曲线的收敛情况。可以看出，未加入扩张状态观测器之前，只在PID控制器的作用下，系统的抗干扰性能极差，无法抵抗外界扰动。加入LESO后，系统能够快速抑制外界干扰带来的影响，提高姿态控制系统的鲁棒性，动态性能较好。并且通过对比加入两阶和加入三阶观测器的曲线可以发现，在加入相同常值干扰的情况下，二者的俯仰角跟踪误差最大值分别为0.93°和0.68°，而加入相同正弦变化干扰时的跟踪误差最大值分别为0.21°和0.16°。两阶LESO更能够减小扰动对姿态角跟踪的影响，这是因为扩张状态观测的阶数越高，相位滞后越严重，降低系统的快速性[13]。

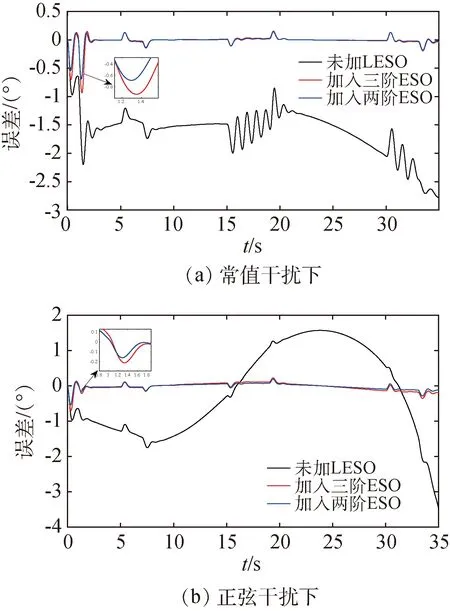
图9 不同情况下俯仰角的跟踪误差曲线

图10～13是常值干扰下加入两阶LESO的仿真结果。在1s时加入常值干扰后，俯仰角会有突变，但在很短时间内重新跟踪俯仰角指令，俯仰角跟踪误差在0.5s内快速收敛，并在±0.2°以内浮动，观测器输出的干扰估计量与理论值会有一定偏差，但是俯仰角速度估计值与理论值一致性较好，能够实现较为准确的指令跟踪。

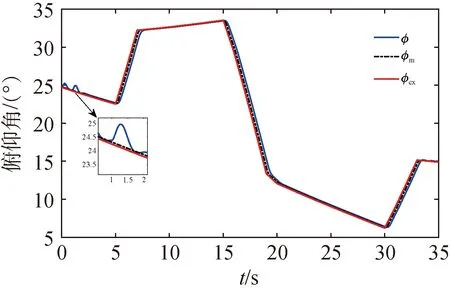
图10 常值干扰下加入两阶LESO的俯仰角指令跟踪曲线

图14～17是在正弦变化干扰后加入两阶LESO的仿真结果。在1s时加入正弦波变化的干扰，和加入常值干扰时类似，姿态角会产生突变但在很短时间内重新跟踪指令，在0.5s内快速收敛，并在±0.3°的误差以内浮动，扩张状态观测器对姿态角速度的估计会受正弦波干扰的影响，但影响不大，同样能够实现较为准确的指令跟踪。

图11 常值干扰下加入两阶LESO的喷管摆角曲线

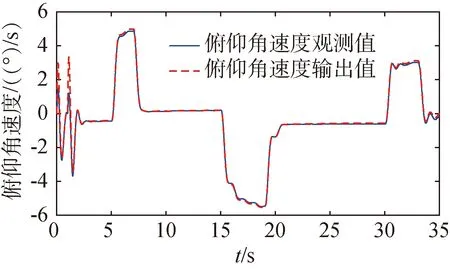
图12 常值干扰下两阶LESO的俯仰角速度估计曲线

图13 常值干扰下两阶LESO的干扰项估计曲线

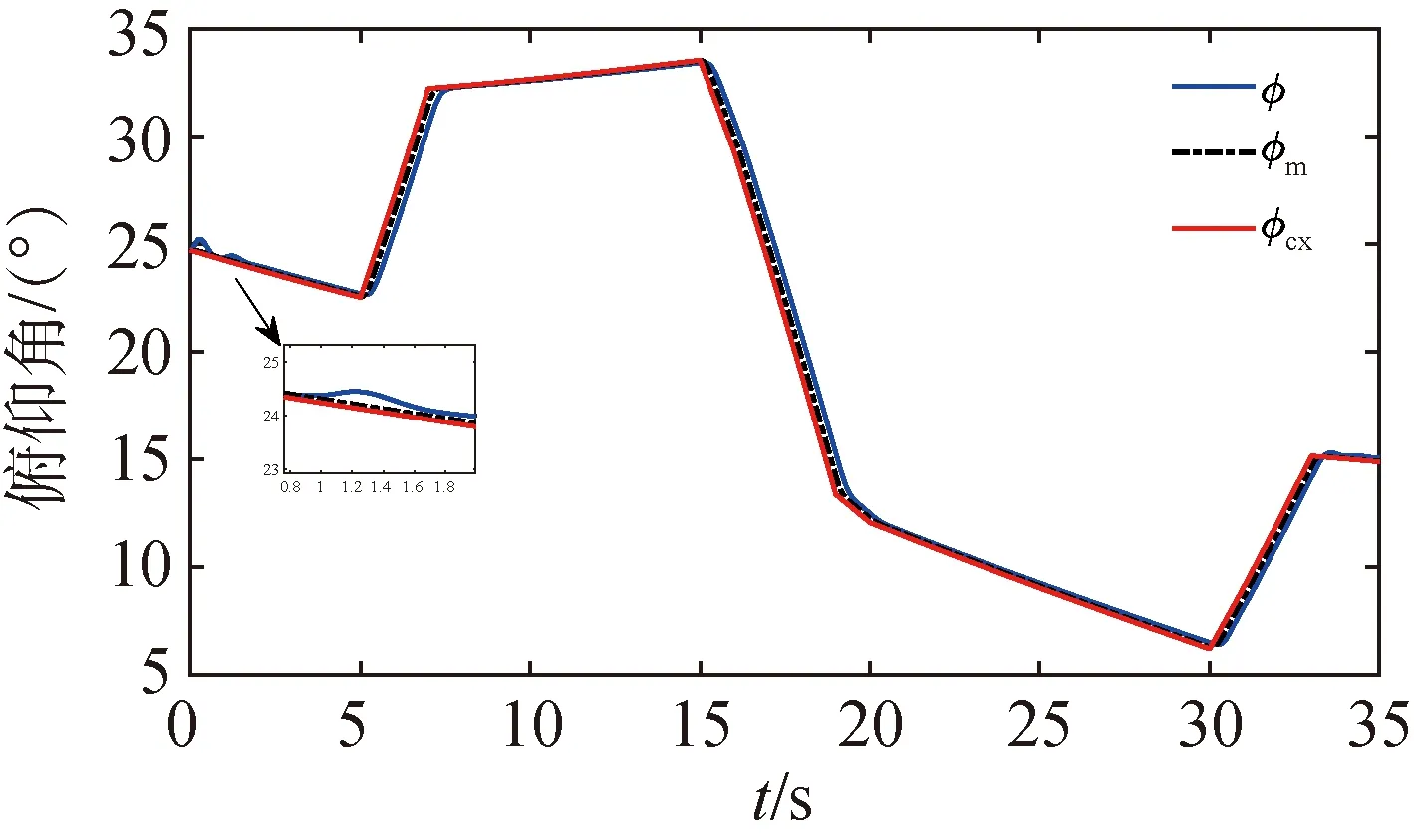
图14 正弦干扰下加入两阶LESO俯仰角指令跟踪曲线

图15 正弦干扰下加入两阶LESO的喷管摆角曲线

图16 正弦干扰下两阶LESO的俯仰角速度估计曲线

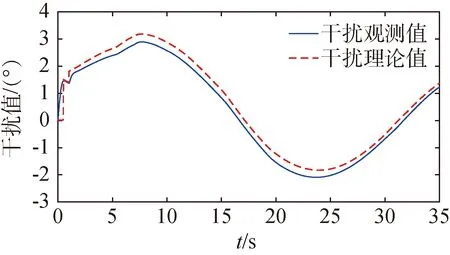
图17 正弦干扰下两阶LESO的干扰项估计曲线

5 结论

提出了一种基于模型参考自适应控制的神经网络姿态控制方法，并加入两阶线性扩张状态观测器，最终实现了姿态角指令的稳定跟踪。主要结论如下：

1) 将表征导弹飞行状态的视速度加入神经网络输入进行训练，获得的PID控制参数自适应调整规律和工程实际较为相近，实现了由计算机代替人工调参、提高了设计过程的智能化，且系统的开环传递函数的相角裕度均大于30°，幅值裕度均大于4dB，姿控喷管摆角未超出限制，满足工程需求；

2) 在加入相同常值干扰的情况下，加入三阶LESO和两阶LESO的俯仰角跟踪误差最大值分别为0.93°和0.68°，而加入相同正弦变化干扰时的跟踪误差最大值分别为0.21°和0.16°，两阶的观测器更能够降低外界扰动对系统的影响。而且无论是加入常值干扰还是正弦变化干扰，经过两阶LESO的控制量补偿，姿态角指令能够在0.5s内很快地重新跟踪指令，实现了扰动的快速抑制，提高了系统的鲁棒性能。