数形结合的思想融入线性代数教学的实践与探索

徐 凯

（四川外国语大学国际工商管理学院 重庆 400013）

0 引言

我国著名数学家吴文俊所说：“在数学的发展过程中，数与形的概念不断扩大，趋向抽象化，但仍有一些对象和运算关系借助几何语言来表示。”线性代数教学过程中大量的公式、定理、推论都是采用严格的演绎论证方法，抽象程度高，逻辑性强。学生在学习知识时很难深刻理解其中的抽象概念和复杂结论，使得学习效率不高[1]。利用几何直观方法，把抽象的问题形象化，结合直观的形象对抽象内容加以理解，可以为代数提供直观背景来发展学生的想象能力，可以消除代数的抽象感[2-3]。因此，在线性代数教学中运用数形结合的思想方法，不仅是学生学好线性代数的需要，而且对培养学生分析问题的能力和养成科学的思维品质都具有十分重要的意义。

1 教学案例分析

本文举例分析线性代数教学过程中的数形结合思想，在教学中运用几何直观与演绎论证相结合的方法，提高教学效果，具体通过几个教学案例说明：

案例一：矩阵的概念和行列式概念不同，不能用数值或者代数式表示，只是把相同性质的数据或代数式列为一个表，对矩阵概念的实质意义难以理解，可以描述通过几何例子形象理解矩阵的概念。

图1：坐标变换公式图

图2：两组向量线性相关性

图3：两种情况的

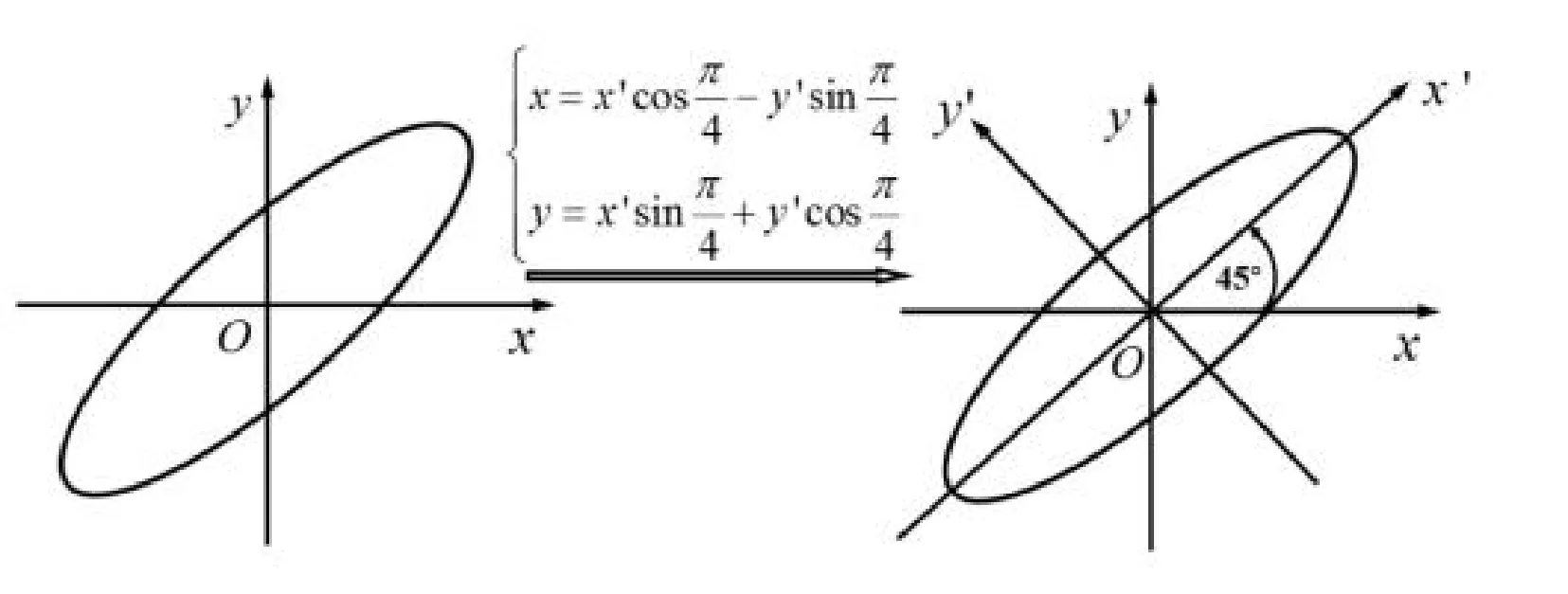
图4：二次型旋转过程图

2 结论

在线性代数教学过程中，数形结合的思想无处不在。比如：向量内积概念[6]可以有三维空间的数量积，通过讲解三维空间内积的几何意义，然后推广到n维空间上；在几何空间中，如果两个向量垂直，那么它们的内积为零。我们从内积出发来推广垂直概念；几何空间中向量的度量性质（如向量的长度、向量间的夹角等）在一般的n维向量中未得到反映；在n维向量空间中，任何正交向量组所含向量的个数n的几何意义是明显的。例如在平面上找不到三个两两垂直的非零向量；在几何空间中找不到四个两两垂直的非零向量等。从几何出发，利用几何直观方法，把抽象的问题形象化，帮助学生理解概念，发现研究思路，有效开展推理、猜想，直至问题解决。