井下管柱力学与控制方法若干研究进展
2021-11-19高德利黄文君
高德利 黄文君
中国石油大学(北京)石油工程教育部重点实验室,北京 102249
1 引言
“井”是人类勘探开发地球中矿产资源不可或缺的信息和物质通道,所谓“油气井”,就是专门用来勘探开发地下油气资源的“井”.油气井工程,就是围绕油气井的建设(钻井与完井,简称“钻完井”)、测量、使用与维护及增产改造等而实施的知识、技术和资金密集型工程.它不仅是贯穿于油气资源勘探开发全过程的基本工程,而且对于地热、地下水及其他矿产资源的勘探开发,以及管道穿越、地球科学钻探等工程都具有重要的实际意义.在油气井工程中,井下管柱是不可或缺的入井工具(图1),是主观控制因素,主要包括钻柱、套管柱、测试管柱、生产管柱及连续管、膨胀管等,其力学行为十分复杂,很难从一般的力学知识中直接找到答案,必须结合实际的工程约束条件进行专门研究(高德利 2006,2018).井眼约束作用是井下管柱力学的本质特征,这也是井下管柱力学理论与细长梁柱理论的主要区别之处.
井下管柱力学最早可追溯到20 世纪五十年代Lubinski (1950)关于直井中钻柱屈曲问题的研究.自此之后,许多学者针对油气井工程中各类管柱力学问题开展了大量研究,并形成了一系列设计方法和控制技术.这些研究工作大致包括:井下管柱屈曲与后屈曲理论、井下管柱摩阻扭矩预测理论、井下管柱安全作业极限理论、底部钻具组合(bottomhole assembly,BHA)力学特性、完井管柱力学、深水管柱力学等,以及相应的工程设计控制方法.上述研究虽然是针对各种特定力学问题开展的,但是它们背后有统一的理论基础.为此,笔者基于细长梁柱理论,推导了受井眼约束管柱的几何方程、平衡方程和物理方程,建立了井下管柱变形控制方程(高德利 1994,1995b),从而为各种特定管柱力学问题研究奠定了理论基础,而井下管柱力学研究由“分”到“合”,在一定程度上标志着井下管柱力学理论体系的建立.
笔者曾在《油气井管柱力学与工程》(高德利 2006)一书中指出:“所谓油气井管柱力学,是指综合应用数学、物理、力学等基础科学的基本理论和方法,采用专门的实验手段,并结合现场采集的数据资料,综合研究受井眼(直井、定向井、水平井及大位移井等)约束管柱的力学行为,如管柱的屈曲行为、动态特性、机械强度及受力和变形等,为油气井管柱与工程的优化设计和作业控制提供科学依据”.井下管柱力学一方面具有坚实的理论基础,另一方面要与工程实践有机结合,能够深入揭示井下管柱的复杂力学行为与失稳失效机理,以期有效促进相关工程设计控制理论和方法的创新发展.
随着油气井类型由常规的直井、定向井发展为水平井、大位移井、多分支井等复杂结构井,实际井眼的垂深和水平位移不断刷新记录,目前都已超过了12 km (高德利等2019),井下管柱的力学行为更加复杂,对经典管柱力学理论方法提出了新挑战.目前,井下管柱力学研究正处于由“合”到“分”的新阶段,以期继续深化各类井下管柱力学问题的创新研究.
“明镜所以照形,古事所以知今.”回顾井下管柱力学七十多年的研究发展历程,正是为了更好地解决油气井工程中日趋复杂的井下管柱力学问题.本文首先介绍了井下管柱的静力学变形控制方程,然后选取了井下管柱力学中的几个重要问题,包括井下管柱屈曲、井下管柱摩阻磨损、井下管柱安全作业极限和底部钻具组合力学特性及其相应的工程设计控制方法,分别介绍了相关研究进展、最新研究成果以及存在的一些问题等,并在一定程度上进行了相关总结与展望.
2 井下管柱的变形控制方程
弹性力学的基本方程包括几何方程、平衡方程和本构方程,是求解弹性力学问题的必要基础.井下管柱作为一种特殊结构形状的弹性体,其基本方程包括几何方程、动量(矩)方程和本构方程.几何方程描述了井下管柱应变与变形之间的定量规律,通常采用Euler–Bernoulli 梁假设或者Timoshenko 梁假设.动量(矩)方程描述了井下管柱运动与作用力的关系,稳态问题则简化为平衡方程,描述了井下管柱上内力与外力的平衡关系.本构方程描述了井下管柱上应力与应变之间的关系,将其与几何方程进行结合,便可得到井下管柱内力与变形之间的定量关系.
基于井下管柱力学的基本方程,并采用了井下管柱不可伸长等假设条件,推导了井下管柱的变形控制方程,从而建立了井下管柱变形、运动和受力分析的理论基础(高德利等1994,2006).在此基础上,忽略方程中的动力因素,可得到静力条件下井下管柱变形控制方程如下
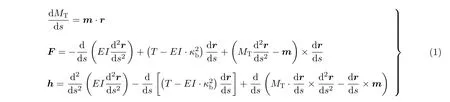
其中,r为井下管柱位置的矢量,m;s为井下管柱的弧长,m;κb为井下管柱变形曲线的曲率,m−1;T为井下管柱上轴向拉力,N;MT为井下管柱上扭矩,N·m;F为井下管柱截面上的内力矢量,N;h为单位长度井下管柱上的外力矢量,N/m;m为单位长度井下管柱上的外力矩矢量,N.
在上述变形控制方程的推导过程中,没有考虑实际作业条件的约束,因而具有普适性.针对具体的井下管柱问题而言,需要从井下管柱变形控制方程出发,引入相应的假设条件和近似处理方法,推导出适用于具体问题的变形控制方程,再进行求解和定量分析.
例如,对于斜直井眼中的管柱,当井下管柱两端的轴向压力达到一定值后,管柱直线状态变得不稳定而进入屈曲状态.假定屈曲状态下管柱与井壁连续接触,忽略管柱弧长与井眼轴线长度的差异,并且将笛卡尔坐标系转换为沿井筒轴线的圆柱坐标系,可推导出井下管柱屈曲控制方程如下(高德利 2006)

其中,θ为管柱在井眼内的角位移,rad;rc为管柱的径向位移,等于井眼的视半径,m;z为沿井眼轴线的长度,近似等于管柱弧长,即;q为管柱的线重,N/m;α为井斜角,rad;其他变量意义同上.
当井下管柱在井眼内运动时,管柱与井壁的相互作用导致在管柱上产生摩阻和扭矩.在井下管柱摩阻扭矩的计算分析中,通常假定管柱与井壁连续接触,且管柱变形曲线与井眼轴线一致.前者假设保证了井下管柱与井壁是相互接触的,可用接触力的大小和方向描述其接触关系;后者则确定了井下管柱的变形曲线,极大降低了求解与计算难度,推导得到井下管柱摩阻扭矩的计算方程如下(高德利等1994)
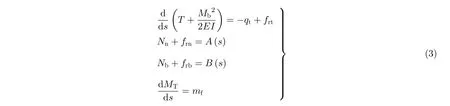
其中,Mb为管柱上弯矩,N·m;Nn和Nb为单位长度管柱与井壁接触力在井眼轴线主法线方向和副法线方向上的分量,N/m;qt为管柱线重在井眼轴线切线方向上的分量,N/m;frt,frn和frb分别为单位长度管柱上的摩擦力在井眼轴线切线方向、主法线方向和副法线方向上的分量,N/m;mf为单位长度管柱上扭矩的损失,主要是由摩阻导致的,N;A(s)和B(s)为两个中间变量,N/m;其他变量意义同上.
底部钻具组合主要由钻头、钻铤、稳定器等部分组成,它是井眼轨迹控制的关键所在.底部钻具组合在井眼约束、重力、浮力、轴向力等作用下,是一个典型的三维梁柱问题.基于井底坐标系,并对管柱上外力、轴向力等进行简化,可推导出底部钻具组合的静力学变形控制方程如下(高德利 2006)
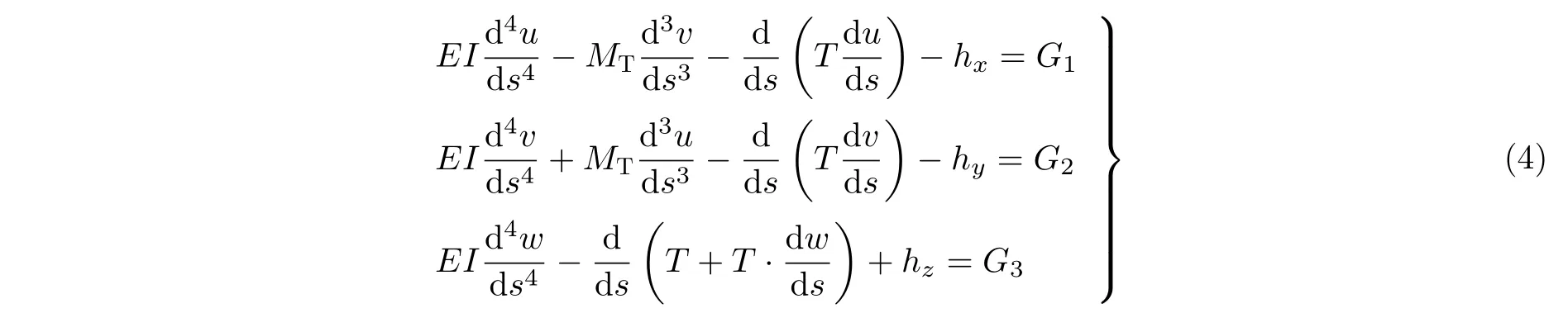
其中,u,v和w分别为BHA 变形曲线在井底坐标系的位移分量,m;hx,hy和hz为管柱上外力在井底坐标系的三个分量,N/m;G1,G2和G3为三个非线性量,对于小变形问题可忽略为零;其他变量意义同上.
实际的油气井工程涉及的影响因素复杂多样,通常需要在现有的井下管柱变形控制方程基础上进行必要的修正,有时要综合利用多个控制方程才能进行求解.
3 井下管柱屈曲与后屈曲行为
井下管柱屈曲是指管柱上轴向压力达到某一临界值时,管柱变形由一种构型突变进入另外一种构型的不稳定性问题.井下管柱屈曲会引起钻进方向改变、井下摩阻磨损加重、井下管具和仪器失效、井下管柱作业困难甚至“锁死”等诸多问题,对安全高效作业造成威胁.开展井下管柱屈曲问题研究,揭示管柱屈曲与后屈曲行为,准确预测管柱屈曲临界载荷,可为井下管柱优化设计与安全高效作业提供理论依据.
相对于欧拉压杆屈曲而言,井下管柱屈曲包含了井眼约束、重力、摩擦力等诸多因素的影响,其力学行为更加复杂.根据井眼几何形状的分类,井下管柱屈曲问题可分成受垂直井眼、斜直井眼(包括水平井眼)以及弯曲井眼等不同井眼约束的管柱屈曲问题.井下管柱屈曲问题的研究方法包括理论法、数值法和实验法,理论法包含梁柱方程、屈曲微分方程和能量法等(Gao &Huang 2015).
20 世纪50 年代,Lubinski 率先研究了垂直井眼中管柱二维横向屈曲(Lubinski 1950)和三维螺旋屈曲问题(Lubinski &Althouse 1962),结果表明,随着钻压(轴向压力)的增大,井下管柱依次经历直线状态、二维横向屈曲状态直至螺旋屈曲状态,并推导了螺旋屈曲状态下螺旋变形与轴向压力的关系.然而,Lubinski 没有揭示井下管柱如何从二维横向屈曲过渡到螺旋屈曲.后续,Wu (1992)研究指出,随着钻压的增大,垂直井眼中管柱依次经历正弦屈曲和螺旋屈曲状态,并推导了两种屈曲模态的临界载荷.
笔者在前人工作的基础上,研究了垂直井眼中管柱屈曲模态转换的全过程(Huang &Gao 2016).随着井下管柱底端上轴向压力的增大,井下管柱依次经历了直线状态、二维横向屈曲、三维横向屈曲、连续接触屈曲和螺旋屈曲五个状态(图2(a)),分别推导了每个屈曲状态转换的临界条件.二维横向屈曲是指管柱在垂直平面内发生二维弯曲变形(图2(a2)),三维横向屈曲是指管柱轴线是一条三维空间曲线(图2(a3),(a4)),连续接触屈曲是指管柱与井壁之间点接触开始转换为连续接触(图2(a5)),螺旋屈曲是指管柱与井壁的连续接触长度达到一个螺距(图2(a6)).

图2
垂直井眼中管柱重力方向与井眼轴线相互平行,垂直于井眼轴线的管柱重力分量为零;斜直井眼内管柱重力同时包含平行于和垂直于井眼轴线的两个分量,因而斜直井眼中管柱屈曲行为不同于垂直井眼.当管柱上轴向力为拉力或者较小的压力时,管柱受到垂直于井眼轴线重力分量的作用而躺在井眼底端,且保持直线状态;当管柱轴向压力增大到某一临界值时,管柱开始脱离井眼底端而呈现蛇形状态,即发生正弦屈曲(图2(b1));随着轴向压力进一步增大,管柱变形曲线转换为螺旋线,即发生螺旋屈曲(见图2(b2)).
Paslay and Bogy (1964)首次利用能量法推导了斜直井眼中管柱正弦屈曲的临界载荷,后续学者Chen 等 (1990)、Miska 等 (1996)也得到了相同的结果.由正弦屈曲过渡到螺旋屈曲是一个非常复杂的过程,还没有一个理论能够完整地描述该过程.目前,解决该问题的主要思路为:开展管柱屈曲室内实验(Salies 1994,Salies et al.1994,邹红华 2002),观察管柱变形特点并测量相关数据,分析过渡过程中管柱轴向力与轴向压缩位移之间的关系,提出过渡过程的假设条件,建立力学模型并进行求解.
Chen 等 (1990)忽略了正弦屈曲阶段的压缩位移,且假设由正弦屈曲转换到螺旋屈曲的过程中,轴向压缩位移变化较大,而轴向压力保持不变,推导得到螺旋屈曲临界载荷为正弦屈曲临界载荷的倍;Wu (1992)假设由初始正弦屈曲转换到螺旋屈曲过程中,井下管柱轴向压力与压缩位移之间是线性关系,得到结果为倍;Miska 等 (1996)假设从初始无屈曲状态到螺旋屈曲的整个过程中,井下管柱轴向压力与压缩位移之间为线性关系,得到结果为倍.Cunha (1995)研究认为加载进入螺旋屈曲和卸载退出螺旋屈曲的临界载荷是不相同的.
笔者基于模拟实验研究,提出了一种更加完整的管柱屈曲状态转换过程假设(图3):正弦屈曲过程中轴向压力与压缩位移之间是线性关系,正弦屈曲结束到螺旋屈曲开始过程中轴向压力保持不变(高德利 2006,Gao &Huang 2015),并采用能量法推导了屈曲临界载荷.基于井下管柱屈曲控制方程,利用管柱与井壁接触判断条件,也推导了管柱螺旋屈曲临界载荷(Gao et al.1998),其结果与能量法非常接近,约为正弦屈曲临界载荷的1.38 倍,略低于Chen 等(1990)的结果,验证了计算公式的合理性.

图3
模拟实验表明(McCann &Suryanarayana 1994),井眼弯曲可增大管柱屈曲临界载荷,提高管柱的稳定性.He 和 Kyllingstad (1995)将弯曲井眼中管柱屈曲问题等效为斜直井眼问题,在计算中将垂直于井眼轴线的管柱重力分量替换为弯曲井眼中管柱与井壁的接触力.后续一些学者,包括Wu 和 Juvkam-Wold (1995a)、Kyllingstad (1995)、Qui 等 (1998)、Mitchell (1999)等,均采用不同的假设条件和求解方法,推导了造斜井眼和降斜井眼中管柱正弦屈曲和螺旋屈曲的临界载荷.这些结果主要适用于仅有井斜变化的井眼,而真实井眼的方位也是变化的,因此需要研究井斜和方位同时变化的井眼中管柱屈曲问题.笔者根据井斜和方位的变化分别定义井斜平面和方位平面,将管柱变形问题分解到这两个平面内进行研究,然后再进行组合,最后得到了三维弯曲井眼中管柱屈曲临界载荷的近似计算公式(Huang &Gao 2019).
井下管柱屈曲研究中通常假定管柱是等径的细长杆,且与井壁连续接触.实际上,井眼内的整个管柱是由许多段管柱单元(或单根管子)顺序连接组成的,单元之间通过接头连接,管柱接头的径向尺寸通常大于管柱本体的直径,导致接头附近的管柱本体与井壁是不接触的.严格来讲,连续接触的假设条件不符合实际情况.Lubinski (1977),Paslay 和 Cernocky (1991)研究了弯曲井眼中带接头管柱受拉和受压时的应力集中问题;Mitchell (2003,2005)研究了在水平井眼中带接头管柱正弦屈曲以及在垂直井眼中的螺旋屈曲问题;Gao 等 (2011)、Daily 等 (2013)、Hajianmaleki 和 Daily (2014)研究了水平井眼中带接头管柱由二维变形转换为三维变形的临界条件.然而,这些研究工作只是聚焦于某一个或几个特殊的管柱屈曲问题,未能全面揭示井下带接头管柱的复杂屈曲力学行为.
针对该问题,笔者综合采用梁柱方程、屈曲微分方程和能量法开展研究,首次揭示了井下带接头管柱变形状态的转换关系,并绘制了相图(图4).井下管柱本体与井壁的接触状态包括无接触、点接触、连续接触和完全接触,管柱的屈曲模态包括无屈曲、横向屈曲、正弦屈曲和螺旋屈曲.将接触状态与屈曲状态进行组合,共有16 种管柱变形状态;综合接触状态转换条件和屈曲状态转换条件,共有20 种临界条件.分别求解获得了各个状态下管柱变形曲线、管柱局部弯矩、管柱与井壁接触力等结果,推导了各种临界条件的计算表达式(Huang &Gao 2014a,2014b,2015;Huang et al.2017,2018a).

图4
在图4中,I,L,S,H 分别代表初始状态、横向屈曲、正弦屈曲和螺旋屈曲;N,P,W,F 分别代表无接触、点接触、连续接触和完全接触;C 代表临界条件.
井下管柱端部的边界条件也是影响管柱屈曲行为的重要因素.借鉴材料力学中梁柱端部约束的分类标准,目前管柱端部边界条件主要包括铰支约束和固支约束.在端部约束下,井下管柱屈曲变形包括过渡段和完全屈曲段,过渡段又可以分为悬空段和连续接触段.一些学者研究了过渡段上管柱变形规律以及过渡段长度等问题(Mitchell 1982,Sorenson &Cheatham 1986,刘凤梧和高德利 1999,Gao &Miska 2009).研究表明,过渡段的长度小于螺旋屈曲的一个螺距.笔者研究发现,铰支和固支约束只是两类特殊的边界情形,提出了一种新的井下管柱边界条件的分类标准(Huang et al.2015b,2015c),并研究了端部约束对管柱螺旋变形状态稳定性的影响规律.其他井下管柱屈曲问题,包括摩擦力、管柱内外液压力(韩志勇 2011)等因素对管柱屈曲行为的影响,也取得了一些研究进展,这里不再赘述.
整体而言,关于井下管柱屈曲行为的研究大都属于静力屈曲范畴.然而,在旋转钻进过程中井下管柱通常处于运动状态,此时井下管柱屈曲控制方程中包含管柱位置变化、惯性力等项,属于动力学屈曲问题.目前管柱动力学屈曲研究很少,仅局限于几个特殊问题(Dunayevsky et al.1993,Gao &Miska 2010a).模拟实验结果表明,动力学屈曲临界载荷小于静力学屈曲临界载荷(张广清等2001),但是尚未能从理论上揭示其力学机理.因此,下一步需要加强对井下旋转管柱动力学屈曲问题的创新研究.
4 井下管柱摩阻扭矩预测理论与设计控制方法
井下管柱摩阻和扭矩,分别是指井下管柱在井眼内轴向运动时产生的轴向阻力和旋转运动时产生的扭矩损失.对于水平井、大位移井等复杂结构井而言,在管柱上的摩阻扭矩作用问题比较突出,是影响工程作业安全的重要因素之一.同时,井下管柱摩阻扭矩载荷计算是井眼轨道设计、钻柱优化、卡点预测、降磨减扭及钻机选型等设计控制的理论基础.因此,开展井下管柱摩阻扭矩预测与控制研究具有实际意义.
20 世纪80 年代,Johancsik 等 (1984)建立了经典的井下管柱摩阻扭矩模型(即软绳模型),该模型将井下管柱简化为无抗弯刚度的绳索.Ho (1988)为克服软绳模型中忽略管柱刚度的缺点,将管柱视为弹性细杆,建立了刚杆模型.其他学者在此基础上做了大量的完善工作(Sheppard et al.1987,Maidla &Wojtanowicz 1987,Lesage et al.1988,Brett et al.1989,李子丰和孔凡君 1993,闫铁等2011).笔者基于井下管柱的静力学变形控制方程,推导了井下管柱摩阻扭矩计算模型的一般表达式,并针对一维、二维和三维井眼约束条件开展了井下管柱整体受力分析(高德利等1994).在上述模型建立过程中,假定井下管柱与井壁连续接触且管柱变形曲线与井眼轴线一致,该假设条件极大降低了求解与计算的难度,但也影响了模型的精度和适用范围.例如,大位移井大斜度钻进过程中管柱容易发生屈曲,管柱接头导致管柱本体与井壁连续接触条件失效等,这些问题超出了经典管柱摩阻扭矩模型的适用范围.
Wu (1995)将管柱屈曲临界载荷以及屈曲引起的附加接触力引入到经典模型中,建立了考虑屈曲效应的井下管柱摩阻扭矩预测模型;McSpadden 和 Newman (2002)、Menand 等 (2006)、Mitchell 等 (2015)研究了带接头管柱的摩阻扭矩问题,将管柱接头以及接头之间的中点作为管柱与井壁的潜在接触点.上述研究中管柱接头效应和屈曲效应是相互独立的,未耦合起来.一些学者直接采用有限元的方法求解井下管柱摩阻扭矩 (刘巨保 2003,Aslaksen et al.2006,Tikhonov et al.2014,祝效华等2019),但也存在数值模拟计算效率低、收敛性差等问题.
近年来,笔者将井下管柱局部力学模型与经典整体受力模型(即摩阻扭矩模型)结合起来,建立了井下管柱局部−整体耦合力学模型(图5).在局部力学模型中研究了井眼几何、管柱接头、管柱屈曲等因素对局部管柱力学行为的影响规律,充分考虑了管柱接头效应和屈曲效应的耦合(Huang et al.2018a,Huang &Gao 2019),再将局部模型的结果引入到整体受力模型中修正相关参数,建立了相应的耦合力学模型(Huang et al.2018c,Huang &Gao 2020).耦合力学模型既考虑了各种局部因素的作用,扩展了模型的适用范围,同时保证了计算的高效性.利用该模型,成功揭示了南海某油田大位移井钻进过程中规律性阻卡的力学机理,并提出了设计控制方法,而常规模型无法解决这个问题.
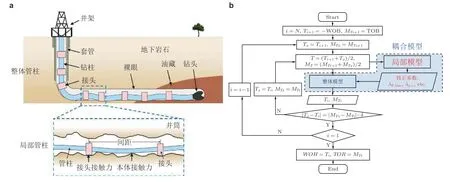
图5
钻柱在井眼内长时间旋转作业时不断磨损套管内壁,使得套管抗内压强度和抗外挤强度有所降低,甚至导致套管磨穿事故(姜伟 2002).套管产生严重磨损时,容易诱发键槽卡钻、井筒完整性失效等井下恶性事故,严重影响了井下作业安全和井的使用寿命.
二十世纪六七十年代,前苏联和美国学者首先开展了套管磨损的理论和实验研究工作,为后续研究奠定了重要基础.目前研究认为,套管磨损机理主要分为四种形式(孙连忠 2012):粘着磨损、切削磨损、磨粒磨损和抛光磨损.粘着磨损是套管内壁局部粘焊导致材料损失,磨屑呈薄片状;切削磨损是井下管柱接头硬质点对套管内壁的微切削,磨屑呈细条状;磨粒磨损是磨粒对套管内壁的微切削,磨屑呈粉末状;抛光磨损为细颗粒对套管内壁的打磨,磨屑呈细粉末状.在实际钻井过程中,这四种磨损行为可能同时存在,但通常以磨粒磨损为主.
影响套管磨损的因素很多,主要包括井眼狗腿度、钻柱旋转速度、钻柱和套管表面粗糙度、钻井液性能及接触力大小等诸多因素.Bradley 和 Fontenot (1975)、White 和 Dawson (1987)研究表明,套管磨损主要由于钻柱旋转导致的,钻柱起下钻的影响可忽略不计.White 和 Dawson(1987)将套管磨损量和摩擦能联系起来,建立了线性的套管磨损效率模型.在该模型中套管磨损体积与摩擦能成正比,与套管硬度成反比.Hall 等 (1994)简化了套管磨损效率模型,认为磨损系数、接触力和运动路程是计算套管磨损的主要参数,其中磨损系数需要通过室内实验或者现场测量数据反演才能确定.Schoenmakers (1987)认为套管磨损形状为单月牙形(图6(a)),基于线性磨损效率的假设,建立了套管磨损面积和磨损深度的预测公式.国内,林元华等(2004)、祝效华等(2015),还有其他学者也做了一些相关的有益工作.

图6
套管磨损实验表明,磨损系数不是一个常数,而是随着套管磨损深度的增加而减小,最后趋于稳定.Hall 和 Malloy (2005)研究了套管磨损体积与摩擦能的非线性关系,提出了门槛接触压力的概念.针对该问题,笔者认为钻柱与套管的接触压力是影响套管磨损过程的关键因素,建立了具有非线性的套管磨损效应模型(Gao et al.2010,Gao &Sun 2012,Sun et al.2012).在该模型中,套管磨损系数随着磨损深度的增加而减小,全面描述了套管磨合磨损和稳定磨损两个阶段,且计算结果与套管磨损实验吻合良好.钻柱屈曲、钻柱涡动、套管椭圆度等因素也与套管磨损过程密切相关,进而建立了考虑这些因素作用下的套管磨损预测模型(谭雷川等2018;Tan &Gao et al.2018a,2018b,2018).
现场多臂测井数据显示,井下套管的实际磨损形状有时不是单月牙,在某些井段的套管上存在多个磨损区域,超出了常规模型的适用范围.笔者提出了套管复合磨损模式(图6(b)),包括月牙之间的重叠、交叉和分离.不同套管磨损模式产生的原因是不同的:重叠的原因是磨损外径发生了变化,交叉的原因是磨损位置小幅度偏移,分离的原因是是磨损位置大偏离.基于套管磨损过程的时间离散化和磨损截面的空间离散化,建立了一种复合模式下套管磨损预测模型.
目前已有许多工程控制方法来降低摩阻磨损,但是其理论基础仍有待于完善.常用的控制方法包括(Aston et al.1998,Schamp et al.2006):井眼轨道优化设计和实钻井眼轨迹精确控制、提高钻井液润滑性、钻具组合优化、安装防磨减扭工具等措施.优化井眼轨道参数,提高实钻井眼轨迹的光滑度,可有效降低钻柱与井壁的接触力和摩阻;利用油基钻井液替换水基钻井液,使用润滑剂、防磨剂、润滑珠等添加剂,可降低井下摩阻系数和磨损系数;在垂直井段和小井斜井段采用高线重钻具以提高有效下入重力,在大斜度井段采用低线重管柱或者漂浮管柱来降低摩阻;防磨减扭工具主要借鉴套管扶正器安放方法来进行安放位置优化设计(Juvkam-Wold &Wu 1992),其原理是通过避免管柱本体与井壁的接触来降低摩阻和磨损.
笔者基于井下管柱局部−整体耦合力学模型,建立了井下减阻工具安放位置和个数的优化设计模型(Sun &Gao 2012,Huang et al.2018c),模型中考虑了减少摩擦阻力、降低阻卡风险等多重目标.计算结果表明,当井眼状况比较好时,建议采用井下减阻工具以降低摩阻;当井眼状况比较差时,不建议采用井下减阻工具以防产生异常的机械阻力,这与现场实践认识相吻合.
目前的管柱摩阻扭矩模型中假定井眼是理想清洁的,无岩屑床存在.然而,定向钻井中岩屑床的存在是难以避免的,尤其在大位移井、长水平段水平钻井中岩屑床问题更加突出.井眼中管柱与岩屑床存在复杂的相互作用,管柱运动会影响岩屑运移,岩屑运移也会影响管柱受力,两者是相互耦合的.现有的摩阻扭矩模型未能考虑管柱与岩屑的相互作用,导致难以揭示岩屑阻卡产生的复杂力学机理.因此,下一步需要将管柱与岩屑看作一个整体,开展两者相互作用的力学机理和风险特征研究.在套管磨损方面,目前套管剩余强度模型主要考虑了单月牙磨损形状,后续应开展复杂磨损形状下套管剩余强度研究.
5 井下管柱安全作业极限预测理论与设计控制方法
随着钻井垂深和水平位移的不断增加,钻完井与油气井工程作业风险不断增大,井下管柱安全作业极限问题俞显突出.井下管柱安全作业极限,是指受地面和井下各种主客观因素约束下管柱可以安全作业的最大井深.开展井下管柱安全作业极限理论研究,揭示限制作业极限的主要因素及其影响规律,可为工程作业风险分析、优化设计及安全控制提供重要科学依据.
图7(a)为全球钻井作业极限的统计数据,大位移井的世界纪录主要集中在英国Wytch Farm、俄国Sakhalin 以及美国墨西哥湾等地区,大位移井的水平位移已超过12 km.国内大位移井记录主要在南海东部,水平位移超过8 km,与世界记录仍有一定的差距(高德利等2019).对于每一口大位移井世界纪录的创造都是当时钻井技术条件和客观约束条件下定向钻井延伸所能够达到的井深极限值,即定向钻井延伸极限.对于任何一口井而言,在特定的主观和客观约束条件下其作业井深都存着一个极限值,也称之为钻井延伸极限.两种关于钻井延伸极限的定义虽然有所差异,但是其内涵是一致的.

图7
2009 年,笔者首次从理论上系统提出了旋转钻井延伸极限的概念(Gao et al.2009),包括三个子概念:裸眼延伸极限、机械延伸极限和水力延伸极限,引领了国内外钻井延伸极限的学术研究.裸眼延伸极限是指裸眼段不发生井眼失稳所能钻达的最大井深,水力延伸极限是指能够保证正常的钻井流体循环和清洁条件下实钻井眼的最大长度,机械延伸极限是指钻井系统在机械性能上可以安全钻达的最大井深.狭义上,井下管柱安全作业极限即为机械延伸极限;广义上,井下管柱安全作业极限是指机械、裸眼和水力延伸极限的综合.本节从广义角度介绍井下管柱安全作业极限的若干研究进展.
国外学者主要通过建立简单模型或者根据钻井经验进行工程作业极限研究.Meertens 和Kloss (1994)针对英国TA-05 大位移井,从井身结构设计等角度开展了钻井风险与作业极限分析;Wu 和 Juvkam-Wold (1995b)开展了垂直和水平井眼中管柱屈曲力学行为研究,认为垂直井眼中管柱轴向压力存在上限值,水平井眼中管柱螺旋屈曲段最大长度为,其中µ为摩阻系数,无因次;rc为井眼的视半径,m;EI为管柱抗弯刚度,N·m2;q为管柱的线重,N/m;并指出螺旋屈曲是限制油管下入极限的首要因素.Gao 和 Miska (2010b)研究了水平井眼中管柱螺旋屈曲力学行为,得到管柱螺旋屈曲段最大长度为,与Wu 和 Juvkam-Wold 的结果有所差异;Rocha 等(2003a,2003b)指出,大位移钻井中地层破裂压力与环空压耗的不同步变化是作业极限存在的重要原因.国内,汪志明和郭晓乐(2008)建立了水力延伸极限的预测模型,闫铁等(2010)建立了机械延伸极限的预测模型,其他学者从地层、钻井装备和水力参数等角度开展了作业极限的研究(Alfsen et al.1995,Rodman &Swietlik 1997,Mason &Judzis 1998,Meader et al.2000,Martins et al.2004,刘维凯 2008,槐庆林和王洪英 2008,任文希等2014).
近些年,笔者基于机械、裸眼和水力延伸极限的定义,综合考虑地面和井下各种工况和约束条件的影响,建立了三类延伸极限的预测模型(李鑫等2016;黄文君 2016;Li et al.2016a,2016b,2016c,2017a,2017b,2019a,2019b;Chen &Gao 2018;李鑫 2018;Huang et al.2018b;Li et al.2020);揭示了旋转钻井延伸极限的整体分布规律,与全球钻井作业极限统计结果基本吻合;揭示了影响钻井延伸极限的主控因素,形成了基于钻井延伸极限的工程设计方法(李鑫和高德利 2017,Huang et al.2018c,Li &Gao 2019,Li et al.2019c,黄文君等2020);基于上述研究成果,构建了钻井延伸极限的理论体系(高德利 2018,高德利等2019),是对常规钻井理论体系的重要发展(图8).上述研究成果在海洋大位移井、陆地页岩气长水平井等复杂油气井工程中获得了良好应用实效.
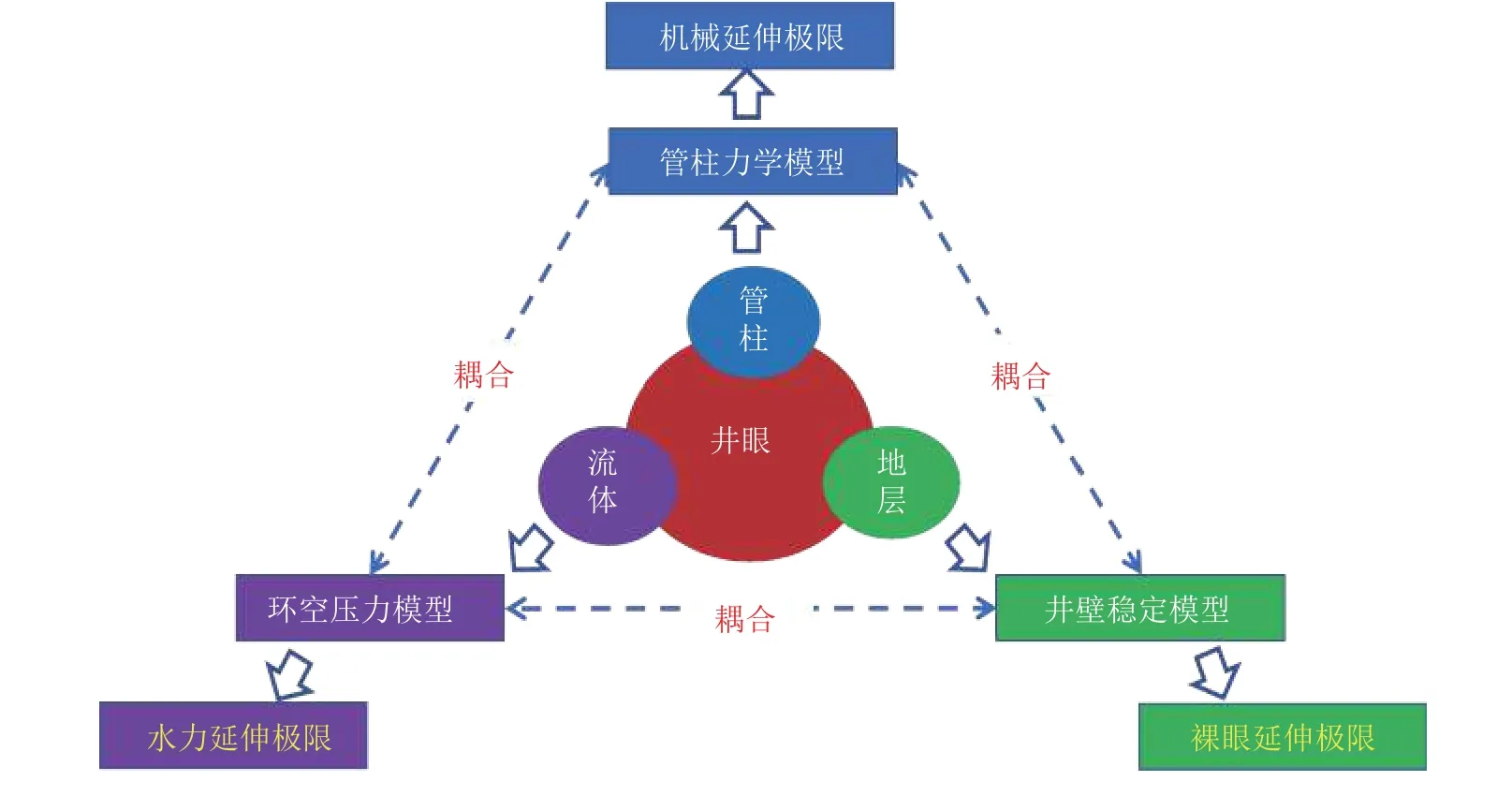
图8
图7(a)和图7(b)的对比结果表明(高德利等2019),理论预测计算延伸极限与实钻统计延伸极限具有相似规律:水平延伸极限随着钻井垂深呈现出“迅速增大−稳定−线性降低”的三段式规律,分别对应浅井、中深井和深井或超深井三种情形.
(1)对于浅井而言,大斜度井眼钻进过程中钻柱容易产生屈曲,钻柱屈曲导致的高摩阻与钻柱有效下入重力小的矛盾是约束定向钻井作业极限的重要原因之一.浅井的垂深变化小,长裸眼段地层压力安全窗口基本不变与环空压耗变化大的矛盾也是限制井眼延伸的重要原因.为了提高定向钻井作业极限,建议采取旋转导向钻井、优化井眼轨道稳斜角、降低摩阻系数、优选钻井液排量等技术措施.
(2)对于深井而言,井眼垂深大导致管柱重力作用显著,管柱重力、阻卡等因素导致的高提拉载荷与地面钻机额定提升能力之间的矛盾是约束钻井作业极限的重要原因之一.深井钻井过程中通常会钻遇多套地层,地层压力系统复杂,复杂地层的窄安全钻井压力窗口与环空压力波动大的矛盾也是限制井眼延伸的重要原因.为了提高作业极限,建议提升钻机性能、优化钻具组合、采用控压钻井等技术措施.
(3)对于中深井而言,水平延伸极限在大斜度井眼稳斜角为atan(1/µ)时达到最大值,其中µ为摩阻系数.目前,创世界记录的大位移井大都为中深井.中深井的水平位移比较大,钻柱旋转产生的高扭矩与地面钻机额定扭矩之间的矛盾是约束定向钻井作业极限的重要原因之一.大斜度段钻进过程中岩屑阻卡等问题突出,井眼清洁所需的高排量与钻井泵额定功率之间的矛盾也是限制井眼延伸的重要因素.为了提高作业极限,建议优化井眼轨道、提高钻机性能、优化钻井参数、采用连续循环系统等技术措施.
常规的钻井设计方法,大致按照井眼轨道设计、井身结构设计、钻具组合设计、钻井参数设计以及其他参数设计的顺序依次进行.常规方法存在两方面的缺点:设计目标中未充分考虑钻井安全作业极限的影响;整体设计简化为多个子设计的串联组合,设计效果难以达到整体最优.笔者以提高井眼延伸极限为目标,建立了钻井优化设计方法,主要包括基于井眼延伸长度约束的钻井液密度和排量窗口设计方法、井下管柱分段优化设计方法等(李鑫和高德利 2017,Huang et al.2018c,Li &Gao 2019,Li et al.2019c,黄文君等2020).最近,笔者基于钻井延伸极限理论,建立了钻井作业风险定量评估方法,该方法可计算一口井每个井眼尺寸下每种作业工况的安全系数(图9),识别出最危险作业工况以及主要限制因素,再进行针对性的优化设计,然后不断重复上述过程.该方法针对作业安全的最短板进行参数优化,子设计的顺序根据当前最危险的作业工况和影响因素动态调整,使得整口井的作业安全系数不断提升,得到更加优化的工程设计结果,可有效克服常规工程设计中的一些不足.

图9
在钻进过程中,钻井参数不断变化,管柱作业风险也随之动态变化.目前,主要采用数据法进行作业风险的实时预测(廖明燕 2007a,2007b),其主要思路为:实时测量和处理数据,利用数据挖掘、机器学习等算法进行分析,进而实现钻井状态监测和异常情况诊断.该方法的主要缺点是:需要大量的现场数据进行训练,无法实现钻井大进尺作业的风险预测.由于钻井过程中测量数据种类少、质量较差,尤其对于新钻井区块而言,钻井数据不足,导致数据法的预测精度难以达到要求.模型法,即基于钻井延伸极限的风险评估法,可有效克服数据法的不足,但需要利用实测数据对模型中关键参数进行动态修正.因此,下一步需要将数据法和模型法相互结合,取长补短,形成一套更加准确和稳定的钻井风险动态评估方法.
6 底部钻具组合的力学特性分析与设计控制方法
普通的底部钻具组合(BHA)主要由钻头(drill bit)、钻铤(drill collar)、稳定器(stabilizer)等结构单元组成,可以看作是一个多跨连续的纵横弯曲梁柱,在钻具重力、井眼约束、钻头破碎岩石及钻井流体压力等作用下,BHA 会产生复杂的力学行为.底部钻具组合力学特性包括静力学特性和动力学特性两部分,静力学研究钻头的侧向力和偏转角以及管柱受力、变形状态等,主要用于指导井眼轨迹预测和控制;动力学研究BHA 纵向振动、横向振动、扭转振动、涡动以及耦合振动等特性,目前主要用于钻柱(钻具)失效分析与控制、疲劳寿命预测等,也涉及井眼轨迹控制问题.
底部钻具组合静力学研究发展至今约有70 年,其理论体系已比较成熟,且在工程中获得广泛应用.1953 年,Lubinski 和 Woods (1953,1955)首次提出了上切点的概念和“钟摆防斜”理论,上切点以上的钻具躺井眼的底边,上切点下部的钻具为底部钻具组合,建立了底部钻具组合的二维力学模型并初步考虑了地层各向异性的影响,为井眼轨迹控制奠定了一个理论基础.Walker(1973)基于最小势能原理进行了底部钻具组合力学特性分析,并提出了钻头倾角的概念,即为钻头处钻具变形曲线的切线与井眼轴线的夹角,现在多被用于评价导向工具的造斜率.Bradley(1975)利用有限差分方法开展了底部钻具组合力学特性分析,认为钻进方向与钻头机械合力方向一致.Ho (1986)推导了底部钻具组合大挠度控制方程,并采用有限差分法进行求解.随后,他(Ho 1987)提出一种钻头与地层相互作用矢量模型,建立了定向钻进方向的预测方程.Williamson 和 Lubinski (1987)、Birades 和 Gazaniol (1989)采用有限元方法,计算了底部钻具组合的造斜率和扭方位率,分析了BHA 弯接头对井眼轨迹控制能力的影响规律.
国内,白家祉和苏义脑(1990)利用纵横弯曲梁法开展了底部钻具组合力学特性分析与井眼轨迹预测,在分析中以稳定器、BHA 与井壁接触点为关键节点,令关键节点处的内弯矩为未知量,建立了纵横弯曲方程组并进行求解;之后,该方法扩展应用到带弯接头的底部钻具组合和弯外壳钻具组合.刘巨保等(1997,2002)利用间隙元法开展了底部钻具组合力学特性分析等.其他学者围绕底部组合力学特性和井眼轨迹控制问题,开展了大量工程应用工作(柏景海等1994,Min et al.2006,唐波等2008,曹向峰等2013).
前期,笔者从井下管柱的变形控制方程出发推导了底部钻具组合的变形控制方程,利用加权余量法研究了底部钻具组合小挠度和大挠度变形问题(刘希圣等1988;高德利和徐秉业 1992,1995);定义了钻头各向异性指数和地层各向异性指数,建立了钻头与正交各向异性地层相互作用模型,提出了有效钻力的新概念和正交各向异性钻井理论(高德利和刘希圣 1989,1990a,1990b;高德利等1989;高德利 1993,1994),建立了一个井眼轨迹预测与控制理论体系(高德利等1994;高德利 1995a,1996).
在底部钻具组合力学特性分析中,稳定器可能会与井壁接触,也可能不接触(图10),如何快速和稳定地计算稳定器与井壁的接触状态以及在井眼中的位置,一直是个难题.近些年,笔者基于稳定器处连续条件,修正了井壁对稳定器支撑反力大小与方向的计算方法,形成了一种稳定器在井眼内空间位置的计算方法,并对上切点位置的确定方法进行了修正,提高了模型的计算效率和精度(郭宗禄等2014,2019).最近,笔者将底部钻具组合力学特性分析方法扩展应用于推靠式旋转导向钻具组合的力学分析研究,提出了一套基于零侧向钻速准则的旋转导向工具造斜率预测方法,并获现场试验验证.
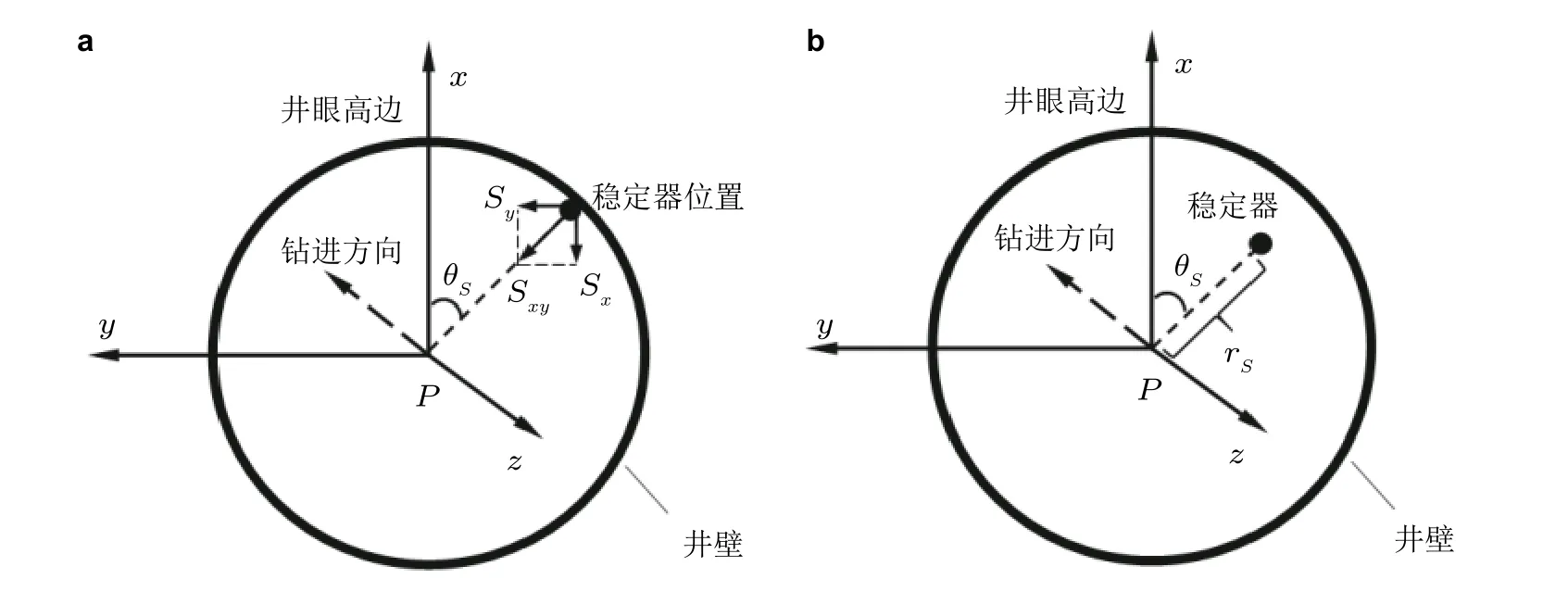
图10
底部钻具组合动力学研究也比较早,许多学者做了大量研究.Millheim 和 Apostal (1981)利用有限元法分析了底部钻具组合的动力学特性以及对定向钻进轨迹的影响.研究结果表明,底部钻具组合包括四种运动状态:低转速稳定态,中转速非稳态,高转速非稳态和高转速稳定态,转速、钻具与井眼间隙等因素与定向钻进轨迹密切相关.Jansen (1991,1992)应用转子动力学理论对钻铤涡动问题开展研究,结果表明:钻铤的运动模式包括正向涡动、反向涡动、周期运动和混沌,其运动规律与某些不确定因素包括稳定器与井眼的间隙、钻铤质量偏心等密切相关.Apostal 等(1990)利用有限元法研究了阻尼作用下钻柱受迫振动问题,求解了底部钻具组合的固有振动频率,揭示了不同振动模式对应的钻柱失效形式.Dunayevsky 等 (1993)研究了钻压波动引发钻柱横向振动问题,建立了钻柱稳定性的判断图版,结果表明:即使钻压很小,当钻柱转速和钻压波动幅度处于非稳定区域时,钻柱将产生横向振动.
国内,管志川等(2003,2013)开展了底部钻具组合的动力学实验研究.结果表明,随着转速的增加,钻具运动模式逐渐由规则摆动转变为规则反向涡动与无规则摆动;随着钻压的增大,逐渐由规则摆动向规则涡动和无规则摆动转变.狄勤丰研究了预弯曲钻具的涡动规律,并利用平衡侧向力法进行了井眼轨迹预测(Di et al.2007,狄勤丰等2010,Zhang et al.2017).国内外很多学者在底部钻具组合动力学方面做了不少工作(署恒木等1990,Melakhessou et al.2003,祝效华等2007,Nandakumar &Wiercigroch 2013,Ghasemloonia et al.2014),此处不再赘述.
笔者研究了底部钻具组合的涡动特性(高德利等1996;高宝奎等1997),建立了基于最小耗损能量的涡动速度判断准则,揭示了钻具涡动的力学机理以及钻具转速、钻具与井眼间隙等因素对涡动方向和大小的影响规律.研究指出,反向涡动导致钻具上产生高频交变应力,容易引发疲劳失效;正向涡动易导致钻具偏磨;无涡动易导致套管偏磨.突破了传统静力学防斜打直理论的限制,提出了基于BHA 涡动的动力学防斜理论(高德利等1995,高德利 2005):大钻压条件下钻具进入屈曲和涡动状态,可同时实现井斜控制和钻井提速的双重目标.近年来,笔者开展了底部钻具组合纵、横、扭耦合振动研究(刘永升等2017,Liu &Gao 2017,Liu et al.2018,刘永升2019),考虑了钻具与井壁的碰摩作用、钻头与地层相互作用等因素的影响,建立了井下钻具稳定性的预测图版.部分学者尝试利用机器学习的方法开展BHA振动和疲劳失效的研究(Christine &Jerome 2018,Prince et al.2019),但是该方法难以揭示BHA 振动的力学机理,其有效性仍有待验证.笔者建议BHA 动力学的研究宜有针对性,要针对特定的定向钻井模式和作业工况,厘清影响BHA 力学行为的主要因素和次要因素,建立合理的确定方法,并通过室内实验和现场应用进行验证.
7 总结与展望
井下管柱力学已经形成了比较成熟的理论体系,为油气井工程优化设计和安全控制提供了重要的理论依据,但这并不表示井下管柱力学的发展变得缓慢甚至停滞.随着油气资源勘探开发向着“非常规、深层、深水、极地”等复杂领域进军,钻完井与油气井工程面临的客观条件更加复杂,对井下管柱力学提出了新的挑战,也提供了新的研究任务.同时,井下测量技术和数据分析方法的不断进步也为管柱力学研究发展提供了新动力.通过综述井下管柱力学的研究进展,笔者认为今后应在以下几个方面加强研究:
(1)突破原有模型的假设局限性,建立更加精确的力学模型.所有的井下管柱力学模型都是基于一定假设条件下建立的,引入假设条件可简化问题的求解,但同时会导致计算结果与真实情况存在差距.因此,需要在原有井下管柱力学研究基础上,解除某些假设条件的约束,例如从井下管柱的静力学屈曲扩展到动力学屈曲,建立更加接近真实情况的井下管柱屈曲力学模型.
(2)引入非管柱因素的影响,开展多因素耦合力学模型研究.目前,井下管柱力学的研究对象主要是管柱本身,将影响管柱力学行为的其他因素当作已知条件或忽略之.然而,在实际的钻井过程中,井眼中的管柱、流体、岩屑、井壁等因素之间存在复杂的相互作用.例如,岩屑会影响钻柱受力,钻柱运动反过来影响岩屑运移,两者之间的作用是相互耦合的,单方面研究难以揭示岩屑阻卡的复杂力学机理.因此,需要综合考虑与钻柱密切相关的诸多因素,建立包括钻柱在内的多因素耦合力学模型.
(3)井下管柱力学与数据方法相结合,实现数据驱动和模型驱动的优势互补.受制于目前井下力学测量技术水平的约束,井下管柱力学测量数据类型少、质量差,导致大数据、人工智能等计算方法的适用性差,需要借助力学模型的结果进行数据的补充和修正.井下管柱力学模型可以克服数据法的缺点,但力学模型与真实情况总是有差别的,且难以确定模型中的某些重要参数,需要利用数据法进行补充.因此,将数据法和模型法结合起来开展研究,以实现井下管柱力学研究的双驱动目标.
(4)加强与工程实践相结合,不断完善井下管柱力学与控制理论体系.长期以来,钻完井与油气井工程对井下管柱力学不断提出新的问题和挑战,从而推动了井下管柱力学与控制方法的创新研究与发展;同时,井下管柱力学与控制方法的研究成果也在不断改变着工程设计控制理念与技术.钻完井与油气井工程实践中遇到的每一个复杂问题,都有可能成为井下管柱力学与控制理论体系的新增长点.因此,要紧密结合工程实践开展研究,不断完善井下管柱力学与控制理论体系,以促进相关工程技术创新发展.
致 谢国家自然科学基金 (51821092,U1762214,51904317) 资助项目.
