深井提升动力学研究

何满潮

中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室,北京 100083

1 引言

随着浅部煤炭资源的日益枯竭,矿物资源开采朝着深部化和大型化方向发展.我国新建和改扩建的大型立井年生产能力已达1000 万吨,开采最大深度已达1500 m (何满潮 2021).在其他国家,如南非金矿,其矿井的深度已达地表下4800 m 以上.《国家“十二五”科学和技术发展规划》提出加强对三深(深海、深地、深空)的研究.在《国土资源部“十三五”科技创新发展规划》中明确提出“2020 年形成至2000 米矿产资源开采”的战略目标.作为深部资源开发技术体系的重要组成部分,深井提升技术能力直接影响到我国深部资源开发战略的顺利实施.为此,在国务院发布的《国家中长期科学和技术发展规划纲要(2006−2020 年)》提出,“重点研究开发煤炭高效开采技术及配套装备”;在《装备制造业调整和振兴规划》中提出要“大力发展新型采掘、提升、洗选设备”.在国内,根据工作原理和结构的不同,速度较低的单滚筒缠绕提升系统使用在施工立井;速度较高的双滚筒单绳缠绕与摩擦提升系统广泛运用在永久立井(如图1所示).

图1

然而对于上述传统的提升方式,提升加速度随着提升速度和高度的增大而增大,易诱发平衡尾绳大摆动、频繁碰摩,其提升效率、安全性等迅速下降而不适用于超深井高速提升.比如:提升深度千米级的辽宁沈阳大强煤矿,其平衡尾绳在运行过程中呈现大摆动状态;提升深度达1500 m的云南会泽铅锌矿,同样在运行过程中易诱发平衡尾绳大摆动.在矿井提升运输过程中,卡罐、打滑松绳、过卷过放等事故经常见诸报道.为了解决提升系统的安全问题,朱真才及其科研团队(朱真才 2000,2003,朱真才等2007,2020,曹国华 2009,曹国华等2007,2009a,2009b,2010,Wang L et al.2018,2019,2020,Cao et al.2015,2017,2018,蔡翔等2018,Wang Y D et al.2014,2018,Yang et al.2019,杨盼盼 2020,Zhang et al.2021,Wang N G et al.2018,2020a,2020b,2021,王进杰2016,王乃格 2019,王磊 2021,王彦栋 2018)构建了立井过卷过放、制动、装卸载、变长度提升钢丝绳、尾绳摆动和张力控制等比较全面的提升系统动力学理论模型以及立体化的安全保护与监测系统,为矿山超深立井提升系统的设计与安全运行提供了重要支撑.李玉谨(2003),李玉瑾等(2012,2014a,2014b,2015a,2015b,2016),李楠等(2015),霍磊等(2015)针对提升装置过卷、卡罐、松绳以及跑车等工况,建立了相应的动力学模型,对事故进行了分析研究,优化了相应过卷缓冲装置的制动性能,并给出了合理的建议;梁敏等(2015),吴娟等(2015,2016),Huang 等 (2020)对立井提升系统的提升绳的垂绳进行了动力学行为的研究,并给出了矿井柔性提升系统极限减速度的计算方法;Jiang 等 (2014),Ma 等 (2016),Yao 等 (2017),Wang G Y 等 (2019)研究了定弦绳和变长垂直提升钢丝绳在由天轮波动引起的周期性外界激励作用下的动力学行为,并研究了弦绳的多源耦合振动特性;Wang 等 (2015,2016),Zhang 等 (2017),Guo 等 (2018)研究了深井提升钢丝绳内部螺旋部件的微动态扭转特性和磨损特性,并研究了钢丝绳在提升过程中与摩擦衬垫的接触摩擦磨损特性,建立了摩擦系数与滑移速度和钢丝绳张力的关系,并使用多体动力学商业软件进行了验证.Kaczmarczyk 等 (1997,2003a,2003b),Arrasate 等 (2014),Crespo 等 (2018)观测了矿井提升过程中提升绳的横纵耦合振动响应特征,并研究了固定式高层电梯系统的建模与仿真,以预测其部件之间的动态相互作用.Ren 等 (2013),Zhu 等 (2013)考虑了提升容器的转动特性,给出了双绳提升系统的横纵耦合振动响应特征.为了对绳索进行建模离散求解,通过假设模态法(Zhu et al.2013)和有限元法等用于离散连续体的方法来求解系统方程.基于能量法,通过第一类拉格朗日方程(Zhu et al.2013,Dvorak et al.2005)或者哈密顿原理来推导连续体的离散能量方程以此得到方程的广义质量、广义刚度、广义阻尼和广义力.Terumichi 等 (1997)基于绝对节点坐标法进行建模,通过变尺度有限元法研究了恒提升速度下提升容器的提升绳的非平稳振动,分析结果表明,柔索的纵向速度通过共振影响振动的峰值振幅.

随着提升深度和载重的增大,平衡尾绳自由悬挂下的立井提升系统的大振动、大摆动等现象逐渐显现.为了揭示自由悬挂柔性绳索类的动力学行为,很多学者考虑通过能够描述大变形、大摆动的绝对节点坐标法对其进行建模描述.Escalona 等 (1998),Berzeri 等 (2000),Shabana 等(2001),Yakoub 等 (2001)基于有限元方法和连续介质力学理论,提出了绝对节点坐标公式(ANCF),并将其应用于二维悬臂梁的动力学建模和数值求解;Zemljaric 等 (2019)提出了利用预计算矩阵和高斯积分相结合的ANCF 内单元广义弹性力模型,以节省运动方程时间数值积分的计算时间.

现有的多绳摩擦提升方式,能够满足浅井的要求,但当提升深度增大,尾绳晃动幅度大,其安全可靠性降低;若深度进一步增大到1800 m 时,其提升能力非常小.现有的摩擦提升方式,其尾绳是摩擦轮式提升机在左右罐笼下部连接的平衡钢丝绳,它在运行时自由下垂,起平衡和稳定罐笼的作用.尾绳的总重量和首绳总重量基本相等,尾绳在运行时不承受其他外力作用,只承受自由下垂重力和自身运行时所产生的旋转、摆动等自身应力作用,这就要求尾绳要有很好的柔韧性抗疲劳性,要求运动时避免旋转消除应力.为避免尾绳在井底回转位置出现相互缠绕,一般在井底设有金属分绳挡梁.除了锈蚀,尾绳在高速运行中由于自身摆动易与分绳挡梁、井内其他设施以及尾绳之间发生碰撞、刮磨以及绞绳现象,长期磨损将导致尾绳断丝断股.

目前,虽然国内外均致力于超深井大型提升系统的高提升能力、高运行速度和高运行安全性的技术突破,在现有的提升系统上进行了初步尝试,但一直无法改变传统多绳摩擦提升系统在超深井、高速度、强时变等特点下自由悬挂平衡尾绳大摆动等问题.2016 年,启动了国家重点研发计划项目“煤矿深井建设与提升基础理论及关键技术”的研究.本项目针对其中的深井提升面临长距离、高速度、重载荷等挑战,以建立1000～ 1500 m 及至2000 m 深部提升基础理论体系,突破高速度提升关键技术为目标,研发深井高速提升成套装备,以铁法煤业集团大强煤矿主井为现场示范矿井,开展深立井预应力调节的多绳摩擦SAP 提升系统的创新应用研究,为建立具有我国自主知识产权的深立井提升系统及装备提供示范,为千米深井筒安全高效运行提供技术保障.下面将围绕国家重点研发计划项目“煤矿深井建设与提升基础理论及关键技术”的提升方面的研究团队的最新研究动态,详述有关深部提升动力学研究方向的最新创新性成果.

2 单元数量自动调整的自由悬挂平衡尾绳提升系统动力学

对于煤矿建立1000～ 1500 m 及至2000 m 的深部建井工程,其松弛状态的尾绳在运动过程中表现出较大的振动变形以及较大的摆动位移的现象,因此基于重大研发项目进行了自由悬挂平衡尾绳的建模与动力学分析,拟揭示自由悬挂平衡尾绳在提升运动过程中的大变形力学特性.

2.1 平衡尾绳的动力学方程

为了揭示自由悬挂平衡尾绳大摆动现象,将传统多绳摩擦提升系统模型简化(如图2所示).

图2

使用绝对节点坐标法得到了平衡尾绳的能量表达式

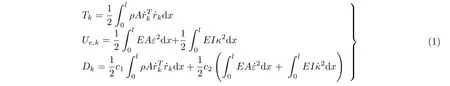
式中,Tk,Ue,k,Dk分别为平衡尾绳单元的动能、弹性势能和耗散能,ρ为钢丝绳密度,r˙k为二维梁单元中心轴上任意一点P的整体位置向量rk对时间t的一阶导数,ek为任意单元节点坐标向量.

任意单元节点坐标向量ek表达式

式中,c1为质量阻尼系数,c2为刚度阻尼系数.ε为纵向变形,E为杨氏模量,A为截面面积,I为截面惯性矩,κ为单元中心轴线的曲率

由式(1)所表示的单元能量以及拉格朗日方程可得自由悬挂尾绳大摆动的动力学方程

式中,Φ=0为约束方程,λ为拉格朗日乘子,Φe为约束方程对坐标的一阶偏导数.若平衡绳的左上端与右上端均选择为固定约束,则约束方程为,具体各项为

式中,θ0和θN表示第一个节点与左容器所形成的夹角以及最后一个节点与右容器所形成的夹角,x0,y0,xN和yN表示第一个节点以及最后一个节点的横坐标和纵坐标.

式(5)中,Fe为平衡绳整体所受到的广义外力项,M为平衡绳整体的质量矩阵,Q(e)为平衡绳的总弹性力矩阵,C(e)为阻尼矩阵.针对式(5),采用广义α 法对数值求解.

2.2 平衡尾绳的单元变换

由于平衡尾绳总是处于U 字形弯曲状态,在单元数量较少时,弯曲段等效单元刚度值较大,无法真实地等效计算出所处节点单元的应力与应变,从而产生伪高频位移响应,容易发散,得不到准确的计算结果.单元长度较小时,所需要的单元数量和自由度数量就会大幅增加,计算量较大,MATLAB 数值计算速率较慢.因此为了快速求解得到平衡尾绳的动力学响应,建立了一种五段式非等长单元数量自动调整的划分方法(5 part non-equal-length,5P-NEL)−中间大弯曲部分段(Part Ⅲ)和两侧直线(Part Ⅰ和Part Ⅴ),以及与之衔接的中部过渡段(Part Ⅱ和Part Ⅳ),如图2(c)所示.中间大弯曲部分段(Part Ⅲ)内含有平衡尾绳弯曲形成的低环,平衡尾绳的横向振动位移较大,弯曲应力较大,故此段内的单元长度应小一些,使得平衡尾绳最低环处显示出较柔软的状态,保证单元等效弯曲应力逼近真实单元应力,防止产生伪高频位移响应,导致结果发散,得不到准确的计算结果.两侧直线段(Part Ⅰ和Part Ⅴ)由于不靠近平衡尾绳最低环,平衡尾绳的横向振动位移较小,单元弯曲应力较小,因此在这两段上,单元长度可以稍大一些,减少单元数量.因此在五段上依次顺序分别划分等长单元lt1,lt2,lt3,lt4,lt5.

当平衡尾绳左端上升的高度距离为lt1(lt1为第一段的单元的长度)时,需要进行一次单元变换,如图3所示.经过单元变换后,左侧第一段的单元数量增加一个,右侧第五段的单元数量减少一个,其余段的单元数量不变,单元变换前后尾绳的总体单元数量保持不变.平衡尾绳节点单元转换流程图如图4所示.

图3

图4

单元变换后的质量、阻尼、弹性力矩阵变为

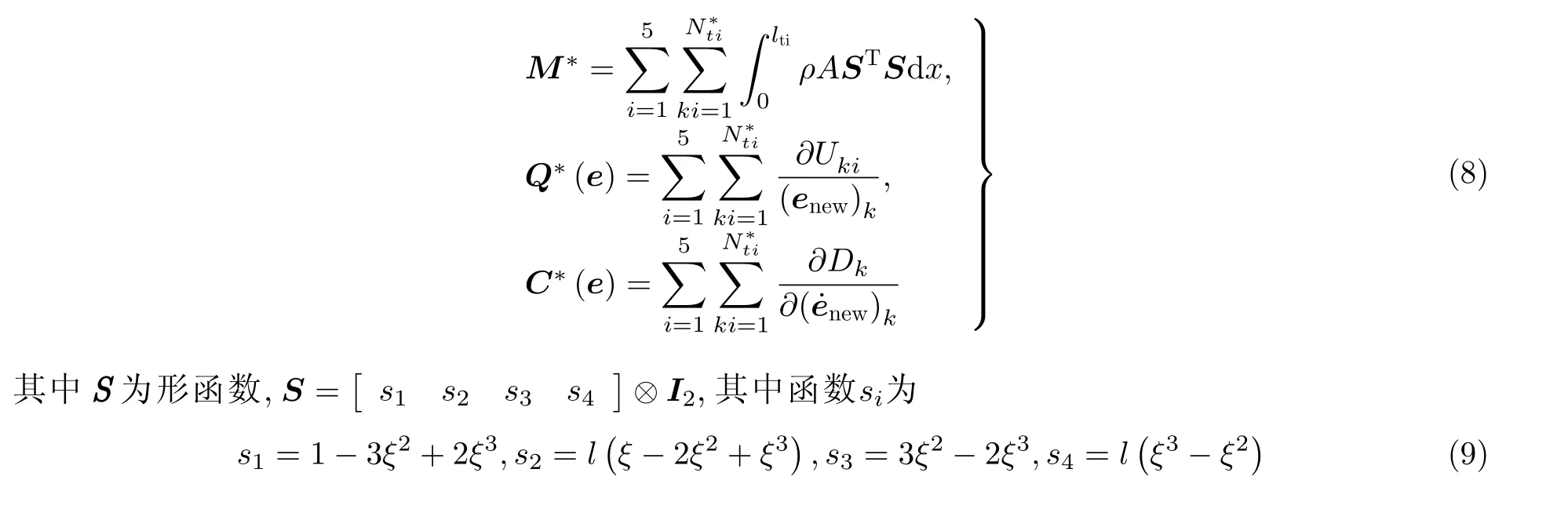
2.3 平衡尾绳的振动特性

参数:匀质平衡尾绳线密度ρ=18.67 kg/m,杨氏模量E=100 GPa,平衡尾绳横截面积A=0.003 m2,两个容器的中心间距D=2.25 m,尾环的长度Lh=44 m;尾绳运行长度Lm=966 m,弯曲刚度EI=145.066 N·m2,运行加速度为0.73 m/s2,运行速度为8 m/s.

平衡尾绳使用五段式非等长单元划分方法进行单元划分,一共划分了577 个单元,而使用等长单元划分方法将会产生5050 个单元,单元数减少88.57%,极大地提高了求解计算效率.

单元转换产生的动能能量的相对误差率如图5所示.从图5可以看出,每一次单元转换后由于速度改变所产生的动能能量的相对误差率均小于0.000 003%,因此由于单元变换产生动能能量误差可以忽略.又因为平衡尾绳所受的重力为常值,因此单元变化对平衡尾绳所受的重力无影响,因此5P-NEL 划分单元方法是可行的.

图5

左右两侧平衡尾绳距离容器中心线最大摆动位移如图6所示,左侧最大摆动位移在0.52 m左右,右侧的最大摆动位移在0.45 m 左右.

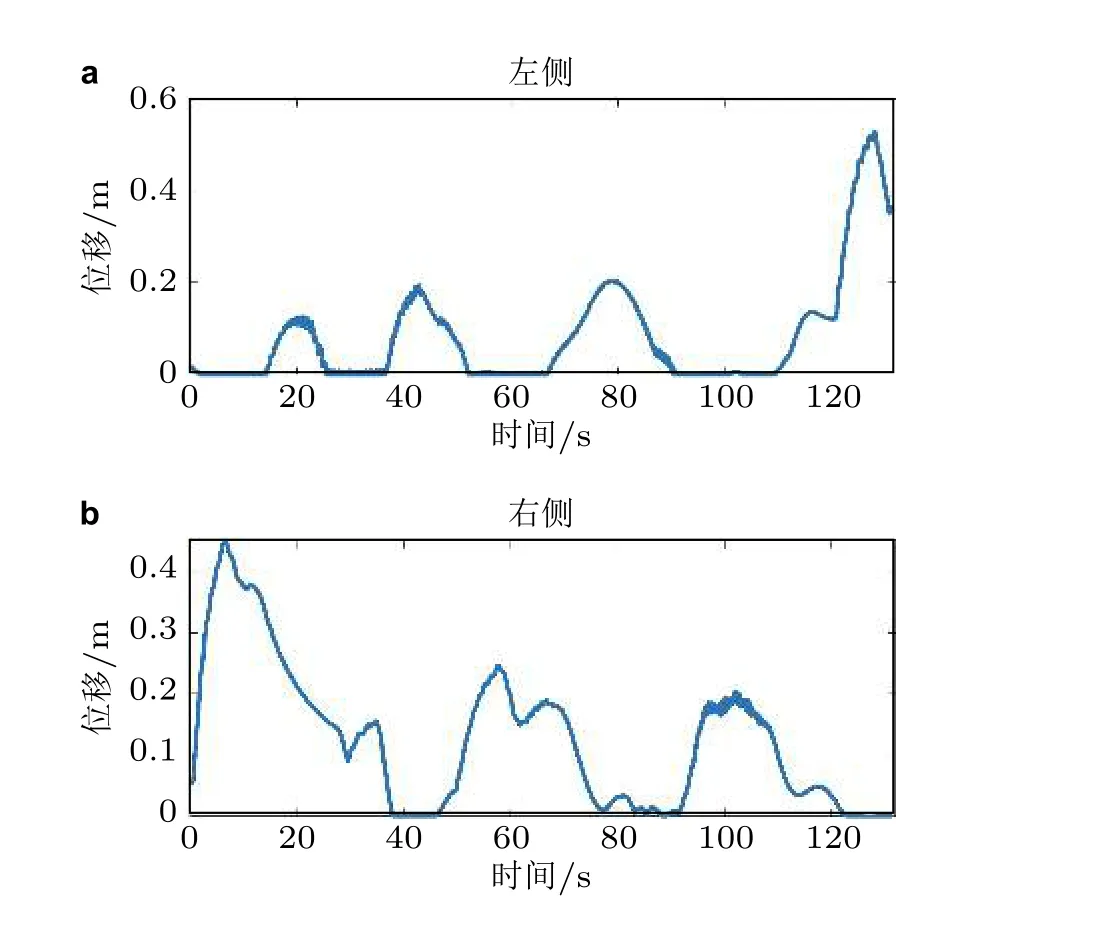
图6

3 平衡尾绳自适应导向下的提升系统动力学

为解决平衡尾绳自由悬挂下摆动幅度大的问题,首先,构建了预应力自适应的平衡尾绳导向下的提升系统(简称SAP 系统),通过建立SAP 系统提升绳−容器−尾绳−调节轮多元耦合动力学模型,揭示SAP 系统的摆动特征,其SAP 提升系统动力学模型如图7所示,其中,除了传统的摩擦提升系统中滚筒带动提升绳运动进而带动提升容器运动的提升方式外,在平衡尾绳6 的底部,增加了调节轮作为导向轮,用于约束底部的尾绳环的运动进而约束尾绳的摆动,调节轮靠自身的重力随动张紧尾绳,起到控制尾绳横向摆动的目的,这里,称之为尾绳摆动自适应抑制系统(SAP系统).

图7

3.1 SAP系统提升绳−容器−尾绳−调节轮多元耦合时变动力学模型构建

基于上述的物理模型,设提升绳和尾绳任意界面的位移场可表示为

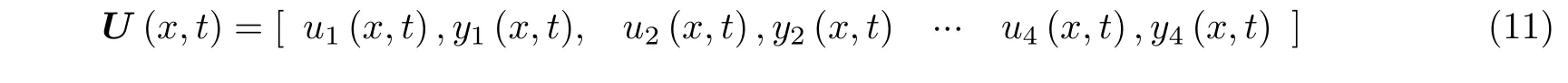
式中,ui为提升绳的纵向振动,yi为提升绳平面内的横向振动.

提升容器和张紧轮的位移场可以表示为

目前锂电池的充电方法很多[7-10],如传统的恒流恒压充电方法、传统的三段式充电法、以及传统的五阶恒流充电方法等,但这些方法具有充电速度慢、充电效率低以及极化现象导致温升过高等缺点[11-13]。

提升钢丝绳任意界面的速度可表示为

将悬吊柔索在t时刻的长度记作Li(t),对应的柔索卷放速度和加速度分别记作vi(t)和ai(t);对于柔索i,将其在点Ai处纵向方向的位移激励表示为(t),在横向方向的位移激励分别表示为(t);将悬吊柔索i在x处、在t时刻的纵向振动位移分别表示为ui(xi,t),横向振动位移分别表示为yi(xi,t).由于柔索横向振动远小于柔索的长度,因此柔索i的真实长度可近似表示为

提升系统尾绳通过尾部调节轮独立进行张紧,调节轮与地面通过张紧弹簧以及阻尼缸连接实现振动控制被动控制的目的,系统的动能,势能和耗散能为

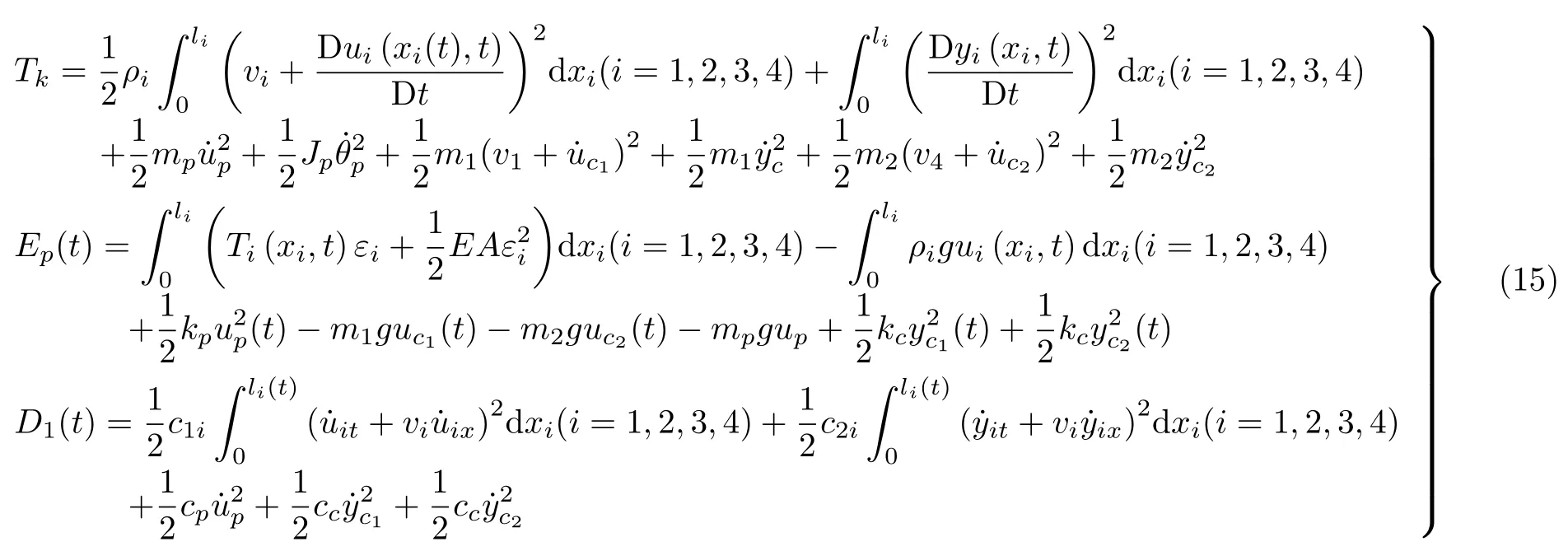
式中,A表示绳子的横截面积,g表示张力加速度,c1i和c2i分别代表提升绳和尾绳的阻尼系数,下标x,t分别表示变量对x,t的偏导,加上点的变量表示对时间t求导;ρi(i=1,2,3,4)是绳子的线密度;vi(i=1,2,3,4)是提升速度;Ti(x,t)(i=1,2,3,4)是提升绳张力和尾绳张力;εi(i=1,2,3,4)是钢丝绳的正应变.这里,.

提升绳和尾绳任意位置的张力公式如下

εi(i=1,2,3,4)可以表示为,采用Galerkin 方法将无限维的偏微分方程转化为有限维的常微分方程,然后再通过数值方法对常微分方程进行求解.为方便分析,首先定义一个新的变量对原变量x进行归一化处理,将相对于x的时变域[0,l(t)]转化为相对于ξ 的固定域[0,1].Galerkin 方法的具体思想可简单描述为:用有限个单自由度三角信号的叠加来模拟所期望获得的无限自由度信号.振动位移采用伽辽金法离散,定义相应的广义位移.

根据链式求导法则,可以得到时间t和空间x的偏导数

基于绳索的连续特性,可以采用假定模态法(AMM)来近似计算绳索的动态位移坐标,尾绳的横向和纵向位移假设如下

这里,N1和N2分别为提升绳和尾绳纵向位移和横向位移的包含离散顺序.qui,j(t)和qyi,j(t)是系统的广义坐标.ψi,j(ξi)和φi,j(ξi)对应的试函数满足系统的齐次边界条件和约束方程,试函数的选择如下

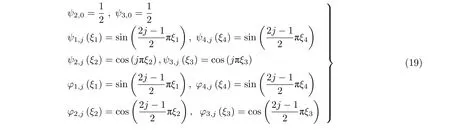
代入第一类拉格朗日方程,通过推导,得到系统的动力学方程

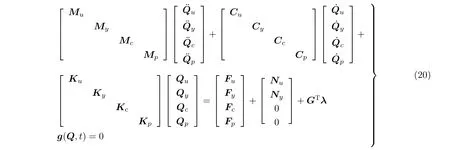
其中Mu(My,Mc,Mp),Cu(Cy,Cc,Cp),Ku(Ky,Kc,Kp)和Fu(Fy,Fc,Fp)分别表示绳索纵向(横向),提升容器纵向(横向)和调节轮对应的广义质量,广义阻尼,广义刚度和广义力.G为约束方程的雅可比矩阵,λ为拉格朗日乘子.Qu(Qy,Qc,Qp)分别表示绳索纵向(横向),提升容器纵向(横向)和调节轮对应的广义坐标.g(Q,t)表示SAP 系统的约束条件,Nu和Ny表示系统的广义坐标耦合矩阵.系统的矩阵和力向量定义如下

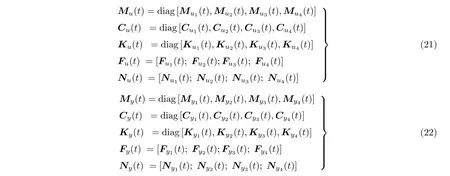
矩阵中元素的具体表达形式Mui,Myi,Cui,Cyi,Kui,Kyi,Fui,Fyi,Nui和Nyi定义如下

由此构建了尾绳自适应摆动抑制系统作用下的SAP 提升系统动力学模型,并采用广义α 算法实现该微分代数方程的求解.

3.2 SAP系统动力学特征

张紧牵引系统(蓝线)与传统(红线)牵引系统纵向固有频率比较如图8所示,传统牵引系统的纵向固有频率远高于张力牵引系统.从图9可以看到,底部张紧轮质量的大小,对于系统纵向振动的振幅以及频率等振动特性无影响,故张紧轮的质量无需太大.

图8

图9

图10显示了不同的导轨导向等效阻尼作用下底部张紧导向轮的纵向响应的时频特性.可以看出,能量集中点主要集中在A 区和C 区.A 区是由于钢丝绳较长,运行加速度突变引起的振幅增大,振动频率约为0.6～ 0.7 Hz.C 区振幅和频率的增大是由于系统共振引起的,振动频率约为1～ 1.1 Hz.在同一频率激励下,共振区的振动频率约为非共振区的2 倍.

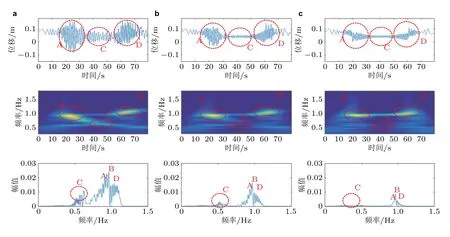
图10

比较可以看出,由于导轨导向等效阻尼的增大,C 区的振幅基本上完全消散.虽然A 区的能量也在耗散,但其耗散速度不如A 区块,在增大阻尼的过程中,以B 点为代表的激励频率逐渐突出,其频率幅值所占的比例逐渐增大.

图11显示了双向张拉牵引系统纵向振动最大振幅随时间的变化.结果表明,随着导轨导向等效阻尼的增大,系统纵向振动的最大振幅减小.特别是在共振C 时,由于导轨导向等效阻尼效应,系统的共振幅度大大减小,甚至消除了共振.

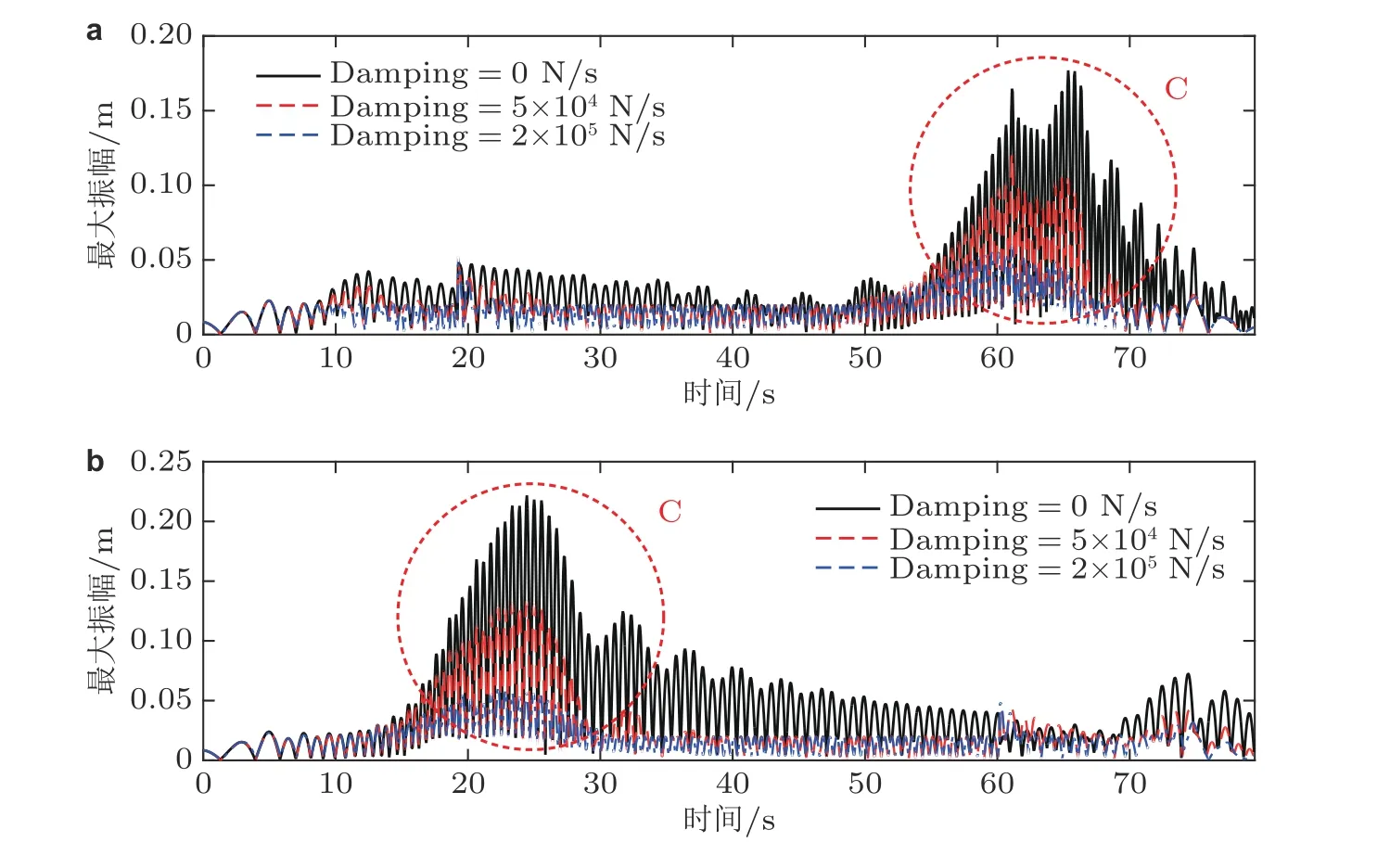
图11

4 平衡尾绳自适应导向下的提升系统非光滑动力学

4.1 SAP系统提升绳−容器−尾绳−调节轮多元耦合非光滑动力学模型

为了抑制尾绳的横向摆动,避免尾绳的相互摩擦与碰撞,提出了在底部尾绳环处增加张紧轮以抑制尾绳摆动的策略,构建了尾绳摆动自适应张紧抑制机构,但是,由于尾绳和底部的调节轮之间接触是单向接触,当由于外界激励幅值或者频率过大以及紧急制动等恶劣工况下系统易发生调节轮与尾绳分离的非光滑动力学行为,导致尾绳张力置零以及绳轮分离等失稳现象,为此构建了非光滑动力学模型以分析系统产生非光滑动力学行为的极限工况,示意图如图12所示.

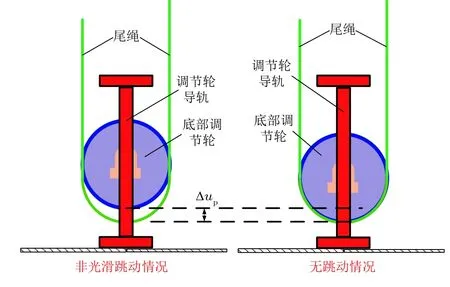
图12

将尾绳和张紧轮之间的纵向约束关系与尾绳底部张力表示成如下的互补关系

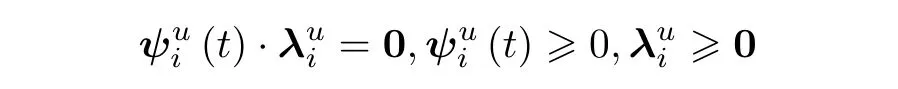
尾绳和张紧轮之间的纵向约束关系称之为单边约束.在容器处的边界条件为双边约束条件,此处考虑系统的双边约束ψb和单边约束ψu分别为

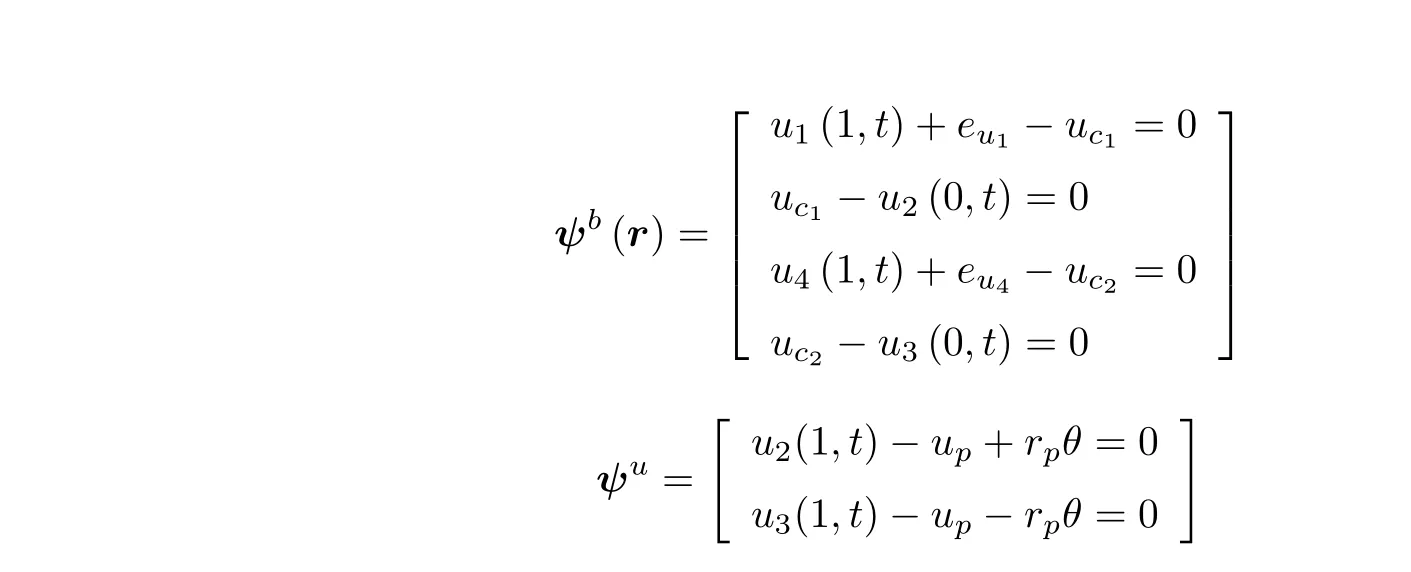
同样根据带约束的拉格朗日方程,可以得到非光滑动力学的微分代数方程组

Mui,Cui,Kui和Fui具体的表达式如下所示

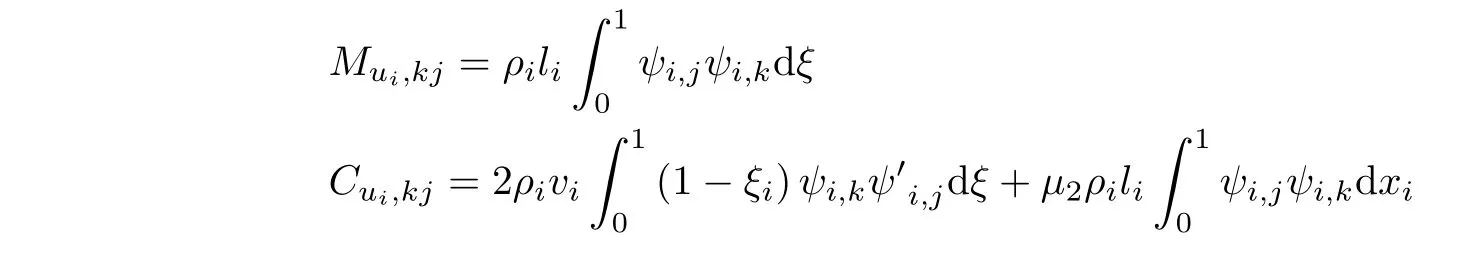
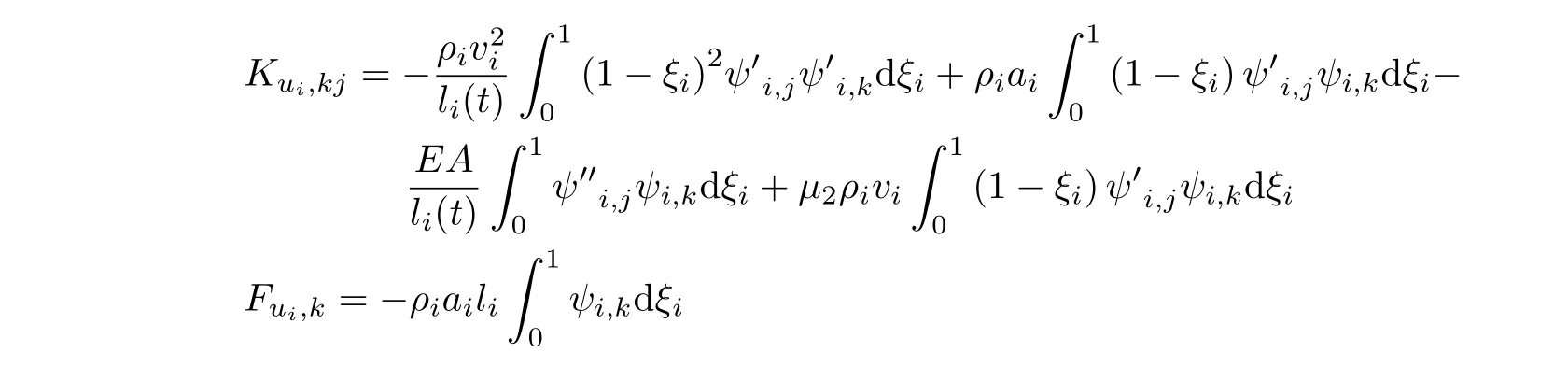
对于非光滑动力学方程的求解,一般情况下首先要对方程在速度水平进行重新描述,首先,将动力学方程乘以Lebesgue 测度dt,得到

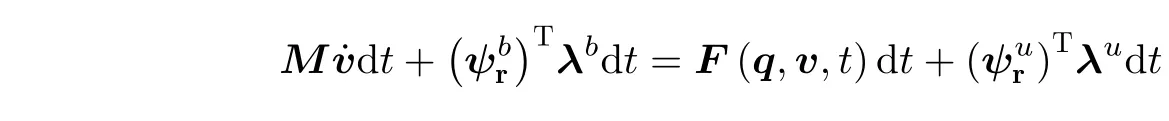
其中F(q,v,t)=Q−Cv−Kq,或者写成如下形式

式中,dib和 diu分别为双向约束力和单向约束力的冲量测度在时间步长内进行积分,其中dv=dt+dw,这里是与广义力F(r,R,t)产生的加速度变量,dw是由于单边约束力和双边约束力产生的微分量度.这样将方程写成如下形式

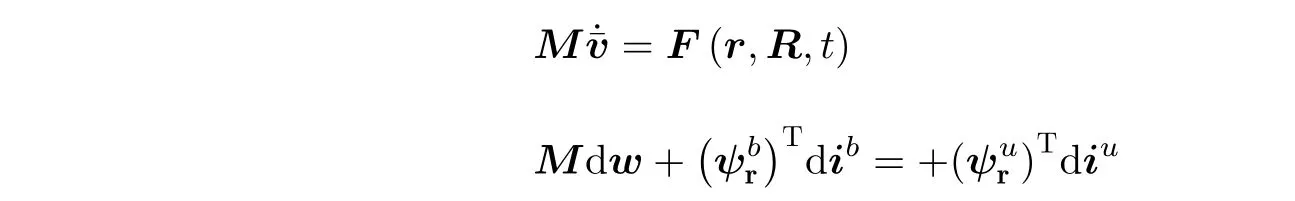
将上面方程离散,可得到方程在速度水平的离散表达式

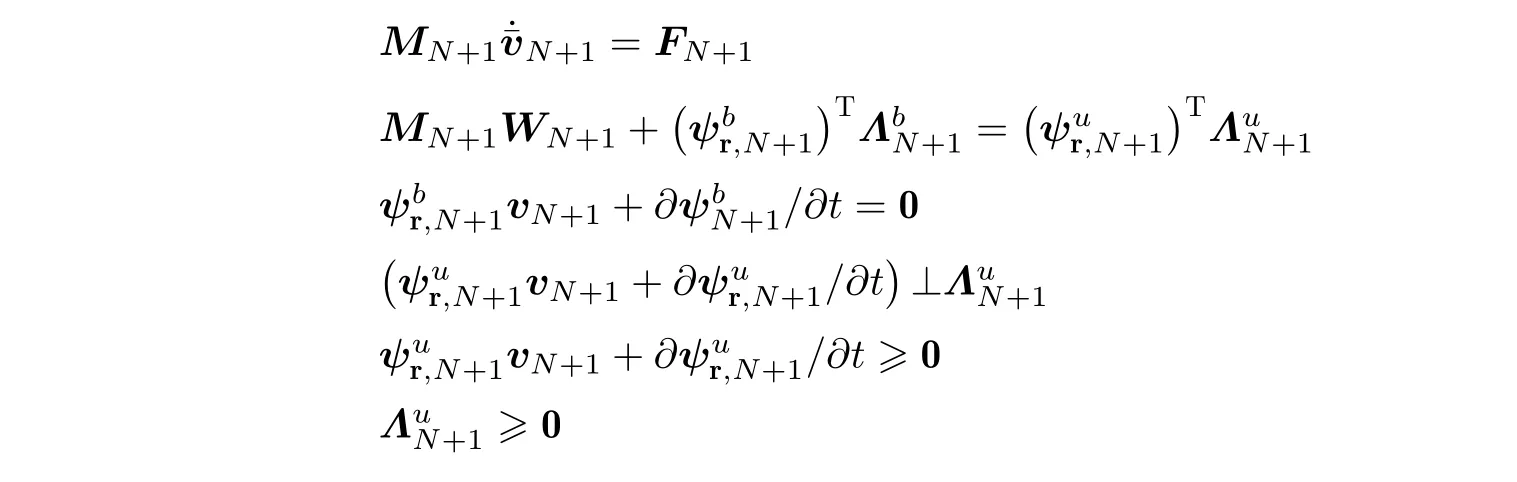
其中,WN+1是一个时间步长内的突变,分别表示关于双边约束和单边约束的拉格朗日方程乘子.

4.2 SAP系统非光滑动力学求解

考虑到尾绳与导向轮之间的单边约束特性,基于构建的单双边约束方程,根据广义α 法(Arnold et al.2007) 的基本迭代形式,可得到非光滑广义α 法的差分方程式及迭代过程为

由此构成一个构建标准形式的线性互补方程(LCP)

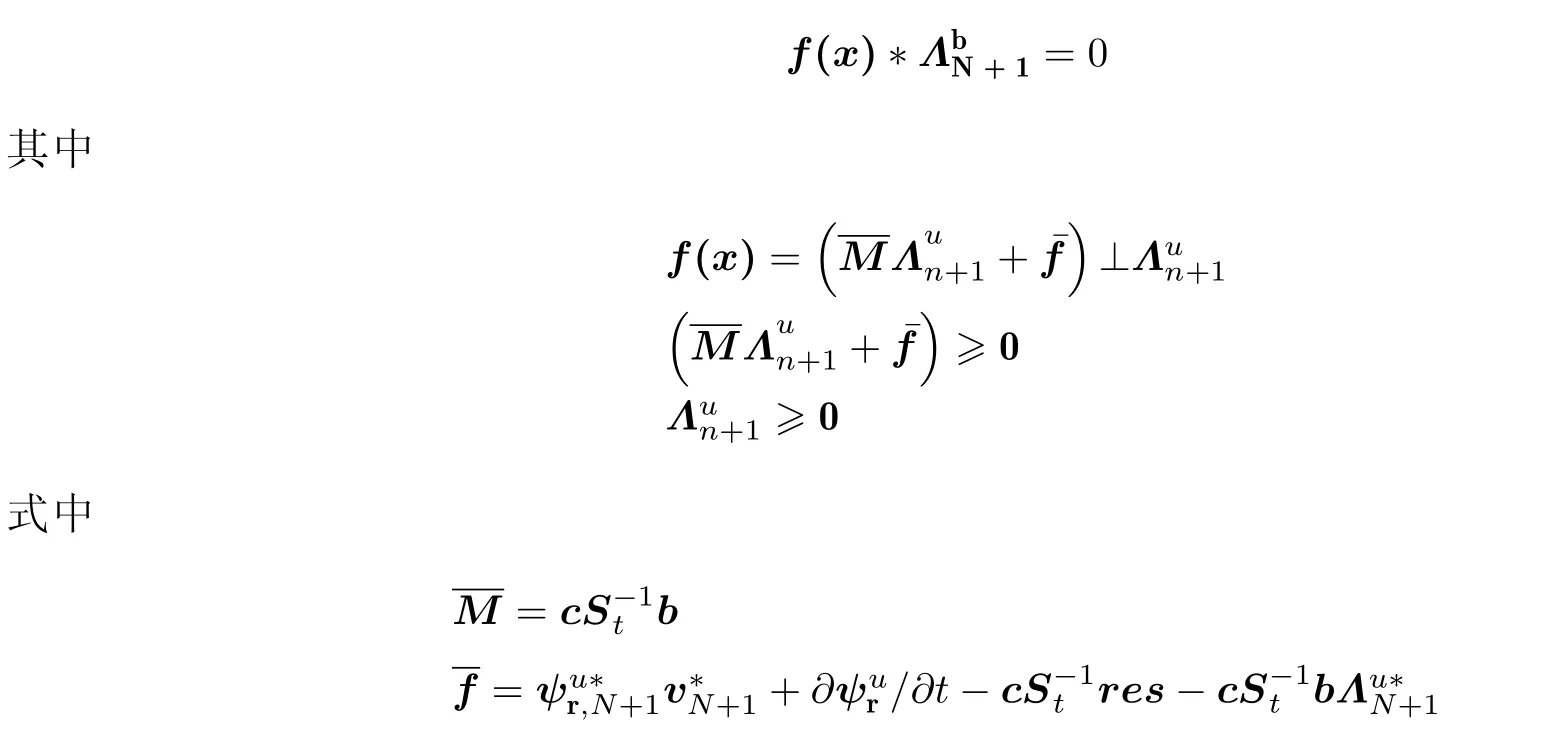
4.3 SAP系统非光滑动力学特性

这里,考虑通过对提升系统不同频率的激励,得到尾绳与调节轮的入绳接触点A(a,b-2)和出绳接触点B(a,b-3)的张力大小以及计算底部调节轮与尾绳的相对位移(a,b-1)如下所示.

基于上述构建的非光滑动力学模型进行分析,当系统的激励以基频振动作用于提升系统时,尾绳的张力均是正值,不会出现张力置零以及张紧轮和尾绳分离的失稳现象,但是随着系统顶部激励频率的提高,导向轮与尾绳接触的初始绳轮接触点A 和最终绳轮接触点B 处的产生了尾绳的动张力置零的情况,进而使得SAP 系统的底部张紧导向轮出现了跳动的情况,对比图13(a)和图13(b)可以看到如图A 中区域所示,故考虑到调节轮等系统部件的稳定性,要严格避免高频激励的情况的发生.

图13

5 SAP提升系统现场试验研究

5.1 SAP提升系统关键装备

为了解决深井提升大摆动、大惯量、大振动问题,项目组研发了适用于深部提升的SAP 提升系统,并在铁法集团大强煤矿首次进行SAP 提升系统试验.SAP 提升系统装置由尾绳调节轮、导向块、轴、轴承座、导轨、上下梁、尾绳防跳槽杆等组成,其在井底的现场安装图如图14所示,SAP 提升系统满载常速运行监控系统如图15所示.

图15

5.2 传统提升系统与SAP提升系统关键参数对比

项目组先后对原提升系统及SAP 提升系统运行中的16 种工况,包括满载(2 m/s,4 m/s,6 m/s,8 m/s)、半载(2 m/s,4 m/s,6 m/s,8 m/s)、空载(2 m/s,4 m/s,6 m/s,8 m/s)、空载(4 m/s,8 m/s)及半载和满载8 m/s 的恒减速制动的尾绳运行监测,对比分析得到以下数据曲线.

(1) SAP 系统与原系统不同工况下尾绳摆动对比分析

加速度为0 m/s2时代表尾绳在各速度(2 m/s,4 m/s,6 m/s,8 m/s)匀速状态摆动情况,尾绳摆动最大值基本出现在加减速过程中.

由图16可以看出,原提升系统满载状态下尾绳最大摆动118 cm(其中左摆73 cm,右摆45 cm),半载状态下尾绳最大摆动108 cm(左摆76 cm,右摆32 cm),空载状态下尾绳最大摆动114 cm(左摆72 cm,右摆42 cm).

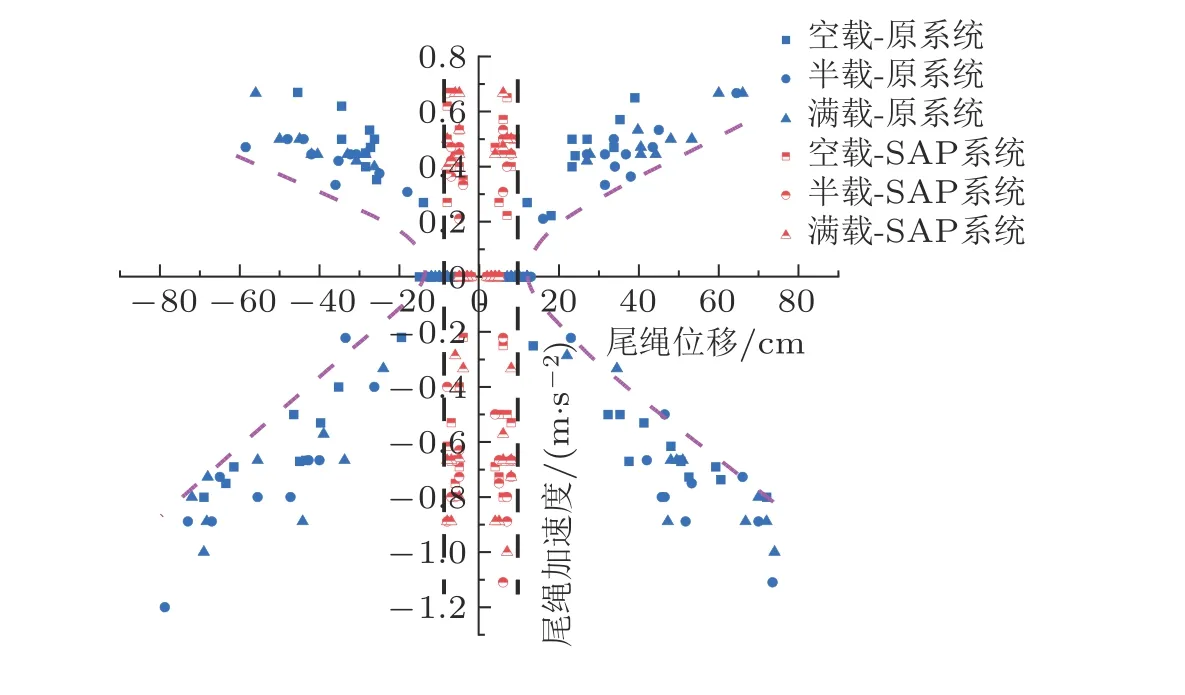
图16

SAP 提升系统在各种工况及不同速度下的尾绳摆动基本稳定在10 cm 以内,尾绳摆动量减小至原提升系统的1/10 左右.

(2) SAP 系统与原系统不同工况下尾绳振动对比分析

由图17可知,SAP 提升系统对比原提升系统尾绳上下振幅减小约30%左右;原系统紧急制动情况下尾绳振动20 余次稳定,持续50 s 左右后稳定,SAP 系统紧急制动情况下尾绳振动9 余次,持续15 s 左右后稳定.

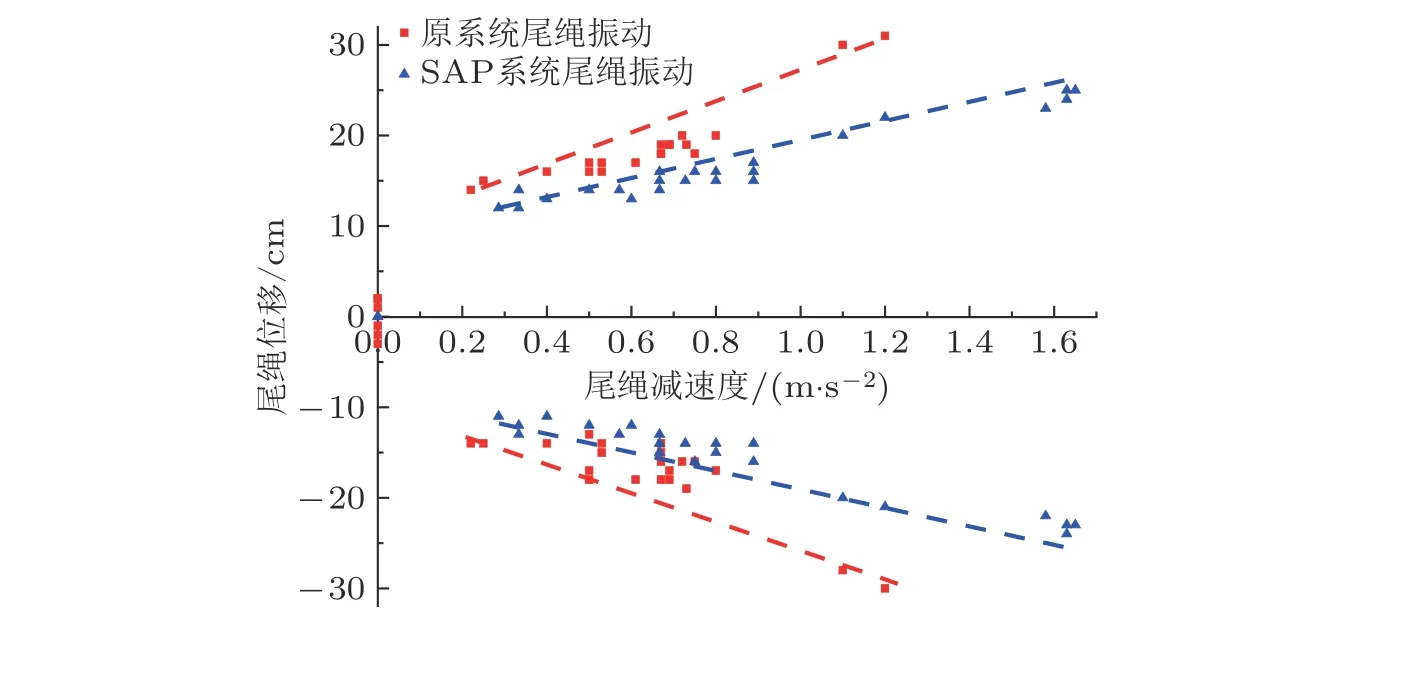
图17

(3)空载时不同加速度尾绳位移

通过图18中的曲线可以看出,尾绳摆动值与加速度近似呈线性关系,随着尾绳加减速度的不断提高,尾绳在各个位置的横向位移也会不断增大,由此说明,尾绳的横向摆动产生的原因就是由于尾绳加减速度的运动导致的,适当的减小系统运行加速度,能够减小尾绳碰撞磨损的危害和风险.SAP 系统有效解决了提升系统运行过程中尾绳大摆动、提升容器大振动等关键问题,提高了提升系统高速运行的安全性.

图18

6 结论

随着年生产能力达1000 万吨,开采最大深度达1500 m 的大型立井的发展,深井多绳摩擦提升系统提升过程中,产生大摆动、大惯量、大振动问题,严重影响高速度、深度化发展.在国家重点研发计划“深地资源勘查开采”重点专项“煤矿深井建设与提升基础理论及关键技术”支持下,建立了单元数量自动调整的自由悬挂平衡尾绳提升系统动力学模型,揭示了传统提升系统诱发平衡尾绳大摆动的机理.提出了以“顶部智能驱动与制动、中部刚柔耦合轻量化容器、底部自适应尾绳导向”系统控制为核心的深井SAP 提升新模式,构建了提升绳−容器−尾绳−调节轮多元耦合下的SAP 提升系统动力学模型与非光滑动力学模型,得到了尾绳摆动特性,揭示了多参数影响下系统的非光滑动力学特性及非线性振动演化规律,为尾绳的大摆动抑制提供了基础数据;研发了平衡尾绳独立导向、提升系统预应力自适应、防杂物跌入、防尾绳跳槽、防相对摩擦打滑的深井SAP 提升配套装备.SAP 系统在大强煤矿千米深井提升工程成功应用,解决了大强煤矿立井提升系统运行过程中尾绳大摆动、提升容器大振动等关键问题,提高了提升系统高速运行的安全性,消除了尾绳大摆动难控制的问题,为深部资源开发提供了理论与技术储备.

致 谢国家重点研发计划专项（2016YFC0600900）资助.