飞行器非线性气动伺服弹性力学

黄 锐 胡海岩 ,2,

1 南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016

2 北京理工大学飞行器动力学与控制教育部重点实验室，北京 100081

1 引言

以飞行器为对象的气动伺服弹性力学主要研究飞行器结构、非定常气动力和主动控制系统之间相互耦合导致的稳定性问题和动响应问题,是先进战机、导弹等飞行器设计的重要力学基础,对保障飞行器飞行安全和提升飞行性能具有重要影响.图1(a)给出气动伺服弹性力学中弹性力、惯性力、气动力、主动控制的相互耦合关系,图1(b)给出飞行器气动伺服弹性(aeroservoelastic,ASE)系统的示意图.20 世纪70 年代末,航空界首次提出气动伺服弹性概念(Feltetal.1979).此后,国内外研究主要针对飞行控制系统诱发的气动弹性失稳、刚弹耦合动力学、颤振主动抑制 (active flutter suppression,AFS)(胡海岩等2016,Livne2018)和突风载荷减缓 (gust load alleviation,GLA)(Moulin &Karpel 2007,Zhao et al.2016)等问题,并有多位学者综述了上述研究在航空航天领域的工程应用进展(杨超等 2015).迄今,对气动伺服弹性力学的研究进展综述大多针对ASE 系统的线性稳定性问题,很少涉及非线性气动/结构效应诱发的非线性气动伺服弹性力学问题.

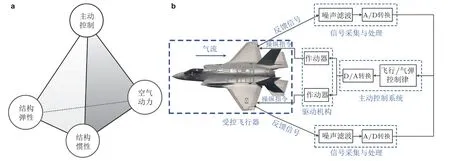
图1

近年来,轻质无人机、可变体飞行器、高超声速导弹等先进飞行器的结构日趋轻柔、可变,而飞行控制系统的通频带变宽、权限增大,飞行器结构的几何非线性、传动机构的间隙、非定常流动的激波振荡和流动分离等非线性效应加剧了ASE 耦合的复杂性,使先进飞行器设计遭遇新的动力学与控制问题,即非线性气动伺服弹性力学.如图2所示,在非线性气动伺服弹性力学研究中,因主动控制系统的参与而额外引入控制面运动产生的气动力反馈回路,加剧了飞行器结构非线性流固耦合动力学的复杂性.

图2

迄今,航空航天界对上述问题的基础研究不足,迫切需要发展新的非线性ASE 理论、高鲁棒性ASE 控制方法,并开展系统的风洞/飞行试验研究.因此,本文介绍飞行器的非线性气动伺服弹性力学研究现状,给出该研究所涉及的非定常气动力、非线性结构动力学、控制律综合、风洞/飞行试验等若干研究进展与挑战,推动学术界和工程界深化对该领域的认识.本文的第2节和第3 节主要讨论具有气动/结构非线性效应的机翼气动伺服弹性力学问题,可视为“小回路受控系统”的非线性ASE 问题.自第4 节起将涉及飞行器整机的非线性ASE 问题,此时需要考虑飞行器的飞行力学,尤其是刚体运动及其耦合效应,可视为“大回路受控系统”的非线性ASE问题.

2 非定常空气动力学模型

空气动力的非定常效应来自于气流经过飞行器时其环量和尾流的变化.非定常气动力研究主要关注飞行器在气流中运动时空气动力随时间的变化规律(Dowell 2015),是气动弹性/ASE 研究不可或缺的重要组成部分.目前,空气动力学界已发展了如西奥道生理论(Theodorsen 1935),亚声速偶极子格网法(Albano &Rodden 1969)、超声速偶极子格网法(Brock &Griffin 1975)等线性化的非定常气动力模型和计算方法,并且在ASE 稳定性分析和控制律设计等方面取得了重要研究进展.上述非定常气动力模型均基于线性化的小扰动假设,无法计入跨声速激波振荡、流动分离等诱发的非线性气动效应.若要精确描述非线性气动效应,则需采用计算流体力学(computational fluid dynamics,CFD)方法.对于非线性气动弹性问题,则需采用计算流体力学与计算结构动力学相结合的直接流固耦合计算方法.但这类方法的计算时间过长,难以用于ASE 控制律综合、非线性ASE 系统的闭环动力学分析等.因此,本节将围绕非线性气动伺服弹性力学研究的需求,介绍非线性非定常气动力的建模方法及其对ASE 系统动力学行为的影响规律.

2.1 非定常气动力系统的非线性辨识

如果将飞行器结构动力学的模态位移作为输入、空气动力系统产生的非定常广义气动力作为输出,则两者间的映射呈现非常复杂的静态非线性和动态非线性,严重影响ASE 系统的动力学行为.已有研究表明,激波振荡和流动分离是产生上述非线性效应的主要因素,可能会诱发飞行器结构出现跨声速“颤振凹坑”、极限环振荡等复杂的非线性振动行为.为了研究上述气动非线性对ASE 系统的影响规律,需要建立既能计入气动非线性效应、又具有较低阶次的非定常气动力模型,进而便于从时域、频域等多个角度研究非线性气动伺服弹性力学问题.

为了克服基于直接流固耦合计算来研究非线性气动伺服弹性力学问题耗时过长的缺点,航空界发展了基于非线性系统辨识理论的非定常气动力模型降阶方法.该方法的主要思想是:将飞行器结构动力学的模态位移作为训练输入,将通过CFD 技术获取的广义气动力作为训练输出,基于非线性系统辨识方法建立非定常气动力的降阶模型.近年来,基于非线性系统辨识的非定常气动力建模方法取得了可喜进展.学者们基于本征正交分解(proper orthogonal decomposition,POD)理论(Hall et al.2000)、谐波平衡法(Hall et al.2002,Yao &Marques.2015)、模糊神经网络(Zhang et al.2012,Winter &Breitsamter 2016)、代理模型(Glaz et al.2010,Liu et al.2014)、非线性Wiener 模型(Huang et al.2014)等建立了多种非定常气动力降阶模型,并在跨声速非线性气动弹性力学研究中取得成功应用.作者学术团队针对二元机翼在马赫数为0.8 的来流下所呈现的跨声速非定常气动力、极限环振荡和拍振现象,给出图3所示基于直接流固耦合计算和基于非线性系统辨识的结果对比.由图可见,非线性系统辨识方法为预测非线性空气动力及气动弹性力学研究提供了高效、准确的建模方法.

图3

虽然基于非线性系统辨识的非定常气动力建模方法已取得可喜的研究进展,但非线性气动伺服弹性力学研究仍面临较大挑战.例如,在飞行器的ASE 系统中,常采用飞行器的控制面作为控制输入,精确预测控制面偏转产生的气动力对ASE 控制律设计、非线性ASE 分析都至关重要.尽管CFD 技术可较为精确地计算控制面的气动效率,但在空气动力网格生成和流场计算中如何处理控制面位移与结构模态位移的协调激励是非常复杂的问题.因为在产生气动力训练数据时,飞行器控制面偏转角度将作为额外的位移输入,与结构模态位移同时作为激励,输入到基于Navier-Stokes 方程描述的空气动力学系统.如何在CFD 环境下定义控制面偏转角度,进而实现其与结构模态位移同时激励时保证气动−结构网格插值精度、广义气动力计算,是非线性系统辨识的关键.为了在不改变CFD 求解器框架前提下计算上述同时激励下的非定常气动力,作者学术团队采用协调网格(blended mesh)方法定义CFD 计算环境下的控制面模态(Huang et al.2015a).该方法忽略控制面与机翼之间的缝隙,将二者视作一个整体曲面.从结构动力学角度,可通过引入控制面模态坐标描述控制面运动.将控制面的固有振型Φδ表示为

式中,x0和x1分别为控制面偏转前后的机翼表面网格位置.函数B2定义为

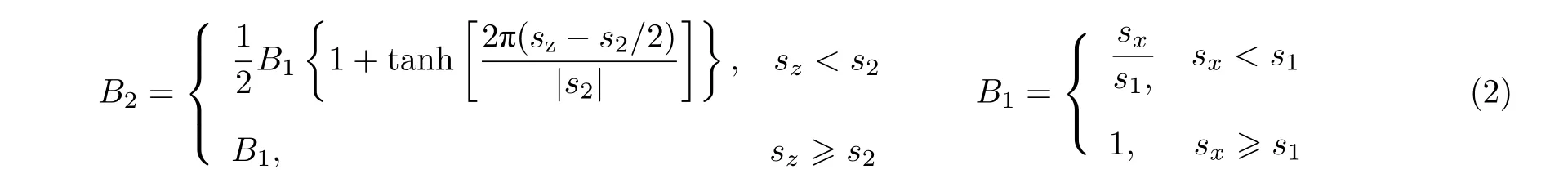
式中,sz是表面网格点与主翼−控制面展向分界线的距离,s2是设定的展向协调宽度(可取为展长的2%);B1用于协调弦向网格,sx是网格未变形前控制面铰链线与控制面区域内任意一点的弦向距离,s1是设定的弦向协调宽度(可取为弦长的5%).图4所示是针对主动控制技术标模(benchmark active control technology,BACT)机翼表面气动网格所给出的控制面模态.由图可见,协调网格方法可采用较为简单的方法得到变形网格,无需对网格生成和流场求解器进行特殊处理.

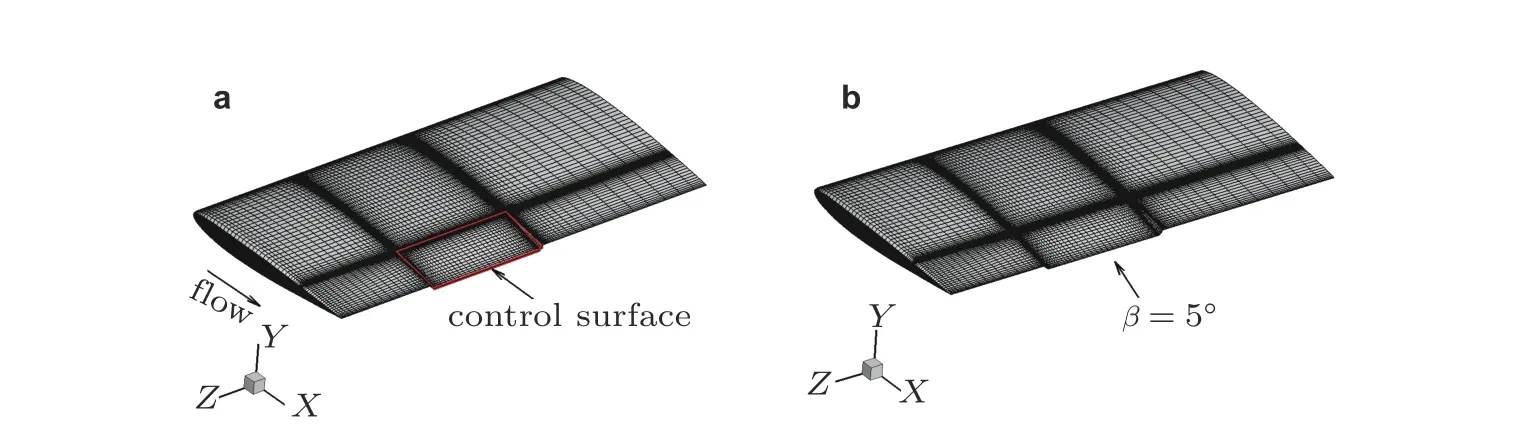
图4

飞行器的ASE 系统是多输入/多输出（multiple-input and multiple-output,MIMO）受控系统,需要在状态空间描述下研究其控制律设计.因此,在状态空间中开展非定常气动力的非线性系统辨识研究,并与结构动力学模型耦合,是开展非线性ASE 系统研究的必然思路.近年来,基于非线性状态空间辨识的非定常气动力建模方法受到了广泛关注(Huang et al.2018),其离散形式的状态方程和气动力输出方程为

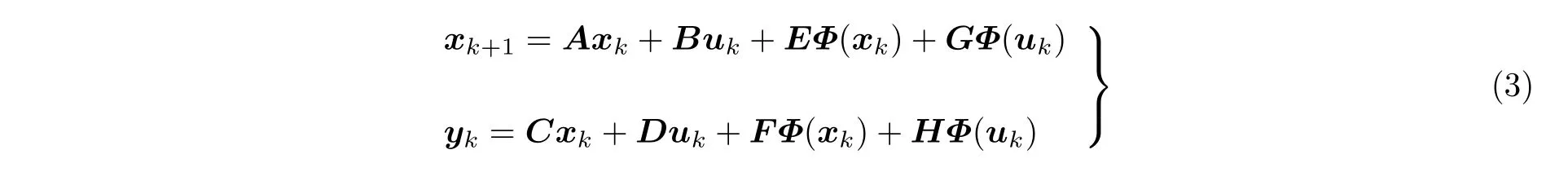
其中k为离散时间步数,xk为气动力状态向量,uk为结构模态位移向量,Φ(·)为非线性函数向量,(A,B,C,D)为待辨识系统的线性部分的系数矩阵,(E,F,G,H)为待辨识的非线性函数向量的系数矩阵.基于式(3)对ASE 系统建模,具有灵活多样的模型结构.例如,非线性函数可以是单层神经网络(Huang et al.2014)、双曲正切函数(Huang et al.2015a)或多项式基函数的组合(Noeel et al.2017).此外,该模型在不同周期内平均的最佳线性近似可为非线性优化提供初值选择.近年来,非线性状态空间辨识方法已应用于迟滞动力学、流体圆柱绕流和非线性ASE 系统的非定常气动力辨识.作者学术团队基于非线性系统辨识的非定常气动力模型,预测了BACT 机翼和三维弹性机翼的ASE 系统动力学行为,图5是对应的频率响应曲线.由图5(a)可见,随着控制面偏转幅值增大,BACT 机翼的频率响应曲线出现向右弯曲,并发生幅值和相位“跳跃”现象.这表明,气动非线性效应会导致ASE 系统呈现“刚度硬化”的非线性.图5(b)所示为马赫数为0.8 时三维弹性机翼的跨声速ASE 系统频响曲线.图示结果表明,预测结果与直接流固耦合计算结果吻合较好.表1给出了两种非线性ASE 系统建模方法在预测频率响应函数时的计算效率对比,非线性系统辨识方法的计算效率明显优于直接流固耦合计算方法.

图5

表1 预测非线性气动伺服弹性系统频率响应曲线的效率对比

2.2 非定常气动力的数据驱动建模

基于非线性系统辨识的非定常气动力建模方法为非线性气动伺服弹性力学研究提供了高效、准确的非定常气动力.然而,基于非线性系统辨识的气动力状态变量并没有显式的物理意义,无法揭示非线性ASE 耦合时的流动特性.在研究飞行器的非线性气动力高效预测、气动伺服弹性振动条件下的流场重构和ASE 耦合失稳的力学机理等问题时,需要获得具有显式物理意义的气动力状态变量.解决该问题的思路是,将CFD 计算获得的非定常压力分布快照作为数据样本,发展基于数据驱动的非定常气动力建模方法,进而建立状态变量具有流场物理特性的低阶非线性气动力模型.与非线性系统辨识研究的不同之处是,在数据驱动建模中,直接以流场计算获取的压力快照pk和飞行器结构模态位移uk为数据样本,即选择

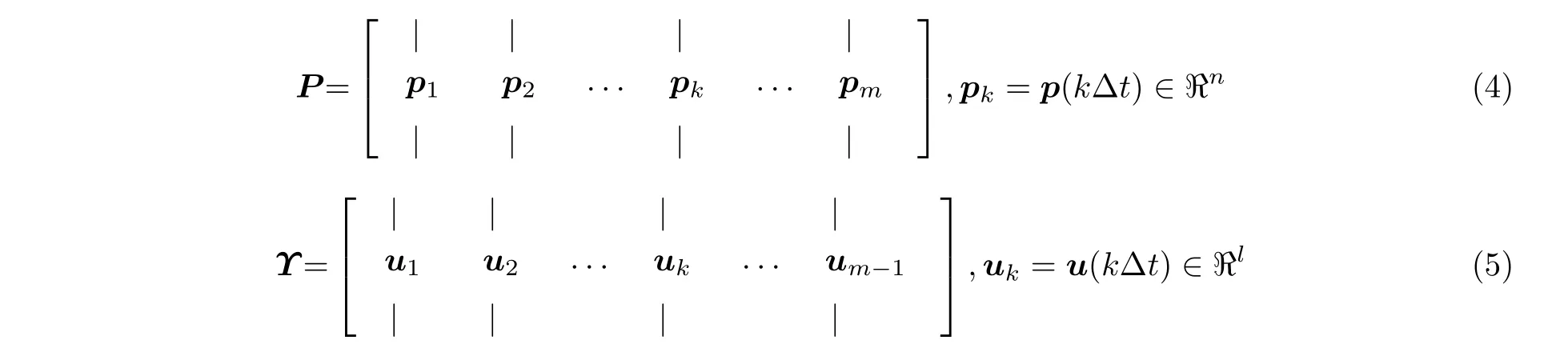
建模的目标是建立非定常流动状态方程

以及广义气动力输出方程

解决上述问题的思路之一是,从复杂动力学系统的海量数据中提取特征模态,通过特征模态上的低阶动力学行为来近似复杂系统动力学行为(Williams et al.2015).已有研究表明,这种模拟复杂非线性动力学系统的方法具有如下优点:一是数据驱动建模方法仅依赖于数值仿真或实验所获取的动力学数据,可以结合未知动力学系统的基本先验知识,建立未知系统的低维数据模型,广泛适用于科技和工程领域的复杂非线性动力系统,并且可启发研究者从数据中认识复杂现象的机理;二是可建立复杂非线性动力学系统的低阶模型,为后续的控制设计提供便利,极大地提高对复杂非线性系统的分析、预测和控制能力.

近年来,随着高性能数值计算和实验测量技术的进步,可方便获取大量复杂流动的高保真数据,给研究复杂流动的数据驱动建模提供了丰富的原始数据.例如,复杂高维流动数据可能会表现出一些典型时空模式,如圆柱绕流中的卡门涡街和跨声速流动中的激波振荡.对这些相干结构的观测和识别,提供了一种建立高维复杂流动的低阶建模方法,即通过识别主导模式上的低阶动力学来近似复杂流动的高维动态特性.复杂流动主导模式的提取通常依赖于模式分解技术.模式分解的方法包括两类:一类是基于POD 算子技术,这需要更多的理论框架或基于Navier-Stokes方程的离散算子.另一种是数据驱动技术,如动力学模式分解(dynamic mode decomposition,DMD);它只将流场数据作为建模过程的输入,不需要先验知识(Taira et al.2017,2020,Berkooz et al.1993,Willcox &Peraire 2002,Schmid 2010).POD 方法根据欧氏范数意义下的最优准则,从流场快照中提取主要空间结构,然后通过Galerkin 投影将Navier-Stokes 方程投影到由POD 模态组成的低维空间.基于POD 和Galerkin 投影的降阶建模方法已分别用于描述不可压缩流动和可压缩流动问题 (Noack et al.2005,Rowley et al.2004).对于可压缩流动问题,实现POD 和Galerkin 投影需要定义明确的内积,包括运动学和热力学变量.此外,通常需要对可压缩的Navier-Stokes 方程进行简化,以方便Galerkin 投影.然而,定义合理的内积和简化Galerkin 投影仍然是应用中的挑战.

动力学模式分解是一种新兴的数据驱动模态分解和降阶建模方法.它提供了一种从仿真或实验数据中提取时空结构的方法,其模式代表不同频率分量对应的相干结构.这种方法也可以看作是求解Hilbert 空间中无限维线性算子Koopman 算子本征模的算法.该方法已被应用于描述各种流动问题,如射流(Rowley et al.2009)、圆柱尾迹(Bagheri 2013)和空腔湍流流动(Seena &Sung 2011).DMD 模式及其对应的频率给复杂流动的底层模式和机理又带来新的认识.尽管DMD 方法已有上述成功应用,但只能在没有外部输入的情况下提取各种流动的特征.为了克服DMD 的缺点,有学者提出了考虑带外部输入控制的动力学模式分解(DMDc)(Proctor et al.2016).在这种方法中,假设输入和快照满足系统状态方程,并组集到一个增广数据矩阵中.通过矩阵逆运算、奇异值分解(SVD)和矩阵相似变换,可以得到状态方程的低阶系统矩阵和输入矩阵.这种带控制的动力学模式分解技术已被应用于非定常流动的流场重构,包括绕圆柱流动和绕机翼流动(Kou &Zhang 2019).其中,将整个流场测量值排列成的快照作为状态向量,尽管只有极少数测量值是独立的.

近年来,非线性气动弹性力学领域的学者发展了一些新的非定常气动力建模方法.Yao 和Marques(2017)采用离散经验插值方法对空气动力学系统进行降维,仅通过几个插值点来近似POD 模态的流场.Opgenoord 等(2018)用流场中涡量和体源密度扰动的最小矩来近似流动状态.然而,在非线性气动伺服弹性力学研究中,非定常数据驱动建模研究仍处于初步阶段.图6给出非定常气动力的数据驱动建模及其在非线性ASE 系统中应用的流程图.如图所示,基于数据驱动的非线性气动伺服弹性力学研究包括高保真非定常流动分析、数据组装与POD 降维、数据驱动建模方法、ASE 耦合分析四部分.

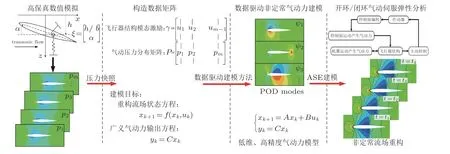
图6

对于非线性ASE 力学研究,基于数据驱动的非定常气动力模型应在飞行器结构的主要工作频带内具有较高的气动力预测精度.以作者学术团队对BACT 机翼的研究为例,图7给出了0 ～25 Hz 范围内基于数据驱动建立的非定常气动力模型的频率响应曲线.图示结果表明,该模型在给定频带范围内的动力学特性与直接流固耦合计算的结果吻合较好.该模型除了可预测广义气动力,还可用于重构气动弹性振动条件下飞行器结构的流场分布特征.图8给出了基于该模型所预测的二元机翼发生跨声速颤振时的瞬态流场压力分布特征,它与直接流固耦合计算结果表现出较好的一致性.

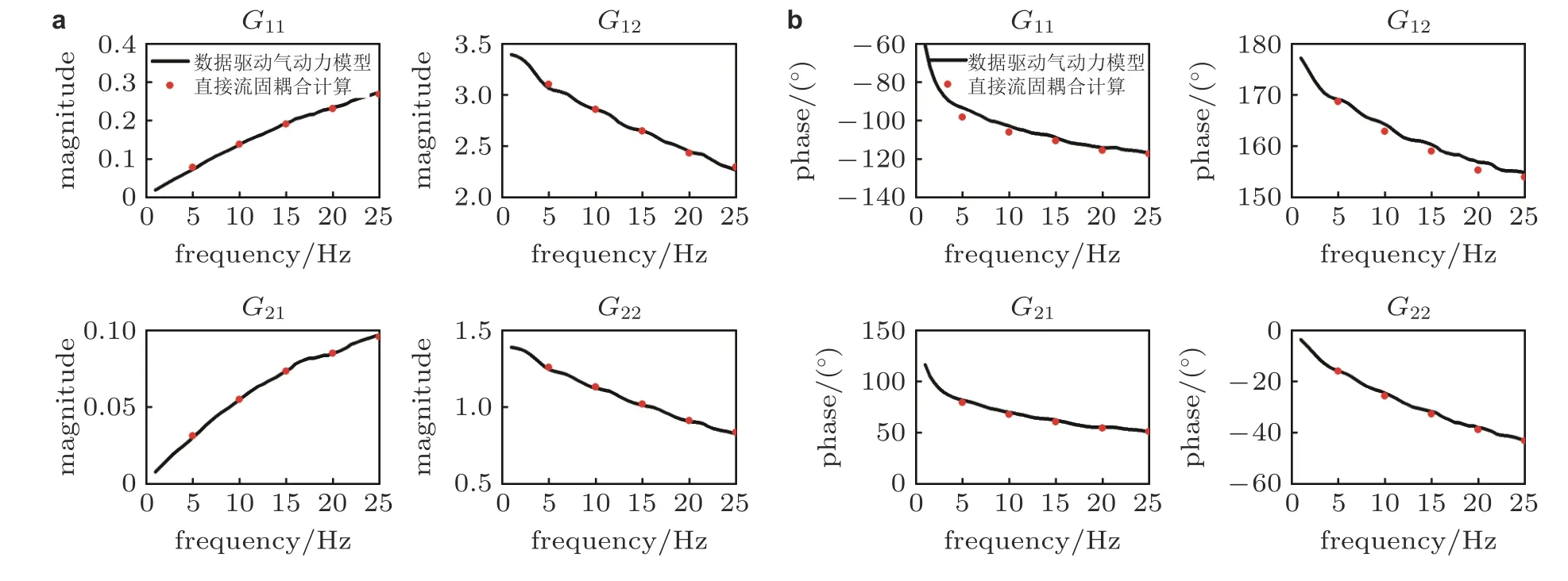
图7

图8

现有的数据驱动建模方法,如POD方法 (Noack et al.2003,Xie et al.2013)、DMD方法(Proctor et al.2016)、稀疏识别(sparse identification)理论(Brunton et al.2016)、Koopman 理论(Rowley et al.2009,Proctor et al.2018)等,在Lorenz 系统、Duffing 振子、圆柱扰流和跨声速颤振等非线性动力学系统的建模中取得了可喜进展,但仍存在如下亟待解决的问题:一是现有数据驱动建模理论大多针对非线性形式已知的动力学系统,对于非线性特征未知的高维、流固耦合动力学系统(如跨声速飞行条件下的柔性飞行器结构),需要深入研究高维动力学数据的稀疏采样与模式分解、非线性函数的选择、数据驱动状态空间模型的辨识等问题;二是现有数据驱动建模方法大多针对系统参数定常的问题,无法考虑系统参数随时间变化的非线性动力学系统建模.对于依赖于飞行马赫数的跨声速空气动力学系统,如何发展参数化的数据驱动建模理论和方法,并开展先进飞行器结构的非线性气动伺服弹性力学分析等尚待研究.

3 非线性结构动力学

近年来,航空航天领域日益关注计入结构非线性效应的ASE 问题,尤其是受控飞行状态下的非线性ASE 问题,因为其严重影响飞行器的飞行安全.从公开文献看,对结构非线性效应的ASE 问题研究并不多见.主要原因在于,该研究方向涉及多学科交叉、研究难度大、门槛高.随着飞行器轻量化结构设计的需求增大、宽速域飞行要求的提升,自然需要对飞行器开展非线性气动伺服弹性力学研究.例如,柔性机翼的几何大变形、高超声速飞行器执行机构的间隙和摩擦、可折叠机翼的双线性铰链刚度等非线性效应,严重影响飞行器气动伺服弹性性能.由于基础研究的不足,导致航空航天界对气动伺服弹性耦合机理的认识不清.目前,考虑控制面间隙的小展弦比机翼和计及柔性机翼大变形的非线性ASE 研究已取得可喜进展(Huang et al.2013,Wang et al.2016),对受控飞行条件下ASE 闭环系统的机理逐步有了清晰认识.对这两方面感兴趣的读者可阅读上述两篇文献,本文不再赘述.相较于固定构型的飞行器而言,可变体飞行器在变体过程中,不仅其非定常气动力随着机翼形状发生变化,而且其惯性、弹性和阻尼特性也同时发生变化,极易诱发不同结构模态参与的多时间尺度的非线性气动伺服弹性问题,给变体机翼技术的研究带来挑战.本节将重点介绍变体飞行器的非线性ASE 研究进展.

3.1 具有时变参数的非线性结构动力学建模

近年来,航空航天界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种不同任务(如巡航、盘旋、机动等)的变体飞行器,图9是其几种典型构型.这类飞行器通过改变自身结构与气动外形,以适应不同的任务需求(Barbarino et al.2011,Li et al.2018).显然,飞行器在变体过程中必须具备工程可接受的ASE 力学特性.由于变体概念的多样性,对各类变体结构的研究现状与进展差异很大.例如,对于翼型变化较大的变体飞行器,由于传统舵机机构不再适用,人们正尝试使用形状记忆合金(Simiriotis et al.2021)、压电材料(Wang et al.2021)等发展新的驱动方式,其技术成熟度尚待提升(Keidel et al.2019).对于翼型变化较小的变体飞行器(如折叠翼飞行器),可采用液压、电机等传统驱动方式完成原理样机的飞行试验(桑为民和陈年旭2009),其技术成熟度较高,但对其ASE 系统的研究尚在进行之中.

图9

对于折叠翼飞行器,机翼的折叠和展开过程涉及结构大范围运动和弹性变形的耦合,本质上属于多柔体系统的动力学问题.当机翼的折叠和展开过程较缓慢时,可视其为准静态变化的结构.此时,折叠角变化会导致结构固有模态发生显著变化,从而引起气动弹性和ASE 系统的不稳定性.因此,必须对其颤振边界进行研究.Snyder 等(2009)研究了Goland 变体机翼和全尺寸变体飞行器中折叠角度、作动器刚度和飞行器质量对结构固有频率和颤振边界的影响,并对其参数敏感度进行了分析.Tang 和Dowell(2008)基于三维VLM 和非线性结构模型建立了具有机身、内侧机翼和外侧机翼的三段式折叠机翼气动弹性模型,随后计算了该模型的颤振边界和极限环振动现象,并与风洞试验结果进行对比.Hu 等(2016)基于DLM 和柔性多体系统动力学方法,建立了若干折叠角下的气动弹性系统,并通过Kriging 方法对系统在其余折叠角时的空气动力影响系数矩阵进行插值计算.研究结果表明,机翼折叠过程和展开过程对气动弹性稳定性产生彼此相反的影响,且该影响随机翼折叠和展开速度的增加而变得更加显著.

作者学术团队基于子结构综合、流形切空间插值等方法,揭示折叠翼模型的颤振特性在结构参数域内的变化规律(Zhao 2012),并且在ASE 系统的稳定性分析、ASE 频率响应的参变特性(如图10所示)和控制律设计等方面取得研究进展(Huang et al.2019).但上述研究仅针对线性化的折叠翼模型进行分析,尚未考虑结构存在铰链间隙等诱发的非线性动力学问题.对于给定构型下的折叠翼模型,采用现有的非线性动力学建模方法可建立其非线性模型.但考虑结构参变效应时,能否高效求解含参变量的非线性气动伺服弹性力学问题成为研究折叠翼在全参数域内颤振特性、非线性气动弹性响应和非线性ASE 系统闭环动力学等问题的关键.

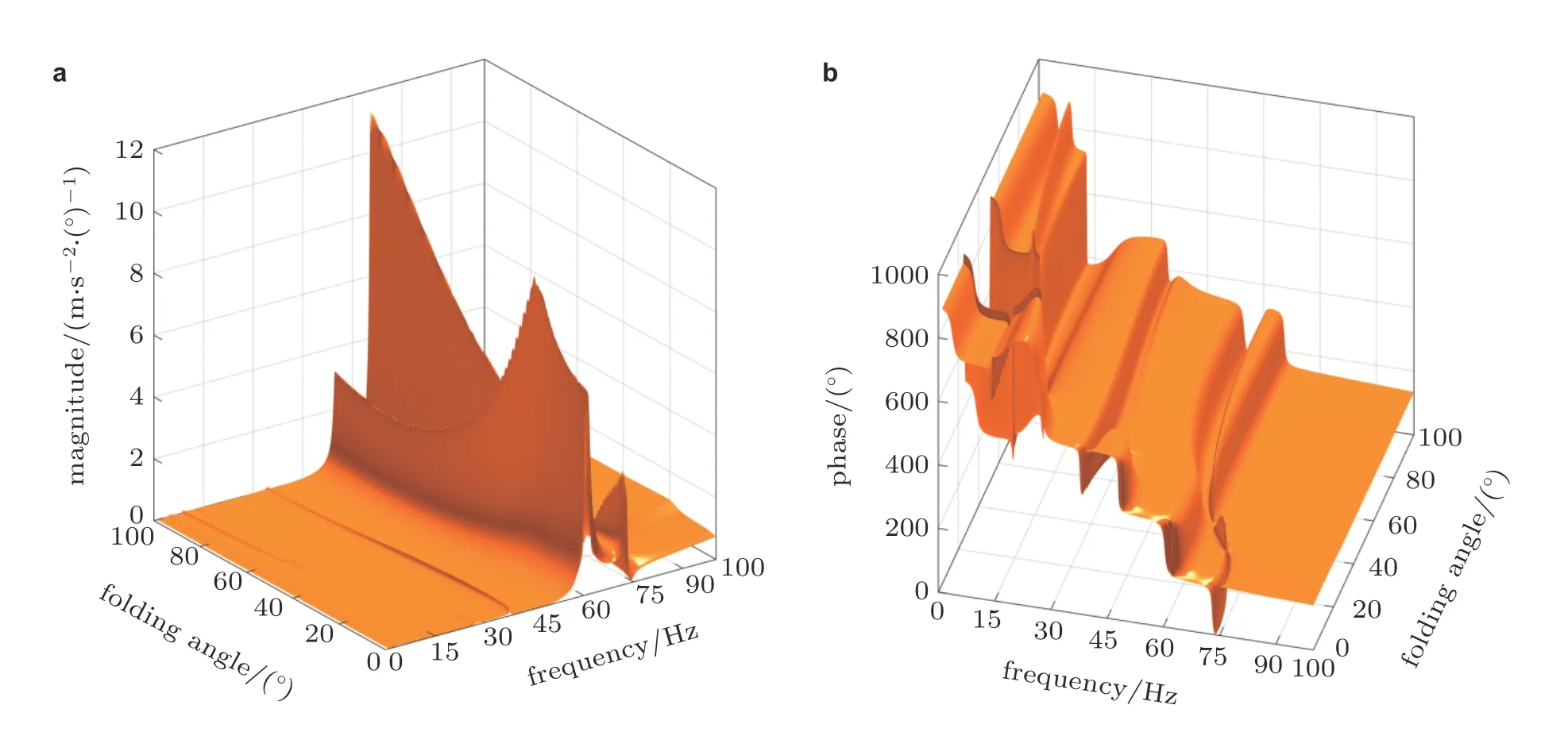
图10

以下针对折叠翼模型的非线性气动伺服弹性力学研究背景,介绍作者学术团队如何研究含非线性铰链刚度的折叠翼参数化建模方法,以及得到的折叠翼的ASE 力学行为.

铰链间隙和双线性刚度是典型和常见的局部结构非线性.对于常规飞行器,它通常存在于舵面与机翼相连的铰链中.对于图11所示的折叠翼飞行器,由于各翼段之间采用铰接连接,铰链处的双线性刚度会诱发飞行器的极限环振动等问题,严重影响飞行器的气动弹性和ASE 系统动力学行为.然而,这种局部结构非线性效应会对折叠翼飞行器的气动弹性力学和气动伺服弹性力学产生何种影响呢? 对该问题开展研究,需要建立考虑铰链双线性刚度的参数化非线性ASE 系统模型,进而从折叠角、铰链刚度、来流速度等多个视角研究折叠翼的非线性气动伺服弹性力学问题.

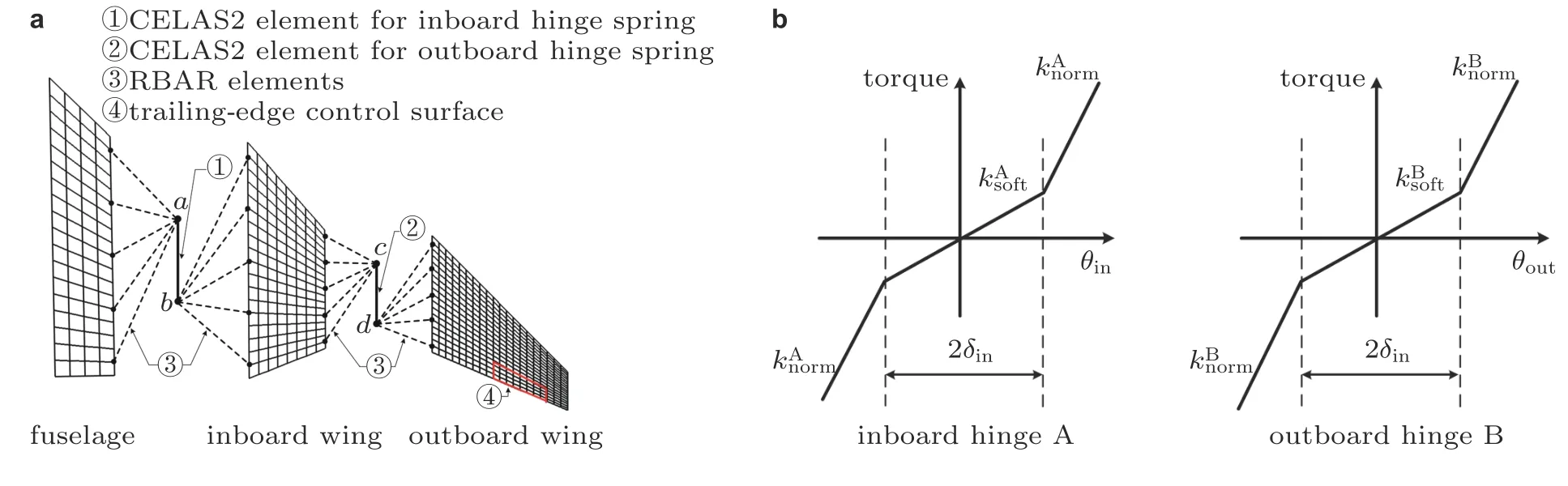
图11

为了克服不同铰链刚度下结构模态坐标不一致以及重复建模过于繁琐的缺点,作者学术团队发展了基于虚拟质量法的参数化虚拟模态建模方法(Huang et al.2021).该方法的主要思想是:将折叠角度和铰链刚度作为参数,在铰链处附加数值很大的虚拟集中质量,生成参数化的广义特征值问题

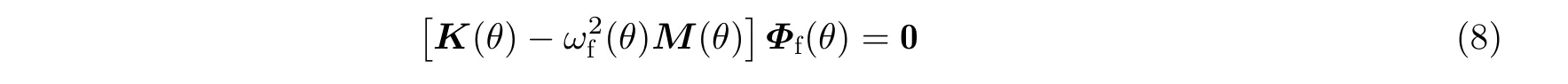
式中M(θ)和K(θ)分别是施加虚拟集中质量后的折叠翼质量矩阵和铰链处于软刚度区间的刚度矩阵,ωf(θ)和Φf(θ)为折叠角为θ时的固有频率和固有振型.当选取一组折叠角和双线性铰链刚度组合后,固有振型Φf(θ)能表征该参数组合下折叠翼的分段线性结构动力学特性.该固有振型对不同铰链刚度配置的折叠翼加权后,其动力学特性维持不变.图12针对4 种铰链刚度参数,给出采用参数化虚拟模态建模方法计算的折叠翼前6 阶固有频率随折叠角变化,该结果与直接有限元计算结果完全吻合.图13给出参数化虚拟模态建模方法预测折叠翼在4 种角度下的前6 阶模态置信度,进一步验证了参数化建模方法的准确性.

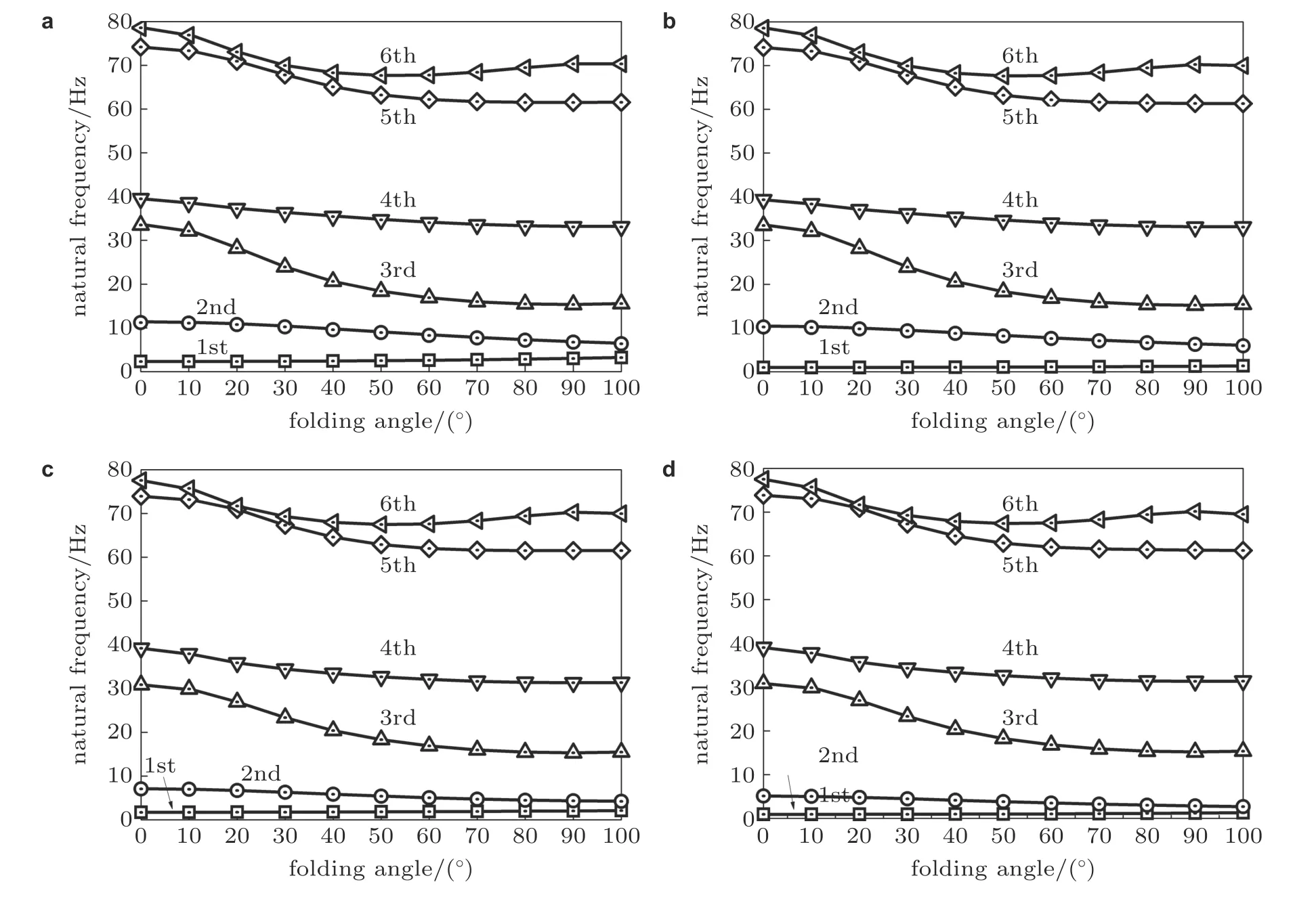
图12

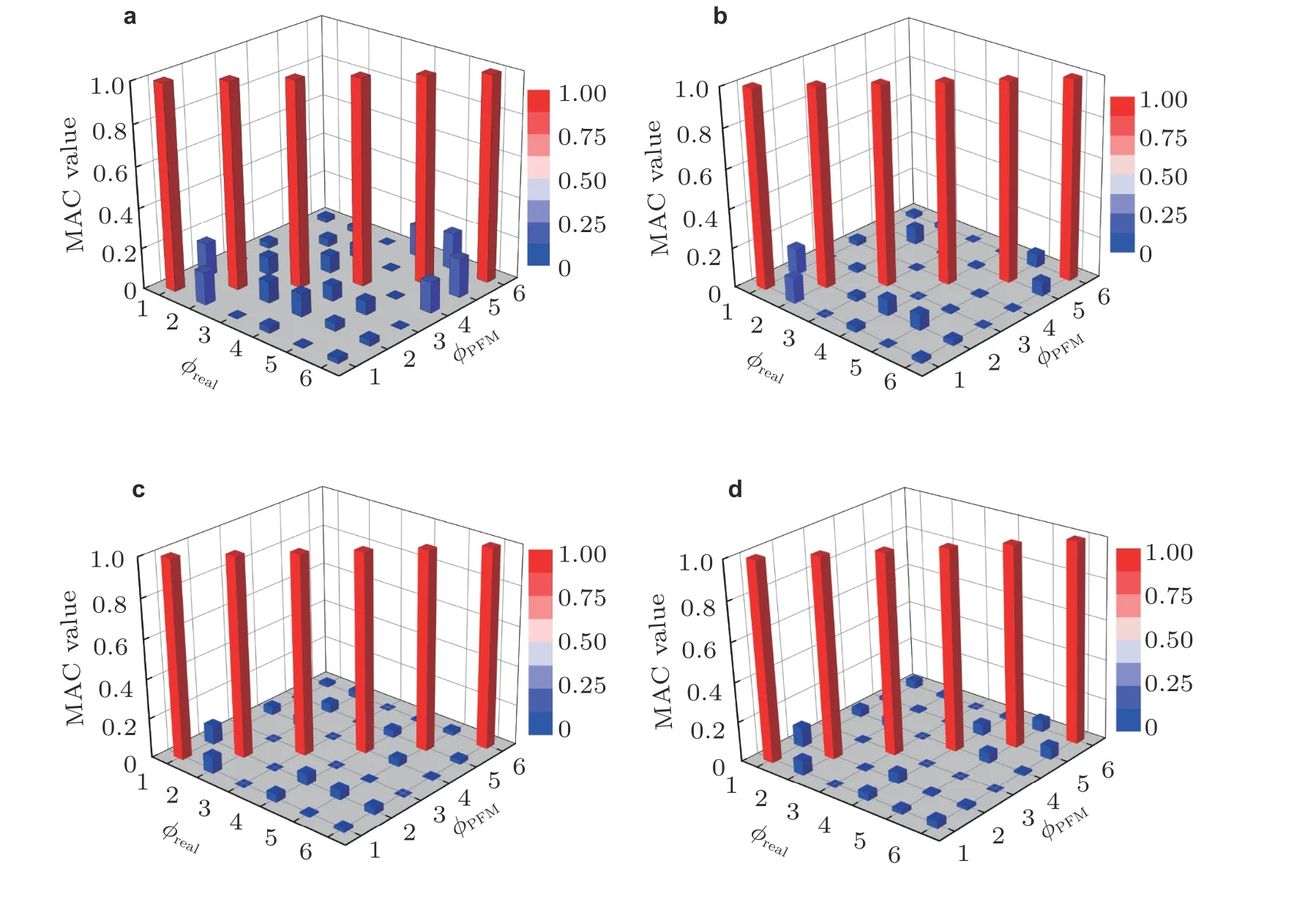
图13

3.2 变体机翼非线性气动伺服弹性力学特性

虽然参数化虚拟模态方法在非线性结构动力学特性分析方面已取得研究进展,但在非线性气动伺服弹性力学研究中仍面临较大挑战.由于在折叠翼动力学方程中,包含随铰链转动变化的刚度补偿项,故参数化虚拟模态方法无法直接用于构建参数化的非线性ASE 系统模型.为了在参数化的模态空间内分析非线性问题,需要引入分段线性的非线性分析方法.根据两铰链的转动角,将非线性ASE 系统划分为9 个参数化的线性子系统,进而将参数化非线性ASE 系统的动力学程表示为

式中Mhh(θ)和Mhβ(θ)分别是折叠角为θ时的模态质量矩阵及控制面模态耦合质量矩阵,ξf(t)是虚拟模态位移向量,β(t)是控制面的偏转角,R(θ,ξf(t))是与铰链转动角有关的分段线性弹性恢复力向量,Qhh(θ,kr,M∞)和Qhβ(θ,kr,M∞)分别是虚拟模态和控制面模态对应的广义气动力矩阵,它们与折合频率kr和来流马赫数M∞有关.在动力学研究中,频响函数是验证系统动力学模型准确性的重要考量.图14给出通过参数化ASE 系统和直接方法计算的0°折叠角度下线性子系统的频响特性的比较.由图可见,在0°折叠角度下,基于参数化模型计算的各线性子系统的频响函数与直接计算结果基本吻合.

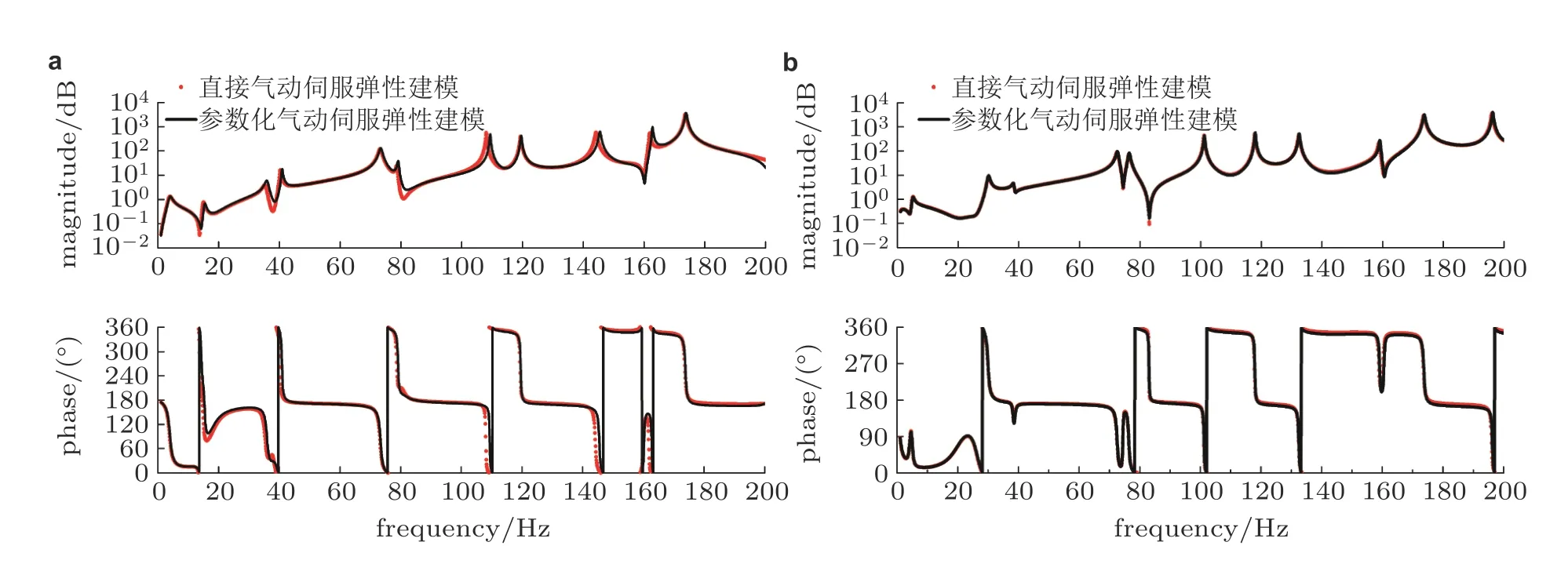
图14

当非线性ASE 系统的控制输入为零时,其响应与气动弹性系统一致.通过分析算例发现,含双线性刚度铰链的折叠翼模型会呈现趋于零的渐近稳定运动、极限环振动、混沌振动和颤振发散等4 种情况.图15是来流速度和折叠角变化时折叠翼位移在Poincare 截面(选择折叠翼某一参考点处位移为零且速度大于零)上的分岔图.如图15(a)所示,在流速为47.5 m/s 时,折叠翼模型的响应由趋于零的渐近稳定运动转为渐近稳定的极限环振动,此时外铰链的运动轨线擦过不光滑的刚度边界.当流速增加到54.8 m/s 时,折叠翼模型的位移呈现非周期性.通过Lyapunov 指数计算验证,这是混沌振动.随着流速增加,混沌运动可继续保持,直到流速超过57 m/s 后发散.随着流速增加,折叠翼模型的响应从渐近稳定逐渐过渡到不稳定,非线性振动的区域基本位于线性颤振边界附近.由于折叠角变化会对颤振速度产生较大影响,故折叠角变化对折叠翼模型的响应影响较为剧烈.如图15(b)所示,当流速处于51 m/s 时,由于小折叠角和90°折叠角的构型颤振速度较高,此时机翼呈现极限环振动或非周期振动;对于40°到80°折叠角与105°折叠角的构型,由于颤振速度较低,机翼发生颤振.同时,两张分岔图都展示了系统动态位移随来流速度变化发生的变迁.

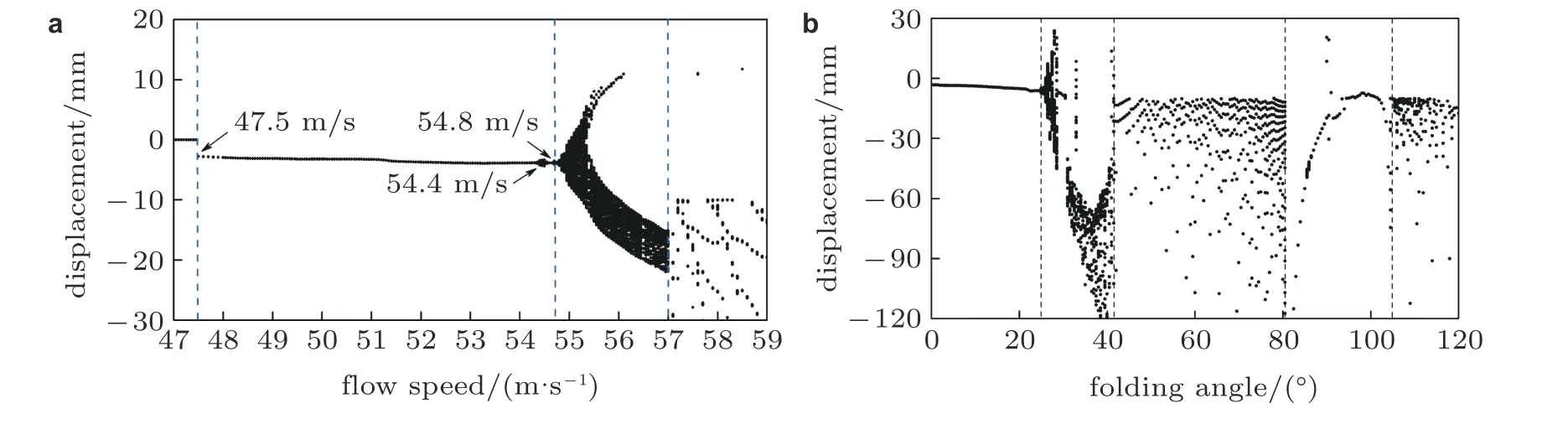
图15

对该折叠翼模型的非线性ASE 系统进一步研究可发现,当流速远低于颤振速度时,系统的气动弹性响应本应渐近稳定;但在控制面偏转激励下,折叠翼位移会呈现混沌.图16是舵面输入分别为3.1Hz 和5Hz 的正弦信号时,折叠翼系统位移在Poincare 截面上的分岔图.有趣的是,在较低流速下,舵面偏转会导致折叠翼呈现混沌振动;随着流速逐渐提高,折叠翼振动的非周期性减弱;最终在30m/s(依然远小于颤振速度)时,折叠翼呈现周期振动.这表明,对于具有结构非线性的折叠翼模型ASE 系统,流速提高引起的气动力变化可部分抵消结构非线性效应,使系统的动力学特性接近线性系统.

图16

对该折叠翼模型进行ASE 系统闭环分析时发现:由于提高了线性子系统的颤振速度,施加控制对系统非线性响应有一定的抑制作用,并不会引起混沌振动.如图17所示,施加控制后,开环系统的极限环振动会出现幅值减小或趋于零的情况;不稳定的开环混沌振动会退化为渐近稳定的极限环振动.因此,当折叠翼模型在颤振速度附近呈现混沌振动等复杂非线性动力学现象时,可以通过主动偏转后缘控制面来抑制或消除混沌振动.

图17

美国国防部高级研究计划局(DARPA)在“变体飞行器结构”(morphing aircraft structure,MAS)计划中明确指出:需要在0.2～0.9 马赫数范围内研究折叠翼变体飞行器在变构型下的气动弹性稳定性问题,进而验证在真实气动载荷工况下变体机翼技术的可行性(Ivanco et al.2007).目前,变体机翼动力学与控制研究多集中在低亚声速区域(0.3 马赫数以下),几乎未涉及变体飞行器在跨声速飞行(马赫数0.8～0.9)时的ASE 力学问题.与低亚声速飞行条件下的变体机翼气动伺服弹性力学研究相比,在跨声速飞行区域研究变体机翼的ASE 力学问题难度剧增,面临众多富有挑战的问题.例如,变体机翼在不同折叠构型下所承受的非定常气动力十分复杂,尚缺乏有效的动力学理论来表征不同折叠构型下变体机翼的跨声速气动−结构耦合动力学系统.再如,当飞行速度进入跨声速区域时,变体机翼在不同折叠构型下的跨声速颤振稳定性的动力学机理尚不清楚,这对在全参数空间内研究有效抑制跨声速颤振失稳的气动弹性控制方法带来困难.

4 气动伺服弹性控制律设计

在飞行器设计中,将设计气动伺服弹性控制律来实现给定的性能指标称为ASE 综合,并以此来提高飞行器颤振边界、保障飞行安全(陈桂彬等 2004,赵永辉和黄锐 2015).具体地说,可将提高飞行器颤振临界速度、减缓突风载荷或机动载荷等作为目标,将布置在飞行器上的传感器所测量的结构振动作为反馈信号,基于ASE 综合理论设计主动控制系统,通过实时驱动控制面偏转,控制飞行器表面的气流分布,从而抑制飞行器颤振或减缓载荷.该技术具有以下优点:一是利用飞行器已有的控制面作为控制输入,不需要对飞行器结构或气动布局进行修改;二是可在保持原有结构刚度甚至适当降低结构刚度的前提下,减缓飞行器的气动弹性效应,进而减轻飞行器结构重量;三是该技术涉及的控制律设计方法可用于减缓由气动弹性振动引起的附加载荷,对提高飞行器飞行品质和疲劳寿命等均具有工程借鉴意义;四是半实物仿真硬件设备和软件技术已相当成熟,可采用高性能半实物系统开展飞行器ASE 风洞/飞行试验.

由于AFS 技术在气动弹性问题中的重要性和难度,它已成为ASE 综合的研究热点,可望为先进随控布局飞机研制、飞行器服役过程中出现的颤振问题提供有效的解决方案.从公开文献看,尚未见AFS 技术成功应用于飞行器工程研制.其主要原因是:AFS 技术难度大、试验周期长、费用高昂、风险高.美国联邦航空管理局(federal aviation administration,FAA)一直致力于推动AFS 技术在飞行器设计中的应用.在FAA 的发起和支持下,著名气动弹性力学家Eli Livne 教授对该领域近五十年的研究进展进行了综述(Livne 2018),并指出AFS 技术需要进一步提升技术成熟度,需要面向考虑非线性效应、不确定性和多输入/多输出的全机ASE 系统开展研究.本节将针对Livne 教授提出的ASE 综合所面临的挑战,介绍近年来对柔性全机模型ASE 综合方面的研究进展.

4.1 气动伺服弹性鲁棒控制

在传统的飞机结构设计中,避免颤振的办法是提高结构刚度.然而,提高结构刚度势必会增加结构重量、降低飞机性能,这与现代飞行器追求更轻更快的理念相矛盾.主动控制技术的发展给解决上述矛盾带来了转机,使飞机设计理念发生了如下跨越式发展:在飞机结构设计中,不再以附加结构重量、牺牲飞行性能为代价来提高结构刚度以回避气动弹性问题,而是通过在飞机机翼表面布置多个可操纵的控制面,并设计主动控制系统驱动其联合偏转,提高机翼控制气流的能力,进而主动调节气动弹性效应.

20 世纪90 年代,美国通过实施“主动气动弹性机翼计划”验证了上述主动控制设计理念(Pendleton et al.2000).近年来,对AFS 技术的研究取得重要进展,有些技术已进行了风洞实验与飞行试验(Livne 2018,Zeng et al.2012,Danowsky et al.2018).例如,作者学术团队(于明礼等2006,2007)采用超声电机作为作动器,研究含控制面的二元翼段的鲁棒AFS 问题,并进行了风洞实验验证.此后,Huang 等(2016)进行了三维小展弦比机翼模型的AFS 和闭环颤振模态辨识的风洞实验研究,利用通过极点配置优化设计的线性反馈控制器有效地抑制了颤振,并对机翼模型的在线闭环颤振辨识进行了探索.在面向飞行器全机模型的AFS 技术研究方面,杨超等(2010)以仿F/A-18A 外形的全机模型为对象,采用线性二次型高斯方法,结合平衡截断法降阶,研究了常规布局飞行器模型AFS 设计方法和特点.Zeng 等(2012)开发了一套基于S4T 风洞实验模型的反馈控制框架,利用鲁棒控制律来抑制颤振和阵风负荷减缓.在上述研究中,尚未考虑飞行器刚体运动对AFS 的影响.

近年来,航空界对先进飞行器在气动效率、续航时间、气动隐身等方面的需求,推动了飞翼布局飞行器技术的发展.这类飞行器一般采用大展弦比机翼以获得较好的升阻特性,并使用轻质复合材料减轻结构重量,以满足长时间续航任务需求.由于这类飞行器结构的重量轻、柔性大,在飞行载荷作用下,机翼会产生较大的弯曲变形和扭转变形,使气动、结构、控制三者耦合系统呈现新的动力学问题.例如,飞翼布局无人机机翼的低阶弯曲振动模态会与机体的刚体俯仰模态耦合,诱发一种新的颤振形态−体自由度颤振(body freedom flutter,BFF).由于刚体模态参与耦合颤振,在抑制飞行器的体自由度颤振时,要考虑全机刚体模态和弹性模态的相互耦合,这对颤振抑制技术研究提出了新的挑战.

Theis 等(2016)针对图18所示美国明尼苏达大学设计的Mini-MUTT 全机模型,用其外侧副翼作为控制输入,用质心加速度、机身刚体俯仰率与翼尖加速度作为输出反馈,基于鲁棒H∞控制律构造增广闭环系统并设计控制器,取得了较好的控制效果.Schmidt(2016)针对洛马公司的BFF06 全机模型,利用“identically located force and acceleration”方法构造双回路闭环系统,抑制颤振并增加模型的阻尼,也取得了很好结果.基于鲁棒控制理论的BFF 主动抑制技术虽有所进展,但现有的控制律设计方法鲁棒性有待提高,抗干扰性能存在显著不足.因此,设计具有高鲁棒性、强抗干扰能力、控制律简单并易于执行的体自由度AFS 系统具有重要的意义.

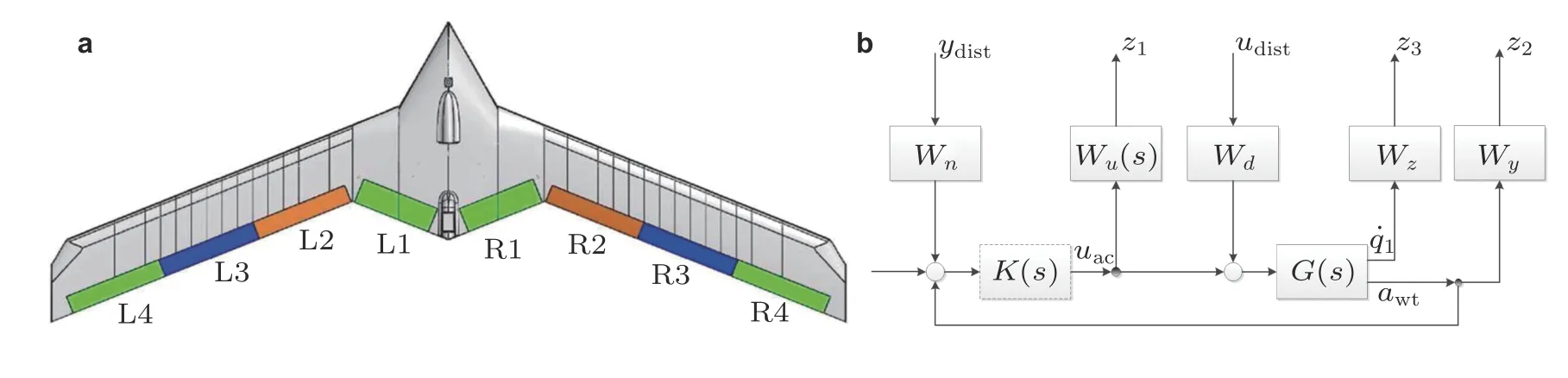
图18

4.2 气动伺服弹性时滞反馈控制

气动弹性控制系统是反馈控制系统,控制回路中存在由A/D 转换、控制器、D/A 转换、数字滤波等环节引起的反馈时滞,严重影响闭环性能,甚至会诱发新的高频颤振现象(Zhao 2011).为了降低上述反馈时滞效应,作者学术团队在控制律设计中考虑反馈时滞量,提出了时滞最优气动弹性控制方法(Huang et al.2012).数值模拟和风洞实验均表明,该时滞最优控制方法可有效抑制三维机翼颤振,且控制性能明显优于传统最优控制(Huang et al.2015b).然而,若将该时滞最优控制方法拓展到柔性全机模型的ASE 综合研究中,则存在控制算法复杂、控制器阶数过高、扩大颤振边界效果不好、鲁棒性有待进一步提高等问题.设计控制律简单、鲁棒性高、适用于全机模型的控制器设计新方法,无疑具有重要意义.

在工程界,PID 控制是最受欢迎的控制律,具有控制律简单,易于机载计算机运行等优点,但也存在鲁棒性不高、抑制效果不理想等缺点.为了提高PID 控制器的鲁棒性和颤振抑制效果,作者学术团队在PD 控制中主动引入反馈时滞,构造如下控制器

其中g1和g2分别为输出反馈增益,,τ为主动引入的反馈时滞量.将式(10)代入ASE 系统的状态方程,并设对应的线性时滞微分方程的解形如x(t)=exp(λt),可得到闭环系统的特征方程为

式中A,B,C分别为ASE 系统的状态矩阵,控制输入矩阵和输出矩阵.当系统处于临界稳定时,具有特征值λ=iω.将其代入式(11),得到

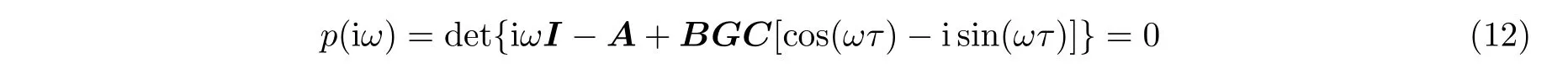
由此可以解得反馈增益

如控制器不含时滞,令τ=0,随频率ω的增加,可以得到一组集合

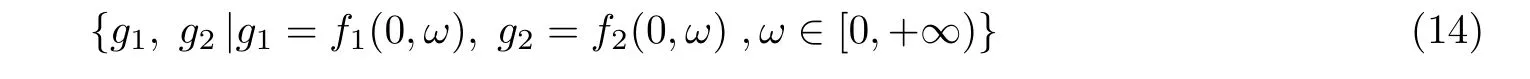
设开环系统在流速低于颤振临界速度时渐近稳定,则闭环系统在上述参数曲线的原点处渐近稳定,在含原点的曲线所围区域也是渐近稳定的,由此可得到使闭环系统稳定的反馈增益和.

当时滞量τ≠=0时,在反馈增益平面的不同子区域内,可选择不同的反馈增益和,将其代入式(12),可得

由于cos2(ωτ)+sin2(ωτ)=1,可构造如下辅助函数

由式(16)解得多个正根ω=ωi,i=1,2,···,将其代入式(16)并根据三角函数周期性,可求得在不同频率下无穷多个满足条件的时滞量,即

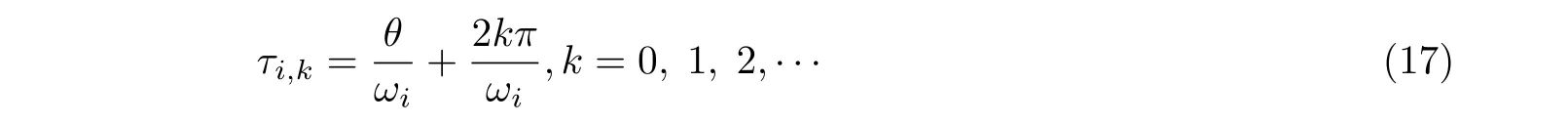
其中θ=ωiτi,0∈[0,2π).为判断此时特征根实部的变化趋势,可利用如下横截性条件(Hu 和Wang 2002)

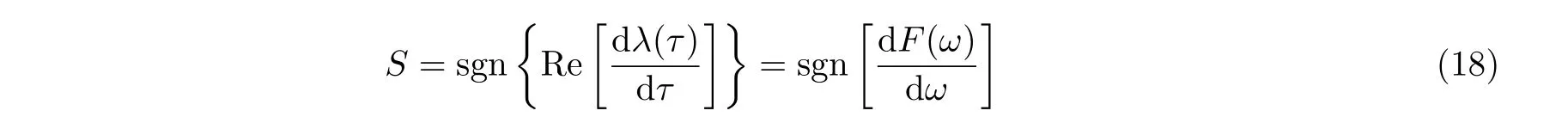
当S >0时,特征根实部将随时滞量增大而增加,上述纯虚根 iω将向复平面右侧移动,变为具有正实部的共轭复根,系统失稳;若S <0,则结果相反.根据纯虚根随时滞量变化的轨迹趋势,可以获得系统稳定性的切换方向.在不同流速下,可使系统从不稳定状态切换为稳定状态的时滞量将构成一系列解区间,它们的交集可使时滞反馈闭环系统在整个流速区域内保持稳定.为了从时滞交集中找到使系统稳定裕度更高、鲁棒性更强的时滞量,可用奈奎斯特图来判断时滞闭环系统的稳定性裕度.为了验证时滞反馈控制的颤振抑制效果,作者学术团队以大展弦比的飞翼布局飞机为研究对象,采用上述方法抑制其BFF.图19是该飞翼布局无人机的外形和开环颤振特性.如图所示,当飞行速度达到26.9 m/s 时,短周期俯仰模态与机翼对称弯曲模态耦合,发生体自由度颤振.图20给出了施加时滞反馈控制后的闭环系统根轨迹分布和基于最小奇异值理论的鲁棒性分析结果.如图所示,上述反馈控制方法可将BFF 临界速度提高到49 m/s,相比开环颤振边界,提高约82%.此外,若考虑闭环颤振边界范围内的控制器鲁棒性,在36.3 m/s 前的飞行速度范围内,闭环系统的鲁棒性都在0.3 以上,提高百分比也达到35%.

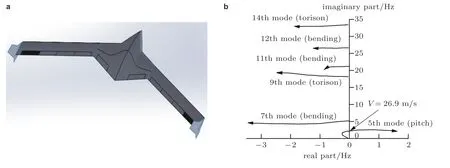
图19

图20

4.3 气动伺服弹性的自抗扰控制

20 世纪90 年代,我国学者提出了自抗扰控制理论(韩京清,1998).该理论在结合跟踪微分器(韩京清和王伟 1994,韩京清和袁露林 1999)、非线性状态误差反馈(韩京清 1995a)以及扩张状态观测器(韩京清 1995b)三大工具后,已发展成为一类新的控制技术.自抗扰控制的核心思想是:将作用于受控对象的所有不确定因素都归结为“未知扰动”,而用对象的输入/输出数据对其进行估计并给予补偿(李杰等 2017).线性自抗扰控制器(linear active disturbance rejection controller,LADRC)(Gao 2003)是对经典自抗扰控制理论的改进,现对其作简要介绍.考察n阶动力学系统

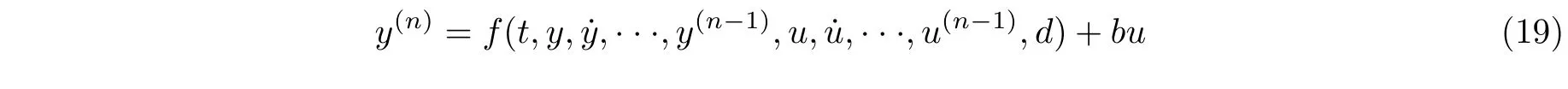
其中t为时间,y和u分别是系统的输入与输出,d为外界干扰.引入参数b的近似值b0,可将式(19)改写为

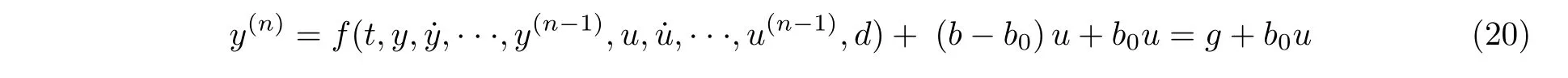
其中g=f(t,y,y˙,···,y(n−1),u,u˙,···,u(n−1),d)+(b −b0)u为广义扰动,包括了系统内部未知动力学特性以及外部扰动.为便于控制律设计,可将式(20)改写为状态方程

其中,xn+1=g为增广状态变量,h=g˙表示未知的扰动.基于状态方程(21),可构建线性扩张状态观测器(linear extended state observer,LESO),获取广义扰动g的估计值gˆ.LESO 形式为

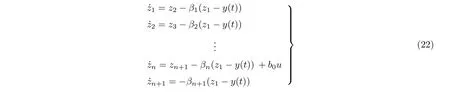
其中,z1,z2,···,zn+1为x1,x2,···,xn+1的观测值,β1,β2,···,βn+1为LESO 参数.观测得到模型状态变量与广义扰动后,可构造式(23)所示的控制器

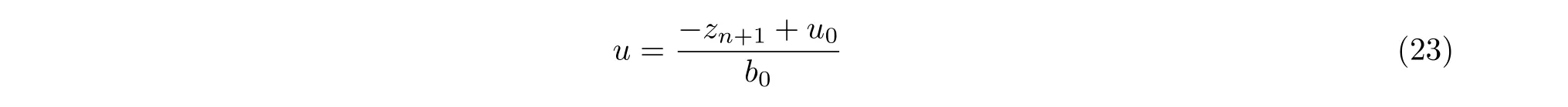
在忽略zn+1的观测误差的情况下,原受控对象被近似转化为一个单位增益的串联积分器模型y(n)=(g −zn+1)+u0≈u0,该受控对象可通过PD 控制器来施加控制

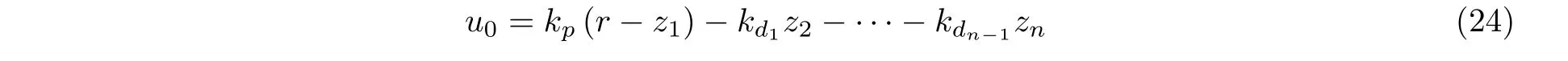
其中r为控制目标,kp,kd1,···,kdn−1为控制器参数.为便于控制器参数整定,可引入极点配置优化方法

其中ωc与ω0为可调节参数.作者学术团队将上述自抗扰控制理论应用于气动弹性控制律设计,研究了考虑参数不确定和测量噪声干扰的BACT 机翼(Yang et al.2017)和三维弹性机翼(Yang et al.2019)的跨音速AFS 问题.数值仿真表明,该控制律可有效抑制较大马赫数范围内的跨音速颤振,并对刚度参数的变化具有强适应性.虽然自抗扰控制技术在飞行器ASE 研究中取得上述进展,但仍面临如下困难问题:一是尽管自抗扰控制理论在原理上具备抗干扰和鲁棒性特征,但缺乏鲁棒性判别方法;二是此前研究均围绕单输入/单输出控制系统的设计,如何设计MIMO 的自抗扰颤振抑制控制律尚值得研究;三是对于飞翼布局飞行器,其体自由度颤振频率较低,而受控系统维数较高,导致控制器参数难以整定.

作者学术团队对MIMO 自抗扰气动弹性控制存在的上述问题进行了探索.以大展弦比飞翼布局无人机的全机模型为对象,研究全机模型的体自由度AFS 的自抗扰控制律设计问题(沐旭升等 2020).首先,基于该飞翼布局飞行器的有限元模型,获得其结构模态参数,进而建立低阶的结构动力学模型;通过偶极子网格法建立飞翼布局飞行器模型的非定常广义气动力矩阵,再通过建立控制面模型、作动器模型以及应用最小状态近似,获得如下ASE 系统的状态方程

其中A,B,C分别为状态矩阵,输入矩阵和输出矩阵.状态向量,输入向量和输出向量定义为

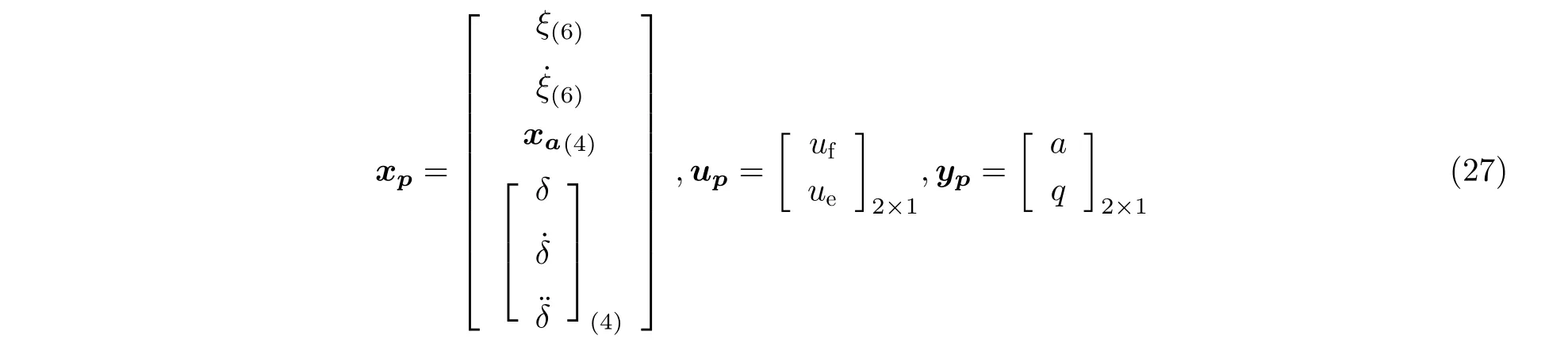
式中uf和ue分别为模型最外侧副翼和机身升降舵的对称偏转指令,a和q分别为翼尖加速度信号和机身刚体俯仰率信号.该ASE 系统的模型阶数为28 阶,其状态向量包括系统的前6 阶对称模态的模态位移与模态速度,4 个气动力滞后项与4 个作动器的状态变量.

鉴于飞翼布局飞行器产生BFF 的机理为刚体俯仰模态与低阶对称弯曲模态耦合,作者学术团队分别设计两个LADRC 构造双回路,进而抑制飞翼布局飞行器模型的BFF.其中,第一个回路以模型翼尖加速度信号为反馈输入,操纵最外侧副翼来抑制BFF 中的弯曲模态;第二个回路以模型刚体俯仰率信号为反馈输入,操纵机身升降舵来抑制BFF 中的刚体俯仰模态.为了基于最小奇异值理论对LADRC 构成的ASE 闭环系统的鲁棒性进行分析,将LADRC 变换为单输入单输出模型,并将设计的两个LADRC 进行并联,构建增广控制器(沐旭升等 2020).由此构建的闭环系统框图如图21所示,其中Ka为翼尖加速度通道的LADRC,Kq为刚体俯仰率通道的LADRC.

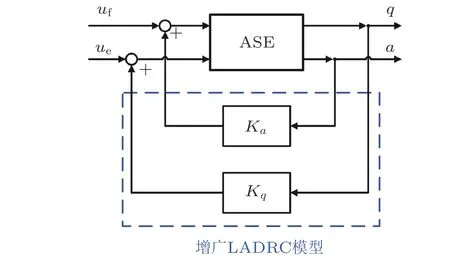
图21

为验证上述MIMO 自抗扰AFS 控制律设计方法的有效性,针对所建立的MIMO 飞翼布局飞行器ASE 模型进行仿真.首先,分析构造的闭环系统的稳定性,对开闭环ASE 系统的根轨迹作对比,如图22(a)所示.由图可见,根据上述控制律设计方法构建的控制器可将系统的临界颤振速度提高至53.5 m/s,比开环系统提高了101.9%.由于实际飞行器模型存在诸多不确定性与外界扰动,因此系统需要具有足够鲁棒性.在工程中,通常将系统的最小奇异值高于0.3 作为鲁棒性达标要求.图22(b)给出ASE 闭环系统的最小奇异值曲线.由图可见,在考虑鲁棒性的情况下,该MIMO 自抗扰AFS 控制器可将系统的临界颤振速度升至38.5 m/s,即提高约45.3%.该仿真结果验证了MIMO 自抗扰AFS 控制律设计方法的有效性,并表明该控制律设计方法具有鲁棒性高、抗干扰能力强、易于执行等优点.

图22

4.4 基于强化学习的控制律设计

现有的气动弹性控制律设计方法,如极小极大控制(Mukhopadhyay 2000)、鲁棒H∞控制、µ综合控制(Waszak 2001)、自抗扰控制(Yang et al.2017)等,均需进行复杂的手动参数调节过程,控制器性能与控制器参数选取息息相关.对于二元机翼或者三维柔性机翼的AFS 问题,由于受控系统的维数较低,手动调参过程尚可达到控制目标.对于整架飞翼布局飞行器,依赖于经验的手动调参过程繁琐且耗时,难以获得最优控制参数.因而,参数整定被称为一门“艺术”,而不是一门“科学”(Gao 2003).

强化学习(reinforcement learning,RL)技术的发展为解决上述问题带来了转机.RL 是机器学习(machine learning,ML)的分支之一.该名词来源于行为心理学,表示生物为了趋利避害而更频繁实施对自己有利的策略.人工智能借用这一概念,把与环境交互中趋利避害的学习过程称为RL.RL 适用于解决诸如控制器参数整定这样的趋利避害问题.许多学者针对基于RL 的控制技术开展了研究.例如,Kashki 等(2008)针对自动稳压器模型,提出了CARLA(continuous action reinforcement learning automata)算法用于整定模型PID 控制器的参数,并将其参数优化性能与粒子群优化算法、遗传算法对比,证明了RL 方法具有更高的效率和性能.Hwangbo 等(2017)基于四旋翼无人直升机的飞行控制提出了一种新的RL 方法.基于该方法训练的人工神经网络可根据直升机的状态参数调整电机转速,从而实现航点追踪与在苛刻初始化下的飞行器稳定控制,手抛直升机的稳定控制实验验证了该方法的有效性.不同于以往的任务级别控制,Koch 等(2019)基于RL 方法,开发了一个用于四旋翼直升机姿态控制的开源高保真仿真环境,分别基于三种最新的RL 方法构建姿态控制器,并将其性能与传统的PID 姿态控制器进行对比,证明了RL方法在高精度、即时的飞行控制需求方面的高效性.上述研究探索了RL 在飞行控制技术方面的可行性.目前,尚未见到将RL 方法用于飞行器ASE 综合方面的研究.飞行器的ASE 系统涉及到气动、结构、控制三者间的耦合效应,研究基于RL 方法的AFS 控制律设计问题比飞行控制律设计更难.

为了解决上述问题,作者学术团队以图23(a)所示的飞翼布局飞行器为对象,获得图23(b)所示的BFF 特性.根据对飞翼布局飞行器BFF 特性的理解,提出如下基于机器学习的AFS 控制律设计方法.

图23

首先,基于RL 的智能体/环境界面,将ASE 模型与AFS 控制器构成的闭环系统建模为RL的环境,并基于DDPG(deep deterministic policy gradient)算法构建智能体.DDPG 算法(Lillicrap et al.2016)是一种基于确定性策略梯度(deterministic policy gradient,DPG)算法的执行者/评论者(actor/critic)方法:一方面,利用评论者网络来近似价值函数,然后利用该价值函数近似值来估计回报值;另一方面,利用估计得到的回报值估计策略梯度,进而更新策略(执行者网络)参数.像Q 学习(Watkins et al.1992)一样,评论者函数q(s,a;ω)可通过Bellman 期望方程学习,其中s为RL 中环境的状态,a为智能体的动作,ω为评论者函数参数向量.执行者函数的学习需要利用策略梯度定理(Silver et al.2014),顺着梯度方向改变执行者网络参数以增加期望回报.为回避直接将Q 学习应用于神经网络造成的不稳定,同时为提高网络学习效率,DDPG 算法引入了经验回放、目标网络、Ornstein Uhlenbeck 过程来解决上述问题.

其次,构建如图24所示的基于机器学习的AFS 控制律设计算法框架.在每一轮次的交互中,智能体基于当前策略生成动作(控制器参数)并施加给环境,而后环境基于动作综合出AFS 控制器并构建闭环ASE 系统,将基于闭环系统稳定性/鲁棒性指标设计的当前环境的观测值与动作的奖励值反馈给智能体,智能体基于观测与奖励来优化策略,于是可在智能体与环境的交互中学习得到最优控制器参数.

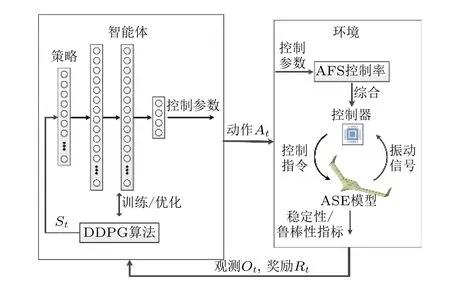
图24

为验证上述算法扩大飞翼布局飞行器颤振边界的有效性,作者学术团队针对飞翼布局飞行器的鲁棒AFS 技术进行了仿真.为给出直观对比,同时给出一组耗时数天手动整定出的鲁棒H∞控制器结果.首先,分析闭环系统的稳定性.图25(a)给出开环ASE 系统、具有鲁棒控制器的闭环ASE 系统、基于机器学习控制器的闭环ASE 系统的根轨迹对比.由图可见,该机器学习方法构建的控制器可将系统的临界颤振速度提高至41.15 m/s,比开环系统提高了52.6%;而鲁棒控制器只能将颤振速度提高约46.9%,且需要繁琐、耗时的手动调参过程.由于实际飞行器模型存在诸多不确定性与外界扰动,因此系统需要具有足够的鲁棒性.现基于最小奇异值理论分析系统的鲁棒性,选择系统最小奇异值高于0.3 作为鲁棒性达到要求.图25(b)给出两种控制器的闭环ASE 系统的最小奇异值的对比.由图可见,在考虑鲁棒性的情况下,机器学习AFS 控制律设计方法构建的控制器可将系统的临界颤振速度提高至36.83 m/s,即提高约36.6%,明显高于鲁棒控制器所达到的28.1%.上述仿真结果表明,基于机器学习的AFS 控制律设计方法可获得控制性能更优的AFS 控制器参数,而且不再需要繁琐、耗时的手动调参过程.

图25

5 气动伺服弹性实验

与非受控的飞行器气动弹性系统实验研究相比,飞行器气动伺服弹性系统实验研究具有成本高、风险大等特点.在世界范围内,对飞行器气动伺服弹性系统进行风洞实验和飞行试验的研究均很少.主要研究难点如下:一是气动/结构的非线性效应导致系统的气动弹性力学非常复杂,现有的气动伺服弹性建模方法难以精确模拟受控系统的动力学行为;二是气动伺服弹性系统是反馈控制系统,测控回路中存在由A/D 转换、控制器、D/A 转换、数字滤波等环节引起的时滞,会严重影响控制器性能,甚至会激发气动伺服弹性系统失稳;三是飞翼布局飞行器等先进飞行器研制对气动伺服弹性系统的实验提出了更高要求,在ASE 系统的设计中必须考虑飞行动力学与结构动力学的耦合效应,而对体自由度进行AFS 实验难度更大.

在Livne(2018)的综述中,详细评述了近五十年来世界范围内关于AFS 和GLA 的风洞实验/飞行试验研究,但对气动弹性控制实验研究存在的学术问题讨论尚不充分.本节介绍针对气动弹性控制实验研究上述难点的最新进展.

5.1 气动伺服弹性系统的实验试验

在飞行器研制过程中,需要开展大量的风洞实验/飞行试验.其中,飞行器气动伺服弹性系统的风洞实验/飞行试验具有较高风险.其主要原因是:受气动/结构非线性效应、非定常气动力计算误差等因素的影响,通常难以建立飞行器气动伺服弹性系统的精确动力学模型,从而导致风洞实验/飞行试验失败.

为了给气动弹性控制律设计提供较为准确的气动伺服弹性系统数学模型,需要对气动伺服弹性系统的理论建模结果进行风洞实验验证.作者学术团队以图26(a)所示的小展弦比机翼为对象,开展气动伺服弹性系统的风洞实验研究(Huang et al.2015b).如图26(b)所示,采用高性能伺服电机驱动机翼后缘控制面偏转作为控制输入,以机翼振动加速度作为输出反馈信号,通过主动控制,构建了具有AFS 功能的三维受控机翼系统.

图26

图27分别给出流速为20 m/s 和26 m/s 时理论建模和风洞实验获得的频率响应曲线对比.如图所示,理论建模得到的幅频和相频曲线与风洞实验结果均存在较大差异.其中,幅频曲线在峰值处的频率值吻合较好,但幅值差异超过一倍之多.产生上述误差的主要原因在于,非定常气动力计算误差、控制面气动力矩计算误差、以及计算固有振型难以与实测固有振型精确吻合.

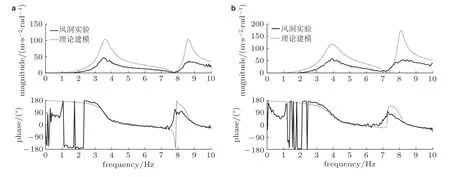
图27

上述气动伺服弹性系统的风洞实验是在低亚声速来流条件下进行的.随着来流速度的增加,三维机翼气动伺服弹性系统进入高亚声速或者跨声速区域时,空气动力的非线性效应变得显著,导致气动伺服弹性系统的理论建模误差进一步增大.此时,即使采用高精度CFD 技术进行非定常气动力建模,也难以准确获得真实气动伺服弹性系统的数学模型.由于高亚声速或跨声速气动伺服弹性系统的风洞实验成本高、测试困难,鲜见公开发表的研究进展.以美国为代表的航空强国分别开展了主动气动弹性机翼研究计划(Waszak &Srinathkumar 1995,Mukhopadhyay 1995)和BACT 机翼(Waszak 2001)的跨声速AFS 风洞实验研究.NASA 兰利研究中心的风洞实验结果表明,基于现有气动伺服弹性理论建模方法获得的频率响应曲线与风洞实验结果差异较大,给气动伺服弹性控制律设计带来挑战.因此,这是气动伺服弹性理论走向工程应用时必须解决的问题.

5.2 气动伺服弹性系统实验的时滞效应

图28是作者学术团队研制的气动伺服弹性系统实验框图.在图中,风洞实验系统的时滞主要来自输入/输出板卡中A/D 和D/A 采样、反馈信号的数字滤波、控制器运算、以及作动器伺服跟踪等环节.随着数字滤波器阶次增加、控制器算法复杂提升,气动伺服弹性系统的测控时滞量将显著延长.以常用的五阶Butterworth 滤波器为例,图29表明该滤波器在截止频率25 Hz 范围内的相位变化斜率可近似为常值.通过换算可知,25 Hz 正弦信号通过该滤波器时将具有约43 ms的时滞.作者学术团队的研究表明,测控时滞对气动伺服弹性系统的风洞实验成败至关重要,43 ms 的输入时滞会严重降低控制器性能,甚至会激发闭环颤振(Huang et al.2012).

图28

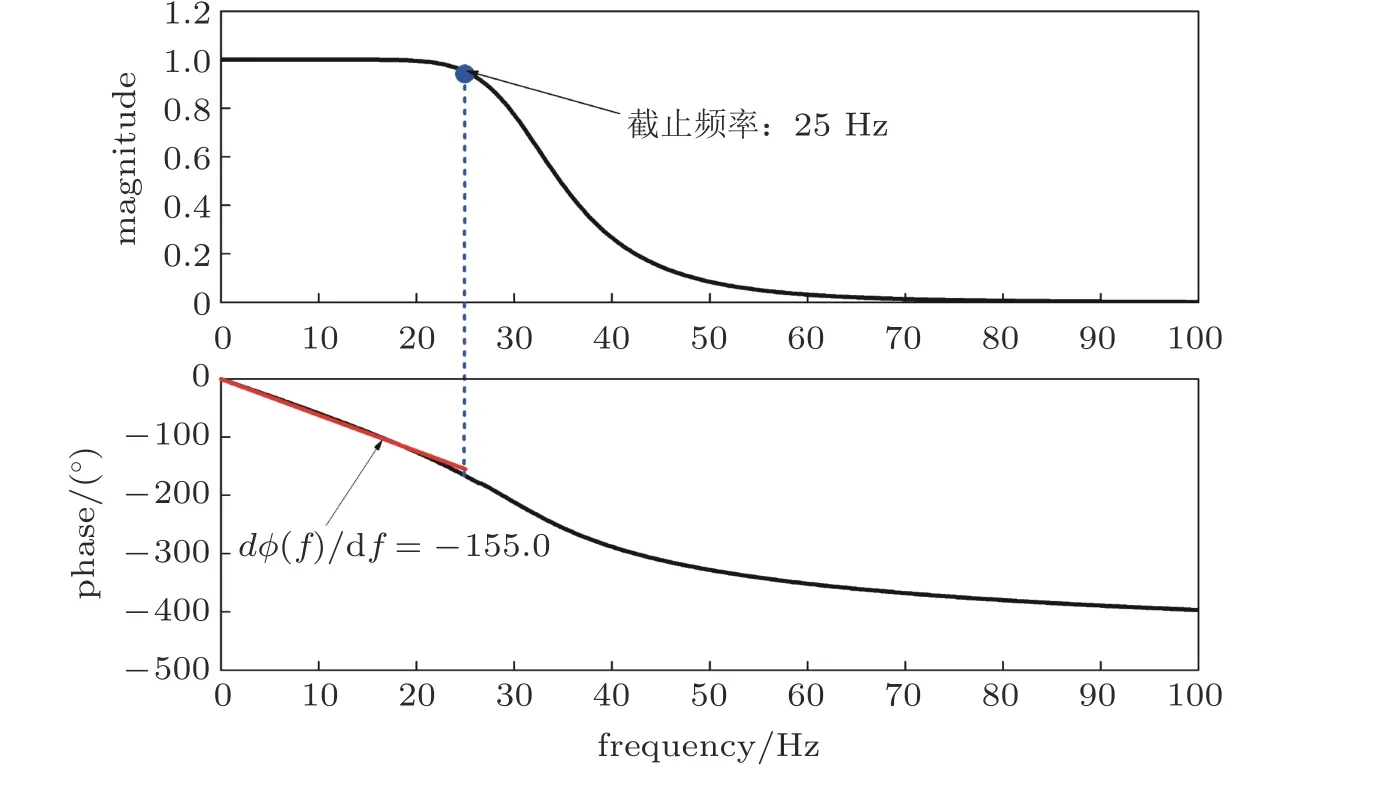
图29

针对气动伺服弹性系统的上述时滞问题,可采用如下两类解决方案:一是以幅值裕度和相位裕度满足指标要求为目标,致力于设计高鲁棒性的气动伺服弹性控制律,通过提高闭环系统的鲁棒性来补偿测控时滞的不良影响.二是将测控时滞作为设计参数引入到气动伺服弹性系统的模型中,基于含时滞的气动伺服弹性系统状态方程进行控制律设计(Zhao 2009,Huang et al.2015b).作者学术团队的研究表明,第二种方案更为简洁和有效,在此作简要介绍.

以含输入时滞的气动伺服弹性系统为例,其状态方程可表示矩阵形式

式中τ为输入时滞量,通常大于测控系统的采样间隔;状态方程中的系数矩阵可参考文献(Huang et al.2015b).将上述状态方程离散化,并引入如下新的状态向量

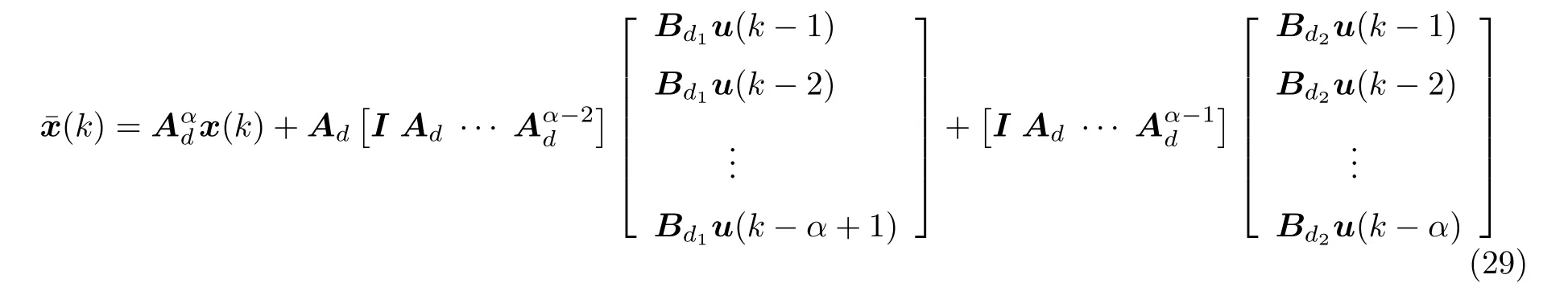
可得到不含时滞的状态方程

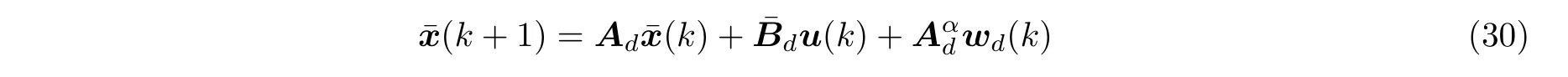
基于上述新的状态方程,可采用最优控制等理论设计控制器.图30(a)给出计入时滞效应的最优控制律的风洞实验执行框图.图30(b)是来流速度为36.5 m/s 时,施加计入时滞的AFS 控制器前后所测量的机翼加速度时间历程和控制面偏转角位移时间历程.由图可见,施加计入时滞的最优控制器后,机翼颤振得到了有效抑制.

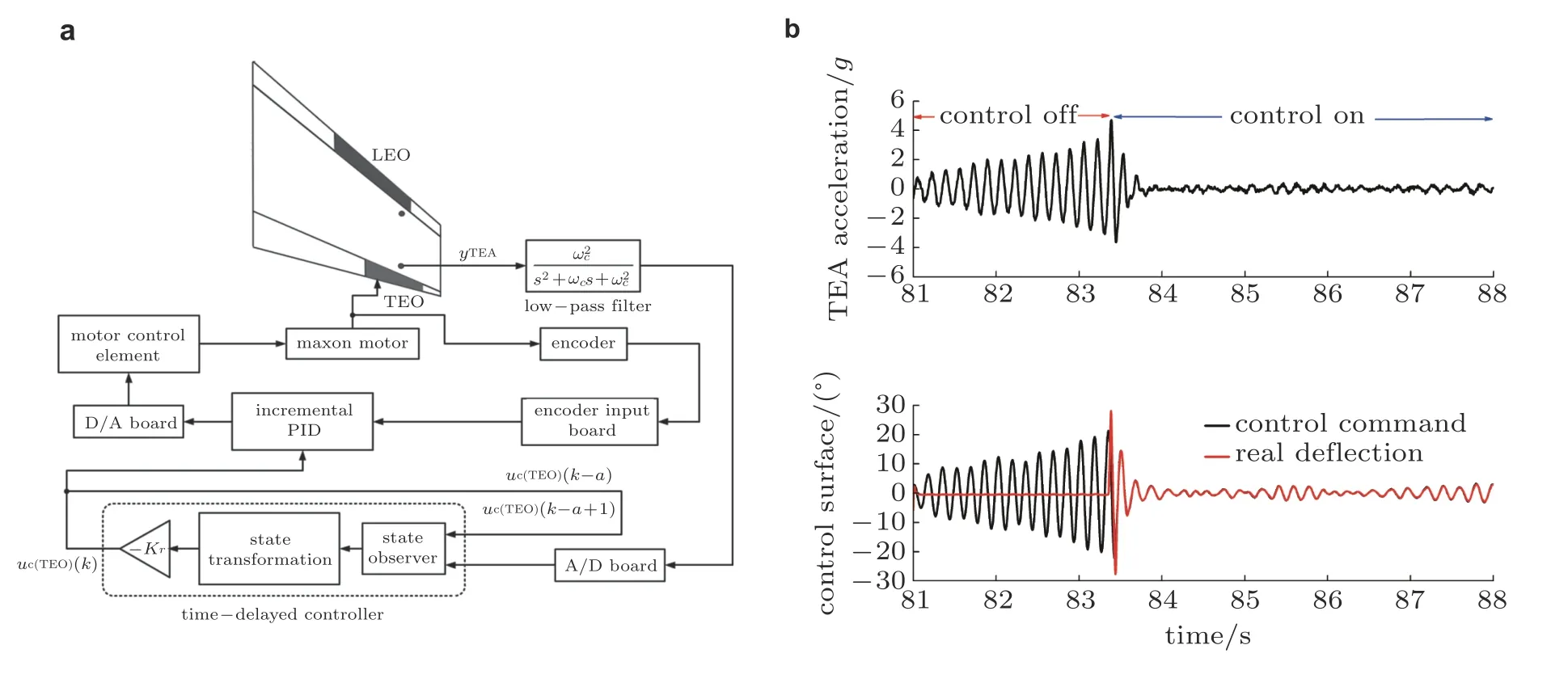
图30

5.3 全机体自由度颤振主动抑制实验

为了研究飞翼布局飞行器的体自由度颤振特性,雷鹏轩等(2021)分析了飞行控制律对飞行器颤振的影响,通过风洞试验与频域计算,获得了不同刚体自由边界条件下的开环/闭环体自由度颤振特性.如图31所示,Li 和Pak(2015)研究了通过优化质量配平对于飞翼布局无人机颤振速度的影响.Moradi 等(2018)通过风洞实验对上述方法及结果进行了验证,获得彼此吻合的结果.

图31

近年来,航空界在新概念飞行器研究中积极采用增材制造技术,利用其可设计程度高、制造周期短的优点,设计和研制用于风洞实验/飞行试验的飞行器模型.如图32所示,美国空军实验室Pankonien 等(2018)利用3D 打印技术研制了飞翼布局无人机半模风洞试验模型,完成了弯扭耦合颤振试验,为其设计后缘变弯度机翼奠定了基础.

图32

Danowsky 等(2018)基于图33中美国明尼苏达大学的柔性飞翼布局无人机飞行试验平台mAEWing1,采用鲁棒控制律、MIDAAS(modal isolation and damping for adaptive aeroelastic suppression)方法和传统的ILAF(identically located accerleration and force)方法设计了AFS 控制器.其飞行试验结果表明,所设计的控制器具有一定效果和良好的鲁棒性.Schmidt 等(2020)设计并制造了第二代柔性无人机mAEWing2,并通过多次飞行测试和地面试验对飞行器结构进行优化,为后续气动弹性飞行试验打下了基础.

图33

6 非线性气动伺服弹性力学研究面临的新挑战

非线性气动伺服弹性力学是为了推动先进飞行器技术发展而形成的多学科交叉研究领域,主要研究飞行器、非定常气动力、主动控制三者相互耦合的非线性动力学系统,解决非线性气动伺服弹性建模、耦合动力学机理分析、控制系统设计等问题.近年来,可变体飞行器、轻质柔性无人机、高效率商用运输机和高超声速飞行器等先进飞行器的技术发展,给非线性气动伺服弹性力学研究提出许多新的挑战.本节围绕上述四类飞行器技术发展的需求,梳理非线性气动伺服弹性力学研究中的工程科学问题.

6.1 飞行器非定常气动力数据驱动建模方法研究

对非定常气动力的非线性效应进行高效、准确建模,是开展非线性气动伺服弹性力学研究的基础.与非线性气动弹性力学研究相比,非线性气动伺服弹性力学研究不仅要分析气动非线性效应对飞行器气动伺服弹性行为的影响机理,还需要设计飞行/气动弹性控制律并进行高保真闭环仿真,从而需要精度高、阶次低的受控系统模型.因此,针对非线性气动伺服弹性力学研究需求,迫切需要研究非定常气动力的高精度、低阶次建模方法.

近十年来,基于非线性系统辨识理论和数据驱动理论的非定常气动力模型降阶方法研究取得了可喜进展,但仍存在如下亟待解决的问题:一是现有非定常气动力模型降阶方法大多通过二元翼段来验证方法的有效性,鲜有研究三维柔性机翼和复杂全机模型的非定常气动力模型降阶问题,没有充分彰显非定常气动力模型降阶研究的生命力和工程价值.对于考虑气动力非线性效应的气动伺服弹性力学研究,针对三维飞行器开展非定常气动力的数据驱动建模难度剧增.因此,需要深入研究非定常气动力数据的稀疏采样、非线性函数的选择、数据驱动气动力模型的非线性辨识等问题.二是数据驱动建模方法大多以模态空间内的广义气动力为辨识目标,构造低阶非定常气动力模型.这类辨识过程视空气动力学系统为黑箱,不考虑飞行器表面的真实流场特性,得到的低阶模型可能是局部最优解.虽然这类建模方法可用于气动弹性/气动伺服弹性稳定性分析,但无法揭示气动伺服弹性耦合的流动特征.因此,需要深入研究以三维柔性机翼、飞行器全机模型的流场参数为辨识目标的非线性数据驱动气动力建模新方法,为非线性气动伺服弹性力学研究提供具有流场参数的非定常气动力模型.

6.2 飞行器非线性时变结构动力学

可变体飞行器设计给非线性气动伺服弹性力学研究带来许多新的挑战和发展机遇.变体机翼技术涉及极为复杂的气动弹性动力学与控制问题,尤其是在宽速域飞行条件下的气动伺服弹性力学问题.以美国洛克希德•马丁公司研制的具有可折叠机翼的变体飞机为例,其变体过程对气动力影响很大,导致飞行控制技术仍不成熟,两次演示验证试验均因闭环稳定性不足导致飞行失败.

面向变体飞行器的研究需求,需要发展新的时变气动伺服弹性力学理论,解决变体过程中飞行器结构时变效应引起的气动伺服弹性建模难题.在机翼受控变体过程中,不仅非定常气动力的非线性效应会随着机翼形状发生变化,机翼的惯性、弹性和阻尼特性也同时发生变化,极易诱发不同结构瞬时模态参与的多时间尺度非线性气动弹性效应,给变体机翼控制技术的研究带来挑战.如果飞行器变体角速率远低于飞行器结构的固有频率,可将变体过程简化为具有慢变参数的结构动力学问题,通过给定的变体参数来表征变体过程.此时,结构模态随着变体参数的变化而变化.因此,需要建立结构模态与变体参数之间的映射关系,发展高效的参变气动伺服弹性建模方法.如果飞行器变体角速率达到与飞行器结构固有频率相同量级时,飞行器结构呈现多柔体系统的动力学特征,即变体过程与结构变形产生非线性耦合.目前,基于多柔体系统动力学方法所建立的飞行器结构模型过于复杂,无法用于非线性气动伺服弹性建模.因此,需要开展多柔体系统动力学模型的降阶研究(Luo et al.2017,Tang et al.2019),在此基础上提出高效的时变结构气动伺服弹性分析方法和控制方法.

对于高超声速飞行器,其空气舵系统(由作动器、连杆、摇臂、舵轴和舵面等活动部件组成)间隙引发的非线性刚度问题是非线性气动伺服弹性力学的研究重点之一.空气舵是飞行器伺服控制系统的重要组成部分,它接受舵面偏转信号后输出控制指令,经过传动机构驱动舵面偏转,控制飞行器的飞行姿势或飞行轨迹.由于加工误差和装配精度等因素的限制,舵传动机构的回转铰链内部存在不可避免的间隙,对机构的动态特性产生不良影响.铰链内的间隙导致销轴和铰链孔之间出现碰撞,使机构产生振动,导致舵面难以精确跟随控制指令,舵系统的控制性能变差.因此,需要研究间隙、碰撞等非线性因素的空气舵非线性结构动力学行为,建立简化的非线性动力学模型与非定常气动力模型相耦合,发展高超声速飞行器的非线性气动伺服弹性建模方法,高效、准确地模拟飞行器的气动伺服弹性力学行为,进而提高飞行器的飞行控制品质.

6.3 柔性飞行器的气动弹性控制与飞行试验

已有研究表明,飞翼布局飞机和可变体飞行器具有复杂的颤振特性,给扩大飞行器颤振飞行包线和保障飞行安全带来巨大挑战.以可变体飞行器为例,其变体过程会引发非定常气动力和结构动力学的时变动力学效应,极易诱发气动弹性失稳.通过增加结构刚度来回避气动弹性效应,会显著增加变体飞行器的结构重量,抵消通过变体方式带来的飞行性能收益.在不增加飞行器结构重量条件下,气动弹性控制技术可望改善变体飞行器的气动弹性稳定性,是先进飞行器轻质化结构设计必须突破的关键技术.

航空科技强国十分重视气动弹性主动控制技术,启动了多项研究计划.由于气动弹性主动控制试验的风险大、费用高、周期长,这些计划均在大型无人机上开展飞行试验.相比之下,我国的飞行试验研究尚有很大差距.为了提升气动弹性控制技术的技术成熟度,需要面向飞翼布局无人机、可变体飞行器等无人飞行器的设计需求,采用理论、计算和实验高度融合的技术路线,发展气动弹性控制律设计的新方法,研究飞机结构−空气动力−主动控制的相互耦合作用机理,揭示结构与气动非线性、时滞效应、不确定性等因素对气动弹性控制系统动力学特性的影响规律,尽早开展大型无人飞行器的气动弹性控制飞行试验.

7 结论

非定常气动力、柔性飞行器结构、主动控制系统的不利耦合给大柔性无人机、变体飞机等先进飞行器研制带来新的挑战,需要发展新的非线性气动伺服弹性(ASE)理论,进而深入研究气动/结构非线性效应、测控时滞、飞行器结构参变/时变效应等对飞行器ASE 行为的影响机理.已有研究主要关注线性ASE 问题,较少涉及非线性ASE 问题.本文面向先进飞行器的研制需求,分别从非定常气动力的非线性建模、非线性结构动力学建模、鲁棒控制律设计、ASE 系统实验四个方面梳理了国内外研究进展,重点介绍了作者学术团队在非线性ASE 力学研究中的若干进展.

非线性ASE 力学属于新的交叉学科研究,对先进飞行器的研制、解决服役飞行器气动弹性问题均具有重要应用价值.从公开文献来看,对该问题的研究并不多见,特别是在面向先进飞行器研制需求的应用基础研究才刚刚起步.在今后一个时期,需要结合大柔性无人机、可变体飞行器的研制需求,开展全机复杂模型和变体机翼的非定常气动力数据驱动建模、变体飞行器参变/时变结构动力学等问题的研究,并持续进行三维复杂模型的非线性ASE 系统风洞试验以及全机模型飞行试验,提高ASE 技术的成熟度.

致 谢国家自然科学基金(11972180,12022203)资助项目.