绕椭球的低速流动研究
2021-11-19丛成华邓小刚毛枚良
丛成华 邓小刚 毛枚良
1 南京航空航天大学航空学院,非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016
2 中国空气动力研究与发展中心,设备设计及测试技术研究所,四川绵阳 621000
3 军事科学院,北京 100010
4 中国空气动力研究与发展中心,计算空气动力学研究所,四川绵阳 621000
1 引言
在一般性研究中,人们通常会将各种飞行工具进行简化处理,如战斗机、导弹、鱼雷、航空飞行器的机身、潜艇、无人水下飞行器、轮船、热气球、飞艇等,都可以简化为轴对称扁平椭球体(下文简称椭球),虽然进行了较大程度的简化,流态基本上是相似的,在一定程度上,可以代表这些飞行工具.由于其应用广阔,详细了解绕椭球的流动特征具有十分重要的工程意义,因此研究人员对绕椭球的流动进行了广泛的研究.对绕椭球复杂流动现象认识的发展是过去70 多年来流体力学发展的缩影.对这类简单外形的研究,也促进了流体力学理论的发展和实验方法的进步.Wang(1976)就是在对椭球绕流的边界层计算中定义了开式分离和闭式分离.
椭球外形非常简单,其外形和无黏压力分布都有解析表达式(Cebeci 和Meier 1987),但绕椭球的流动却异常复杂,甚至远远超出想象.在黏性流动中,按照流动条件的变化,流场的主要特征有驻点流动、局部边界层增厚、流向涡、回流区、强烈的黏性和无黏干扰、受强压力梯度影响的三维边界层流动、流线扭曲、横流分离、自由涡层的形成和演化、转捩等,包含了三维流动的几乎所有基本现象,其中最主要的是分离形成的涡旋运动.
涡旋运动是流动运动的基本形态,是流动结构的主要组成部分.涡之间的复杂相互作用也是流体运动中产生复杂结构的重要原因.因而,涡运动的研究一直是流体力学的重点,因此多年来绕椭球的流动一直是流体力学研究的经典实例.从现实的观点看,理解和预测复杂的流场是为了设计最佳的流动装置,对于指导飞机机身和潜艇艇体等交通工具的设计具有十分重要的工程意义.
对绕椭球的流动开展的大量研究工作,从类型上可以分为实验研究和数值模拟研究,在实验研究中,在风洞、水洞、水槽中对椭球绕流采用了不同的表面流态显示方法,测量流场也采用了不同的仪器.在数值模拟研究中,从求解边界层方程到求解雷诺平均的N-S 方程(Reynolds averaging Navier−Stokes,RANS),最近发展到采用大涡模拟(large eddy simulation,LES)、分离涡模拟(detached eddy simulation,DES)甚至直接数值模拟(driect numerical simulation,DNS),求解绕椭球的流动,采用的湍流模型从代数湍流模型,到应用成熟的k −ωSST(shear stress transport)模型、雷诺数应力模型等.
在计算流体力学(computational fluid dynamics,CFD)代码验证中,研究人员也喜欢采用外形简单但流态较为复杂的外形,绕椭球的流动是很好的算例之一(Dallmann 和Herberg 1995).在转捩的数值模拟研究中,绕椭球的流动也经常作为经典的算例之一.
绕椭球的流动从低速、跨声速(Matthews 1952)、超声速(Newsome 和Adams 1988)到高超声速(郑世超 2019,Schonauer 和Straub 1975)都有广泛的研究,本文主要考虑低速流动,马赫数小于0.4 的情况,在这个马赫数下,气流可压缩性的影响基本可以忽略,因此如果未特别说明,实验和数值模拟时均指不可压缩的情况.
绕椭球的定常流动是复杂的,按照雷诺数不同,流动可分为层流流动、过渡流和湍流流动(Cebeci 和Meier 1987).在相对较高的Re时,流动基本是湍流流动.在有攻角的情况下,贴近壁面流动的边界层会脱离壁面出现分离,边界层从壁面分离后留下的空间形成回流区,回流区会被逆向流动填充,并形成涡流,甚至二次涡流(Simpson 1996).流动分离或许是流体力学中还未得到解决的最重要的物理现象,其根本原因在于流体是有黏性的.分离现象的研究对理解转捩、再附也是非常重要的.分离的周向位置和分离拓扑高度依赖当地边界层的状态,如图1,尾部出现横流分离.

图1
按照气流来流方向的不同,本文将其分为小攻角(小于6°)、中等攻角(6°~30°)、大攻角(30°~45°)和特大攻角(45°~90°)流动.随攻角增加,椭球上的分离向头部移动,如图2所示.随攻角增加,流动形态也发生了很大变化,三维边界层从再附和无旋涡流,变成分离流和由旋涡主导的有旋流动.在大攻角和特大攻角时分离呈现明显的非对称,分离流结构具有明显的非定常特性.

图2
即便是在0°攻角时,椭球尾部也可能出现分离.在小攻角和中等攻角时(参考图1),当流动沿周向从迎风面向背风面流动的过程中,在椭球两侧,气流卷起形成第一个分离涡,形成分离面,分离涡在顶部对称面处和顶部死水中心区域再附.分离线大致与纵轴平行.如果一次涡的强度足够强,在首次分离的尾部,会诱导形成二次分离,气流卷起形成第二个旋涡,位于第一个分离涡的下方.当二次分离区的强度足够强时可能会诱发第三次分离.流动中,主涡可能与一个或多个更小的涡相伴,这依流动条件而定,每个旋涡都有相应的分离线和再附线.攻角小于30°时,椭球两侧的流动和分离基本呈现对称分布.也有研究者认为,当攻角大于15°时,在旋成体的固定位置上,背风面的旋涡会同时和交替地起伏(Hoang 和Telionis 1991).
飞行器为了获得高机动性和高敏捷性,往往需要进行大攻角飞行(张毅锋 2010).在大攻角时(30°~45°),在较低Re时(约103以下量级),流动还能保持对称,但在较高Re时,流动会呈现明显的非对称分离和非定常旋涡流(Zilliac 1989).根据求解边界层方程的结果,在背风面对称线上,对于f=6 椭球,其层流边界层分离的临界攻角是42°(Cebeci 和Khattab 1980).在特大攻角时(45°~90°),流动呈现明显的非定常特性,并出现侧向力.
这些分离以及旋涡之间的干扰使得三维边界层高度扭曲,椭球绕流场的分离对攻角α、雷诺数Re、来流速度U∞、来流湍流度TuI、表面粗糙度都非常敏感,这些因素彼此之间相互诱导、作用形态非常复杂,使得人们对于其背涡的形成机理、流场结构、发展及演变特性等的研究变的更加困难(张丹和郭雪岩 2008).其中对椭球表面涡结构和受力分布影响最显著的是攻角和雷诺数,基本上,分离的幅度和旋涡的强度随攻角的增加而增加.对椭球绕流的研究也主要集中在椭球体表面涡流分布和流动分离方面.
2 参数与坐标系定义
定义椭球的主轴长度为L= 2a,副轴长度为D= 2b,坐标原点设定为椭球头部中心.长细比定义为f=L/D=a/b.诸如椭球类的流线型物体,其长细比为4~8 时,阻力最小(Dorrington 2006).对流线型轴对称外形,在宽范围的长细比范围内,Hoerner 公式(Cd=4f1/3+6f−7/6+24f−8/3)计算阻力系数有很好的一阶近似,如图3所示(Dorrington 2006).

图3
因此在过去的研究中,最常见的长细比为4 和6,这两种比例的椭球在高雷诺数范围内有大量的实验信息,流动经历了转捩,有研究者认为长细比为4 的椭球涡流特性更丰富(Su 和Tao 1996).在航空航天领域,这两种长细比的流场特征很具有代表性,因为采用较大的长细比,在机动过程中,能有效改善其操纵性,但长细比越大,低速时的性能越差,需要采用大攻角飞行提高升力(刘伟和杨小亮 2008).
在讨论流场前,必须建立坐标系,在分析三维流动时,坐标系的选择非常重要,因为应力、梯度、流动角等变量有不同的方向,在流动中,根据坐标系的定义不同,流动状态的描述也不尽相同.
在椭球流动中,坐标系一般有两种设定方法,一种是体轴坐标系,是一种与模型相固定的坐标系,当椭球水平放置时(长轴平行于地面),沿椭球的长轴为x轴,垂直方向为y轴,按照右手坐标系设定z轴.这个坐标系主要用来讨论近壁面的横流.第二种是全局坐标系(global coordinates),也称为风洞坐标系(wind tunnel coordinates)即与来流方向相关,远场来流的方向为x轴,z轴与体轴坐标系相同,按照右手坐标系设定y轴,这个坐标系是第一种坐标系的惯性系,这个坐标系主要用于流动模拟和讨论尾迹.坐标系如图4所示,起点是椭球的前端.为了更好的说明绕椭球的复杂流动,还可以定义更多的坐标系,如探针坐标系(probe coordinates)、物面坐标系(body surface coordinates)、自由流坐标系(free steam coordinates)、壁面并行坐标系(wall collateral coordinates),这里不再一一介绍,具体可以参数文献(Madden 和Simpson 1997).上述讨论的所有坐标系都是正交坐标系和右手系.

图4
沿流向站位:定义不同站位的截面时,沿x轴方向,定义不同的站位.椭球前端为x/(2a)=x/L=0,椭球尾部为x/(2a)=x/L=1.
周向角:定义周向角度ϕ时,迎风面对称面上ϕ=0°,背风面对称面上ϕ=180°.关于站位和周向角,下文若无特殊说明,都采用这种标注方法.
迎风面与背风面:基于体轴坐标系定义,以子午对称面将椭球分为两部分,受气流上洗的为迎风面,受气流下洗的背风面.
雷诺数:在定义雷诺数时,若无特殊说明,特征长度都是基于椭球的主轴长度L= 2a,特征速度采用远场来流速度U∞,密度ρ为来流密度,由于全文都采用了不可压缩假设,全流场范围内密度保持为常数.由于温度变化范围小,黏性系数µ也为常数.
攻角:攻角α在全局坐标系中定义,即来流方向与椭球主轴的夹角.
三个速度矢量(U∞,V,W):在全局坐标系下定义,自由来流速度为矢量U∞,沿y轴方向为V,沿z轴方向为W.
涡量:在全局坐标系下定义.涡量矢量方向与全局坐标系的三个坐标轴方向保持一致.

流动梯度角:在全局坐标系中定义.
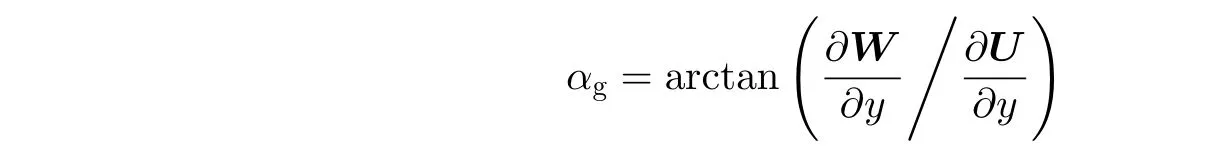

对椭球绕流的认识是从实验和理论研究开始的,在理论方面,从研究小范围分离开始,发展了边界层反方法、边界层分析理论和其他近似分析方法,对于旋涡运动,也发展了类似于边界层的积分近似方法.在实验研究方面,压力测量技术、表面摩阻测量技术以及流场显示技术的发展,也使得对椭球的分离流场和旋涡运动的定量研究有长足的进步,因此下文先介绍实验和理论研究方面的进展.随后介绍在数值求解椭球绕流方面的内容,尤其是近年来,数值求解N-S 方程技术得到了很大发展,绕椭球的分离流场和旋涡运动都可用N-S 方程的数值求解方法给出.
早期的研究主要集中在表面流态和流动分离上,实验和计算方法都发挥了明显的作用.椭球后部尾迹的研究较表面流动晚得多.
3 实验和理论研究
实验是发现新现象和验证理论所不可少的手段,在计算无法进行或计算精度不能保证时,实验是必须依靠的手段.对椭球绕流的实验研究,反映了实验方法和手段的发展,如压力、摩阻等参数的测量及流场显示技术等,对流体力学的发展起了重要的作用(张涵信和周恒 2001).
3.1 椭球绕流场分离的定性描述
绕椭球分离流动的空间结构主要为离开物面的边界层卷起形成的分离涡,分离涡离开物面的位置即为分离线.完整地描述分离流动需要了解流场的三维信息,二维分离有许多可用的分析方法,三维分离却很难用公式定义(Chang 1961),一般只能通过实验研究,可视化对理解流动分离的本质就显得尤为重要.早期通过实验测量三维数据比较困难,而测量表面摩擦力等二维信息则容易得多(祝成民和忻鼎定 2002).几十年来,研究者通过烟雾、染料、油流、氢气泡等方法对绕椭球的流动进行了可视化,例如,利用混有颜料的油在物面上流动形成条纹,可以方便地显示物体表面摩擦力线,因为在分离线每一侧的近壁低速流体都被迫朝着分离区,靠近分离线的涂料会加速,通常偏向分离中更高速一侧,这是使用表面油流可视化的关键基础.
通过研究椭球的表面摩擦力线结构可以推测分离流的空间结构.但早期受限于实验条件和测试技术的发展,一般着眼于层流流线的可视化,因为层流分离时边界层形成的分离涡个数较少,流场结构是较少涡旋相互作用的结果,对层流分离的研究有利于研究涡相互作用的规律,能够对绕椭球的流动进行定性描述.即便是层流,椭球的表面摩擦力线图谱仍呈现出复杂的结构(Su 和Tao 1996).表1为给出的实验条件.
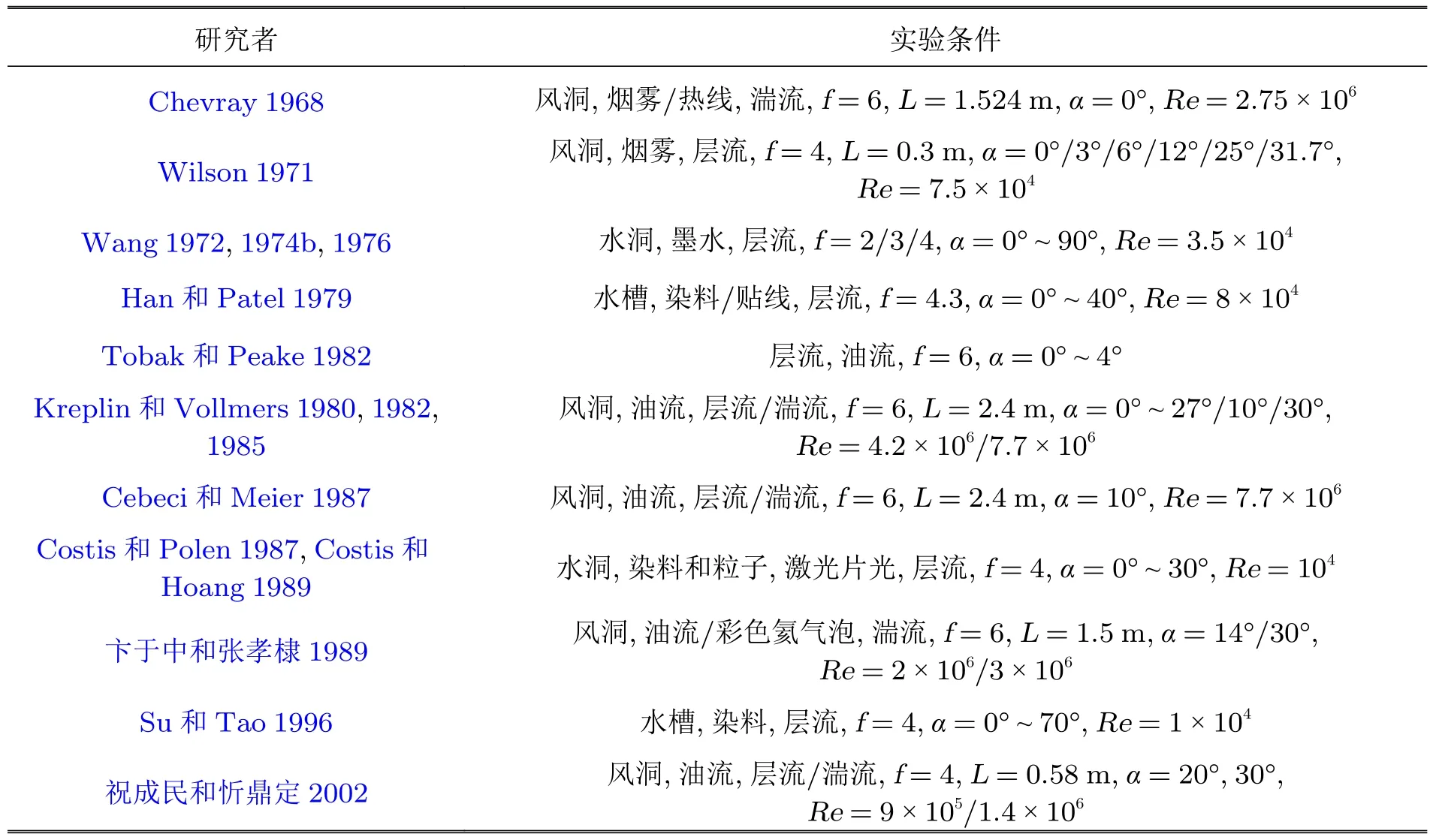
表1 实验条件
Wang(1972)最早开始研究绕椭球的三维分离,基于对称面边界层求解方法,分析了椭球在有攻角情况下的分离模式,表明分离是自由涡层与分离泡之间的融合.攻角较小时,分离泡占据主导,攻角变大时,自由涡层占据主导.攻角继续变大时,分离泡再次占优.Wang 为验证求解结果进行了实验,如图5所示,R是旋涡的起点,S是分离点.在分离点S之前出现旋涡R,反驳了之前通常所认为的概念,即在分离点之前不存在回流.在下游方向上,变平的、接近一致的速度型导致了分离的延迟.
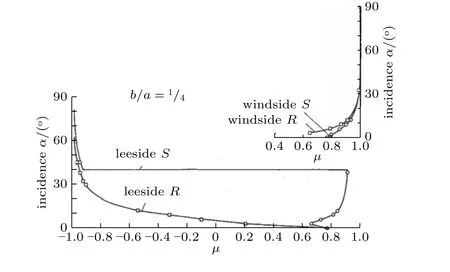
图5
Wang 将迎风面和背风面的旋涡起点和分离点相连,椭球被划分为三个区域,如图6所示,区域A是规则的边界层区域,区域B是内嵌的涡流区,区域C是分离区.攻角<6°时,区域B很薄,边界层的概念仍是合理的,反向的速度V在边界层内部形成了内嵌的旋涡.当攻角增加后,区域B增厚,不再是严格意义上的边界层.

图6
区域A与区域C是容易识别的,区域B受攻角和外形影响,差异很大.12°攻角时,背风面上R与S相距较远,区域B覆盖了背风面大部分.区域A显示边界层特性,区域B则与边界层特性相距甚远,如V反向、边界层增厚,可能已经出现了部分分离.但仅仅V反向,而U未反向,疑似分离肯定只是一类周向分离.而且,靠近对称面处,由于极限流线能仍能从区域A 穿向区域B,分离区必须在两端都是开放的.也就是说,分离线不能与对称面相交叉.区域B是V反向,是开放区域.区域C是U,V都反向,是闭合区域.区域B内的流动更复杂,存在再附和二次分离.如图7所示.
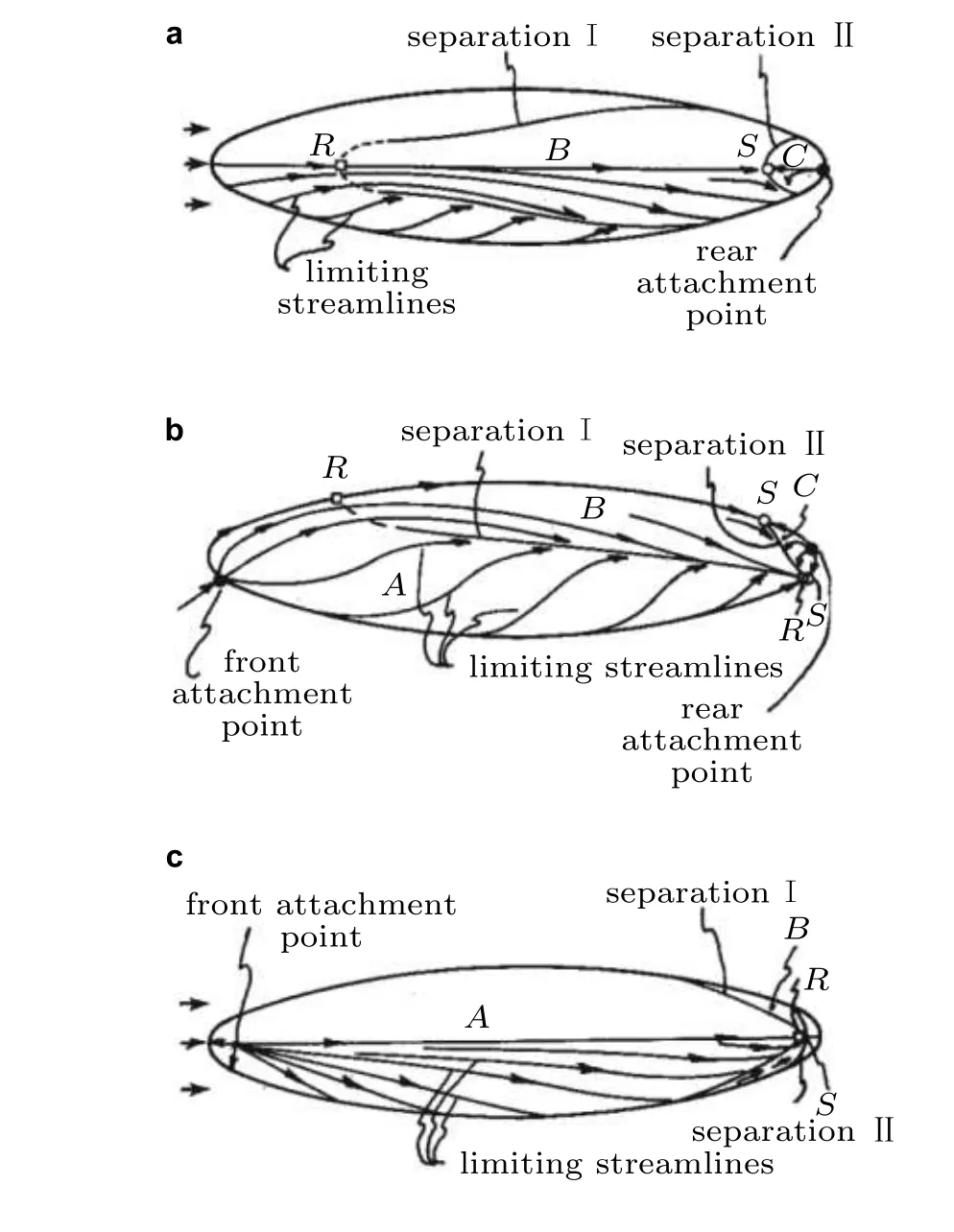
图7
图8给出了12°攻角时随椭球长细比倒数变化时R与S的变化.在迎风面上,R与S总是很接近.在背风面,随着椭球长细比倒数变小,比值小于0.5 后,分离点总是后移的,而旋涡起始点总是前移的.换句话说,越是细长体,流动对攻角的变化越敏感.

图8
通过在背部释放烟雾的方式观测分离点,其局限性是非常明显的,其精度也不高(Wilson 1971).采用染料则精度得到了一定程度的提高.如图9所示,图中黑色区域是染料染色形成的,在尾部,两侧两个相对较亮的区域,表明存在两个闭式分离.在背风面的对称面及附近,流动保持再附.染料一直停留在附近的壁面上,直到在尾部支撑底座附近出现少量的染料.两侧看上去像是闭式分离(分离泡类型)的流动,实际上是大范围的横流区域.图中的无黏流线是通过在边界层外缘释放染料所标记的.

图9
通过图9可以看到,在分离线前缘的流场结构还不清楚.看上去两条分离线转向并合并在一起.这个区域附近的摩阻线的详细模式也还不是很清楚.当攻角为6°~30°时,在一次分离和二次分离之间存在一个有很强的横流区域,再附的染料沿着两条分离线离开物面,形成开式分离,如图10所示.图中的区域I 对应上图9中的黑色区域,在背风面的对称面及附近,流动保持再附.图中类似脑叶外形的区域2 和3 就是前述的横流区域,脑叶的上游和下游边界实际上是分离线.这与Wang 的结果是类似的,Han 和Patel(1979)在实验中也观测到了这一现象.
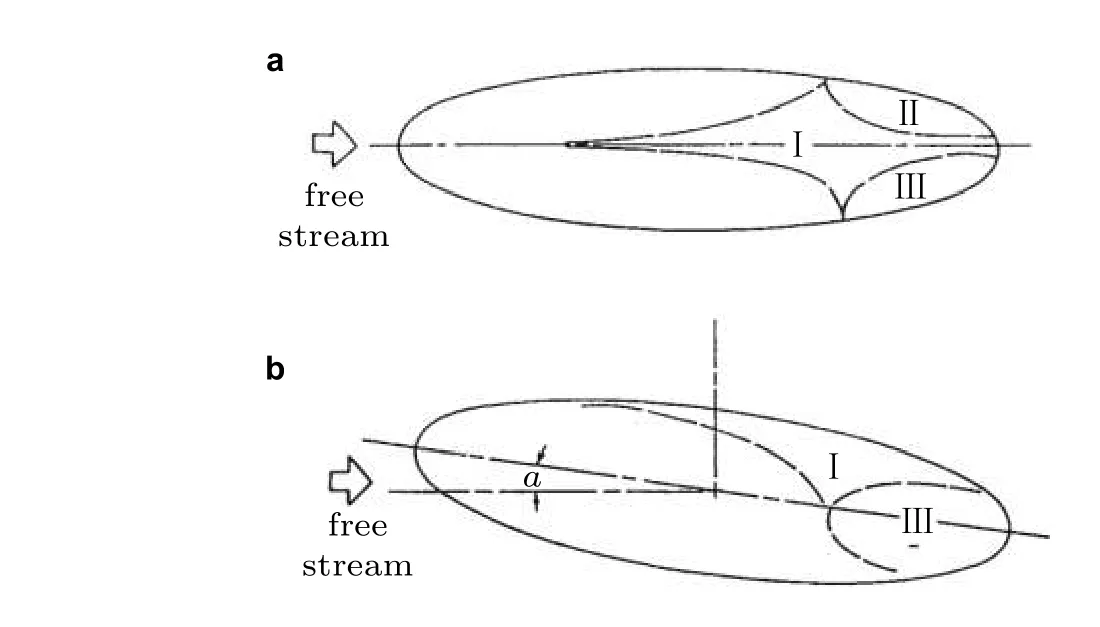
图10
图11给出了按照实验结果所绘制的流场示意图,当攻角为6°~30°时,会分别从一次分离和二次分离线处开始形成两个脱落涡层,从涡层的前缘可以看到,流动形成开式分离,涡层的落脚点处为分离线.一次分离线和二次分离线之间的区域就是就是图10中的区域2 和3.在这个区域内速度剖面是起伏变化的,在横流方向上有很大的分量.随流动发展,这两个涡层很快合并形成一个单独的涡层.因此Re较高时,上游可能是层流,但区域2 和3 已转变为湍流(图9).Kreplin 和Vollmers(1980,1982)在实验中也发现,在这个攻角范围内,背风面分离区的流动会突然由层流转变为湍流.
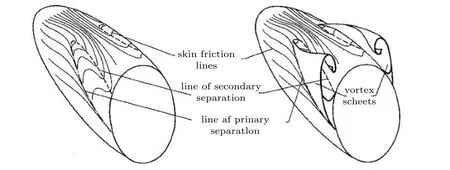
图11
图12是通过染料获得的壁面摩阻和涡层示意图,侧面脑叶内的摩阻线看上去像是S 型.Cebeci 和Khattab(1981)在求解边界层方程时,当在背风面被迫中止积分时,接近达到或非常接近零轴向剪切应力的点,所形成的曲线也是S 型的.一些研究者求解N-S 方程时都清晰地捕捉到了上 面 提 到 的S 型 摩 阻 线(Rosenfeld 和Israeli 1988,Rosenfeld 和Wolfshtein 1992,Zilliac 1989,Shirayama 和Kuwahara 1987).
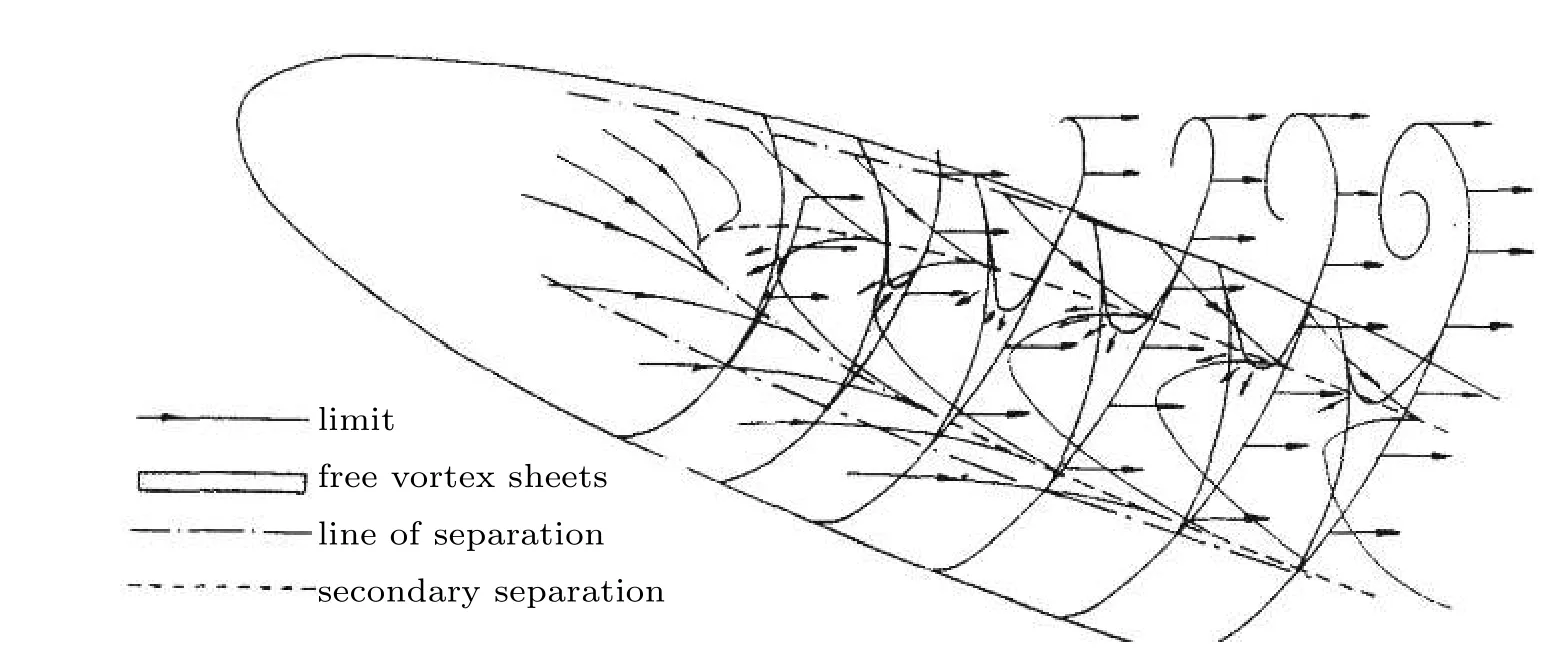
图12
Ahn 和Simpson(1992)研究了雷诺数对流态的影响,认为在流动中存在区分一次分离线特征的临界雷诺数,大约为Re=2.5×106.大于临界Re时,随Re增加分离线不会改变周向位置,但会向椭球的前部移动和背风面方向移动,在更高的Re时,横流分离的影响是主要的.对于较低的超临界Re范围,攻角对一次分离位置的影响没有高Re那么显著,当攻角超过15°时,可能有一对三次分离,其特征与其他分离线是相同的.
欧洲磁悬浮列车研究中设计和建造了一种高速移动轨迹测试系统,用于磁悬浮交通工具模型的气动性能测试,列车头部外形与椭球基本是类似的,使用热线风速计测量了模型后的流场、湍流度和壁面摩阻,以及在前端的转捩位置(Tyll 和Liu 1996).Siclari 和Ende(1995)采用求解RANS 的方法展示了磁悬浮列车尾部的CFD 分离流线,与测试结果基本保持一致,如图13所示.在尾部形成一对向上卷起的横流分离涡,形成尾迹.两个对转的涡诱发了涡旋运动,在这对旋涡间形成下洗,流动保持再附.

图13
国内关于椭球绕流的定性实验与国外几乎是同期开展的.卞于中和张孝棣(1989)在哈尔滨空气动力研究所1.5 m×1.5 m 开口低速回流风洞中测量了截面速度分布及边界层.用表面油流法测出了模型表面上的流态分布,使用彩色氦气泡法测出了模型背风面上5 个截面处的流动参数分布.在攻角α=14°时,在x/L=0.493 处还未分离,到了x/L=0.652 处,流动出现了两个强度不同的旋涡,涡区面积不大,随着旋涡向尾部移动,涡区面积越来越大,分离呈现出轻微的不对称.在α=30°时,在椭球头部附近开始出现分离,在x/L=0.493 处形成两个很明显的不对称涡,到了x/L=0.652 处,对称面一侧物面附近形成一个二次涡和一个三次涡,而且,背风面上的两个涡开始合并,在x/L=0.825 处,两个一次涡合并为一个涡,如图14所示.

图14
尽管油流显示技术已经是研究固体壁面附近流动的常用手段,但在实际应用中仍存在一些问题.最主要的问题是实验效果不易控制.油流实验的效果由模型的几何形状和所用涂料的质量决定.对表面摩擦力较大的流动(如三角翼绕流),比较容易形成清晰的油流条纹,此时涂料的质量对实验效果的影响较小.对摩擦力较小,流场复杂的流动,涂料的质量则起关键作用.后一种情况在分离流的研究中经常遇到,也是油流实验的困难所在.配制油流涂料是油流实验最困难的环节,往往要花几天甚至十几天的时间配制涂料.而且隔一段时间再做不同实验时,上次实验的配方往往不能使用,还需要从头开始配制涂料.在已发表的与油流实验有关的论文中,对实验方法的介绍通常很简单,很难从中找到可靠的方法以获得清晰的油流条纹.祝成民和忻鼎定(2002)对原有的油流实验方法做了改进,新的方法容易掌握,在实验中也很可靠,减小了配制涂料的难度.他们所用涂料以320 目钛白粉作颜料,以200 号硅油和航空煤油作溶剂.
采用上述涂料研究了椭球表面摩擦力线结构(祝成民和忻鼎定 2002).实验在北京航空航天大学流体力学研究所的回流开口风洞中进行,风洞湍流度小于0.3%,风速分别为22.5 m/s 和35.0 m/s,速压不均匀度小于3%.为了研究湍流状态下的流动,在x/L=0.15 处设置了宽5 mm 的粗糙带.将直径约1 mm 的金刚砂用胶水均匀黏贴在模型表面,沙粒约占粗糙带面积的三分之一.实验证实这种方法可以有效地使粗糙带后的边界层流动转变为充分发展的湍流.
Re=1.4×106,α=30°时,层流状态下,一次分离线在尾部终止,在终止处观察到油流涂料的集聚,吹风很长时间此处涂料仍不见减少,推测此处表面摩擦力较小,可能存在表面摩擦力线结点或焦点.图15(d)是采用二阶迎风格式的数值计算结果(Rogers 和Kwak 1990),从中可以看到一个汇聚结点(图15(d)中圆圈所示部分),数值计算得到的是流场的定常解,而实际流动是弱非定常的,在这样高的雷诺数下,数值计算的结果可以作为参考来研究主要的分离线和再附线,不能用于研究流动的细微结构.图15(c)中显示的二次分离线与一次分离线的起点相距不远,两者之间是狭长的再附区.三次分离线起始于椭球后部背风面,延伸到支杆附近后向下偏折.
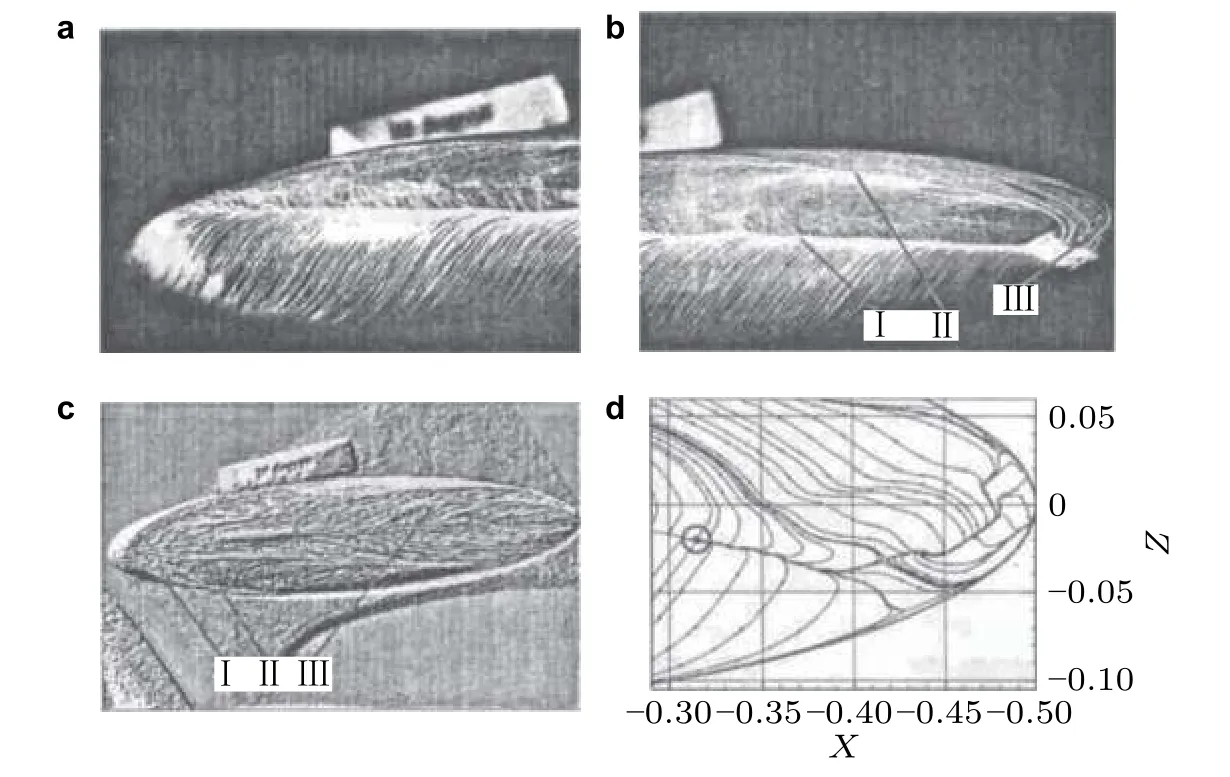
图15
Re不变,当α=20°时,椭球表面摩擦力线的拓扑结构与α=30°时相同,但分离线的位置发生了很大的变化.总体看,三条分离线的位置更偏向下游,一次分离线和二次分离线向下游偏移的距离较小,三次分离线向下游的偏移则非常显著.从图16中可以看到α=20°情况下的三次分离线比α=30°情况下短了许多,其长度约为α=30°时的二分之一.
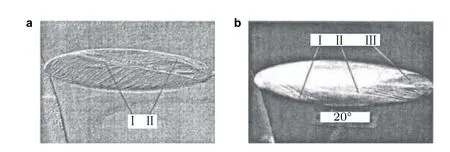
图16
当流动为湍流时,分离线和再附线的位置和拓扑结构与层流状态有很大不同,如图17 所示.在α=30°时湍流状态下只观察到两条.湍流状态下一次分离沿周向被推迟了,一次分离线的位置更靠近椭球背风面对称线;二次分离线的起点约在x/L=0.55 处,二次分离线的长度与层流状态相比缩短了一半.二次分离线的起点也比层流状态下模糊,这表明在该点附近二次分离涡处于较强的非定常状态.在湍流状态下,一次分离线一直延伸到椭球尾部支杆附近.在终止处油流涂料的集聚很弱,其位置在紧邻支杆处.
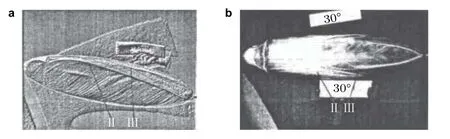
图17
湍流状态下,当α=20°时(图18),椭球的表面摩擦力线具有与α=30°时相同的拓扑结构,但各分离线的位置不同程度地偏向下游.与α=30°时相比,一次分离线和二次分离线之间的再附区明显缩小.
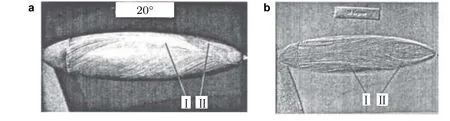
图18
从祝成民和忻鼎定(2002)的研究可以看到,在相同的Re下,湍流推迟了流动分离.分离的推迟又减少了主分离涡诱发次级分离涡的空间,因此,与层流时的3 条分离线相比,湍流时分离线减少了一条,而且二次分离线长度也大大缩短.在层流时很严重的涂料集聚,在湍流时变得很弱,这主要是因为湍流边界层中,高能量的主流离壁面较近,增大了表面摩擦力.
图19(Wetzel 和Simpson 1998)油流所显示的迎风面分离倾向于距离前缘过远,误差产生的原因可能是重力效应,或者是流场和油流混合物间的直接干扰,因为在靠近分离的位置,会发生油流的淤积.而且油流还会影响转捩,导致流场结构出现改变,在有些条件下(如大攻角)误差非常明显,因此油流试验一般用于定性分析.

图19
上述的分析都是基于流动现象的定性研究,没有采用一些特征参数表征流动的分离.对这类流动可视化的解释是存在怀疑和争论的,因为不同的研究者使用了不同的长细比和Re,流动可视化技术本身也受限于分离后的非定常特性,以及染料在低剪切和低速区域的扩散也受到限制,而正是在那些地方,才能发现流动拓扑中最感兴趣的方面(Kim 和Patel 1991).因此无论是染料、油流还是氢气泡方法,都只能对流场进行定性描述,因为这些实验方法会影响流场的发展.即便采用了一种小型装置可以测量边界层流动(Cebeci 和Meier 1987),但受限于当时的技术,无法测量边界层底层的参数,对三维分离的说明仍然是较为欠缺的.由于说明三维分离需要完整的流场信息,需要更为精确地测量才能更为准确地说明流动问题.
3.2 椭球绕流场分离的定量研究
绕椭球的分离流和旋涡运动使流场发生重大变化,改变了流动的压力分布、摩阻分布,甚至产生脉动压力,为定量描述流场变化,需要更为精确的测量.随着测量技术的进步,近年来的实验研究能够给出较多的湍流分离细节方面的测量数据,可以较为完整地描述三维流动的信息.包括采用热线探针(hot wire probe/hot wire anemometer)、热膜(hot-film probe/hot-film sensor/hot film gage)、激光多普勒风速计(laser Doppler anemometer,LDA)、激光多普勒测速仪(laser Doppler velocimeter probe,LDV)等装置进行压力、速度、湍流应力和壁面剪切应力的测量,有些测量装置可以安装在模型内,少量的压力孔、剪切应变测量表和探针可以在模型内绕着主轴旋转,能够在周向获得更多的流场细节(Constantinescu 和Pasinato 2002).其中热膜摩阻幅值测量是最容易和最精确的技术之一,LDV 耗费较大,同时受到需要知晓分离线方向的限制,但仍能提供分离区的细节.表面热膜测量所提供的摩阻数据,能够得到详细的表面拓扑,形成对分离的全局认识.这既揭示了椭球分离流动的重要物理特性,又为检验和验证各种求解器提供了大量的实验数据,对分离现象的研究取得了重大进展.表2给出了相关的实验条件.

表2 实验条件
德国的Kreplin 和Vollmers(1980,1982)第一次进行了较为系统的定量实验,相关实验条件见表2.实验在德国哥廷根DFVLR(现在的DLR)3 m×3 m 风洞中进行,椭球采用玻璃纤维制造,壁面用4 mm 厚的树脂加固.采用热线探针(hot-wire anemometer probe)测量了不同攻角和Re下相应的表面流动、平均压力、局部剪切应力、平均速度.采用热线获取壁面剪切应力是较为容易和精确的技术,而且表面摩擦力结构能够给出分离的全局认识和表面拓扑细节.为了解分离模式,他们也进行了油流实验.
从图20和图21可以看到,在椭球绕流的流场测定中,压力对分离的标识是最不敏感的,但压力脉动局部极小值、壁面摩阻局部极小值与分离的位置相关性很好.分离线会在剪切应力大小的局部最小附近.
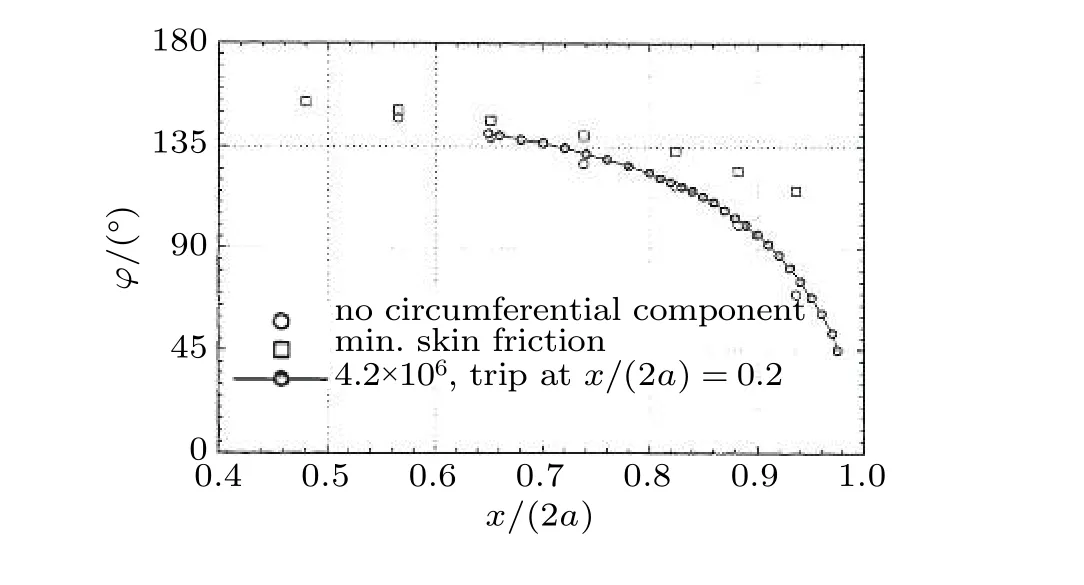
图20

图21
Cebeci 和Meier(1987)为了确认数值求解边界层方程所获得的结果,在DFVLR 的3 m ×3 m 风洞中采用相同的模型重复了实验,来流速度为55 m/s,来流湍流强度为0.2%.实验中使用了颗粒转捩带,将平均直径为0.7 mm 的金刚砂粉喷在x/L=0.2 处,转捩带的宽度为20 mm.沿流向布置了42 个压力计接口,并且可以绕主轴旋转.测量靠近边界层的量时,采用一种小型化测量装置,能够潜入到边界层以下,装置由两个互相垂直的呈现V 字形的镍膜组成的12 个热膜测量仪,以及物面上薄的塑料箔片,等间距的嵌入模型中.热膜测量到了壁面剪切应力相关的脉动信号.沿周向每隔2°测量一组压力数据,在不同站位,沿周向测量了30~80 个位置.以无量纲的形式给出了其速度型、积分量、壁面剪切应力和压力系数,并绘出了表面摩擦力线.当地速度根据探针所测量到的量,采用伯努利方程和偏航修正来计算,如图22和图23所示.
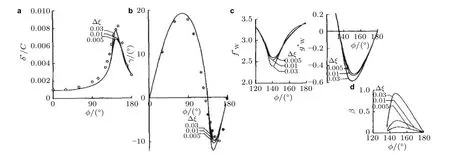
图22
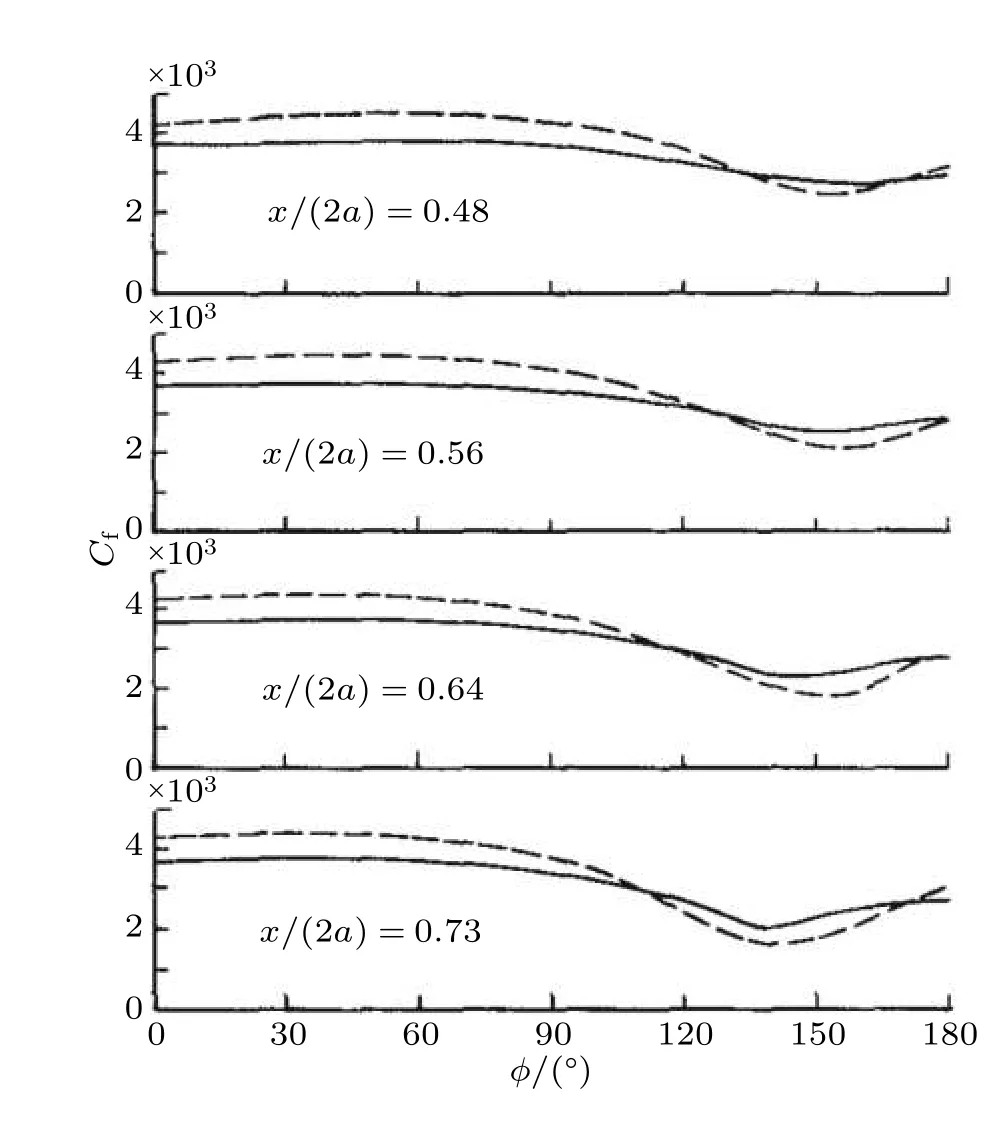
图23
在当地总压保持常数时,假定这个区域就是边界层的边界.尽管这在流动发展到背风面时会导致很大的困难,这是因为背风面导致边界层变厚的静压是未知的.那些厚的边界层是更难解释的,甚至在对称面上也是如此,因为这代表了一种处于轴对称边界层和全三维边界层的中间状态.
自然转捩导致了流动分离,而本文的强迫转捩,流动在整个物面保持再附.通过采用强迫转捩,测量了10°攻角下绕椭球的流动特征,如图24所示.与先前的自然转捩相比,强迫转捩时,边界层在整个物面上保持再附.在流场的一定区域,测量的表面压力与从无黏流动方程获得的压力分布是有差异的.因此使用无黏流方程所获得的压力分布作为边界条件求解边界层方程,在表面压力有差异的位置将无法获得与实验结果相近的解.
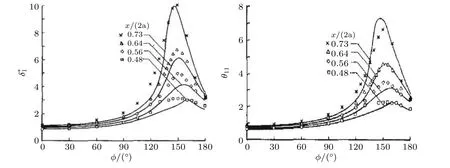
图24
Cebeci 和Meier(1987)通过检验具有指向的摩阻数据,从摩阻数据趋势得到了有用的物理特性,测量了物面摩阻的方向,提供了测量分离拓扑的最直接的方式.传感器仅仅依赖于热交换和摩阻间的关系,这种关系倾向于至少是单调的,实际上,精度在幅值大小上是5%以内,在方向上是10%以内.误差主要是由于认为对流体的加热被假定为是极快的,时间可以忽略,并且与湍流边界层和分离流快速混合.在攻角约为10°时,误差是明显的,因为此时分离才渐渐形成,旋涡较弱,总体上来说带有更多的不确定性.
后来,美国维吉尼亚理工学院的Simpson(1996)针对f=6 的椭球开展了长达十多年的研究.实验是在州立大学1.8 m×1.8 m 稳定性风洞中开展的,该风洞为闭口回流亚声速风洞,实验段长度为7 m,自由流湍流度约为0.03%.椭球采用铝制框架,壁面覆盖玻璃纤维,堵塞度为1.3%.为了固定转捩位置,增加实验的重复性,在x/L=0.2 位置使用了周向转捩带,其直径为1.2 mm,高度为0.7 mm,间距为2.5 mm.转捩带总宽度为20 mm.
Barber 和Simpson(1991)使用五孔探针、X 型热线风速仪测量α=10°,Re=4.0×106时的流动,没有使用转捩带,流动自然转捩.主要对x/L=0.7 与x/L=0.8 两个站位进行了测量.由于五孔压力探针和交叉热线(即X 型的热线探针)的使用,边界层内层的数据需要排除在外.为了能够更为清晰的分辨分离,将坐标系转换为体轴坐标系.从图25中给出的除主流外的其他两个速度分量矢量曲线图能够清晰的看到分离涡区域.
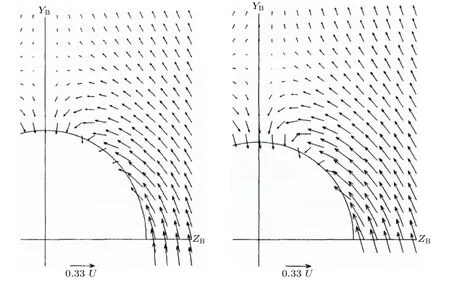
图25
从图26可以看到,沿着椭球的周向和轴向,边界层的增长都是非常明显的.与Kreplin 的结果对比可以发现,在更高Re时,位移厚度会增加,最大位移厚度的位置会向背风面移动.这可能与边界层转捩相关,Re越大,转捩发生的位置越靠近椭球前部,越早发生生转捩,湍流边界层开始增长的越早.在马上就要出现分离的前面位置,压力梯度对湍流产生了结构性改变,边界层会显著增厚,湍流长度尺度明显增加(Simpson 1996).因此,数值模拟时,在马上就要发生分离之前的区域,需要非常精细的网格分辨率,甚至比分离区或者再附区域都还要高(Manhart 2004).

图26
Townsend 结构参数A1 的估算表明,椭球的三维边界层分布与二维边界层是相似的(图27),而对x和z方向涡黏性的估算表明在边界层内涡黏性不是各向同性的(图28).因此在CFD 中,采用各向同性模型不能给出精确的结果,这在下文会详细讨论,这里不再赘述.

图27
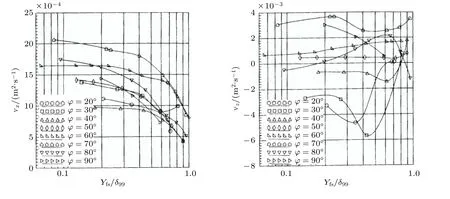
图28
将估算的混合长Lm与广为接受的按照二维理论流动模型计算得到的混合长Lm2d相比,表明二维模型预测的值偏高,如图29所示.

图29
从图30给出的信息可以看到,剪切应力角和流动梯度角在整个边界层内的对比,表明两个角并不呈一直线.在边界层的边界上,剪切应力角大于平均速度梯度角,而在物面上,剪切应力角较流动梯度角延后.

图30
为了更好地理解流动模式,即横流分离,采用油流可视化研究了自然转捩条件下雷诺数和攻角对边界层转捩和分离的影响(Ahn 和Simpson 1992).α=20°,Re=4.2×106时初始分离发生在x/L=0.6,φ=145°位置,分离在x/L=0.762 位置充分发展,根据流线的聚拢,判定分离在φ=123°位置,如图31所示.
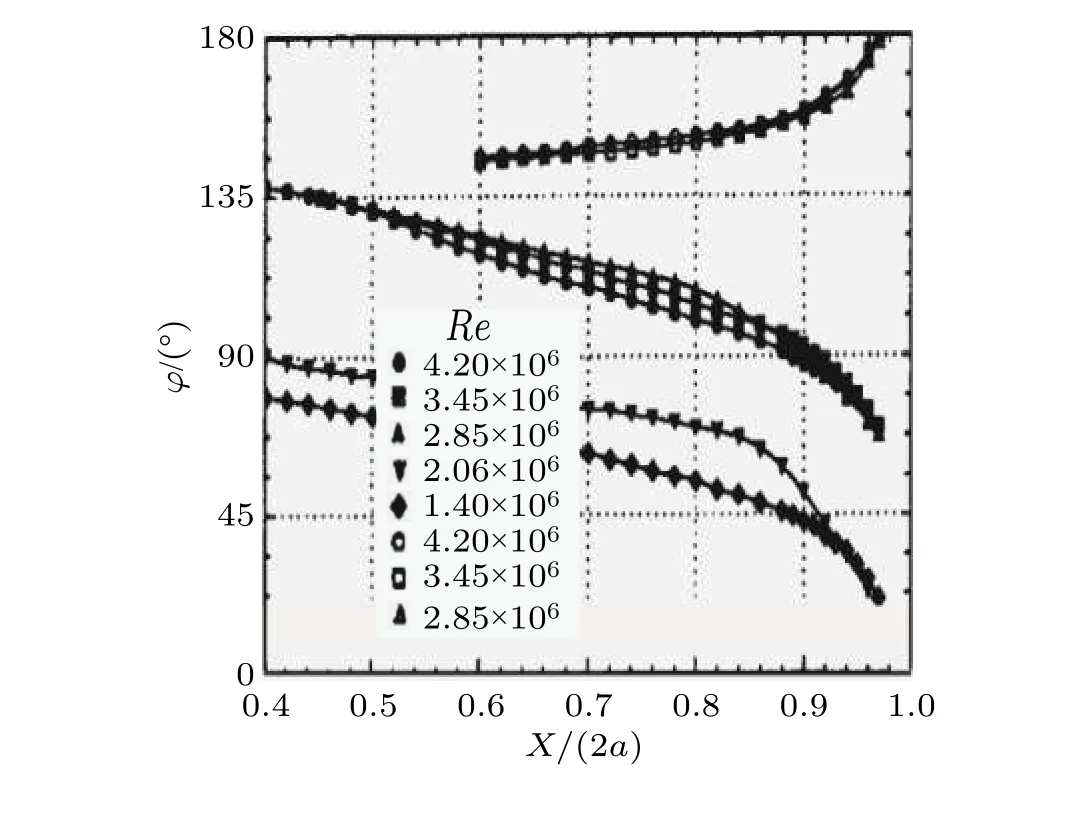
图31
通常热线是不能距离壁面太近的,因此很难获得黏性底层的数据.而对三维壁面受限流动,近壁区域是最重要的区域,速度型的偏移主要发生在那些地方,测量必须要十分靠近壁面,才能测量黏性底层的参数变化.Barberis 和Molton(1995)第一次将LDV 安装在模型内部进行了测量,采用三分量LDV 和三孔压力探针测量了α=20°,Re=5.6×106(f=4 椭球一半与轴线同样长度圆柱体,后部斜切45°)的流场,包括边界层和旋涡结构,测量仪器安装在模型内部,探针可以测量非常靠近物面的三维边界层分离.通过观测发现,边界层逐渐发展,逐渐剪切形成旋涡卷起,然后进入到有序的旋涡中.从图32中可以看到,在800 mm位置,两个矢量基本保持同步,在这个位置下游,除了靠近壁面的薄层外,两个矢量之间方向上的差异开始增加,剪切应力矢量明显落后于速度梯度矢量.这时边界层的扭曲度增加,在速度梯度矢量方向和剪切应力矢量方向之间的差异也增加.对这种类型的流动,基于各向同性假定的湍流模型是不足以进行数值分析的.因为各向同性假定的前提是剪切应力矢量和平均速度梯度矢量是同一方向.

图32
为了克服传统激光多普勒测速仪系统的限制,能够对黏性底层进行测量,Chesnakas 和Simpson(1996)采用了一种创新性的小型化测量装置LDV,如图33所示,为了避免对近壁流场造成干扰,将探针装置放在椭球体内部,通过厚度为0.75 mm 的莱克桑(Lexan,一种高强度透明塑料聚碳酸酯)来观测,测量可以非常靠近壁面,从距离壁面0.1 mm(位于黏性底层,y+≈ 7)到边界层外缘范围内的湍流结构都可以测量,包括横流分离区内贯穿边界层的高精度、高空间分辨率的三个速度分量、雷诺应力张量、速度三重积,再现了边界层内湍流的三维效应,不确定度在1%以内,在此之前很少有可用的类似数据.测量主要集中在x/L=0.762,φ=123°这个位置,从以前的研究得知,这个位置靠近分离线,流动变化剧烈.边界层以外采用热线风速计进行测量.每个边界层位置都测量了14~17 个径向位置.
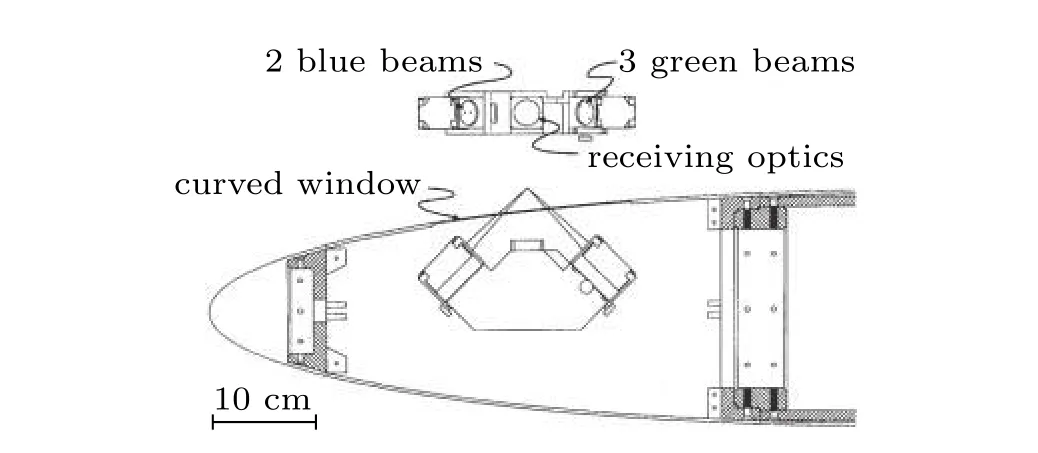
图33
图34,在x/L=0.762 位置,正应力的最大值在边界层内距离壁面是十分远的,大约是y+=12 位置.且占完全的主导地位,的值都非常小.
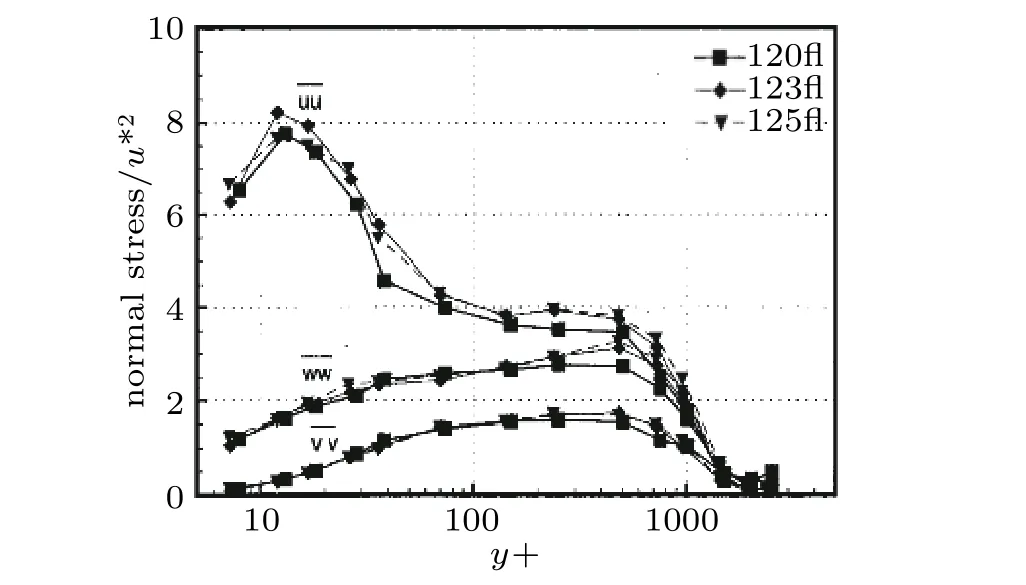
图34
速度三重积主要是用来评估湍动能方程中的耗散项.速度三重积表明在分离线附近,三个方向湍流结构变化都很迅速,如图35所示.

图35
速度型按照Spaling 类型的壁面律进行匹配来计算壁面摩阻.图36三维流动中,摩阻极值是滞后于三维分离线的.x/L=0.6 站位的摩阻局部极低值与Cebeci 和Meier(1987)实验所测量得到的位置非常接近.x/L=0.4 站位的最小摩阻点在150°,而Kreplin 和Vollmers(1985)的测量结果为160°.

图36
图37在整个边界层的大部分范围内,流动梯度角与剪切应力角是不同的,二者存在很少的关联,这表明涡黏性不是各向同性的.Rosemann 和Staeger(1996)也进行了实验和数值计算,分离区的各向异性湍流也通过减小涡黏性和混合长得到了证实.前文提到,Barberis 和Molton(1995)通过增加速度梯度和剪切应力矢量之间方向上的差异也证实了湍流的各向异性.另外,从图37还可以看到,在整个边界层内,湍流生成项和耗散项占据主导.对这种逐渐分离的情况,在分离位置,非平衡湍流效应很强,特别是三重积.在这种分离中,有一些证据表明存在小的非定常流动.
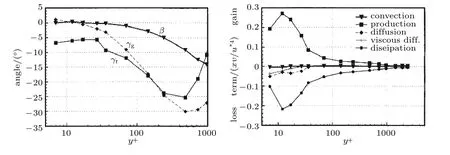
图37
对于旋涡与三维分离的发展是如何相关的,以及分离、再附连同旋涡是如何影响边界层发展的.Chesnakas 和Simpson(1997)的实验分析了这个问题,将测量集中到x/L=0.772 站位,对边界层内的平均速度和脉动速度、平均压力和脉动压力等量进行了测量,结果表明,在大攻角下,流体经过椭球体时,在背风区两侧发生三维分离,其分离剪切层会以螺旋状演化.
图38的流线显示有单个分离,分离起点在123°位置,在165°方位上方存在一个近似1.5 cm厚度的旋涡.压力最低点在90°方位,气流加速绕流模型,之后压力升高,直到出现分离,在分离区,压力处于扁平态.通过LDV 识别到了这样一个最小的速度区域.在这个坐标系中,二次流的流线识别到了分离背风面一侧的低速槽(low velocity trough),也就是在横流分离的背风面某个位置有一块速度非常低的区域.该结果是在与分离线相一致的坐标系中给出的,看上去这个低速槽正好处在分离的位置.Hedin 和Berglund(2001)在LES 模拟中也出现了低速槽.
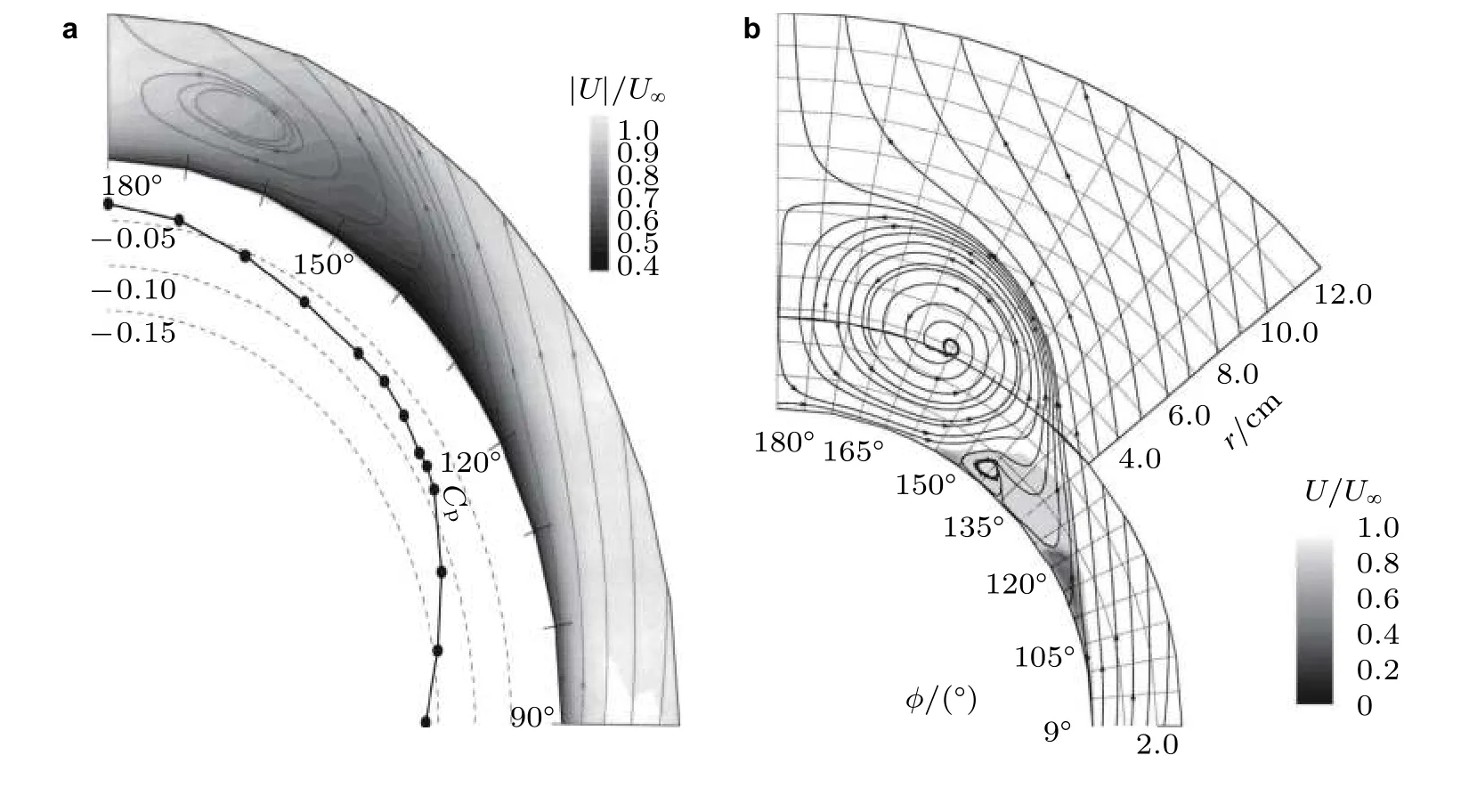
图38
图39中摩阻最小的位置在分离位置下游的某个位置.严格来说,摩阻局部最小不能表征分离,摩阻局部最大也不能表征再附.但从Kreplin 和Vollmers(1985)的测量结果可以看出,摩阻局部最小与分离位置基本相符,因此至少在椭球绕流中可以认为摩阻局部最小表征分离.Wetzel和Simpson(1998)也认为壁面摩阻局部最小的位置,定性与分离位置相对应.综合来看,即使摩阻不能精确预测分离,那么准确地测量摩阻,意味着能够合理地预测分离位置.

图39
螺旋度是涡量和速度的点积,可以用来识别流向涡,也能用来定位旋涡的位置.又可以用来识别三维分离.图40中白线表示0 螺旋度.正螺旋度表征了二次涡,负螺旋度最大的位置是第一次分离的中心.
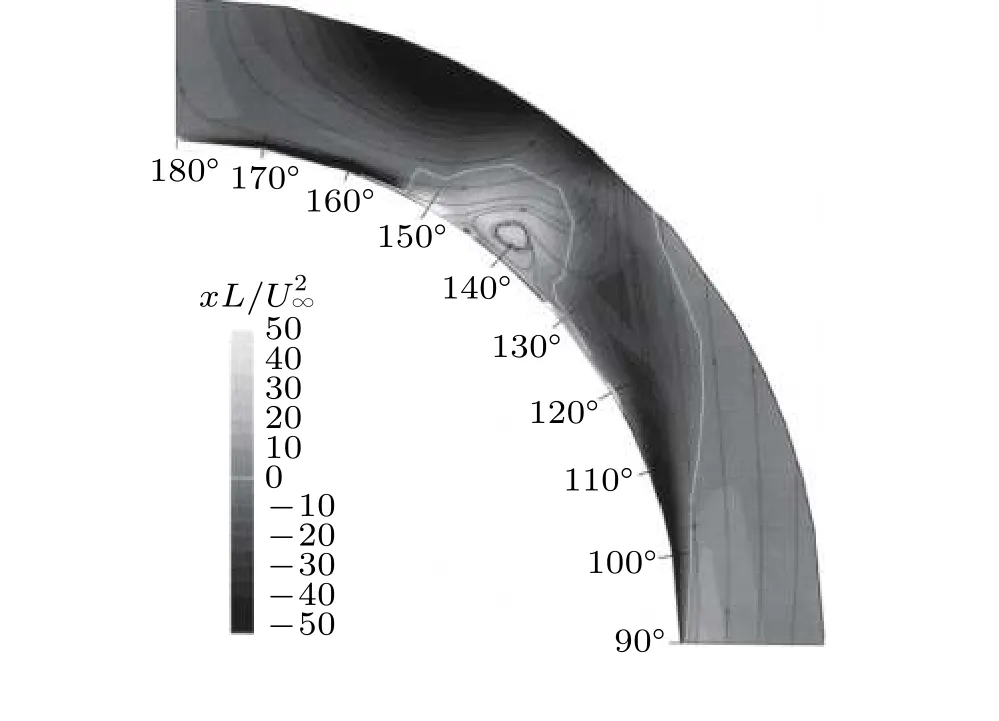
图40
图41,在整个边界层内剪切应力角与流动梯度角相近,气流显示各向同性.在边界层外,二者差异增大,涡黏性呈现越来越重的各向异性.涡黏性的各向异性对速度剖面和剪切应力角都有很大的影响(Ragab 1982).因此对于强三维流动,为准确辨识分离区域内的流场变量,必须使用基于涡黏性各向异性假定的湍流模型.而大多数成熟的工程所用的湍流模型对涡黏性都做了各向同性假设,即假定剪切应力角和平均流动的角度相同.

图41
在上述工作的基础上,Wetzel 和Simpson(1998)对横流分离进行了进一步分析,横流分离的特点是开式分离,因为分离线在物面上有一个自由终点.Yates 和Chapman(1992)也认为许多类型的分离在物面上有特定的奇点,横流是个特殊的例子,它并非起源自唯一的奇点,而是起源自驻点,如同所有的流线一样.Han 和Patel(1979)的实验和Wetzel 和Simpson(1998)的实验都验证了Yates 的观点.
图42中横流方向上的摩阻分量Cflat,与速度W方向相同,在分离位置接近0.这些数据是在体表面坐标系中给出的,而不是垂直于分离线的坐标系中(作者注:这与Chesnakas 的分析方法完全不同,因为Chesnakas 是在分离坐标系中给出相关数据的),因此在分离处并不是精确的等于0.总摩阻幅值的极小值与平行于模型轴向的摩阻分量的极小值相对应,换句话说,这表明在U速度分量,也就是平行于模型轴向的分量,在近壁面处也有一个局部极小值.Wetzel 和Simpson(1998)和Goody 和Simpson(2000a)建立了通过壁面剪切应力的幅值局部极小是三维横流分离最简单和最精确的识别标志之一.这是由于横流分离位置低速区域的存在,导致摩阻幅值较小.壁面剪切应力在再附和大的旋涡位置则达到很大的局部极大值.Cebeci 和Meier(1987)认为壁面剪切应力幅值最小并不是分离的严格定义,但在椭球流动中用来识别分离的效果不错.

图42
图43给出了Chesnakas 和Simpson(1997)与Wetzel 和Simpson(1998)中摩阻的差异,他们在相同的风洞中采用相同的模型进行了测量,Chesnakas 比Wetzel 的测量值低大约30%(10°攻角时)到50%(20°攻角时).这些数据测量的位置有轻微的不同,Chesnakas 位于x/L=0.77,Wetzel 位于x/L=0.729,然而这种差异更多的是由于所采用的测量技术不同所导致的,Chesnakas 是采用LDV 测量的速度型拟合壁面律曲线后计算的摩阻,Wetzel 是热膜直接测量的.虽然二者在数据大小上存在差异,在分布趋势上是一致的,也就是说基本不影响对流场特征的判断,可以看到,在两个攻角下,摩阻的局部极小值和局部极大值基本是吻合的.

图43
Goody 和Simpson(2000a)的测量结果显示(图44),近壁面的湍动能(turbulence kinetic energy,TKE)也遵循这一规律,即在分离位置达到局部极小值,分离区域的上升气流将TKE 带离壁面,而二次再附区将TKE 带回到壁面.
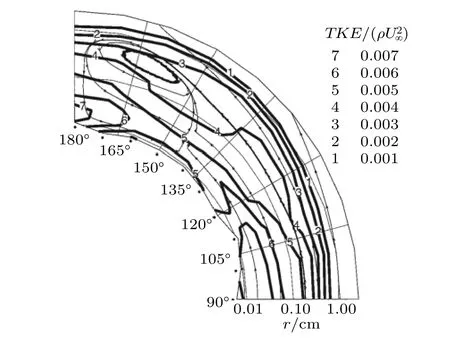
图44
国内关于椭球绕流的定量研究在时间上与国外基本一致.卞于中和张孝棣(1989)在风洞中用激光测速仪测量了边界层,在测量中采用自由转捩.图45表明,在α=14°,在x/L=0.652 处,迎风面上的边界层很薄,背风面上的边界层是典型的二维湍流边界层.还可以看出,边界层的分布相对于子午面是不对称的.

图45
后来,严崇禄和曹露洁(2002)分析了分离后主附着涡剪切层内的涡量结构及其分布,认为椭球绕流场分离剪切层内的离散小涡特征,与三角翼尖前缘的分离流动内的离散小涡特征是一样的,为此对流场内的涡量分布以及离散小涡与主涡之间的关系,在北京大学低湍流度风洞进行了实验,来流湍流度为0.08%,椭球材质为有机玻璃.六线涡量探头由三组xz平面的X 型探头(热丝两两相距1 mm)和一组位于xy平面的X 型探头(热丝两两相距2 mm)组成.探头的外形尺寸为6 mm×6 mm,探针的外缘距离壁面的距离可以控制在1~1.5 mm 范围内,即探头中心距离壁面4~4.5 mm.实验的采样频率为100 kHz,实验测量的速度不确定性小于.
在x/L=0.75(注意,他们所选的截面与其他所标注的不同,这里的截面位置是按照全局坐标系所选取的截面)湍动能,雷诺应力u′v′的分布见图46(图中的标值为原值的100 倍).可以看出,湍动能高值区主要集中于分离流两侧的主附着涡的中心附近,而在脱落涡的左上方有低值区域,这是由于平均速度梯度和雷诺剪切应力都很小,造成湍动能的产生项在该区域也很小,湍动能的分布与Goody 和Simpson(2000a)得到的测量结果相符合.湍动能各个分量的最大值分别为0.0213,0.0341 和0.34.与比较,非常小,所以湍动能的贡献主要来自于项,这说明剪切分离对平均流向速度U和脉动速度u′的影响很小.雷诺应力的最大值位于湍动能低值区域的边缘,这说明雷诺应力分布与平均速度梯度的分布是不相同的.在分离流脱落涡附近区域,其湍动能产生项是正值,这验证了分离流内湍动能是通过吸收平均动能来维持的结论.
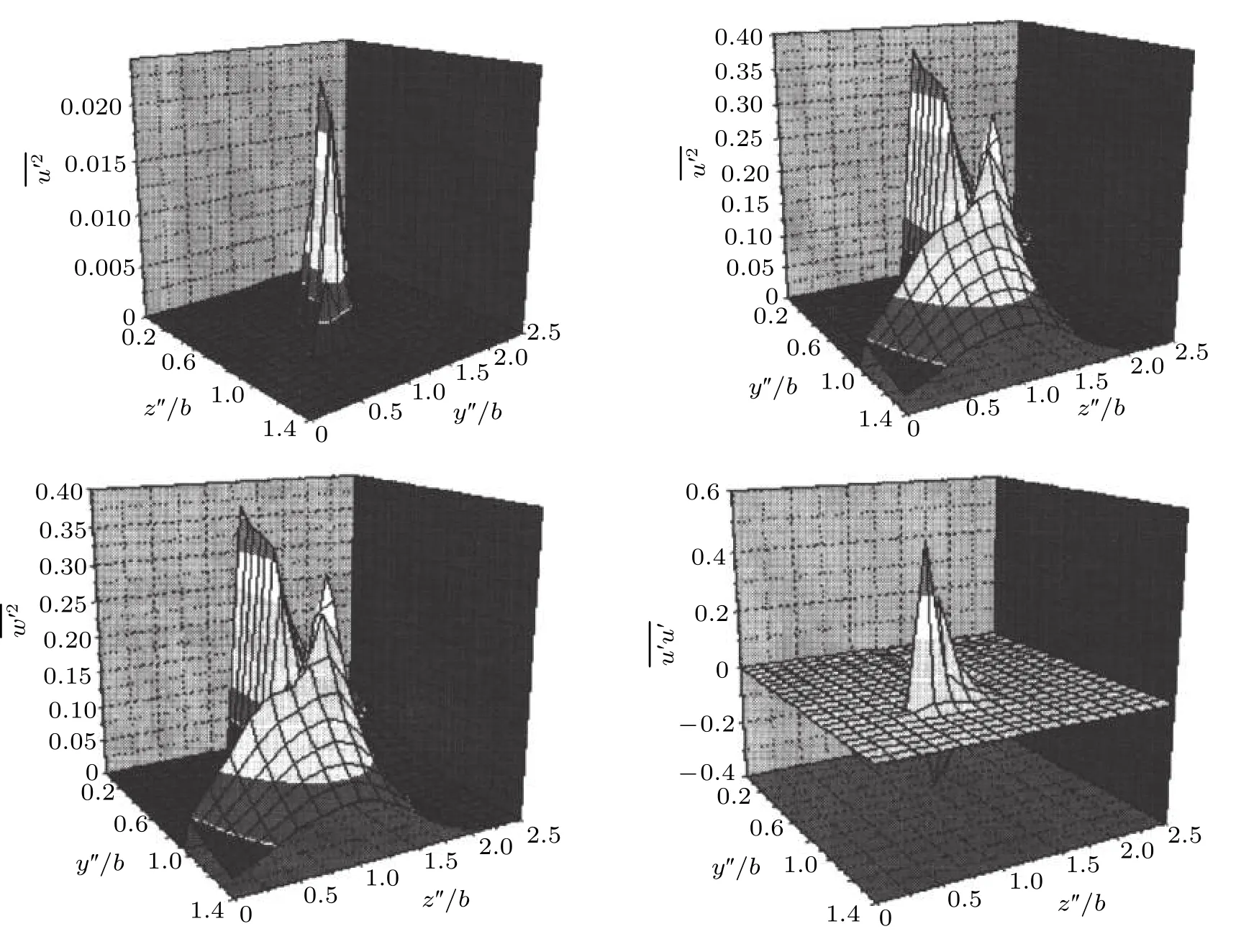
图46
图47给出了截面A-A上的Ωx的涡量分布(其他两个截面未给出).由沿流向三个测量截面的结果可以看出,沿流向其主旋涡自前向后逐渐扩大,且主旋涡中心位置向椭球外侧移动,并逐渐向上抬高.
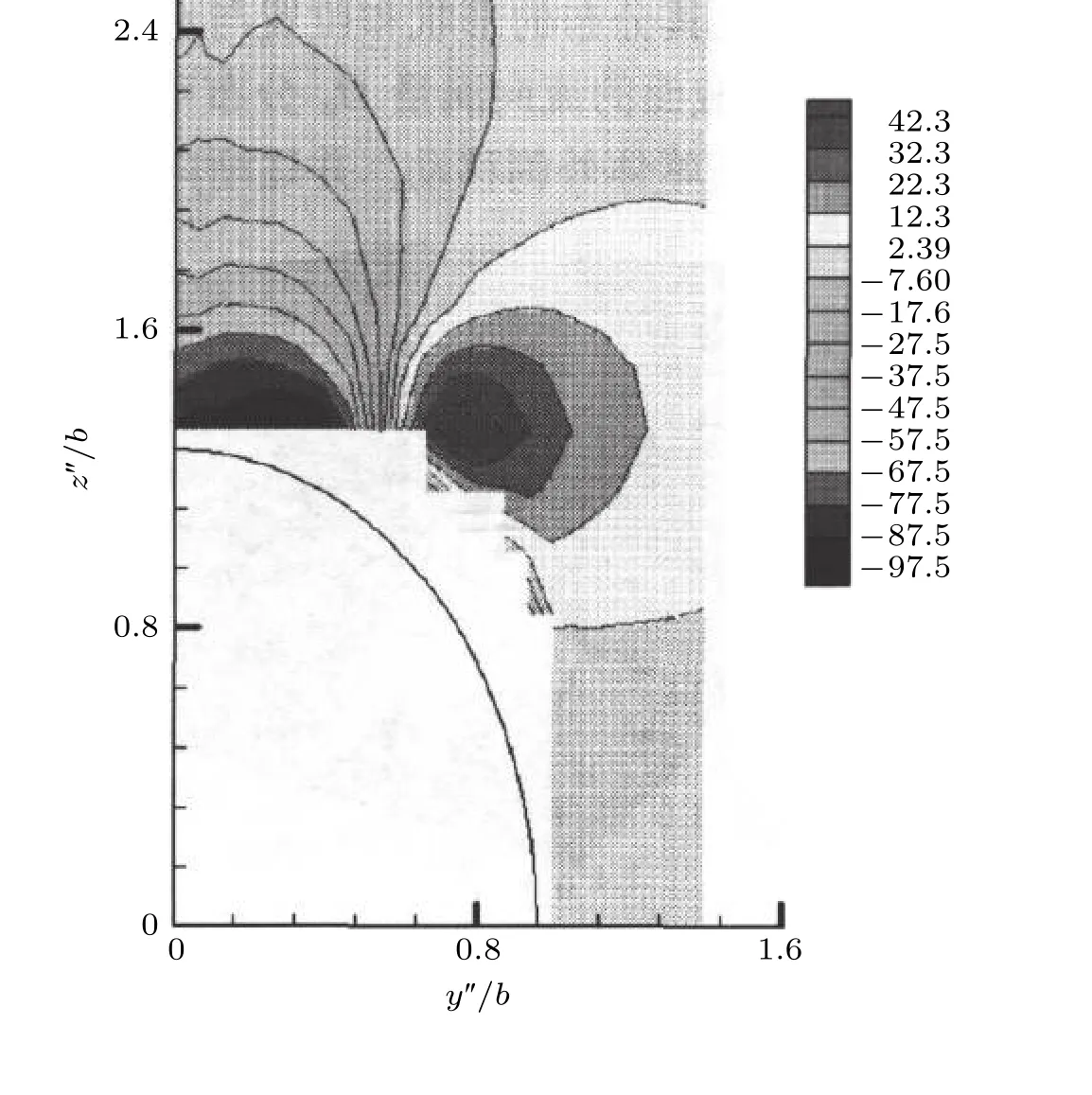
图47
背风面分离流内附着大涡外缘剪切层的特性,采用单丝热线探头测量流向速度脉动量u′,对u′及其湍动能进行频谱分析,可以得到分离剪切层内离散小涡的频率分布,通过判定经过某一截面内离散小涡的湍动能最大值所在的几何位置,得到了背风面分离流内主附着涡的剪切层的外缘轮廓曲线.这与六线涡量探头确定的背风面分离流内附着主涡的外缘轮廓形状是一样的,位置相互吻合.该曲线与水槽中用氢气泡做的流动显示结果(图48左上角)和用六线探头测量的结果(图47)相比较,三者符合得很好.而流动显示照片是在Re=8×103的条件下获得的.在截面A-A上测得的Ωx分布,其中心位于(1.5,0.8)处.而用频谱方法得到的分离流内主附着涡剪切层外缘轮廓的曲线,其中心位于(1.5,0.7),二者几乎重合,这表明用频谱分析法来确定背风面分离流中主附着涡剪切层外缘轮廓曲线是可靠的.这也从另一方面说明椭球在大攻角时所产生的分离剪切流,如同三角翼前缘分离流一样,背风面上方的主附着涡外缘层是由一系列的离散小涡构成的,虽然两种分离对象的形状截然不同,但所构成分离流动的小涡特性,二者相同.Goody 和Simpson(2000a)也认为其流动的主要特征是流场中存在着由剪切流分离引起的脱落涡,并且伴随主涡还有许多个离散小涡,而每个小涡的演化又与其各自的分离线有关,其相互作用会形成高度扭曲的三维螺旋状的剪切层.

图48
3.3 椭球绕流场分离的辨识
过去的研究主要集中在两个问题上,一是分离线的本质,二是三维分离的起源.椭球绕流分离的识别问题,其实关系到对三维定常黏性流动分离的识别或者如何识别分离线的问题.边界层稳定理论、流线谱稳定性理论、剪切层理论都可以用来解释或预测分离问题,但这些预测都有着先天的缺陷,在小攻角范围内准确性较高,在大攻角下往往不能合理预测.
Prandtl 认为逆压梯度是流动分离的必要条件,这一经典理论对于层流适用,对于湍流则还存在很多问题(熊英 2019).Chang(1961)认为分离是壁面上出现的回流.在绕椭球的横流分离流动中,是没有流动反转的开式分离.Constantinescu 和Pasinato(2002)则认为回流和剪切应力消失这两个众所周知的效应,并不总是与三维分离相伴随.Wang(1972)认为分离线是壁面极限流线的包络.Wang(1975)、Cebeci 和Khattab(1981)使用有限差分获得边界层方程的数值解表明,在靠近壁面流线聚集到一起形成包络线的位置,求解过程会出现中断,他们认为求解中断的位置为分离线.van Dommelen 和Cowley(1990)将分离描绘为由于流体单元沿着其运动路径奇异收缩而形成的前锋面.Delery(1992)认为三维分离导致了旋涡结构的形成,分离起源于黏性层的卷起,黏性层初始是包含在薄薄的边界层中的,在压力梯度的作用下,从物面弹起进入到外部的平均流中.也就是说,某个流体层具有较大的壁面法向速度,将气流带离物面,形成分离.在二维定常流动中,通常认为零剪切应力的地方就是分离发生的位置,在分离点下游,剪切应力的值为负,速度的纵向分量与主流方向相反.再附后,摩阻由负转正.图49中二维分离沿流向形成分离泡,也称为旋涡,流线形成封闭的曲线.分离区最外侧的线称为分离线.在三维流动中,用零剪切应力定义分离是不充分的,甚至是无效的,因为旋流区可以脱离物面而剪切应力并没有消失,除了有限的几个点,这些点被称为临界点或奇异点.同时由于在三维流动中剪切应力是矢量,很难识别分离的存在和精确位置.

图49
为了对三维分离形成直观的认识,必须找到一些基本的流动变量来识别分离位置,比如压力、速度、涡量、摩阻、流向角等.早期研究认为,在出现分离的地方,这些参数的分布都没有快速改变或出现极值(Yates 和Chapman 1988).在CFD 中,分离位置也不是直接计算得到的,也需要得到与实验中相同的基本量,因此CFD 中会遇到同样的问题.
分离位置是涡量较为集中的区域.在三维分离流中,涡量在整个流场中的变化是平滑的,没有间断,无法定义旋涡的范围和涡核.对横流分离,物面上或者与分离相关的气流中,没有三维临界点,也没有与分离层边界相对应的唯一流线.在分离起始点的下游,流场具有所有分离流的特性,即在物面上极限流线有很强的聚集特性,气流中有涡量的集中区域,在螺旋流线区域内那条具有最小曲率的流线就是旋涡的中心线,这条线具有最大归一化螺旋度,是分离层的边界,这依然无法识别分离的准确位置(Yates 和Chapman 1992).
从流动图像上看,通过极限流线是可以识别分离的.Lighthill 认为壁面极限流线收拢的概念可以看作是三维流动分离的判据.Tobak 和Peake(1982)认为三维流动分离的一个必要条件是摩阻线聚拢为一条线,但却不是分离的充分条件.Chapman(1986)也认可这一结论,摩阻线收拢到一条特别的摩阻线是必须 的,但 还不足以描述分离线.Costis 和Telionis(1988)、Costis 和Hoang(1989)认为椭球的分离线大致平行于体轴,相对于来流方向是倾斜的,由此提出了一个在二维分离中不存在的三维分离特征,即在三维流动中,边界层内代表涡量的涡线(即涡量矢量方向)不再平行于分离线.Wetzel 和Simpson(1998)认为绕椭球的分离线源自一个或多个临界点,在定常流动中,在靠近壁面处,摩阻线是极限流线的投影,椭球上的开式分离是通过摩阻线的收拢所反映的.
张涵信(2002)对这些争论做了总结,给出了判定三维流动分离的条件,他证明,当用N-S 方程描述黏性流动时,给出的分离线是壁面极限流线的收拢渐近线,且本身也是极限流线.只有当用边界层方程描述分离流动时,给出的分离线才可能是壁面极限流线的包络.
在绕椭球的流动中,横流分离是由于背风面剪切层(或旋流区)明显加厚和具有相对较大法向速度分量流体层的形成而产生的,这个分离层和分离线有一致的边界,在迎风面和背风面的流体间有一个交界面.剪切层增厚能否看作分离,其最本质的是由于分离而离开物面的流体是否与外层无黏流之间存在交互作用,没有相互作用,则认为出现了分离.分离使得法向边界层破碎(离开物面或中断),此时垂直壁面的速度分量的值产生了间断,导致流体从物面出现了明显脱离.在分离的相反一侧产生了气流聚集区域(Simpson 1996).van Dommelen 和Cowley(1990)从Lagrangian 观点描述了三维分离的特征,认为在分离位置,奇异性的渐近结构是准二维的,位移厚度会快速增加,形成新月形的山脊.从图50给出的位移厚度分布可以看到,在靠近分离时,位移厚度确实出现了明显的加厚,但却完全无法显示分离的起点(Wetzel 和Simpson 1998,Patel 和Baek 1985).
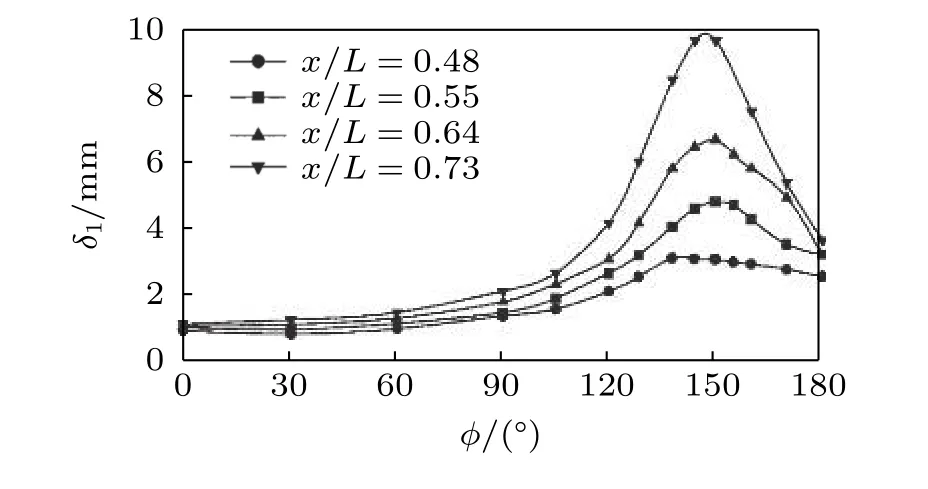
图50
为了识别椭球横流分离的准确位置,Wetzel 和Simpson(1998)使用几组不同的数据评估了识别三维横流分离位置的参数和技术(图51和图52).前面提到,摩阻的局部极小值在椭球的横流分离中可以作为识别分离的最简单和最精确的标志之一.零横流速度也尝试用作分离标识,因为物面分离线是极限流线,垂直于分离线的横流速度必须为0.二次流流线的位置依赖于坐标系,这是因为所有流线上的横流速度,在一个与流线相切的坐标系中,都等于0.通常,横流分离线大致与体轴平行,但为了精确,速度数据必须转换到与局部分离线相切的坐标系中,因此,全局数据要求知道分离线的方向.采用不同的横流速度辨识分离位置,结果差异很大.因此小的坐标转动,会导致所识别的分离线有很大移动,修正分离位置也有相对较高的不确定性.
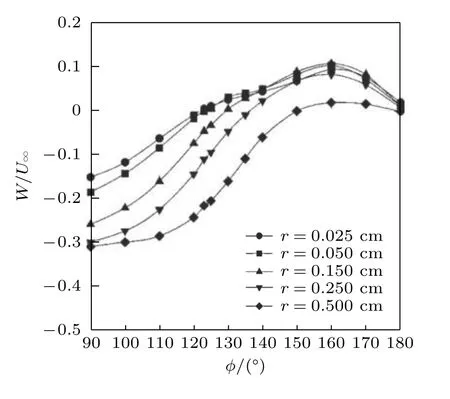
图51
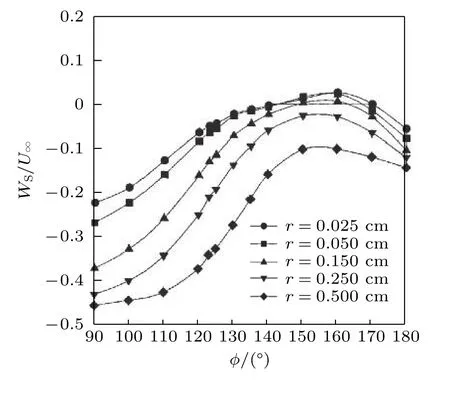
图52
在靠近分离的位置,壁面法向速度是最大的,然而最大的壁面法向速度与分离位置并不精确对应.分离层是垂直物面的,很快就会朝背向扭曲,远离物面.而且,速度测量在局部和全局测量要求之间有明显区别,使用方向上片面的假定(即假定方向一致)将会是局部不准确的,除非首先获得全局信息.相比之下,摩阻则没有这种特性,它不依赖于坐标系.因此很难使用法向速度作为分离的直接判据,因为与近壁的非零速度相比,实验中测量的不确定性与之相比显得太大了.在CFD 中也很难使用法向速度作为分离的直接判据,因为根据黏性流的壁面条件,与近壁的非零速度相比,截断误差或者是数值噪声与之相比也显得太大了.
压力数据可以用来表征大范围分离的存在,但压力对分离的标识是最不敏感的,图53可以看到,压力几乎不能用来标识分离位置.原因是空间给定点的压力受到整个流场很强的影响.在分离区(图中用摩阻的局部最小表示了分离点),压力分布非常平坦.很难在这个曲线上指定一个起点.
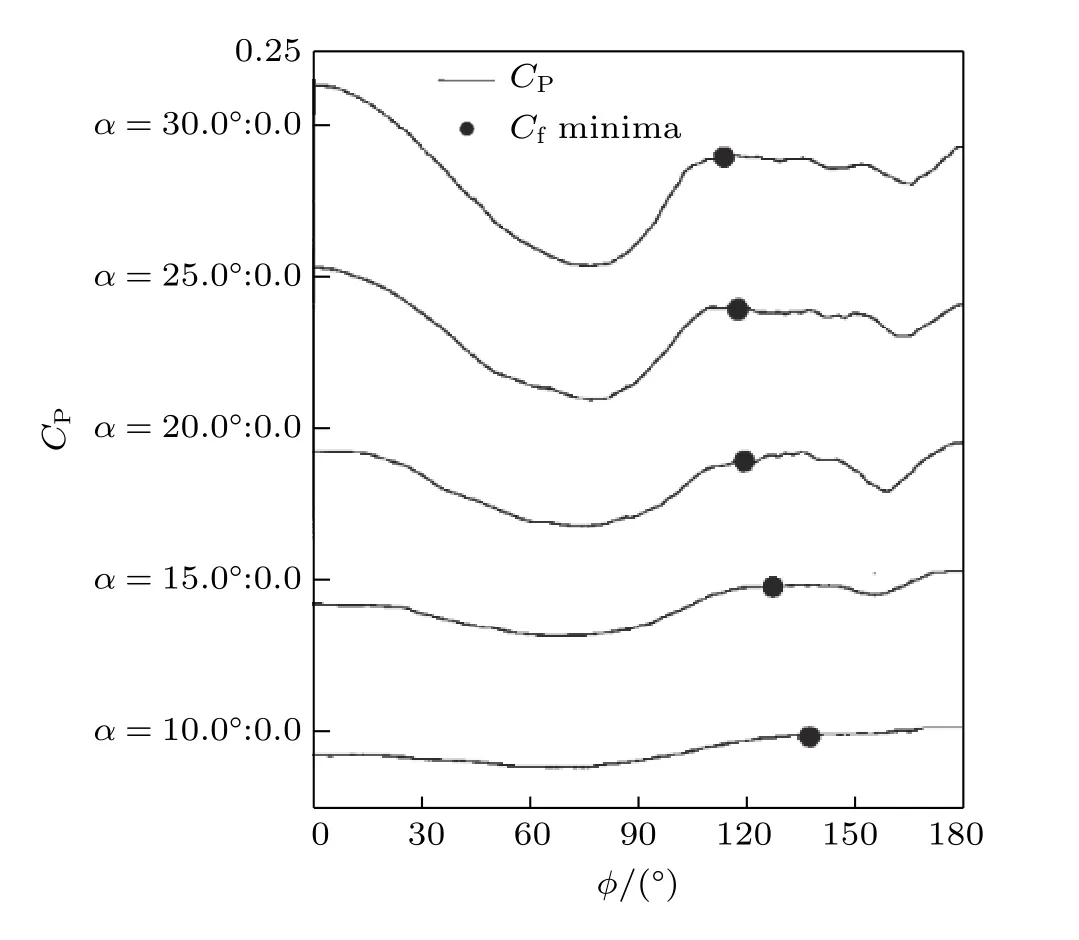
图53
虽然压力无法标识分离位置,但压力脉动极小值与分离的位置相关性很好.如图54所示,在靠近分离的位置,压力脉动达到最小值.测量时,沿周向的间隔为5°,如果能够测量间隔更小,或许对分离点的辨识会更精确.表面压力脉动低的区域直接就是湍动能低的位置,可以认为,迎风面的分离,增长的湍流边界层让压力脉动增加,在靠近分离的位置,大范围的出流,连同分离,一起将湍动能带离壁面,因此分离时压力脉动减小.背风面的分离,大涡分离流场产生了非常大湍流结构,导致压力脉动增加.分离并不是严格意义处于压力脉动最小的位置,但这确实是一个很好的非直接标识,如同摩阻幅值一样.实际操作中,表面压力脉动的精确测量很困难,这源于复杂的修正问题、非常宽频的要求、大量的数据需要统计.

图54
图55给出了不同方法获得的分离线,可以看出,油流所识别的分离明显靠前了.尽管测量时的雷诺数不同,但当Re>2.6×106后,尾部的横流分离对雷诺数是非常不敏感的(Ahn 和Simpson 1992).LDV 体轴测量的数据提前了15°.将速度数据转换到平行于分离线后,分离的位置推后了大约20°,为143°.这种数据修正的方向是正确的,但相对摩阻最小的位置推后了大约5°,这主要是由于分离线方向角上的不确定性.从图中也可以看到,恒流传感器和恒温传感器测量结果也存在一定的差异.采用不同的实验技术,分离线的差异也非常大.
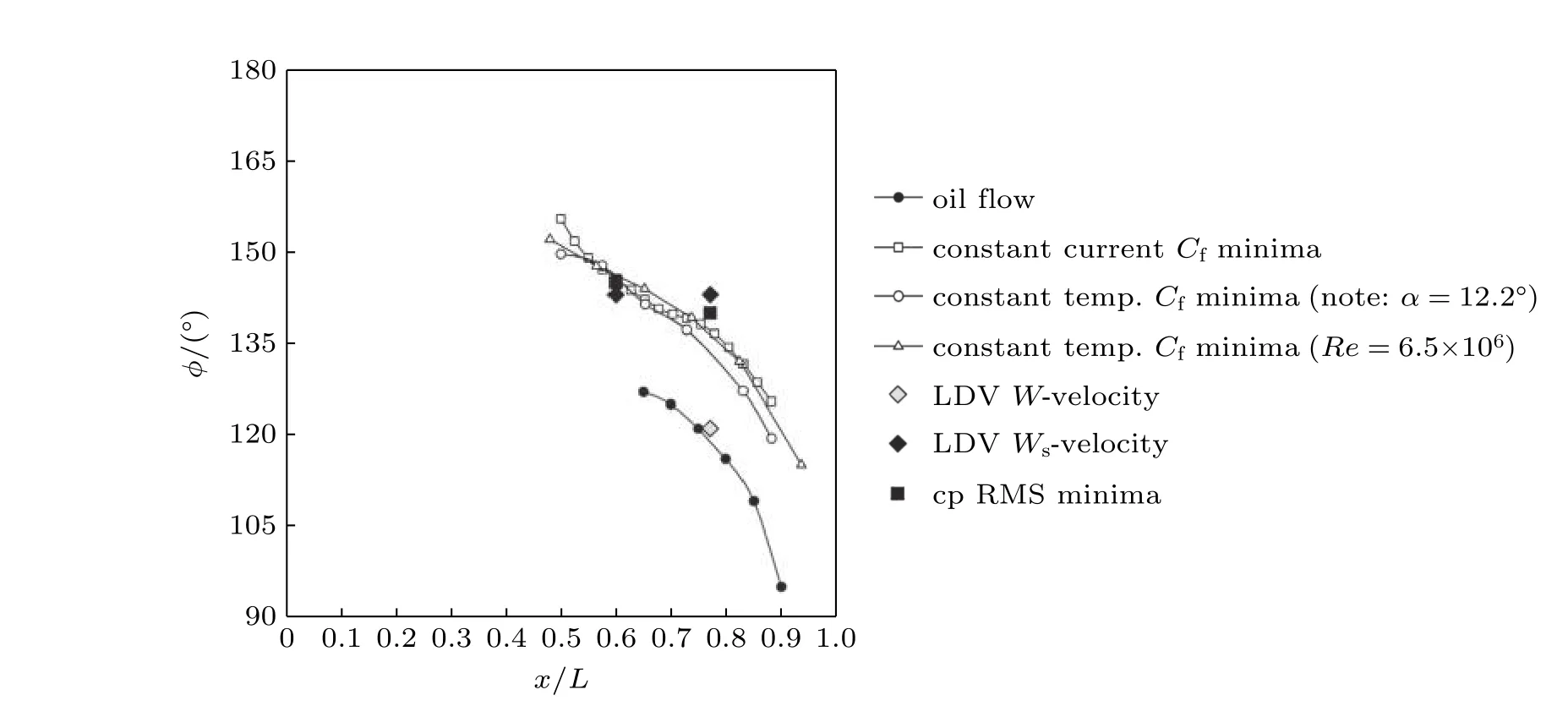
图55
从图56可以看到,摩阻大小局部最小的位置与二次流矢量改变方向的位置是一致的.
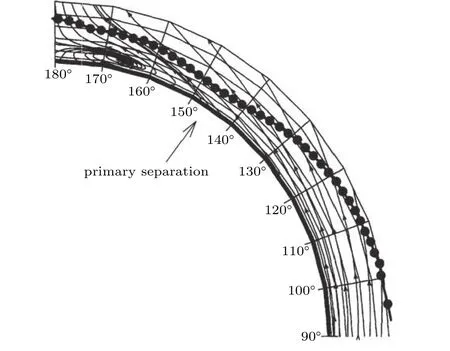
图56
3.4 椭球绕流场分离的拓扑研究
绕椭球的流动是研究三维分离流拓扑的基本测试问题.三维分离流研究的前提是对其流场的理解,通过流动现象和拓扑分析能够较为清楚的分析分离流的特征.通过现象分析三维流动分离,为识别流动中的细小特征,如二次涡,对实验精度和精细度的要求比较高.因此早期开始研究分离时,都是从摩阻线型式与流场之间的拓扑关系开始的,根据流场中临界点(critical point)或奇异点(singular point)(下文统称为临界点)和摩阻线的模式对分离进行分类,如图57所示,这是对二维平面分离定义的,实践证明,这个定义也适用于三维问题(Delery 1992).

图57
对流动分离的研究,有两种不同的方法,一种是现象学方法(Wang 1972,1975),一种是使用拓扑的数学方法(Tobak 和Peake 1982),拓扑归类方法为分离流动的描述提供了一种精确和简洁的方法.要从物理上理解三维分离,必须使用临界点理论对流场结构进行合理分析(Delery 1992).Chapman(1986)对定常流动提出了一种更为全面的方法,如图58所示,与拓扑方法相似,通过将有色染料喷涂到物面上,根据摩阻图像上临界点的类型将流动分为:附着流、二维分离、三维一次分离、三维二次分离、三维组合分离等.在微分方程理论中,拓扑结构能清晰地给出常微分方程奇点分布的形态,从而能够定性地描述微分方法所表达的积分曲线.在定常分离流场内,分离流动的图像可用流线来表达,如果能给出流线方程奇点的形态及分布,分离性状也能得到清晰的描述(张涵信 2002).

图58
在绕椭球的分离流动中,分离线源自一个或多个临界点(Wang 1972,1974;Chapman 1986).分离涡可能起始自某条线,这条线却并不是从某个临界点起源的,如图59所示.

图59
Wang(1976)基于极限流线的分析定义了开式分离和闭式分离,根据临界点和摩阻线的模式对三维分离进行了分类,如图60所示.

图60
图61给出了开式分离和闭式分离的空间结构.开式分离,分离不是从鞍点传出的,或者说分离线在物体表面有起始点.从流线的观点看,即物面极限流线分离后并没有再汇合.闭式分离是一种奇异分离,分离线被定义为通过鞍点(即临界点)的一条线,且在这个位置的壁面剪切应力消失,或者说分离线在物体表面没有起始点(从流线的观点看,即在物面流线上存在分离交叉后闭合形成的封闭区域).
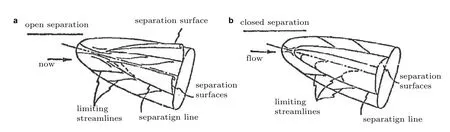
图61
在小攻角时,以闭式分离为主,此时,分离线与从不同驻点起始的极限流线是完全分离的.随攻角增加至中等攻角,流动分离从闭式分离转变为开式分离,流动中存在类似龙卷风的旋涡,其旋转轴垂直于物面,从同一驻点起始的极限流线从两侧靠近分离线.在椭球的每一侧各形成一条分离线,因此在背风面对称面上没有连接到一起.攻角增加至大攻角、特大攻角时,流动又呈现闭式分离(Wang 1976),如图62所示.

图62
在一种流动中,不能简单的认为只存在一种分离类型,如图63,开式分离和闭式分离是同时出现的(Wang 1976,Han 和Patel 1979).Wang 提出的关于三维分离类型和开式分离的发展,得到了很多研究者的认可,在实验和数值计算中都进行了复现.同时在数值模拟研究中也得到广泛应用,并且已经作为阐释CFD 结果的基础.

图63
Han 和Patel(1979)通过在椭球的前端释放染料观测到了攻角变化时表面流线模式的变化,有两种基本的分离模式,一种是自由涡层类型的分离(free vortex type separation),即Wang提出的开式分离,另外一种是分离泡类型的分离(bubble type separation),在横流分离中,对于分离的流体,如果在足够高的雷诺数下形成层流横流分离,经历转捩并再附在物体表面所形成的拓扑即为分离泡(Wetzel 和Simpson 1996).分离泡类型的分离即Wang 提出的闭式分离,这种分离是一种奇异分离,因为分离线会通过,或者是与临界点相连,且在这个位置的壁面剪切应力消失.在很低的攻角时,分离是闭式分离.攻角在6~30°之间时,椭球上有两条开式分离线,这是由于染料沿着两条开式分离线是再附和抬起的.由于湍流倾向于抹平分离流中的细节结构,叠加染料实验的精度不够,在分离附近的流动细节没有捕捉到.Han 还采用贴线法研究了雷诺数和分离对流动的影响,确认了由Wang 提出的三维分离的定性特征.Han 还通过求解边界层方程研究了摩阻线型式与流场之间的关系,当出现闭式分离时,分离从临近的区域将流动分隔开,边界层理论不再适用.将不同攻角下,椭球层流分离线的位置与Wang 数值求解边界层方程的结果进行了对比,由于明显的黏流与无黏流干扰的存在,两种结果有定性差异,尤其是在高攻角时.
Costis 和Polen(1987),Costis 和Hoang(1989)实验中也观测到了同样的现象,在3°~30°攻角范围内,开式分离占优势;而当攻角小于3°和大于30°时,绕椭球的分离线是闭合的,在这种情况下,在分离线上可以识别两个临界点.Cebeci 和Su(1988a,1988b),Ragab(1986)通过求解边界层方程获得了绕椭球的层流模态,在计算中确认了开式分离的存在.开式分离中,表面摩阻线聚集在分离线的一侧(Simpson 1996),如图64所示.在分离线每一侧的近壁低速流动聚集在一起,形成了收敛的摩阻线,并与分离线相融合,同时在靠近分离线的位置产生了相对较大的壁面法向平均速度.从许多油流可视化的实验来看,在分离线每一侧的壁面摩阻线看上去都是在有限的角度上接近分离线的.然而,那些收敛的摩阻线必须在切向上接近分离线.
Tobak 和Peake(1982)对绕椭球的层流流动进行了研究,给出了时间平均的油流显示结果,分析了流场中的节点(node point)和鞍点(saddle point)的数量和分布,形成了简单的拓扑规则.在横流中,能够很清晰的定义流动模式.根据流动现象,定义了两种类型的三维分离流动,第一种是图65(a)的全局分离(global separation),Wang 称为闭式分离(Tobak 提出的全局分离中不包含分离泡模式),在小攻角和大攻角时出现,与Wang 的结论基本一致.对于全局分离,在物面上总是存在一个与流动分离相关的临界点(即分离鞍点).从这个分离鞍点出发的线就是分离线,在这条线上与物面相交的是分离层,并延伸到下游的气流中,这是与Wang 之间共通的地方.但Costis 和Hoang(1989)不支持分离线的起始点处是鞍点的说法.这个分离层在气流中有一个边界,与一条线相对应,这条线或从三维临界点出发,或从物面临界点出发,这条线是唯一的,对于定常流,它就是流线,代表了一种对旋涡中心线的实际和精确定义.
Tobak 和Peake(1982)定义的另外一种分离是图65(c)的局部分离(local separation),Wang称为开式分离,Chapman(1986)称为横流分离(crossflow separation),这种类型的分离是旋成体的一种分离特征,是由横流逆压梯度主导所引起的分离.流动最明显的特征和有争议的点是开式分离线的发展.Tobak 认为局部分离线从附着的节点(也就是前驻点)出发,朝着其他摩阻线收敛的方向前进.当极限流线汇聚在一起,流体被迫离开物面时形成局部分离.当局部分离出现时,流场中没有突然的变化,因此分离的起始点不容易定义.而且也没有与局部分离相关的鞍点,分离线也就不能定义为通过鞍点的某条线.但分离线大体上可以定义为摩阻线的收拢线.由于没有精确的数学定义,Tobak 认为很难确定这条线是否是摩阻线的延续.Wang 认为这条线可以起源于物面上的任何地方,也没有沿着摩阻线前进,因此证明这条线是包络线或极限流线是很困难的.由于开式三维分离时没有表面临界点,定义开式分离线的上游起点位于多条摩阻线第一次收敛为一条线的位置(Yates 和Chapman 1992),如图65(c)所示.Tobak 认为Wang 提出的开式分离和闭式分离的描述并不足够缜密,开式分离并不是真正的分离.表3给出了分离类型与对应关系.

表3 分离类型与对应关系

图65
国内的苏文瀚(Su 和Tao 1996)在水槽中将染料以0.04 m/s 的速度喷出,辅以激光片光技术观测到了椭球流动模式的变化,如图66所示.攻角在3°~15°时,未封闭的气泡在椭球尾部形成,气泡的上游边界是封闭的分离线,在闭式分离线前面,自由剪切层从开式分离线上脱落.因此,开式分离是由于三维边界层中两股相反的横流气流相遇并聚集而形成的.在当前实验条件下,在很小的攻角时,出现了开式分离,封闭的分离线永远不会破碎,仅会改变外形和拓扑结构.低攻角时,尽管出现了开式分离,但还没有涡流形成.
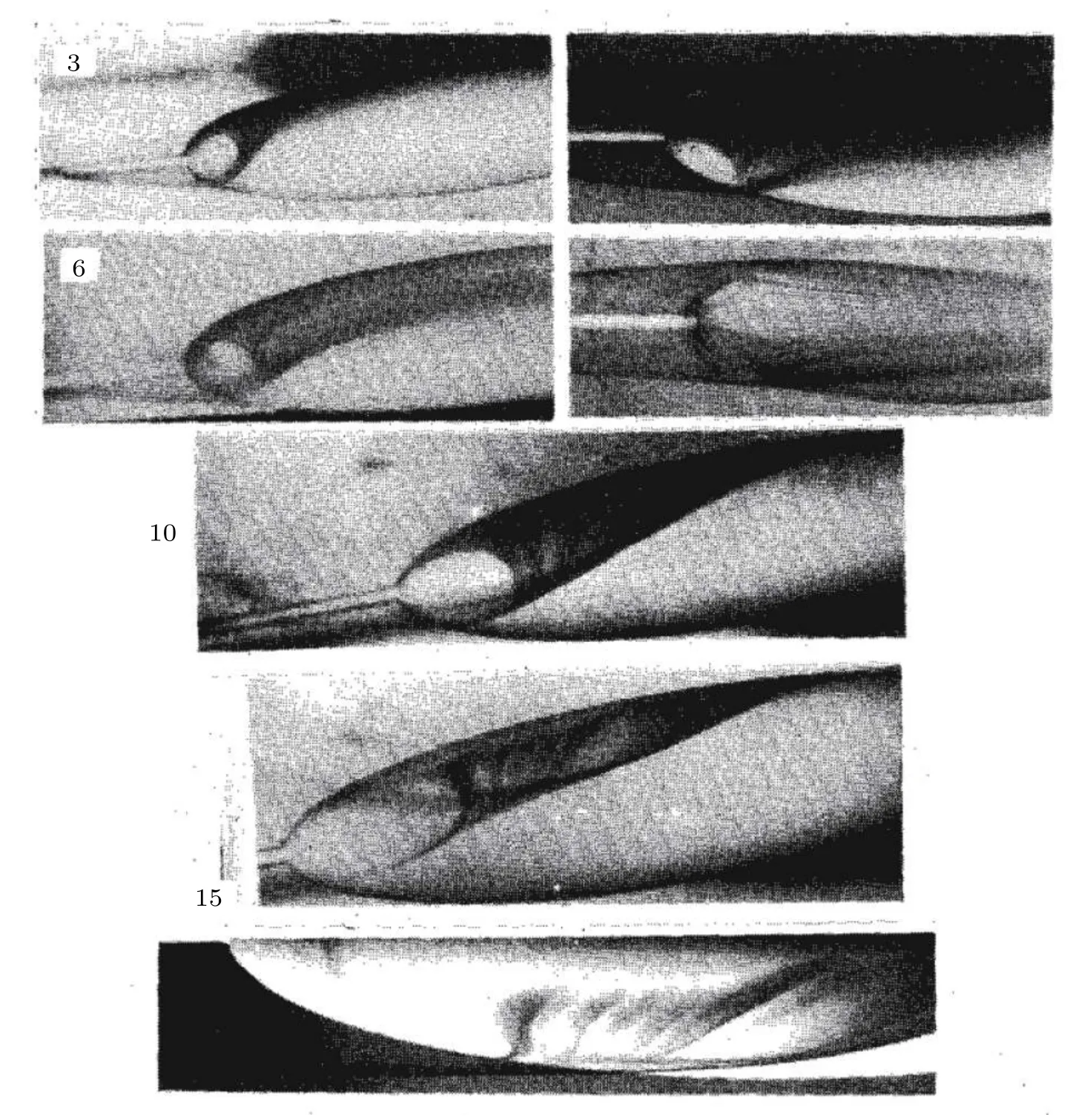
图66
如图67所示,当攻角超过15°时,从开式分离线脱落的自由剪切层卷起进入到较弱的旋涡中,但还没有形成涡核.当攻角增加时,开式分离线和气泡继续前移.当攻角超过30°时,从一次分离线脱落的自由剪切层卷起进入到椭球上方聚集的旋涡中.气泡的外边界变成了一次分离线尾部的部分,因此仅气泡前部的一部分是开式分离线.当攻角超过45°时,椭球上方的涡破裂,被称为破裂涡.流场变成非定常和非对称的.在攻角超过65°时,两条开式分离线相交,变成了一条封闭的分离线.这是另外一种类型的旋涡:垂直旋涡从一次和二次分离线的尾部部分脱落.流动是弱非定常的.当攻角继续增加,流动变成非定常涡脱落.
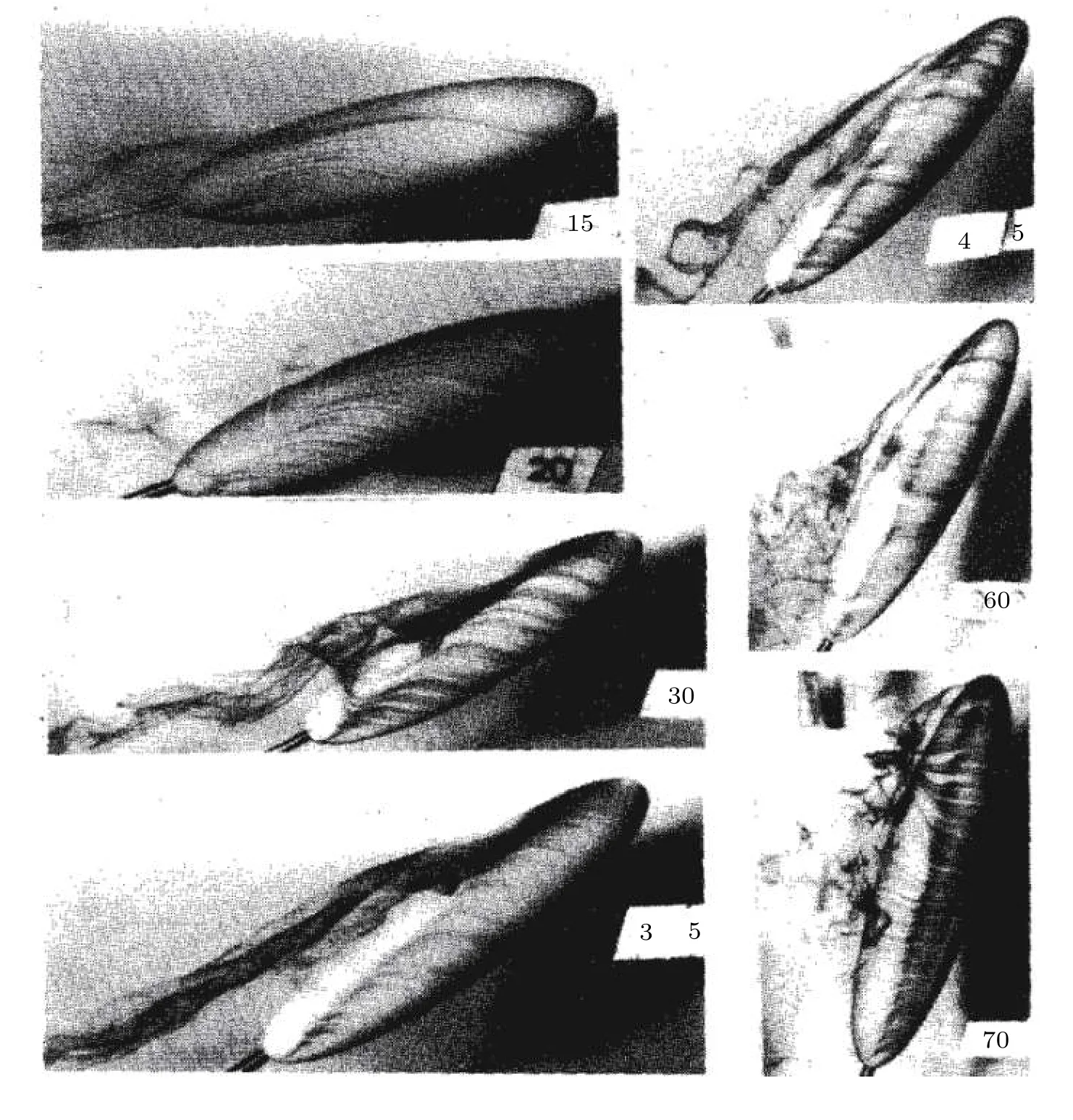
图67
开式分离中分离面的自由边界是螺旋流线,这个螺旋流线是环绕着涡轴的,不是与涡轴相一致.图66~图68显示了在开式分离的起始点没有任何的临界点,包括椭球表面和所涉及的流场中.然而,开式分离导致在近物面的气流面上形成了褶皱,它刚好是一个尖头突变,壁面上的这个尖点可以用作定义和识别开式分离的起点.
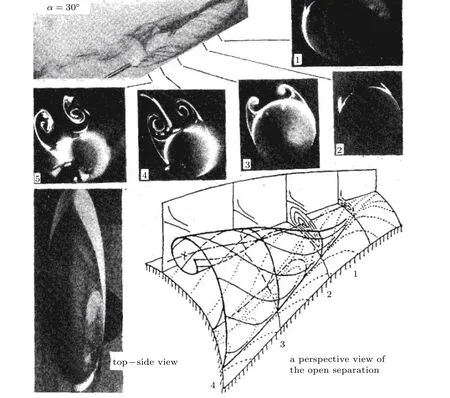
图68
3.5 分离对气动力的影响
分离流动和旋涡的运动,本质上是一种三维非定常黏性流现象,会使流场发生重大变化,从而影响椭球的气动特性(张丹和郭雪岩 2008).边界层分离几乎总是与不希望的各种效应相随(Chang 1961).分离会引起能量损失,并伴随着流线的偏离和回流.当分离出现时,导致升力减小、阻力增加、压力场的非定常脉动放大、由非对称前体涡所致的不可控偏航等.从工程观点看,对定常非对称流场结构的研究是重要的课题.尤其是攻角大于6°后,绕椭球的流动会出现横流分离,横流分离决定了靠近尾部的速度场分布和物面的压力分布,进而影响推进、机动性能和控制性能(Ahn 和Simpson 1992).一些特定现象,如随机偏航和水平螺旋等,都是由定常非对称流场所产生的侧向力所引起的(Kubota 和Arai 1983).尾部背风面的横流分离会导致非定常的力和力矩(Karlsson 和Fureby 2009).
气动力计算和分析对有效的控制操作、稳定性分析、合理设计等方面起着重要的作用,研究其气动特性具有十分重要的意义.同时,为了优化设计,考虑到性能和特色,研究者对类椭球这种外形的气动力测量是很有兴趣的,需要知道流场在不同运行条件下的详细信息,因为飞行器需要最小的阻力(Radwan 1988).Sanjeevi 和Padding(2017)计算了不同攻角和雷诺数下长椭球和扁椭球的阻力系数.直到Re=2.0×103,长椭球的阻力系数都遵从正弦平方律,这源于压力分布也遵从这一规律.但扁椭球即便是到Re=100 都不遵从这一规律,主要是受到较强的诱导阻力.对于长椭球,升力系数也能找到等价的理论方程,其近似是合理的,这一公式适用于很高的Re(即前文提到的Hoerner 公式).
图69给出了高雷诺数范围内椭球阻力系数的测试结果(Dress 1990),在测试的雷诺数范围内,阻力都是以不规则的方式变化的,与低雷诺数时阻力系数的有规律分布完全不同.Boltz 和Kenyon(1956)(图中文献12)测试的雷诺数范围与Dress 研究的范围没有重叠部分.但可以发现,Boltz 给出了非常低的阻力系数.Newcomb(1988)(图中文献14)使用磁浮平衡系统测量了与Boltz 相同的外形,虽然雷诺数不同,但测量得到的阻力系数比Boltz 大得多.Newcomb 测量的数据总体上比Dress 的数据稍微高一点,因为他们没有进行堵塞度和浮力修正.
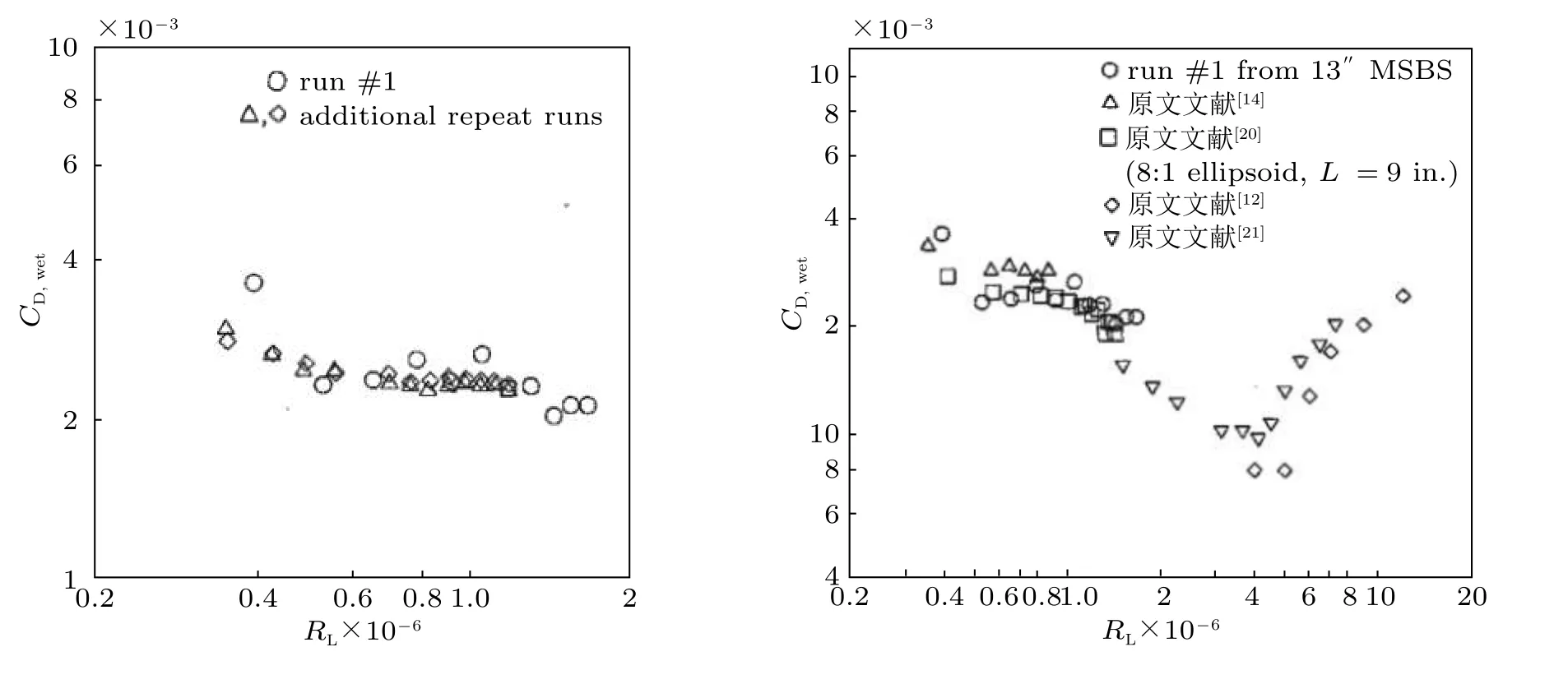
图69
Holt 和Garry(2016)研究了f=6、Re=1.4×106椭球的近地效应,转捩带设置在x/L=0.15 位置.如图70,可以看到,在距离地面小于0.3L时,攻角小于10°时,升力系数都是减小的,这是由于椭球和地面之间气流加速,使得靠近尾部的压力减小所致.随着离开地面距离的增加,升力减小的幅度降低.当距离地面大于0.3L后,对升力系数的影响逐渐减小并趋于零.在超过20°的大攻角时,地面效应有助于升力的提高,这可能是由于地面效应使得有效攻角增加了.
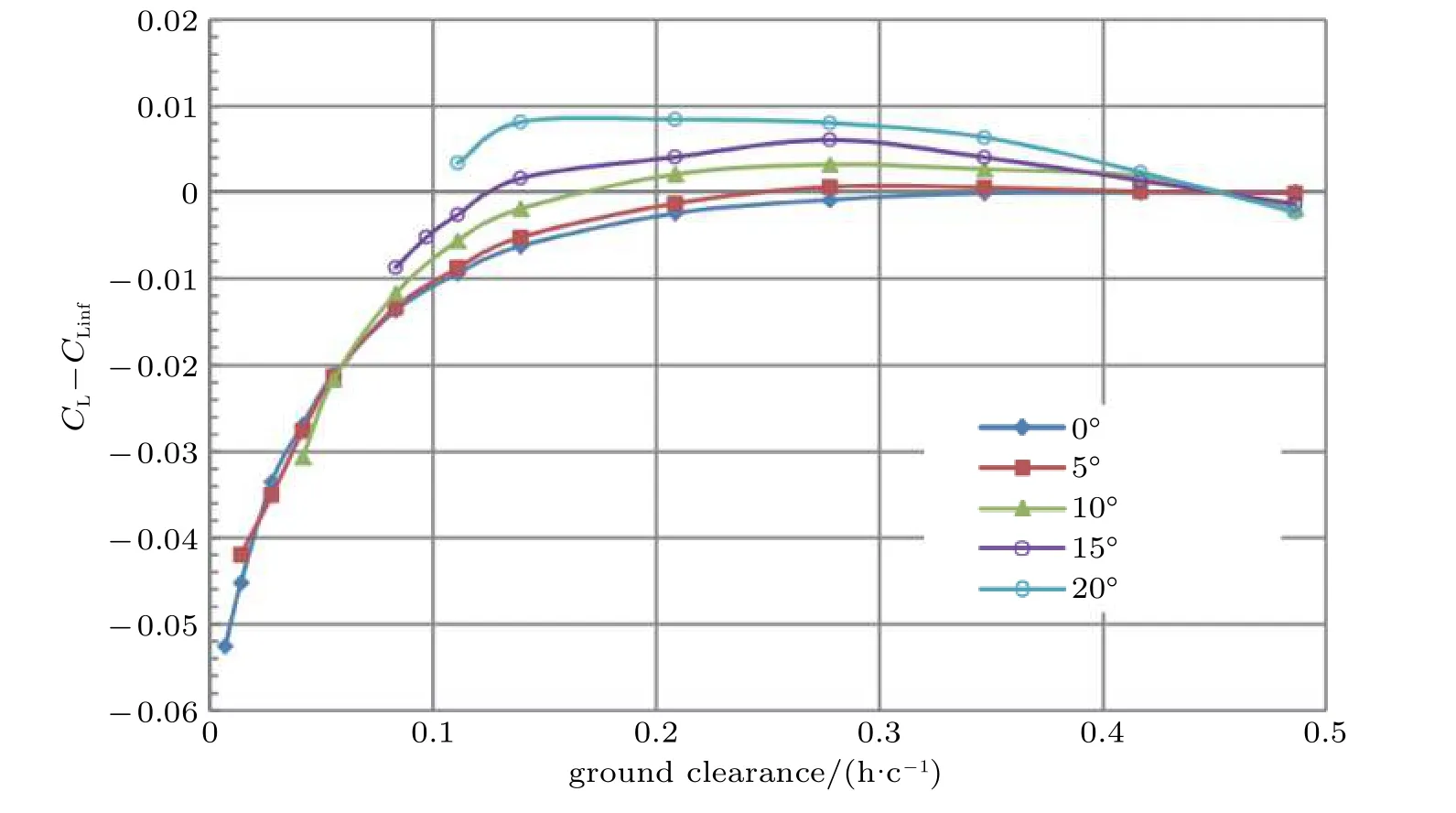
图70
地面效应对升力的影响,主要在于其影响了椭球的流态,Holt 和Garry(2016)通过求解RANS 的方法给出了距离地面0.15L时地面效应对一次分离和二次分离位置的影响,从图71可以看到,地面效应对二次分离的位置基本没有影响,一次分离的位置明显提前了.
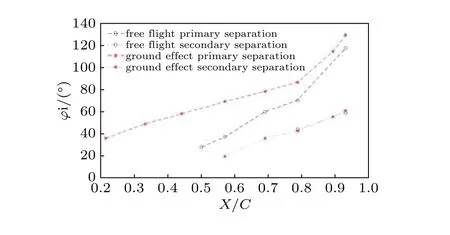
图71
攻角超过15°后,随攻角增加,就会出现小雷诺数效应,在力和力矩方面就会出现差异,可能是前部层流分离的影响(Ahn 和Simpson 1992).因为在较大攻角时,椭球对称面的两侧形成两个较大的附着涡,背风面的这两个主附着涡伴有低压,因而对椭球体产生额外升力,即非线性涡升力,可用来提升其气动特性(Chesnakas 和Simpson 1997).可见,随着攻角的增加,伴随分离流结构的变化出现了一系列的受力变化.Kim 和Rhee(2003)通过CFD 给出了f=6,Re=4.2×106时升力系数随攻角变化的曲线(图72),可以看到,随攻角增加,曲线的斜率是逐渐增加的,这主要是非线性涡升力增加的原因.
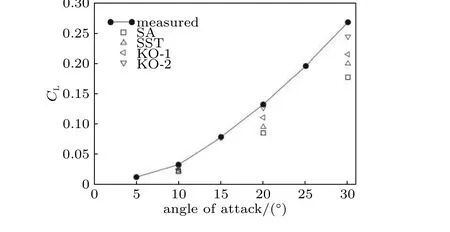
图72
国内的卞于中和张孝棣(1989)在哈尔滨空气动力研究所2.5 m×3.5 m 低速回流风洞中测量了f=6 椭球的气动力,从图73侧向力系数随攻角的变化可以看出,当攻角大于15°以后,不同速度下的侧向力系数均随攻角增加而增大.模型受侧向力作用与其周围的具体流态相关,模型在不同攻角时其背风面上的流动出现分离后形成了涡,涡在其开始形成和发展的一个小范围内是对称的,随着向下游移动开始变得不对称起来,攻角越大越明显,且左边的涡比右边的涡强.
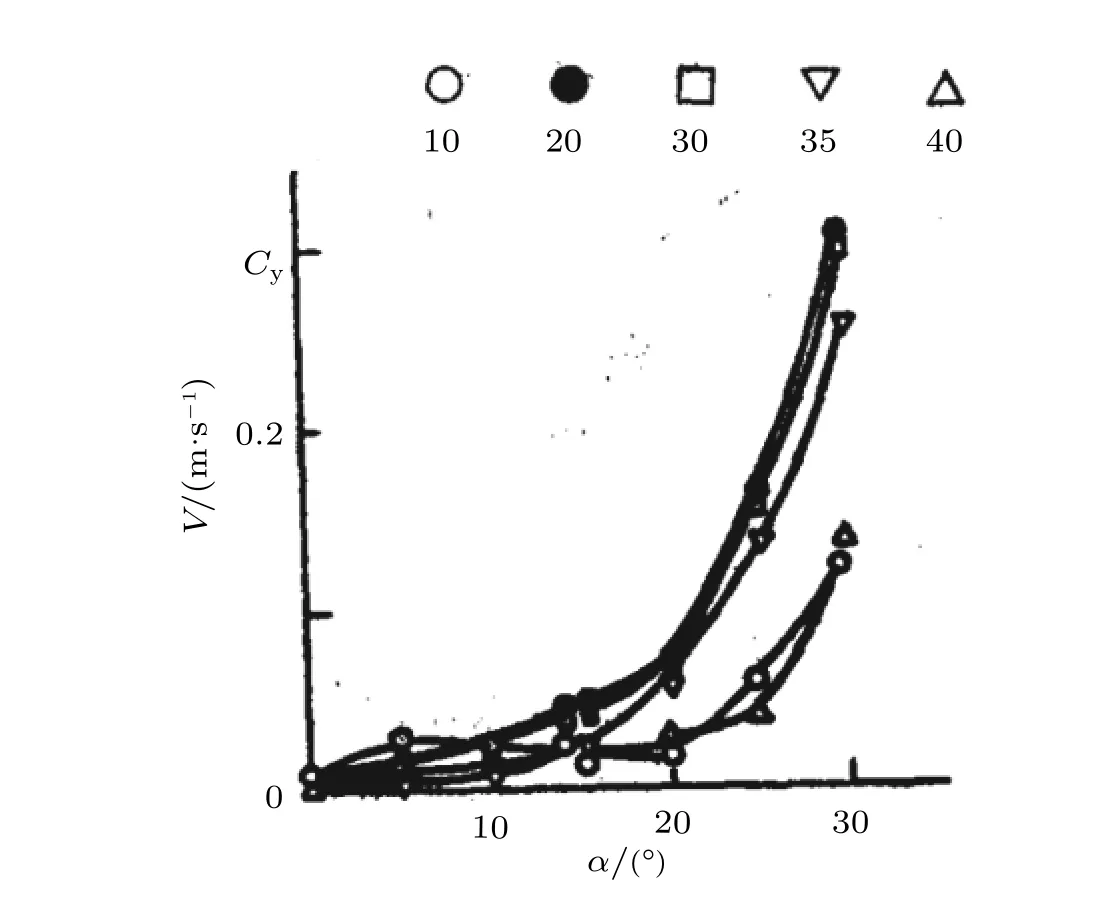
图73
刘沛清和邓学蓥(2002)实验研究了椭球头细长旋成体大迎角绕流非对称侧向力的时均值和脉动值,实验是在北京航空航天大学流体力学研究所的低速风洞中进行的.实验段湍流度为1%.模型前部为f=6 椭球体的一半,后部为长度4D的圆柱体.在大迎角下,作用在椭球上的时均气动力除升力Cl和阻力Cd外,还有非对称的时均侧向力Cc,定义为


其中ρ∞为来流密度,S为参考截面积.
对于椭球头旋成体,侧向力出现的起始迎角为32°,图74给出了不同周向位置时均侧向力随攻角的变化曲线.侧向力出现的攻角范围约为32° <α<70°.当攻角超过70°后,侧向力消失.
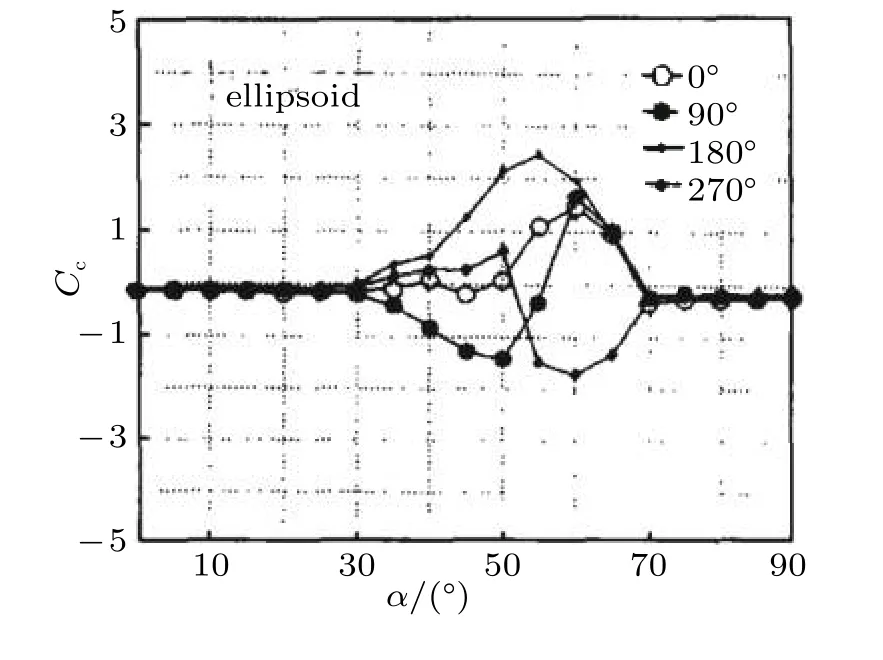
图74
为检测侧向力低频大振幅分量的脉动特性,在实验中测量了侧向力的时间过程,图75给出了椭球头旋成体侧向力在不同迎角下的脉动过程及其功率谱密度分布.在迎角0°~40°范围内时均升力系数和阻力系数实验结果和由横流理论预测的结果基本一致.侧向力瞬时值的时间过程表明,类椭球旋成体大迎角绕流非对称背涡具有明显的非定常特征,反映在侧向力系数过程线上是一个非周期的随机或间歇过程,侧向力的脉动过程由不同频率和振幅的分量组成.

图75
随着迎角从30°增加到70°,低频分量的振幅开始发展并不断增大,但主频基本保持2.0 Hz 不变.图76给出的脉动侧向力均方根值随迎角的变化表明,脉动侧向力均方根值随迎角的增加而增大.

图76
侧向力的非定常性是明显的,且非定常过程是由不同振幅和频率的分量组成.图77给出了脉动侧向力功率谱的密度分布,可以看到明显的三个不同频率的峰值区,其中,低频大振幅分量由分离涡核的振动引起,对应非对称分离背涡的振颤,中等频率分量由类似Karman 涡的脱落引起,高频小振幅分量主要由分离剪切层中的小尺度旋涡和来流湍流度引起.

图77
3.6 分离产生的噪声
在三维剪切流中,压力脉动,特别是在那些有流动分离的区域,是相当重要的噪声和振动源(Goody 和Simpson 2000a).椭球尾部背风面的横流分离可能产生脉动压力并放大脉动压力,相当多的噪声正是由于这样的分离产生的,如果脉动压力增大,可能会使椭球出现颤振和抖振,影响结构强度和稳定性.尽管这一现象非常普通,但压力脉动的来源却没有得到很好的理解,也很难数值模拟,目前主要还是通过实验的方法进行研究.
图78和图79给出了10°攻角时x/L=0.6 站位背风面上三维横流分离的壁面湍流压力脉动能量谱,使用uτ作为速度尺度,使用v/uτ作为长度尺度,在高频区域,压力谱都出现了急速下坠.与二维边界层内层的下坠速度相似,即ω−5.在具有相关性的区域,uτ最小,v/uτ最大,也具有最小的湍流结构.
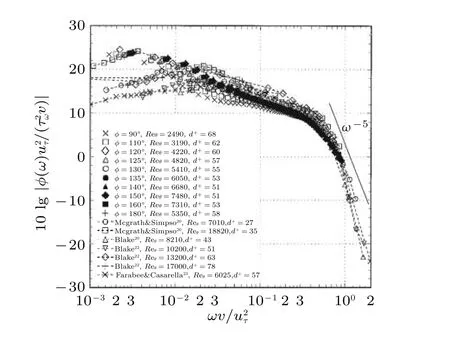
图78

图79
按照边界层内有内层(黏性区域)尺度和外层(最大的涡)尺度的说法,在高雷诺数时,在二维边界层的内层,压力谱中内有重叠的区域,在重叠区域内,内层和外层的尺度是相容的.理论上在这个频率范围内,压力谱应该按照ω−1的速度减小,因为在对数律层内,湍流结构的对流速度接近局部平均速度,然而,在重叠区域内测量得到的谱延迟减小速度为ω−1.压力谱在中等频率范围的变化主要是受雷诺数的影响.随雷诺数增加,重叠区域的范围也增大(Goody 2004).低频谱的贡献主要是来自最大的剪切层结构,那些大的结构的能量谱贡献度随雷诺数的增加而增加.高频尺度下是不受雷诺数影响的.这要求当雷诺数增加时,在中等频率范围内,在能量谱上需要有很大的延迟.
在剪切应力很大的区域,壁面区域产生了很强且高频的能谱含量.在那些有相对较小的外层平均速度梯度的地方,有较小的低频贡献度.这些特征在椭球两侧及更大攻角时大涡度的情况下都会出现.因此,在那些位置,能谱的值在中等频率上接近常数.由此导致物面上的压力脉动均方根分布反映了高频壁面区域贡献度的重要性.边界层分离区域,压力脉动均方根偏差具有局部最小值,但是再附位置和大旋涡情况下,那里的压力脉动均方根偏差具有局部最大值.(在靠近横流分离的区域,表面压力脉动有局部最小值,而在靠近再附和大脱落旋涡下,那里的表面压力脉动具有局部最大值.)
由于没有前面提到的外层变量尺度,使得更低频率突然下跌,如同10°攻角时一样(图80).在x/L=0.600 站位和1 kHz 位置,谱的值有三个局部最大值,130°靠近一次分离,145°靠近二次分离刚发生的位置,160°靠近脱落涡的涡核.直到出现一次分离,谱的值都随周向角增加而逐渐增加的.在160° <φ<180°之间谱值是减小的.在一次分离附近和迎风面位置,在周向角110° <φ<135°之间,谱分布有一处很强的下陷.当气流从迎风面向背风面流动时,由于外层中薄的加速边界层具有较低的平均速度梯度,那里有大量的低脉动水平、低频的大尺度湍流气流.由于靠近壁面层的结构具有相对较大的uτ,产生了高频气流.而在中等频率(60 Hz~5000 Hz 间)附近,能量谱基本保持常数,之所以存在这样一个中等频率的谱区域,是由于外层的大尺度运动和靠近壁面黏性主导的区域之间缺少重叠的频率结构(Goody 和Simpson 2000b).继续向背风面移动,由于边界层增厚和大尺度的分离结构,低频分量增加,相反,高频分量随着uτ的减小而降低.继续移动到大尺度旋涡时,由于外层较低的平均速度梯度,低频分量继续减小.然而,由于uτ较大,使得高频分量增加.同样地,中等频率附近基本为常数.注意到90° <φ<180°周向角位置的谱值是相等的.

图80
从脉动能量谱可以看到,这是一个复杂的三维非平衡流.物面上的高频压力脉动能量谱尺度是变化着的.靠近分离区位置的壁面剪切应力比较低,那里有很少的高频含量,但是来自外层的低频量的贡献度相对是很大的.物面上压力−速度的空间修正系数,主要是为了检测强烈影响脉动压力的湍流流动的位置.这种流动的泊松方程显示p和v之间是强相关的.图81给出了相关系数和脉动速度v.在半径为0.1~0.2 cm 之间有高湍流的流体存在.Rpv最大的负值出现在平均速度剖面半对数区域的外层(在剪切应力坐标系中).物面压力脉动与速度脉动结构的相关性很强,特别是速度v通过泊松方程,以Rpv的形式表征了外层区域流场特征的影响.一次分离的迎风面和一次旋涡的背风面,在100 图81 在低攻角时,压力谱和脉动压力的值与平衡流的测量结果还具有可比性.在分离位置附近,由于壁面剪切应力较低,高频分量是小的,而来自外层的低频分量相对是较大的.在壁面剪切应力较大的区域,壁面区域产生了很强的高频分量.在外部区域平均速度分布具有相对较小梯度的位置,低频分量具有更小的贡献度.这些特征都发生在周向角90°和大的旋涡下,因此这些位置的谱值在中等和较高频率时基本保持常数. 湍流绕流钝体时产生压力脉动,从而产生声波的传播(Cianferra 和Armenio 2018).不同外形的物体,其频率和幅值是不同的.Cianferra 通过采用壁面解析的LES,重现了Re=4430 的湍流流动,水底声学远场采用FW-H 方程类比进行分析.结果表明流线型的类椭球物体其产生的压力信号幅值比钝体外形要低一个量级,如图82所示,f=6 的椭球,在靠近尾部的区域出现了回流区,这个回流区与圆球和方柱相比都是较小的,主涡的直径约为0.28D,尾部出现分离的位置约为2.7D.对FW-H 方程中不同项对噪声的贡献的分析表明,对于钝体(如方柱和球),线性项对总共噪声信号的贡献明显大于非线性项.而对流线型物体(如椭球),则刚好相反,线性项对总噪声信号的贡献明显小于非线性项,因为其自身外形使得载荷噪声非常小(Cianferra 和Armenio 2018). 图82 绕椭球的流动,对转捩带是非常敏感的,而且转捩带的直径对尾迹形态也有影响(Karlsson 和Fureby 2009).采用砂粒在x/L=0.23 位置固定转捩后(图83),阻力系数明显增加,这是由于转捩后流动成为湍流,湍流对总阻力系数的贡献远大于较小层流分离区的贡献.而固定转捩设定在x/L=0.75 位置后,阻力系数总体是降低的,这可能由于较低雷诺数时,边界层的厚度比砂粒厚,所以阻力轻微降低. 图83 在Re<2.5×106时,转捩效应特别重要(Ahn 和Simpson 1992).当Re<2.08×106时,整个绕流被层流分离包裹,并且在背风区尾部随着湍流再附,当2.08×106 图84 图85给出了30°攻角情况下再附和分离位置处局部最大的压力脉动值.对于低攻角情况,峰值脉动压力水平是不存在的,不能用来判断分离的位置.在转捩带的上游,在大攻角时,层流流动会出现分离,进而转捩、再附、二次湍流分离,两个分离线在转捩带的下游融合(Wetzel 和Simpson 1998). 图85 图86给出了这个分离涡的平均二次流线,可以清晰的分辨一次分离(S1)、二次分离(S2)、三次(S3)分离和一次再附(R1)、二次再附(R2).这些分离和再附的位置对相邻气流之间的动量湍动能输运是很敏感的. 图86 Wetzel 和Simpson(1996)对比了转捩带的影响,从图87的油流照片上可以清晰的看到,转捩带对流动有影响.他们还根据油流照片绘制了流动图谱,靠近背风面位置(周向角90°)的层流经过转捩带后成为湍流,而背风面较远位置处在转捩带前已经成为湍流.但有研究者认为求解RANS 时是否模拟转捩带对结果的影响很小,使用低雷诺数修正的k-ω模型,其结果与实验要符合的更好(Kim 和Rhee 2003). 图87 为进一步确定转捩带大小对绕椭球(L=0.87 m,D=0.102 m)流动的影响,Ashok 和Buren(2015)采用三种尺度的转捩带进行了实验研究,图88给出了椭球下游x/D=10 站位的速度云图,在三种尺度的转捩带下,尾迹中都有一个强旋涡和一个弱旋涡,两侧旋涡的强度受到转捩带直径的影响,转捩带直径小于0.8 mm 时几乎无影响,大于1.6 mm 才对流场有影响. 图88 大长细比椭球的尾迹吸引了很多空气动力学和海洋水动力学领域研究者的兴趣.前面提到,潜艇、导弹和水下运输工具都和椭球有相似的外形.设计者通常比较喜欢这种外壳形状,当入流方向与主轴成一直线时,它的流线型细长体外形有良好的阻力性能.考虑到它的性能,源于机动性方面的考虑,研究倾斜椭球后的尾迹也变得很重要. 在早期的研究中,重点是气动力系数和靠近椭球的流动细节,诸如表面流态、边界层、分离,有些关注了很靠近椭球的尾迹.由于尾迹更为复杂,且范围更大,实验测量很困难,采用简化的数值方法也很难模拟,受限于计算资源,早期很少通过数值模拟研究椭球的尾迹,因此椭球尾迹研究的进展较慢. Chevray(1968)是最早开展尾迹研究的,实验条件如表1,测量范围一致延伸到椭球下游18D的位置.采用在前端释放烟雾的方式进行了可视化,如图89所示,大量密集的烟雾进入旋涡区域内,扰动了真实的流动结构,这种方法给出的分离区仅可以作为参考. 图89 Chevray 测量了椭球后自维持区域的轴对称尾迹发展的平均特性(图90),确定了其流动模式,推导得出了尾迹发展平均特性的分析表达式,在远场区域的尾迹中,所推导的方程与已知的幂律是一致的.在近流场区域,实验结果与方程给出的结果也符合较好. 图90 Chevray 还通过动量方程和平均能量方程检测了雷诺应力的幅值,如图91所示.法向雷诺应力在三个坐标方向相对幅值的变化,表明旋涡没有保持任何初始的优先方向,当流动向下游发展时,显示了一种朝向各向同性状态的明显趋势.剪切应力的分布揭示了在湍流生成过程中,壁面剪切应力超过自由剪切应力的原生重要性.流线型椭球的雷诺剪切应力水平比相应钝体的水平低得多.椭球的尾迹大约是在尾部3D~ 6D的范围内建立的.而圆盘的尾迹是在15D范围内建立的(Carmody 1964). 图91 后来,Morgan 和Hughes(1978)采用有限元方法,利用普朗特混合长假定,求解了f=6,Re=2.75×106椭球后的湍流剪切流动问题,给出了其轴对称尾迹.之后很多年都没有研究人员开展关于尾迹的研究.直到近年来,随着测试和计算技术的发展,对尾迹流动的研究逐渐增多,但也多集中在低雷诺数范围. 对于类似椭球这样的轴对称模型,早期的研究都假定其尾迹是对称的.在攻角10°和20°时都没有出现非对称涡脱落(Goody 和Simpson 2000a).但Johnson 和Patel(1999)的结果显示,椭球后周期性脱落的发夹涡,导致尾迹呈现非对称性.Ashok 和Buren(2015)在低速风洞中使用立体粒子图像速度仪(stereoscopic particle image velocimetry,SPIV)做了进一步研究,如图92所示,测量了中等和高雷诺数(主要是Re=2.4×106)下类椭球潜艇模型的湍流尾迹.在有攻角的情况下,尾迹中有一对长度上保持非对称的流向涡,较弱的涡很快就扩散了,由于缺少进一步的扩散,较强的旋涡一致延续到很远的下游,形成非对称的尾迹,同时也引起了模型的侧向力.这说明,非对称性是这类相似尾迹流动的本质特征. 图92 Tezuka 和Suzuki(2006)对此有进一步的研究,在一定范围的自由来流雷诺数(Re=4.0 ×103~7.0×103)范围内,流动呈现非振荡、轴对称(α=0°情况下)和非振荡非对称流动(在非0 攻角下,α=0°~30°).他们使用Chiba 方法研究了不同攻角下绕椭球的流场,这是一种三维全局线性稳定性分析方法.结果表明非振荡非轴对称(和非振荡非对称)模式的放大因子是最大的.当放大因子变为0 时,流动从非振荡对称(或轴对称)流动转化为非振荡非对称(或非轴对称)流动.为了明确在有攻角情况下非振荡非对称流动出现的原因,采用低速风洞进行了实验,流动图像显示,在Re=6.5×103左右,流动模式是非对称的,在Re=3.5×103左右,流动模式是对称的.因此存在两个临界雷诺数,一个是从定常轴对称转换为定常非轴对称,另外一个是从定常非轴对称转换为振荡流动.f=6 椭球,在α=30°时,在Re=7.1×103左右很小的范围内,流动变为定常非对称流场.如图93所示,烟线显示了在α=10°时,绕椭球的流动可以呈现定常非对称模式. 图93 实现类椭球外形飞行器的安全操控,应急操控以及保持稳定运动状态具有重要的意义,所以对非稳态甚至极端情况下的受力和运动状态的研究非常重要(熊英 2019).类椭球体的操控状态一般分为稳态、准稳态和非稳态操控.稳态操控运动是指恒定速度的平动或者转动操控.准稳态操控运动是指一种相对“缓慢”的运动状态的改变.非稳态操控运动是指此刻运动状态明显依赖于上一运动状态的非恒定速度的操控运动.无论是自主运动还是操控运动,都是在外力的作用下在流场中运动,并伴随着位置和姿态发生变化.亚临界雷诺数下细长体的机动性能体现了这一特性(Zeiger 和Telionis 2004) 准定常有严格的定义:如果流动不受流动历程的影响(历史效应),是一种时间平均的现象.也就是说,如果等价的定常现象g是某个参数x的函数,那么如果x随时间变化,而g仅仅是x(t)的函数,在任何其他方式上都不是t的函数,那么g就是准定常的(Wetzel 和Simpson 1996).由于机动过程的复杂性,绕椭球的时间相关机动特性大部分只能通过实验获得,并且实验是非常昂贵且复杂的,这导致实验研究并不多见.表4给出了开展非定常机动实验的一些实验条件. Hoang 和Wetzel(1994a,1994b)在实验室条件下,第一次对全湍流条件下的机动问题进行了研究.在维吉尼亚工学院和州立大学风洞中,用一个名为DyPPiR(dynamic plunge-pitch-roll)的三自由度(俯仰、横滚和升降)实验装置对俯仰过程中椭球表面流场进行了研究,测量了不同周向角处的压力分布.在1/3 秒短时间内,椭球体的俯仰角从0°变化到30°,绕重心旋转,等效无量纲俯仰速率为0.047. 图94给出的俯仰机动的压力数据表明,在20°至30°高攻角时,背风面的旋涡在物面上诱导生成很强和具有黏结性的旋涡运动,在背风面x/L=0.44~0.77 站位的压力分布上产生了吸气峰值.而在模型的尾部,在压力剖面上,吸气峰值并不显著,这意味着背风面的旋涡上升并离开物面,或者是由于一部分涡破裂而耗散了.这个现象其他研究者在细长旋成体上通过流动可视化和压力测量也发现了(Zeiger 和Telionis 2004).因此对于椭球这类轴对称物体,当非定常快速俯仰时,分离流和旋涡运动可产生非定常的超升力,从而进一步使飞行器产生超速机动. 图94 图95给出的压力分布可以看到,机动过程中流场是高度非定常的,与定常态的流动特征相比,出现了十分明显的偏离,压力分布不是准定常的,这意味着在相同的攻角下,与定常流动没有相关性,也就是说不能采用某个有效攻角计算非定常流场作为机动过程的流场. 图95 在相同攻角下,与定常流动相比,压力脉动在背风面达到了局部最大要更甚一些(图96).由于大攻角下,定常流动的分离位置靠近压力脉动局部最大的位置,可以判断非定常机动能够进一步引起背风面的分离延迟.并且,随攻角增加,背风面的旋涡出现的越来越快,并逐渐朝椭球的上游移动. 图96 如图97所示,在回转机动过程中,在压力分布剖面图中背风面没有出现峰值,这表明模型上的剪切层分离还没有发展到背风面的旋涡中,或者是背风面的旋涡可能已经从模型上发展到很下游的远场尾迹中.采用准定常近似对于回转机动是无效的. 图97 非定常流动相比于定常流动有明显的滞后,导致了不同的流动拓扑,与定常状态相比,在机动期间,所有位置的分离都推迟了,这说明定常和非定常流动发展过程中是存在差异的.回转机动时物面压力分布与纯粹的上仰机动和定常流动都有明显差异.回转机动能够较单纯的上仰机动产生更高的升力,这也表明俯仰速率越高,产生的动态升力越高.如图98所示 图98 在非常低有效攻角(约1.15°)下进行俯冲运动时,非定常运动的模型看上去仅对一些孤立区域的表面压力系数有影响,即头部和尾部,如图99所示.头部和尾部压力分布的共同改变产生了上仰力矩.因此在纯粹的俯冲机动过程中,经历了绕重心的旋转,即向下俯冲时,可能会遇到所不愿看到的前端抬头现象,最大俯仰力矩刚好出现在机动结束前. 图99 后来,Wetzel 和Simpson(1996)采用热线测量椭球俯仰加滚转机动时的横流特性,通过壁面剪切应力的局部最小值来识别分离位置,图100给出了定常和俯仰机动过程中的分离线,与定常态相比,一次分离、二次分离和再附线由于俯仰机动而延迟. 图100 攻角越大,这种效应越明显,一次分离涡的位置大约会延迟10°,如图101所示,这是因为机动时所受到的逆压梯度更小,因此边界层分离延迟了. 图101 准定常和非定常气动力方面存在明显的差异(图102).在准定常方法中,机动飞行器的气动力仅依赖于模型的瞬时状态(包括攻角、侧滑角、控制面的偏斜等),而在完全非定常空气动力学中,隐式的时间依赖性,或者说是历程的过程影响都要包含在内.这一结果已经将非定常流动演化的重要性明确的展现出来,表明了定常流动和非定常流动之间的明显差别.后来,Hosder 和Simpson(2001)测量了类椭球的潜艇外形,结论与Wetzel 和Simpson(1996)基本一致. 图102 Wetzel 采用Goman 和Khrabrov(1994)提出的非线性方法,即一阶延迟模型,成功拟合了实验数据,如图103所示,看上去分离的延迟与边界层内的对流速度相关. 图103 对于延迟模型,Granlund 和Simpson(2009)做了进一步研究,对稳态、准稳态和非稳态操控下细长体的受力和力矩进行了研究,如图104所示.稳态运动时,在6°小攻角下,流动未呈现分离状态,力和力矩同攻角之间是线性关系,随着攻角的增加,横流分离在背风区形成涡流,此时力和力矩同攻角之间是二次关系.同时,随着攻角的增加,压力的中心向后移动,不稳定性降低,对于椭球体,涡升力对压力位置变化的影响是恒定的并且限制了最大俯仰力矩.总之,非稳态俯仰纵摇运动操控实验表明非稳态力和力矩不同于准稳态运动,不能用简单的时间滞后模型. 图104 实验时,需要机械支撑装置将模型支撑在试验段的模型区.机械支撑装置引入了支撑干扰效应,这一点早就已经认识到了,也发展了相应的支撑干扰修正方法.数值模拟研究表明,尾支撑对模型气动力有一定的影响,主要影响模型的轴向气动系数,对俯仰力矩系数、法向力系数的影响很小,对模型前体的影响非常小,对流场的影响主要集中在尾部边缘处(吴天佐 2014).椭球上的支撑干扰效应也基本上如此. Dress(1990)在低速风洞中,采用自由支撑无干扰的方式对f=7.5 椭球的阻力进行了测量,攻角为0°.如图105所示,参考面积和长度都选用无尾撑的数据.带有尾撑后,阻力系数明显降低.原因可能有两个,一是尾撑相当于使得椭球长细比更大,阻力系数降低,二是尾撑起到了改变和破坏模型尾部的分离尾迹区的作用.另外,随着雷诺数增加,尾撑的影响增加,这可能是随雷诺数增加,层流分离点逐渐向后移动,下游的尾迹区尺寸减小,尾撑通过改变尾迹进而对流动有了更显著的影响. 图105 Amob 和Otsuki(2016)使用没有机械支撑装置的方法来避免尾撑干扰,使用一种理想的自由支撑系统:磁悬架平衡系统(magnetic suspension and balance system,MSBS),通过由线圈产生的环绕磁场和包裹在模型内的永久磁铁之间的作用将模型悬浮在试验段中,气动力可以通过控制线圈的电流来测量.如图106所示.在MSBS 中,诸如压力等物面的物理量却很难获得,因为这需要遥感测量系统.但流动可视化可以提供一些关于绕模型流场的有用信息.为此他们仅进行了一些初步的实验. 图106 Ambo 采用MSBS 研究了f=6,Re=5×105椭球(L=0.252 m)尾部的流动分离,同时采用发光油流技术进行了可视化.自由来流速度为30 m/s,攻角为0°和5°.即便在零攻角时,模型尾部都呈现了复杂的层流分离模式.为了评估支撑干扰的影响,进行了系统的实验,采用小的多余物来模拟支撑系统的干扰.干扰物放置在顶部中心线上,如图107 所示.实验表明,多余物对分离模式有明显的影响,即便其直径小到0.5 mm 时也会明显影响流动.在多余物的下游,分离出现了延迟,这意味着分离模式的改变是由于多余物后的层流边界层转捩引起的. 图107 图108中攻角为0°时流场呈轴对称状态,沿流向有两个周向线x/L=0.8 和x/L=0.95,在x/L=0.8 的上游,流动是附着流,x/L=0.8 位置的周向线是分离线,在这个位置,流动出现了层流状态的边界层分离,在分离流内部形成了复杂的流场.在x/L=0.95 位置的周向奇异线在过去的研究中没有观测到.在这条线的下游,流动是反向的.图109(a)是基于这种解释给出的表面流线,关于这种解释还存在很大的空白,需要测量速度场以便进一步理解流动过程.图108(b),攻角为5°时,分离模式变得更为复杂,表面流线呈现高度的三维结构,实验中观测到了开式分离. 图108 图109 图109(b)中显示了侧面的流线,迎风面的流线朝着奇异线聚集,在模型的侧面形成一条斜线,在这条线的上游,流动是附着流,在这条线上边界层出现了分离,并卷起形成涡层.在背风面,观测到了三条奇异线,在这些线的终点末端,油流是停滞的.这些线表明流动中出现了多个纵向涡.在椭球的末端区域,气流从尾部向上游流动,流线朝着由背风面起源的分离线聚集,注意到,在分离线的末端,形成了一个螺旋点或者是焦点.受到油流技术的限制,无法给出更多的流场细节,因此他们没有进行更为详细的拓扑分析. 从前面Ambo 和Otsuki(2016)的实验可以看出,椭球上小的突起物对流场有显著的影响,当然,他们的实验是为了模拟支撑干扰.由于绕椭球的流动非常复杂,对椭球物面很小的改变,都会对流动状态造成显著影响.在日常研究工作中,实验模型的表面常因制造或保管不善而存在表面缺陷,如表面有裂纹或凹凸不平等,这些缺陷会影响绕模型的近壁流动,改变壁面摩擦力线结构,从而产生虚假的拓扑结构,这是流体力学研究所关心的(祝成民和忻鼎定 2002). 在进行流场测量时,在椭球表面增加测量仪器同样会影响流场结构,如图110所示,椭球表面增加传感器后的一次分离位置存在明显差异,通过油流实验可以观测到,增加传感器后,在分离区的前部,传感器对流动几乎没有影响,在后部延迟了分离(Wetzel 和Simpson 1996). 图110 图111给出了椭球表面增加传感器后的二次分离位置差异,从实验结果可以看到,传感器对二次分离的影响更大一些(Wetzel 和Simpson 1996). 图111 国内的祝成民和忻鼎定(2002)采用油流法实验观察了物体表面颗粒突起对表面摩擦力的影响,层流状态下,分离线附近的颗粒突起会显著影响分离线的形状,如果雷诺数减小,颗粒对分离线的影响也会减小,直到微弱状态.实验观察到的颗粒影响仅局限在壁面附近.实验条件如表1所示. 为观察模型表面缺陷对油流谱的影响,实验中,在模型下方的迎风面放置两粒直径约为1 mm的金刚砂(金刚砂为不规则多面体,未准确测量直径).在雷诺数为1.4×106时,这两个细小颗粒对油流谱产生了明显的影响.从图112(a)中可以看到颗粒后的分离涡将未加颗粒时完整的一次分离线分为三条.将未加颗粒时的一次分离线称为原始分离线,将受颗粒影响而分开的三条分离线依从前到后次序称为第一、二、三条分离线(在图112中用阿拉伯数字标出).第一条分离线起始部分就是原始分离线前半部分,在遇到第一个颗粒的分离涡后分离线抬升,呈弧形向上接近二次分离线,然后与二次分离线平行向下游延伸,在x/L=0.89 处折向下.第二条分离线是原始分离线的中间部分,其起始部分为第一个颗粒的右分离涡所形成的分离线.当第二条分离线遇到第二个颗粒的分离涡时其方向改变,然后与第一条分离线一样呈弧形向上折转后再向下延伸.第三条分离线的起始部分与第二条一样,是第二个颗粒的右分离涡所形成的分离线.第三条分离线的后半段即是原始分离线的后段.由于靠近椭球尾部的流动已处于非定常,油流谱未能显示一分为三的三条分离线是如何终止的.当把雷诺数降为9.0×105后,这两个颗粒对油流谱的影响明显变小.从图112(b)中可以看出,第一个颗粒的影响已可以忽略.第二个颗粒的影响仅仅使一次分离线的后段出现向上的弧形. 图112 当流体流过颗粒时,在流场下游会形成旋转方向相反的两个涡.如果这两个涡形成的时间不长,它们的尾部是连着的,形成一个涡环.如果周围流动均匀,涡环逐渐被主流拉长,最终会形成类似于三角翼前缘涡的两个涡,这里称颗粒形成的涡为二型涡.如果物面有多个颗粒并且之间的距离很小,不同颗粒的二型涡就会碰到一起,涡之间的相互作用使二型涡破碎,流动紊乱,形成湍流.祝成民和忻鼎定(2002)实验所用转捩粗糙带就是利用这个原理使流动由层流人为地转变为湍流.如果颗粒相距很远,不同的颗粒的二型涡仍将保持层流流动.壁面附近两个颗粒产生的二型涡的左半部分旋转方向与主分离涡相反,两者相遇后削弱了主分离涡导致分离沿周向推迟,分离线上移.相对于主分离涡,颗粒产生的二型涡很弱,二型涡对主分离涡的影响局限在壁面附近.二型涡的右半部分旋转方向与主分离涡相同,当它与主分离涡相遇时,使削弱的主分离涡强度得到恢复.受油流显示精度的限制,祝成民和忻鼎定(2002)的实验没有显示出主分离涡与二型涡相互作用的详细情况.降低实验风速后,两颗粒产生的二型涡减弱,影响区域减小,颗粒对流动的影响减小.实验观察到的油流谱变化反映的是两个颗粒的二型涡对分离流动的影响.具体地说,对椭球绕流,由于分离涡的位置和方向控制了分离线的位置和走向,上述结果说明了两个颗粒对原始分离线所对应主分离涡的影响.这种影响归纳为两点:首先,在远离壁面的区域主分离涡所受影响很小.如果只看第一条分离线的前部及其他两条分离线的后部,可以看到它们仍然保持了与原始分离线相同的位置和走向,这说明主分离涡的位置没有因颗粒的作用而改变,受影响的只是壁面附近的流动.其次,近壁区流动受到的影响与雷诺数有关,雷诺数越大,颗粒的影响越显著. CFD 是借助一定的数学方法离散流体力学方程组,并通过计算机来求解流场离散点,进而研究流动过程、受力等流体力学问题,它是理论流体力学、数值方法和现代计算机科学的结合,由于控制方程是偏微分方程,难以用解析方法求解,而实验方法也有一定的局限性,所以CFD 方法在流体力学研究、航空飞行器和相关的交通工具设计中的应用深入而广泛.在一些特殊情况下,CFD 是可能提供流场详细资料的一种方法(张涵信和周恒 2001). 数值模拟验证通常采用简单外形,即所谓的通用外形.从前面的实验可以看到,椭球虽然外形简单,却有三维流动的所有基本现象,而且丰富的实验数据为验证数值模拟结果提供了参考,因此在三维计算中经常作为考核CFD 程序的验证算例.要系统的验证CFD 代码,需要识别流场拓扑的改变是由于物理流动的分叉,还是数值模拟效应,数值模拟必须保证不能让网格、分辨率、格式等,从物理上影响拓扑.对于壁面受限的流动,需要同时考虑壁面压力梯度和壁面剪切应力,即如何识别旋涡.同时要对比不同的模拟条件,如雷诺数、马赫数、不同边界条件等,同实验结果或其他人的数值结果进行对比(Dallmann 和Herberg 1995).在非定常模拟中,需要研究瞬时流态的拓扑变化,需要识别非定常分离流动中的静态特性.瞬时流场的分析应该允许识别静态流动特征,例如,分离线可能的局部位置,或者是非定常流中的涡核(Dallmann 和Herberg 1995). 虽然椭球外形简单,但计算中面临的困难却很大,尤其是大攻角时湍流起主导作用,并对椭球的气动力和流场结构有极强的影响.影响大攻角旋涡分离流动数值模拟的因素很多,主要包括湍流模型、隐式算法、计算网格和数值黏性等,除隐式算法外,其他几个因素都与黏性有关,可见黏性在大攻角计算时的重要性(张毅锋 2010).不同计算格式的数值黏性不同,包括人工黏性和格式精度带来的数值耗散,网格的疏密也会影响数值黏性的大小.为准确而有效地模拟大迎角湍流流动,发展了很多强有力的分析方法,以便更深入地认识和解释流动的物理机制. 绕椭球的流动中强烈的各向异性效应控制了剪切应力,即便是在远离分离的区域也是这样(Simpson 1996).湍流结构相对平均流结构的滞后需要通过应力输运方程来模拟.因此,三维分离的性态用代数模型计算得到可信结果是很困难的(Simpson 1996).尤其是攻角较大时,背风面的流动采用CFD 是很难模拟的(Gee 和Cummings 1992,Sung 和Griffin 1993,Chesnakas 和Simpson 1996).要想更好的理解湍流模型对流动特性的影响,需要更多的实验数据来支撑(Gee 和Cummings 1992). 由于实验观测的困难性,很多实验方法都是单点测量或整体测量,不能提供流场细节.即便是针对某一具体的流动情况展示了流场结构的细节,也缺乏系统的研究,例如攻角梯度变化很小时对流动的影响、雷诺数变化时对流动的影响.对理论研究来说,恰恰需要能提供流场细节的方法.CFD 不受此限制,变更计算条件简单,在CFD 中可以尽可能的发现更多的流场细节.但由于前述CFD 研究的不确定性,这些细节是否能够真实的反映流场也未可知,但对实验和理论研究还是提供了一些参考. 绕椭球流动的数值求解的发展,基本反应了近几十年来计算流体力学的发展,早期计算求解的是边界层方程、抛物化N-S 方程或薄层N-S 方程,后来计算求解的则是N-S 方程和RANS.近年来,随着计算机技术的发展,LES,DES,DNS 等逐渐用于求解绕椭球的流动. Van Dommelen 和Cowley(1990)采用理论方法确认了椭球赤道平面上的分离过程,采用Lagrangian 数值格式,给出的结果与欧拉方法计算的结果符合很好,但明显更精确.在分离位置,欧拉方法的计算过程被打破,但Lagrangian 计算可以继续,在壁面上未分离的涡量层,与非定常分离过程有相似的特征,在有限的时间内会消失. 早期采用不同的数值格式求解边界层方程(如表5所示),特别是这些方程与无黏流方程相耦合,能够为理解分离提供很多的支持.根据我们的认识,Wang(1972)是第一个对椭球的对称面进行边界层计算的.随后很多研究者都通过求解边界层方程对椭球绕流进行了计算,他们求解的都是层流边界层方程,没有模拟湍流.在求解过程中,为了计算过程能够顺利推进,边界层以外的速度场或压力分布需要指定,或者是通过求解势流方程获得,这是一种精确解(Cebeci 和Khattab 1981),或者是根据实验测量的数据(Wang 1974b).Vollmers(1982)给出了指定边缘速度初始值的方法,其幅值是根据实验所获得的压力,采用伯努利方程计算,方向是采用势流解的方向.这两种指定方法在预测分离或增厚的边界层方面没有任何显著的变化,获得的结果基本是相同的,这也表明了一阶边界层理论的局限性(Patel 和Baek 1985).或许采用二阶精度的边界理论能够提高求解穿越边界层压力梯度的精度(Radwan 1988).这是因为流动的主要特征是分离,尤其是在靠近背风面的位置,边界层方程在求解分离流动上的局限性所导致的误差更大,因此主要归结于边界层方程近似所带来的原理性误差(Patel 和Baek 1985).但Ragab(1985)则认为采用实验所获得的压力分布求解边界层方程得到的结果与实验更为符合. 表5 求解边界层方程的计算条件描述 Wang(1972,1975)使用固定在椭球上的坐标系进行求解,为了把计算扩展到整个物面,沿着对称面那条线,采用了一种分离的准二维计算过程,必须指定沿着这条线的初始边界层剖面分布.获得了绕流椭球大部分表面的解,但由于数值失稳,没有获得尾部的解.因为闭式分离是一种奇异分离,分离线经过或与临界点相连,这种分离从临近的区域将流动分隔开,随攻角增加,楔形的分离线沿着物面一侧向上游延伸,超过分离线的区域边界层理论不再适用.而且,沿着通过可到达区域末端的无黏流线,这种奇异性会被传导到下游站位(Cebeci 和Khattab 1981).Tai(1984)在流向上使用幂律剖面分布求解沿流向的流动,采用Mager 剖面分布求解横向流动,攻角大于10°后由于大范围的横流,定量上出现了偏离.因此采用具有奇异性的边界层理论无法确定分离线的位置和外形(Patel 和Baek 1985). 虽然不能确定分离线的位置,却能够获得对称面临界点的起始位置.Wang 通过边界层近似方法所计算得到的相应临界点位于x/L=0.724.其他研究者也得到了相近的结果,Cebeci 和Khattab(1981)为0.72,Ramaprian 和Patel(1981)为0.73,而Rosenfeld 和Wolfshtein(1988,1992)通过求解简化N-S 方程得到的结果为0.75,他们之间的差异可能是由于在边界层近似中对黏性和无黏干扰处理方式的不同而引起的. Wang(1974b)在对倾斜椭球对称面三维边界层的分析的基础上,进一步给出了攻角为0° ~90°时的边界层特性,以及长细比从1 到0 近乎圆柱的椭球的流动特性.随攻角增加,横流速度型的横向导数出现反向,纵向速度型逐渐扁平化,后面这个特征在二维湍流边界层中是长期都知道其存在的,Wang 在三维边界层中也观测到了这一现象,这与Wilson(1971)的实验结果是相符合的,这增加了求解边界层方程结果的可信性和重要性. 由于边界层方程的局限性,在周向速度出现流动反向的区域,边界层方程处理这一区域是极端困难的,很多研究者为了解决这一问题,提出了很多有效的办法,提高了边界层方程求解的精度.如Hirsh 和Cebeci(1977)采用盒子格式和ADI 格式(假定横流速度梯度是常数)求解,在没有横流逆流的区域,两种方法的结果是相同的,当出现横流逆流后,两种方法的结果出现差异.Cebeci 先后通过使用坐标转换方法消除边界层方程中椭球前端外形的奇异性(Cebeci 和Khattab 1980)、使用特征盒子格式获得了周向流动回流线的位置和对称面上最上游的零摩阻临界点(Cebeci 和Khattab 1981)、采用无黏流方程获得的自由流边界条件和稳定性理论提高数值求解的精度(Cebeci 和Meier 1987).Patel 和Baek(1985)通过逼近分离涡层的的方式能够处理较弱的周向反流.Radwan 和Lekoudis(1986)和VanDalsem 和Steger(1987)则通过在分离区通过指定壁面剪切应力和尾迹中心速度的方式获得了成功,以反演模式(inverse mode)通过指定反演强制函数(inverse forcing functions)能够克服边界层方程的奇异性,在靠近分离线位置没有任何奇异行为,避免了分离附近计算出现中断的问题,尽管这种方法不是很精确,但却是有效的.因此使用这种形式来研究黏性和无黏干扰过程以及光滑壁面的三维分离问题是可行的,这种方法也为较弱周向反流提供了一种解决方法. 后来,Radwan(1988)采用四阶精度的两点紧致格式求解了绕椭球的亚声速黏性流场.Telionis 和Costis(1983),Costis 和Telionis(1984,1988),Costis 和Hoang(1989)提出流线方法和涡格方法(vorte lattice)来计算无黏流动和分离涡层的非定常发展过程,采用基于局部相似的近似边界层方法用来计算开式分离线,这种方法假定绕过一般物体的边界层流动与绕过特殊外形物体的流动是局部相似的,而特殊外形物体边界层的解是较为容易得到理论解的.当尾迹增长时,两种格式在定位分离线时出现相互干扰,导致无法定位分离线.图113给出了瞬时分离线.可以看到,与无黏解(Telionis 和Costis 1983)符合的很好.分离线最终的位置,还不是很长时间后的解,看上去与通过流动可视化给出的分离线(Telionis 和Costis 1983)非常接近.边界层的解虽然有些粗糙,但与涡格方法相耦合,可以确定分离线的位置,而且当尾迹增长和卷起时,可以确定分离线随时间变化的位置,脱落涡的强度可由简单的近似公式来确定.这种方法比求解完整的三维边界层方程简单,但结果的精度值得商榷,特别是对一些非传统外形的构型. 图113 由于定常边界层方程在分离区域无法进行计算,一些研究者提议求解非定常边界层方程.Cebeci 和Stewartson(1984)使用非定常边界层方程求解椭球以均匀速度起动的流场,非定常状态的解很快接近定常状态的解,并且在攻角大于41°后,随时间增加,背风面出现回流区域,沿流向的位移厚度出现了显著的峰值,形成了一种奇异类型的分离.Ragab(1985,1986)假定椭球是从静止突然起动的,在旋涡演化期间的短时间段内,获得了关于椭球两侧分离线的部分信息. Wu 和Shen(1991,1992)提出了一种非迭代、时间推进的数值格式求解三维非定常层流边界层方程,解决了几何上的奇异性和椭球从静止突然起动的非静止驻点问题.从拉格朗日(Lagrangian)的观点看,物理上出现分离是显而易见的,在二维算例中发现的靠近分离位置的某种奇异特征在椭球计算中也发现了,也就是在流向上,某一流体块突然爆发,变形成为一个零厚度的流体包,随后边界层局部厚度快速增长,这种爆发首先出现在对称面的某个点上,然后沿横流方向朝背风面传播,是否会形成封闭曲线或者到达背风面对称面则与攻角有关.对0°攻角,离开椭球物面的分离位置,其投影形成了一条闭式曲线,环绕着椭球.在有攻角的情况下,如图114所示,由于攻角的存在,对称性遭到了破坏,在迎风面的对称面上,很强的位移速度首先进行演化,然后朝向背风面的对称面,在分离位置的边界层会发展为新月形的山脊,随后被猛推到主流中.Van Dommelen 和Cowley(1990)采用奇异性渐近理论也得到了相似的结论. 图114 在t=0.11 时(图115),靠近椭球的末端,位移速度的云图迅速演化成细长的肾形山脊,当从对称面以某种程度上温和的方式下降离开时,在流向上有很剧烈的梯度.这些条状的云图的建立,证明了van Dommelen 和Cowley(1990)渐近分析的结果.在分离之前的奇异性结构恰好是准二维的,流向的长度尺度比横向的短得多.事实上,由van Dommelen 和Cowley(1990)所推测的边界层厚度云图的外观,与图115(b)所示的位移速度分布是非常相似的. 图115 如图116所示,尾部区域形成封闭的气泡,有轻微的非对称,这称为定常分离.Chapman(1986)将之称为第一类型的分离.回流区的尺寸会随时间增加而增加,但气泡保持闭合.Cebeci和Su(1988,1988)根据其计算,气泡会逐渐从背风面打开,那些融合的极限流线也会改变成为开式分离. 图116 严家祥和席德科(1989,1991)采用三维积分边界层法并结合流线法确定涡层型流动分离,如图117所示,压力分布由实验测量得到,边界层边缘处流线会聚的位置近似地决定分离线的位置.分析表明,涡层型分离不仅与壁面极限流线的收拢有关,而且还与边界层边缘处的会聚有关.壁面极限流线的收拢并不是引起涡层型流动分离的充要条件.因为在某些情况下,即使壁面极限流线收拢,涡层型流动分离也可能不发生,这是由于三维流动分离不但与黏性滞止及流向反压梯度有关,而且还与横向压力梯度有关,即使流向反压梯度使得流线偏向侧方,而横向压力梯度很小,流动仍然可以不分离.对于绕椭球体带迎角的流动,由于背风面流线弯曲,必然和来自迎风面的那些流线会聚而产生分离面,分离面和物面的交线称为分离线,因而形成涡层型分离.事实上,会聚的轨迹线是处于包络线以上的,流线会聚后,就产生涡流,并建立起带有某些间歇性的分离面.从水洞中流场显示观察到,伴随不对称涡的拖出,分离面交替地向两侧摆动.这种现象在大迎角小雷诺数下展示得尤为清楚. 图117 严家祥在求得边界层参数后,获得了椭球的无黏和黏性流线,图118为流线的比较,由于黏性效应,使得黏性流线变陡而偏离了无黏流线,产生这种现象的原因是由于横流速度所致.将计算结果与水洞的观测结果进行了对比,二者基本一致. 图118 图119给出某流线上三个典型点处的流向、横流速度型以及它们的合成速度型.由于横向速度型由正转负,故使得黏性流线先向上偏而后向下偏. 图119 北京航空航天大学的忻鼎定( Xin 2000)也开展了大量的实验和数值模拟工作,考虑到了压力梯度效应和涡黏性的变化历程.转捩点设置在x/L=0.575 处,边界层外侧的速度通过求解势流方程来获得.摩阻上的差异主要是在背风面的尾部区域,这可能是流动分离后,采用基于边界层的势流解无法描述分离流动所导致的,如图120 所示. 图120 Kim 和Patel(1991)认为使用经典的边界层方程计算,不管所采用的方法,在分离区内都无法再继续计算.也有研究者曾做了一些尝试,如交互的或反向边界层方法来处理分离,困难之处在于推进过程的合理选择.考虑到数值计算的困难性,在理解三维边界层的演化时,也只有很少的收益.事实上,基于边界层方法本身就不可能处理分离相关的所有问题,因为流动出现分离后本身就是难以理解的.求解过程被打断导致经常把分离这一物理现象弄混淆,而且这也增加了关于在某种特定情况下分离类型的讨论. 早期,受到计算方法和计算资源的限制,采用求解边界层方程的方法解决绕椭球的流动问题,获得了一些有益的结果,但受到边界层方程本身局限性的影响,当遇到分离线时,困难会成倍增加,考虑到在分离附近数值求解边界层方程的误差,以及边界层方程在分离区是无效的事实,这些方法的效果多是存疑的.采用边界层方程求解绕椭球的流动,分离位置对求解方法非常敏感,小的误差可能导致分离位置与实际相差很大.为了获得分离区的特性,同时计算方法和计算机计算能力的发展,20 世纪90 年代开始,人们尝试采用求解N-S 方程的方法,这使得了解分离后的区域变得可能. 表6给出了求解简化N-S 方程的条件.Rosenfeld 和Israeli(1985,1988),Rosenfeld 和Wolfshtein(1992)通过对控制方程中沿流向的扩散项进行简化,得到了抛物化N-S 方程,方程的数量和因变量的数量与未简化的N-S 方程相等,因此方程在分离区仍是有效的,而抛物型边界层方程则是无效的.采用曲线正交坐标系和原始变量求解,结果显示,在层流区域,与实验结果符合不错,并根据摩阻线型式和分离线外形对开式分离和闭式分离两种模式进行了讨论,与Wang(1975)的结论是一致的.Yates 和Chapman(1988,1992)也求解了抛物化N-S 方程,结果表明速度和涡量场在旋涡中心线位置,方向是一致的,在旋涡中心线上,速度大小、涡量大小、静压、密度都处于极值状态.虽然依然无法精确识别分离位置,但提供了一些参考. 表6 简化的N-S 方程及层流计算条件描述 雷诺数对流动有重要影响,Re=100 时背风面就开始出现定常分离(Zamyshlyaev 和Shrager 2004).Zilliac(1989)计算表明,在Re=1.0×103时,背风面的流动是对称的,而当Re=8.2 ×105时,背风面的流动呈现非对称性,通过水槽拖曳和风洞实验进行了证实.中国科学院袁礼(Yuan 2002)在不同攻角(α=10°/30°)的两个雷诺数(Re=3.0×103/1.1×104)下都得到了定常解,流场是对称的,他采用隐式全近似储存(full approximation storage,FAS)多重网格和人工压缩性方法求解,在解粗网格差分方程时,对Neumann 边界条件采用增量形式进行更新,离散方程采用三种不同的隐式格式,包括修正的点高斯松弛,标准的高斯−赛德尔线性松弛、Beam-Warming 的ADI 格式,对流项使用三阶迎风MUSCL 格式和对称TVD 格式进行离散,黏性项采用二阶中心差分.结果表明,无限制函数的MUSCL 格式比TVD 格式对流场结构有更好的分辨能力,在分离附近布置更精细的网格能够提高结果的精度.Rosenfeld 和Israeli(1985,1988),Rosenfeld 和Wolfshtein(1992)认为需要在分离区域附近布置更多的网格. 对不可压缩流,雷诺数是反映流场复杂性的重要参数.雷诺数大范围的变化意味着流场复杂程度的大范围变化.通过实验来大范围的变化雷诺数存在很大的困难.在普通风洞内风速变化有限,通过改变风速难以得到较大的雷诺数变化范围.一些特殊的风洞可以通过改变流体密度调节实验雷诺数,但这样的风洞造价高昂.变更模型尺寸也受到造价和风洞尺寸的限制.而通过CFD 变化雷诺数则简单的多.祝成民研究了流场结构随雷诺数的变化,计算结果系统地显示了分离结构随雷诺数的变化情况及分离涡的空间结构(祝成民和忻鼎定 2003b).这对Wang(1972,1975)之前的发现也是一种有益的补充和完善. 在较高雷诺数的椭球绕流中,表面摩擦力矢量场的奇点较多.使用前驻点指代椭球表面摩擦力线图谱中正对来流的奇点.将表面摩擦力线图谱中下对称线上、前驻点之后的第一个奇点称为下回流点,上对称线上、前驻点之后的第一个奇点称为上回流点.经过这两个点之后,上下对称线上的表面摩擦力线方向变为与来流相反.上下回流点反映了在对称面上分离发生的位置.在图121(a) (b)和图122(a)只有两个奇点时,上下回流点合二为一,即为后驻点. 图121 图122 图123给出了不同雷诺数下的分离涡系,可以发现α=10°和α=30°的涡系性质不同.α=10°时流动结构主要由椭球尾部穿过对称面的涡旋控制,此涡旋是由闭式分离的边界层形成的.随着雷诺数的增大,椭球尾部出现上下两个涡旋,上涡旋起的作用较大,它是背风面分离的边界层直接卷绕形成的,在它的作用下,椭球表面产生回流区.开式分离在较大雷诺数时才出现,其对流场结构的影响较小.从计算结果看,α=10°时是以闭式分离产生的涡系为特征的. 图123 如图124所示,α=30°时,当Re=500 时开式分离即已出现,并随着雷诺数的增大逐渐增强,但形成穿过对称面的涡旋则需要更大的雷诺数.在椭球尾部穿过对称面的涡旋形成后,由于其强度远小于椭球侧面开式分离的主分离涡,流场的结构仍由主分离涡控制.在雷诺数增大后,增强的主分离涡诱导产生二次分离涡,在椭球表面上形成二次分离线.二次分离线的方向与主分离线近乎平行. 图124 从流场的空间结构图上看,在计算的大部分雷诺数下,α=30°时流场中最明显的涡结构是与主流方向基本一致的主分离涡,分离涡系显示出开式分离的特征.图125给出了α=10°和α=30°时的典型空间涡结构. 图125 在所计算的雷诺数范围内,表面摩擦力线奇点的变化有一定规律.除了众所周知的奇点数随雷诺数增大而增多外,表面摩擦力线图中的上下回流点的位置也呈现规律性变化.不同雷诺数下回流点的位置列在表7中.α=10°时,在Re=500~5000 的范围内,上回流点的位置随雷诺数增大逐渐向下游移动,而下回流点的位置则向上游移动,主分离线则向上游凸出,这使分离区的面积逐渐增大. 表7 不同雷诺数下回流点的位置(°)(祝成民和忻鼎定2003b) 由于α=30°时椭球绕流主要受开式分离产生的主分离涡的影响,上回流点随雷诺数增大向下游移动的趋势不如α=10°时明显,下回流点的位置则体现出与α=10°时相同的趋势.上下回流点的这种变化趋势反映出随雷诺数增大边界层分离逐渐提前,分离涡逐渐增强.增强的分离涡的卷吸使上对称线的分离推迟. 从20 世纪90 年代开始,随着计算机和计算方法的快速发展,从求解边界层方程、简化NS 方程过渡到了N-S 方程,这使得了解分离后的区域变得可能.在求解N-S 方程的诸多方法中,RANS 是应用最广泛的,它并不直接求解N-S 方程组,而是求解雷诺平均方程来获得所需要的流场物理量.雷诺平均方程是由N-S 方程组经过系综平均后得到的,描写了湍流在整个区域中平均数量(动量、能量等)的传递. 对于一个复杂流场,在求解N-S 方程时,要获得工程设计能够使用的数据,一般需要几百万个网格点(张涵信 1998).RANS 的优势是计算量小,计算效率较高,在工程中得到了广泛应用.其不足之处在于,一是只能给出湍流的平均运动和相应的物理量,不能精确描述脉动量,二是有很多雷诺平均的封闭模式,但是没有一个普适的湍流模式.层流状态下的分离流动研究较充分,可以使用数值模拟方法得到完整的流动信息,而湍流状态下的分离流动目前还没有完全有效的计算方法(祝成民和忻鼎定 2002).这主要是指雷诺平均的封闭模式,即湍流模型的问题. 湍流流动模型很多,大致可以分为四类. 第一类是湍流输运系数模型,是Boussinesq 于1877 年提出的,模型的任务就是给出计算湍流黏性系数的方法,根据建立模型所需的微分方程数目,可以分为零方程模型(即代数方程模型)、一方程模型(如Spalart and Allmaras 的S-A 模型)和两方程模型(如k-ε和k-ω模型). 第二类是直接建立湍流应力和其他二阶关联量的输运方程,如雷诺应力输运模型(Reynolds stress trasport models,RSM). 第三类是LES,前面两类是以湍流的统计结构为基础,对所有旋涡进行统计平均,LES 把湍流分成大尺度湍流和小尺度湍流,通过求解经过修正的N-S 方程,得到大旋涡的运动特性,而小旋涡运动还是采用上述模型求解. 第四类是LES/RANS 混合方法. 目前,在工程领域中,甚至是预测非定常分离流动,主要的手段都是基于求解RANS 方程.事实上,在没有分离或回流的情况下,对于定常流动,RANS 方程叠加湍流模型有足够的精度和效率,能够对整体参数提供合理的数据,比如力和力矩系数等,只是在预测湍流应力等数据细节上能力不足.然而,对于非定常流动,或者是更为复杂的大范围分离流动、大尺度不稳定流动过程,准确地预测关键的物理过程总是非常重要的,这时就很难找到一个足够可靠的物理模型.早期求解RANS 方程时,由于椭球绕流中具有很强的湍流尾迹,导致数值方法遇到了很大的困难(Ragab 1986,Vatsa 和Thomas 1987),因此研究重点多集中在计算方法的改进上,而很少关注流场细节等物理现象.其计算条件如表8所示 表8 RANS 方法叠加代数湍流模型的计算条件描述 4.4.1 B-L 等代数湍流模型 B-L(Baldwin and Lomax(1978))模型为平衡型双层代数模型,形式简单,计算量小,无需确定边界层厚度,可较好地模拟附体流动,对于较小的局部分离流动,也有一定的模拟能力,因此在早期得到了广泛应用.从应用结果看,当流动出现明显分离时,模拟结果与实验值差异较大.采用与J-K(Johnson-King)模式类似的指数形式合成涡黏性系数,可有效提高格式的鲁棒性. Ramamurti 和Sandberg(1994)采用一种预处理隐式有限元求解器,速度和压力都采用同阶的线性外形函数.在x/L=0.44,x/L=0.56,x/L=0.896 三个站位,压力分布与实验值差异较大,而无黏计算的压力与实验值非常接近.在x/L=0.6 位置摩阻与实验较为吻合,在x/L=0.772 摩阻位置与实验差异较大.可能的原因有两个,一是B-L 模型本身在面临大范围分离时存在有一定的局限性.二是Ramamurti 采用非结构网格计算Fmax存在问题. Vatsa 和Thomas(1987)在B-L 模型中改变了搜索Fmax值的方法,从迎风面开始搜索,以物面作为起始点,沿径向向外移动.Vatsa 采用美国CFL3D 程序的初始版本,对比了两种通量方法对计算结果的影响.第一种是基于隐式通量差分分裂方法(flux difference splitting,FDS),依靠迎风差分提供人工耗散.而第二种是基于显式中心差分方法(central difference,CD),依赖显式可控量的人工耗散方法.实验(Cebeci 和Meier 1987)时转捩线是在x/L=0.2 位置,计算时保持相同.当α=10°,Re=1.6×106时,转捩线基本位于一次分离线的下游,因此CFD 认为全场均为层流流动,与实验(Cebeci 和Meier 1987)时保持一致,计算得到的物面压力分布与实验结果相一致,但下游的摩阻计算结果和实验结果存在较大差异,这主要是由于湍流尾迹的存在所引起的,当前的数值方法还无法克服这一困难.当α=10°,Re=7.7×106时,计算时转捩线设置在x/L=0.2 位置,结果显示它处于分离线前,摩阻的计算结果与实验存在较小差异,这说明雷诺数越低时,结果对假定的转捩位置越敏感.当α=30°,Re=7.2×106时,仅在椭球前端存在很小的层流区域,计算时在相应位置打开湍流模型,结果与实验结果吻合的很好.总的来说,FDS 的结果比CD 的结果稍好,主要是有更低的人工耗散.后来,Wong 和Kandil(1989),Hartwich 和Hall(1990)重复计算了Vatsa 和Thomas(1987)的算例,Wong 采用VOR3DI和CFL3D 两个程序进行计算,VOR3DI 仅在物面压力分布上可接受,摩阻的预测较差,而CFL3D 的结果与实验值符合较好.Hartwich 使用VOR3DI 模拟到了横流分离模式,首先是层流分离泡,随后分离剪切层中发生转捩,并形成一次旋涡. 由于大攻角绕流时椭球会出现横向分离,并导致多个脱落涡,引起非线性干扰,B-L 模型的预测性能和稳定性出现了问题,仅改变Fmax计算方法的效果还不够明晰,一些研究者对B-L 模型进行了其他修正.Gee 和Cummings(1992)在F3D 程序中对其进行了横流修正,但还是没有捕捉到二次分离线,背风面的压力也要比测量值高,所得到的涡黏性值也比较大,导致一次分离涡的活跃度很低.Sung 和Griffin(1993)做了两个调整,一是零攻角下尾部区域内对混合长尺度的估算方法,二是提高了对Fmax第一个峰值的搜索算法,调整后对横流分离的预测精度明显提升,进而提高了有攻角时对力和力矩的预测精度,如图126所示. 图126 国内开展的相对较晚,温功碧和陈作斌(2004)基于人工压缩性方法提出一种中心与迎风混合算法,半离散方程的左端采用中心差分,右端数值流量采用迎风Roe 近似算法,其精度可达三阶.压力和摩擦系数与实验符合,在分离涡旋区计算值与实验有差别,这或许是由于湍流模式不够精确的缘故.图127是层流表面摩擦系数沿周向的分布,可以看出,其趋势与边界层解是相同的,摩阻最小值在周向120°附近,较边界层解(Rosenfeld 和Wolfshtein 1988,1992;Hirsh 和Cebeci 1977)的值低. 图127 图128为攻角10°的湍流表面压力沿周向的变化.除了接近后缘(如x=0.83)与实验(Hoang 和Wetzel 1994b)相差明显外,计算值与实验符合较好.总体而言,密网格比粗网格更接近实验.计算结果在后缘与实验的差别或许由于湍流模式的缘故.Sheng 和Taylor(1995)采用B-L 模型也有相似的结论. 图128 Deng 和Zhuang(2002),向大平和邓小刚(2005),丛成华和邓小刚(2011)采用一种新型的微可压缩模型(slightly compressible model,SCM)求解,在周向的背风区和分离线附近对网格加密,转捩位置x/L=0.2 与实验一致.图129给出了椭球表面的极限流线图,可以清晰地看到椭球表面的一次分离线、二次分离线和二次分离的再附线. 图129 图130给出了与实验和可压缩N-S 方程结果的对比,从摩阻分布的情况来看,SCM 和NS 方程的计算结果完全重合,在分离区外与实验结果的吻合程度相当好,在分离区内计算结果比实验结果略微偏大,但趋势完全一致.这种摩阻的差别可能是由于B-L 模型不能很好地模拟分离区内非平衡湍流流动所致. 图130 图131为对称面压力分布,压力系数除了在背风面尾部区域与实验结果存在差异外,与实验结果符合得非常好.尾部的差异估计是由于实验中支杆的影响造成的. 图131 图132给出了沿流向不同站位的周向摩阻分布.可以看出,在迎风面上,SCM 得到的摩阻系数比实验结果稍大,优于Vatsa 和Thomas(1987)的计算结果.在背风面上,SCM 计算的局部极值与实验结果符合较好. 图132 为了克服较强的压力梯度,特别是较强逆压梯度的湍流边界层,Johnson 和King(1985)于1985 年提出半方程J-K 模型,这是一种非平衡代数模型,通过求解一个关于最大雷诺剪切应力(由湍流动能推导而来)变化的常微分方程以模拟上游对下游的影响,该模型有很多的改进版本,统一称为J-K 模型,这里不再详细叙述. 4.4.2 一方程和两方程模型 三维分离的性态用代数湍流模型计算得到可信结果是很困难的(Simpson 1996),因此还需要使用更为复杂的湍流模型,表9给出了相应的计算条件. 表9 RANS 方法叠加一方程和两方程湍流模型的计算条件描述 Kim 和Patel(1991)使用k-ε模型,阐明了流动拓扑和分离模式的变化,确认了之前Wang(1975)得到的一些结论,同时得到了一些使用代数湍流模型计算中没有出现的分离流细节,第一次证明了复杂湍流模型在绕椭球的高雷诺数湍流问题中较代数湍流模型具有明显的优势.最重要的特征是在低攻角时椭球的一侧存在螺旋点或焦点(图133),在较高攻角时仍能短暂看到,确认了早前流动显示中的观测和推论(Ramaprian 和Patel 1981). 在较低攻角和中等攻角时(图133和图134),在椭球尾部,总是有一处闭式分离区域,这个区域可以通过物面摩阻线或极限流线的临界点来识别.随攻角增加,这个点向椭球的上游移动.临界点的类型和数量与攻角相关,当攻角增加时,临界点数量增加,在临界点中,有螺旋点,或焦点,表示龙卷风类型的旋涡是从这些点起源的,然后弯曲进入尾迹中. 图133 图134 综合图133~图135可以发现,在0°攻角时,绕椭球的大部分流动都是轴对称的,但在分离附近,流动变成三维的.打破这种对称性的可能是数值方法的问题,但这是在任何数值求解中都无法避免的.5°攻角时流动分离是闭式分离.开式分离从10°攻角开始出现,此时极限流线聚集成为一条单独的线.当攻角增加时,一次分离线向上游移动.在15°时,看上去存在另外一条开式分离线.这条线随攻角增加也向上游移动,当30°攻角时,有一次分离线和二次分离线,在它们之间还有一条再附线. 图135 如图136所示,根据不同攻角的计算流场,发现分离线与背风面的纵向涡是相关的.这些旋涡变得越来越大,离开椭球一定的距离.最好是通过轴向速度亏损和低压来识别这些旋涡的核心.其他的量,诸如轴向涡量,二次运动、螺旋度密度、归一化螺旋度,尽管有用,但不是涡核位置好的识别工具.在30°攻角时,从椭球体上发源的有三个明显的涡对. 图136 从Kim 和Patel(1991)的研究结果可以看到,k-ε模型在处理大范围分离时还面临较大的问题.Tsai 和Whitney(1999)使用k-ε模型得到的压力系数分布与实验结果符合的很好,复现了一次分离、二次分离及再附,但采用壁面平板律计算得到的摩阻系数与非直接测量的实验结果(Chesnakas 和Simpson 1997)差异较大,将壁面律中的经验常数由5.2 根据经验调整为0.454 后,得到的摩阻系数与热膜直接测量的数据(Wetzel 和Simpson 1998a)有很好的一致性.祝成民和忻鼎定(2003b)采用两种形式的k-ε模型:Jones−Launder 模式(简称为J-L 模式)和Shih-Lumley 模式(简称为S-L 模式),考虑了低雷诺数湍流效应,与实验数据(Kreplin 和Vollmers 1982)对比发现,在没有发生分离时,两种湍流模式计算的平均流场与实验结果符合较好.在分离发生后,分离结构与实验差别较大,分离区的表面压力系数分布与实验值定性相符. 虽然较代数湍流模型对分离区的模拟精度有所提高,在实际使用中,也遇到了很多问题.这就需要根据实验结果对参数进行修正.Liu 和Zheng(1998)使用k-ω模型计算得到的雷诺应力较实验值明显偏大.Kim 和Rhee(2003)在Fluent 商业软件中对k-ω进行低雷诺数修正后,与实验结果(Wetzel 和Simpson 1998a)相比精度明显提升,图137中KO-1 表示原始的k-ω模型,KO-2表示进行了低雷诺数修正. 图137 Constantinescu 和Pasinato(2002)对S-A 模型中的雷诺应力使用了非线性本构关系(图中标注为S-A NL),计算精度有提升.图138给出了壁面上的气流转向角,在x/L=0.6,预测得到的转向角小于135°,同实验(Chesnakas 和Simpson 1997)相比稍微有些滞后,在150°附近测量值变化剧烈,与第一次和第二次分离的位置相对应,在x/L=0.77 位置,CFD 预测与实验结果有些差异. 图138 Constantinescu 和Pasinato(2002)也对比了大范围分离区内不同模型的模拟能力,如图139所示,S-A 模型进行了旋流效应修正(标注为S-A RC),从结果可以看到,RANS 和DES 的结果是相似的,趋势与实验结果(Wetzel 和Simpson 1998a)都是吻合的,不同模型在横流分离区的差异不大,但DES 不采用显式湍流模型(标注为No Modle)时与实验结果差异较大. 图139 Scott 和Duque(2004)也得到了相似的结论,采用OVERFLOW 软件对比了不同代数湍流模型(标注为BB,Baldwin-Barth)、一方程和两方程湍流模型的影响,从图140中可以看到,在大范围横流分离区内,无论是迎风面,还是背风面,摩阻系数与实验值(Chesnakas 和Simpson 1997)的差异都较大,仅有BB 模型和k-ωSST 模型完整识别到了一次分离、二次分离和再附区.结合Constantinescu 和Pasinato(2002)的研究,一方面说明了当前的湍流模型在处理大范围分离时有一定的效果,另一方面也说明仅通过对当前模型的修正是无法从本质上提高求解精度的. 图140 其他一些研究者更多是偏向数值方法和工程应用方面的研究,如Scott 和Duque(2004)研究了网格分辨率对流动的影响后,认为在周向必须有足够的网格点才能捕捉由于分离所致的压力梯度变化,这一结论在前文已经提到.Huang 和Lin(2009)采用WENO 格式加预处理的方式求解原始变量的N-S 方程,预处理在求解中提升了低速流动的求解精度.Holt 和Garry(2016)采用Fluent 商业软件研究了类椭球外形飞行器的近地效应. 国内也开展了一些相关研究.如邱磊(2004),邱磊和邹早建(2005)采用k-ε模型与Kim 和Rhee(2003)进行了相同的计算;肖昌润和刘巨斌(2007)采用k-ωSST 模型进行了计算,如图141所示,α=20°时压力分布与实验值(Wetzel 和Simpson 1998a)基本吻合,实验曲线在140°处压强系数有一个小幅的下降,显示这是由于流动的二次涡所致,计算没有能够计算出这种二次涡引起的压强变化,实验表明背风面上压强系数的极小值点(图中的160°位置)与流动的二次分离相对应,计算结果在此角度与实验结果有明显差别. 图141 摩阻则与实验结果(Wetzel 和Simpson 1998a)有明显差异(图142),在30°大攻角时出现了强二次分离,实验的分离点分别位于周向125°和150°左右.计算结果与实验结果间存在一定的差别,一是与实验结果相比计算结果偏小,二是分离点的周向位置角稍有不同.一次分离位置角较小,说明横向绕流分离靠前.由于摩阻与当地的速度分布和湍流黏性系数有关,出现这两种差别的原因可能是计算的湍流黏性系数偏小,横流湍流度不够强,导致壁面切应力较小和分离较早发生.前文提到,根据实验结果,在分离区外缘湍流黏性是各向异性的,而一方程和两方程模型中都假定湍流黏性是各向同性的,这也是原因之一. 图142 陈亮中(2010)采用无人工转捩的全湍流方式进行了计算.图143显示出物面压力系数分布的计算结果和实验测量值比较吻合,给出了分离区域内较为平直的压力分布特点.k-ωSST 模型更为精细地模拟出了分离线和再附线附近流场的压力分布细节,显示出k-ωSST 模型模拟大分离流动的较强能力,S-A 模型则稍微高估了流场中分离和再附区域内的压力变化. 图143 图144给出了不同流向位置处截面的物面摩阻系数分布.实验结果显示在迎风面转捩发生前的层流区域内,摩阻系数有一段较低的平直分布,而计算得到的结果却高出很多.过了转捩区后,计算结果和实验测量值的吻合程度大大提高. 图144 图145给出了x/L=0.5 站位横截面的流线分布,可以判定截面流线中共包含有4 个半鞍点S′和1 个鞍点S以及2 个结点N,奇点总数满足张涵信(1997)给出的适用于任何截面的奇点数目拓扑规律,即 图145 其中I(C)为绕截面内边界闭曲线上的Poincare 指数,在该截面上I(C)=1.两个湍流模型对主涡位置和大小的模拟结果是一致的.k-ωSST 模型给出的二次涡在尺寸上略大于S-A 模型的结果. 图146给出的是物面流线分布,可以看出,两个湍流模型都模拟出了流场中存在的一次分离和二次分离,相比之下,S-A 模型给出的二次分离和二次再附的位置稍微靠后一些,这是由于SA 模型过高地估计了湍流效应,推迟了分离流动的出现.对比可以发现模拟椭球这种复杂的大分离湍流流动,k-ωSST 和S-A 模型是效果比较好的湍流模型,S-A 模型的计算结果稍逊于k-ωSST 模型的结果,但采用S-A 模型的整体计算效率则高于k-ωSST 模型. 图146 过去几十年开展的绕椭球体的大量RANS 模拟可以看到,RANS 在全局预测能力上有很好的表现,在局部上,如气流方向角和摩阻等细节上还有些差距.同时也认识到,各向同性涡黏性湍流模型不能完全辨识分离区的旋涡,这主要是归结于对分离区内涡黏性的过预测倾向,以及湍流各向同性的潜在假定. RSM 直接建立湍流应力和其他二阶关联量的输运方程,可以得到各向异性的湍流黏性系数,能够考虑湍流各向异性对流场的影响.而绕椭球的大攻角流动中,湍流应力分布是高度各向异性的,因此求解这样的三维分离流,需要采用RSM,计算条件如表10所示.Kim 和Rhee(2003)采用基准的雷诺应力输运模型,得到的结果与实验存在明显的差异,后来,他们通过调整长度尺度方程提升了二阶矩封闭模型的性能,结果有较大改变,求解精度明显提升. 表10 RSM 计算条件描述 Morrison 和Panaras(2003)采用线性涡黏性k-ω模型和显式代数应力模型(explicit algebraic stress models,EASM)进行了计算,计算中模拟了模型尾部的支撑杆.实验中没有指定转捩位置,CFD 中将转捩点设置在x/L=0.2 位置.如图147所示,在边界层内,EASM 模型所预测的湍动能较k-ω模型低(其中n是到物面的距离). 图147 图148给出了湍动能分布,在x/L=0.524 站位,沿周向每个位置,边界层内的最大湍动能的极小值与分离位置符合的很好.在再附边界层区域,EASM 模型所预测的最大湍动能较低,而在一次分离和二次分离区域,所预测的最大湍动能偏高.这表明通过考虑湍流黏性的各向异性,确实能够对流场参数的分布起到作用. 图148 Alpman 和Long(2005)采用雷诺应力模型,求解12 个耦合的非线性偏微分方程,横流分离点的平均压力和周向位置都与实验符合较好(图149),压力分布与Kreplin 和Vollmers(1985)的实验结果一致,仅在很靠近尾部时有些差别,可能是由于涡量场的数值耗散所致.当旋涡沿着纵向移动时,旋涡从物面远离,一直到网格比较稀疏的区域,带来了较大的数值耗散. 图149 三维分离是很难模拟又比较难懂,不像二维分离,前面提到,三维分离很少与壁面剪切应力的消失相关.绕椭球的流动,气流在背风面一侧发生分离,并卷起旋涡形成涡层(Chesnakas 和Simpson 1997),这样,在分离一侧的摩阻线朝着分离线渐近收敛(Wetzel 和Simpson 1998a).在高攻角时,二次分离出现在更高的周向角上,如图150所示,沿着表面摩阻线的不同站位的涡量图说明了这个问题.从图中可以清晰的看到摩阻线是向着分离线渐渐靠近的.在椭球尾部,刚刚在分离线后,形成了旋涡.在上部的背风面一侧观测到了二次分离. 图150 表11给出了与Kreplin 和Vollmers(1985)所测量的x/L=0.738 站位一次分离和二次分离位置的对比,可以看到,计算得到的分离点与实验值是非常接近的,两个分离位置的差异在3°左右. 三维分离的另外一个标识是,在靠近壁面的分离点附近,纵向速度分离局部最小(Wetzel 和Simpson 1998a).图151给出了x/L=0.738 站位的纵向速度云图.纵向速度最小的位置(图中黑色区域)就是一次和二次分离点,这与实验测量的结果(Wetzel 和Simpson 1998a)相符合. 图151 摩阻系数的测量(Wetzel 和Simpson 1998a)是非常困难的,实验中总是包含一些不确定性.从图152中可以看出,采用RSM 模型获得的摩阻系数分布趋势与实验结果是完全一致的,局部极小值的位置也基本符合,但在数值上,CFD 和实验结果间还存在一些差异. 图152 RSM 中线性涡黏性模型假定剪切应力角和平均流动的角度相同.而前文指出,流动梯度角和剪切应力角在边界层的大部分范围内都不同(Chesnakas 和Simpson 1996),因此,RSM 在绕椭球的大攻角流动计算中与实验结果仍然还存在一些差异是可以理解的. 大涡模拟技术(large eddy simulation,LES)被认为是目前湍流流动数值模拟中最有效的工具之一,因为它不是模拟,而是求解包含大能量尺度的运动,也就是动量输运.其基本思想是对NS 方程进行过滤,对大于网格尺度的湍流脉动进行直接求解,能够更好地捕捉湍流的瞬态特征,小尺度湍流脉动选择合适的亚格子模型进行模拟,小尺度的运动是各向同性的,容易模拟,如果亚格子模型选择的合适,能够得到真实的瞬态流场,提高了数值模拟的准确性.LES 避免了直接计算小尺度的脉动,数值模拟的时间和空间步长都不如DNS 精细,从而减小了计算量,降低了对计算机资源的要求,其消耗的资源介于DNS 和RANS 之间.采用LES 时的计算条件如表12所示. 表12 LES 计算条件描述 Wikstrom 和Svennberg(2004)在LES 的计算结果中观测到了复杂的非定常现象,且不能使用RANS 捕捉到.这说明LES 的计算精度有明显提高,捕捉到了流场中一些实验中观测到的其他流场细节,进一步验证了实验结果,也肯定了CFD 的模拟能力和精度. LES 中最重要的是计算亚格子网格应力,特别是近壁面区的模型(张涵信 2016).Hedin 和Berglund(2001)对比了亚格子模型对结果的影响,所有亚格子模型与实验结果定性保持一致,在定量上还有些差距.如图153所示,在两个攻角下,气流速度最高的位置在椭球两侧,也就是说绕椭球流动时,气流加速,这也正好处于一次涡的下方,攻角越大,这种效应越明显.气流速度最低的位置刚好位于分离线的下游.在两个攻角下,两条分离线之间可以看到一个流体的低速槽,这个区域与速度脉动的最大值、压力脉动的最小值相对应.前文已经提到,实验(Chesnakas 和Simpson 1997)中也观测到了低速槽.分离线下游的这个低速槽之所以存在,是因为一次涡卷起了近壁面的低动量流体,接着,在一次涡本身和分离线之间的这股气流加速.当攻角增加,旋涡足够强时,这股近壁处的低速气流中的一部分冲出该区域进入旋涡中.这可以从图153(b)中观测到,在类似手指状的低速气流从壁面一直朝着旋涡的核心方向延伸,湍动能云图表明,在分离位置,二次流流线的提升与湍流气流薄层的提升是相伴的.这个湍流薄层看上去被一次涡从边界层拖拽到了旋涡核心中.这种效应越靠椭球后部越明显,但两个位置都可以观测到.湍动能最大的区域与低动量气流区域相对应,与一次涡的下游拐角也是相一致的. 图153 Farhat 和Rajasekharan(2006)采用静态LES(static large eddy simulation,S-LES)没有捕捉到二次旋涡,后来他们使用一种基于变分多尺度方法的动态版本LES(variational multiscale,VMS,VMS-LES)捕捉到了一次旋涡和二次旋涡(图154),可能是由于静态LES 方法产生了过度耗散. 图154 Alin 和Fureby(2005)证实了LES 能够精确计算绕类椭球的潜艇在0°侧滑角和0°俯仰角时流场的能力(图155),后来,Alin 和Fureby(2007)对比后认为LES 较URANS 能够给出更好的压力分布,而速度分布,只有LES 能够给出合理的计算结果,尤其是在x/L=0.772 位置,方位角为90°时,如图153(c)所示,在体表面坐标系中给出的三个速度分量,LES 都精确捕捉到了速度型沿椭球体的变化,而且准确预测到了攻角的影响.这个位置的速度型受到一次涡的强烈影响,这是因为分离涡位置很小的角度误差,将导致速度型出现巨大的差异. 图155 Karlsson 和Fureby(2009)对比了攻角小于20°下RANS、DES、LES的计算结果,其中LES 采用了不同的亚格子模型,发现结果的分散度很高,其中DES 和带转捩带的LES 的一种亚格子模型与实验结果吻合的很好.对于LES,通常不会考虑模拟转捩带,因此对于近壁面的处理和模拟就显得非常重要.如图156(a)所示,使用LES 配合转捩的方式,分离出现了延迟,在流线从椭球的侧面发出之前,椭球前端的极限流线被推后了,为第二个旋涡外面的第一个圆形涡的发展给出了空间.DES 模型没有带转捩带的模拟也给出了相似的结果,如图156(b).这两个结果与图19(b)的实验结果(Wetzel 和Simpson 1998a)定性符合的很好. 图156 Ranjan 和Menon(2015)对LES模型进行了改进,采用混合双层LES(two level simulation LES,TLS-LES)方法对湍流进行多尺度模拟,这种混合双层LES 方法,考虑了传统的LES 方法,又去除了一些传统LES 方法的限制.在TLS-LES 方法中,流场变量被大尺寸算子分为大尺度变量和小尺度变量,而不是采用传统LES 方法中的空间过滤方法,这样就避免了空间过滤操作中的很多限制.但从实际效果看,这种方法的精确度值得商榷.从图157压力系数分布上可以看到,在椭球的前半部分和后半部分分别呈现过预测和欠预测.计算中,迎风面压力系数由正转为负值是在x/L=0.5 站位,而实验中,由正转为负是在x/L=0.25.沿周向分布与实验值符合较好,但幅值在50°~120°之间与实验有差别.这些差异可能来自于实验条件上的差异,主要是尾部支撑的使用,在CFD 中没有模拟撑杆,也有可能是模型的敏感性和所使用的大尺度网格.因为从物理上看,靠近壁面的大涡尺度是较小的,将LES 运用到高雷诺数流动中时,在边界层的处理上需要额外的经验. 图157 前面提到,在工业应用中得到广泛应用的RANS 方法,其在计算附体和小分离流动时可获得令人满意的结果.但由于所有湍流模型的涡黏性各向同性假设,导致很难准确模拟大范围的分离流动,RANS 方法的这种缺陷促使人们发展了可直接求解大尺度运动并仅模拟小尺度运动的LES 方法.LES 可以较为准确地模拟分离流动以及与几何相关的大尺度非定常运动,所花费的资源仅需DNS 的很小部分.但是,当模拟边界层流动时,LES 所需的计算资源与DNS 几乎相当,另外,LES 方法的近壁模式尚不成熟,不能完全分辨出高雷诺数边界层的近壁湍流结构,所描述边界层的增长和分离不准确. 为解决工程实际需要,克服RANS 方法模拟分离流动的不足,同时提高LES 方法模拟边界层流动的效率,提出了一种描述非定常湍流流动的方法:RANS/LES 混合方法.其基本思想是用RANS 的湍流模式计算小尺度湍流脉动所控制的近壁附体流动区域,在远离壁面的区域,将湍流模型耗散项中的湍流尺度参数用网格尺度与一常数的乘积代替,使其形成大涡模拟中的亚格子雷诺应力模型,用LES 方法模拟包含远离壁面核心流的大尺度运动,并将它们有机地结合起来.这种方法在经验范围内是可行的,但缺乏统一的理论基础,因为LES 是建立在空间滤波基础上的,其流动与时间有关,而RANS 是建立在时间平均基础上的(张涵信 2016). 混合方法有很多,诸如尺度自适应模拟(scale-adaptive simulation,SAS)、分离涡模拟(detached eddy simulation,DES)等.雷诺平均的概念和空间滤波看上去貌似不兼容,因为在动量方程中它们具有不同的附加项(雷诺应力和亚格子应力),这就形成了混合模型.应用较多的还是Spalart 和Deck(2006)提出的DES,利用RANS 预测边界层的增长和分离,使用LES 模拟远离物面的那些受外形影响和分离区内的非定常大尺度的运动.通过对分离流动的模拟,证明DES 具有很强地模拟分离流动的能力,且可以很好地模拟物体表面的流动.由于DES 集合了各自方法的优缺点,且利用对方的长处有效地弥补了自身的不足,在当前有限的计算条件下,成为可以准确而高效地模拟几何相关、三维非定常湍流流动的一种切实可行的办法.由于在近壁区域采用RANS,因此,前文提到的一方程和两方程湍流模型,都可以与LES 相结合,形成多种DES 方法,如表13所示. Constantinescu 和Pasinato(2002)使用商业CFD 代码Cobalt 进行了研究,如图158所示,背风面的压力系数与实验(Chesnakas 和Simpson 1996)符合很好.迎风面在分离出现前与实验结果吻合的很好,出现分离后,尾部与实验结果有差异,可能是因为实验中有支撑的影响. DES 对边界层内沿流向的速度型辨识非常好,如图159所示,在x/L=0.6 站位某周向角处的速度分布与实验(Chesnakas 和Simpson 1996)符合很好,近壁区域显示出了对数律分布.近壁边界层内其他两个方向速度中,w与实验基本保持一致,而v与实验差异较大. 图159 即便是采用DES,计算得到的摩阻值仍然较实验值偏小,如图160所示,x/L=0.77 站位的摩阻分布,总的趋势与实验结果一致,但缺少峰值的变化.例如局部最小在150°附近用于识别分离位置,计算结果在那个位置附近出现了拐点,但没有清晰的二次局部极值,与实验相比,这说明计算中有一个很弱的脱落涡结构.对比可以发现,RANS 和DES 所得到的摩阻分布没有本质区别,很难区分不同模型的精度. 图160 DES 在分离位置的压力分布也没有显现出独特的优势(图161),x/L=0.77 位置的压力系数分布,与摩阻分布显示了相似的效应,在通过压力系数第二局部极小识别涡脱落方面,计算结果相比实验要弱得多. 图161 在DES 中,近壁边界层的分离仍是由RANS 模型确定的,因此对分离位置预测的精度没有明显提升,图162给出了一次分离和二次分离线,采用两种不同测量方法得到的实验结果(Wetzel和Simpson 1996)来推断分离的位置.总的来说,一次分离的位置,DES 得到的结果与实验符合很好,仅在x/L=0.3 站位附近与实验有差异,但与实验相比,DES 预测的一次分离和二次分离位置的起始点都有些延迟,例如一次分离处于x/L=0.4 稍微的下游. 图162 从Constantinescu 和Pasinato(2002)给出的结果可以看到,由于DES 在近壁处采用RANS 模型,外层采用LES,导致DES 仅在远场的求解精度得到了提升,对物面压力和摩阻的辨识并没有实质性的提升.Scott 和Duque(2005)采用商业软件OVERFLOW 也验证了这一点,图163给出了x/L=0.77 站位的速度型,该位置刚好处于二次分离的下游,背风面压力下降最小的位置,在y+<10 时RANS 和DES 的结果是几乎完全相同的,但当y+>100 后,DES 预测精度有明显提升.关于这一点,从升力和力矩的预测上也有明显的证明,DES 和传统的湍流模型所预测的升力都较实验结果小,但都准确预测到了俯仰力矩(Scott 和Duque 2005). 图163 国内的研究者对基于不同湍流模型的DES 方法进行了比较.肖志祥(肖志祥和陈海昕 2006,Xiao 和 Zhang 2007)对比了B-L DES 和S-A DES 两种方法对结果的影响(图164),两种方法均可以较好地模拟压力的细节变化以及主分离线的位置,B-L DES 方法计算的背风面旋涡较弱,尤其在x/L=0.48 和x/L=0.56 两个截面,而S-A DES 方法在这两个截面的计算结果与实验吻合非常好.遗憾的是,S-A DES 方法计算的分离区域和分离强度在x/L=0.64 截面后较实验和B-L DES 方法的值都大. 图164 于向阳和刘巨斌(2011)对基于SA 和k-ωSST 的DES 进行了对比,速度压力采用SIMPLE(semi-implicit method for pressure linked equations)方法解耦,如图165所示,计算得到的压力系数与实验数据(Wetzel 和Simpson 1998a)趋势较一致;在迎风面上S-A DES 略高于实验值,而kωSST DES 更接近实验值,两种方法都捕捉到背风面局部极小值点的位置,但在数值上还略有差别;S-A DES 在计算背风面旋涡能力上稍有优势,特别是Cv=30 时,在背风面上与实验值吻合较好,而Cv=40 时,数值计算结果略小于实验值,且在背风面局部极小值点的捕捉上提前约5°,从这里也可以看到,在湍流模拟中,湍流黏性系数的计算是极其重要的. 图165 从壁面摩阻系数看,即便是在靠近椭球头部的位置,计算得到的壁面摩阻系数与实验值(Wetzel 和Simpson 1998a)还有一定差别存在;在分离位置的捕捉上,根据摩阻系数局部极小值与分离点位置相对应的条件,分离点分别位于120°和150°处,S-A DES 对一次分离点捕捉较好,而k-ωSST DES 得到的一次分离点的周向位置滞后约8°,Cv=40 时能够捕捉到二次分离点,但在位置上略提前5°. 为防止出现网格诱导分离问题,Spalart(2009)提出了延迟分离涡模型(delayed detached eddy simulation,DDES),DDES 模型对长度尺度进行了重新定义,使得DES 能够检测到边界层,并且在边界层内部保证完全的RANS 模式.国内胡偶和赵宁(2017)采用基于k-ωSST 的DDES 模型得到的结果与实验值吻合较好,如图166所示,通过物面的极限流线分布展示了一次分离线的位置S1,二次分离线的位置S2与二次涡再附线位置R2,一次分离再附线的位置R1位于z=0 对称面附近. 图166 表14将x/L=0.77 站位处的分离位置与再附位置进行了对比,可以看到S1与S2的值与实验吻合很好,R2的位置与计算值(Xiao 和Zhang 2007)相近,显示出DDES 对大分离流动问题的模拟能力. 表14 分离点、再附点位置的计算结果比较 为定量分析背风面流动情况,图167中给出了横截面上沿周向的压力系数分布,可以看到,即便是在二次分离下游,对压力分布的预测也与实验值(Wetzel 和Simpson 1998a)基本完全吻合,仅在靠近背风面对称面处的第二局部极小值大小和位置的预测上与实验有差异. 图167 图168中给出了x/L=0.77 站位4 个方位角的无量纲速度分布.φ=90°时速度分布与实验值吻合良好.u/U∞(U∞为来流速度)呈现出对数分布趋势,在yn/L ≈3.0×10−3达到最大值;v/U∞的值很小,几乎接近零,较之于实验值稍稍偏大;w/U∞的值也在yn/L ≈3.0×10−3到达最大值,与测量结果完全一致.φ=120°时u/U∞与w/U∞随法向的变化更为陡峭,该站位位于背风面流动分离区域,3 个方向的速度型计算结果与实验值(Wetzel 和Simpson 1998a)吻合很好,这说明DDES 能够在流动分离区域正确地捕捉边界层分离.φ=150°位置处于二次涡结构附近,从图168(c)中可以看出,u/U∞的结果与实验值吻合良好,但是v/U∞与w/U∞的结果却存在明显的差异,这说明DDES 在分辨较弱的二次分离涡时还存在困难,得到的分离涡强度较实验值小得多,Constantinescu 和Pasinato(2002)也有相似的结论.φ=180°时u/U∞和w/U∞与实验值吻合良好 ,v/U∞较实验值稍稍偏大. 图168 DNS 是在不引入任何封闭模型的前提下对N-S 方程直接求解.这种方法能对湍流流动中最小尺度的涡进行求解,可以获得湍流场的全部数值信息,但是要对高度复杂的多尺度不规则湍流运动进行直接数值计算,必须采用很小的空间步长和时间步长才能分辨出湍流中详细的空间结构及变化剧烈的时间特性,即使对于最简单的湍流,也需要规模巨大的计算机资源.在DNS 中,由于需要模拟最小尺度的旋涡,三维网格数至少需要正比于Re2.25,而总的计算量正比于Re3(Chapman 1979).举例来说,对于前文实验中经常涉及的Re=1.0×106,其网格数量为3.16×1013,计算量为1018,根据当前的计算能力,在工程计算中,这几乎是不可承受的,因此DNS 目前还只能用于较低Re的流动中. Khoury 和Andersson(2010)第一次将DNS 应用于椭球的模拟,对f=6,α=90°椭球绕流进行了细致的研究,网格量为1.5 亿.在亚临界状态Re=1.0×104时,图169(a),在子午平面和极轴附近,层流边界层从椭球前侧的表面分离,在那些位置,小尺度的旋涡被冲入尾迹中.从图169(b)(d)可以看到,分离剪切层从最初始就是不稳定的,剪切层从椭球表面分离后,涡层内很快就出现了剪切层失稳,涡丝在方向上大致与椭球的主轴保持一致,涡丝相对是比较长的,但还没有扩展到整个展向上.随后这些涡丝向下游发展,出现扭曲变形,在近场尾迹中逐渐破碎.这种情况与图169(c)赤道平面的情况是完全不同的.在这种情况下,分离的剪切层暂时保持层流,在椭球后驻点的上游,在较早的起始阶段,出现了Kelvin−Helmholtz 失稳.随后,层流剪切层被打碎成小尺度的旋涡,形成椭球形涡街,近场的尾迹流动已经演化为湍流状态. 如图170所示,Std从极点向着赤道平面逐渐增加,并在赤道平面达到极值0.156,在极点附近,流动是由更多高频率的模态所主导的,这使得Std从0.015 增加到0.5.这些高频模态与极轴区域相关,控制脱涡模态的高频模态,使其被限制在距离极点1D的范围内.高频模态可以归结于分离剪切层内的Kelvin−Helmholtz 失稳.从图170b看到,局部Red与局部Std呈现线性关系,这说明沿着椭球的展向方向脱涡频率是常数.尽管沿着展向的截面积是变化的,脱涡频率却是相同的.也可以看到,中线段的间隙与某个展向位置是相对应的,在这个位置,高频模态比低频的脱落涡模态具有更多的能量.这些高频模态与剪切层失稳相关,在主轴下游3.5D位置清晰可辨(图170a).随着向下游发展,这些模态逐渐减弱,到下游9D位置,这些高频分量就无法识别了,而更低频率的脱涡模态就占据优势了.在相同的亚临界雷诺数下,Constantinescu 和Squires(2004)在圆球的CFD 研究中也认为高频模态与剪切层中的Kelvin−Helmholtz 失稳相关,但大尺度涡脱落的St比圆球明显低很多. 后来,Khoury 和Andersson(2012)对f=6,α=90°椭球Re=50~300 黏性层流流动的尾迹进行了研究,如图171所示.Re=50 和Re=75 时,边界层从椭球表面分离,形成大范围的回流区,但流动仍保持定常层流,且流动以子午面(meridional plane)和赤道面(equatorial plane)保持对称.分离位置都非常靠近极点,在赤道面上,分离点分别位于φ=138°和φ=124°,可以预见,随着向极点靠近,局部雷诺数是逐渐减小的,分离点会向背风面移动.在子午面上,两个雷诺数状态下的流线图基本无差异.而在赤道面上则存在明显差异,Re=50 的流线图与Re=40 长圆柱的流动类似,在椭球后形成两个反向旋转的涡,Re=75 时,反向流动看上去像是起源于椭球下游4.2D位置的一个源,与圆柱后的定常尾迹完全没有可比性. 图171 在Re=100 时流动虽然还保持层流,但已经呈现明显的非定常特性,St=0.109,关于子午面的对称性被打破,关于赤道平面仍保持对称.图172是流向速度为0 的界面,在Re=100 时其外形如舌状,舌根部分与两个反向旋转的旋涡相对应,而舌尖部分则是由于出现了周期性发夹涡.Re=150 时舌尖部分变宽,关于赤道平面仍然保持着对称性.在Re=200 时,尾迹拓扑的复杂程度明显增加,但舌根部分仍较为平滑,此时非定常层流流动有两个明显的频率,在任何平面内都不再保持对称.在Re=300 时,尾迹拓扑变得非常不规则,非定常尾迹流甚至变成了过渡流,脱涡频率为St=0.151. 图172 远场尾迹在空间上都不再保持对称(图173).Re=100 和Re=150 时,从椭球两侧依次脱落形成发夹涡,形成阶梯形态但呈相反分布的涡结构,与圆球单侧脱落的尾迹相反.在靠近椭球的位置,其尾迹云图仍保持椭球的形状.大约距离椭球15D后主轴与副轴的流动成一线.在x/D=10 截面,所有雷诺数下,尾迹外形还能反映椭球的外形比例.然而在10D的下游,圆周的外形已经明显不同.尽管尾迹外形并不是完全平滑,主轴的尾迹和副轴的尾迹已经成为一线.这说明在下游10D的某个位置,主轴和副轴之间发生了转换,也就是说,在某个确定的下游位置,横断面的尾迹发生了演化,导致主轴和副轴发生了交换,这种特别的现象在椭圆和矩形射流中经常发现,但在非对称尾迹流中,轴的转换却很少发生.其尾迹与有限长度圆柱尾迹非常相似,与圆球后的轴对称尾迹也有相同的特征. 图173 Jiang 和Gallardo(2014)对f=6,α=45°,Re=50~1.0×103(其Re基于短轴直径)的流动进行了研究,网格数量为1.8 亿.由于攻角较Khoury 和Andersson(2012)小,直到Re=200 时椭球后的尾迹都是定常的,流场结构关于子午面对称.如图174所示,在Re=1000 时,尾迹仍保持层流,较近的尾迹由涡街所主导,强横流引起了开式分离,但流动仍保持定常,除了非常靠近椭球尖端约0.2D左右的区域,流场关于子午面是对称的.从大约4D位置开始,流场关于子午面开始呈现非对称状态,出现了局部振荡,振幅小于0.01U.这部分的尾迹由一对反向旋转的涡组成,尾迹偏向强涡一侧,另外一个较弱的涡也被强涡包裹了一部分,此时尾迹可能处于非定常的边缘,但没有出现涡脱落或者涡丝摆动.同时力和力矩也没有任何迹象的变化显示非对称或非定常.回流区的长度从上极点到下极点显著减小,在靠近较低的极点时,回流消失.尽管平面对称性被打破,但尾迹在x/D=14 之前仍保持定常流动. 图174 后来,Jiang 和Gallardo(2015)将雷诺数增加至3000,由于流动更为复杂,网格数量增加至7.5 亿.如图175所示,此时尾迹不再保持层流,从本质上来说是非定常流动,从起始位置就是高度非对称的,涡结构出现了极度扭曲.椭球后剪切层从物面分离后形成很多旋涡,当旋涡离开椭球后的阴影区后,旋涡的一部分破碎成小尺度的旋涡,旋涡的另外一部分,看上去像是螺旋涡,在x/D=6 和x/D=8 两个站位可以发现,存在两个与主流涡量的符号相反的涡量集中区,这些正涡量起源于螺旋涡,而螺旋涡起源于椭球下端的极点. 图175 在体轴坐标系中画出了流线,由于其速度场是从xyz平面投影到ξz平面,图中的流线并不是真正的流线(Johnson 和Patel 1999).虽然不是真正的流线,但仍反映了流场的一些特性,例如,近椭球的尾迹流动由一对反向旋转的旋涡主导,在图176的瞬时图像中无法分辨这一对旋涡,因此瞬时流态与时均流态间存在差异. 在一定的长度范围内,在螺旋涡内部机械能是守恒的(图177中的〈Cp〉 +(〈uax〉/U0)2).轴向速度从椭球的下端(x/d=−2)开始增加,一直持续到x/d=1,达到第一个峰值,约为1.1U,大于自由来流速度,这源于三维分离:涡街从椭球的分离线上脱落,将涡量释放到近场尾迹中.由于分离线相对于自由来流方向是倾斜的,所释放的涡量有平行和垂直于分离线的分量(Zeiger 和Telionis 2004).在当前条件下,气流从椭球的底端向前端逐渐发展,涡量沿着分离线被释放掉,所释放涡量的平行分量有助于涡街的卷起,而垂直分量则引起了轴向速度的增加.从图177还可以看到,当维持旋转的方向不变时,在螺旋涡管内,在旋涡中心,轴向流动经历了从最大到最小的突然改变.这种尾迹的严重非对称性要归于全局失稳,可能会影响其机动性能. 图177 非对称的压力场导致了很强的侧向力,侧向力和流场呈现周期性振荡状态,从图178可以看到St=0.0733,这是非常低的,侧向力的增加占阻力的比例约为70%,与同样条件下圆球侧向力增加的占比是相同的,但圆球的St=0.137 则大得多(Johnson 和Patel 1999).另外,从速度信号中还可以发现存在二次谐波,其频率约为主频2 倍.而同样条件下圆球侧向力的时间变化显示了更低的频率占据主导,比阻力的变化St=1.3~1.4 的频率要低(Constantinescu 和Squires 2004). 图178 网格量增加至21 亿(Strandenes 和Jiang 2019),对相同模型Re=4000 的研究表明,如图179所示,尾迹是高度非对称和非定常的,两个主要的涡结构从椭球剪切层中发展,一个明显比另外一个强.侧向力与Re=3000 时有明显改变,涡核内部的压力也改变了.这表明流动是高度的过渡流.在靠近椭球处,较弱一侧的旋涡,有一处区域的轴向速度为负值. 图179 在这个回流区内,气流从椭球的后部进入,然后朝前流动,与来流相反,然后通过一个主要的涡结构从回流区流出.这个回流以前没有发现过,靠近这个区域存在明显的Kelvin-Helmholtz 剪切层失稳,如图180所示. 图180 从上面的结果可以看到,目前DNS 已经应用于相对较低雷诺数湍流流动的模拟,能够提供非常丰富的湍流特征,成为研究低雷诺数湍流物理机理的手段之一.在多数时间,DNS 被用于辅助理论来研究湍流的特性,可以启示我们更新对湍流结论的认识,发展更新的湍流描述方法,验证模式理论,验证LES 方法及LES/RANS 混合方法等(张涵信 2016).考虑到计算资源和连续流条件,对于绕椭球的高雷诺数流动,目前还无法实现,从这个意义上说,目前DNS 还无法用于解决工程实际问题. 非定常流动演化的重要性已经通过实验(Wetzel 和Simpson 1998b)进行了明确的展现,流场显示了丰富的三维复杂湍动剪切流的特性,如滞流、强压力梯度和大曲率流线下的三维湍流边界层、横向流动分离、自由层与附着涡旋的生成等,这些特性在飞行器作有攻角飞行和潜艇作操纵运动的绕流流动中很典型.实验(Wetzel 和Simpson 1998b)表明了定常流动和非定常流动之间存在明显的差别.椭球机动时,流动是高度非定常的,要想将其处理为定常或者准定常来模拟是很困难的,因为准定常方法不足以捕捉机动过程中力和力矩的演化过程(Alin 和Fureby 2005).特别是,在非定常机动过程中,惯性力是极度重要的(Alin 和Fureby 2005). 由于实验非常昂贵且十分复杂,还需要满足一定的条件,通过实验来研究的高成本和数据采集的局限性极大限制了对非稳态流动演化过程的深入研究,所以一些学者利用CFD 方法对非稳态操控问题进行研究,绕椭球的有攻角流动经常用作数值算例,以深刻理解飞行器在机动过程中前体复杂流动的发展.非定常计算过程中面临的问题主要包括:时间离散方法、网格结构形式(结构网格、非结构网格、混合网格)、动网格方法(张来平和邓小刚 2010).非定常机动的计算条件如表15所示. 表15 非定常机动计算条件描述 尽管使用RANS 加上湍流模型模拟非定常湍流还存在一些争议,但目前来看,对于大尺度的工程问题,考虑到当前可用的计算资源,这仍是唯一可行的方法(Liu 和Zheng 1998).Taylor 和Arabshahi(1995)对匀速俯仰运动的椭球体进行了数值模拟,高攻角时,压力分布差异较大,没有提供更详细的流场特征.近年来,得益于计算方法和计算能力的发展,对非定常机动过程数值模拟的有效性和效率得到了很大发展.Rhee 和Hino(2002)将体力加入到N-S 方程中来考虑坐标系的惯性运动,而Kotapati-Apparao 和Squires(2003)使用商业CFD 代码Cobalt 进行计算.从研究结果看到,非定常机动时,流动较定常状态发生了明显的延迟,表面流态也呈现明显差异,分离位置在周向角约115°.由于机动过程中所受到的逆压梯度更小,边界层分离延迟了(Wetzel 和Simpson 1998b),CFD 计算得到的一次分离较定常计算延迟了约5°,而实验结果(Wetzel 和Simpson 1998b)延迟了10°.这说明标量涡黏性湍流模型还不能够完全辨识背风面分离区的涡流,同时也表明,非定常流动现象不能通过将定常或准定常计算结果简单的外推来理解.虽然机动过程中流态呈现明显差异,但定常流动计算(Hedin 和Berglund 2001)和实验(Wetzel 和Simpson 1998b)中观测到的低速槽,在机动过程中仍然存在(图181),低速槽出现的原因前文已经做了分析,这里不再赘述. 图181 如图182所示,数值模拟对边界层内速度型的辨识非常好,DES 预测的速度型与实验结果一致,精确预测到了这个位置边界层的转向. 图182 在非定常机动过程中,采用RANS(Rhee 和Hino 2002)和DES(Koatpati-Apparao 和Squires 2003)所计算得到的摩阻趋势基本保持相同(图183),在α=20°时基本相近,在α=30°时差异稍大,但与实验值(Wetzel 和Simpson 1998a)相比都偏小,这在前面定常流动中也得到了相近的结论.这导致大攻角时,计算得到的升力较实验值明显偏小. 图183 图184给出了压力系数分布,在α=10°时,与实验结果相比,采用DES 得到的压力分布更好,RANS 的结果要差一些. 图184 国内温功碧和陈作斌(2004)在非定常计算时以零攻角解作为初场进行计算,椭球作下沉运动,如图185所示,除了接近后缘的位置外,其他截面计算的压力系数分布与实验都符合很好.正如实验所指出,除了头部和尾部外,非定常下沉运动对压力几乎没什么影响,但压力分布的非定常效应会产生一俯仰力矩(Hoang 和Wetzel 1994b),计算结果也获得了这一特征. 图185 图186给出了不同攻角时的压力系数分布,攻角在15°以下时,只要不是太接近后缘,计算值与实验值(Hoang 和Wetzel 1994a)基本符合.对于大攻角,在椭球后半部,计算值与实验值差别较大,计算的背风面第二个涡的位置和强度与实验不符,这说明在分离区湍流模式需要改进. 图186 熊英(2019)数值模拟了密度分层流中椭球自由俯仰振荡和受迫俯仰振荡的流场.自由衰减俯仰振荡时(图187),椭球上下搅动周围流体,在椭球体左右两侧形成四个对称涡环,密度的垂向分层限制了涡环的垂向传播,也加速了涡环的消失,这种限制助长了水平运动的发展.这种差异产生的涡升力导致升力系数极值的产生.在这种条件下,随着来流速度的增加,阻力系数不升反降,这说明,对于自由俯仰振荡的椭球体,“负阻力”现象仍然出现. 图187 高频受迫俯仰振荡时,起始攻角为45°,振幅为2°,按照正弦波形式运动.图188给出了流场时间演化的压力云图和密度等值线图,内波以纺锤形向上下延伸拓展,并且最终受到分层效应的抑制而发生弯曲.内波的辐射源点除了椭球体的头尾两个端点,还包括椭球体从头到尾的2/3 处.辐射源点在椭球体左右两侧形成四个对称涡环,涡环的生成是一个单一趋势的过程.内波流向以斜上行波和斜下行波的形式传播.展向内波具有先双峰,后单峰,持续性好,波形稳定的特点,随着流速的增加,展向垂直下行内波包络内的密度等值线呈螺旋状.内波在传播的同时也穿越着密度层,并克服层间的自由剪切作用产生涡旋,涡旋伴随着局部低压,低压对周围流体产生吸附作用.振荡橢球受到的黏性剪切力具有周期性变化的性质,其变化周期与振荡周期一致. 图188 椭球在密度均匀流和密度分层流中六自由度自主运动时,受不同的表面压力和涡分布的影响,椭球体的运动姿态变化是不同的,如图189所示,在密度均匀流中,当Re=1.0×104时,在前端逐渐拉出一条辫子涡,这条辫子涡伴随着向下的压力,使椭球头部一头栽下去,随着自由下落,其攻角逐渐变小,甚至为负.当Re=4.2×106时,从椭球尾部附近开始逐渐有环状涡脱落,而在椭球体表面,从椭球的尾部开始逐渐向两侧形成向上运动的表面涡.在密度分层流中,椭球的下落速度明显减慢,体积效应激发内波以孤立波为主,并伴随着非线性随机内波. 图189 虽然数值模拟方法研究椭球体非稳态运动取得一些进展,但是在动边界计算模型建立、流固耦合方法等方面仍然有许多问题没有解决(熊英 2019).在学术界,到目前为止,关于非定常分离的判据还存在争议(张涵信和张树海 2012).在绕椭球的定常流动中,可以采用壁面摩阻系数局部最小作为分离的判据,但在非定常机动过程中,分离是否还能够采用壁面摩阻系数来识别是值得商榷的. 转捩是流体物理研究中最重要的基本问题,研究一般采用理论方法、实验方法、数值方法(李存标 1998).在绕椭球流动的转捩研究中,主要还是基于实验方法和数值方法.Patel 和Baek(1985)通过逼近分离涡层的方法对绕椭球的分离流进行了计算,在Re=1.6×106时,流动是层流主导,在Re=7.2×106时,流动包含了层流、过渡流和湍流区域.忽略或使用不准确的转捩位置会导致预测得到的气动力性能出现明显的误差,因此预测转捩在工程上有着明确的需求.转捩是一个复杂的现象,其具有差异很大的机理,影响椭球绕流场转捩的因素很多,诸如雷诺数、马赫数、自由流湍流度、压力梯度、攻角、壁面粗糙度、壁面曲率、层流边界层的发展情况等(符松和王亮 2007).根据时空发展特性(即转捩机理的不同)将过渡流转换为湍流细分为:流向T-S(tollmien-schlichting)波和横流C-F(cross-flow)波主导的自然转捩,分离泡转捩,回流转捩,旁路转捩(bypass transition,也有译作跨越转捩),Taylor−Gortler 涡致转捩、前缘附着线转捩等.在椭球流动中,T-S 波引起的不稳定性和横流C-F 波不稳定性是最主要的机制,基于不同转捩机理进行建模,可精细化构造专门的转捩模型.虽然对不可压缩湍流,其转捩机理在原则上已经清楚了,但完全依靠理论预测转捩仍然是不可行的,因为来流条件的扰动特性未知(张涵信和周恒 2001). 对转捩实验,目前仍有不少问题需要研究,不是有了低湍流度风洞就可以解决的,实验中的背景扰动如何和实际流动条件相似,即使是低速流动的情况也还没有完全解决.降低风洞的湍流度可以降低测试结果中脉动的低频、高幅值部分,但不能消除更高频率的信号部分,如图190所示.在风洞实验中,湍流度的增加必然会激发非常低频的模式.这种现象还没有得到解释,在高湍流度环境中进行测试,为了获得有意义的数据,需要特别注意(Zeiger 和Telionis 2004). 图190 早期,Boltz 和Kenyon(1956)在NASA Ames 的13 英尺低湍流度低速压力风洞中测量了f=9(铝制)和f=7.5(钢制,覆盖玻璃纤维和树脂)椭球在α=0°时的边界层转捩特性,给出了转捩雷诺数.第一次对椭球绕流场转捩进行系统研究的是Kreplin 和Vollmers(1985),实验在德国哥廷根DFVLR(现在的DLR)的3 m×3 m 风洞中进行,在实验中通过在固定位置采用转捩带,增加了分离的稳定性.采用热线探针测量了壁面局部剪切应力,局部剪切应力的演化提供了关于边界层从层流到湍流发生转捩的详细信息. Kreplin 关于椭球绕流场转捩的实验是第一次较为系统的实验,至今也再未有研究者对此进行系统实验研究,因此他们的实验数据经常被作为数值模拟的对比参考数据.限于当时的实验条件,或者是作者的疏忽,当时进行实验时风洞的来流湍流度未知.后来一部分DLR 的工作人员称该风洞来流湍流度约为0.2%,此湍流度下徐晶磊和周禹(2019)采用KDO(turbulent kinetic en- ergy dependent only)转捩模型进行计算,未发生转捩.后来很多研究人员以Kreplin 的结果进行转捩数值研究时,采用了不同的来流湍流度,取值范围在0.1%~1%.但转捩位置与自由来流的湍流度是强相关的,通过在试验段入口安装增湍网来改变自由来流湍流度,f=6,α=20°时分离和再附位置随来流湍流度的变化而出现很大的变化(Panzer 和Simpson 1995).数据如表16所示. 表16 超临界转捩时不同站位的二次分离的周向角(Panzer 和Simpson 1995) 实验数据的不易获得性及非定常机动的要求,使得对数值模拟预测转捩的需求越来越高.静态过程中,采用黏贴转捩带的方式可以较为准确的预测转捩性能,但在机动过程中,采用黏贴转捩带的方法可能不适用,因为在机动过程中,由于改变了顺压和逆压梯度的区域,导致转捩点的位置随会时间明显改变(Panzer 和Simpson 1995).数值模拟预测转捩最重要的是计算模型.直到现在,仍缺少预测转捩的有效工具.早期曾采用鞍点方法计算转捩,使用边界层方程的求解作为稳定性分析的输入数据(Cebeci 和Stewartson 1980).后来尝试采用求解N-S 方程获得的边界层数据来计算转捩,从前文可以得知,RANS 方程及其相关的雷诺应力封闭模型描述充分发展湍流的精度是可以接受的,但却不能比较准确地给出从层流到湍流的转捩位置.面对日益增加的转捩需求,研究人员绕开RANS 方法,主要根据实验现象来给出判断转捩的方法.例如,传统的稳定性分析使用线性稳定性理论(linear stability theory,LST)分析方法,即黏性流动的平行流小扰动线性稳定性方程(Orr-Sommerfeld,O-S 方程),基于此发展的 eN方法成为稳定性分析和转捩预测的重要方法.基于实验现象发展的转捩方法还包括引入间歇因子法和引入层流湍动能法.这些方法从湍流结构及其时序、空间发展中抽象出反映转捩的参数,用以驱动流动转捩,模型的构造方法、技术完全不同于基于统计平均的传统湍流模型(徐晶磊和周禹 2019). 德国DLR 的Stock(2006)对f=6 椭球绕流场转捩进行了详细模拟(图191),通过对比,绕椭球流动的压力分布和摩阻,采用势流理论描述无黏流,在再附的层流边界层区域中,采用三维层流边界层方法来描述黏性流动是足够的. 图191 如图192所示,当攻角增加时,迎风面的转捩点向下游移动,而背风面的转捩点在攻角大于5°后,持续向上游移动.上游和下游转捩线的分割点在方位角50°左右,在这条方位角线上,α=15°~29.7°,x/L=−0.5~0.5 之间,转捩位置基本上是相同的.Stock 在两个风洞中进行了实验,α=0°~30°,雷诺数范围为1.5×106~4.3×107,测量的转捩位置与计算结果基本一致. 图192 德国DLR 的Krumbein 和Krimmelbein 团队近年来一直致力于转捩研究.Krimmdlbein 和Radespiel(2005,2009)在TAU 代码中耦合eN方法,使用无黏流线作为积分路径进行N因子的计算,使用线性稳定性理论分析椭球绕流的转捩问题.如图193所示,α=10°时,纯粹横流所致的转捩区域得到了发展. 图193 后来Krimmelbein 将稳定性分析代码、边界层计算与RANS 求解器相耦合来预测转捩.定常计算采用低速预处理和隐式LU-SGS 时间积分格式,采用S-A 模型,网格约280 万,在椭球表面等间距分布31 条流线.结果如图194所示,靠近迎风面和背风面对称线的转捩是由T-S 波引起的,这些位置的流动呈现更多的二维流动属性.对低雷诺数(Re=1.5×106,Ma=0.03,α=10°)流动,转捩纯粹是由T-S 波失稳所致,与实验结果符合很好(图194(a)),高雷诺数(Re=6.5×106,Ma=0.13,α=10°和15°)时,在转捩过程中,横流失稳的作用越来越突出,当攻角10°时(图194(c)),转捩线的一部分明显是受到T-S 波和横流波同时激发的,一部分区域是纯粹的横流转捩.当攻角增加到15°时(图194(e)),纯粹横流转捩的区域发展为很大的一片区域.对这两种情况,CFD 预测得到的转捩位置与实验比较一致,但都稍微靠近上游. 图194 由于攻角较大时,横流失稳所致的转捩是主要原因,他们将一种修正的转捩模型应用到TAU 代码中,在预测椭球绕流场转捩区域上有较好的效果,一些物理量也比较准确,诸如压力、摩阻、升阻力系数等.在低雷诺数时,转捩仅仅是由于椭球表面的T-S 波失稳引起的,而更高的雷诺数时,攻角5°和10°的转捩是由T-S 波和横流失稳引起的.到攻角15°时,转捩完全由横流失稳主导(Grabe 和Krumbein 2013).为能够准确预测回流转捩和分离诱导的转捩,他们采用一种转捩输运模型与雷诺应力模型相耦合形成包含9 个输运方程的新的转捩和湍流模型,在预测椭球绕流场转捩区域上也有较好的效果(Nie 和Krimmelbein 2018a,2018b). 后来,他们对程序进一步扩展,增加了RSM 对横流转捩的预测,还进行了网格收敛性的研究,网格采用三棱柱混合网格,所有的计算采用自由湍流延迟,来流湍流强度0.2%,入口黏性比为2.如果采用二阶格式,边界层内至少分布128 个网格点才能使用RSM 模型更为准确的模拟转捩,椭球表面大约分布了2 万个三角形,如图195所示. 图195 α=5°时,图196(a),实验测量得到的壁面摩阻系数是对称的,转捩发生在约x/L=0.4 站位,CFD 预测的摩阻系数分布都没有出现对称性,同时迎风面上没有预测到转捩,可能是基于螺旋度的雷诺数(helicity-based Reynolds number)在这个区域太小而不能激发横流转捩,因此γ-Reθt-CF-He SST 模型、γ-Reθt-CF-He RSM 模型都无法预测迎风面的转捩.或者是在这个攻角下,迎风面的转捩是由T-S 波失稳激发的.在背风面,这两个模型都预测到了转捩起始点,与实验符合较好.γ-Reθt模型假定迎风面沿再附线的T-S 波是容易激发的,但结果证明,转捩过程比纯粹的流向转捩要快,因此没有捕捉到转捩起始点.当然,与再附线转捩相关的转捩机理,在另外两个模型中也是缺失的. α=10°时,图196(b),实验测量的转捩位置约为x/L=0.25,转捩区域的前缘几乎是直线.而γ-Reθt模型预测的转捩位置过于靠近下游,诱导了层流分离.γ-Reθt-CF-He SST 模型、γ-Reθt-CFHe RSM 模型无论是在转捩起始点位置还是转捩线外形上都较为准确地预测到了横流失稳主导的转捩,但也存在一些小的差别,尤其是迎风面上,情况与5°攻角时相似,但差异没有那么明显. 图196 图197给出α=15°时的情况,实验测量的摩阻系数分布在x/L=0.5 站位出现明显的间断.背风面的的转捩是由T-S 波失稳引起的,而在椭球中部,转捩是由横流失稳所主导的,因此出现了明显的T-S 波失稳和横流失稳的干扰.γ-Reθt模型只能预测背风面的T-S 转捩,γ-Reθt-CF-He SST 模型、γ-Reθt-CF-He RSM 模型捕捉到了两种转捩机理,但间断没有那么明显.在迎风面,三个模型都没有预测到对称面上的转捩起始点,并且起始点都朝背风面移动了,与攻角5°和10°相仿. 图197 图198为更大攻角的情况,α=20°和α=24°时,实验中,迎风面对称面处流动保持层流.背风面由于出现了层流分离而发生了T-S 转捩,横流转捩大约出现在x/L=0.15 站位.γ-Reθt模型只能预测到椭球前缘由分离所诱导的转捩.γ-Reθt-CF-He SST 模型、γ-Reθt-CF-He RSM 模型能够预测到横流转捩,但都轻微的太靠近下游.在下游区域,预测的结果与实验符合较好. 图198 近年来,国内也开展了一些关于椭球绕流场转捩的数值模拟研究.鞠胜军和阎超(2017)将γ-Reθt-CF 转捩模型引入开源standford university unstructured(SU2)计算流体力学分析平台中,考虑到γ-Reθt-CF 转捩模型对流向T-S 波和横流波不稳定性引起转捩的判定均是完全基于当地变量,而S-A 湍流模型计算效率高,因而将转捩模型与湍流模型相结合.L=1.2 m,远场湍流度为0.1%,湍流黏性系数与层流黏性系数比为10.图199分别给出了采用原始γ-Reθt模型与γ-Reθt-CF-SA 模型数值模拟得到展开后的椭球表面摩擦系数分布云图.三角形离散点为实验值(Kreplin 和Vollmers 1985),圆形离散点为使用线性稳定性理论计算所得的转捩位置(Krimmelbein 和Krumbein 2011),方形散点为使用γ-Reθt-CF-SST模型计算所得的转捩位置(Krimmelbein 和Krumbein 2011).总的来说,γ-Reθt-CF-SA 模型与γ-Reθt-CF-SST 模型的预测的转捩位置与实验值及线性稳定性理论分析的结果比较相近,且远优于原始γ-Reθt模型的计算结果.γ-Reθt-CFSA 模型能正确地预测出三维流动中的横流不稳定性引起的转捩现象.但在迎风侧φ=0°~50°位置没有很好地预测出转捩点的位置,需要对模型作进一步的修正. 图199 图200中方形散点为使用γ-Reθt-CF-SST 模型计算所得的转捩位置(Krimmelbein 和Krumbein 2011),原始γ-Reθt模型预测的转捩区的面积远远小于γ-Reθt-CF-SA 模型与γ-Reθt-CF-SST 模型,这是由于原始γ-Reθt模型只能预测由T-S 波不稳定性引起的转捩,而其他两个模型能预测出由T-S 波不稳定性和横流波不稳定性共同作用所诱导的转捩. 图200 徐家宽(2019)考虑了壁面粗糙度的影响,壁面粗糙度给定3.3 μm,Kreplin 和Vollmers(1985)实验中椭球的粗糙度约为3.3 μm,自由来流湍流度为0.1%,网格数量为800 万,使用横流驻波转捩预测模式,结果如图201所示,横流失稳现象捕捉良好. 图201 将两个站位的摩擦力系数曲线与实验数据进行了对比(图202),结果显示,对顺压区的横流驻波失稳和转捩之后的分离、再附现象均捕捉得较为准确. 图202 为了进一步验证方法,他们还对另外两个状态也进行了转捩预测,如图203所示,在大迎角高雷诺数状态下,椭球迎风面就会发生横流失稳,预测所得的转捩位置与实验数据吻合较好,可见这种方法对于横流驻波失稳现象的捕捉是较为合理和准确的. 图203 为了促使转捩发生,徐晶磊和周禹(2019)计算给定湍流度为0.6%,图204(b)是根据实验给出的转捩线推断出的摩阻分布.KDO 转捩模型预测的转捩线相对后移,这是合理的,因为计算中给定的是光滑壁面. 图204 从这些计算结果可以看到,由于湍流黏性的模拟问题没有解决,导致摩阻的计算结果不准确,尤其是在大范围分离区内,因此即使计算方法和计算能力提高,也无法完全解决转捩问题.但通过对转捩现象认识的逐步加深,可以进一步提高转捩预测的精度.当前对T-S 转捩与横流转捩的机理和辨识已经较为准确,数值模拟结果与实验结果基本相符,但对再附转捩的认识还不够清晰,尤其是迎风面,因此椭球绕流转捩的研究还需要依靠实验. 椭球虽然外形简单,但绕椭球的流动却非常复杂.在基础研究和工程设计中,其外形具有很高的代表性,几十年来,很多研究者对绕椭球的流动进行了大量研究. 绕椭球流动的边界层是涡量高度集中的区域,边界层分离后,带有高涡量的流体失去了壁面的限制,会自发卷绕成螺旋形,在流场中形成涡旋.在绕椭球的流动中,分离线是极限流线的收拢渐近线,摩阻系数局部最小可以作为流动分离的判据之一,摩阻系数局部最大可以作为流动再附的判据之一.随攻角从0°到90°增加,绕椭球的流动从闭式分离转变为开式分离,最后又形成闭式分离.当攻角大于15°后,绕椭球的大范围分离会形成侧向力,且侧向力是非定常脉动的.而且随攻角增加,椭球后的尾迹也从对称流动过渡为非对称流动、明显的非定常非对称流动.椭球表面的突起物或凹陷对分离线的形状和位置有影响. 椭球非定常机动过程中,一次分离和二次分离会出现明显延迟,攻角越大,这种效应越明显.快速俯仰时,分离流和旋涡运动可产生非定常的超升力.俯仰速率越高,产生的动态升力越高.非定常机动不能作为定常流动或准定常流动处理.与定常流动相比,对非定常机动过程的模拟,与实验结果的差距还要大一些. 对绕椭球流场的研究,主要还是依靠试验方法和数值模拟方法. 在试验方法上,早期采用油流、烟雾、染料、氢气泡等常规实验方法,可以用于绕椭球流动的定性描述,20 世纪末期开始采用LDV 等较为精确的方法,可用于定量描述.但最新的一些试验技术还未见应用到绕椭球的流场测量中,缺少高精度的实验结果,诸如压敏漆等非接触测量方法,即便是PIV(particle image velocimetry)这种较为成熟的技术也未见应用,这导致绕椭球的平面和空间流场还缺乏丰富的实验数据,比如椭球表面和空间上压力分布的连续变化特性.这导致对大范围分离情况下的非定常特性和涡结构不能有效辨识.在支撑装置上,一般的尾部支杆会对尾部流场带来较大的影响,采用磁悬架平衡系统可以消除尾部支撑的影响,但用于大攻角流动还存在问题.近年来发展了诸如风洞虚拟飞行技术、风洞模型自由飞技术、绳系支撑技术等先进技术,目前未见到应用到绕椭球流场的实验中. 在数值方法上,求解RANS 的湍流模式仍然是解决绕椭球大范围分离流动主要工程方法,但LES 和DES 等方法目前也逐渐得到广泛应用.在大攻角绕流中,摩阻的计算结果与实验值相差较大,这说明对湍流黏性的模拟还存在问题.DNS 只能用于较低雷诺数的情况,在高雷诺数流动中还不适用.根据NASA 的一项研究认为,到2030 年前,RANS 仍然会是CFD 分析中的重要组成部分,CFD 对湍流,尤其是带有明显分离的流动,其精度和可靠性仍然严重受限,在RANS 上的进展不可能克服这种不足,因此使用LES 在未来可能更实际,这阻碍了算法方面的根本进步,为了克服这种障碍,混合的LES-RANS 和壁面模拟的LES 可以提供更好的前途,尽管仍然有明显的问题存在(Slotnick 和Khodadoust 2014). 对于绕椭球流场的转捩问题,提升实验的准确性较为困难,主要是测量技术在时间和空间分辨率上还存在不足,导致流场数据不够丰富,无法表征旋涡结构的时空演化特性和演化机制(潘翀和王晋军 2011).另外,在转捩实验中,对来流品质要求很高,诸如来流湍流度、背景噪声等.在数值方法上,还需要继续提高对流场结构的辨识,尤其是大范围分离区内旋涡结构的精确辨识.在未来一段时间内,依靠数值方法的提高完全解决这一问题还有难度,由于数值模拟能够提供丰富的流场时空信息,与实验相结合并进行数值修正是目前解决转捩问题的关键所在. 从国内的研究来看,近几十年来,实验开展的很少,数值模拟研究的成果较为丰富.与数值模拟相比,实验是极其复杂并昂贵的,同时由于高校等研究机构缺少高品质的风洞,很难开展椭球流场精确测量这类基础研究,而一些拥有高品质风洞的机构,很少有机会开展这类研究.CFD 因为其经济性,是非常有吸引力的,尽管有很多因素影响CFD 的精度,诸如湍流模型的不足、计算能力不足等.由于目前实验测量对流场细节的把握还有待提高,需要CFD 丰富的流场数据进行辅助,因此对于椭球流场的研究,需要实验和CFD 相互补充,才可能比较完整地解决这一问题. 致 谢江苏高校优势学科建设工程资助项目.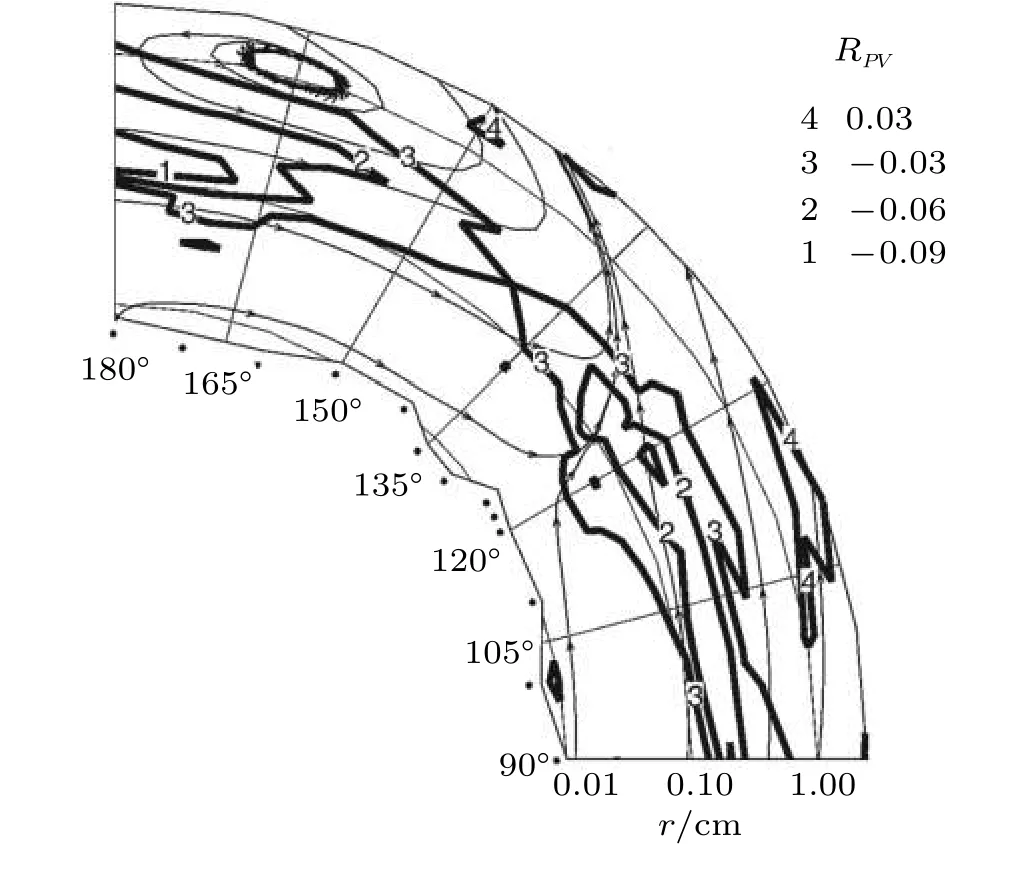
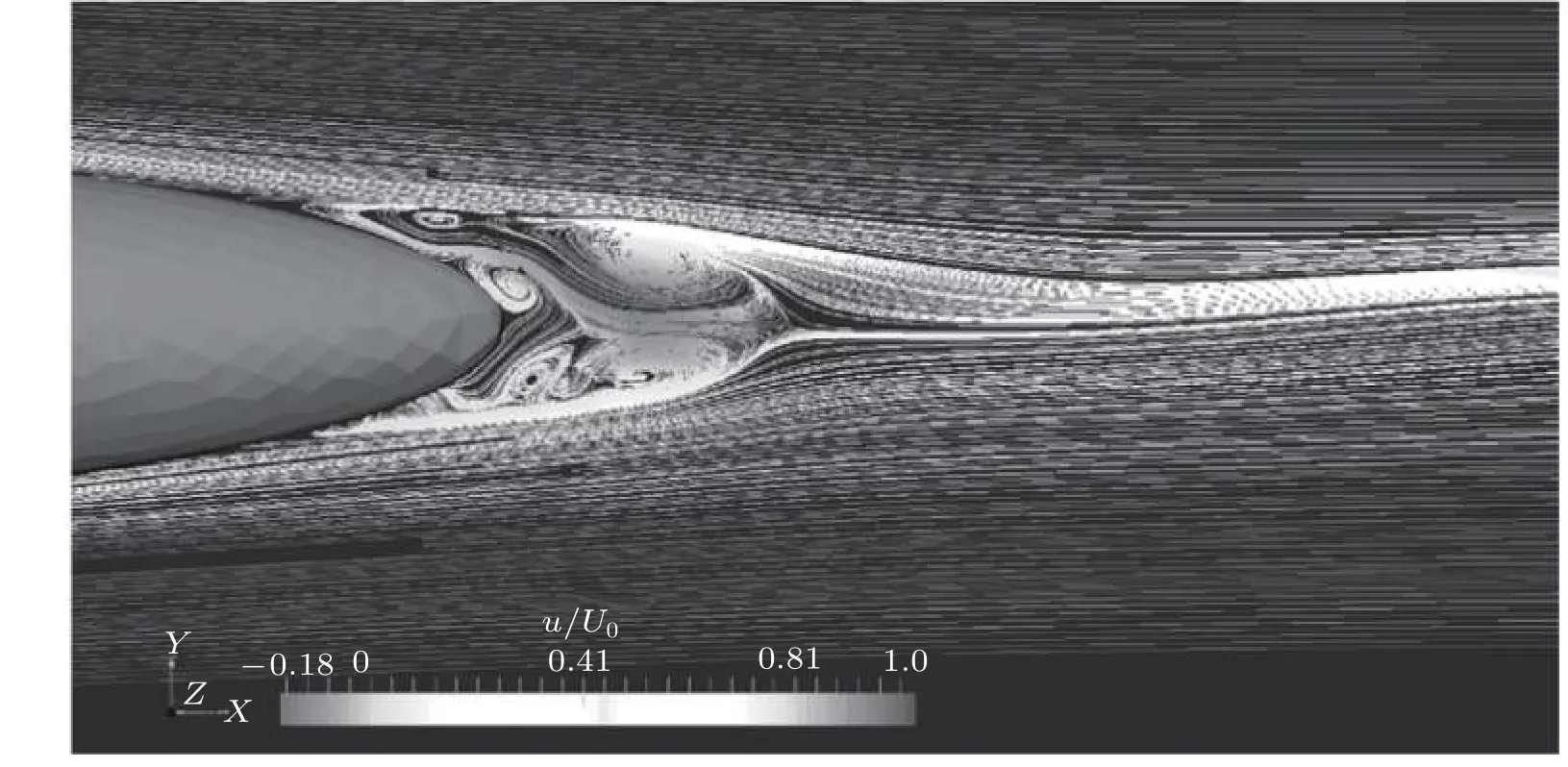
3.7 转捩带的影响
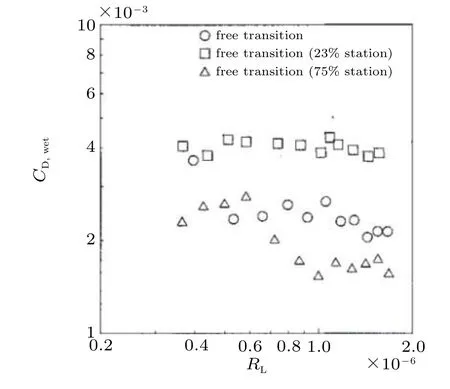
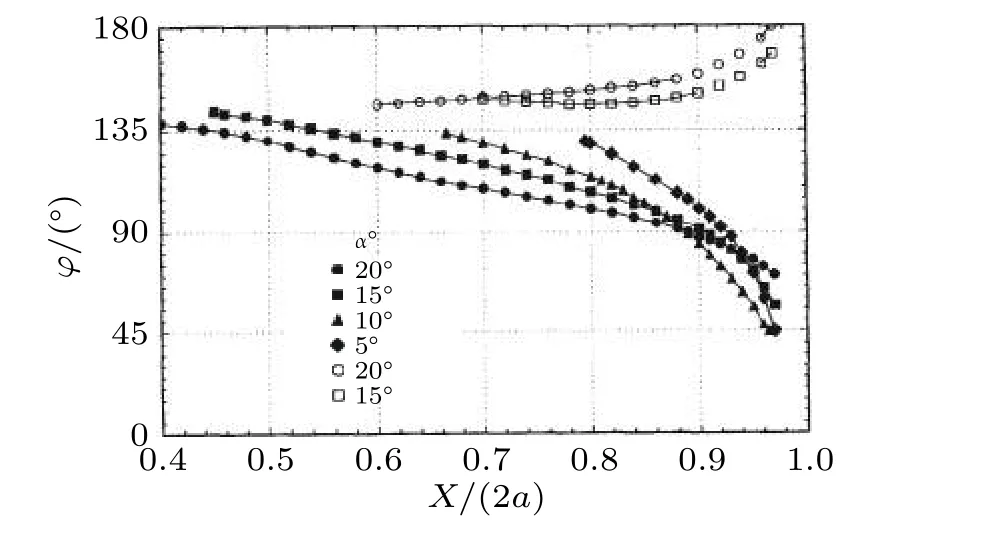
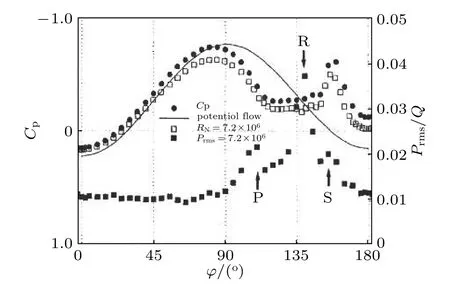
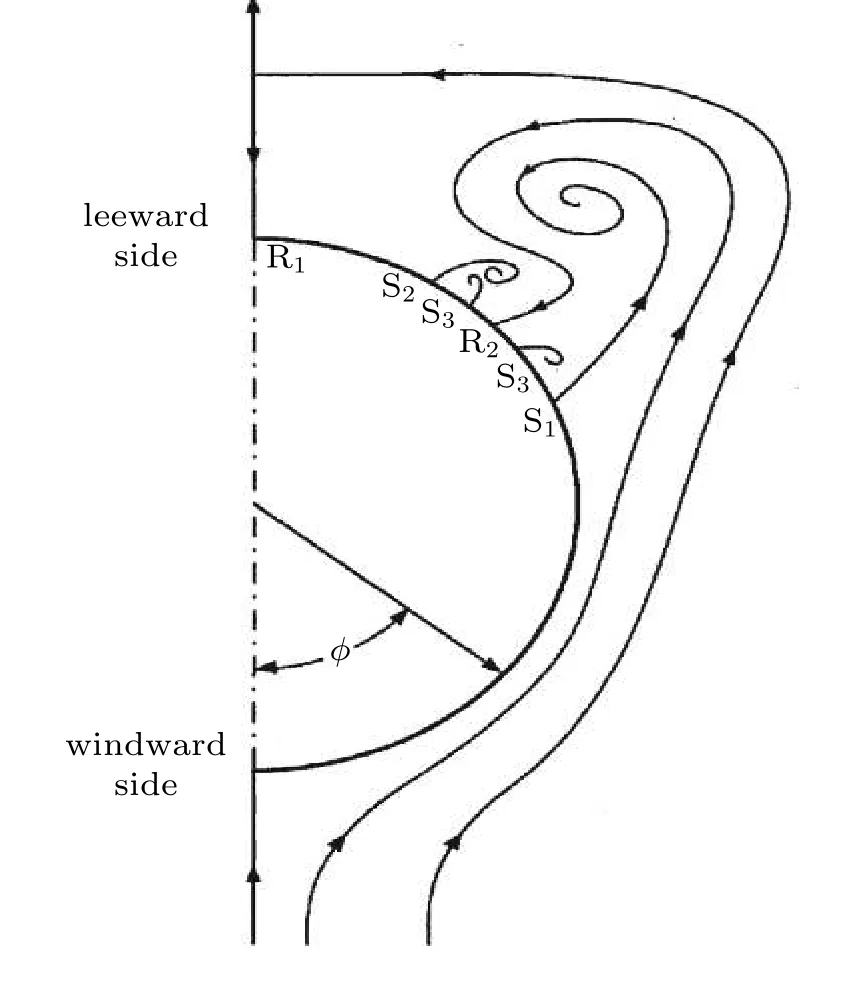


3.8 分离后旋涡的演化过程
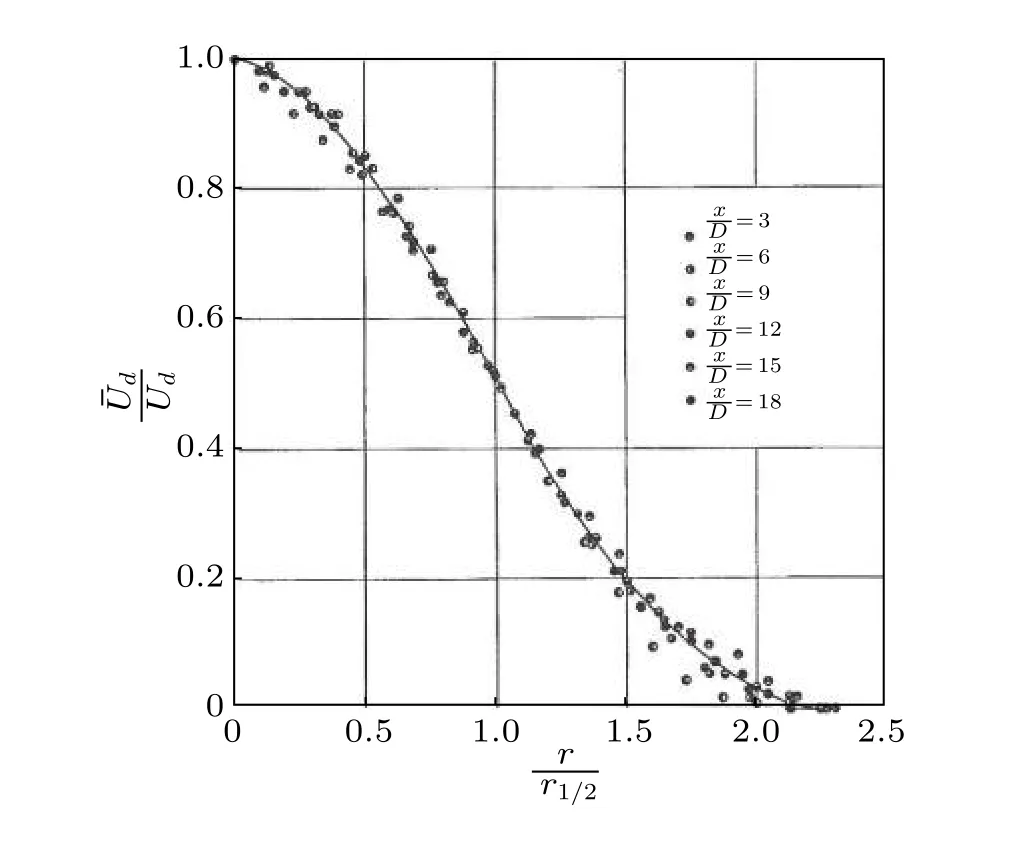
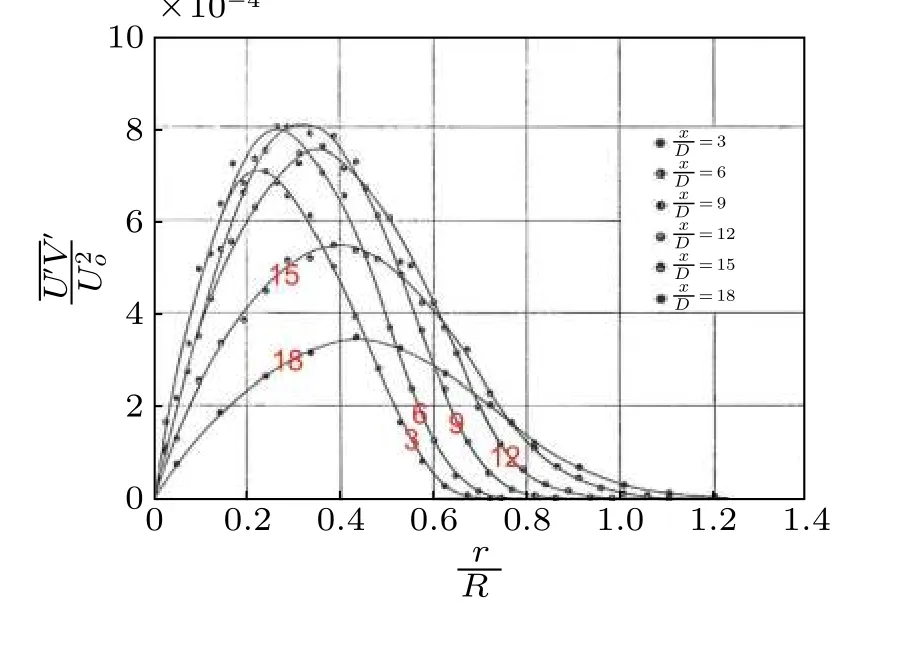
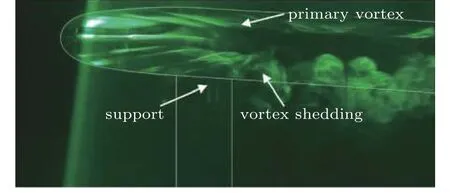

3.9 非定常机动实验
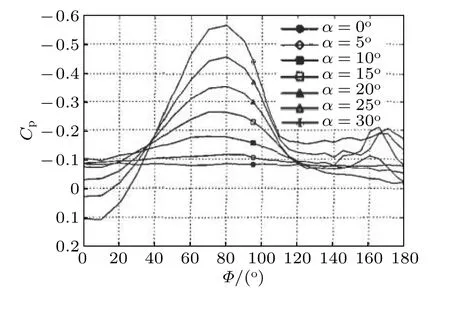
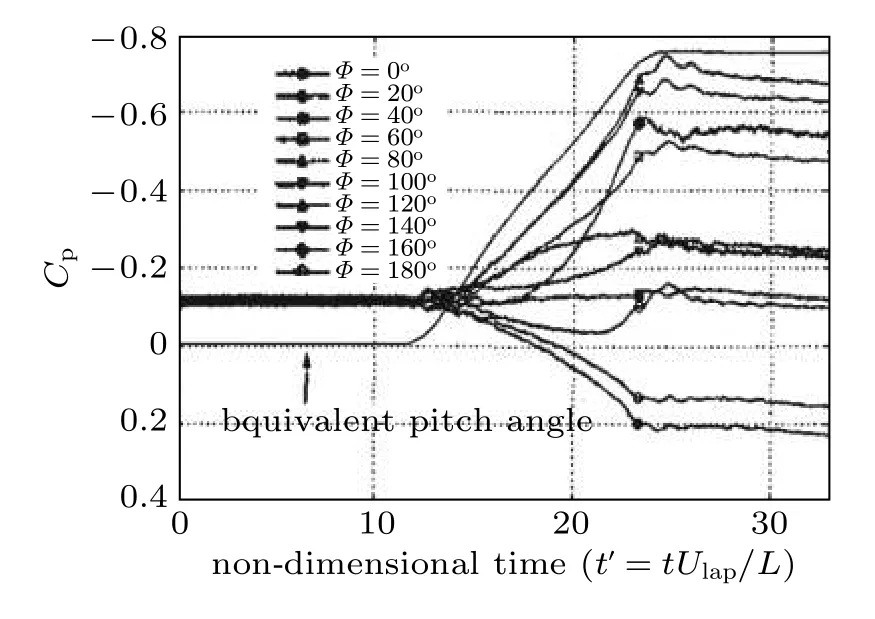

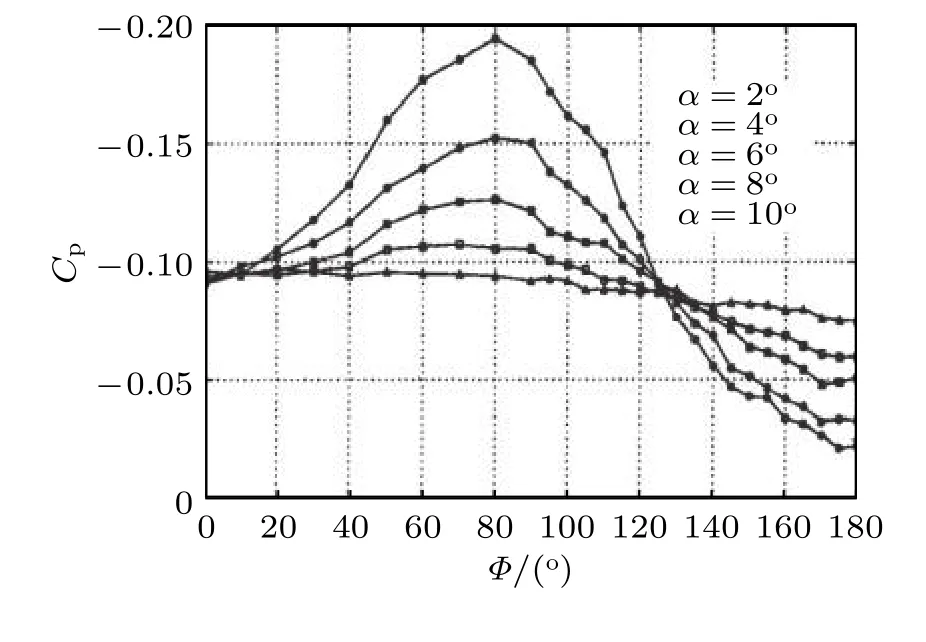
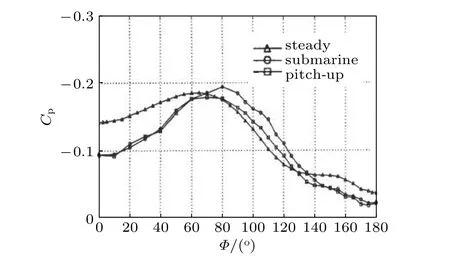


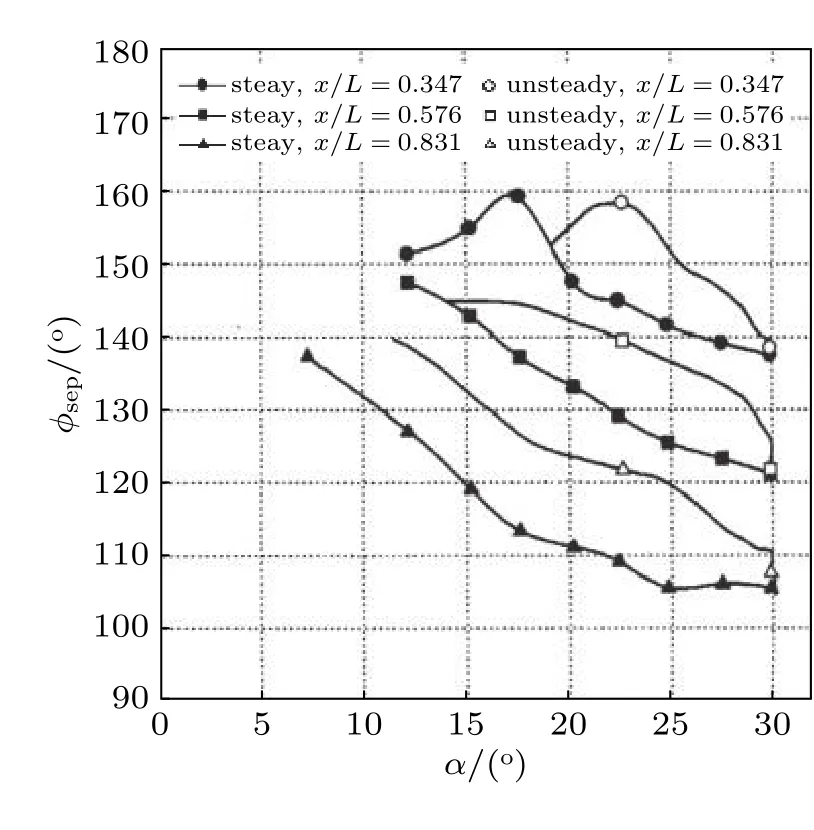

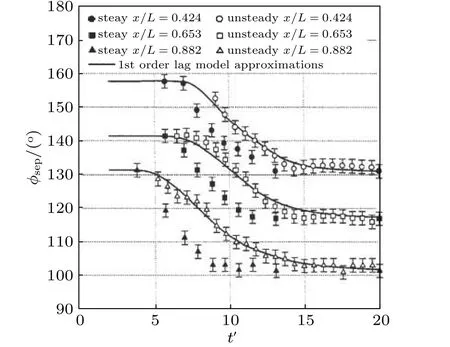
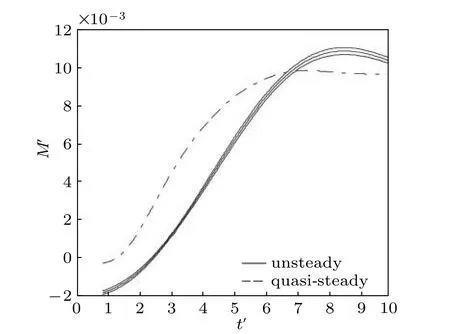
3.10 尾部支撑对流动的影响
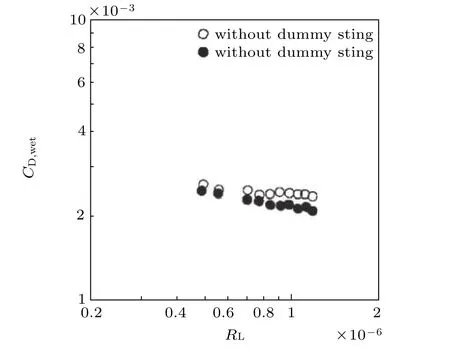


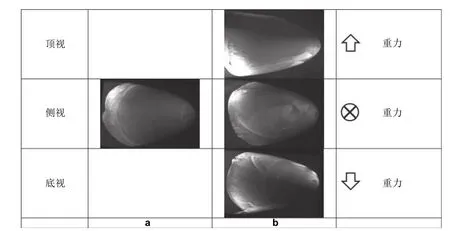
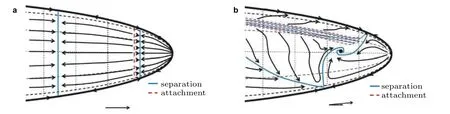
3.11 突起物对流动的影响


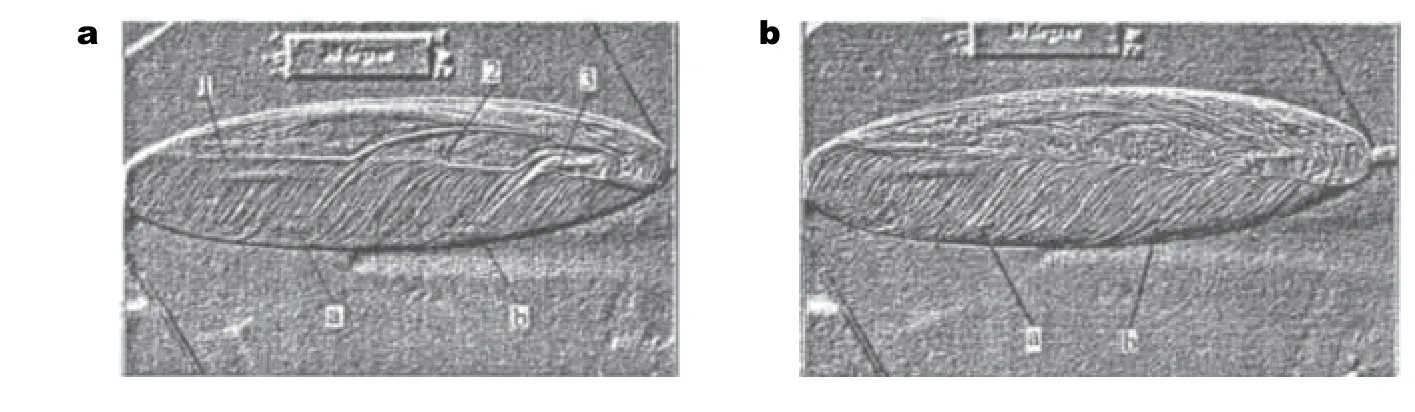
4 数值模拟研究
4.1 欧拉方程及渐近理论
4.2 三维边界层方程


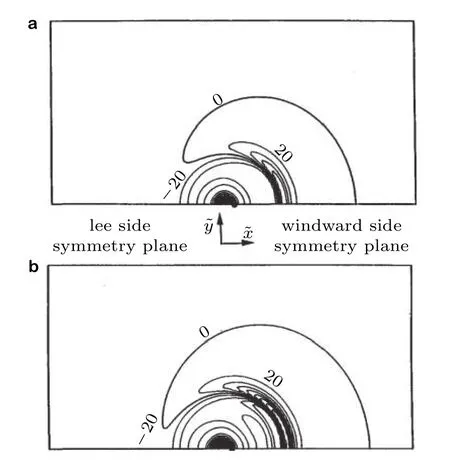
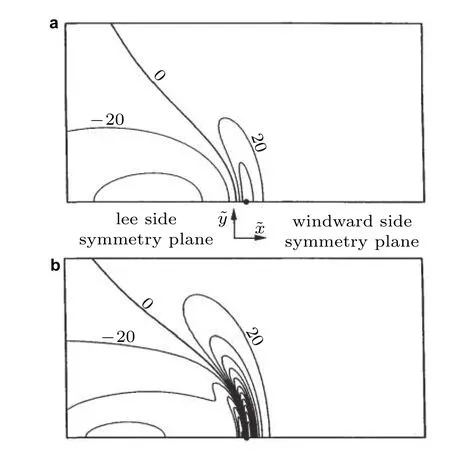


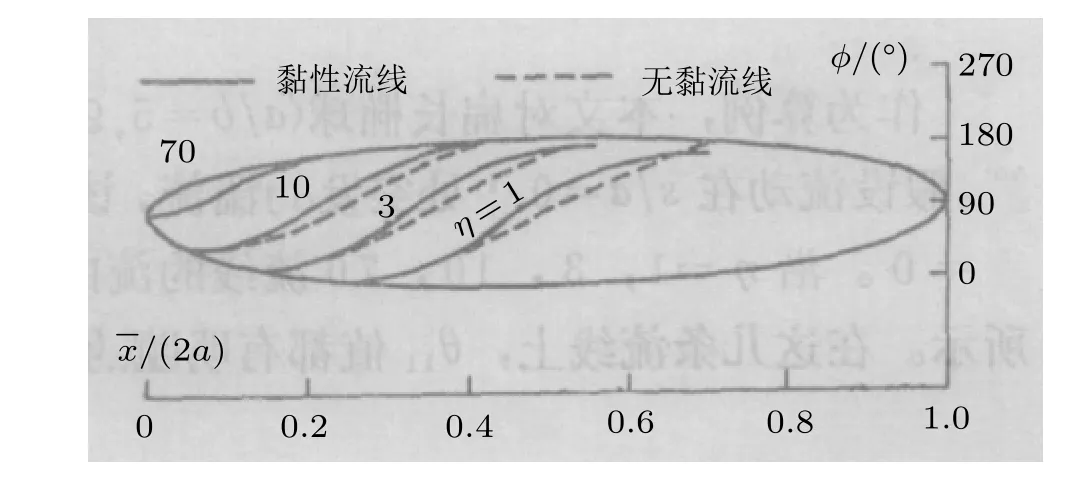
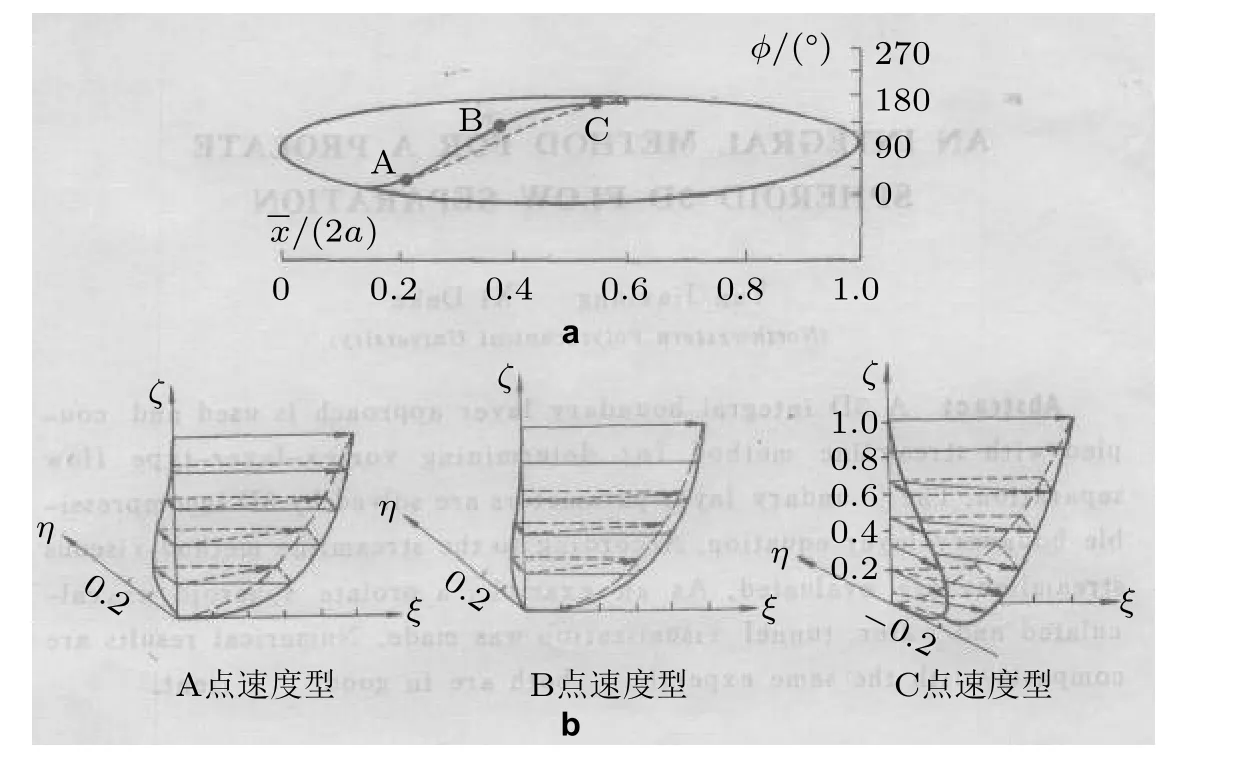
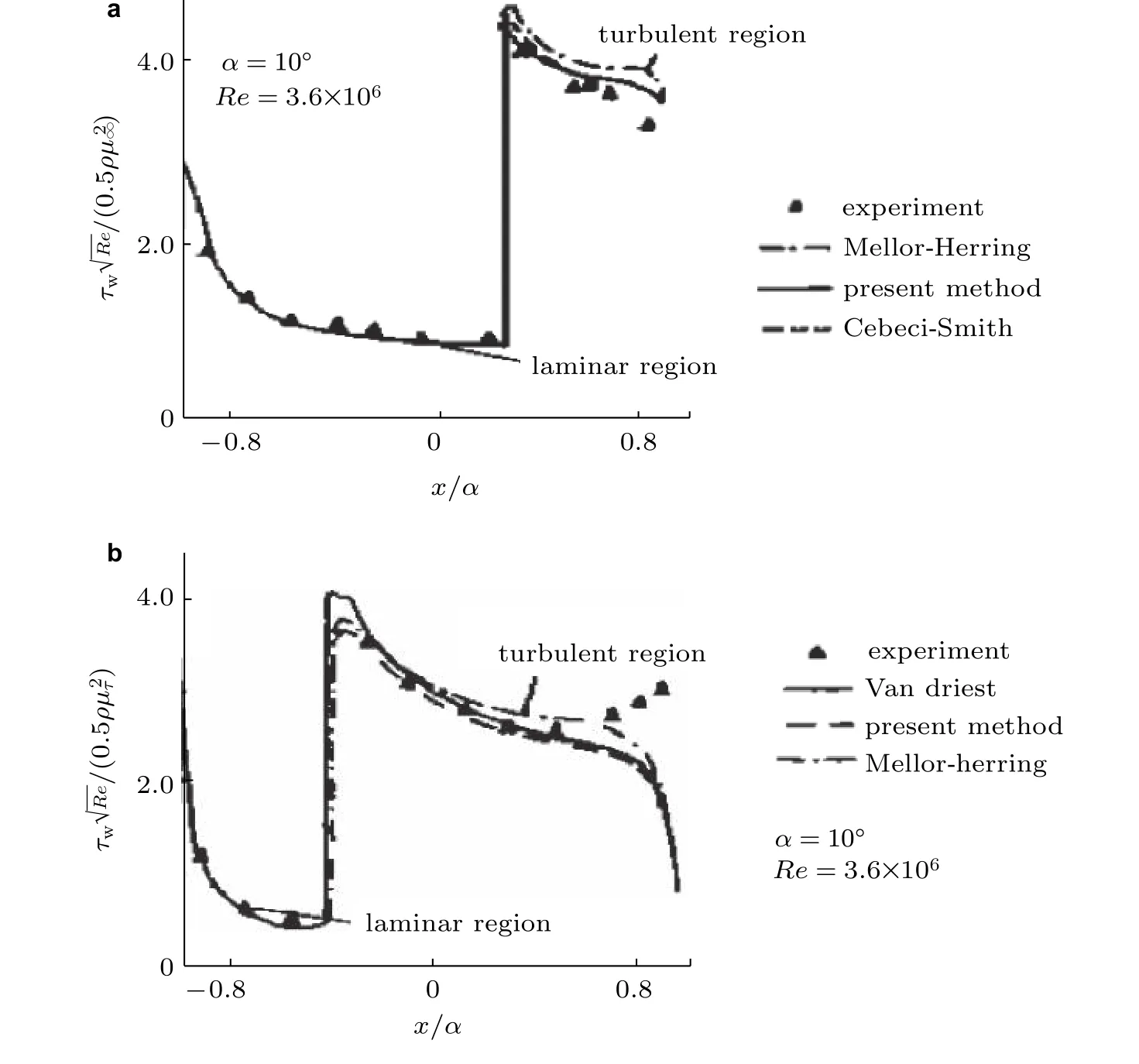
4.3 简化的N-S 方程及层流
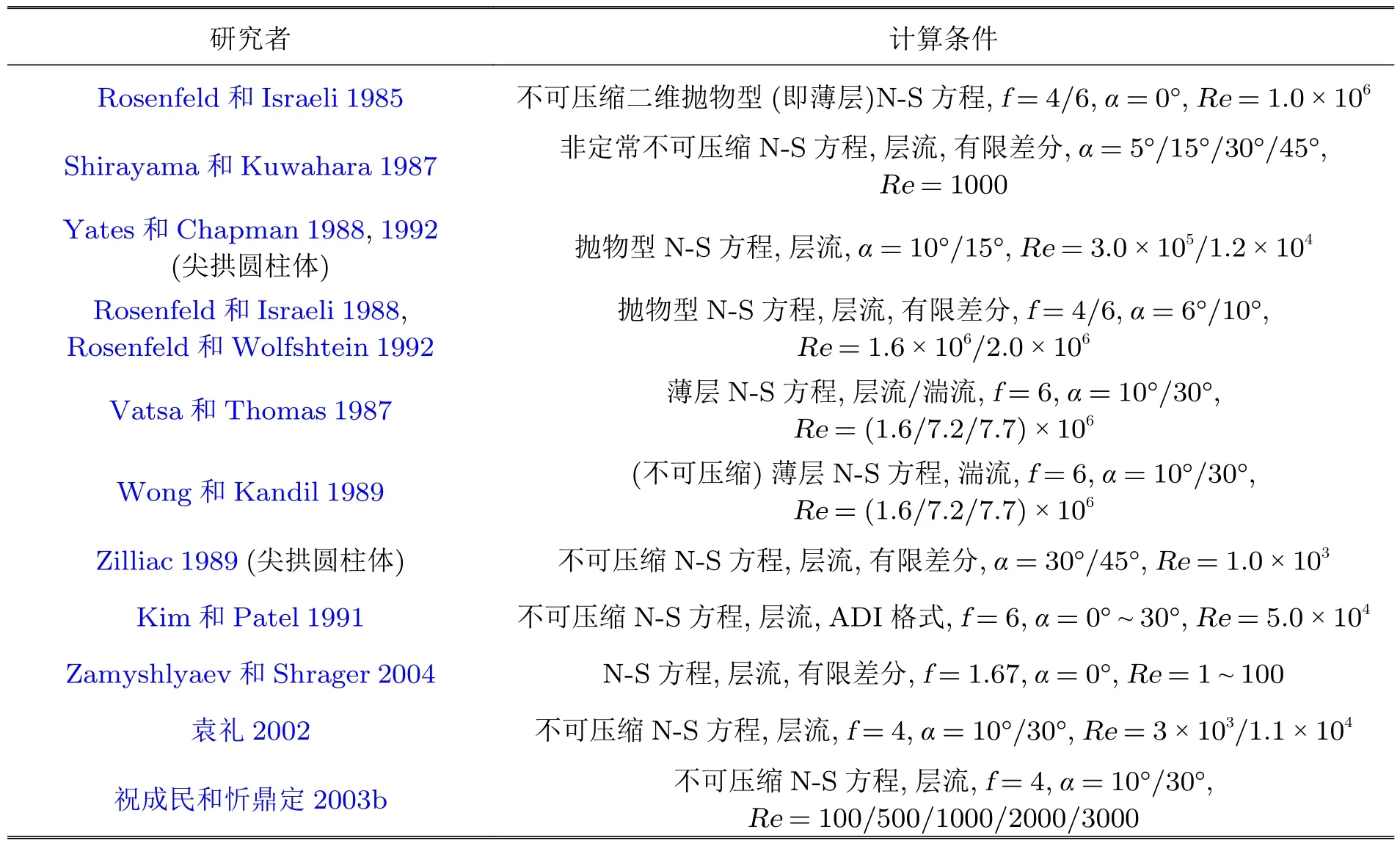
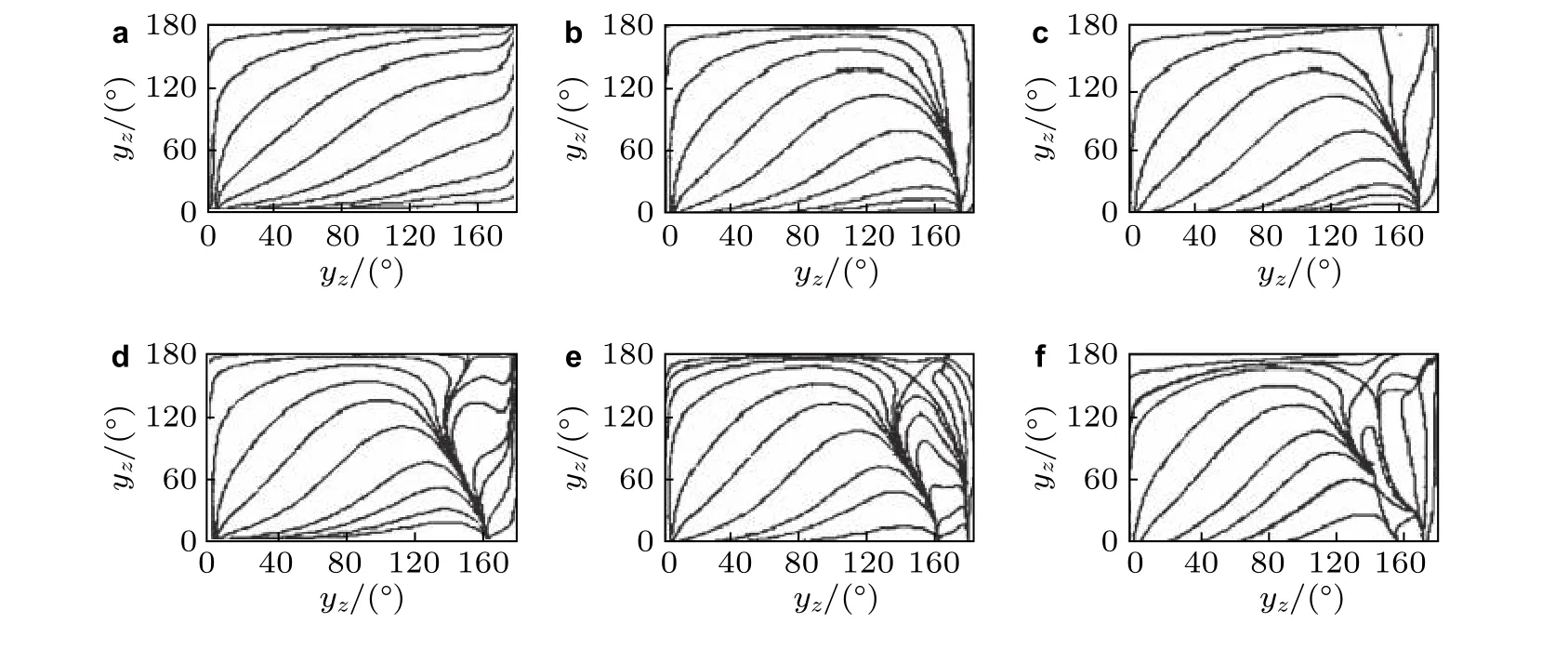
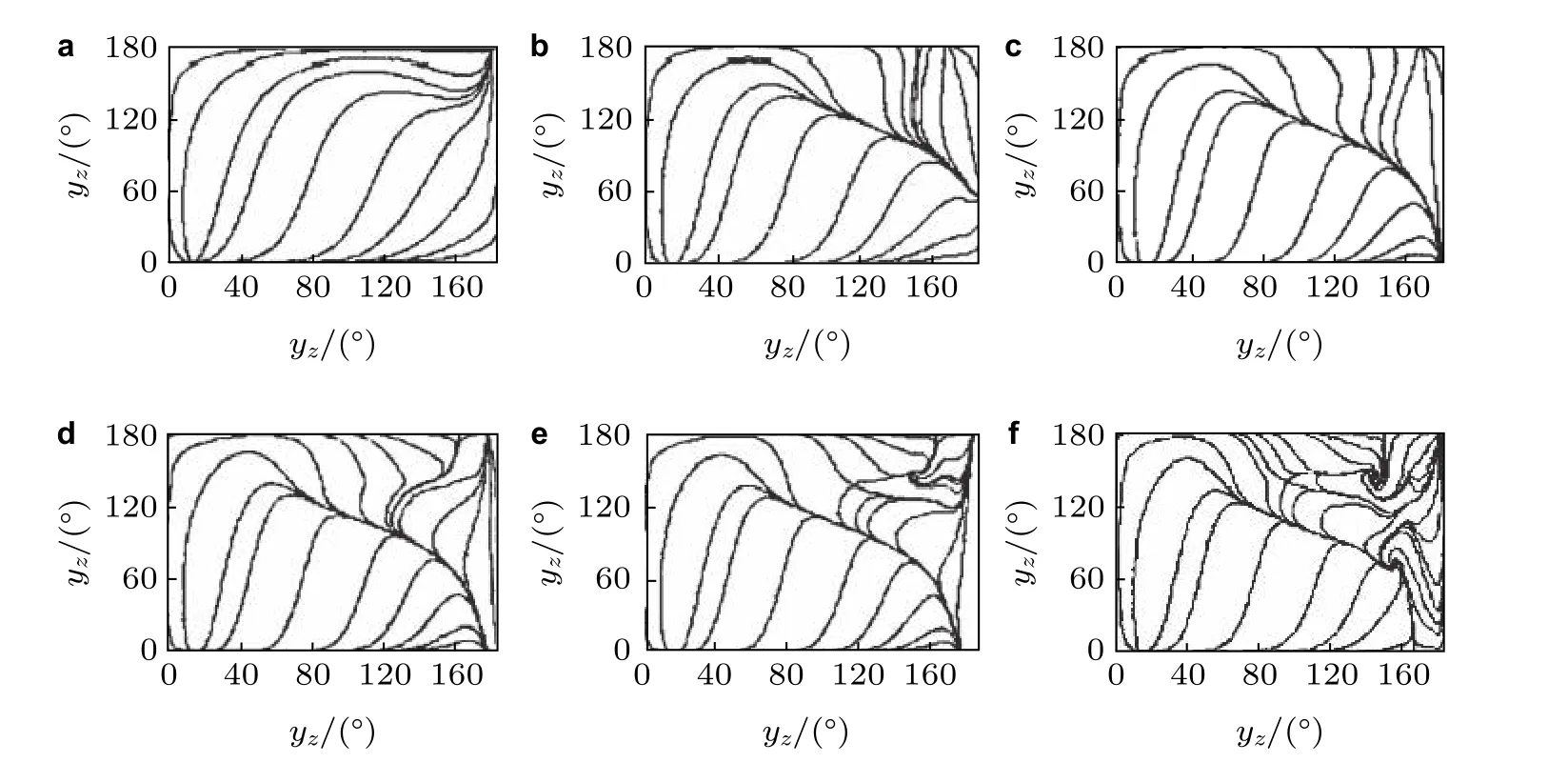
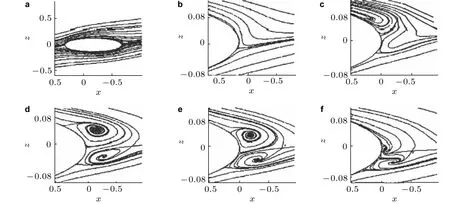


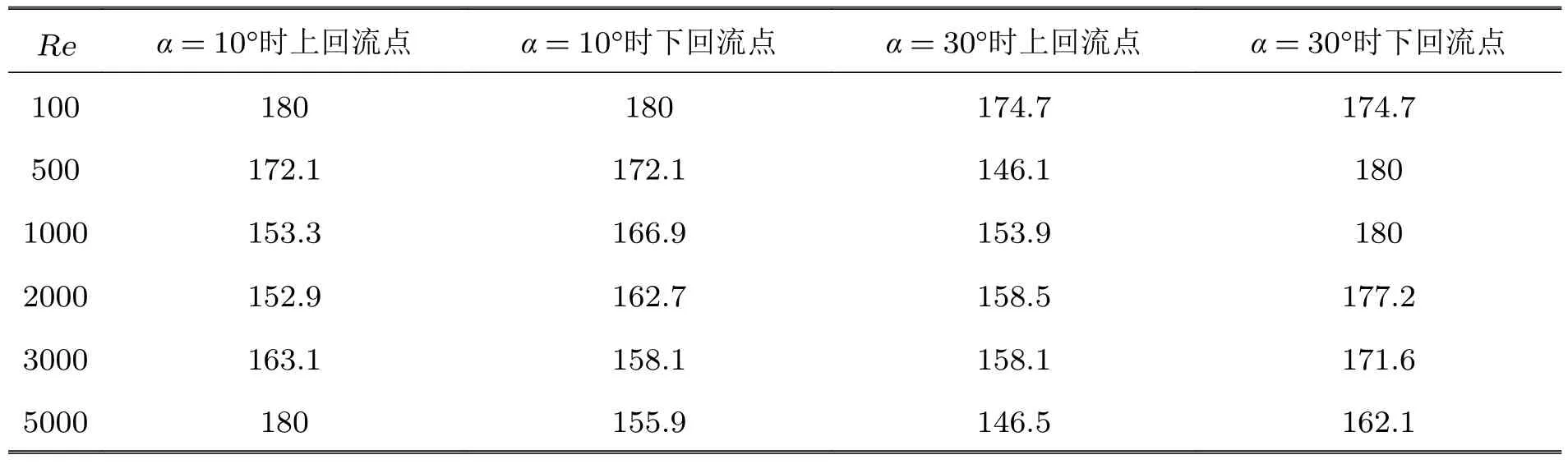
4.4 RANS
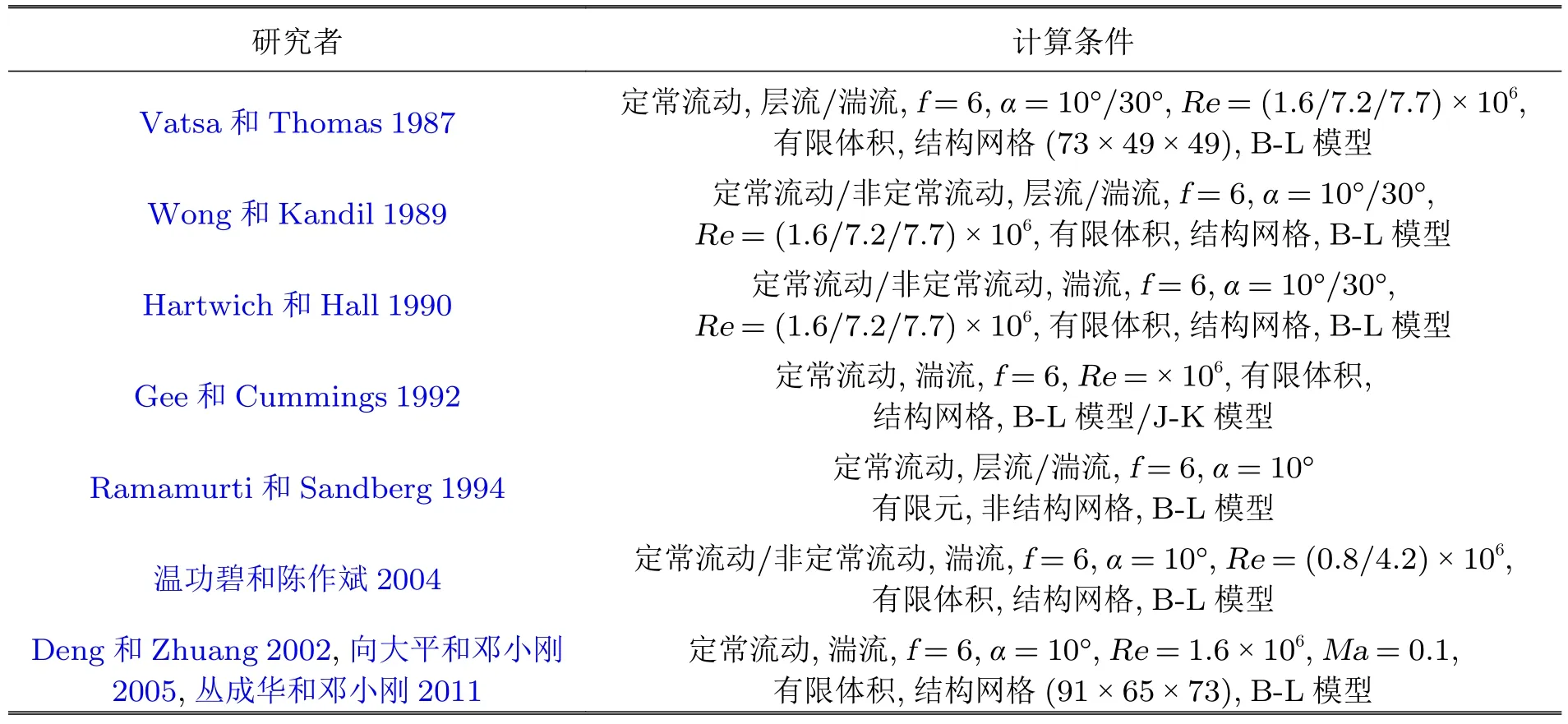
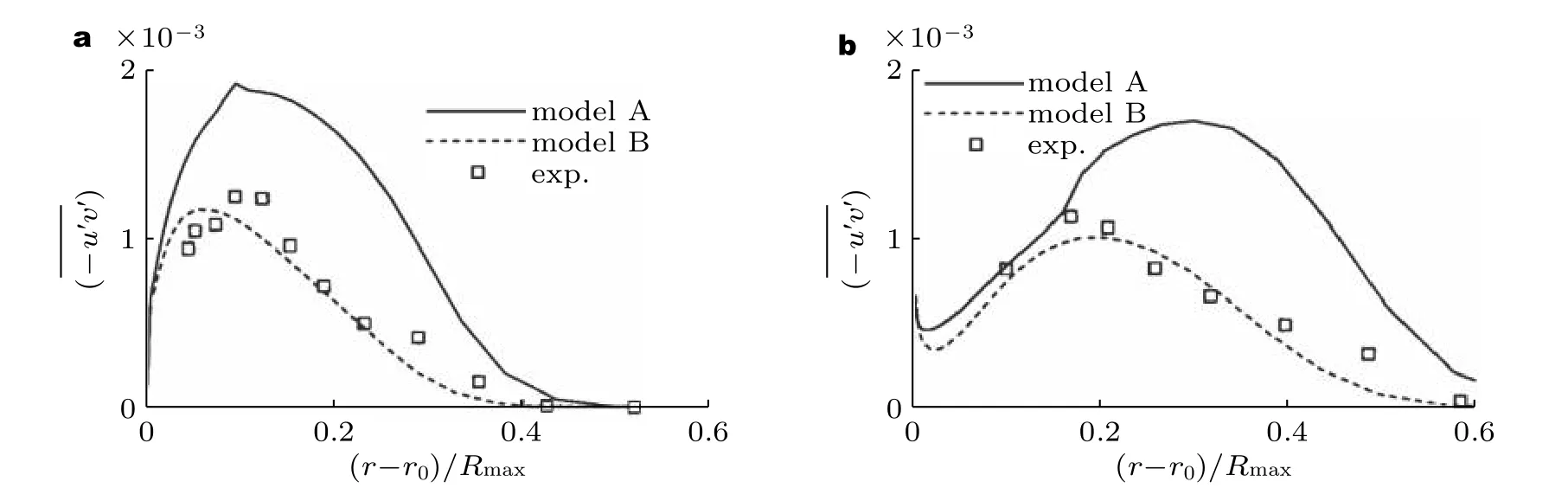

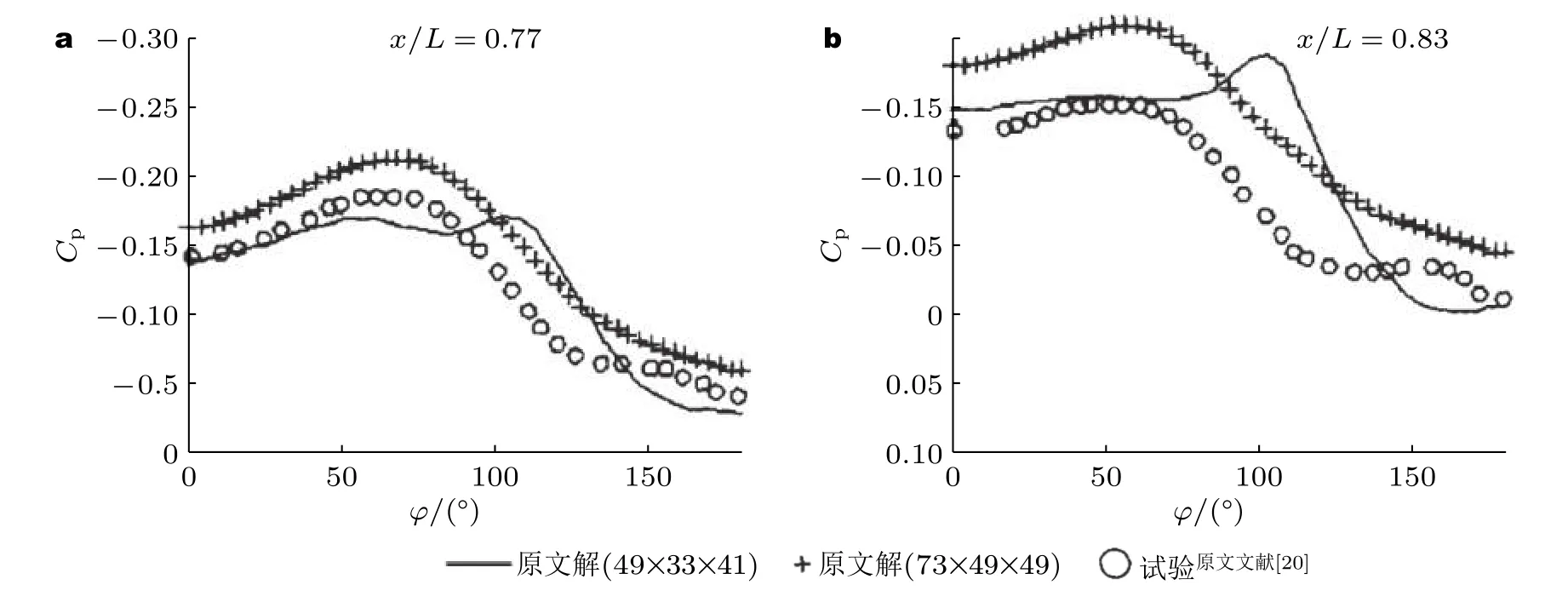

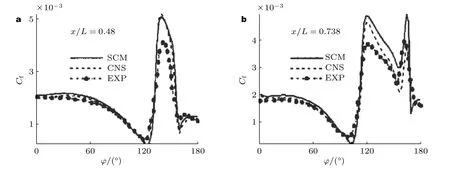

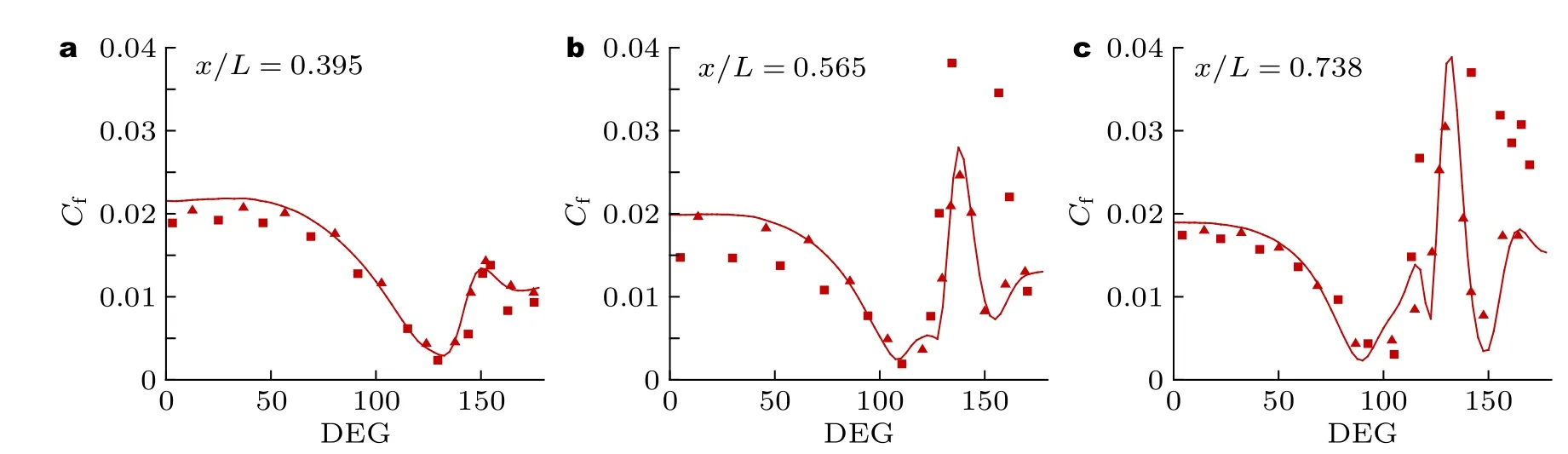


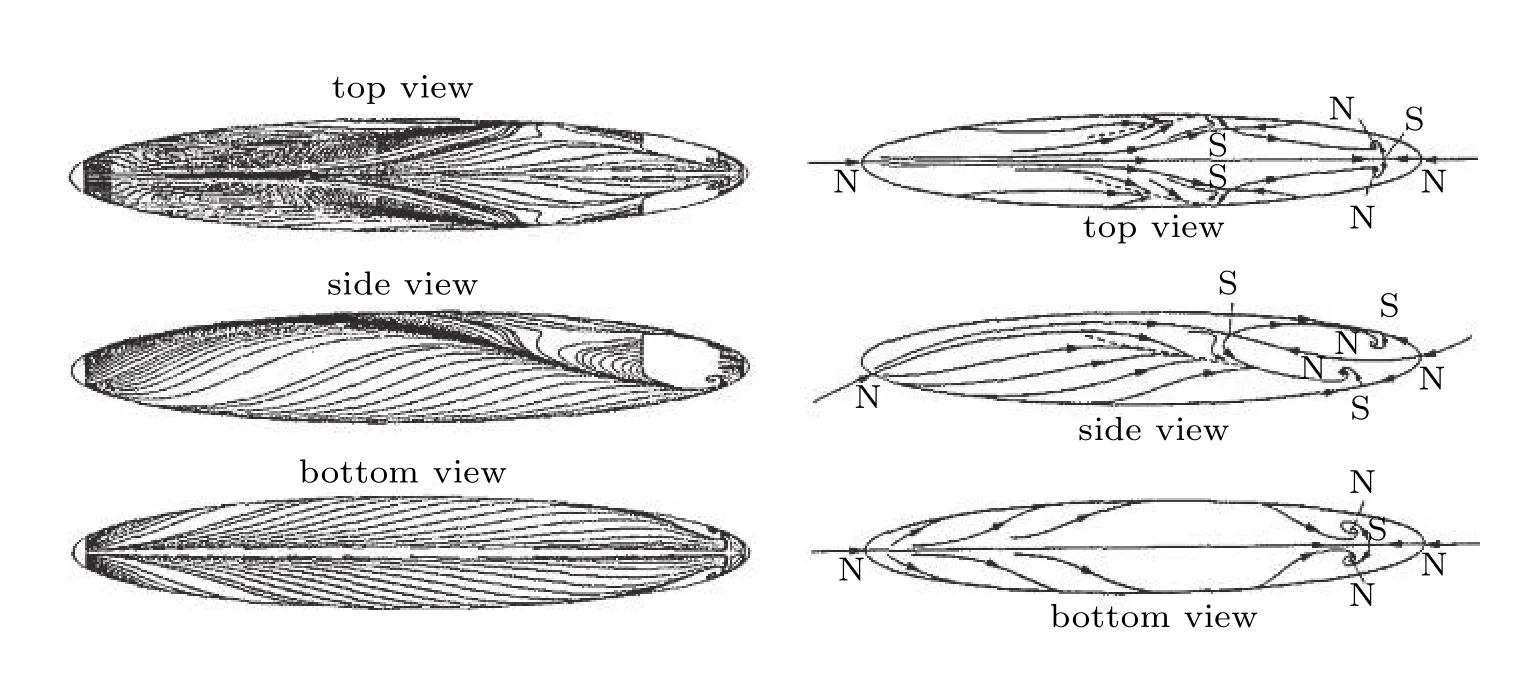

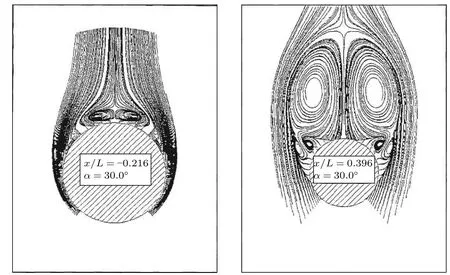
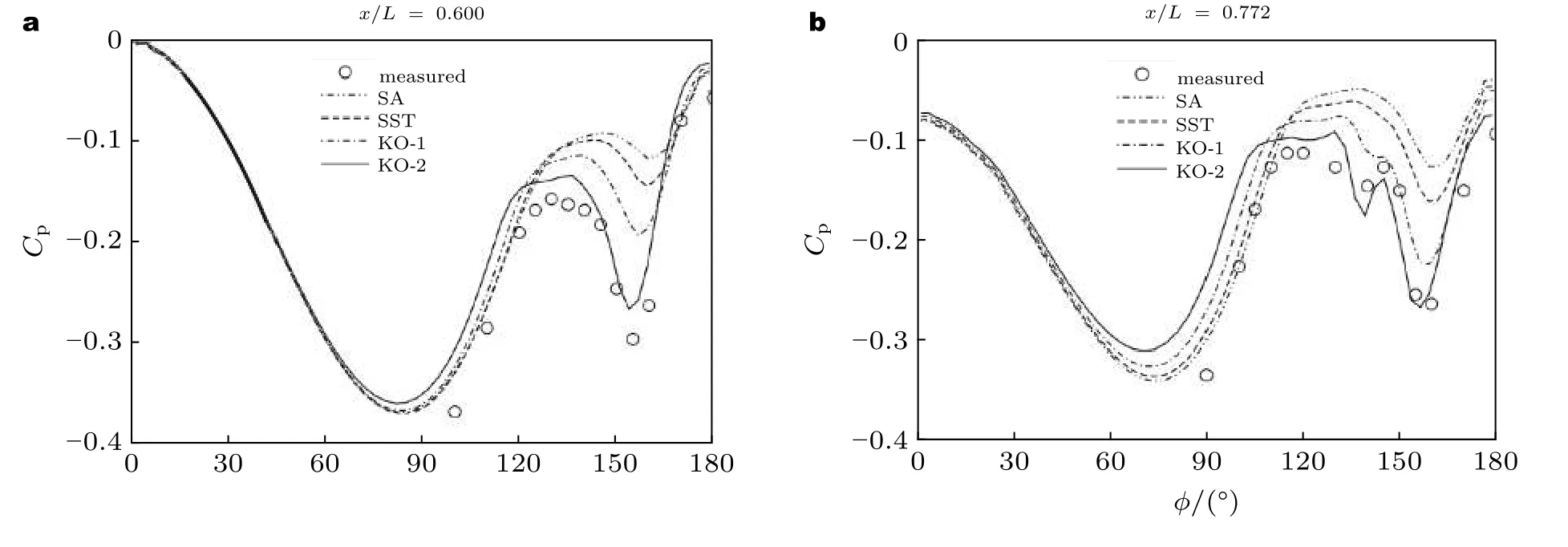
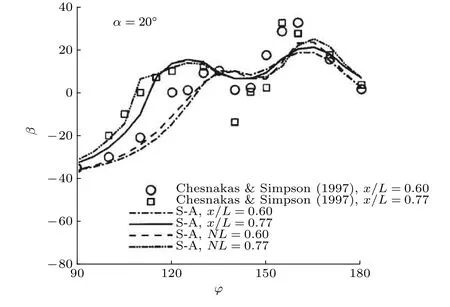

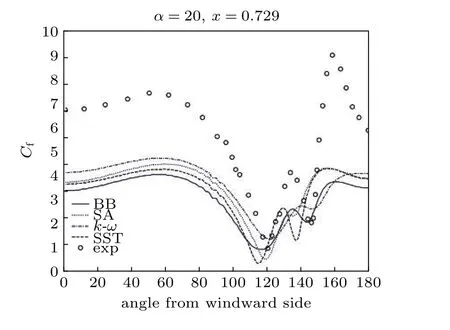
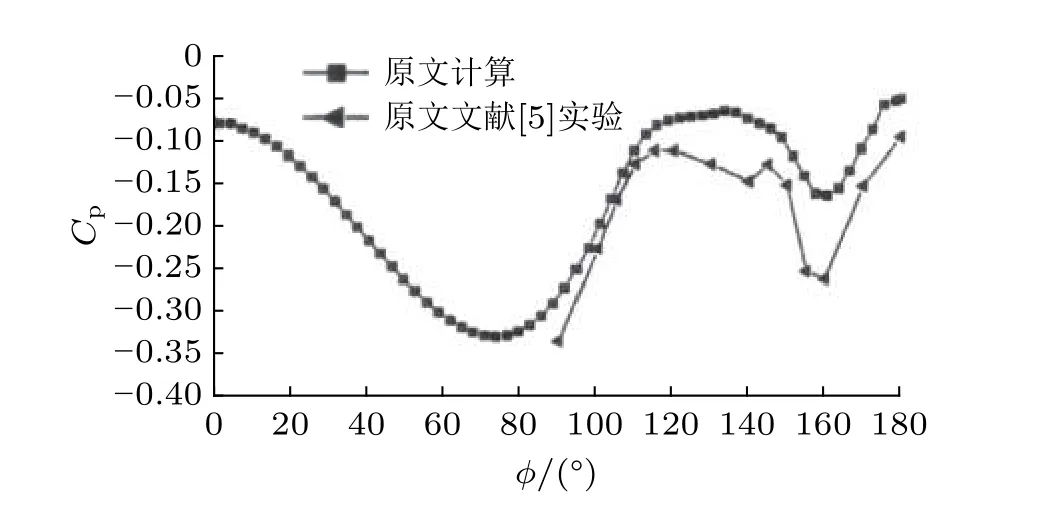
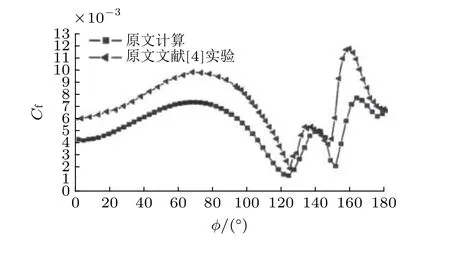
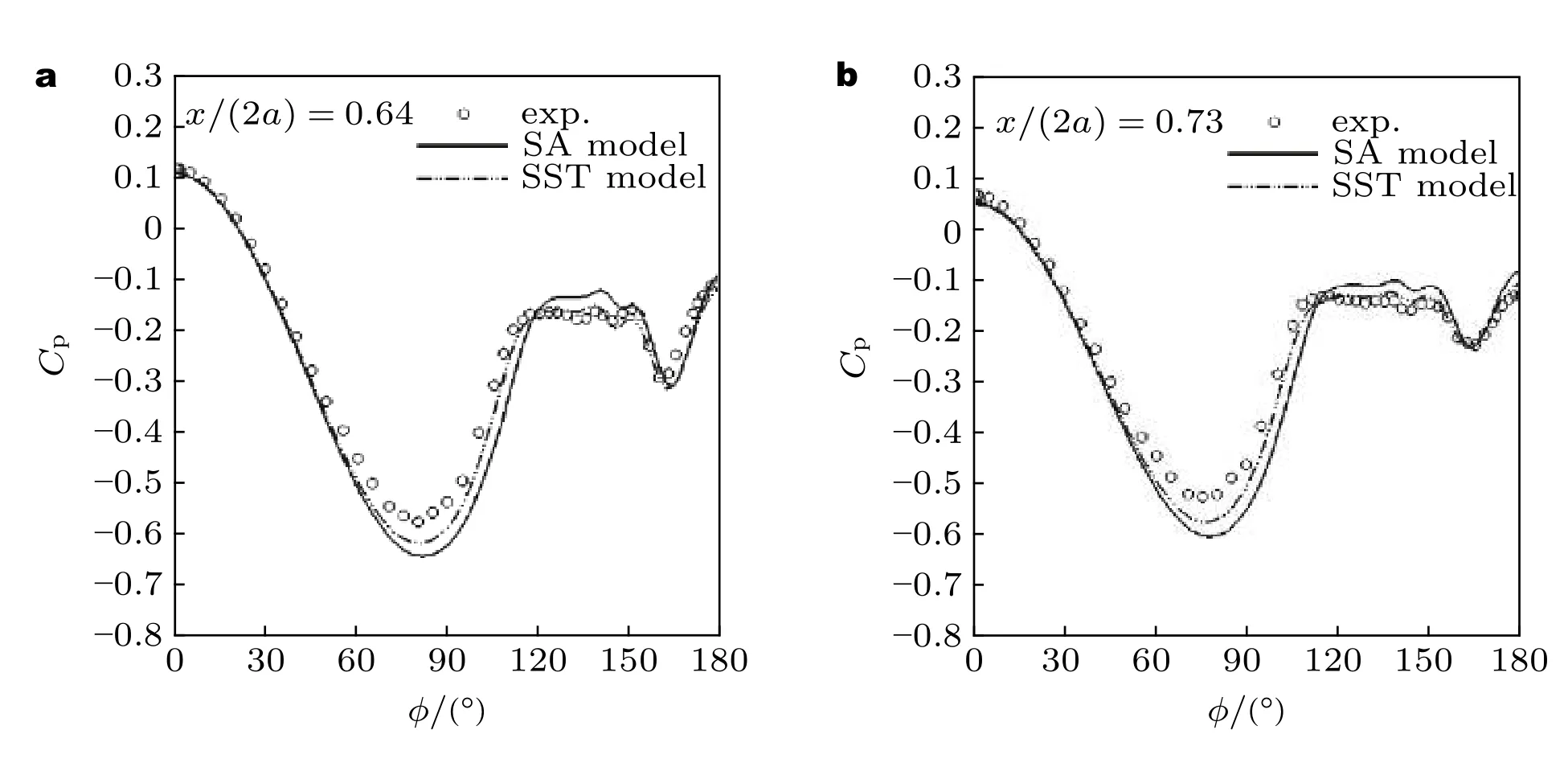
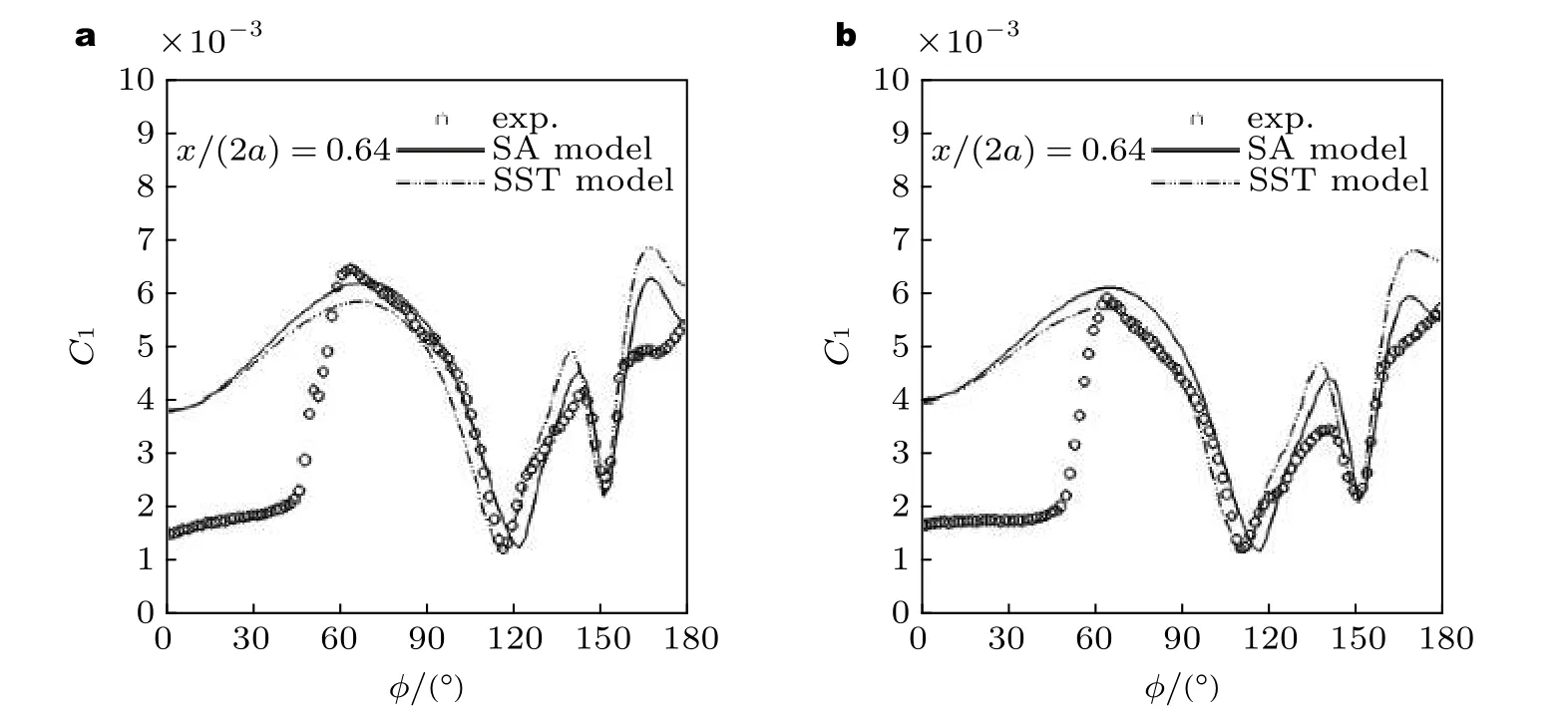
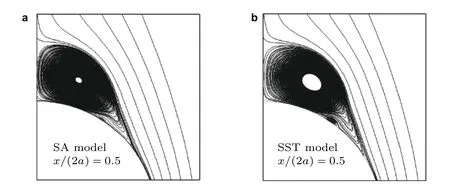
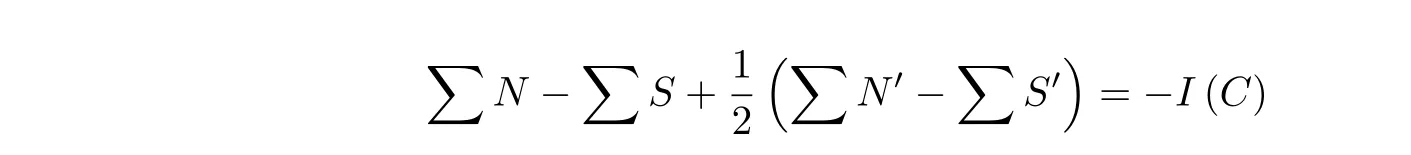
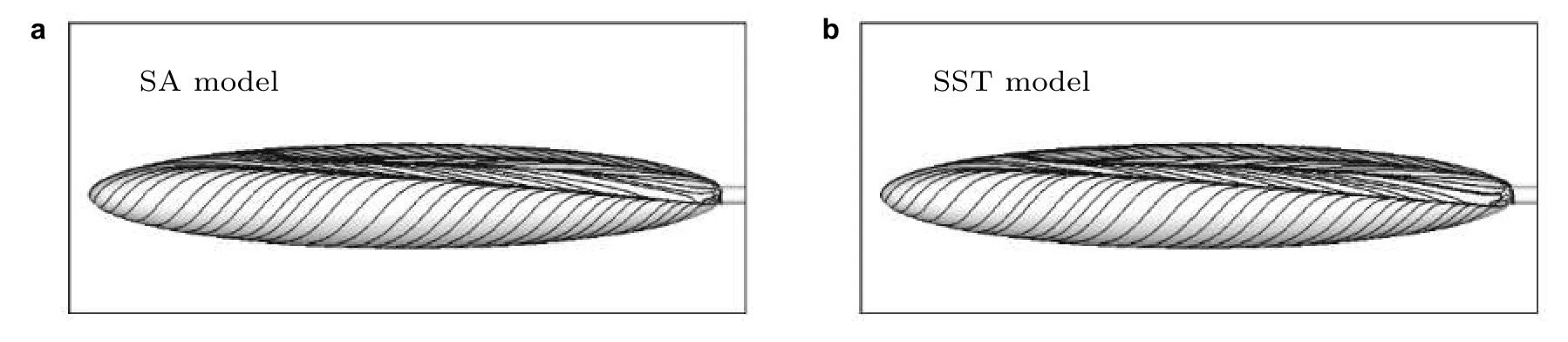
4.5 RSM

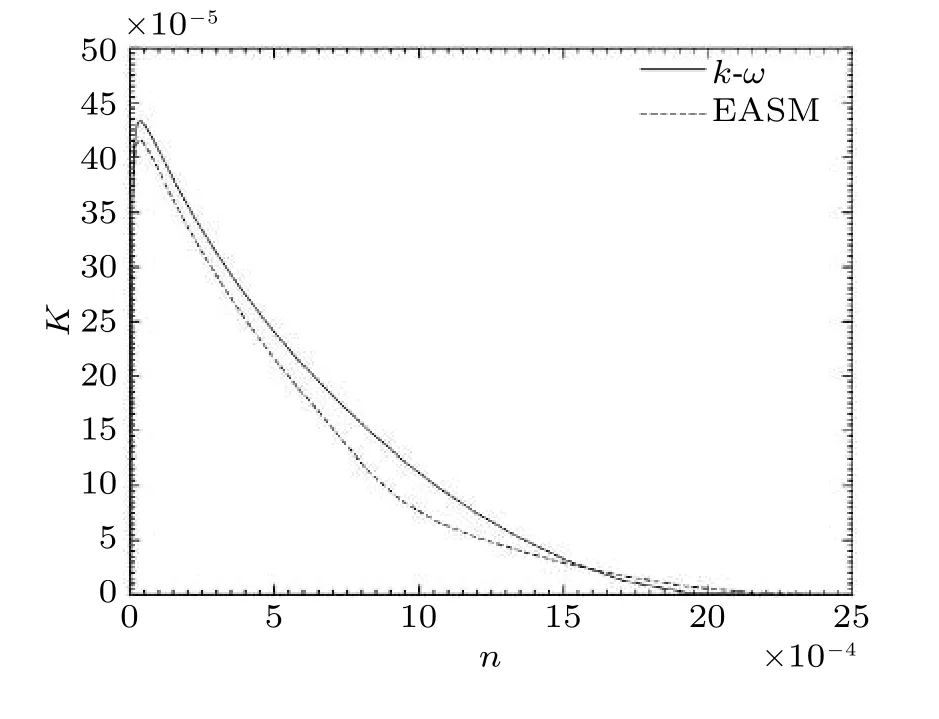
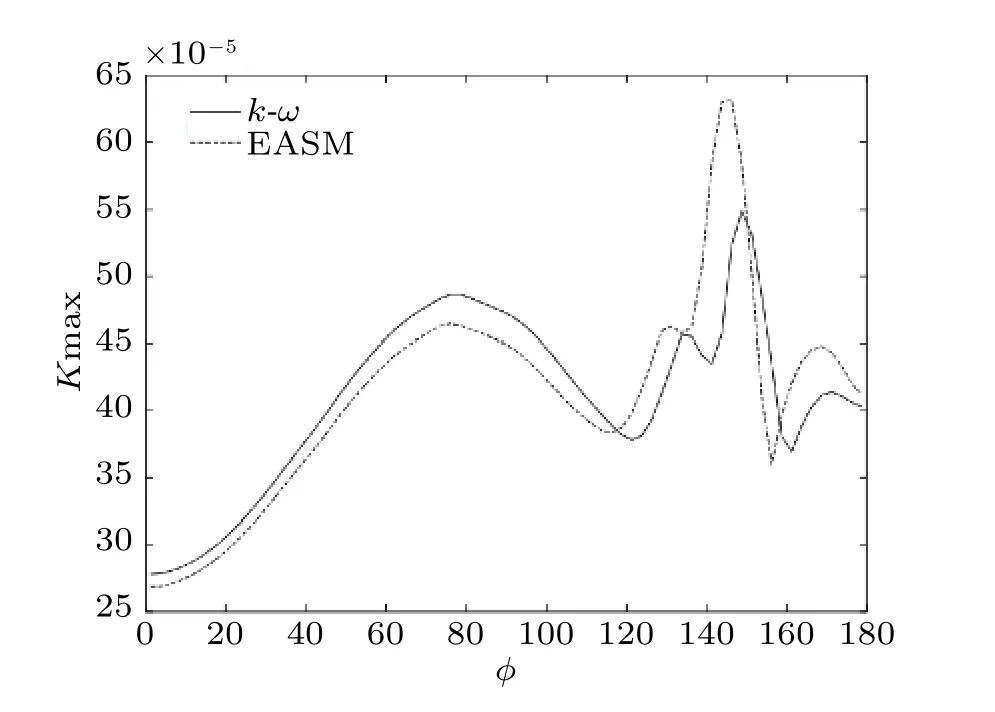

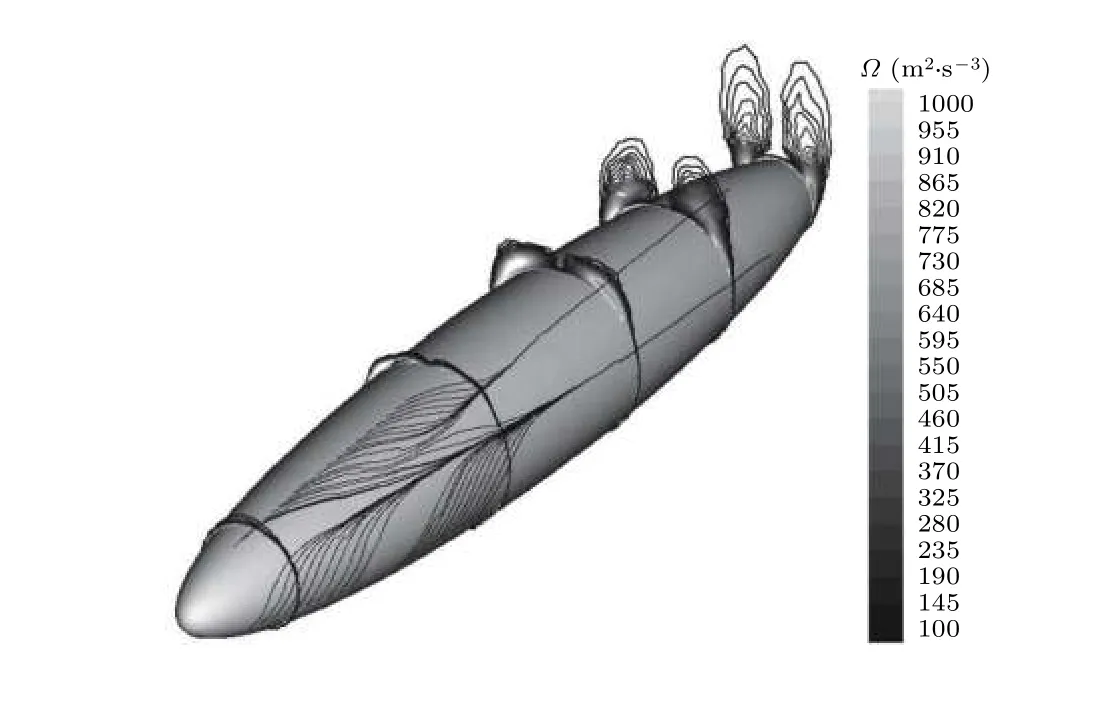
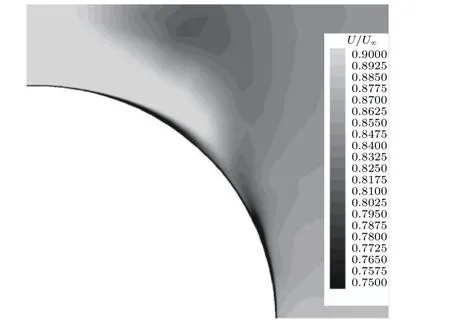
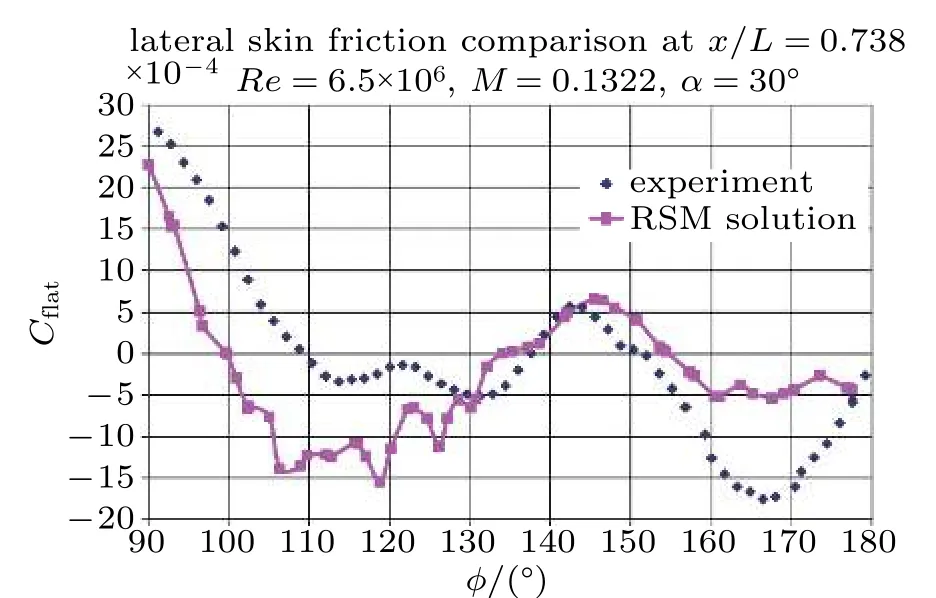
4.6 LES

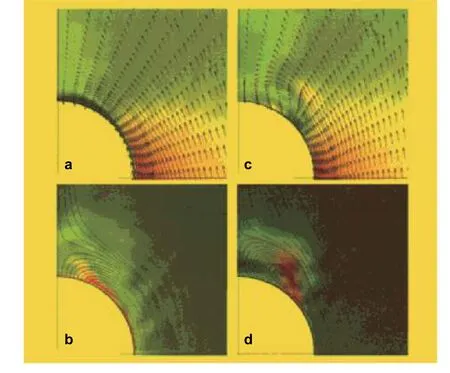

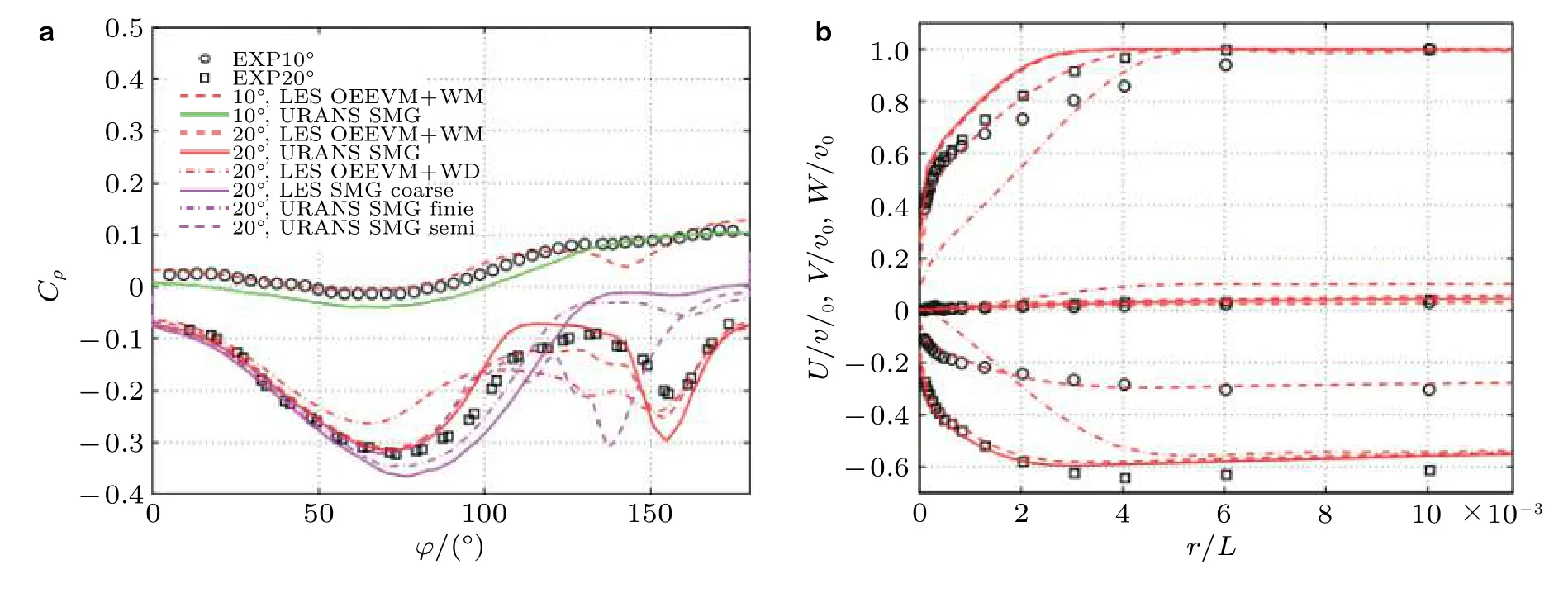
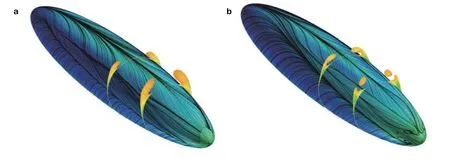

4.7 LES/RANS混合方法
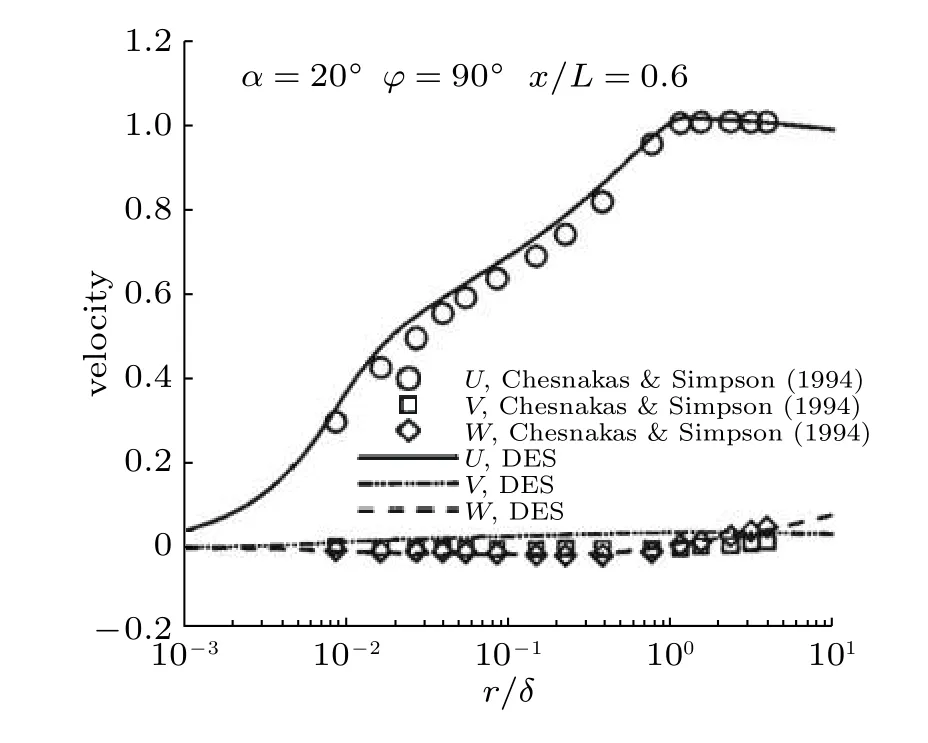
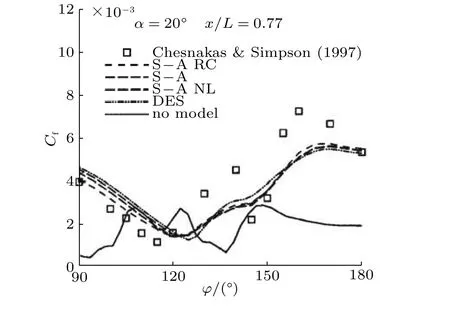
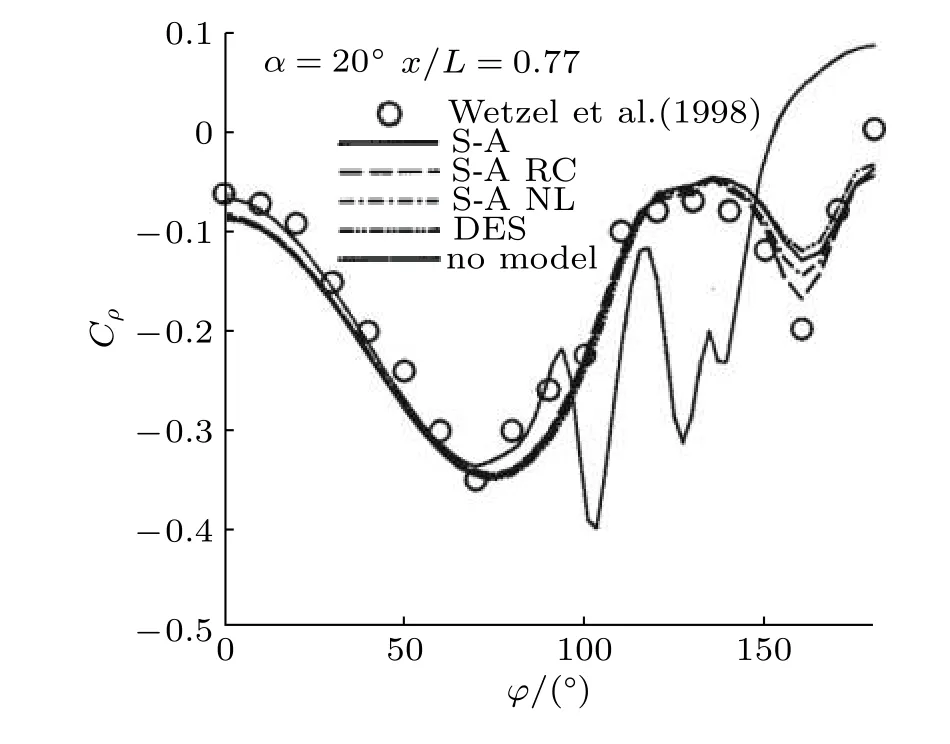
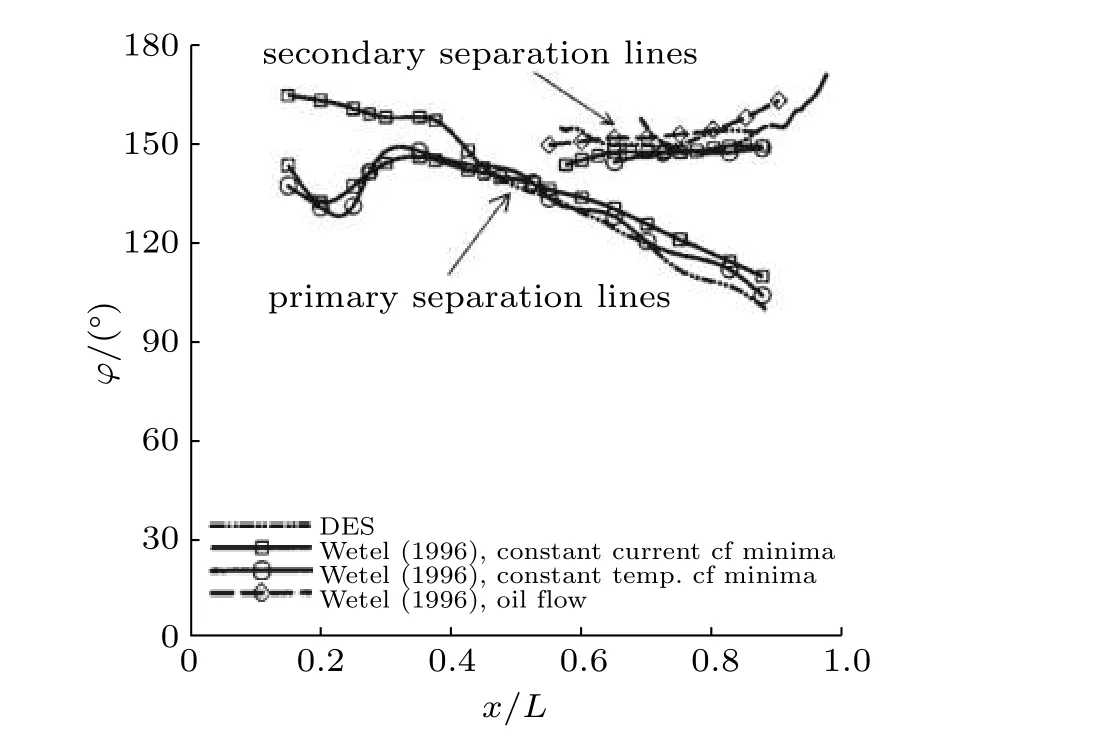


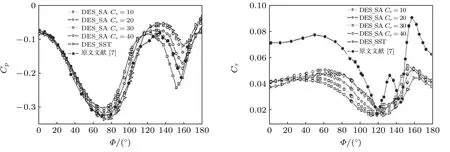


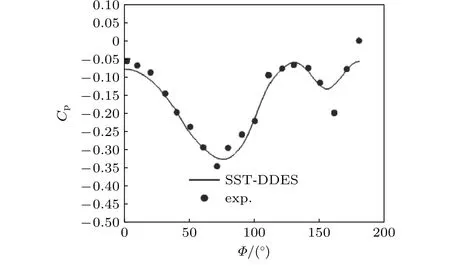

4.8 DNS






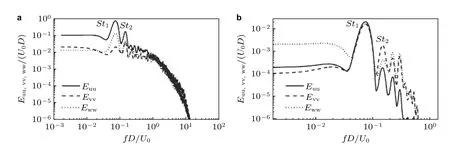
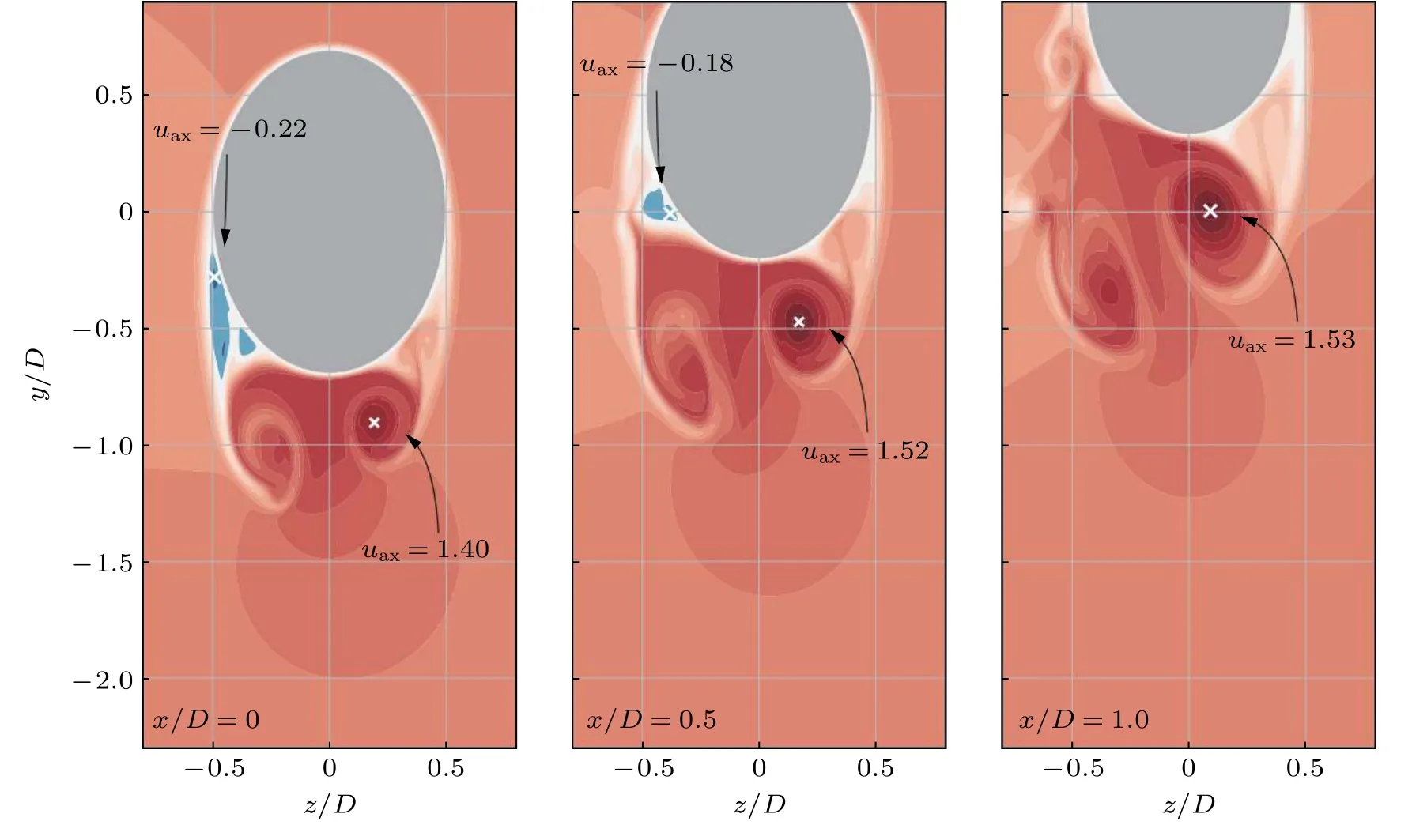
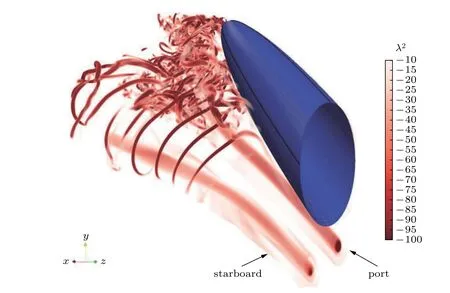
4.9 非定常机动过程的模拟


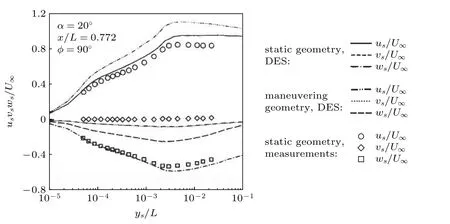



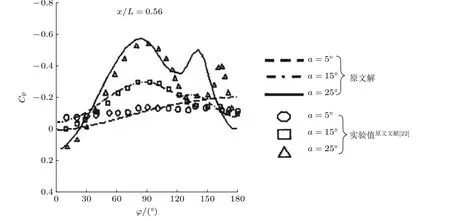
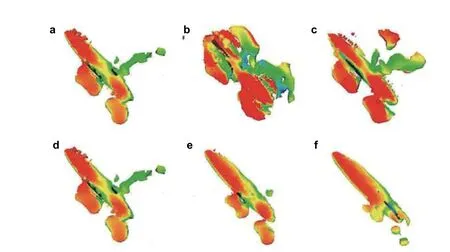
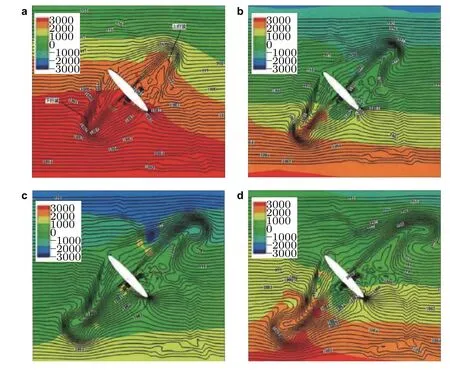

5 椭球绕流场转捩的研究
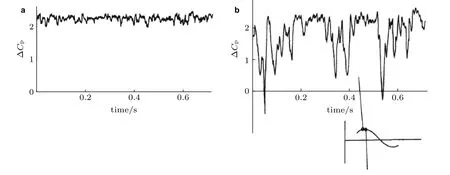
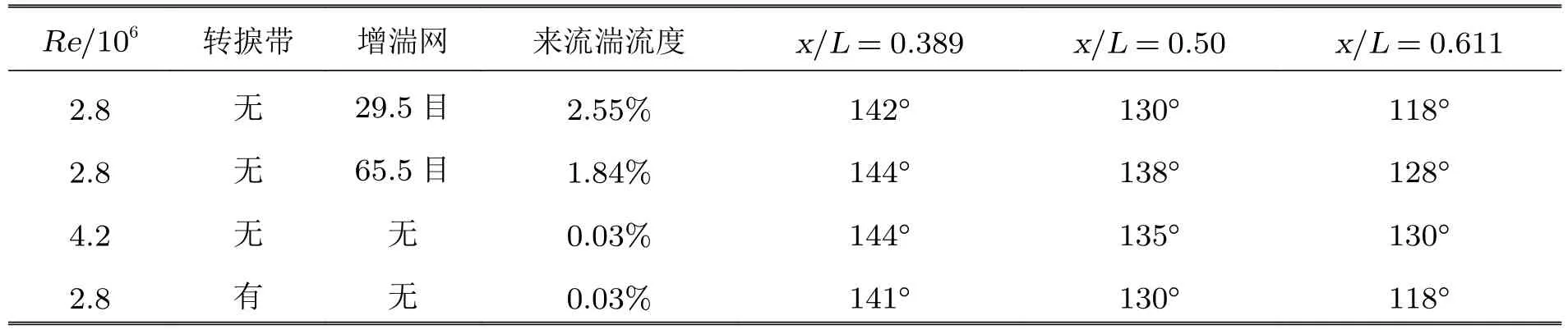
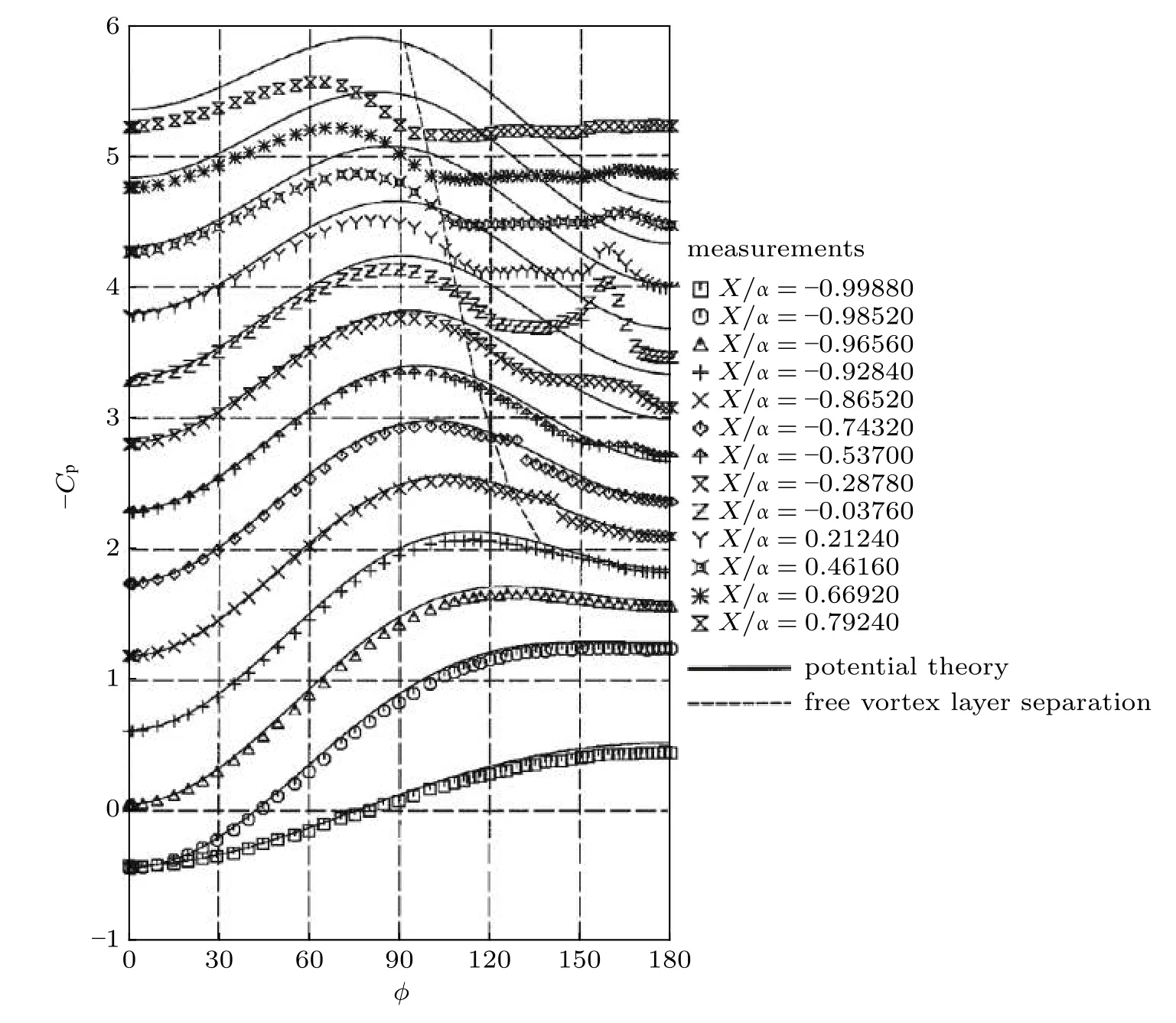



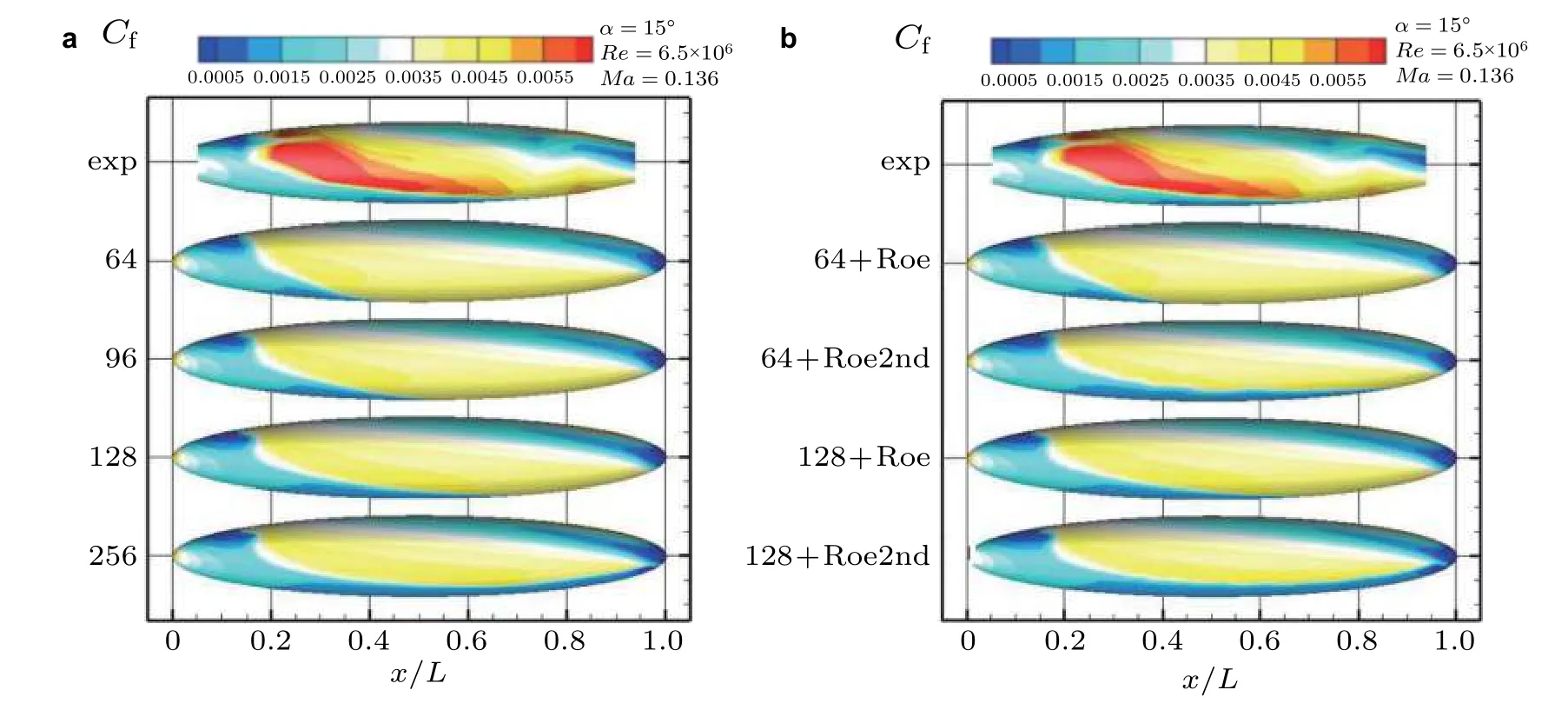
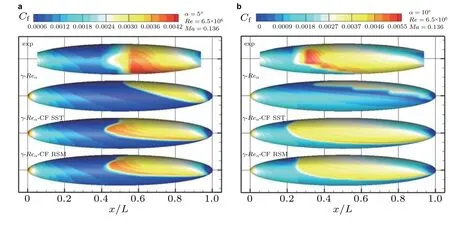
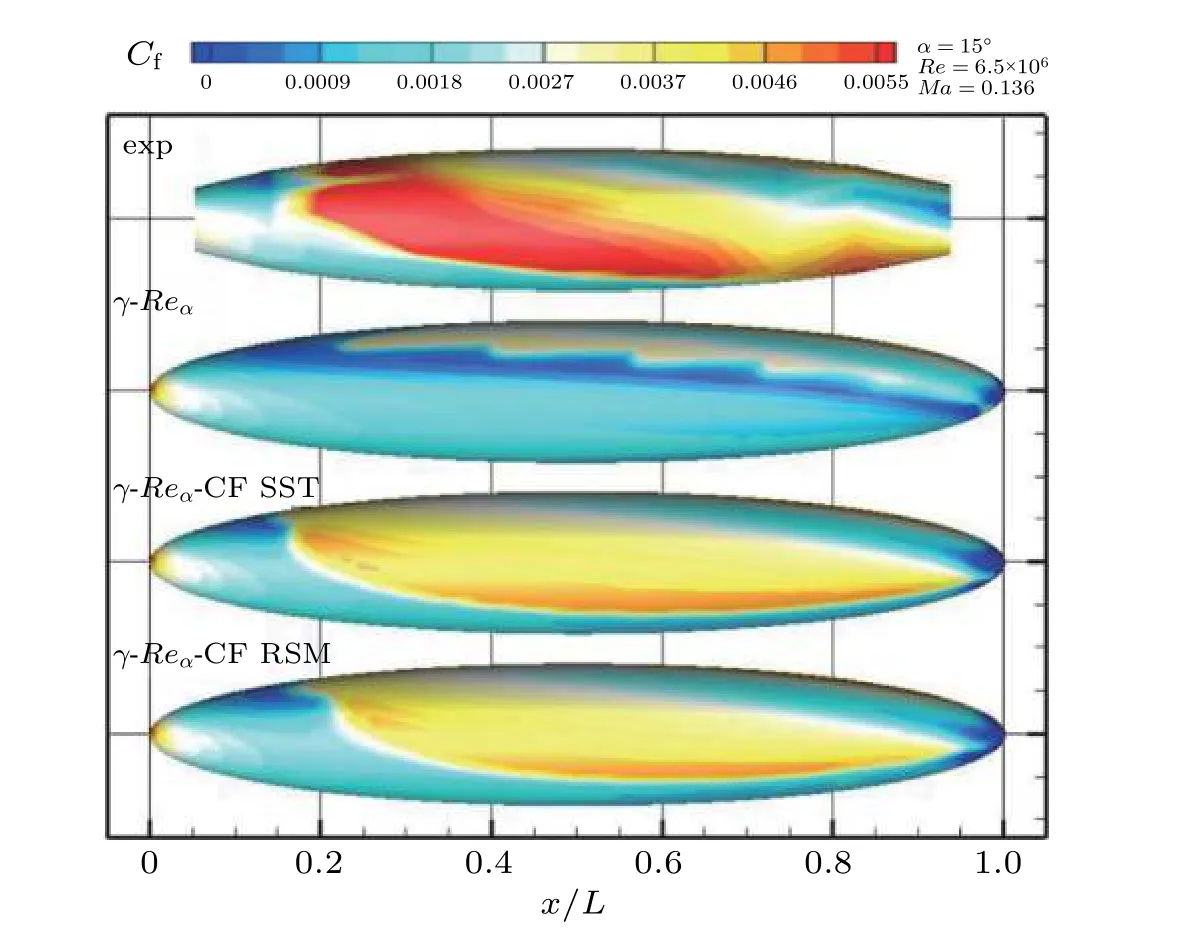
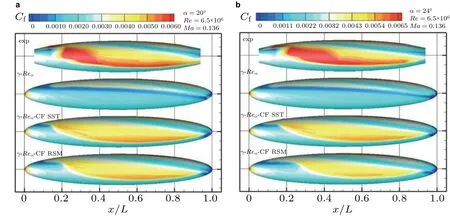
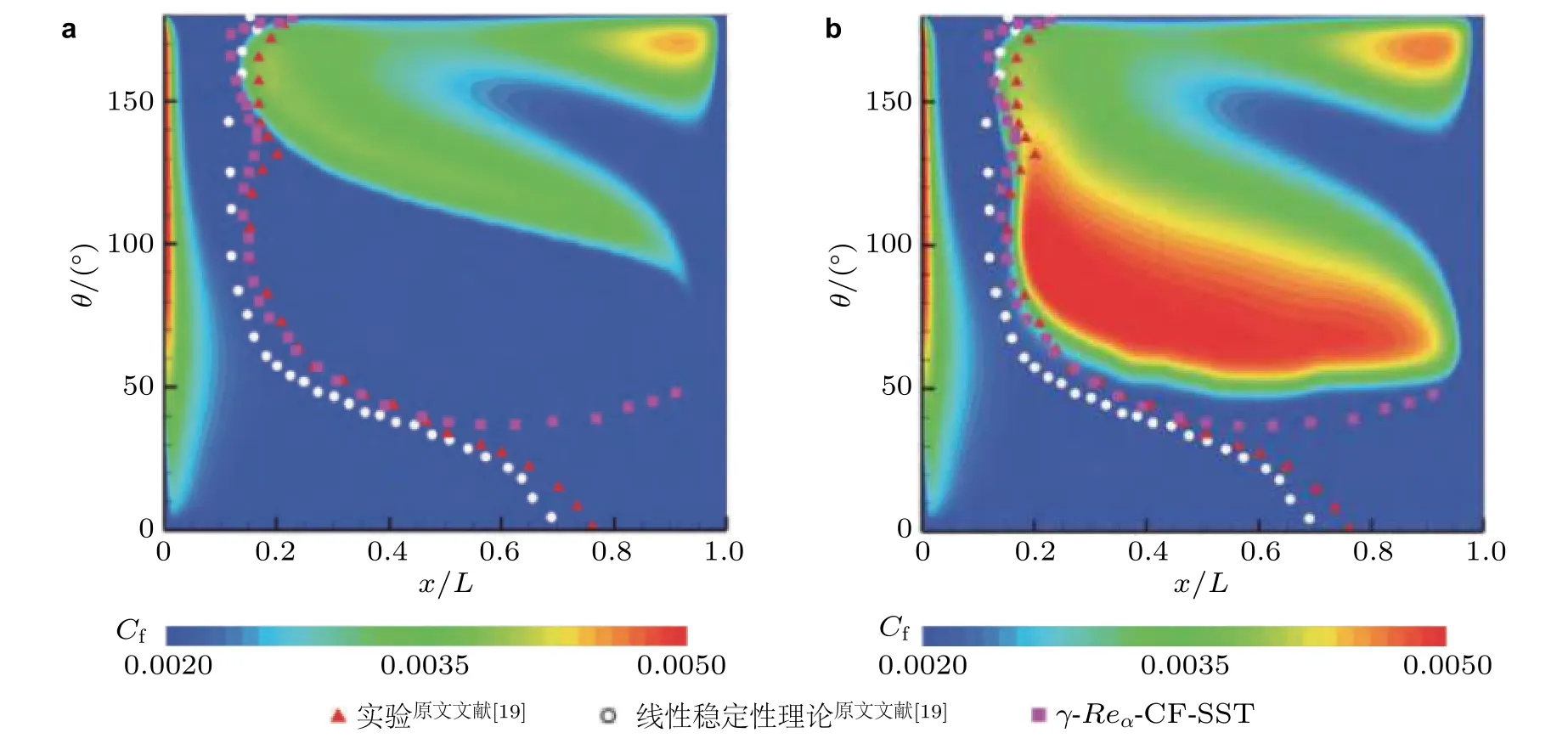




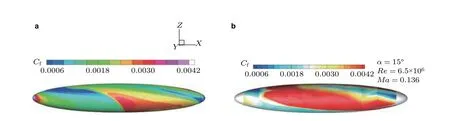
6 结论和展望
