基于数字图像投影技术的三维液膜流动测量研究
2021-11-19宋华振兆环宇朱程香王正之李海星朱春玲
宋华振,兆环宇,朱程香,王正之,田 伟,李海星,朱春玲,*
1.南京航空航天大学 航空学院,南京 210016;2.上海交通大学 航空航天学院,上海 200240 3.上海飞机设计研究院,上海 201210
0 引言
飞机结冰是飞机飞行中常见的一种现象,对飞行安全危害极大。当飞机穿过含有过冷水滴的云层、结冰温度较高时,过冷水滴撞击飞机表面后在气流的驱动下形成水膜。水膜表面波特性分析可以有效地研究水膜流动和传热特性,对探究飞机结冰过程中的质量分布及热量传递意义重大。随着实验技术的进步,非侵入性的液膜高度分布测量技术被广泛应用,其中包括激光诱导荧光技术(Laser Induced Fluorescence,LIF)、反射波技术和图像处理技术等。
LIF 技术被广泛应用于定常流可视化测量,其原理是在液体中添加荧光剂,根据荧光剂所激发的荧光强度来判断流体的速度、高度和温度。Li 等[1]开发了一种分子标记技术,可以同时测量飞溅水滴的尺寸、速度和瞬态温度等参数。Johnson 等[2]开发了一种荧光成像系统,量化了等温条件下薄膜在平坦表面上的瞬态行为。常士楠等[3]利用激光诱导荧光技术测量了一定条件下水膜流动的高度和表面波动特性。
反射波技术中较有代表性的是基于色散共焦位移计的测量方法。该方法通过色散镜头将光源射出的宽光谱复色光进行光谱色散,形成不同波长的单色光,每一个波长都对应一个光源到被测物体之间的距离,通过计算被感测到的波长换算距离。Rishikesan 等[4]利用色散共焦传感器评估不同加工表面的轮廓参数,以此来测量微观水平表面的光洁度。冷梦尧等[5-6]利用色散共焦位移计对高速气流驱动下的平板水膜流动进行测量,得到了高速气流剪切作用下的气液波动界面剪切因子。
基于图像处理的结构化光技术也是实现非侵入式高度测量的一种方式,近年来也受到流体动力学界的关注。该技术将已知的光图案主动投影到物体上,并从一个或多个视点捕获的光图案中提取三维表面形状[7]。Cazabat 等[8]通过投射等距条纹来重构扩散薄膜的剖面高度,研究不同温度下的薄膜爬升特性。Cobelli 等[9]使用数字条纹投影系统进行实验,以测量水流的表面变形。Hu 等[10]开发出数字条纹投影系统,并使用该系统定量测量风驱动下的水膜和溪流在平板上的瞬态行为。
在上述测量技术中,LIF 技术凭借着其非侵入式测量和低信号−噪声比特性得到了广泛应用。但LIF技术的荧光强度通常依赖于温度,在不可控变温过程(如结冰)中很难使用LIF 技术对流体薄膜高度进行定量测量。反射波技术虽然可以对几乎任何材料进行高精度无侵入式测量[11],但是无法实时测量三维流体流动的全貌。基于图像处理的结构化光技术虽能实现非侵入式流体全貌的复现,但也存在图像处理过程相位变化复杂、流体三维全貌预测精度较低等问题[12]。
数字图像投影技术(Digital Image Projection,DIP)具有时间分辨功能,是一种全区域水膜高度的测量方法。相比于其他基于图像处理的结构光技术,DIP 技术可以通过更简单的图像处理方法在采集的图像中提取被测物体的三维表面全貌,且测量精度较好。Zhang 等[13]应用该技术测量NACA0012 翼型表面水膜和溪流随风速变化的流动过程,复原了水膜在不同风速下的三维全貌,但未建立水膜流动与外界条件间的关系式。国内在DIP 技术方面的相关研究较为少见。
为验证DIP 技术在流体测量中的可靠性与准确性,本文自主设计搭建了DIP 测量系统和平板水膜流动实验台,进行了一系列水膜流动实验,并利用标准件对DIP 系统测量精度进行了测试。
1 DIP 测量技术
1.1 DIP 测量技术的原理
DIP 测量技术的基本原理如图1所示。摄像机、投影仪和实验基板形成三角形布局。在目标流体未流过实验基板之前,投影仪投射网格图像于实验基板,此时摄像机采集实验基板上的网格图片作为参考图像。当目标流体流过实验基板时,网格图片将投射于流体表面并发生变形,摄像机记录此时的变形网格作为测试图像。通过分析测试图像和参考图像对应点的位移,就可以重构被测物体的三维形状。
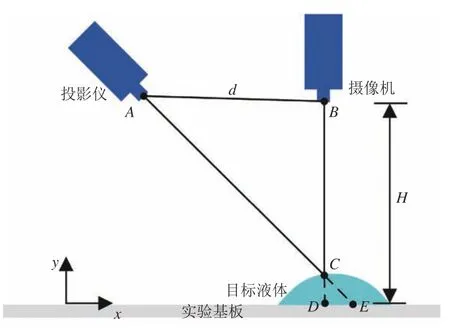
图1 DIP 技术原理图Fig.1 DIP technology diagram
为了将测试图像和参考图像对应点的位移转换为目标流体高度分布,DIP 系统需要标定,以建立高度与位移之间的关系。
建立如图1所示的坐标系,y方向高度为0 的平面为后续测量的参考平面。实验基板上无任何目标流体时,任意网格点投影于点E;当流体流经实验基板时,原投影于点E的网格点将投影于关注点C。若此时摄像机的采集方向垂直于实验基板,根据相似三角形原理可得:

则此时关注点C处的流体高度为:
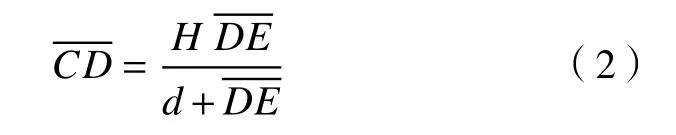
距离d通常远大于上式可简化为:
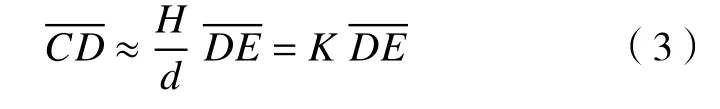
对于给定的DIP 系统,H为摄像机到实验基板的高度,H和d是固定的,因此参数K 为常数,可由标定方法确定;可通过测量测试图像和参考图像之间关注点C处的位移来确定;通过式(3)就可以得出流体流经实验基板时关注点C处的高度信息,从而复原流体的整个三维全貌。
1.2 DIP 测量的图像互相关算法
DIP 测量系统使用图像互相关算法[14-16]来确定测试图像与参考图像之间的关注点C处的位移量。在参考图像和测试图像的特定区域分别选择一个小窗口作为关联窗口,计算两关联窗口的相关系数。相关系数R以下式表示:
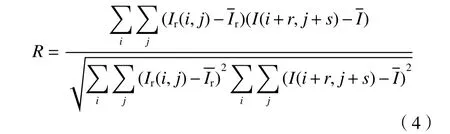
其中,Ir和I分别表示从参考图像和测试图像中获得的关联窗口的图像强度,和为相应的平均强度值;i和j分别表示水平方向和垂直方向,(r,s)为图像位移量。通过找到相关系数的峰值位置就可确定两关联窗口的位移量,即关注点的位移量。图2 展示了一个规则网格的参考图像和由测试板上的长方块产生的关注点移动的测试图像,使用上述算法即可得到红框内的网格点的位移量。

图2 网格点位移图Fig.2 Grid intersection displacement diagram
1.3 DIP 系统的标定方法
对于一个给定的DIP 系统,测试图像和参考图像中对应点的位移随着目标物体的高度变化而呈线性变化。DIP 标定可用于确定测试图像关注点的位移量与实际高度的转换系数K。如图3所示,通过数字投影仪将网格图像投影到实验基板上。实验基板水平安装于升降台顶部,升降台高度(即实验基板在y方向上的位置)用微米级驱动器调整。摄像机用于捕获投影在实验基板上的图像,所获取的图像被存储在计算机上用于图像处理。
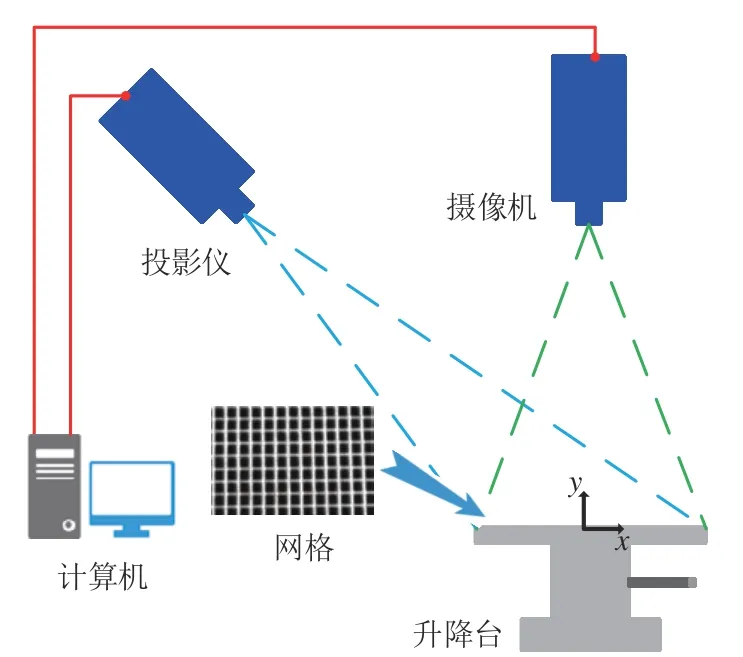
图3 DIP 标定示意图Fig.3 DIP calibration diagram
在DIP 标定过程中,通过调整升降台的高度,将测试板以某一间隔移动到y方向上的多个位置,获取测试板上投影的网格图像,再利用图像互相关算法对图像进行处理。以y=0 处的图像作为参考图像,计算测试板在其他位置时的关注点位移量,从而得到图像网格点的位移值。图4 为测试板在不同高度时的测试图像网格点的像素位移量。从图中可以看出,高度与网格图像点的位移量之间的关系可以用线性函数拟合,符合式(3)的线性关系。标定过程得出的线性比例因子即为DIP 测量系统的K值,且K值是一个常数。
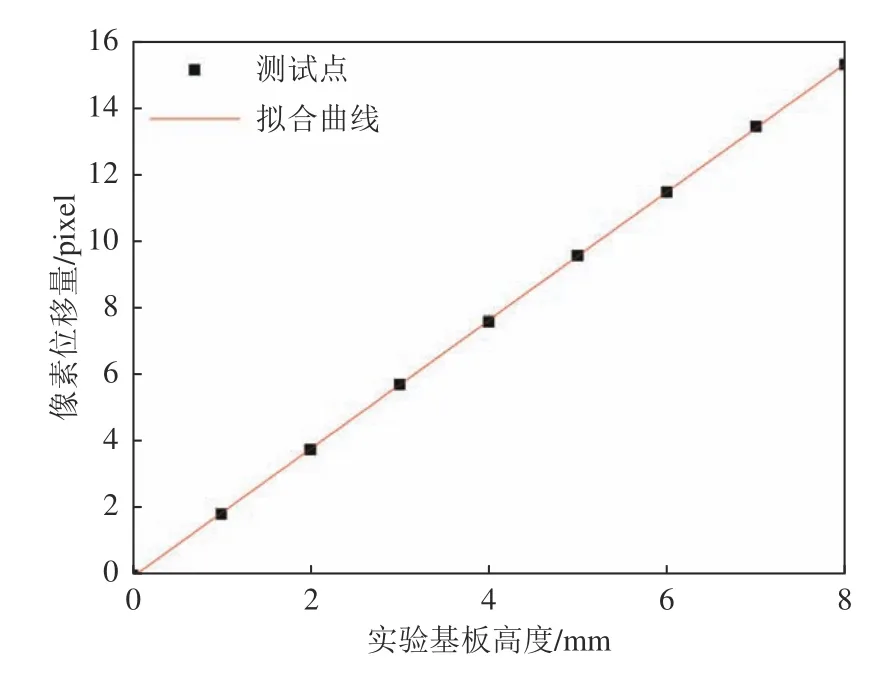
图4 DIP 标定结果图Fig.4 DIP calibration result diagram
2 DIP 技术测量平板水膜流动
2.1 实验台
图5 为平板水膜流动实验台。风道气流经收缩段整流后进入实验段,为保证气流均匀,在收缩段上游设置蜂窝器和阻力网。实验段横截面为300 mm×75 mm。为方便更换实验基板,实验段顶部采用可拆卸的玻璃盖板。实验基板为抛光铝材,其下装有升降台。实验基板的一端开有出水槽,出水槽连接供水箱,供水流量通过高精度齿轮泵进行调节。

图5 平板水膜流动实验台Fig.5 Flat water film flow test setup
2.2 实验台精度测试
为了测试DIP 系统的测量精度,使用DIP 系统测量了长宽高为1200.0 mm×1000.0 mm×0.5 mm 的实验基板。首先对DIP 测量系统进行标定,得出系统的K值。随后获取参考图像和测试图像,使用图像互相关算法计算参考图像与测试图像之间关注点的位移量。最后,根据K值和位移量计算得到实验基板的高度分布。图6(a)给出了实验基板高度h'分布的DIP 测量结果。实验基板的高度分布已知,DIP 系统的测量精度可以通过测得的高度分布与实际高度分布进行定量比较评估。DIP 测量误差分布如图6(b)所示。测量结果显示,实验基板中间区域测量误差较小(2% 以内),上下两侧的测量误差在2%~5%之间。这是由于投影仪的投影方向与摄像机采集方向需呈一定角度,而DIP 系统配置的摄像机垂直于实验基板,因此,投影仪倾斜投射出的网格在实验基板中部区域聚焦较好,网格点清晰,而两侧区域聚焦较差,网格点模糊,增大了测量误差。此外,DIP 系统部件的搭建角度和摄像机分辨率的限制也是造成DIP测量误差的主要原因。由DIP 测量原理可知,投影部件与摄像机部件之间的夹角越大,DIP 测量系统单位距离的网格点像素位移量越大,测量精度越高。受实验条件的限制,本文DIP 测量系统的部件夹角为81°。在图像互相关算法原理中,摄像机的分辨率越高,图像互相关算法计算出的最终位移量精度越高。本文实验摄像机的分辨率为4×106pxiel,拍摄区域面积为80 mm×120 mm。
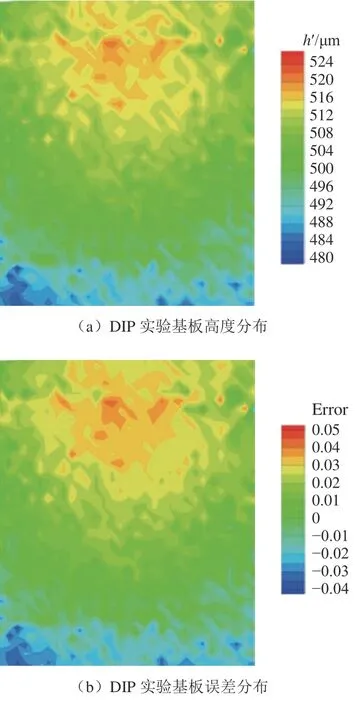
图6 实验台精度Fig.6 Test setup precision
为说明DIP 测量系统对毫米级高度测量的精度,本文在已搭建好的水膜流动实验台上使用DIP测量技术进行3 mm 高度范围内的梯度测量。引入色散共焦位移计同时测量,将其测量结果作为参照。在图3所示的实验台基础上将色散共焦位移计垂直于实验基板固定。由低到高等间隔升高升降台,每次升高500 μm,共6 次。每次升高升降台后,采集网格测试图像并同时记录色散共焦位移计测量结果。该实验重复3 次,最终结果取平均值,如图7所示。从图中可以看出:两种测量方式得到的结果均呈现出良好的线性趋势;随着测量高度增大,共焦位移计与DIP 测量系统的测量误差均增大。相较于DIP 测量,共焦位移计的测量误差随着实测距离越来越大。这是由于共焦位移计有特定的测量距离范围,当超出测量范围时,共焦位移计不能很好地聚焦待测平面,导致测量距离越大、测量误差越大;这也可以反映出在3 mm 高度范围内,当测量高度较大时,DIP 测量技术的精度优于色散共焦位移计。
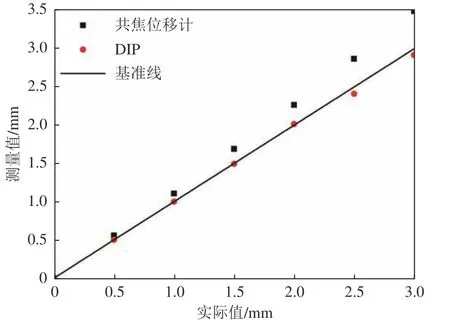
图7 测量结果对比图Fig.7 Comparison of measurement results
2.3 平板水膜流动实验结果
在水膜流动中,水膜雷诺数定义为:

其中,Q为水膜质量流量,W为水膜润湿宽度,μw为水的动力黏度系数。
在实验中,流场风速Ua=17 m/s,水膜雷诺数Ref范围为16.5~188.6。为增大水表面的反射性,在水中加入1%体积比的白色乳胶漆。通过落球法测试配置液体在温度为20 ℃时的动力黏度μw=0.985×10–3Pa·s。在实验段上部空间,使用Texas instrument DLP450 型投影仪投影方形网格图像,同时使用PCO HS4 型高速摄像机采集图像,采集频率为100 Hz,曝光时间为1 ms。摄像机匹配镜头型号为定焦尼克尔105 mm。图8 显示了实验基板水膜的参考图像和变形的测试图像,h为水膜高度。投影的单个方形网格尺寸为2.8 mm×2.8 mm,网格条纹宽度为0.8 mm。与参考图像(图8(a))相比,测量图像(图8(b))由于存在水膜而显著变形。将参考图片与测量图片使用图像互相关算法进行计算,计算过程中的关联窗口设置为2.4 mm×2.4 mm 的方形窗口。图8(c)展示了经过三维重构后获得的水膜流过铝板表面的高度分布。

图8 实验采集图像与计算结果对比图Fig.8 Comparison of test photo and calculation
本文开展了不同雷诺数下的水膜流动实验,水膜高度的DIP 计算结果如图9所示,L为水膜流动长度。整体上,水膜的高度随着水膜雷诺数的增大而增大。水膜雷诺数在16.5~23.6 范围时(图9(a)和(b)),润湿区域的水量较少,风速对表面波的传导影响较大,此时水膜整体较薄,无法形成稳定的表面波传导。随着水膜雷诺数的增大(图9(c)~(f)),润湿区域内的水量逐渐增多,水膜在气液界面剪切力的作用下形成表面波。随着水膜雷诺数的增大,水膜表面波越来越向润湿区域中心集中,中心润湿区域的水膜高度越来越大。当水膜雷诺数继续增大到165.0及以上时(图9(g)和(h)),实验设定的风速不能够以稳定的表面波向后发展水膜。

图9 水膜流动DIP 计算结果(Ua=17 m/s、Ref =16.5~188.6)Fig.9 DIP calculation results of water film flow(Ua=17 m/s and Ref =16.5-188.6)
为了更好地研究水膜雷诺数对水膜表面波形的影响,分别取水膜雷诺数为16.5、70.7、188.6 的DIP计算结果的中间截面剖面曲线,如图10所示。Ref=16.5 时,水膜表面波呈现出振幅小,周期短且不稳定的特性。Ref=70.7 时,润湿区域内水膜的高度整体增大,水膜表面波振幅和周期均较稳定。Ref=188.6时,在水膜平均高度增大的同时,出现了表面波振幅较大、周期较长的现象。因此,在特定风速下随着水膜雷诺数的增大,水膜表面波呈现出振幅逐渐增大、振动频率逐渐降低的波动特性。

图10 水膜剖面表面波形图Fig.10 Water film surface wave profile
3 实验模型验证
3.1 平均水膜高度结果验证
在水膜高度较薄、水流速度较低的条件下,水膜流动可简化为二维不可压缩层流流动。对Navier-Stokes 方程进行简化得出水膜高度的关系式[3]为:
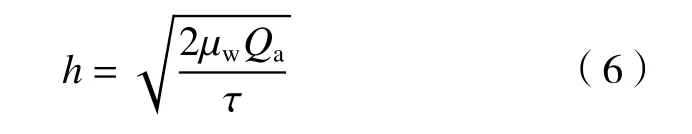
其中Qa为上游流入的单位润湿长度水的体积流量,τ为气−液界面剪切力。借鉴气−液两相分层流研究的经验[17],界面剪切力可以表示为:
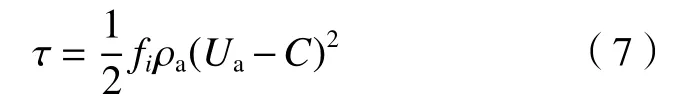
其中,fi为界面剪切系数,通过实验结果测得;ρa为空气密度;Ua为空气主流速度;C为气−液界面波的相位速度,由于C远小于气流速度,故在计算中忽略[18-19]。对于平板边界层模型[20],界面剪切系数fi=0.074(Rea)−0.2,其中Rea=UaH/υa为气流雷诺数,υa为空气运动黏度系数。通过式(6)和(7)可得水膜高度与水膜雷诺数之间的关系为:
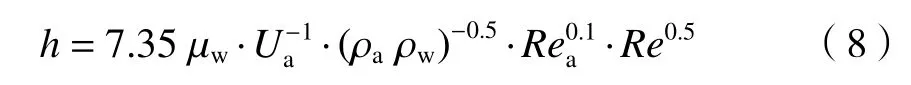
本文测量了8 个水膜雷诺数状态下10 个时刻的水膜高度分布,并将结果平均化处理得到平均水膜高度。平均水膜高度h¯与雷诺数的关系如图11所示,用幂函数拟合得到其关系式为:


图11 平均水膜厚度对比图Fig.11 Comparison of average film thickness
如图11所示,实验得出的拟合曲线与理论推导曲线整体趋势相近。但是水膜雷诺数的实测值略大于理论推导值,并且该趋势随水膜雷诺数的增大逐渐明显。这是由于随着水膜雷诺数的增大,水膜的流速增大,水膜流速增大到一定程度时形成的表面波为滚动不稳定状态。此时水膜的表面波将影响气−液界面剪切力τ的计算,随水膜雷诺数增大而增大,理论推导曲线与实验曲线差别逐渐增大。因此,当水膜雷诺数增大到一定程度时,需考虑水膜表面相位速度对水膜高度的影响。此外,本文的理论曲线基于一系列假设推导得出,这对比较结果也带来一定影响。随着水膜雷诺数的增大,水膜高度增大,DIP 投影网格清晰度降低,加大了图像互相关算法的误差,这也使得图像处理结果误差增大。
3.2 无量纲水膜高度结果验证
为进一步验证DIP 测量技术应用于平板水膜流动的可靠性与准确性,特引入无量纲水膜高度。将平均水膜高度与剪切应力相结合进行无量纲化,定义水膜无量纲高度h+为:


表1 列出了以往文献及本研究的无量纲水膜高度的计算模型,其中Kosky & Staub 模型[21]为水平冷凝环状流模型,Rishikesan 模型[4]为基于色散共焦位移计测量的平板水膜流动模型,Hughmark 模型[22]为等温条件下的上升流模型。与前两者比较,Hughmark 模型将气−液两相的质量流速、管直径和流体的物理性质作为研究变量来预测水膜高度,本文预测模型与之类似。各模型计算值结果如图12所示。可以看出,虽然本文研究对象与Rishikesan 模型的研究对象均为平板水膜流动,但是本文使用的DIP 测量方法与Rishikesan 模型的单点共焦位移计测量方法最终测量误差存在差别(如图7所示),从而导致这两种模型存在偏差。本文测量水膜高度方法虽与其他文献的测量方法不同,但应用到水膜无量纲高度的模型中,与其他研究模型计算结果的趋势具有良好的一致性,更为接近Hughmark 模型,误差在5%以内。
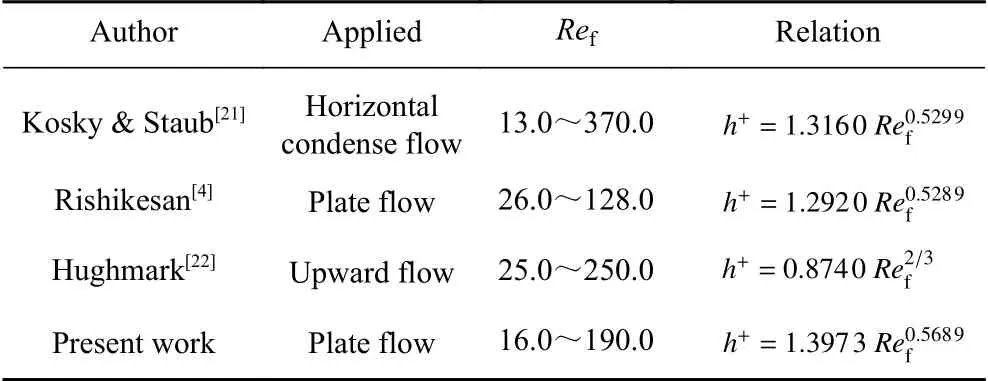
表1 无量纲水膜厚度模型Table 1 Dimensionless Film Thickness Models
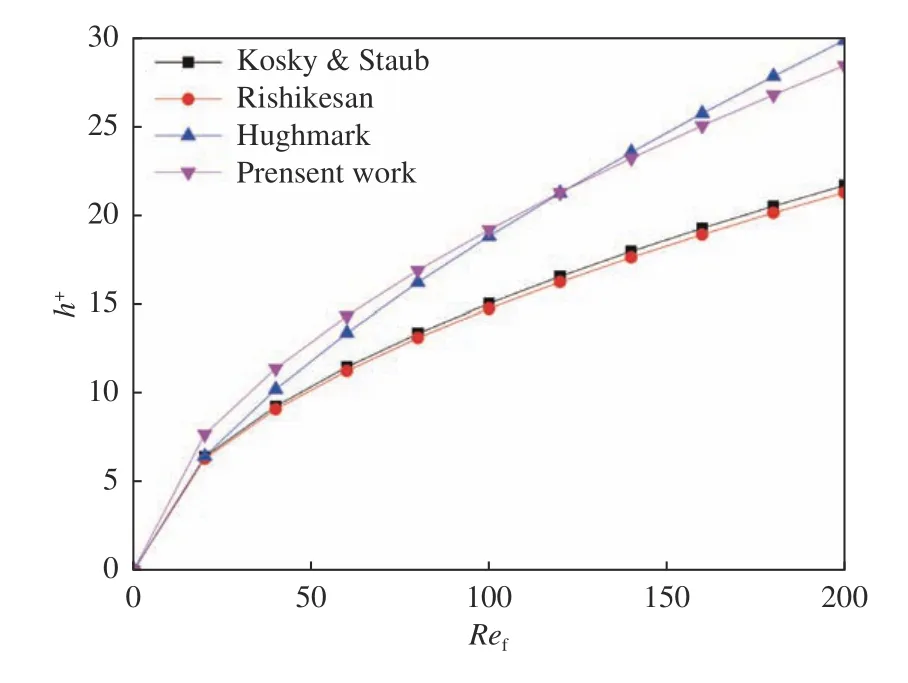
图12 无量纲水膜厚度对比图Fig.12 Comparison of Dimensionless Water Film Thickness
4 结论
本文介绍了可实现非侵入定量测量的DIP 技术,说明了其测量原理、标定方法,并将其应用于平板表面水膜流动的定量测量,最后将测量结果与理论推导和文献结果进行对比得到以下结论:
1)DIP 测量技术可对流体流动的三维全貌进行复原。本文复原了平板水膜表面波随雷诺数的形态变化。
2)DIP 测量技术拥有良好的精度。在本文的实验台参数设置下,DIP 系统的测量误差小于5%。高度在3 mm 以内的测量,DIP 测量技术精度优于色散共焦位移计。
3)平板水膜流动实验结果显示:在风速17 m/s状态下,随着水膜雷诺数的增大,平均水膜高度整体增大;当水膜雷诺数增大到一定程度(Ref>165.0),水膜向中间聚拢,呈现出中间区域高于两侧区域的现象。随着水膜雷诺数的增大,水膜表面波呈现出振幅逐渐增大、振动频率逐渐降低的波动特性。
4)测量与理论推导发现:水膜表面波相位速度的定量测量是影响本文平均水膜高度测量的关键因素,会导致实测值与理论推导值的差别随着水膜雷诺数的增大而增大。
5)无量纲水膜高度与水膜雷诺数的关系模型与文献中的模型吻合良好,再次证明了DIP 技术在流体薄膜测量中的可靠性与准确性。
