一种应用于水流的纹影特性光流测速算法

黄天立，王 倩

上海交通大学 机械与动力工程学院，上海 200240

0 引言

作为流动类型判断、压力计算等的基础数据，流速是流体力学研究中最为重要的参数之一。流速测量技术是开展流体相关实验研究和工程应用的重要技术手段，对于研究基本物理现象和深入解释流动机理具有重要意义。在过去几十年里，流速测量技术不断发展，经历了从介入式到非介入式、从单点到平面再到全场、从低速测量到超声速测量的过程[1]。传统的流速测量主要为介入式测量，包括皮托管（Pitot tube）、热线热膜风速仪（HWFA,Hot Wire Film Anemometer）等，不足之处是会对流场产生较大的扰动。近年来发展了基于图像处理技术的流速测量方法，包括粒子图像测速（PIV,Particle Image Velocimetry）、基于纹影成像的速度测量等。PIV 是目前最常用的全场测速技术，通过在流场中布撒示踪粒子，以脉冲激光片光源入射所测流场区域，采用相机连续两次或多次采集粒子图像，通过互相关算法求得流场速度分布。在示踪粒子浓度较低时，也可对单个粒子进行测量，即粒子跟踪测速技术（Particle Tracking Velocimetry,PTV）[2]。纹影成像基于折射率与密度梯度的关系将透明工质流动可视化，是一种常用的流场观察方法。近年来，有学者结合互相关算法和光流算法，探讨了利用纹影图像测速的可能性。与PIV 相比，纹影图像测速以普通光源代替激光光源，节省了成本，且无需添加示踪粒子，可以实现无扰动测量[3]。对于可压缩湍流边界层内的流动，因难以添加示踪粒子无法使用PIV 方法，采用纹影图像测速则可获得较好结果，已被应用于激波、边界层、带电流场及腐蚀性流场等的定性和定量研究中[4-6]。此外，纹影成像测速具有高帧频采样的独特优势，仅需普通光源（如LED、氙灯等）即可获得微秒级曝光时间，可采用高速相机的最高帧频。因此，研究纹影图像测速方法有助于推动流场测速技术的发展和测速方法的推广应用[7]。

基于纹影图像的测速方法主要分为互相关法和光流法两大类。互相关法将纹影图像中的显著运动结构（如涡团、边界）作为追踪对象，运用互相关算法计算速度场。Kegerise 等[8]进行了点热源的轴对称湍流羽流实验，通过PIV 方法测得中心面速度，并对互相关算法的积分效应进行了评估。结果表明，PIV 方法和互相关法的归一化平均流速剖面一致性较好。互相关法的偏差误差有两项，一是由窗口的平均效应引起，二是由纹影系统无法观测到过小的羽流边缘温度梯度引起，最终可能导致高达中心线速度10%的偏差误差。随机误差来自时间间隔的不确定性和互相关算法，局部流速的平均随机误差为7%～8%。根据偏差误差和随机误差得到羽流中心线上速度估计的总不确定度为8%，羽流边缘附近最大测量不确定度为中心线速度的10%～12%。

光流法基于物体在视网膜上的成像原理提出，能够实现运动目标的检测、跟踪等功能[9]，可以基于单个像素获得速度矢量，具有较高的空间分辨率和测量精度。目前应用最广泛的光流算法基于Horn 等[10]提出的刚体运动假设发展而来。光流算法假设运动物体在连续两帧图像上的亮度保持恒定，从而得到一个包含亮度与速度u、v的约束条件，即为物理约束条件。Horn 等[10]提出了邻域内像素点速度不能相差太大的假设，由此得出空间平滑约束条件，从而将速度求解问题转化为一个包含了物理约束和空间平滑约束的最优化问题，可以通过变分法对能量方程进行最小化得到速度场。由于光流法的约束条件是针对刚体性质提出的，Martínez-González 等[11]将传统光流算法应用于自然对流流场纹影图像，计算结果仅能显示主流运动趋势，准确度和精度均较低。

为得到更适用于流体性质的测速方法，许多学者对光流法的约束条件进行了改进。Suter[12]引入了二阶散度–旋度空间平滑约束形式，可根据运动特征调节散度和旋度项的相对比重，能较好地保留流体特性。Liu 等[13]针对纹影/阴影成像以及PIV 等流场可视化手段，推导了通用形式的投影运动方程，构建了具有流体特性的物理约束条件，误差分析表明，光流法的不确定度与图像亮度梯度成反比，与两帧连续图像之间的时间间隔成正比。Arnaud 等[14]结合纹影亮度方程与连续性方程推导了新的亮度守恒约束，采用二阶形式的空间平滑约束，提出了符合流体运动特点的纹影特性光流测速算法。Wang 等[15]在纹影特性光流测速算法中加入金字塔算法和鲁棒优化等算法，优化后的算法能够得到连续性较好的速度场，并能捕捉更多精细的流动结构。梅笑寒等[16]分析了纹影特性光流测速算法因权重系数取值不当而产生的两种错误，并给出了权重系数的合理取值范围。

上述研究大都针对气体流场，气体折射率与密度的关系满足Gladstone-Dale 定律[3]。目前针对液体流场的纹影测速方法还鲜见于文献。与气体不同，液体折射率与密度的关系更为复杂，由Lorentz-Lorenz公式联系，一般通过测量给出[17]。在液体中，水是流体研究中应用最为广泛的工质，关于水的密度的研究已经比较充分。因此，本文从水的折射率–密度关系出发，基于光流法推导适用于水的纹影亮度方程，构建新的物理约束条件，采用Wang 等[15]的优化算法求解速度场，对浮力羽流纹影图像进行分析，并与互相关算法、光流算法的计算结果进行对比。

1 算法原理

1.1 互相关算法

对于时间间隔Δt的图像序列，当Δt适当小时，第二帧图像相对于第一帧图像有微小位移和变形，此时两帧图像存在相关性。用互相关算法估计图像位移场，除以时间间隔Δt，即可得到速度场估计，这种测速方法称为“图像相关测速法”[8]，其算法原理如图1所示。

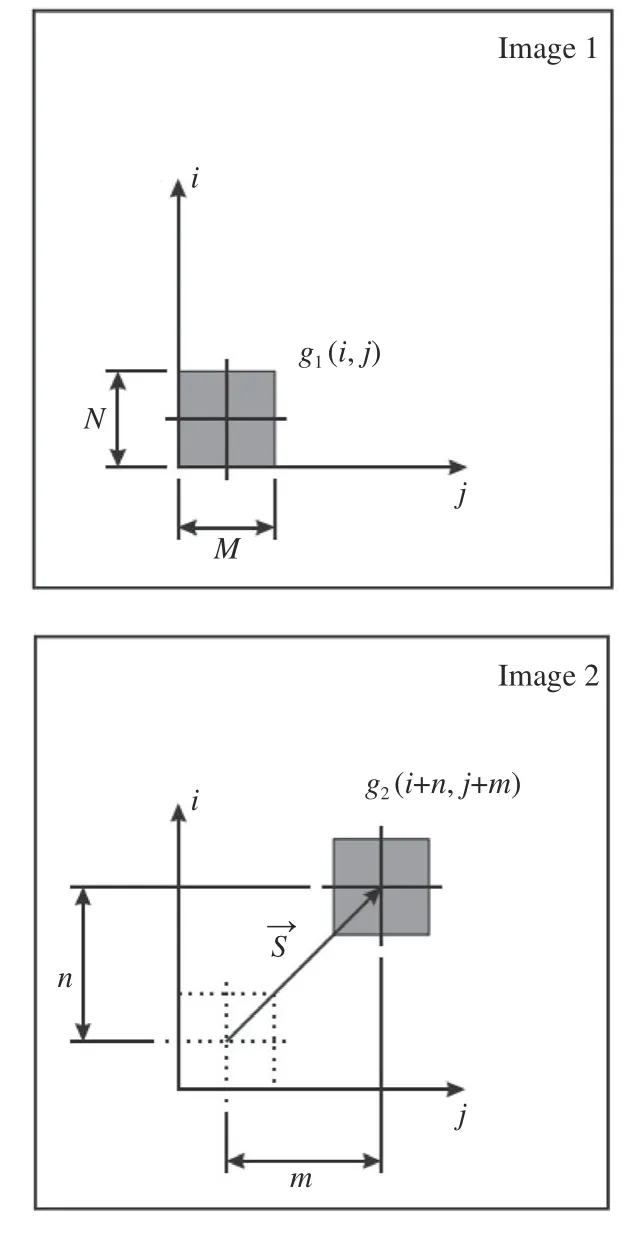
图1 图像相关测速法原理[8]Fig.1 Schematic of image-correlation velocimetry algorithm[8]

互相关算法是在两帧图像中划分若干窗口，通过计算窗口间的互相关函数（Cross-correlation function）最小值来得到窗口区域的最佳匹配关系，从而估计图像位移场。互相关函数的表达式如式（1）所示。式中，M和N表示在第一帧图像中选取的窗口区域大小为M×N个像素；（i,j）表示区域内某点坐标，g（i,j）表示该点的亮度值，m和n分别表示该点可能的水平位移和垂直位移；D（m,n）取最小值时，对应的m和n即为窗口区域最佳的位移估计。将整个图像划分为若干窗口，即可通过式（1）求得全场位移估计。

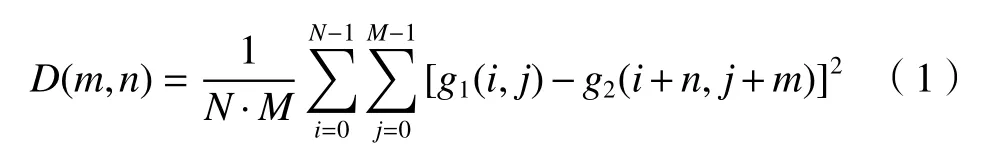
1.2 光流算法

光流算法假设图像亮度值I（x,y,t）是关于坐标（x,y）和时间t的连续函数，某一物体在t时刻和（t+dt）时刻的亮度相等：

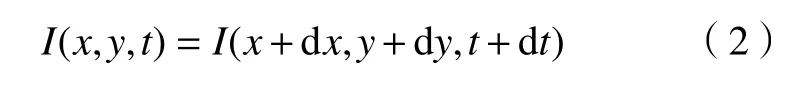
将等式右边进行泰勒展开，消去I（x,y,t），再除以dt，即可得到亮度守恒约束方程：

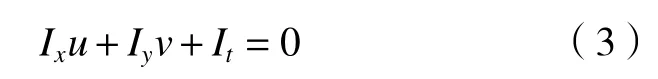
Horn 等[10]提出了空间平滑约束假设：相邻点具有相近的速度，u和v应满足方程：

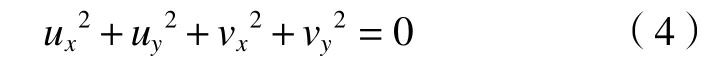
从而将速度场求解转化为一个最优化问题，构建能量泛函：

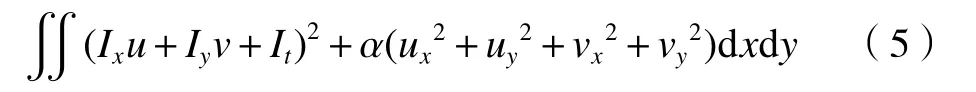
式中，α为正则项的权重，用于平衡正则项在能量泛函中的影响。将式（5）代入变分法中的欧拉–拉格朗日方程，得到两个等式：

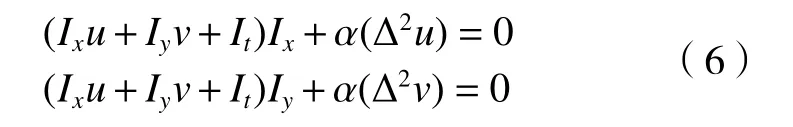
将等式离散化，再进行迭代求解，即可得到全场速度u和v。

1.3 液体纹影特性光流测速算法

在扩展光源纹影系统中，从光源发出的光束通过透镜后，形成平行光穿过测试区域，再由第二个透镜汇聚形成光源像，光源像经刀口遮挡部分光线后，在像平面上形成纹影图像。当测试区域的折射率均匀时，像平面的背景亮度为IK，其值与刀口的位置有关：

式中，h为刀口平面垂直于刀口方向上光源像的宽度，a为未被刀口遮挡的光源像宽度，I0为无刀口遮挡时的背景亮度，如图2所示。a越小，像平面的背景亮度越暗，纹影图像就越清晰、灵敏度越高。通常设置a/h= 0.5，此时刀口平分光源像。

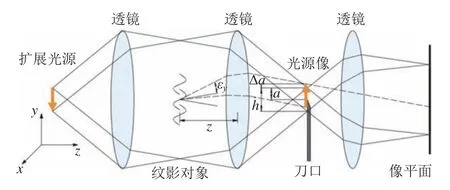
图2 扩展光源纹影系统示意图Fig.2 Diagram of schlieren system with an extended light source

测试区域中某点的密度变化会改变该点附近的折射率，经过该点的光线将发生偏折（偏折角为εy），光源像在垂直于刀口的方向上产生偏移Δa，被刀口遮挡的光线数量改变，使得像平面上该点对应位置的亮度发生变化[7]。亮度变化与折射率满足以下关系：

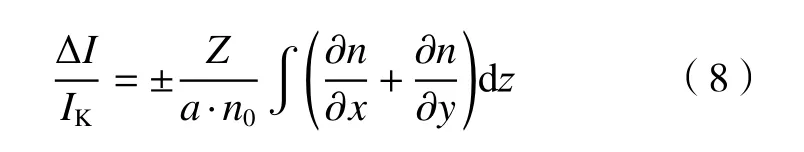
式中，ΔI表示折射率变化引起的像平面上的亮度变化，Z为测试区域距第二个透镜的距离，n为测试区域点（x,y,z）的折射率，n0为周围介质的折射率，z为刀口平面的法向，即光轴方向。

式（9）为Weiss 等[18]给出的水的密度ρ与波长λ、折射率n的关系式，相关具体参数如表1所示。在100 kPa 下、水温0 ～100 ℃时，水的密度如表2所示[19]。

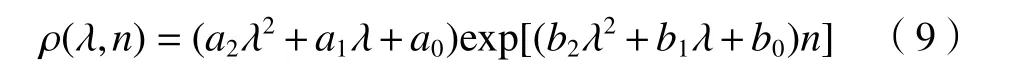
表1 与水的密度相关的参数Table 1 Coefficient related to the density of water

表2 水温0～100 ℃时水的密度Table 2 Density of water in the range 0-100 ℃

根据表2，当波长在可见光范围时，通过对数据点的拟合，可将式（9）近似化简为：

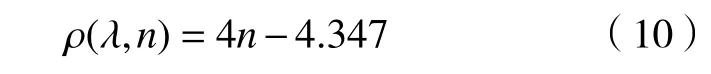
由此可以得到亮度变化与密度的关系：

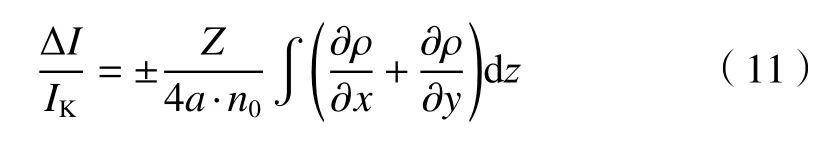
当测试区域为一个薄层时，光轴方向上的密度变化可以忽略，上式简化为：

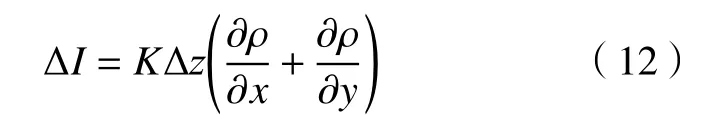
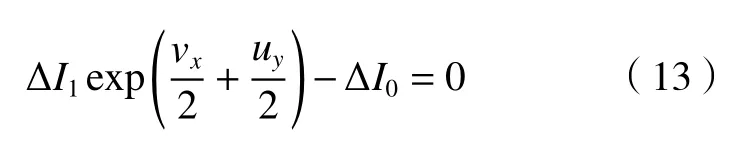
式中，下标0 和1 分别代表第一帧图像和第二帧图像，数据守恒项为：

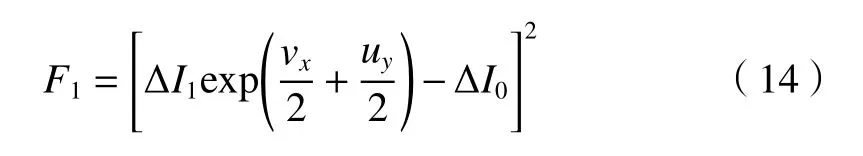
空间平滑约束建立了测试区域内相邻点的速度联系，光流算法中的式（4）可对低散度和低涡量速度场进行估计，但不适用于流体速度场。Suter 等[12]提出的二阶散度–旋度平滑约束被证实能够较好地保存流体特性，表达式如下：

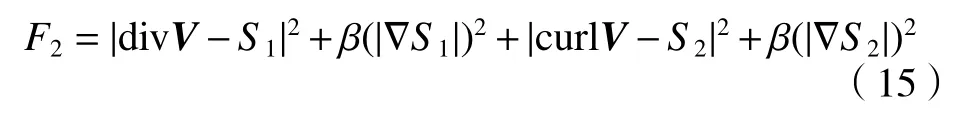
式中，F2为正则项，S1和S2为引入的两个标量场，作为散度、旋度的计算值以简化能量泛函。β为标量场的权重，β越大，速度场计算值越平滑；β越小，平滑约束越弱，可能造成速度场的剧烈变化。

根据数据守恒约束和空间平滑约束构建能量泛函：

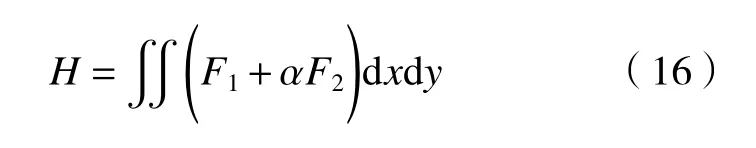
式中，正则项权重α用于平衡正则项F2在能量泛函中的影响。α取值过小时，正则项在能量泛函中比重较小，数据项易受噪声干扰，较弱的平滑约束可能引起计算发散。与传统光流法类似，应用变分法对式（16）进行最小化即可得到速度场，详见文献[20]。

2 实验与计算

2.1 实验装置

浮力羽流发生装置参考了Gono 等[21]的PIV实验台布置，主要由透明水槽、粒子混合腔、流量计、水泵和恒温水槽等组成，如图3所示。透明水槽盛装冷水，底部开口（边长2 cm）通过上升管道连接粒子混合腔，其后依次与流量计、水泵和恒温水槽串联。

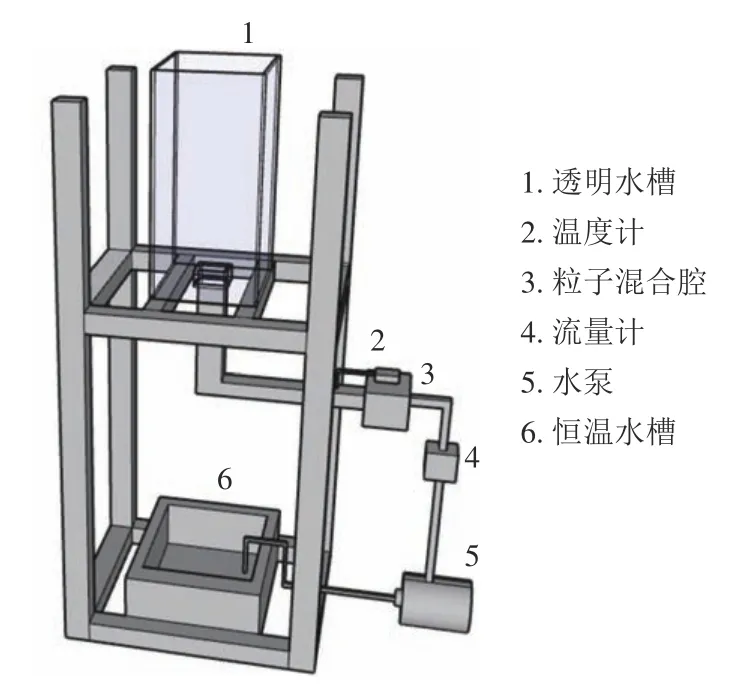
图3 浮力羽流发生装置示意图Fig.3 Diagram of buoyant plume generator

拍摄纹影图像时，混合腔内无需添加粒子，保持恒温水槽内热水温度恒定，通过水泵和流量计将热水以一定流量泵入粒子混合腔，待腔内热水温度稳定后，打开上升管道，热水从透明水槽底部开口缓慢流入，在浮力作用下形成羽流缓慢上升。实验工况为：混合腔内热水温度30 ℃，透明水槽中冷水温度15 ℃，热水流量保持为192 mL/min，透明水槽底部开口处热水平均速度为8 mm/s。

纹影光路采用了“Z”形双反射镜纹影系统，主要由点光源、聚光透镜、（刀口）狭缝、抛物面镜、刀口和高速相机组成，布置方案如图4所示。

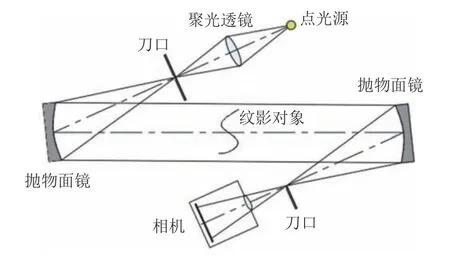
图4 “Z”形纹影装置示意图Fig.4 Diagram of Z-type Schlieren arrangement

在纹影系统中，抛物面镜之间的距离约为其焦距的2 倍，测试区域布置于平行光路中央。点光源发出的光线被聚光透镜汇聚后通过狭缝，经抛物面镜反射形成平行光穿过测试区域；受流场影响，平行光发生偏折，经抛物面镜汇聚后被刀口遮挡，最终在高速相机成像平面上呈现纹影图像。

以卤素灯作为实验光源，光源功率300 W。两个抛物面镜直径0.3 m、焦距3 m。相机为Photron FASTCAM SA-Z，图像尺寸为1024 pixel × 1024 pixel，采样频率500 帧/s。标定点距离100.0 mm（以千分尺测量），图像中两点距离802 pixel，由此计算得到图像空间分辨率为0.1247 mm/pixel。

2.2 计算方法

采集实验的纹影图像数据后，分别用互相关算法、光流算法和液体纹影特性光流测速算法（后文简称“液体纹影测速算法”）对图像进行计算。

互相关算法的计算由PIVlab 完成。PIVlab 是一个基于互相关算法的MATLAB 工具包，可用于数字粒子图像测速（DPIV）分析，也可用于其他环境（如细胞内流动、沙砾变形等）的分析[22]。PIVlab 的分析过程如下：首先对图像进行前处理，采用自适应直方图均衡化对图像进行增强，可将检测有效向量的效率提高4.7% ± 3.2%[23]；在计算环节，依次将窗口边长设置为64、32 和16 pixel，进行3 轮离散傅里叶变换，每轮结果在随后轮次中用于补偿窗口区域，降低由粒子位移引起的信息损失，同时提升分辨率[24]；最后手动设置速度阈值以过滤异常值。

光流算法采用Sun 等[25]的优化光流算法，综合平均端点误差为0.319 pixel/帧[20]。光流算法参数设置为：时间分辨率50 帧/s，空间分辨率0.1247 mm/pixel。

液体纹影测速算法的参数设置为：时间分辨率50 帧/s，空间分辨率0.1247 mm/pixel。多组计算结果表明，权重系数α= 300、β= 100 时能得到收敛的计算结果。

3 结果与分析

3.1 实验结果

高速相机在10 s 内记录了5 000 帧纹影图像，通过观察可知羽流呈现周期性变化，周期为1 s。分别进行瞬时速度场和平均速度场分析：分析瞬时速度场时，选取的两帧纹影图像间隔20 ms（如图5所示），分别以互相关算法、光流算法和液体纹影测速算法对两帧图像进行计算，导出速度矢量图、速度云图和涡量图；分析平均速度场时，选取100 对间隔为20 ms 的图像序列进行计算，对垂直方向的速度场v进行平均，导出平均速度矢量和云图。

图5 原始纹影图像Fig.5 Original schlieren image

3.2 瞬时速度场分析

互相关算法的计算结果如图6（a）所示。从速度矢量图可以看出，在浮力作用下，热流体在冷流体中向上运动，形成湍流结构。从速度云图可以看出，羽流速度由下至上逐渐增大，出现最大值后又逐渐减小，速度最大值约为0.04 m/s。为了清晰对比3 种方法的差异，将速度云图局部放大，如图7所示。从图7（a）可以看出，互相关算法的空间分辨率不高，边界层呈锯齿状，出现了一些速度与主流差距较大的块状区域。从涡量图则可以看出，局部出现了一些较大的涡量。

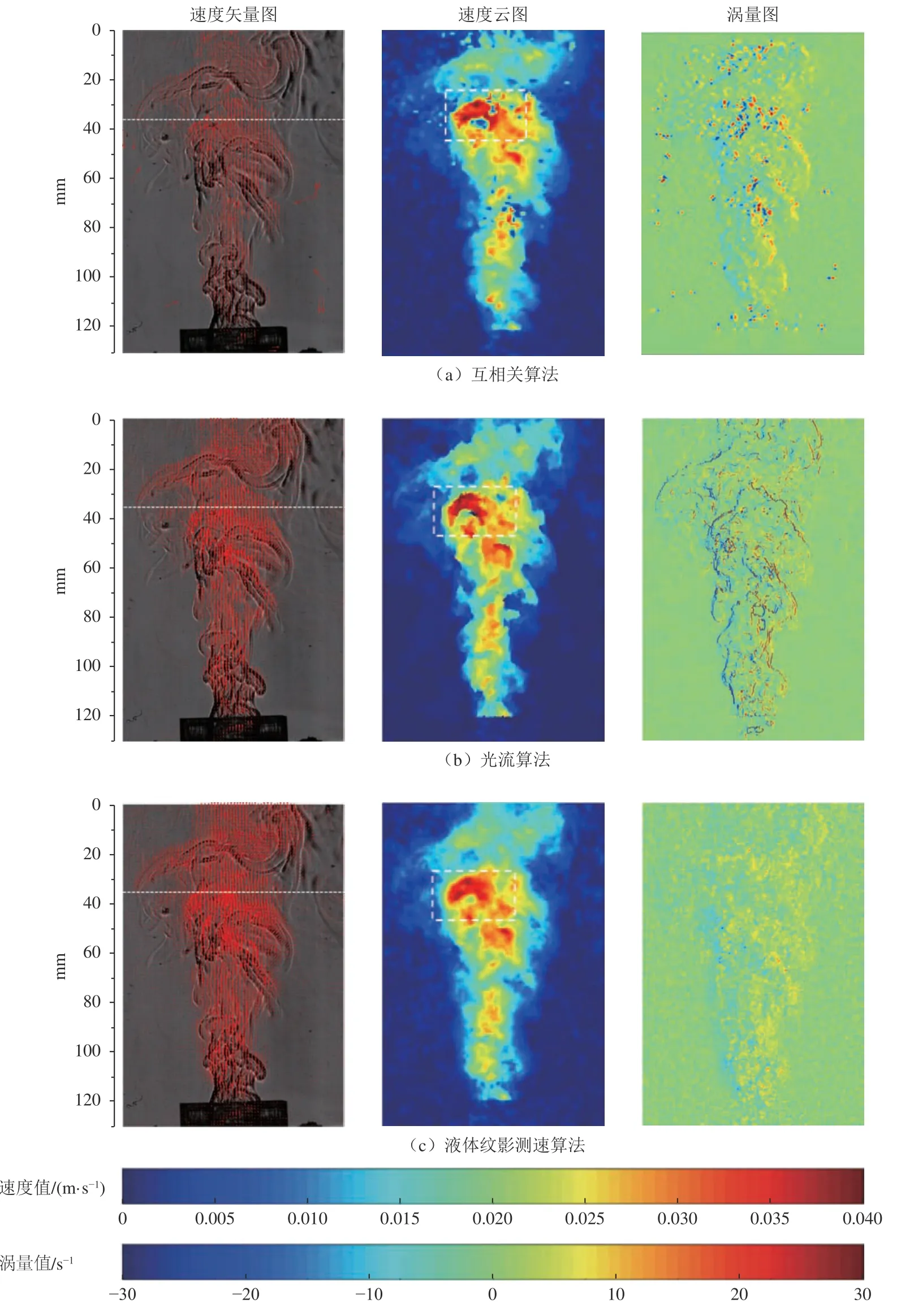
图6 3 种方法计算的流场速度结果Fig.6 Velocity results of three methods

光流算法计算结果如图6（b）所示。从速度矢量图可以看出，速度矢量基本位于主流范围内，在边缘处速度急剧减小，主流外部区域的速度接近于零。从图7（b）可以看出，速度等值区域呈块状分布，即在主流内部速度分布相对统一，而在边缘处变化明显，表现出较大的速度梯度。从涡量图可以看出，涡量沿流动结构边缘呈明显的线状分布，在边缘处有较大的涡量值，而在主流内部涡量较小，在高速区和低速区之间没有平缓的过渡。

液体纹影测速算法的计算结果如图6（c）所示。从速度矢量图可以看出，速度矢量在边缘处逐渐减小，即便是微弱的流动也能显示出速度矢量。在图7（c）中，没有出现过大的速度梯度，体现了流体连续变化的特性，而且流动结构的边界较厚，符合边界层的特点。从涡量图可以看出，涡量结果均匀分布于左右两侧边界，体现了流体的剪切和旋转特性。

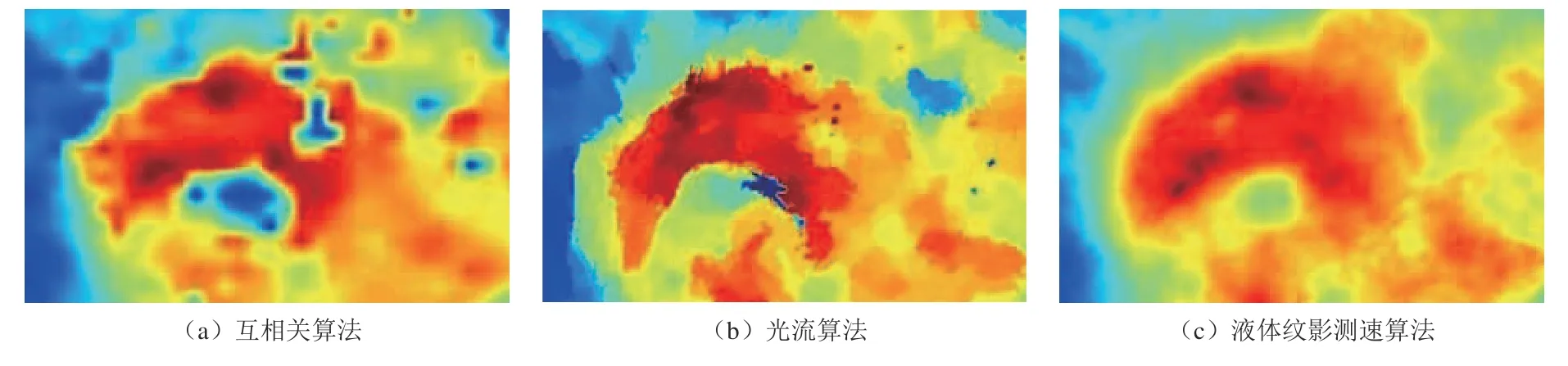
图7 3 种方法计算流场速度的局部展示Fig.7 Velocity contour of the selected part using three methods

提取垂直速度分量v沿图6 白色水平虚线的分布，如图8所示。通过比较速度分布曲线发现：3 种方法得出的速度值在整体趋势上较为接近，但在局部位置存在一定差异。互相关算法和光流算法均在20～30 mm 范围内表现出较大的速度梯度，在30～50 mm范围内出现了一些离群值；而液体纹影测速算法得到的速度场连续性更好，没有出现离群值。

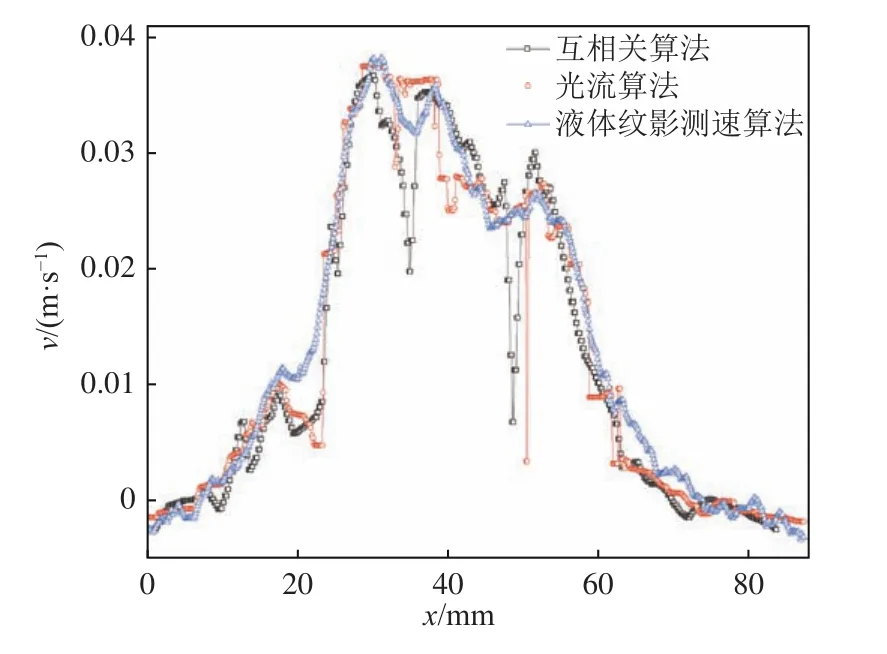
图8 垂直速度分量沿直线的分布Fig.8 Distribution of vertical velocity component along a line

对比3 种算法，由于窗口尺寸限制，互相关算法的精度和空间分辨率受到影响，当追踪对象超过窗口范围时易产生错误矢量；光流算法的空间平滑约束条件会使速度相近的相邻点的速度越来越相近，最后整体保持较为统一的速度，如同刚体一般，没有考虑流体特性；液体纹影测速算法采用二阶散度–旋度正则化导出的空间平滑约束条件，结合纹影亮度方程和流体连续性方程导出了适用于液体的物理约束条件，可以辨别流体内部的细微差异。通过对比可以看出，采用了具有物理含义特性方程的液体纹影测速算法具有更好的连续性，能捕捉更多流场细节，没有出现明显错误，整体性能优于另外两种算法。

3.3 平均速度场分析

采用3 种算法对100 对时间间隔为20 ms 的图像序列进行计算。测试流场的速度主要为垂直方向，因此导出y方向速度分量v的平均速度云图和矢量图进行对比，如图9所示。图中v0为热水在透明水槽底部开口处的平均速度，d为底部开口边长。

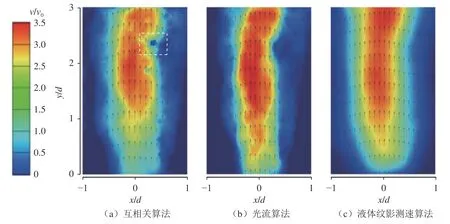
图9 垂直速度分量的平均速度云图和矢量图Fig.9 Mean velocity contours and vectors of vertical velocity component

从图9 可以看出：垂直方向上，垂直速度分量v随着与底部开口距离y的增大而增大，在y/d= 2 时达到最大值，之后随着y的增大而减小；水平方向上，羽流的宽度随着y的增大而增大，体现了垂直于中心线的动量扩散。

互相关算法得到的平均场如图9（a）所示，白色虚线框内部区域显示计算出现了离群值，此外，在y/d< 1 的区域，速度值与其他两种方法相比偏低；光流算法得到的平均场如图9（b）所示，羽流边缘区域速度梯度仍然较大，过渡不平缓，主流区域速度略高于其他两种方法；液体纹影测速算法得到的平均场如图9（c）所示，速度场近似于轴对称分布，没有出现离群值，羽流边缘区域速度梯度较光流算法更小，速度缓慢减小。上述对比结果表明，液体纹影测速算法的计算稳定性以及对流体运动特性的体现优于其他两种方法。

4 结论

本文提出了一种基于高速纹影系统的水流流场测速算法。应用该算法计算了浮力羽流速度场，与互相关算法、光流算法的计算结果进行了对比。该算法结合纹影亮度方程和流体连续性方程导出了适用于水流的物理约束条件，采用二阶散度–旋度正则化作为空间平滑约束条件，计算结果体现了流体内部的细微差异，得到了边界层速度。与光流算法相比，该算法能捕捉到微弱的流动结构，保留更多细节，避免了过大的速度梯度；与互相关算法相比，该算法精度和空间分辨率更高，更加稳定，不易产生错误矢量。