谐波平衡法在压实土体参数识别中的应用研究

李光英

（北京华商远大电力建设有限公司，北京 100070）

0 引言

压实质量连续检测技术基于振动轮—土系统动力学模型，通过对压实过程中振动轮的加速度信号进行实时分析来得到土体的压实指标值[1-2]。与传统抽样“点测法”相比，压实质量连续检测技术具有压实状态实时显示、全过程压实质量监控等优点，近年来，此技术在土体压实方面已经得到了广泛的应用[3]。

建立准确反映土体压实状态的指标是土体压实质量连续检测技术的重要内容，许多学者在此方面已进行了大量的研究。Thurner H 等[4]首先通过现场试验，分析了土体压实状态和振动轮加速度基频及一阶谐频的关系，提出CMV 指标并验证了其适用性。但由于CMV 指标仅包含振动轮加速度信号的一阶谐波，当土体在松散状态时，其可靠度较低。Thompson M 等[5]基于经典轮-土动力模型，定义压路机传到土壤中能量的大小为指标ω，ω 值越大，则土体状态越密实。Mooney M A 等[6]根据加速度信号的频谱提出了总谐波失真指标THD，但由于此指标对土体压实状态非常敏感，其适用性有待进一步验证。Vennapusa P K R 等[7]基于经典轮-土动力学模型，绘制压实过程中轮-土接触力和振动轮竖向位移关系曲线，并定义此曲线的割线模量Evib来反映土体压实状态。Facas N W 等[8]提出利用土体刚度指标评价土体压实状态的思路，并根据轮-土接触力和振动轮竖向位移曲线，定义最大位移对应的接触力与最大位移的比值为指标k，但所求k 值并非真实的压实土体刚度。窦苏广等[9]基于谐波平衡对非线性参数进行识别，提高了识别的精度。孙广利等[10]对土钉强变形进行模拟，得到了滑移区域和安全系数。

上述指标中，CMV，THD 指标仅基于振动轮加速度信号频谱分析来判定土体压实状态，并无明确的力学意义。Ω，Evib和k 虽然基于经典振动轮-土动力学模型，具有明确的力学意义，但由于从能量角度或从力-位移曲线得到相应指标，并未充分提取振动轮的加速度信号信息。

为此，本文利用土体刚度作为评价指标的思路，基于经典振动轮-土动力学模型，引入谐波平衡识别法识别土体参数。对振动轮加速度信号进行快速傅里叶变换，建立土体参数的识别方程并利用最小二乘法进行求解，得到具有明确力学意义且包含振动轮加速度信号高阶谐波信息的土体压实状态评判指标——土体刚度指标ks，且此ks值为真实的土体刚度值。最后通过仿真试验对此法识别精度进行分析，验证了谐波平衡法在振动压实土体参数识别中的可行性。

1 压实质量连续检测技术

1.1 原理

传统压实质量检测方法基于抽样检测法，费时费力、代表性差且不能实时监控压实质量。由于压实计和微电子技术的发展，瑞典的GEODYNAMIK和德国的BOMAG 公司于20 世纪90 年代共同提出了压实质量连续检测的思想，并已应用于道路、铁路路基、大坝等压实作业中。安装于压路机上的GPS 接收机，通过GPS 卫星实时获取土体对应的坐标。另一方面，安装于压路机振动轮上的加速度计用来获取压实过程中振动轮的加速度，控制器通过对此加速度信号进行分析处理，实时显示相应的压实指标值及土体压实状态，实现压实质量连续检测。电台负责将压实过程中的数据汇总传送到基站，实现压实作业远程控制。

1.2 土体刚度对检测指标的影响

土体压实过程中，随着土体逐渐密实，土体刚度随之增大。而振动轮加速度响应会随土体刚度增加而含有更多的谐波，具体见图1。

图1 土体不同压实状态对应的频谱图

由图1 可知，在压实过程中振动轮加速度信号频谱图会随着土体刚度变化发生实时的变化，而压实指标CMV，CCV 仅分析了加速度的部分谐波，不能准确反映土体处于松散（仅含基频）或密实（含高次谐波）状态时的压实情况。所以，利用土体刚度指标实时评价土体压实质量是一个更合理的方法。

2 振动压实过程土体参数识别

2.1 轮-土动力学模型

利用谐波平衡识别法识别压实土体参数时，需确定合理的振动轮-土动力学模型，本文采用经典振动轮-土动力学模型[8]。假设轮-土始终接触，模型简图及受力分析如图2 所示。

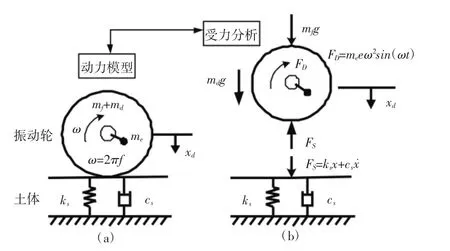
图2 经典振动轮-土动力学模型及受力分析

由图2 列出该模型的动力学方程，见式（1）~（3）：

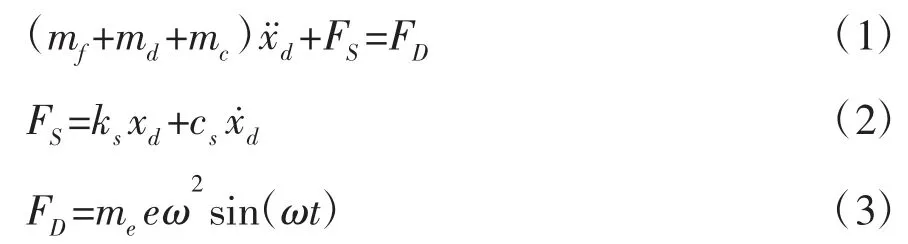
式中：mf，md，me为压路机机架、振动轮与偏心块的等效质量；xd为振动轮位移；ks为土体的刚度；cs为减振器与土体的阻尼；ω 为激振器的角速度；FD为偏心块产生的激振力的幅值；FS为轮-土接触力。

将式（1）改写为动力方程标准形式，如式（4）：

2.2 识别方程建立

由于压路机激振力FD为周期激励，由式（4）可知也为周期响应，满足运用谐波平衡识别法的条件[9]。为了建立质量比μ，固有频率ω0的识别方程，在激振力FD的一个激励周期[0，T]内，将及 λsin（ωt）展开成傅里叶级数形式，见式（5）~（6）：

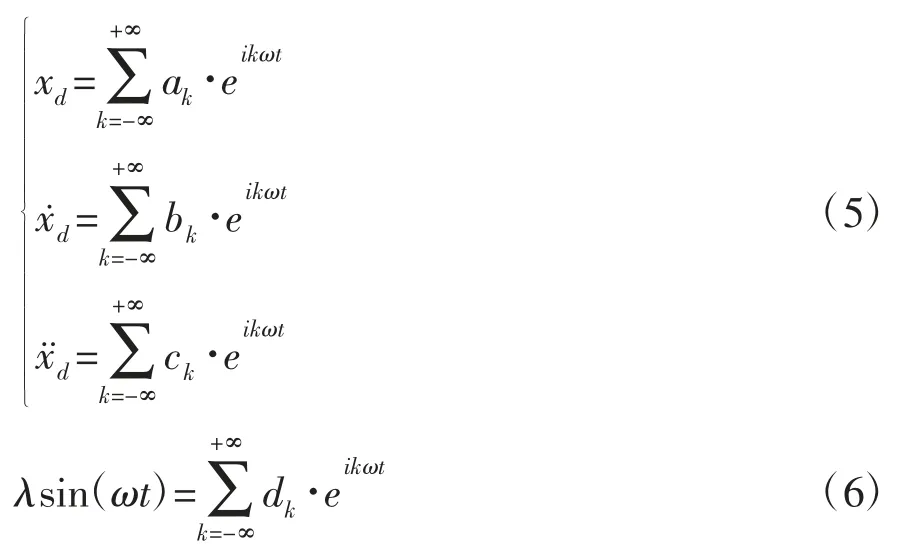
振动轮加速度及 λsin（ωt）的傅里叶系数 ck，dk计算如下：

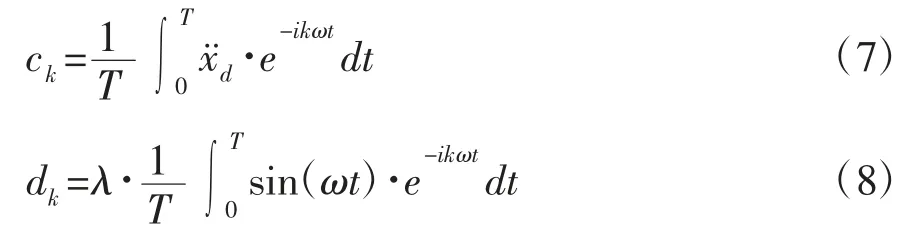
由于压实质量连续检测系统采用加速度计量，可实时获取振动轮加速度信号，故振动轮位移与速度的傅里叶系数ak，bk可由加速度傅里叶系数ck推导得到，具体见下式。

将式（5）~（6）代入式（4），可得下式：

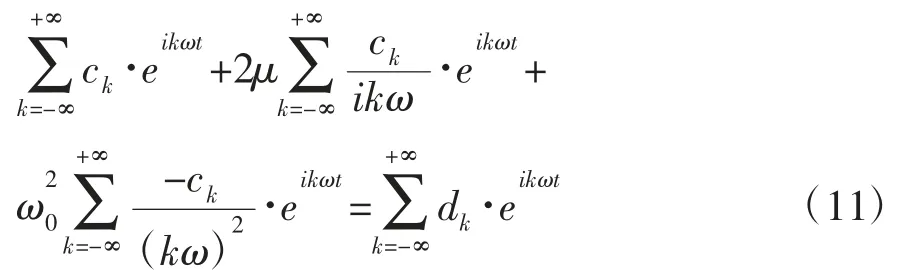
根据振动轮-土系统响应的第k 阶谐波平衡，式（11）可改写为：

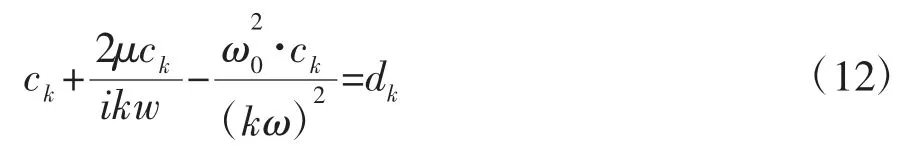
故式（11）或（12）即为所需识别的土体参数质量比μ，固有频率ω0的识别方程。

2.3 土体参数求解

由于快速傅里叶变换存在的误差，式（12）可通过最小二乘法进行求解，定义式（13）：

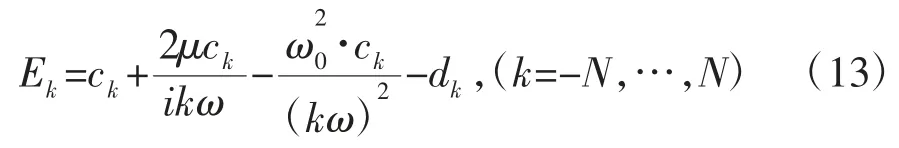
用式（14）表示式(13)的误差平方和：

分别取谐波数k=-N，…，N，就可以得到2N+1个方程来求解待定参数，实现参数识别：

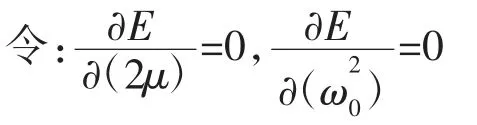
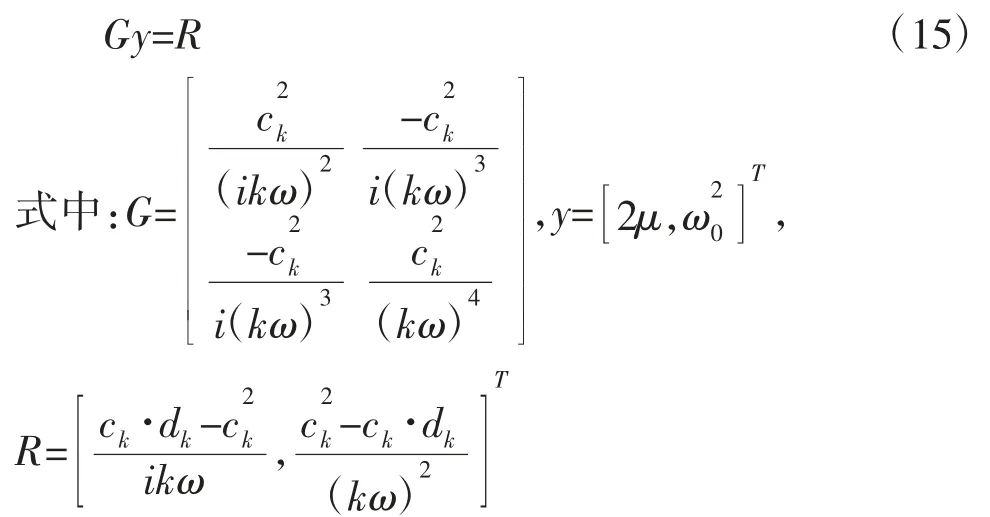
求解式（15）的方程组，可求得质量比μ，固有频率 ω0的值，由式（4）即可得到土体参数 ks，cs。

2.4 土体参数识别算法

由上推导可知，利用谐波平衡识别法识别土体参数大致可分为振动轮-土动力模型选取、振动轮-土系统动力响应傅里叶变换、最小二乘法求解待定参数3 个过程。根据下述算法思路，可编制相应的程序进行土体参数识别。

a) 确定振动压路机的参数：mf，md，me和 FD。

b) 获取并输入压路机激振力的一个激励周期[0，T]内的激振力信号及振动轮加速度信号。

c) 对激振力及加速度信号进行快速傅里叶变换，定义所需最大阶数N，并求得振动轮加速度傅里叶系数{c-N，c-N+1，…，cN-1，cN}及激振力傅里叶系数{d-N，d-N+1，…，dN-1，dN}。

d) 根据{c-N，c-N+1，…，cN-1，cN}及{d-N，d-N+1，…，dN-1，dN}，求得式（13）的系数矩阵 G，y，R。

e) 调用最小二乘法程序，根据所求系数矩阵G，y，R，识别出参数 μ、ω0。

3 参数识别仿真实例

3.1 模型参数选取

为了模拟压路机现场压实工况，mf，md，me，ω 及FD采用龙工LG520A 型号压路机实际施工时的数据。

同时，为了使模拟更加接近实际工况，模型中土壤的刚度ks及阻尼cs根据半无限弹性锥模型进行计算，具体如下：

式中：G 为土体最大剪切模量；ν 为土体泊松比；a 为轮宽度的 1/2；b 为接地印痕宽度；ω 为含水率；ρd为土体密度。G，ν 等各个参数根据参考文献[11]进行选取，ν=0.35，G=6.72 Mpa。

最终确定的仿真模型参数汇总于表1。

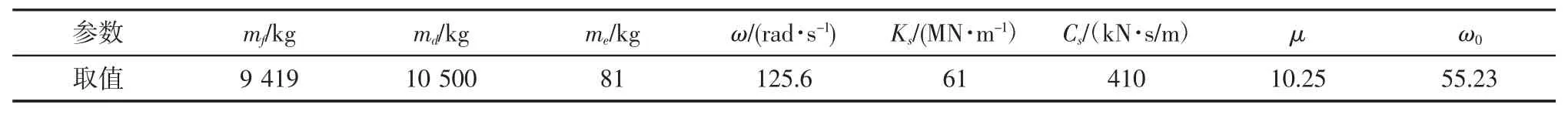
表1 动力模型参数取值

3.2 识别过程

将表 1 参数代入式（2），并设定初始值 xd（0）=0，x¨d（0）=0.1，步长为 0.001，利用龙格-库塔法求解此动力方程，得到振动轮加速度信号如图3 所示。将得到的振动轮加速度信号进行快速傅里叶变化，得到加速度相应的谐波分析图如图4 所示。

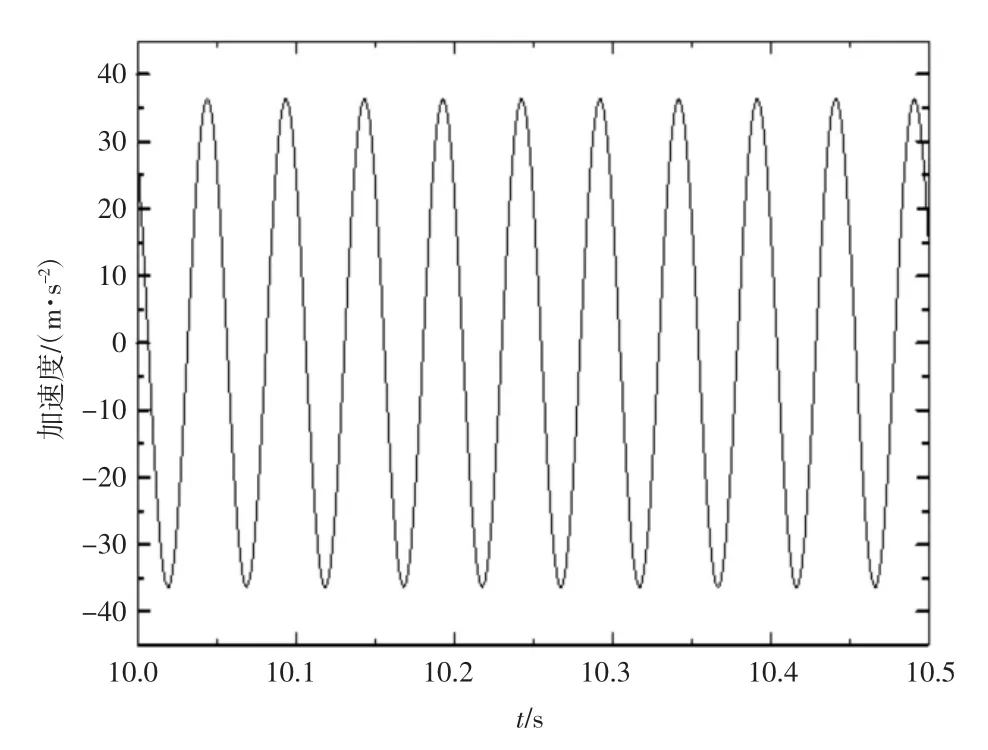
图3 振动轮加速度时间历程图

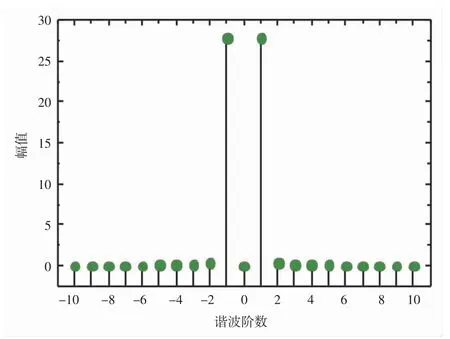
图4 振动轮加速度的谐波分析图

3.3 识别结果及分析

调用最小二乘法程序，求解得到动力模型参数μ，ω0识别结果，根据 μ，ω0推算出土体参数 ks，Cs值。识别结果及误差分布见图5~图6，选取部分谐波数对应的结果汇总于表2。

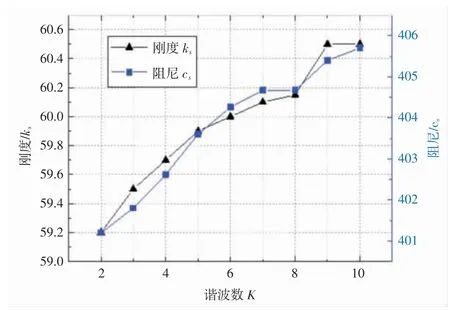
图5 刚度、阻尼识别结果分布图

图6 刚度、阻尼识别误差分布图

利用谐波平衡识别法识别土体参数，最终得到质量比μ，固有频率ω0并最终球的土体参数刚度ks和阻尼Cs的值。刚度和阻尼随着谐波的增大呈现增大的趋势，而两者的识别误差则随着谐波的增大而减小。

由表2 可得，真实值与采用谐波平衡识别法得到的结果比较相近，识别结果误差均＜3%，且识别误差随着谐波数的增加而递减。

表2 动力模型参数识别结果

为进一步验证参数的精度，将误差最大（K=2时）的识别结果代入原动力方程中进行仿真，并对比识别后的轮-土系统和真实轮-土系统的一个周期内的加速度信号和相图，具体如图7~图8 所示。

由图7 相似度矩阵可知[12]，振动轮加速度真实解与识别解的相似度为0.994 5，非常接近1，说明利用识别的土体参数得到的振动轮加速度信号与原加速度信号非常相似。图8 中两相图的相似度为0.996 2，进一步说明根据识别参数求解得到的振动响应与真实响应非常相近。

图7 振动轮加速度时间历程图

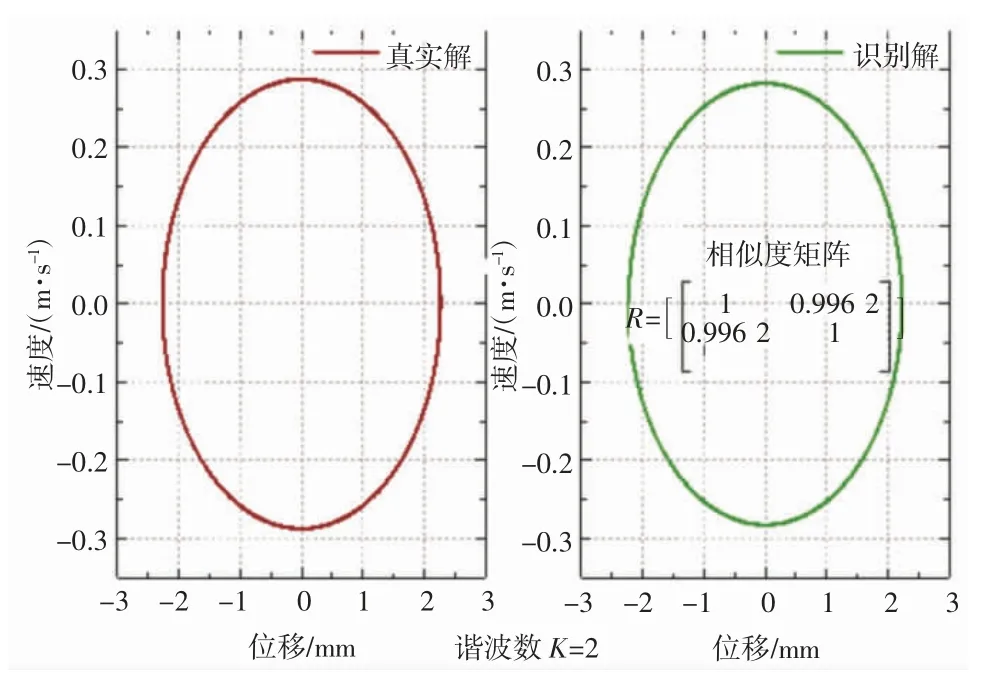
图8 轮-土系统真实解与识别解的相图

由此得到结论，用谐波平衡识别法得到的土体刚度指标ks具有高可靠性，且具有明确力学意义，能够准确反映土体的压实状态，且由于ks考虑了高阶谐波信息，与仅仅考虑低阶谐波信息的CMV 与CCV 等指标相比，能够适用于更多土体状态的评价。

4 结论

1）在分析现有压实质量连续检测指标存在不足的基础上，引入谐波平衡识别法，利用快速傅里叶变换和最小二乘法，推导出压实土体参数识别方程，并编制了相应识别程序。

2）仿真试验结果表明所有识别误差均＜3%，且识别误差随着谐波数的增加而递减，说明该识别程序具有很高的识别精度。

3）将识别的土体参数代入原动力方程，得到的振动轮加速度信号与原加速度信号的相似度为0.994 5，由此验证了利用谐波平衡法识别的土体参数具有很高的可靠度，可准确反映土体的真实参数。

4）与现行指标相比，谐波平衡法识别的土体刚度指标ks既有明确的力学意义且含有加速度信号的高阶谐波信息，能够更加真实的反映土体压实状态，该土体刚度指标可以为的土体压实质量连续检测提供新参考指标。

5）本文的土体刚度指标是基于经典轮-土动力学模型提出的，未考虑土体的非线性特性，下一步研究可在考虑土体非线性特性的基础上识别出更符合实际压实工况的土体刚度指标。