基于GO法融合共因失效的接触网可靠性分析

刘仕兵，李 俊，仇智圣，马志方

(华东交通大学电气与自动化工程学院，江西 南昌 330013)

1 引言

随着我国电气化铁路建设的普及，特别是高速铁路的迅猛发展，列车是否能安全平稳运行，得到了社会的广泛关注。无备用的接触网系统是整个供电系统的薄弱环节[1]，考虑到牵引供电系统运行的可靠性和经济效益，有必要对接触网的可靠性进行充分地分析。

我国科研人员对接触网可靠性的研究起步于20世纪90年代。万毅等[2]采用马尔可夫理论和数理统计的原理，建立关于接触网可靠性分析的数学模型，为接触网可靠性分析提供了一种有效方法。王佳培等[3]把贝叶斯网络法和故障树分析法结合起来，建立接触网系统的贝叶斯网络模型，并对其关键元部件进行了可靠性分析。谢将剑等[4]基于遗传算法，建立了威布尔分布可靠性模型，并计算了牵引供电系统的有效寿命；赵琼等[5]将故障树法运用到接触网可靠性分析中，并进行了定量和定性分析，但计算过程较为复杂。陈民武[6]将GO法应用到牵引变电所的可靠性评估中，建立基于GO法的可靠性模型，找出了牵引变电所中的薄弱环节。

以上研究对接触网可靠性评估具有一定的参考价值，但接触网系统的全部设备均在户外运行，受环境的影响比较大，在恶劣环境的情况下，可能造成接触网系统2个以上部件同时失效，如果没有考虑共因失效，将造成模拟值与实际值之间产生一定量的误差。接触网系统属于可修系统，本文考虑系统各部件之间的共因失效，选取共因失效β因子搭建模型，结合Markov模型，导出可修部件的共因失效概率随时间t的近似表达式，并建立系统GO图。用MATLAB绘制出系统相应的可靠度变化曲线，计算出各可靠性指标，通过定性分析，找出接触网系统的薄弱环节。

2 共因失效

对于一些复杂系统，共因失效(CCF)是由环境、设计和人为因素等方面造成2个或2个以上部件同时失效。分析系统可靠性时，假如不考虑系统存在的相关性，认为系统各单元发生故障时是相互独立的，则分析结果容易产生一定的偏差[7]。一般分析共因失效的模型有：β因子模型、α因子模型、多希腊字母模型、二项失效率模型等。

假设系统中某一部件总的失效概率Qt由共因失效概率QC和独立失效概率QI组成。通过引入β因子，表示某一部件共因失效率与总的失效概率的比值[8]

Qt=QI+QC

(1)

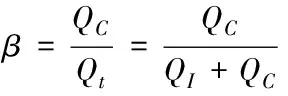
(2)

当部件使用寿命服从指数分布时，假设共因失效故障率λC和独立失效故障率λt为常数，且数值较小，则

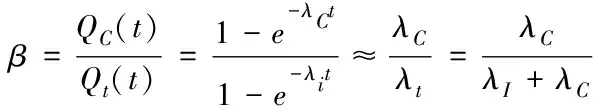
(3)

3 基于GO法的共因失效模型

3.1 GO法理论基础

GO法是一种系统可靠性的分析方法，其分析过程以成功为导向，通过对GO模型的计算确定系统成功概率。GO法根据GO图对系统进行可靠性分析，通过对系统特性的分析，确定系统逻辑框图，并按相应规则绘制出GO图，GO图与系统图基本处于一一对应的关系。GO图中，操作符表示系统中的单元或者是各单元之间的逻辑关系；信号流的作用是连接操作符，表示信号的输入和输出。不同类型的操作符代表不同的功能和运算规则。根据GO图及操作符的运算规则能实现系统可靠性分析的GO法分析。

GO法起源于美国Kaman科学公司，美国军方用于分析武器系统的安全性和可靠性[9]。GO法具有通用性、简洁性和高效率、低成本等优点，在航天航空、核电站、石油化工、军工及交通物流等领域的可靠性和安全性评估中得到广泛应用[10-12]。本文将基于GO法考虑共因失效，对电气化铁路接触网系统进行可靠性分析。

3.2 考虑共因失效的GO法算法

GO法根据GO图计算系统平均工作概率，并得到系统可靠性参数。工程可修系统通常是服从指数分布的，考虑系统中存在m个共因失效组，各组包含2个或2个以上的共因失效单元，由GO法导出系统含有共因失效的成功概率R

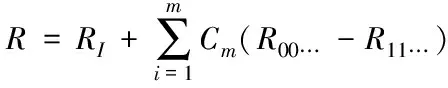
(4)

式中：RI表示系统不考虑共因失效的成功概率，Cm表示第m组共因失效概率，R00…和R11…分别表示共因组内所有单元成功概率都取0和成功概率都取1时，系统的成功概率。

考虑A、B两个可修部件存在共因失效，共因失效故障率为λC，A的故障率λA=λ1+λC，维修率为μA；B的故障率为λB=λ2+λC，维修率为μB。有2个部件的共因失效组，共有5种状态，状态0：两部件正常工作；状态1：B正常工作，A发生故障；状态2：A正常工作，B发生故障；状态3：A、B发生共因失效状态4：A、B两部件非共因的同时失效。根据Markov理论，当Δt很小时，从t到t+Δt的状态转移图，如图1所示。

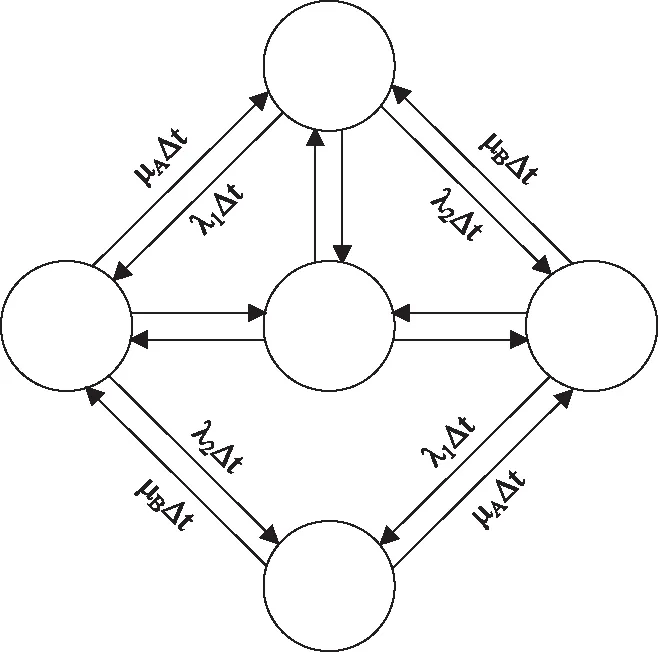
图1 两可修部件系统状态转移图

若初始时刻，两部件处于共因失效的概率为γC，则A、B发生共因失效的概率随时间t的表达式为

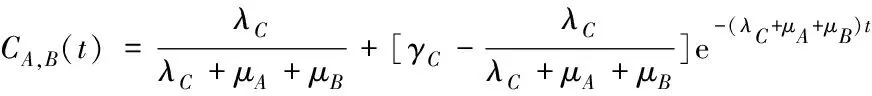
(5)

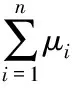
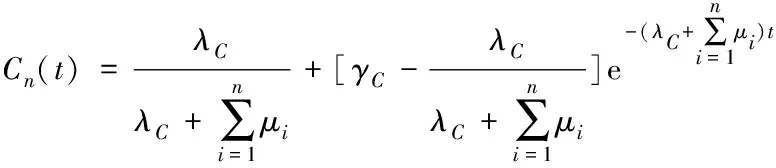
(6)

4 实例分析

接触网系统具有可修复性，属于可修系统，在系统的可靠性分析中，假设系统是服从指数分布的。接触网系统由接触线、承力索、吊弦、线夹、定位装置、斜腕臂、水平拉杆、绝缘子、承力索座、定位环、套管、支柱与基础等几部分组成。只有当所有部件处于正常工作状态，整个系统才能正常运行，若任何一个部件发生故障，系统将停工，因此这些部件在逻辑上是串联的。以某电气化铁路接触网系统为例，其示意图如图2所示。

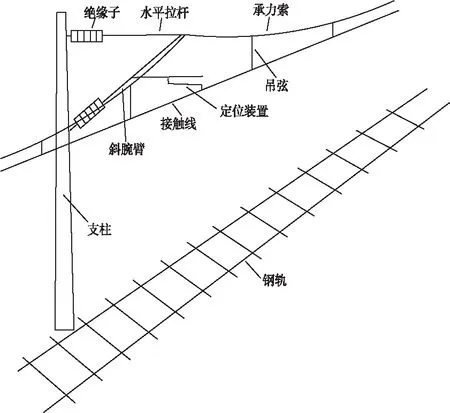
图2 电气化铁路接触网系统示意图

对各部件的故障和维修情况进行记录，可以得到每个部件的故障率和维修率数据，本文采用文献[13]的统计数据，如表1所示。

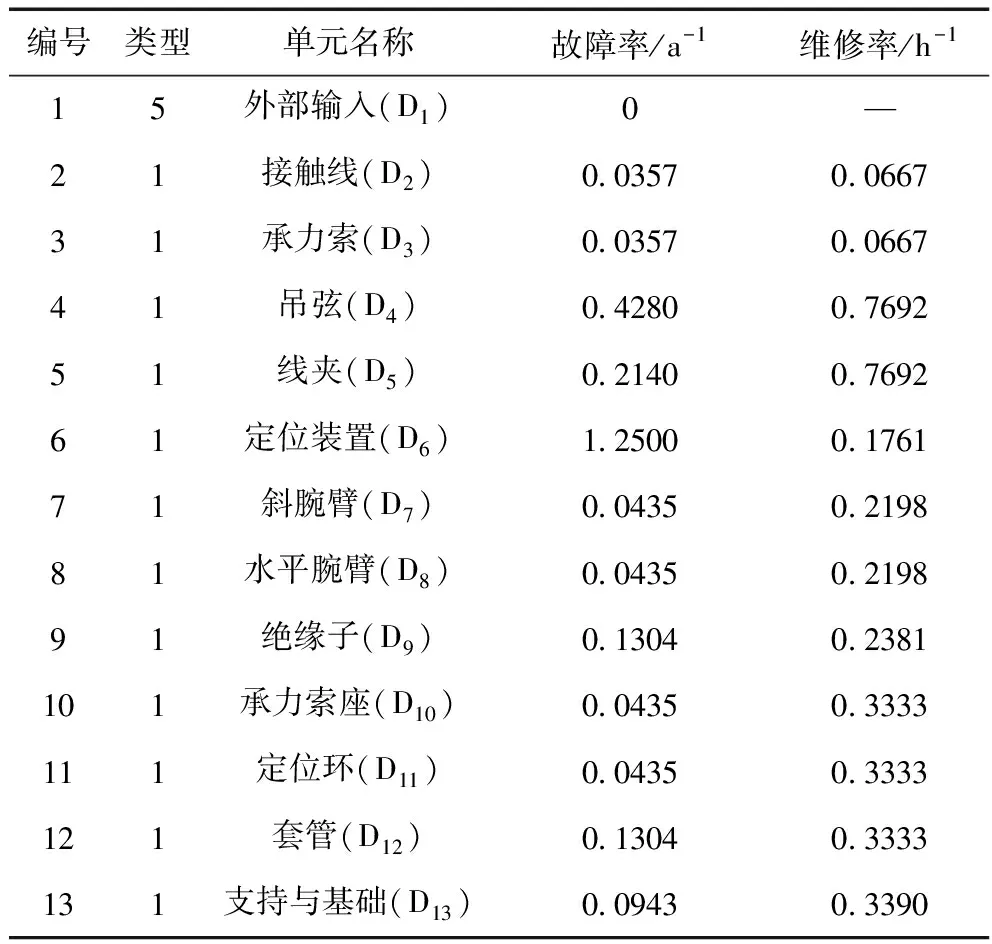
表1 接触网系统可靠性参数

4.1 建立考虑共因失效的接触网系统GO图

经过对接触网系统结构特性的分析，建立接触网系统等效失效模型，如图3所示。

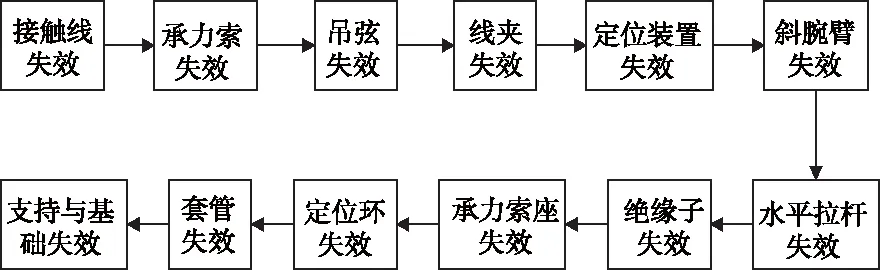
图3 电气化铁路接触网系统等效失效模型

根据接触网系统等效失效模型，按一一对应原则，建立系统GO图，如图4所示。操作符内的M-N，M表示操作符的类型，N表示各单元编号，具体类型及编号见表1。接触网系统由牵引变电所提供电能，所以用信号发生器(类型5)表示电能输入，作为初始输入信号；其余部件只有成功和故障两种状态，用类型1操作符(两状态单元)即可。GO图中的信号流“13”是系统的最后输出，表示整个系统的成功概率。本文由于不分析牵引变电所的可靠性，故假设信号发生器的成功概率为1。

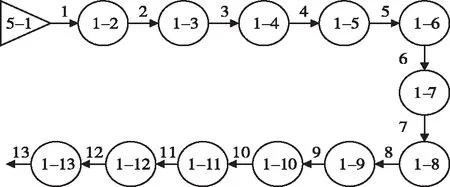
图4 接触网系统GO图

接触网的某些部件发生故障而处于故障状态，其它没发生故障的部件也随即停止运行，并且工作状态维持不变，直到故障部件成功修复，这些部件才能恢复正常工作[14]。因此这些部件不是独立的，其能否正常工作与其它部件是否发生故障有关，具有停工相关性，且停工故障次数I=1，此时两状态单元输出信号的故障率与等效维修率为

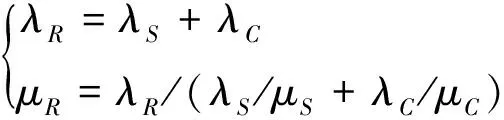
(7)

式中：λC，μC为操作符本身故障率与修复率；λS，μS为输入信号故障率与修复率；λR，μR为输出信号故障率与修复率。

4.2 接触网可靠性定量分析

4.2.1 未考虑共因失效的接触网成功概率

在不考虑共因失效的情况下，接触网可靠性定量分析是通过GO图算出系统的成功概率及各可靠性指标。建立GO图后，输入故障率和维修率数据，按信号流方向逐个对操作符进行GO运算，直至系统的输出信号，得到系统的可靠性参数。

在接触网系统GO图中，操作符编号2～13的12个单元组成串联结构，且都是两状态单元。因为停工故障次数I=1，所以在未考虑共因失效时，串联结构不会2个以上单元同时出现故障。因此串联结构的等效故障率是所有单元故障率之和；其故障率与维修率的比值是所有单元的故障率与维修率比值之和。计算串联结构等效故障率和等效维修率的表达式为

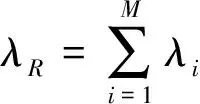
(8)

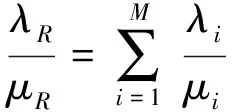
(9)

式中：λi和μi分别表示串联结构中各单元的故障率和维修率。

对接触网GO图中的串联结构进行定量分析，计算等效单元的等效可靠性参数，如表2所示，并在接触网系统中用等效单元代替串联结构，然后进行GO法的直接计算。

表2 操作符2～13的等效可靠性参数

接触网的失效过程满足以下特点：①接触网失效过程无记忆；②系统中任何一个单元发生故障，系统就无法正常工作，相当于一个串联系统；③各部件的故障率和维修率近似为常数；④状态是可识别的[15]。因此接触网系统可以看成是一个符合马尔可夫过程的可修串联系统的马尔可夫模型。故接触网的可靠度R(t)为

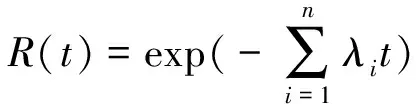
(10)

4.2.2 考虑共因失效的接触网成功概率

接触网系统的所有设备均露天运行，当外部环境发生突变时，可能导致接触网系统多个部件同时发生故障，即共因失效。但接触网在实际运行时，2个以上部件同时发出现故障的可能性很小，因此分别从接触悬挂和支持装置中各选取1个共因失效组(即D2和D3，D10和D11)，每个共因失效组含有2个部件，且故障率与维修率一样，故采用β因子作为接触网系统共因失效模型，共因失效组中包含独立失效因子和共因失效因子，见表3。

表3 共因失效组分解

共因失效部件的故障率可分解成独立失效故障率和共因失效故障率，见表4。假定在初始时刻，接触网系统故障率为零，维修故障部件时，维修工数量不变，共因失效部件修复后能正常工作，则共因失效维修时间是独立失效时维修时间的两倍，相应2组共因失效维修率为μ13，μ14。

表4 接触网共因失效组故障率分解

运用MATLAB仿真，绘制出考虑共因失效前后，系统可靠度随时间变化曲线，定位装置和吊弦的故障率较高，同时绘制出其不可靠度变化曲线，如图5所示。

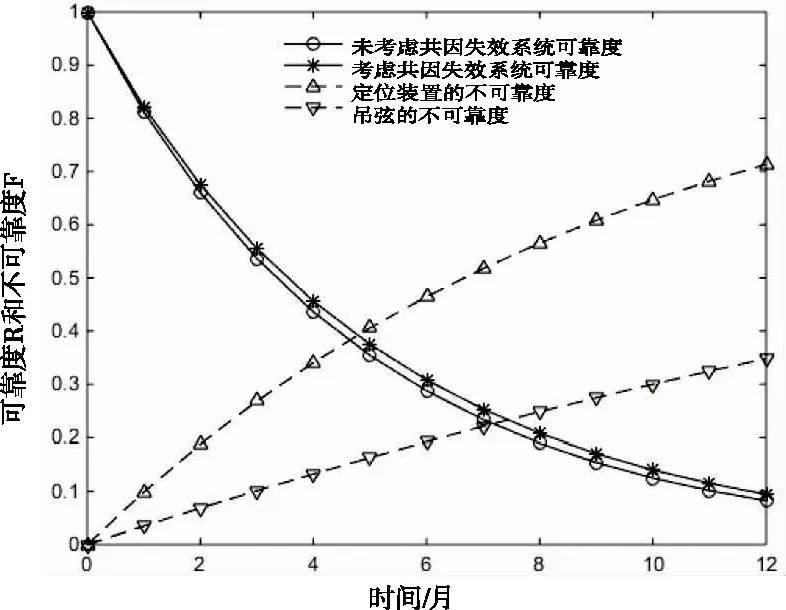
图5 系统可靠度及部件不可靠度变化曲线

从图5可知，在1年的运行时间内，系统的可靠度随着运行时间的增加而明显下降，考虑共因失效后，系统可靠度要大于未考虑共因失效时的情况。而且随着运行时间的增加，定位装置和吊弦的不可靠度增长较快。是否考虑共因失效，会使接触网系统的可靠度产生一定量的偏差，因此在接触网的日常检修中应充分考虑部件发生共因失效的情况。

4.2.3 接触网各可靠性指标

接触网系统是一个具有停工相关性的可修系统，系统运行足够长时间后达到稳定。

接触网的平均无故障工作时间

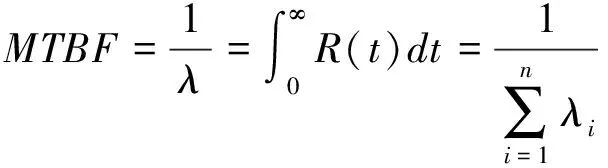
(11)

接触网的平均维修时间

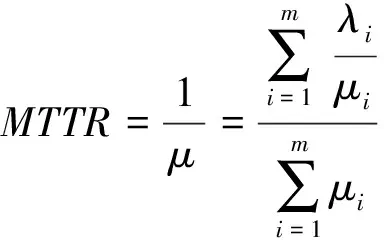
(12)

接触网的稳态可用度(平均工作概率)

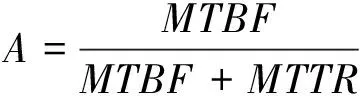
(13)

单位时间平均故障次数

(14)

根据接触网系统可靠性GO法运算规则，得到接触网考虑共因失效前后的各可靠性参数，如表5所示。

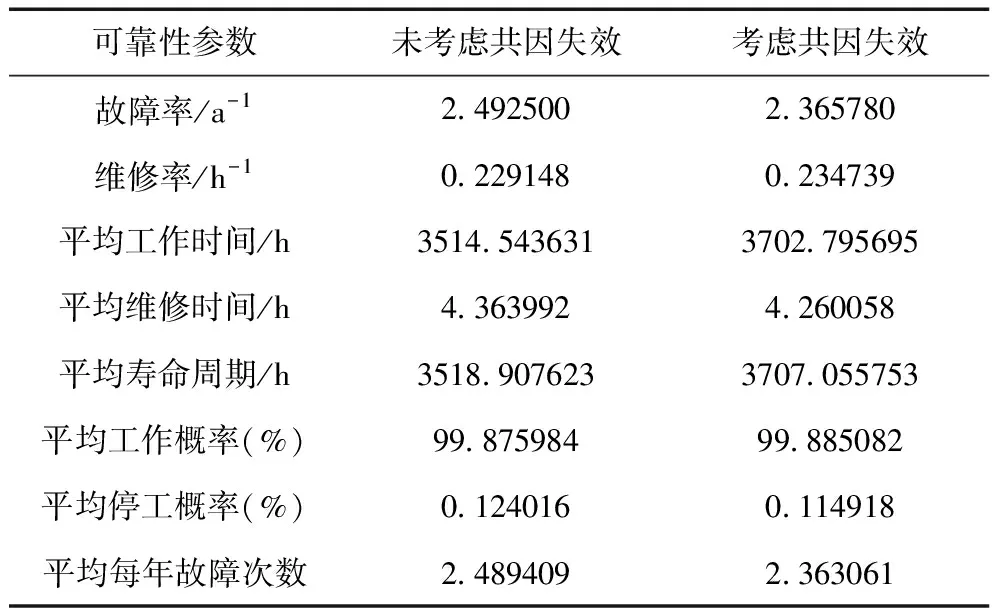
表5 接触网可靠性参数

4.3 接触网可靠性定性分析

该接触网系统GO图中共有12个功能操作符，表示系统的各个功能单元。首先计算一阶割集，假设某个操作符处于故障状态，其成功概率为零，其它操作符状态概率不变，如果此时计算出系统的成功概率为零，则该操作符的故障状态即为系统的1个一阶割集。所有功能操作符按此方法进行分析，可找出系统的全部一阶割集。通过直接定性分析，得到该系统共有12个最小割集，全部为一阶割集，列于表6内，同时给出最小割集的发生概率。最小割集的发生概率为割集内部件故障概率的乘积。最小割集中操作符故障状态的组合代表系统功能部件故障事件的组合。

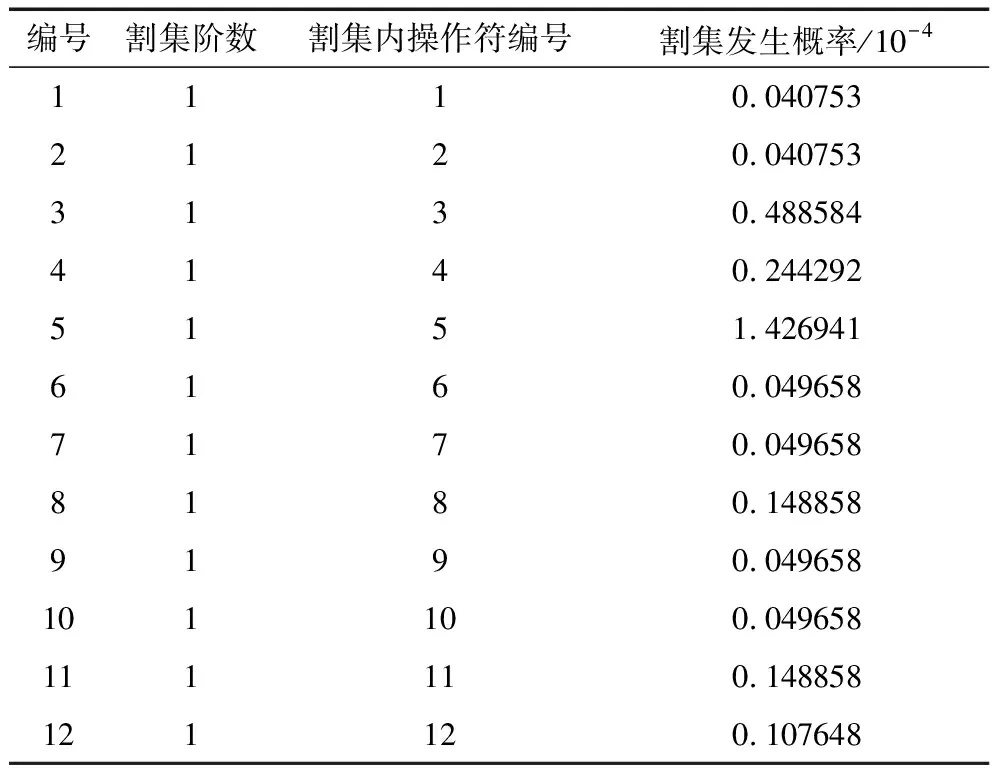
表6 接触网系统最小割集

由表6可知，系统中割集发生概率最大的是定位装置，割集发生概率为1.426941×10-4，是接触网系统中最薄弱的环节；其次是吊弦，割集发生概率为0.488584×10-4。因此，应加强对定位装置和吊弦的定期故障维修。

5 结论

1)通过对系统可靠度变化曲线进行对比，考虑接触线和承力索、承力索座和定位环的2组共因失效后，系统可靠度要大于未考虑共因失效时的情况，为接触网的日常检修提供了一定的理论依据。

2)在接触网系统的可靠性分析中，若未考虑维修因素，随着时间的增加，系统可靠度明显降低；考虑维修因素后，系统的平均工作概率稳定在99.885082%，因此，当接触网发生故障时必须及时抢修。

3)根据求出的系统最小割集可知，系统中割集发生概率最大的是定位装置，其次是吊弦，这两个部件是系统中最容易发生故障的部件，与工程现场的实际情况相符，验证了GO法的适用性和准确性。所以在接触网的日常检修中应加强对定位装置和吊弦的重点维护。