翼伞系统动力学建模与分段归航设计

刘佳玺，刘党辉，刁俊昌

(1. 航天工程大学研究生院，北京 101416；2. 航天工程大学宇航科学与技术系，北京 101416；3. 31700部队，辽宁 辽阳 111000)

1 引言

航天运载器的精确定点以及无损回收一直是各国学者不断探索研究并急需解决的技术难题[1]，20世纪60年代，法国人贾尔伯特(JALBERT)首次提出了“冲压翼伞”的概念，基于冲压翼伞的空投系统以及运载器回收系统开始进入人们的视野，通过对翼伞系统合理的动力学建模以及归航设计，可以大幅度提高空投系统以及运载器回收系统的精确性[2]。

在1978-1984年间，Goodrick先后建立翼伞系统纵向平面的3DOF模型以及6DOF[3]模型开始，国内外学者对翼伞系统的动力学建模进行了较多的研究，翼伞系统的8DOF[4]、9DOF[5]、12DOF[6]动力学模型相继建立。6DOF模型是将翼伞与载荷看做刚性连接，系统在整个归航阶段主要以滑翔为主。更高自由度的动力学模型主要用于分析物、伞系统间的相对运动特性，其中8DOF与9DOF模型是将伞体和回收物间通过长度恒定的吊带相连，而12DOF模型更是考虑到了吊带的弹性形变，这对详细分析翼伞系统归航中突风作用、雀降操纵以及系统设计参数优化等提供了更精确的理论依据。本文主要研究的是翼伞系统的归航设计，而归航设计旨在分析系统质心的运动规律，了解飞行轨迹以及飞行性能。6DOF模型可以直观清晰的描述系统的基本运动特性，而且相对较为简单，而更高自由度的模型建立较为复杂，不利于归航过程中的轨迹以及系统控制器的优化。只有当需要获得更多信息，并进一步了解系统各组成部分--伞体以及回收物之间的相互影响时，才需要建立更高自由度的动力学模型。所以本文采用翼伞系统的6DOF模型进行归航设计。

对于翼伞系统而言，轨迹规划不仅要实现安全地着陆，更要保证着陆精度，以及能量控制在允许范围之内等多项要求。当前，翼伞系统轨迹规划的研究方法大致可分为三种：简单归航法[10]，最优控制归航法[11]以及分段归航法[12]。相比于前两者，分段归航操纵简单，鲁棒性强，可以实现逆风对准，在实际工程中应用越来越广泛。

2 翼伞系统六自由度动力学模型

2.1 翼伞系统的附加质量

由流体力学概念可知：附加质量是物体在流体中做加速运动时产生的，当物体运动速度大，而加速度和尺寸小时，则运动的阻力主要由物体粘性摩擦引起；而当速度很小，加速度和尺寸很大时，运动的阻力主要产生于克服周围流体的惯性阻力。降落伞的开伞过程属于后者，其次降落伞通常在空气中运动，伞的平均密度与空气的密度相当，附加质量与伞体本身质量处于同一量级，因此在计算降落伞的开伞动载以及运动分析中必须考虑附加质量。

附加质量和附加质量惯性矩是个矢量，不同于物体质量是个标量，它与物体的运动方向有关。根据流体力学理论，在六自由度运动方程中，附加质量和附加质量惯性矩表示为6×6的矩阵，共36个分量[2]。由于附加质量具有对称性mik=mki，所以其中只有21个独立分量，其中m11，m12，m13，m22，m23，m33称附加质量，m44，m45，m46，m55，m56，m66称附加质量惯性矩。而对于具有轴对称的降落伞来说

m12=m13=m23=m45=m46=m56=0

附加质量分量只存在于m11、m22、m33，附加质量惯性矩只存在于m44、m55、m66，其表达形式为[2]

本文采用Barrows提供的附加质量矩阵形式，对于平直翼而言，其计算公式如下[7]

由于翼伞展向是圆弧形，真正的附加质量计算公式要根据拱高以及展向弯曲弧度等参数进行修正，如图1所示。由参考文献[7]可知，平直翼与拱形翼在数值精度上差异小于2%，本文为计算方便，直接应用平直翼的附加质量计算公式以简化计算。

图1 翼伞平直翼与拱形翼示意图

2.2 翼伞系统六自由度模型

2.2.1 基本假设

1)翼伞是展向对称的，伞衣完全张满后具有固定的形状(后缘的下偏操纵除外)；

2)载荷所受阻力远大于升力，对其升力忽略不计；

3)载荷与翼伞刚性连接成为一个整体；

4)伞衣的压心和质心重合，位于弦向距前缘1/4处；

2.2.2 翼伞系统气动力与力矩分析

对于翼伞气动力的计算，最可靠的方式还是飞行试验，但是由于飞行试验耗资巨大并不能满足日常学术研究的需求，而对于风洞试验，也因翼伞的柔性特质而难以实现。近年来，随着CFD技术的广泛应用，通过数值计算以及计算机仿真获得翼伞气动力参数的方法发展迅猛。为分析翼伞单侧下拉的转弯运动，目前广泛采用的是Goodrick的分片处理的工程方法，国防科技大学的熊菁[4]采用的是试验数据以及工程分片处理相结合的方法来计算翼伞的气动力以及气动力矩。对于本文，对翼伞系统的合力Faero以及合力矩Maero进行分解并逐一计算，最终得到气动力以及力矩的表达式

(1)

(2)

2)在计算作用在伞体上的气动力时，需要用升力减去阻力，其表达式如下

(3)

3)在计算附加质量产生的力矢量时，根据1.1得到的翼伞系统附加质量，可以得到翼伞系统附加质量产生的力矢量表达式为：

FF=-mFaC

(4)

4)在计算系统所受重力时，需要将惯性坐标系转换到体坐标系上，又因为重力加速度g只作用于惯性系的Z轴，所以重力的表达式为：

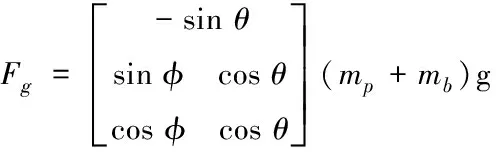
(5)

接着对翼伞系统的力矩关系进行分析，因为系统所受重力不可控，可以不考虑重力产生的力矩，只计算气动力矩(MA)以及附加质量作用力所产生的力矩(MF)，所以翼伞系统合力矩的表达式为

Maero=MA+MF

(6)

1)在计算翼伞系统的气动力矩时，可将气动力矩分解为滚转力矩，俯仰力矩，以及偏航力矩，其表达式可由参考文献[8]给出

(7)

2)在计算附加质量的作用力矩时，根据2.1得到的附加质量惯性矩，可以得到附加质量作用力矩的表达式为

(8)

2.2.3 翼伞系统动力学方程

求翼伞系统动力学方程时，首先根据2.2.2推导的翼伞系统所受合力以及合力矩的分量，得到力与力矩的平衡方程。因为翼伞在左右下拉后缘进行转弯或减速(雀降)运动时会产生襟翼偏转δa和δs，从而对气动力和气动力矩产生影响，所以需要加上修正量ΔFA和ΔMA则翼伞系统力与力矩的平衡方程为

(9)

(10)

其中，I为翼伞系统伞体和载荷转动惯量之和。

接下来就可以建立含附加质量的翼伞系统六自由度动力学方程

(11)

(12)

通过翼伞系统力与力矩的平衡方程对VC与ω进行迭代求解，将其带入翼伞系统六自由度动力学方程中，便可以实时求出模型的六个状态量，从而得到翼伞系统在整个归航过程中的运动轨迹，这样对了解翼伞系统的运动特性有非常重要的参考作用。

3 翼伞系统分段归航设计

3.1 分段归航方案

分段归航的轨迹大致可以分为三段：向心飞行-目标接近段；盘旋削高-能量消耗段；逆风对准-雀降着陆段，如图2所示采取分段归航极大简化了归航过程中系统的操纵过程，并且有利于实现各个参数的优化。

图2 翼伞系统分段归航过程示意图

图3 传统分段归航方案

如图3所示，传统的分段归航方案是在离目标区较近的下风区做转弯运动不断消耗高度，直到满足最终条件时逆风雀降着陆，这样的归航模式简单，不会出现复杂的操纵变换，但是对于整个归航任务来说，必须尽可能控制着陆能量，以防在紧急情况发生时着陆精度有所保证。传统的分段归航方案转弯半径较小，对于翼伞系统而言，转弯半径越小，翼伞后缘所需的下拉操纵量越大，所需要消耗的能量也就越多，而且过小的转弯半径需要极大的转弯角速率，在转弯初期会造成物伞系统之间较大的相对运动，不利于系统的稳定性。

图4 新型分段归航方案

在新的归航方案中，如图4所示为了减小能量损耗，主要以直线以及大圆弧为运动形式，只有在两者衔接处采用小圆弧过渡，在投放点高度合适的情况下，可以通过改变圆弧大小来调节轨迹，确保了回收精度。

3.2 轨迹计算

如图4所示，A点为初始点，δ为初始飞行方向角(初始运动方向与X轴正向的夹角)，B点到C点为目标接近段做滑翔运动。D点到E点为能量消耗段，F点到O点为雀降着陆段做减速运动，β1,β2,β4为过渡段的圆弧角，其转弯半径为Rmin,β3为能量消耗段的圆弧角。

以坐标原点作为目标点，归航轨迹随着初始点的变化而变化，设整个归航过程中翼伞系统的滑翔比保持恒定为k，由以上分析可以得到系统归航的目标函数：

(13)

该目标函数反应的是设计轨迹的水平飞行距离与初始高度所对应的水平飞行距离差的绝对值。

4 仿真分析

4.1 翼伞系统基本运动特性分析

翼伞的基本运动特性包括无下拉的滑翔运动，单侧下拉的转弯运动以及双侧下拉的减速运动(先不考虑雀降)。

设置模型参数，初始投放高度为(0，0，3000)m，初始速度为(14，0，5)m/s，系统的初始角速度、欧拉角等都设置为 0，翼伞系统自身的结构以及气动参数可由参考文献[8]得到，在运动过程中的操纵见表1。

表1 翼伞系统操纵方式

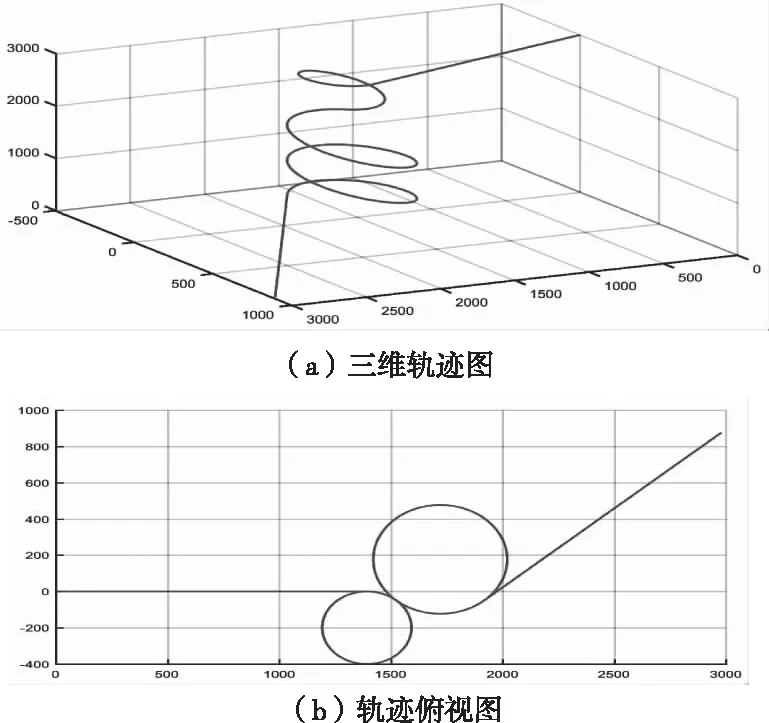
图5 翼伞系统运动轨迹示意图

随着操纵方式的变化，翼伞系统的三个姿态角也会随之变化，如图6所示。

图6 翼伞系统姿态角变化曲线

对图形分析可以得到，前50s以及50s到100s之间均是直线滑翔运动，此时滚转角与偏航角不发生变化；俯仰角在每次改变操纵时会发生一定范围的波动最终趋于某一恒定值。

在100s到200s之间以及200s之后均做单侧下拉的转弯运动，其中转弯方向由下拉量的正负决定，转弯半径的大小由下拉量的绝对值决定，且绝对值越大，转弯半径越小。滚转角与翼伞的运动状态相关，且转弯半径越大，滚转角的绝对值越大；俯仰角会发生小范围波动最终继续趋于稳定，单侧下拉的操纵对俯仰角产生的波动不大；偏航角根据转弯方向的不同按照不同的速率恒定变化。

4.2 翼伞系统分段归航轨迹优化

设置初始条件：A(1000，-400，1260)，初始方向角为60度，最小转弯半径为120m，Rm∈(400，600)，滑翔比k=2.8，水平速度为18.4m/s，过渡段的圆弧角小于180度。

利用几何关系求最优轨迹可以理解为参数优化的问题，可利用计算机智能算法仿真解决。利用遗传算法设置初始种群的大小为100，交叉概率为0.7，变异概率为0.2，最大迭代次数为1000，在满足约束条件下利用matlab遗传算法工具箱的ga函数迭代求解出目标函数的最优值，最终得到整个归航过程所需的所有几何参数如下

图7 新型分段归航方案轨迹俯视图

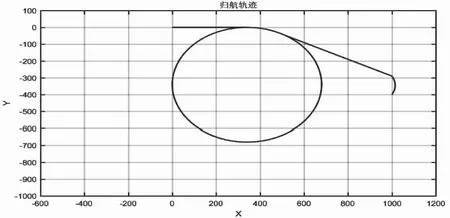
图8 传统分段归航方案轨迹俯视图

由翼伞系统动力学模型可得翼伞单侧下偏控制量与转弯半径的关系见表2．

表2 翼伞下偏控制量与转弯半径关系表

图9 分段归航方案控制图

经计算，相比于传统分段归航方案，新型分段归航方案所耗能量小，转弯半径大，对系统的能量控制以及稳定性更具有优势。

5 总结

本文对翼伞系统的六自由度动力学模型做了详细的推导，对其中附加质量，气动力以及气动力矩的计算方程做了归纳与总结。其次，利用分段归航轨迹的几何特性确定了各段的参数，并利用遗传算法对各参数进行了优化，得到了在满足投放高度的情况下任意投放点到目标点的轨迹曲线方程。最后对传统分段归航方案以及新型分段归航方案做出了对比，得到新型归航方案对翼伞系统归航过程的能量控制以及稳定性有更强的优势。