基于改进动态规划的无人机搜寻航迹规划研究

钱 宇，祝祯祎

(中国民用航空飞行学院，四川 广汉 618307)

1 引言

近几年来，世界范围内出现越来越多的自然灾害，例如洪水、地震、台风等，这些灾害覆盖面积广、房屋摧毁数量多。无人机作为一种新兴无人驾驶技术的载体，具有重量轻、航时长、机动性能好等优势，在救援的过程当中发挥越来越重要的作用[1]。为了满足无人机快速高效地进行定点搜寻工作[2]，需要根据已知的障碍物环境和其物理性能约束规划一条耗时最少、航程最短的航迹。

针对无人机航迹规划技术，国内外学者提出了很多高效的航迹规划算法，主要分为传统经典算法和现代智能算法[3]。传统经典算法包括人工势场法[4](Artificial Potential Field，APF)、模拟退火算法[5](Simulated Annealing Algorithm，SAA)等。这类方法容易陷入局部最优解，在规划空间较大时搜索效率低，相比之下，现代智能算法收敛程度更好，时间复杂度更小，应用范围更广。其中包括A*算法[6]、遗传算法[7](Genetic Algorithm，GA)、蚁群算法[8](ACO)等。经过几十年的发展，这些算法在某些具体场景下仍然有一定的局限性，因此提出了许多改进算法。程泽新等[9]将遗传算法用于无人机航迹规划中，对进化变异的策略进行改进并结合启发式搜索方程，可以加快收敛的速度并更有效地获取可行路径，但是由于是基于概率的选择机制，仍然存在陷入局部最优的可能性。刘永琦等[10]提出在三维环境中修剪扩展节点，降低传统A*算法的网格节点计算量，提高了路径搜索速度，然而并未详细阐释改进A*算法的搜索流程。

动态规划算法(Dynamic Programming，DP)是由美国数学家R.E.Bellma求解多决策问题时提出的一种优化算法，特点在于搜索效率高，结果稳定可靠，从而受到广泛的关注。它将一个问题分解成若干个互相联系的阶段，对每个阶段作出决策，逐个求解，但是在实际应用中性能会受到影响。谭峻强等[11]详细地阐述了动态规划算法的基本思想，并将其用于求解最短运输距离，耗费时间短，结果清晰明了；但是当问题的规划空间变大时，时间复杂度也会相应地增大。孙健等[12]在突发威胁的环境下，结合动态规划算法和切线法可以实时地获得一条合理规避障碍物的航迹，但是飞行过程中需要多次切换方向并且存在多余的航迹点，整个飞行航迹距离相应地变长。

为了解决航迹规划耗时长以及冗余节点的问题，研究首先利用双向动态规划算法把搜索空间重新规划为两个对称区域，减少参与多阶段决策的状态点总数；之后基于优化后的搜索区域，在区间内验证度量函数满足四边形不等式并找到使节点之间欧氏距离最小的决策范围，进一步减少冗余节点的数量，以期得到一种在航迹最优性和规划速度上效果更好的规划算法。

2 无人机航迹规划建模

无人机从起始点到终止点的搜寻过程中，为了减少耗费的时间，需要在空间中规划一条最优的飞行路径。选择在三维空间中对无人机的静态航迹进行仿真建模。假设条件如下：

1)无人机的飞行方向不会指向初始点。

2)只能在规定的空间内进行路径规划。

3)忽略无人机的大小，将其简化为质点。

4)搜寻过程中只考虑障碍物的威胁。

2.1 三维空间栅格化

为了能够计算出满足约束条件的航迹规划

表达式，需要对无人机搜索的整个空间进行离散化

{(x，y，z)|a≤x，y，z≤bx，y，z∈Z}

(1)

在三维坐标系中，令无人机经过的航迹点qi(i=1，2…n)的坐标为(xi，yi，zi)；障碍物区域表示为(xj，yj，zj，r)，整个规划空间如图1所示。其中空心正方体表示为空间离散后的节点，红色实心正方体A和B分别表示无人机搜寻过程的起始点和终止点，球体代表空间中的障碍物区域。

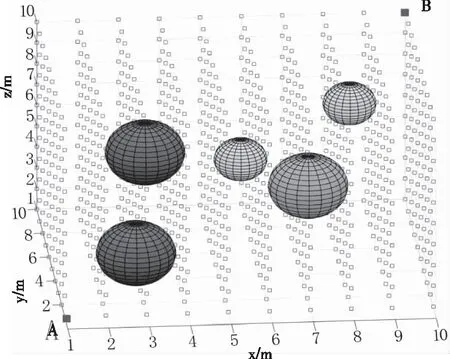
图1 无人机航迹规划空间栅格化

2.2 约束条件

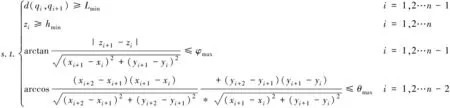
研究考虑最小航迹长度、最大转弯角、最大爬升角/下降角、最低飞行高度等约束。约束条件如下

式中，Lmin为无人机最小航迹长度，θmax为无人机最大转弯角，φmax为无人机最大爬升角/下降角，hmin为最低飞行高度。qi为空间航迹点，(xi，yi，zi)为航迹点的坐标，d(qi，qi+1)为相邻航迹点(qi，qi+1)的欧氏距离。

2.3 代价函数

航迹规划的代价函数[13]是评价航迹优劣的一个重要的标准。影响三维航迹规划的主要因素包括航迹长度代价L、飞行高度代价H和威胁区的威胁代价T，分别表示为

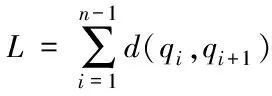
(6)

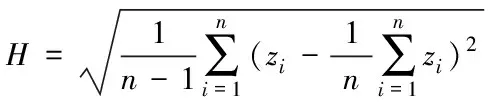
(7)

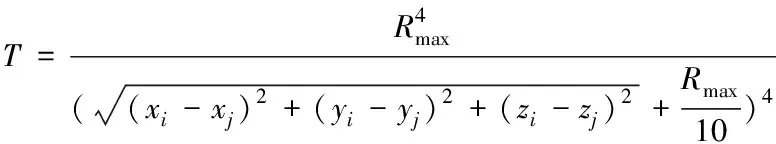
(8)

这里Rmax表示威胁区的最大作用距离，k表示威胁区的个数， (xj，yj，zj)表示威胁区中心坐标。

航迹总代价J与相应的权系数w1、w2和w3表示为

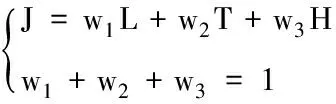
(9)

可以得到无人机航迹规划模型

min(w1L+w2T+w3H)

(10)

3 航迹规划算法

动态规划算法通常将问题划分为若干个相互关联的阶段，通过找到使每个阶段都达得最优效果的决策序列，来获得整个问题的最优解。利用动态规划算法进行无人机搜寻任务航迹规划，在优先考虑整体的思路下，确定每个状态的最优值，最终可以得到整条搜寻航迹的最优策略。

无人机航迹规划中，在初始状态确定，而结束状态不确定的情况下，自底向上的逆序法效率更高；相反在结束状态确定，而初始状态不确定的情况下，自顶向下的顺序法效率更高[14]。因此在航迹规划中确定了初始状态和结束状态的基础上，顺序法和逆序法都可以使用。研究采用逆序法进行建模分析。

无人机从初始点A搜寻到终止点B的总航迹，可以划分为n个阶段，每个阶段表示为k(k的取值为1，2…n)，第k阶段的状态为fk；第k阶段状态为fk的决策变量表示成vk(fk)。若确定了第k阶段的状态fk和选择的决策vk(fk)，则k+1阶段的状态fk+1也可以确定，常用式子fk+1=M(fk，vk(fk))表示。规划过程表示为：

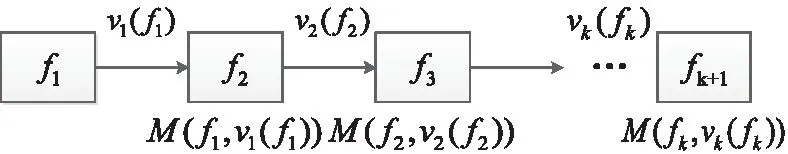
图2 搜寻规划流程图

航迹点和距离信息存储在动态规划表中，从终点开始利用逆序法向前进行规划，依次找到花费最小的前向节点。将指标函数中第k阶段的状态fk到第k+1阶段的状态fk+1之间的花费定义为两点之间的欧氏距离d(fk+1，fk)，第一阶段到第k阶段花费度量值之和w表示为

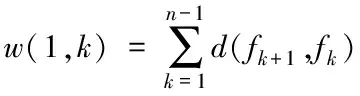
(11)

已知阶段1的状态A和阶段n的状态B，单向动态规划的逆序法模型

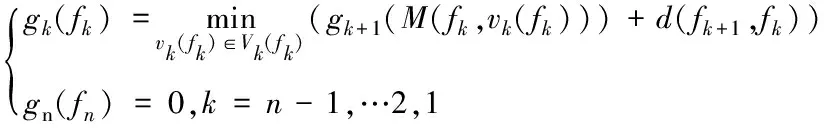
(12)

gk(fk)表示第k阶段末状态fk到结束点B的最优指标函数值；gn(fn)代表结束点状态B。同理，顺序法的动态规划模型可以表示为

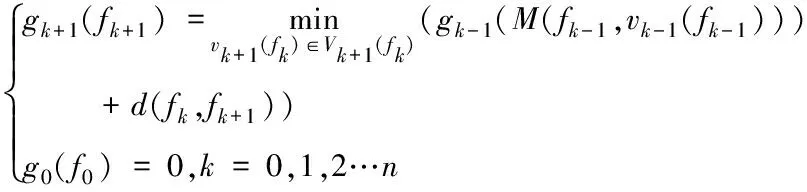
(13)

其中，gk+1(fk+1)表示为初始状态A到第k+1阶段末状态fk+1的最优指标函数值，g0(f0)代表初始点状态A。当搜寻出从A到B的最优航迹时，其中每一段子航迹也是最优的，满足动态规划的最优子结构性质；函数通过作用于后部子过程，得到一个在以往计算中的最优状态，不会对下一步的决策起到影响，满足了无后效性原则；通过将航迹规划得到的状态存储在内存表中，略增加了空间复杂度，但解决了子问题的重叠性。

4 算法改进策略

4.1 状态总数优化

动态规划算法在搜寻过程中，需要遍历整个搜索空间中的状态点寻找最短航迹，当问题规模较小时， 可以取得很好的效果， 但是当规划空间增大，问题中状态总数增多时， 规划耗时变长。针对此问题，双向动态规划算法在保证全局最优的同时，也提高了算法的规划速度。

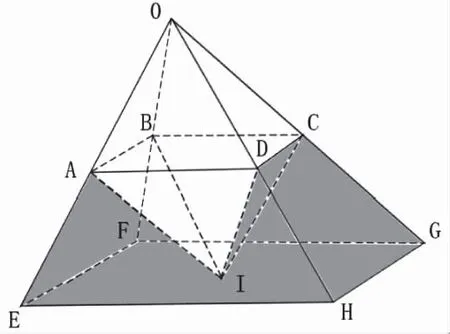
图3 双向动态规划算法分析

如图3所示，单向动态规划的计算空间区域为五面体OEFGH，但是双向动态规划的计算空间区域为五面体OABCD与五面体IABCD之和；图中灰色区域是双向动态规划相对于单向动态规划少计算的状态区域；令顺序法和逆序法的最优交汇处在第k阶段，选取状态点的过程需要满足

qk∈N∩qk∈B=1

(14)

其中qk表示为第k阶段选择的状态点，顺序状态点存储在内存表N中，逆序状态点存储在内存表B中。

4.2 状态转移过程优化

动态规划算法通过计算每个阶段中所有符合约束的状态点来寻找最短路径；状态转移过程就是，把原问题分解为两个子问题，利用求解过的前一状态和此状态上的决策得到当前的状态。状态转移所涉及的状态数目影响了动态规划算法的时间效率。因此在优化决策量的基础上减少所涉及的状态数目，提高运算量。

将状态转移中度量值定义为w(i，j)，航迹规划过程中的状态转移方程表示为

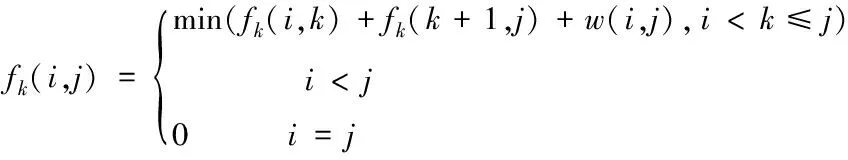
(15)

度费用，fk(i，j)表示区间(i，j)上的最短路径。在区域OABCD中，根据式(11)度量函数w(i，j)属于单调递增，区间(i，j)包含于(i′，j′)，可以验证其满足包含关系单调性

w(i，j)≤w(i′，j′)，(i，j)⊆(i′，j′)

(16)

在式(16)的基础上对距离函数w进行分类讨论，得到度量函数w(i，j)满足四边形不等式：

w(a，c)+w(b，d)≤w(b，c)+w(a，d)a≤b≤c≤d

(17)

根据式(16)和(17)，通过归纳法可以得到，最短路径函数也满足四边形不等式

fk(a，c)+fk(b，d)≤fk(b，c)+fk(a，d)

(18)

Pk∈{(x，y，z)|a≤x，y，z≤bx，y，z∈Z}为第k阶段决策集合，令p(a，b)为fk在(a，b)区间内取最小值时的决策，通过反证法可以得到

p(a，b-1)≤p(a，b)≤p(a+1，b)

(19)

根据式(19)，在保证航迹距离最短的情况下，双向规划的决策范围大大缩小，进一步排除了冗余的节点，存储计算过程更加高效。优化后的状态转移函数可以表示为

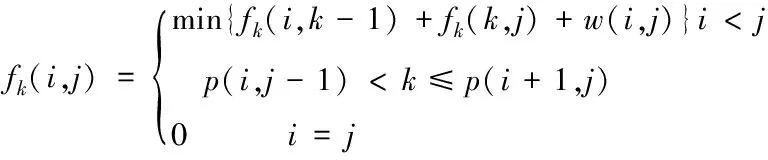
(20)

其中状态转移方程的区间长度L=j-i，v(i+1，j)和v(i，j-1)的长度为L-1，区间的长度为n个，对于确定的长度L，其包含的状态有n个，因此时间复杂度为O(n2)。改进之前，根据式(15)可知算法的时间复杂度为O(n3)。在改进过程中，分析状态之间的关系，得出最优决策具有单调性质，因此在计算过程中减少了状态转移考虑的状态数，提高了算法的时间效率。

4.3 改进动态规划算法流程

改进动态规划算法计算流程如下：

1)初始化数据，包括搜索空间、障碍物坐标和无人机约束函数。

2)三维空间栅格化，若搜寻点不在障碍物区域内，通过式(14)确定顺序法和逆序法交汇阶段k。

3)在顺序法的基础上，结合改进状态转移函数式(20)搜寻前k阶段的路径点，利用d(fk+1，fk)计算距离并把信息全部存储在内存表N中。逆序法同理，将数据都存储在内存表B中。

4)若内存表N和B中存在相同的状态集P，则把两个表中存储的状态点和P连接起来，计算相应的距离。若不存在，则返回步骤2)。

5)找出最小的距离，并输出。

算法流程图如图4。

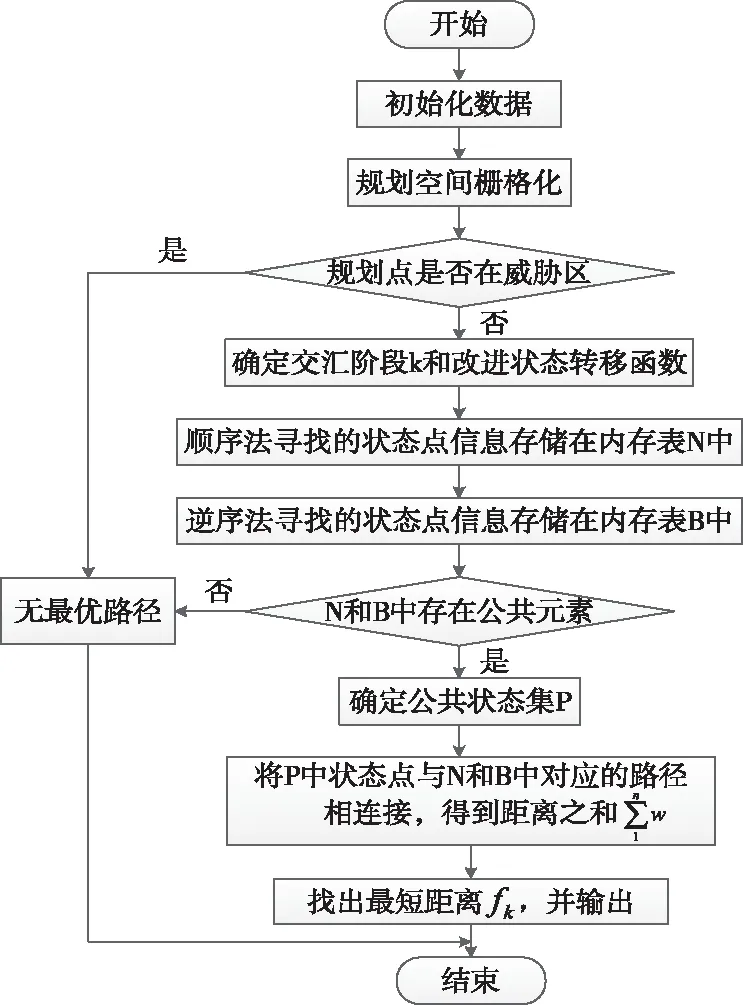
图4 改进动态规划算法流程图

5 仿真与结果分析

为了验证算法的性能，研究利用遗传算法、动态规划算法和改进动态规划算法进行了仿真计算。

仿真条件为：无人机的起始点为(1m，1m，1m)，终止点为(10m，10m，10m)；当无人机在搜寻过程中，可以利用立体摄像机获取障碍物的位置坐标，最小航迹长度为1m，最大转弯角50°，最大爬升角60°。障碍物的位置信息如表1。

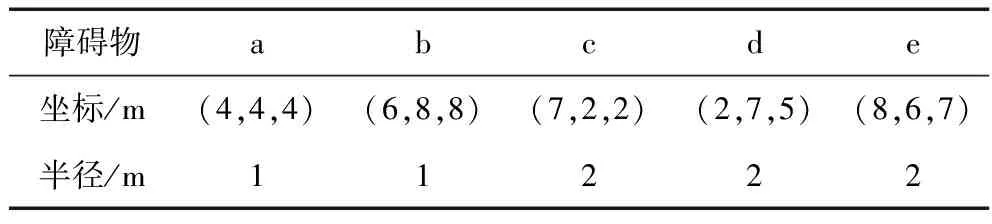
表1 障碍物信息表

仿真结果航迹对比如图5、图6，不同算法的航迹总长度及计算时间如表2所示。

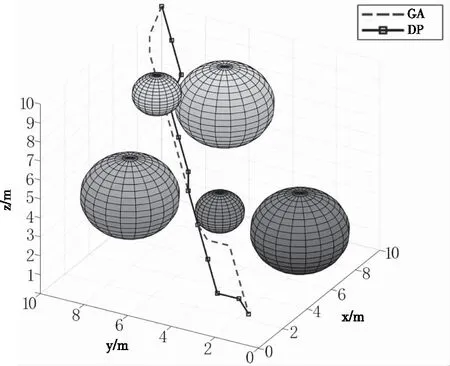
图5 DP与GA算法航迹规划对比图

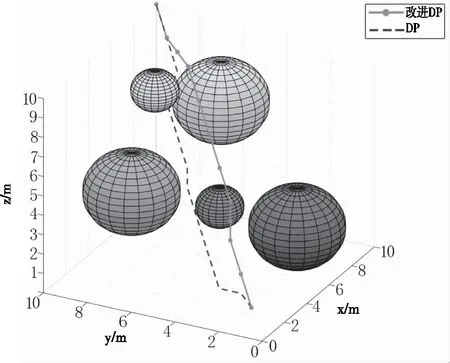
图6 改进DP与DP算法航迹规划对比图

图5显示出遗传算法规划了一条可行的搜寻航迹，但是相对于动态规划算法，不是一条最优航迹，主要是遗传算法在航迹规划后期收敛速度变慢，容易陷入局部最优，使得计算效率变低；无论是在规划速度还是航迹最优性都是动态规划算法更好，利用空间换取时间，存储了每个状态点之间的距离，但是还会产生冗余。图6中，改进动态规划算法计算的状态点的数量相比于动态规划算法更少，解决了空间占据过多的问题，因此规划速度更快，消耗时间更短；并且通过状态转移优化策略减少了冗余节点，航迹长度更优。三种算法的仿真结果如表2。

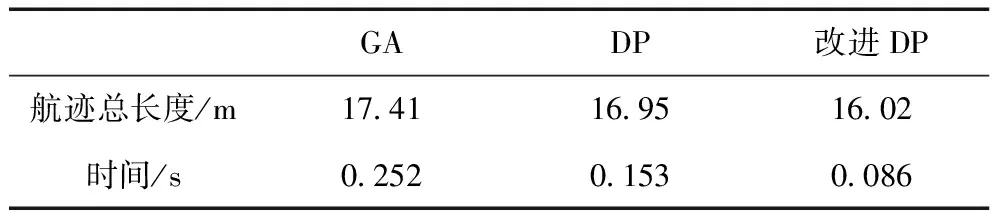
表2 不同算法仿真结果对比

结果表示，在航迹点数量方面，改进DP算法相对于GA算法减少7.9%，相对于DP算法减少5.4%；在时间效率方面，改进DP算法相对于GA算法提高65%，相对于DP算法提高43%。仿真结果验证了改进动态规划算法耗时短，搜寻距离小。

6 结论

1)改进动态规范算法减少了状态转移过程的计算量和存储量，加快了规划速度；优化了航迹节点数量，缩短了整个搜寻的时间。改进动态规划算法能够很好的规划一条代价最小、航路最优的航迹。

2)针对动态规划算法存在维数爆炸，耗时长的问题，结合双向动态规划算法的并行搜索特点和决策变量的优化策略得到一种改进动态规划算法，并将其运用在无人机灾后定点搜寻任务规划中。