基于一维深度卷积自动编码器的刀具状态监测方法
2021-11-17杨国葳李宏坤张明亮黄刚劲
杨国葳, 李宏坤, 张明亮, 黄刚劲
(大连理工大学 机械工程学院,辽宁 大连 116024)
近年来,高速铣削加工领域已经成为先进加工制造业的重要组成部分,其优势在于极高的加工精度、极快的加工效率和极好的加工表面质量[1]。在实际的加工生产过程中,刀具作为直接与被加工件接触的切削工具会不可避免的产生磨损现象。研究表明,由于刀具磨损和破损而导致的计划外停机是造成加工效率降低和生产成本提高的主要原因[2]。因此,在加工过程中,对刀具状态进行实时监测具有重要意义。
刀具的状态监测主要分为直接监测法和间接监测法。直接监测法对刀具进行直接测量,主要包括光学图像法,接触式电阻测量法和放射性元素法。直接测量法测量精度高,但是必须进行离线监测,会造成切削过程不连续,产生延长加工时间的问题,不利于实际应用。间接监测法主要是基于信号分析和机器学习算法,也是传统的刀具磨损状态监测方法。通常首先采集加工过程中的切削力信号,振动信号,电机电流与功率信号等,然后人为的对原始信号进行特征提取,最后采用机器学习算法,实现刀具磨损状态识别。如赵帅等[3]对主轴电流信号的时域、频域、时频域进行特征提取,通过主成分分析(principal component analysis,PCA)对提取的特征进行降维处理,最后利用随机森林得到刀具磨损的分级评估结果;程灿等[4]通过遗传算法合理选择特征参数,利用支持向量机(support vector machine,SVM)实现了刀具磨损量的预测;吕震宇[5]通过散布矩阵分析特征参数对刀具不同磨损状态的敏感程度并对高度敏感特征进行降维处理,最后利用隐马尔科夫模型(hidden Markov model,HMM)识别刀具磨损状态。上述基于机器学习的方法虽然实现了刀具磨损状态的识别,但仍然存在两个弊端:① 算法模型的识别准确率很大程度上依赖于对信号的特征提取和特征选择的手段,十分依赖专业知识。并且,为了提高识别精度,需要研究更深层次的特征提取方法,极大增加了算法模型的复杂程度;② 人工提取特征可能会由于领域知识的限制而导致原始信号中与刀具磨损相关性很高的特征信息丢失。
近几年来,深度学习由于其强大的自适应提取特征的能力而受到了很大的关注。在刀具状态监测领域也得到了广泛的应用。相比于机器学习,深度学习最大的优势在于其可以通过多层神经网络充分学习信号的本征信息,不需要大量的人力和知识来进行人工特征提取与筛选[6]。李宏坤等[7]通过压缩感知技术对电流信号有效值的频域数据进行降维压缩处理,然后使用堆栈稀疏自编码器对刀具状态进行分类。王丽华等[8]提出了一种基于堆叠降噪自编码器(stacked denoising autoencoder,SDAE)的刀具状态识别方法,将时域原始AE信号经过快速傅里叶变换到频域,利用频域信息作为模型输入,有效地提取出了反映刀具磨损的特征信息,并在实际应用中取得了100%的识别准确率。Huang等[9]融合三向铣削力信号和加速度信号的时域、频域和时频域的特征信息,利用卷积神经网络(convolutional neural network,CNN)实现了刀具剩余寿命的预测。Martinez-Arellano等[10]利用格兰姆角求和域(Gramian angular summation fields,GASF)将力信号转换为二维图像,利用卷积神经网络实现刀具磨损状态识别,识别率达90%以上;Zheng等[11]利用小波包变换和短时傅里叶变换提取铣刀铣削力信号的时频特征,以此训练卷积神经网络实现高速铣刀的状态监测,识别率达99.40%。虽然上述模型在刀具状态监测上已经取得了较好的识别效果,但是依赖于对数据进行的预处理手段,当利用原始时域信号作为模型输入时,模型的识别效果并不理想。
为了解决上述问题,本文提出一种基于一维深度卷积自动编码器(1-D deep convolution autoencoder,ODCAE)的刀具磨损状态监测方法。不需要繁琐的预处理手段,而是直接对原始电流有效值信号进行分类。以主轴电流有效值作为模型的输入,首先对网络进行无监督预训练。然后保留编码部分以保存最优权值,为初始化用于模式识别的有监督网络提供更好的起点。最后利用样本标签进行有监督微调,实现刀具磨损状态的识别。
1 算法描述
1.1 一维卷积神经网络
卷积神经网络属于多级前馈神经网络,主要包含卷积层、池化层和全连接层。其中,卷积层和池化层的主要作用是特征提取,全连接层主要是根据提取的特征实现分类或者回归。
1.1.1 卷积层运算
卷积层主要是利用卷积核与输入信号的局部区域进行卷积运算,提取输入信号的局部区域特征。不同于全连接神经网络,卷积层由于具有局部连接和权值共享的特点,因此可以利用更少的参数获得更加丰富的特征。卷积层的计算公式为
Yi=F(Yi-1⊗Wi+bi)
(1)
式中:Yi表示第i层卷积层输出特征;⊗表示卷积操作;Wi表示连接第i层和第i-1层的权值向量;bi表示第i层的偏置向量;F表示非线性激活函数。
1.1.2 池化层运算
池化处理也叫做降采样处理,所以池化层又叫做降采样层,是对不同位置的特征进行聚合统计。在卷积神经网络中,池化层可以有效地简化网络计算的复杂度,避免过度拟合。常用的池化处理有均值池化和最大值池化,均值池化是以池化层输入的平均值作为输出,最大值池化是以池化层输入的最大值作为输出。二者的数学描述为
Pi=maxYi-1
(2)
(3)
式中,Pi表示第i层池化层输出特征。
1.2 一维深度卷积自动编码器
传统的用于模式识别的卷积神经网络由于权值的初始化是随机的,所以很容易使模型陷入局部最优解,从而导致模型的识别精度下降[12]。自动编码器[13]可以通过无监督训练的方式提取基于输入信号本身的固有特征,使网络的权值信息只源于信号本身。基于此,本文将一维卷积神经网络与自动编码器相结合,构建一维深度卷积自动编码器。通过无监督预训练的方式为实现模式识别的有监督网络提供更好的起点,避免从0开始训练网络。模型结构框图如图1所示。网络参数更新采用传统的误差反向传播算法。
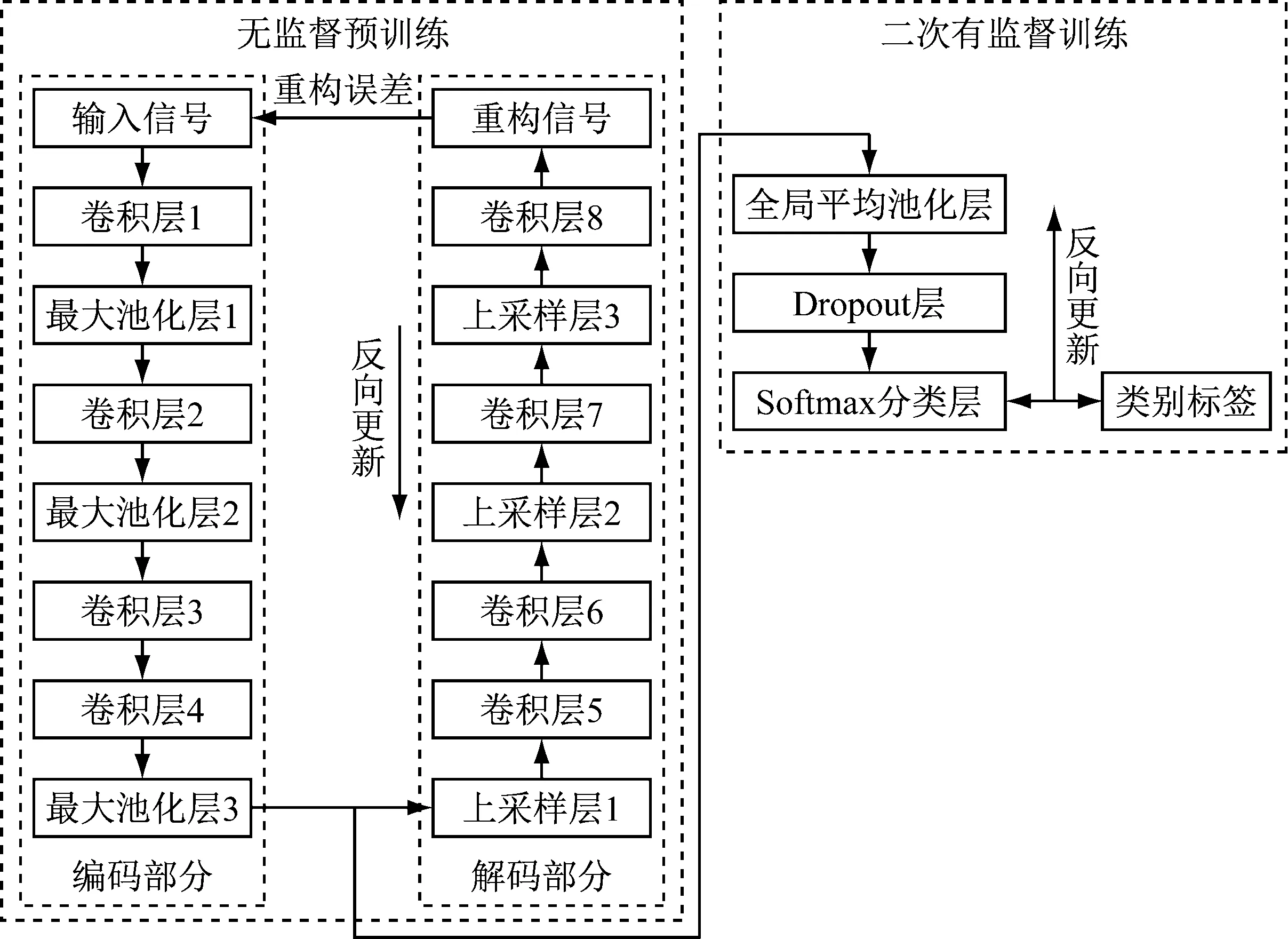
图1 ODCAE网络结构
在无监督预训练过程中,最大池化操作是编码部分的最终输出。在解码部分,可以通过反卷积操作得到与原始输入信号相同的数据维度。但是,由于反卷积操作容易出现矩阵块重叠的问题[14]。因此在本模型中,采用上采样和卷积操作还原输入信息,达到预训练有监督网络的初始权重的目的。在上采样操作中常采用合适的内插值算法来进行输出维度的扩张,在本文中,采用复制插值的方法进行原始输入信号的维度复原。即将上采样层的每一输入特征元素重复4次,赋值给待插入的序列位置,得到4倍于输入维度的特征维度。通过逐层叠加,得到与原始输入信号维度相同的输出特征。在预训练阶段,损失函数为均方误差函数(MSE),具体公式如下
(4)
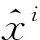
在二次有监督训练过程中,利用全局平均池化层代替传统卷积神经网络中的全连接层,减少模型的训练参数。通过Dropout方法防止深度网络产生过拟合现象。模型的输出层为Softmax分类层,Softmax函数可以将一个具有任意实数的k维向量压缩成另一个k维实向量,每个元素的范围在0~1之间,所有元素的总和为1,因此它通常用于估计不同类别的概率。具体公式如下
(5)
式中:C表示输出层神经元个数,即所分类别的个数(本文中C=6);a表示Softmax层的C维输入向量;yi是一个常数,用于表示第i个类别的概率。
通常以Softmax为输出层激活函数的多类神经网络的损失函数设定为交叉熵,具体公式为
(6)
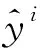
2 基于ODCAE的刀具磨损状态监测流程
ODCAE监测模型包括无监督预训练和有监督微调。具体诊断流程如图2所示,具体步骤如下:
步骤1采集机床主轴三相电流信号,将其融合成电流有效值信号,将电流有效值归一化至[0,1]之间,作为ODCAE模型的输入。
步骤2利用CAE进行无监督预训练,保留由提取的短序列向量组成的编码部分,用来保存最优的权值信息。
步骤3以无监督训练阶段获得的权值作为有监督网络的初始权重,利用样本标签和Softmax分类器再次对网络进行有监督微调,实现对刀具不同磨损状态的模式识别。
步骤4将测试样本输入训练好的网络模型中,得到分类识别结果。
3 试验结果与分析
3.1 试验设计
试验所用机床为台湾东昱精机公司生产的CMV-850A型立式加工中心,主轴电机为FANUC公司生产的β12/8000i型三相异步电动机,主轴传动方式为同步带传动。铣削电流信号采用瑞士LEM公司生产的LT 108-S7型闭环霍尔效应电流传感器获得,采样频率设为4 096 Hz。刀具为台湾Di牌2刃硬质合金平头立铣刀,试验所用数量为1把,直径12 mm,螺旋角30°。工件材料为40Cr。试验所用设备及采集、加工工件如图3~图6所示。
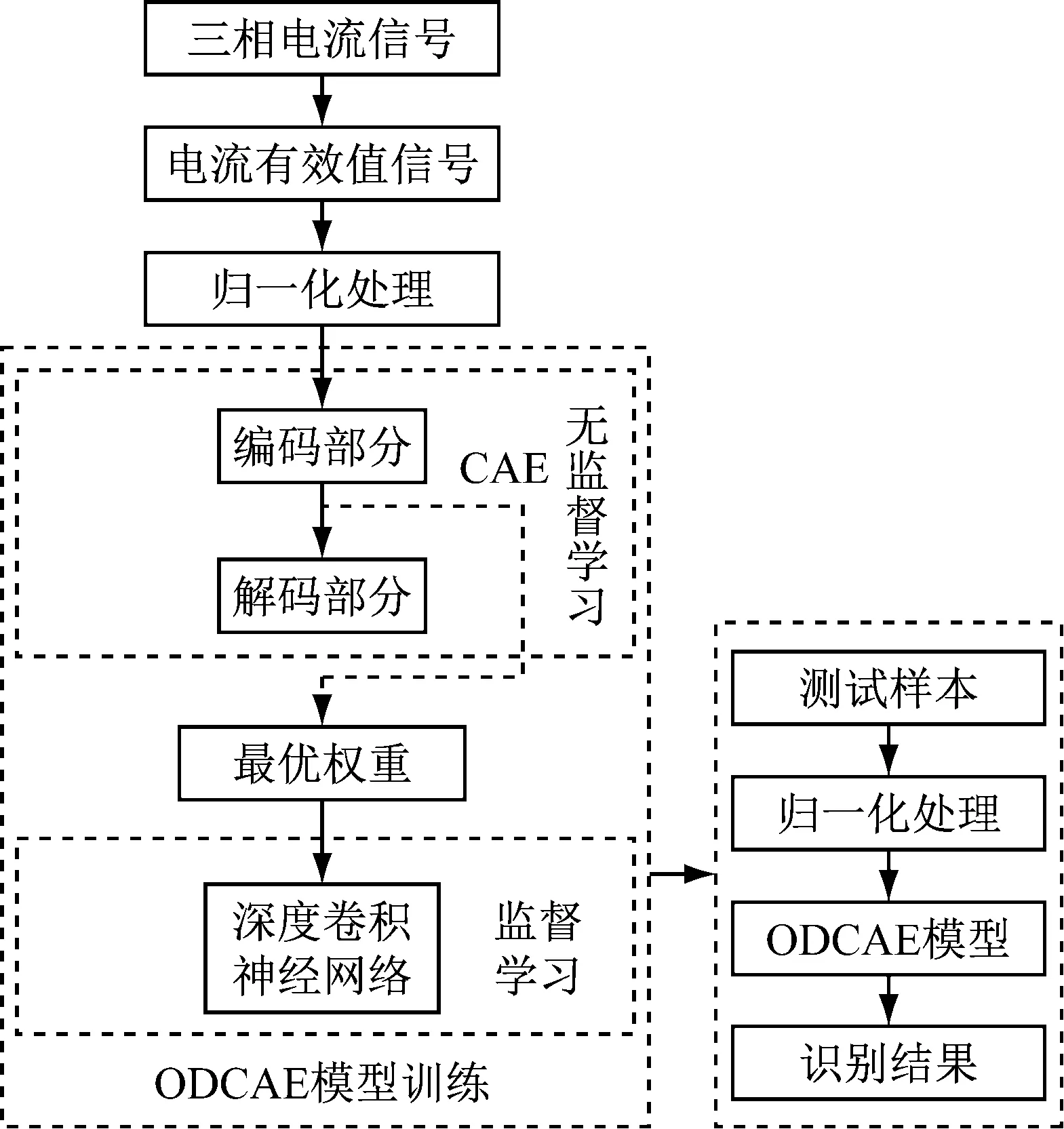
图2 刀具磨损状态识别流程图Fig.2 Flow chart of tool wear state recognition


为了测试模型在变工况条件下对刀具不同磨损状态的识别能力,在表1中设置9种不同的工况,进行循环重复加工并采集主轴电流信号。同时,为了加快刀具磨损,在铣削过程中不使用切削液,通过干铣的方式人为的将刀具磨损至不同的磨损状态。通过测量每组工况下,每次走刀后刀具后刀面的磨损量,对数据进行标记。将采集到的三相电流信号Iu,Iv,Iw根据式(7)融合为三相电流有效值Irms,根据式(8)将融合后的Irms值归一化至[0,1]区间,以此作为网络模型的输入样本。
(7)
(8)
式中:Imax为电流有效值的最大值;Imin为电流有效值的最小值。
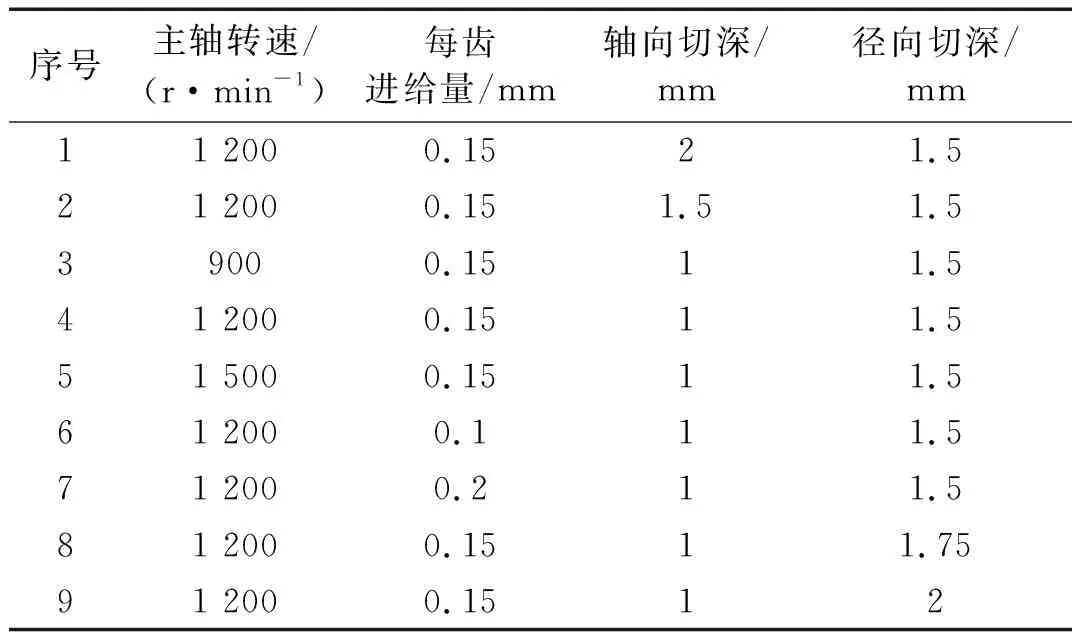
表1 加工参数
3.2 样本与标签制作
根据刀具后刀面磨损量的不同,将刀具磨损划分为6种不同的磨损状态。每种磨损状态样本数量均为200个,共获得1 200个样本,每个样本大小为2 048个点。样本标签根据刀具的不同磨损状态设定为1~6并转化为独热编码形式。取数据集的50%,即600个样本作为训练集,用于训练神经网络。300个样本作为验证集,用于调整网络的超参数。剩余300个样本作为测试集,用来最终测试模型识别精度。具体数据集划分情况如表2所示。
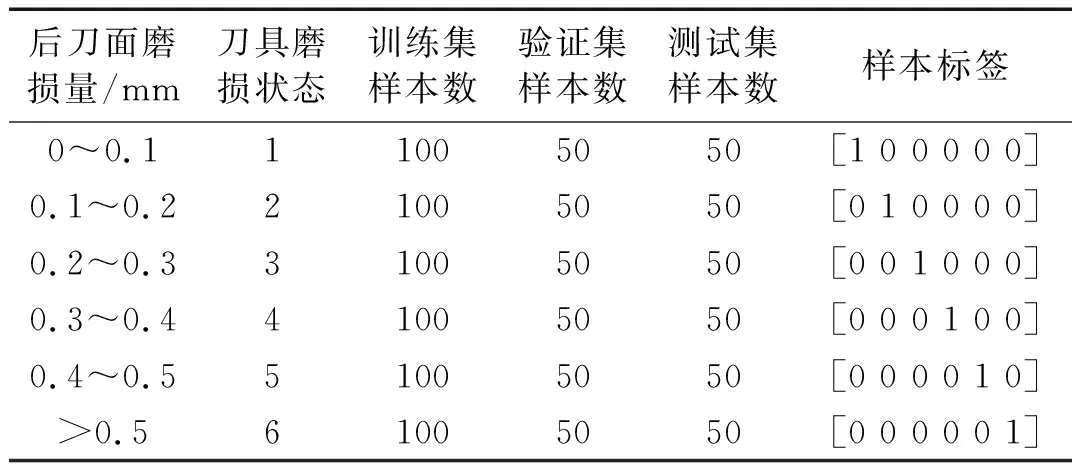
表2 数据集划分
3.3 网络超参数选择
3.3.1 优化算法的选择
梯度下降算法是一种常用的神经网络优化算法。然而,由于难以从理论上解释它们的优缺点,该算法通常被认为是黑盒优化器。为此,对以下常用的梯度下降优化算法(Adam、AdaGrad、RMSprop、SGD)进行实验比较,选择合适的优化算法。不同优化算法下,训练集损失值和验证集平均识别准确率如图7所示。
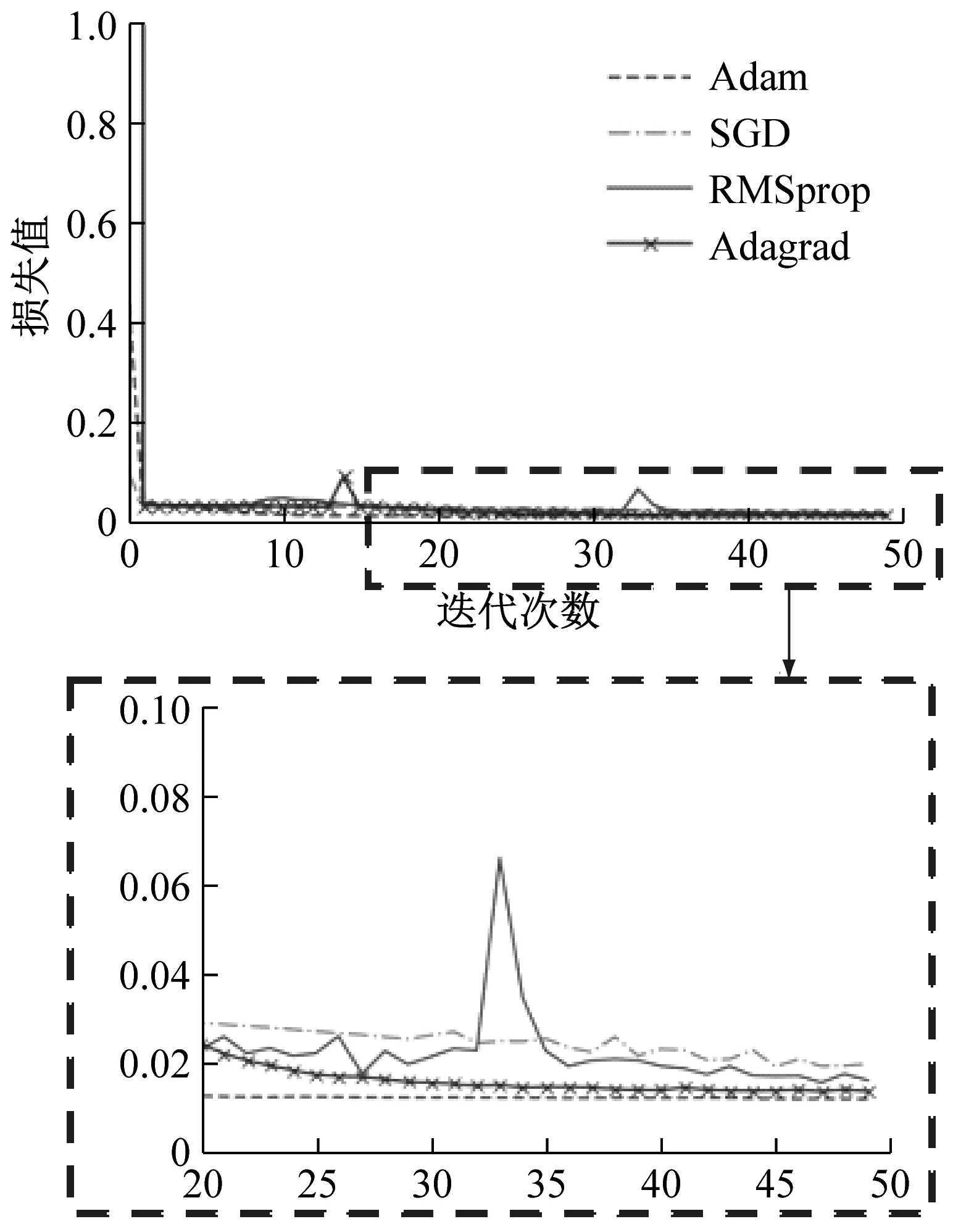
(a) 训练集下无监督学习损失值变化曲线
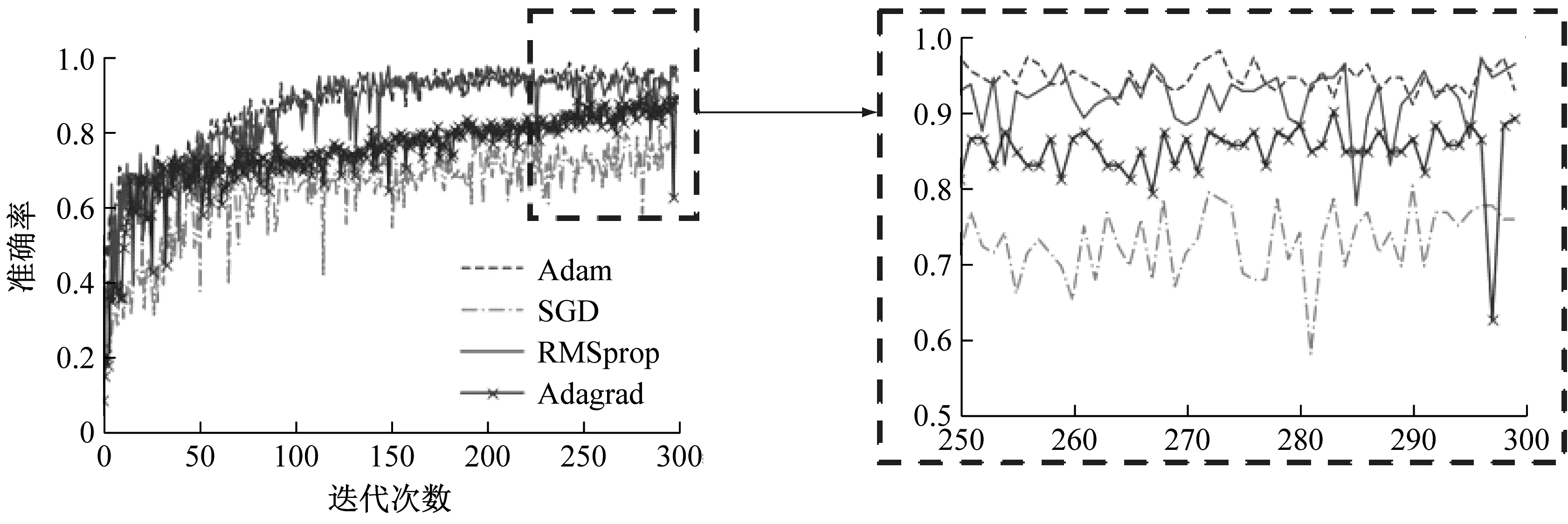
(c) 验证集下有监督学习准确率变化曲线图7 不同优化算法损失值与准确率变化曲线Fig.7 Loss and accuracy curves under different optimization algorithms
由图7可知,在无监督学习和有监督学习过程中,AdaGrad和SGD算法不仅收敛速度慢,而且训练误差较大,在有监督学习过程中尤为明显。Adam和RMSprop算法在训练过程中都获得了较小的损失函数值和极大的识别准确率,但Adam算法相对来说比较稳定,算法的鲁棒性优于RMSprop。因此,选择Adam算法来训练模型。
3.3.2 批处理大小的选择
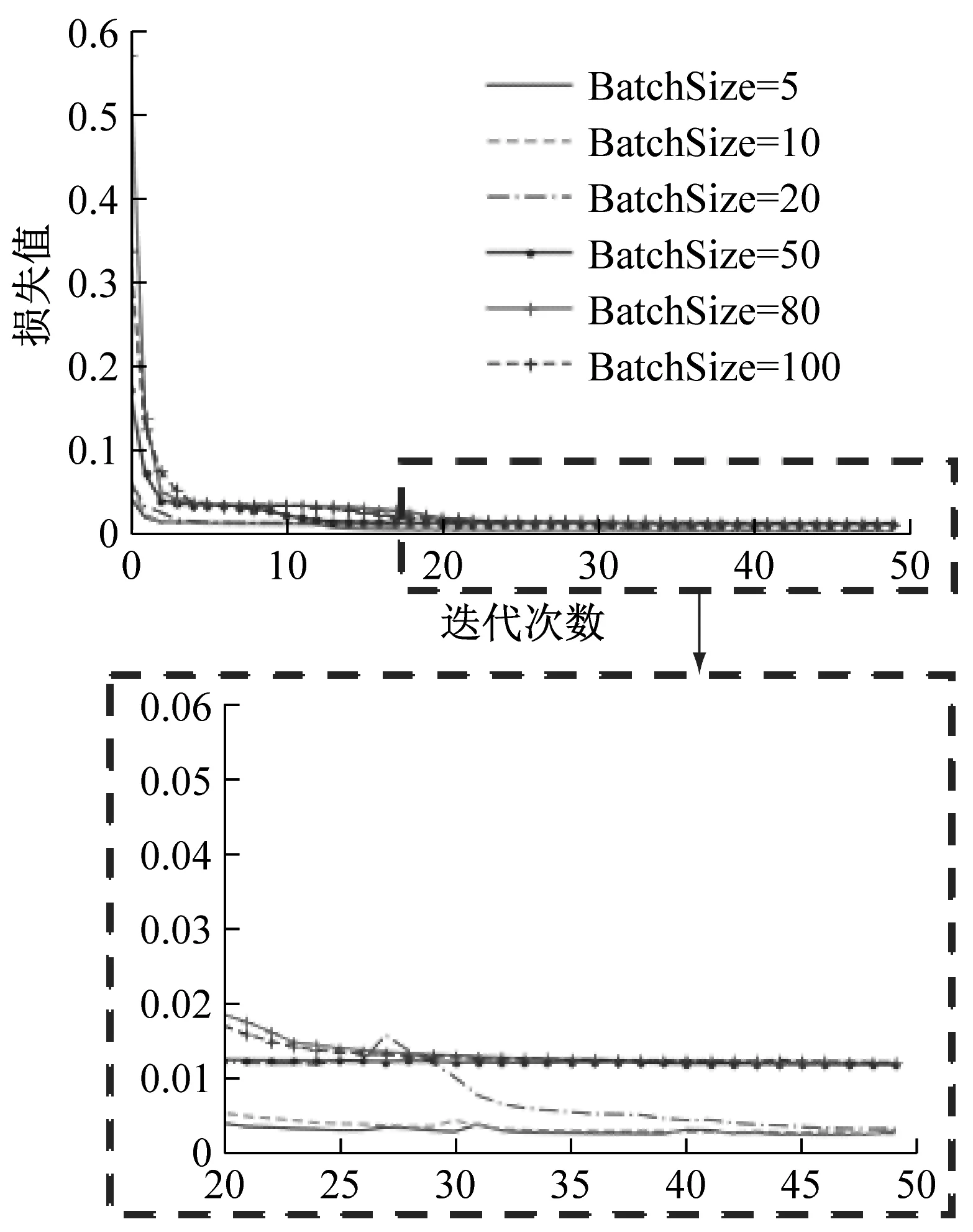
在神经网络的迭代训练过程中,批处理大小的选择会直接影响网络的收敛方向和准确率[15]。因此,在实验中对不同批量大小进行对比分析,选择使训练结果最优的批处理大小。不同批处理大小的训练集损失函数,验证集上整体平均识别结果如图8所示。
由图8可知,当批处理尺寸为5、10、20时,模型在训练过程中收敛速度较快,训练集上的损失函数值很小且相差不大。但是只有批处理大小为20时,模型在验证集上的识别率最高,网络也比较稳定,因此数据集批处理大小选择20。
3.3.3 卷积核尺寸大小的选择
通过研究发现,不同的卷积核尺寸会对神经网络的准确率产生不同的影响,对于非常小和非常大的核尺寸,模型的识别精度是非常不稳定的[16]。因此,在实验中设计不同的卷积核尺寸进行对比分析,选择合理的卷积核尺寸大小,使模型达到最优。不同卷积核尺寸的训练集损失值和验证集平均识别准确率变化如图9所示。
由图9可知,不同卷积核尺寸对无监督学习阶段的影响较小。但是当卷积核尺寸为3和5时,模型在有监督训练过程中收敛速度十分缓慢而且训练集上损失值很大。当卷积核尺寸大于7时,模型的收敛速度明显提高,训练集上的损失值很小,特别是卷积核尺寸为10和13时,模型的收敛速度最快。但是通过验证集上识别准确率对比曲线可以看出,只有卷积核尺寸等于13时,模型在在验证集上的识别精度最高。因此,网络的卷积核尺寸最终选定为13。
(a) 训练集下无监督学习损失值变化曲线

(c) 验证集下有监督学习准确率变化曲线图8 不同批处理大小损失值与准确率变化曲线Fig.8 Loss and accuracy curves under different batch sizes
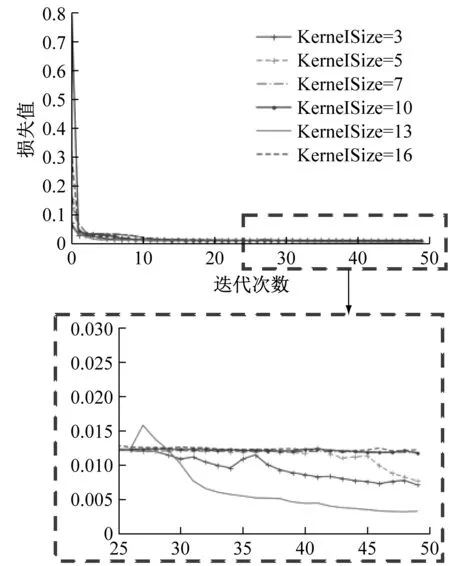
(a) 训练集下无监督学习损失值变化曲线
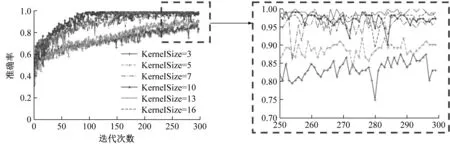
(c) 验证集下有监督学习准确率变化曲线图9 不同卷积核尺寸损失值与准确率变化曲线Fig.9 Loss and accuracy curves under different kernel sizes
3.3.4 网络层数集单元数选择
为了提高模型的识别精度,增加网络模型的深度和各特征提取层单元数是有效措施之一。但是,过度增加网络深度和单元数也会使网络精度停滞甚至下降,同样也会增加模型复杂度[17]。因此,在模型建立过程中,从平均识别准确率和训练时间两个方面,选择最优的网络层数和各特征层单元数,对比结果如表3所示。

表3 不同网络结构下ODCAE识别结果
由表3的对比结果可知,随着网络特征提取层数量的增加,对提高网络识别准确率是有帮助的,但准确率却并不是随着网络层数的增加而提高。另一方面,网络层数和各层单元数的增加,还会增加模型的复杂程度和训练时间。因此,选择平均识别准确率最高,训练时间较少的模型3作为刀具状态监测的网络结构。
通过上述对比分析,确定模型优化算法为Adam,批处理大小为20,卷积核尺寸为13,网络结构为模型3。关于模型的具体参数细节如表4和表5所示。

表4 无监督学习网络参数
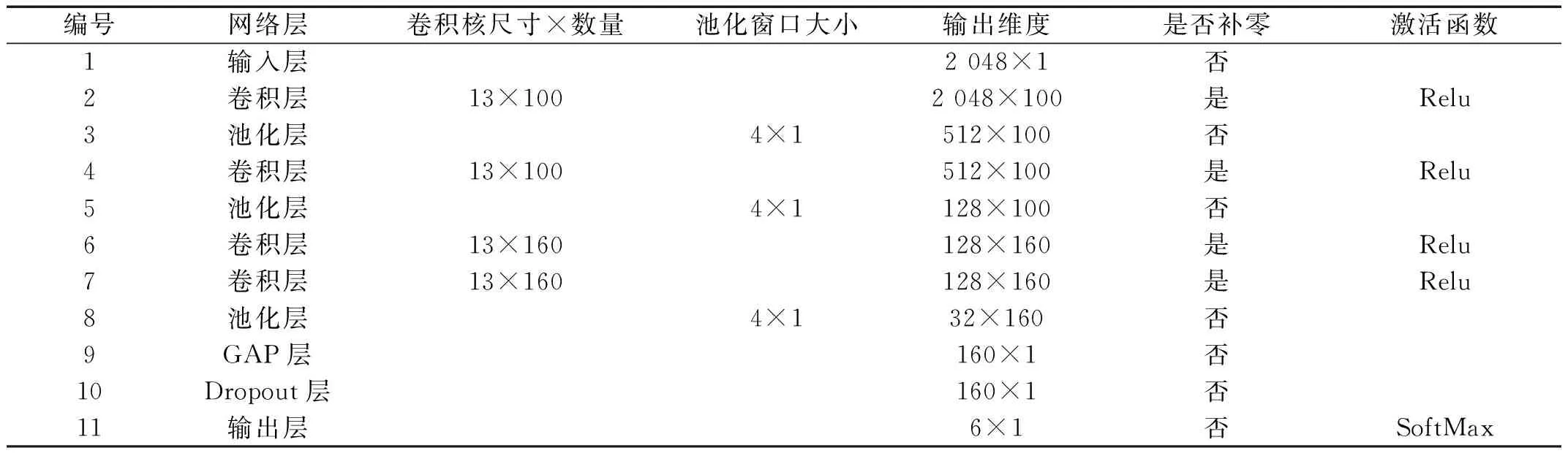
表5 有监督学习网络参数
3.4 测试结果分析
为了深入了解网络的特征提取能力,将无监督学习阶段对不同磨损状态的重构信号提取出来并做可视化分析,结果如图10所示。
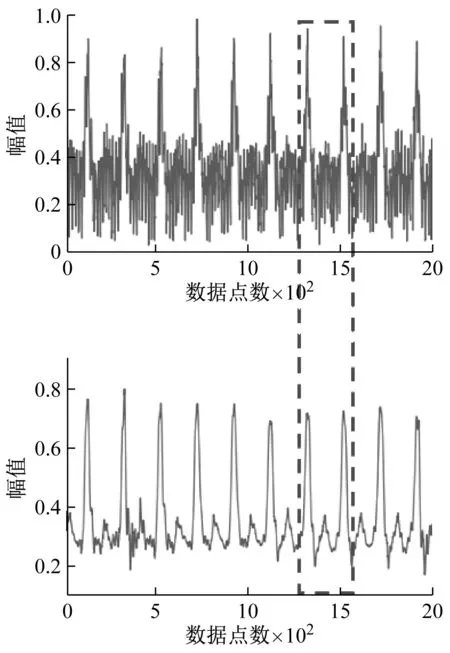
(a) 磨损状态1
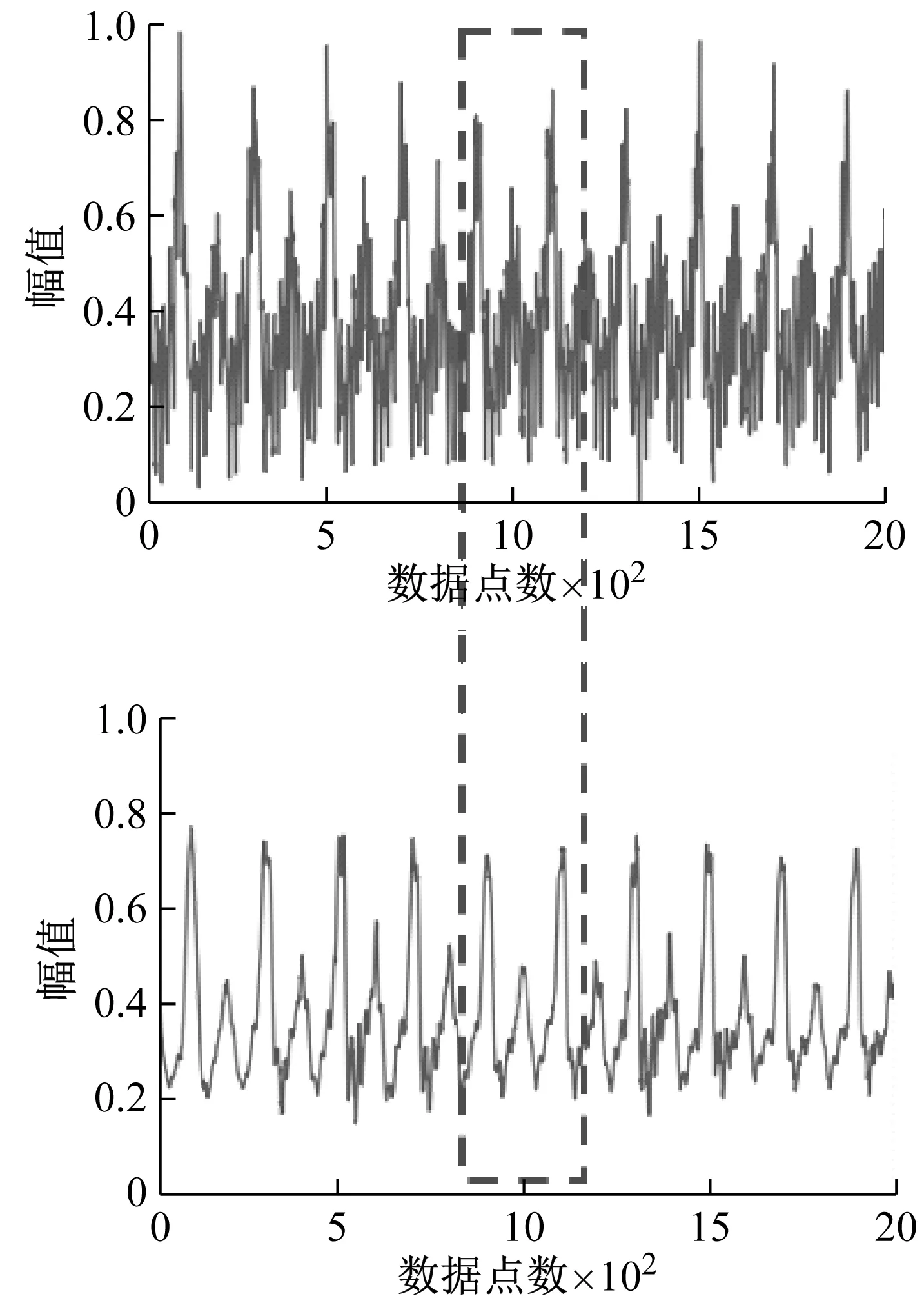
(c) 磨损状态3

(e) 磨损状态5
由图10可知,在网络无监督预训练阶段,重构信号中的噪音相比于归一化后的原始时域信号有明显的减少,这说明网络在进行预训练的过程中具有一定的抑制噪音的作用。另一方面,由于铣削加工为断续加工,刀具在旋转过程中,切削刃每次切入和切出工件都会产生明显的冲击信号。通过对比可以发现,重构信号中的冲击信号明显比原始时域信号平滑了很多并且更加显著,这说明网络的预训练还具有特征增强的作用。
为了进一步衡量模型的识别质量,在评判准则中引入卡帕系数。具体公式如下
(9)
(10)
式中:po表示总的识别精度;pe用式(10)表示;C表示类别;n表示样本总数;ai表示第i类真实样本个数;bi表示第i类预测样本个数。K值越大,模型识别效果越好。
当通过训练集和验证集调整网络超参数结束以后,利用训练好的网络模型在测试集上测试模型的识别精度。用于表示模型识别结果的混淆矩阵如图11所示。图11中0~5对应6种不同的磨损状态,坐标纵轴表示实际的磨损状态,横坐标表示网络预测的磨损状态。具体识别结果如表6所示。
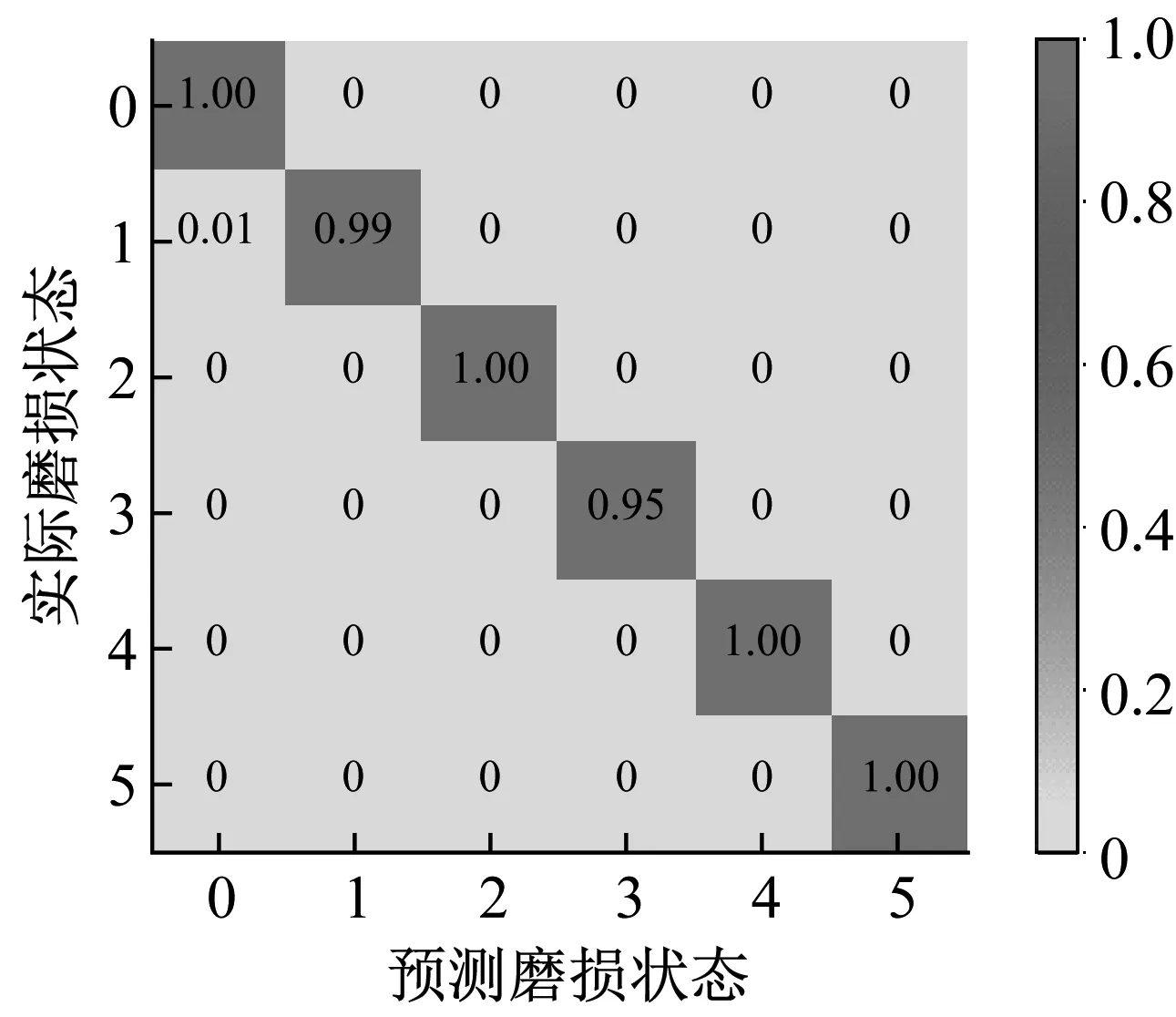
图11 测试集混淆矩阵Fig.11 Confusion matrix in the test set
由测试结果可知,ODCAE模型对不同的磨损程度的识别准确率最高可达100%,最低为95%,平均识别率达99%,卡帕系数0.984 0,充分说明本文提出的模型能够稳定且高精度的识别不同的刀具磨损状态。
3.5 一维卷积自编码器与其他方法的对比
为了突出ODCAE网络的识别能力,将SVM、文献7中堆叠降噪自编码器(SDAE)、传统一维卷积神经网络(1-DCNN)[18]与本文提出的模型作对比分析。SVM模型采用高斯核函数,人工提取原始信号中时域,频域,时频域的共19个特征,其中,时域特征包括:均值、峰峰值、方差、有效值、偏斜度、峭度值、波形因数;频域特征包括:重心频率、频率方差、均方频率、平均能量;时频域特征为通过3层小波包分解得到的8组小波包能量。传统一维卷积神经网络和堆叠降噪自编码器的参数是根据参考文献设置的。

表6 测试结果
不同模型在测试集上测试结果如表6所示。由表1中识别结果可知,本文提出的基于ODCAE的算法模型在测试集上的识别效果和模型稳定性最佳,进一步表明了ODCAE在刀具磨损状态识别上的优越性能。

表7 不同模型测试结果
为更加直观的验证本文提出方法具有优越的特征提取能力,利用t-SNE降维技术对人工提取的特征、SDAE最后一层隐含层、1-DCNN和本文方法最后一层卷积层提取得到的特征进一步降维成二维并可视化,结果如图12所示。

(a) 人工提取特征

(c) 1DCNN最后一层卷积层提取特征
由图12可知,本文提出的方法可以将每类磨损状态都聚合到一起,不同磨损状态之间边界分明,充分体现了ODCAE对时域信号特征信息的深度挖掘能力。
4 结 论
本文提出了一种基于一维深度卷积自动编码器的刀具磨损状态监测方法,合理选择网络超参数,避免了传统算法模型在模式识别前需要进行的繁琐的预处理过程,能够自适应的提取原始信号中表征刀具不同磨损状态的特征信息,实现了高精度的刀具磨损状态识别。在无监督预训练阶段,ODCAE能够很大程度的抑制原始信号中的噪音信息,具有一定的特征增强的作用。与传统的机器学习算法、一维卷积神经网络(1-DCNN)和堆叠降噪自编码器(SDAE)相比,ODCAE模型识别准确率可达99%,卡帕系数为0.984 0,表明利用ODCAE提取得到的特征信息与刀具不同磨损状态之间的相关性更强,能够准确且高效的实现刀具磨损状态识别。
在实际加工生产中,特别是在高精度复杂型面的加工过程中,除了多样的切削条件以外,加工过程本身的复杂性、走刀路径的多样性、切削液和系统噪声的干扰性以及刀具在实际加工生产中磨损的随机性都会给刀具的状态监测带来模糊性和不确定性。因此,在今后的研究中,考虑将深度学习与多传感信息融合技术相结合,多方面捕捉实际生产过程中刀具磨损的动态信息,进一步研究传感器信息与刀具状态之间的映射关系。
