基于概率主成分分析的结构健康监测数据修复方法研究
2021-11-17罗尧治万华平YUN沈雁彬
马 帜, 罗尧治, 万华平, YUN C B, 沈雁彬, 俞 峰
(浙江大学 建筑工程学院,杭州 310058)
鉴于大型结构的重要性以及发生结构破坏事故的严重性,越来越多的大型结构安装了结构健康监测系统[1-4]。结构健康监测是指利用现代传感和通讯技术,实时监测结构服役阶段(甚至施工阶段)的结构响应和环境变量,运用合理有效的信号处理方法从监测数据中提取能够反映结构健康状态的特征量,进而对结构的服役状况、承载力等进行评估,为结构的运维管理提供科学依据[5-6]。基于健康监测数据对结构状态的评估结果的准确性依赖于大量且高质量的监测数据。在长期监测过程中,由于监测设备故障、供能中断、数据传输故障等诸多因素存在,监测数据缺失情况不可避免。因此,有必要对缺失数据进行修复,为结构健康状态评估的提供完整和可靠的数据。
缺失数据修复已成为结构健康监测领域的重要研究课题,研究较为广泛。数据修复方法包括压缩传感方法[7]、神经网络方法[8-9]、多元线性回归方法[10]、贝叶斯多任务学习方法[11]等。其中压缩传感方法通过对原始数据构造随机采样矩阵,根据采样数据修复原始缺失数据,不需要额外的参考数据。但是该方法要求待修复数据在某些正交基上具有稀疏特征,对于稀疏性较弱的数据的修复效果较差,例如日常环境荷载作用下的结构应力响应监测数据。其余数据修复方法则通过建立缺失数据与参考数据间的相关关系,利用参考数据对缺失数据进行修复,例如采用荷载输入数据或未缺失数据对缺失数据进行修复。其中多元线性回归方法假设缺失数据与参考数据的关系为线性,未考虑潜在的非线性关系,因此具有一定的局限性。神经网络方法和贝叶斯多任务学习方法能够较好的建立缺失数据与参考数据间的非线性关系,因而有着较高的修复准确率。但是这两种方法需要采用各测点均完整的监测数据来建模,当完整监测数据较少时,得到的预测模型精度难以保证,会影响数据修复的效果。为此,针对日常环境荷载作用下各测点均存在数据缺失,完整监测数据较少的情况,本文引入了概率主成分分析方法对结构健康监测数据进行修复。
概率主成分分析(probabilistic principal component analysis,PPCA)[12]是主成分分析(principal component analysis,PCA)的一种概率形式。PPCA能够在完整数据较少时,利用最大期望(EM)算法找到各组数据间的隐含关系,进而对缺失数据进行修复,无需对完整数据进行训练。此外,PPCA能够量化数据修复值的不确定性,给出修复结果的置信区间。基于以上优势,PPCA在结构健康监测数据修复领域有着很大的应用前景,但是目前还缺乏相关的研究。本文结合PPCA的特点,针对不完整的多测点响应数据建立PPCA模型,对各测点的健康监测数据进行修复。武夷山旋转观众席的实测数据用来验证方法的有效性,并讨论了不同测点数目、数据缺失类型和缺失率、以及选取的主成分个数对修复效果的影响。另外,在不同数据缺失工况下,对比了PPCA、PCA、多元线性回归、K最近邻法以及压缩传感方法五种方法的数据修复效果,结果表明PPCA的数据修复效果最佳。
1 主成分分析
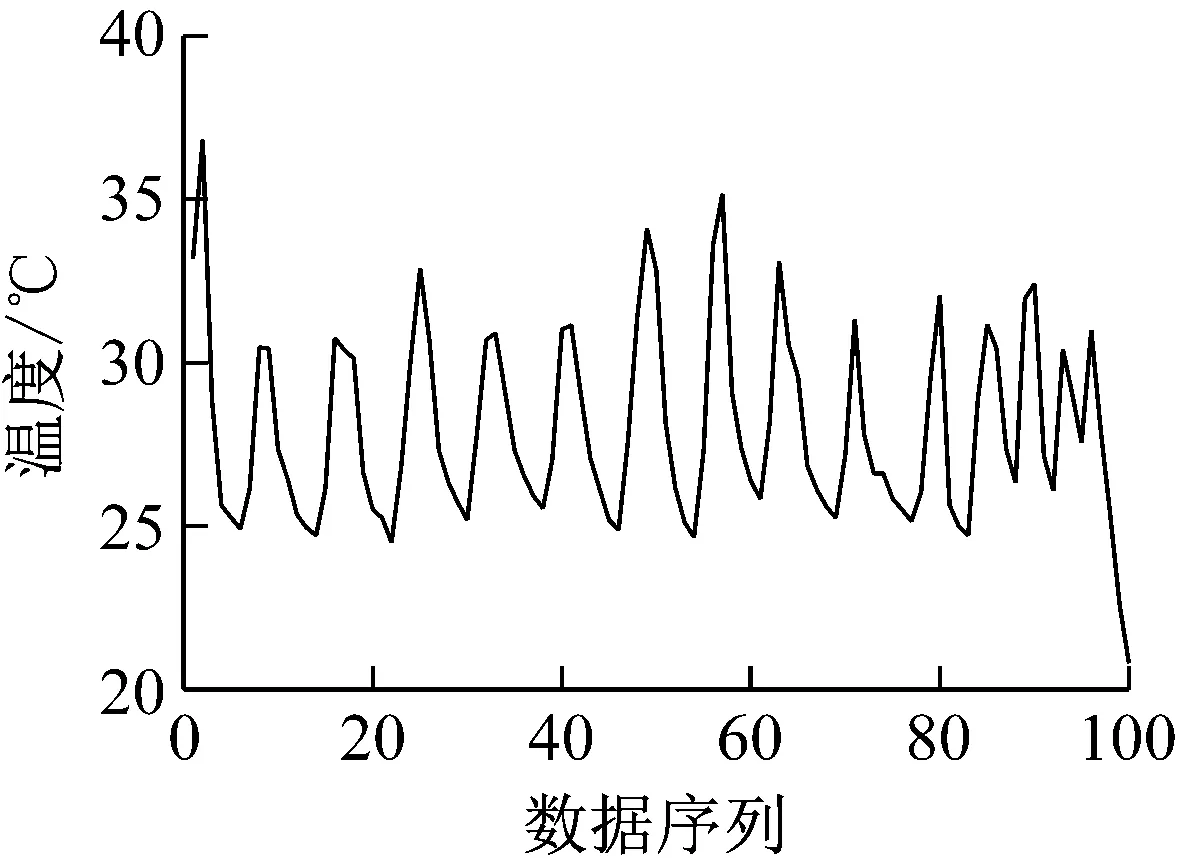
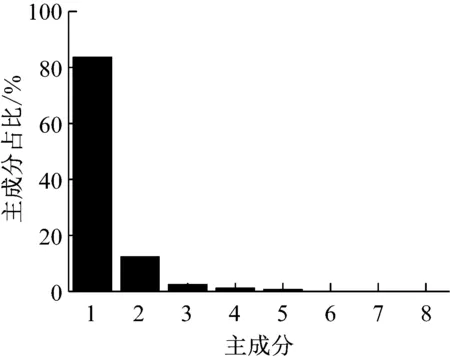
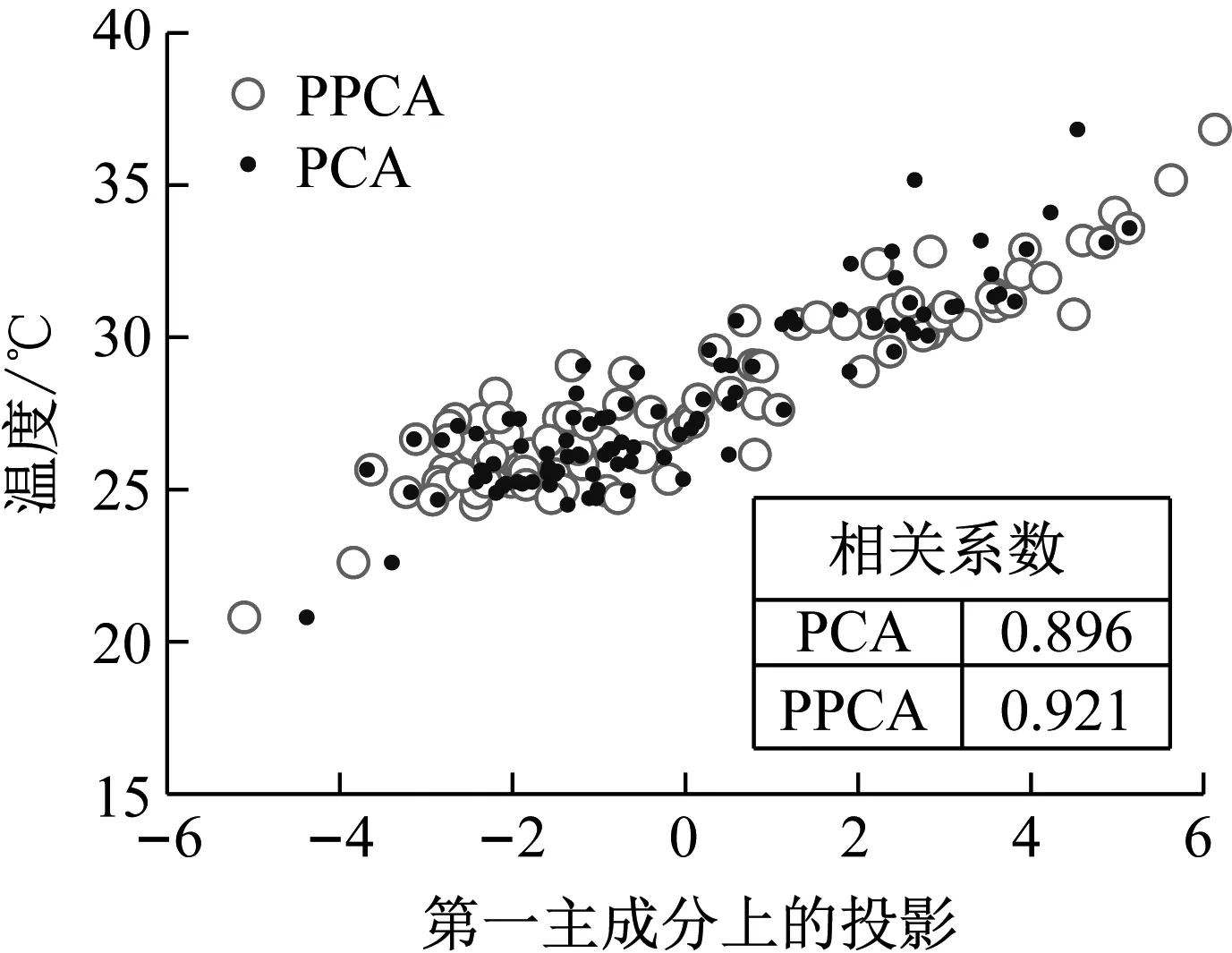
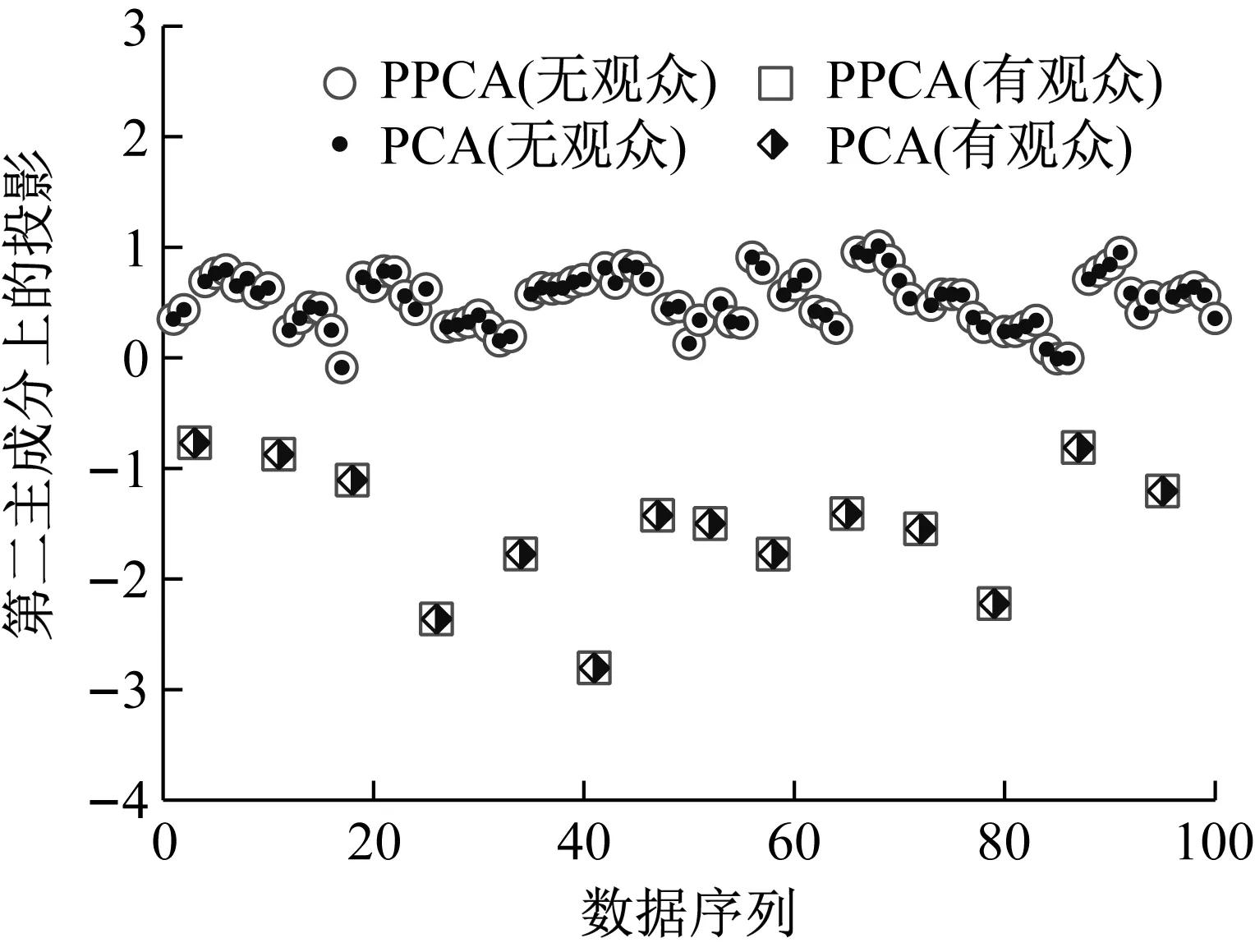
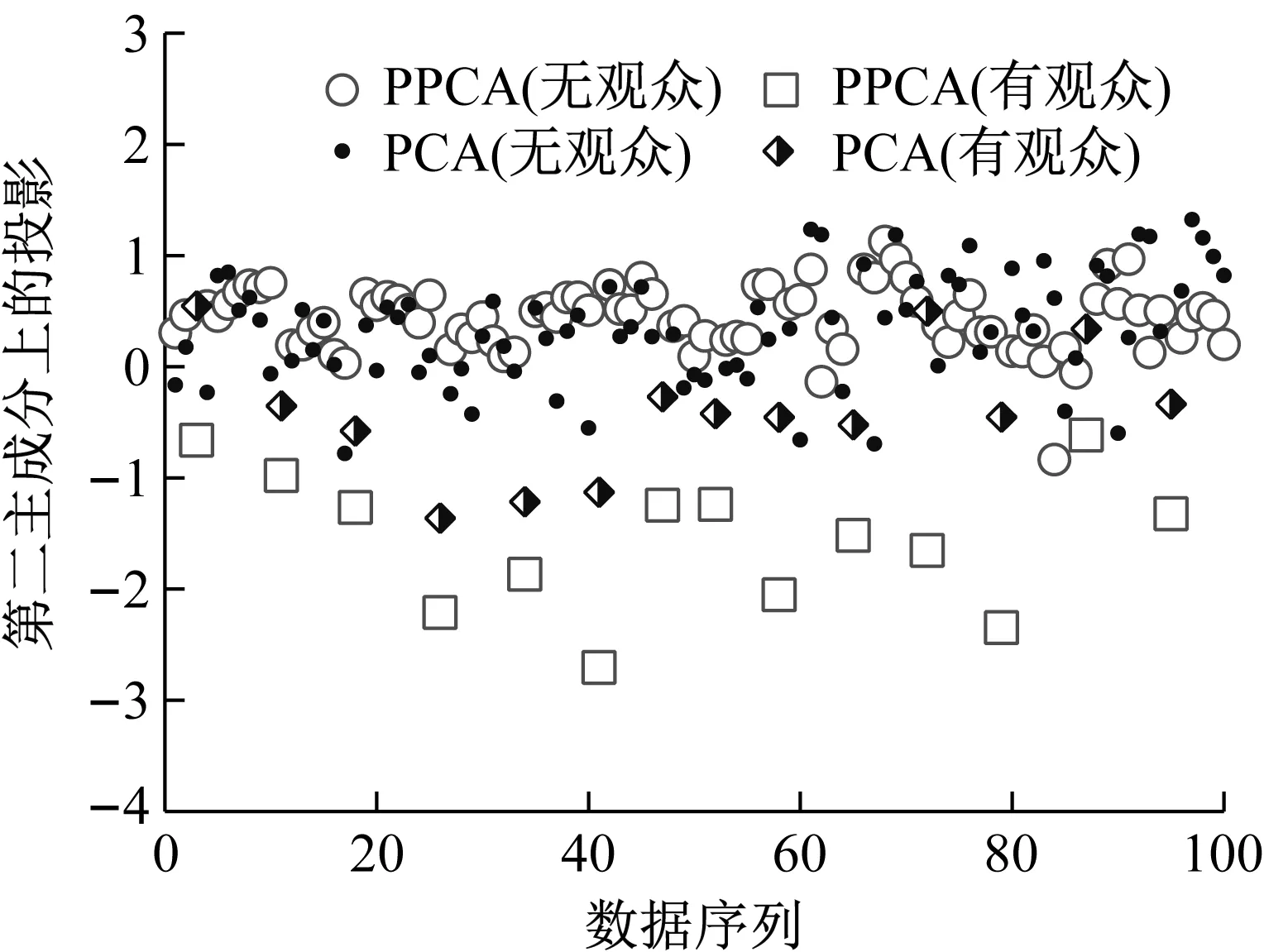
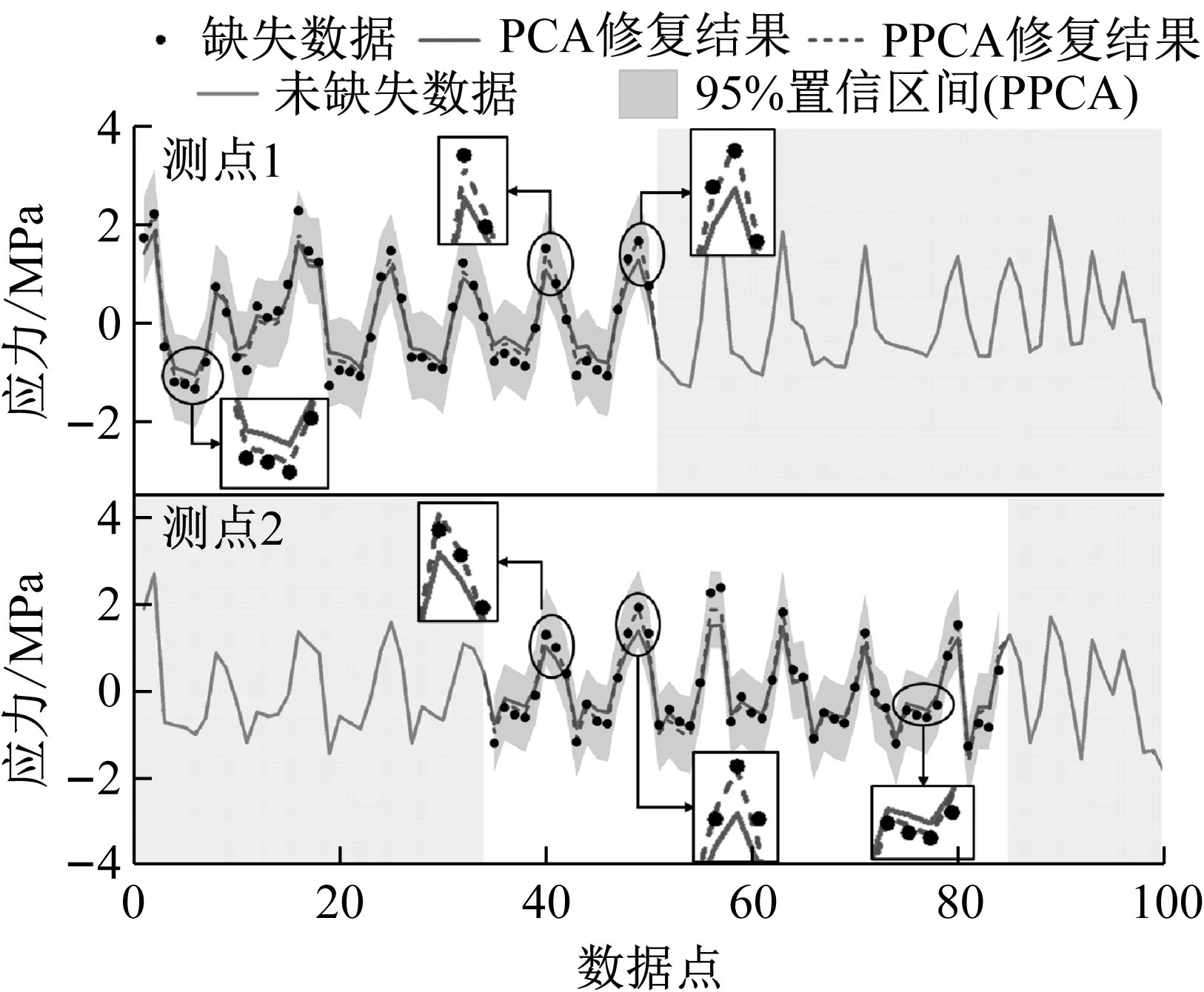
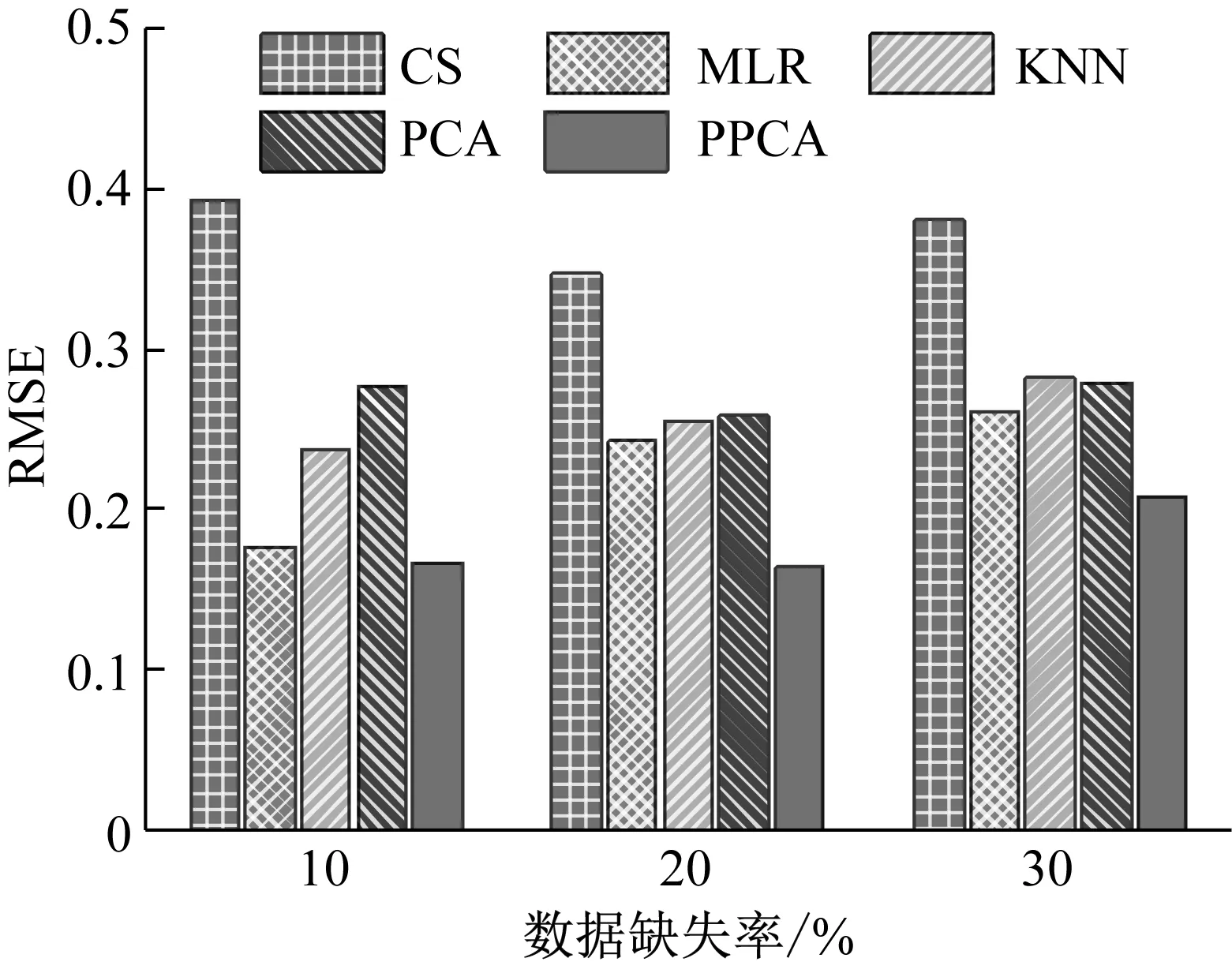
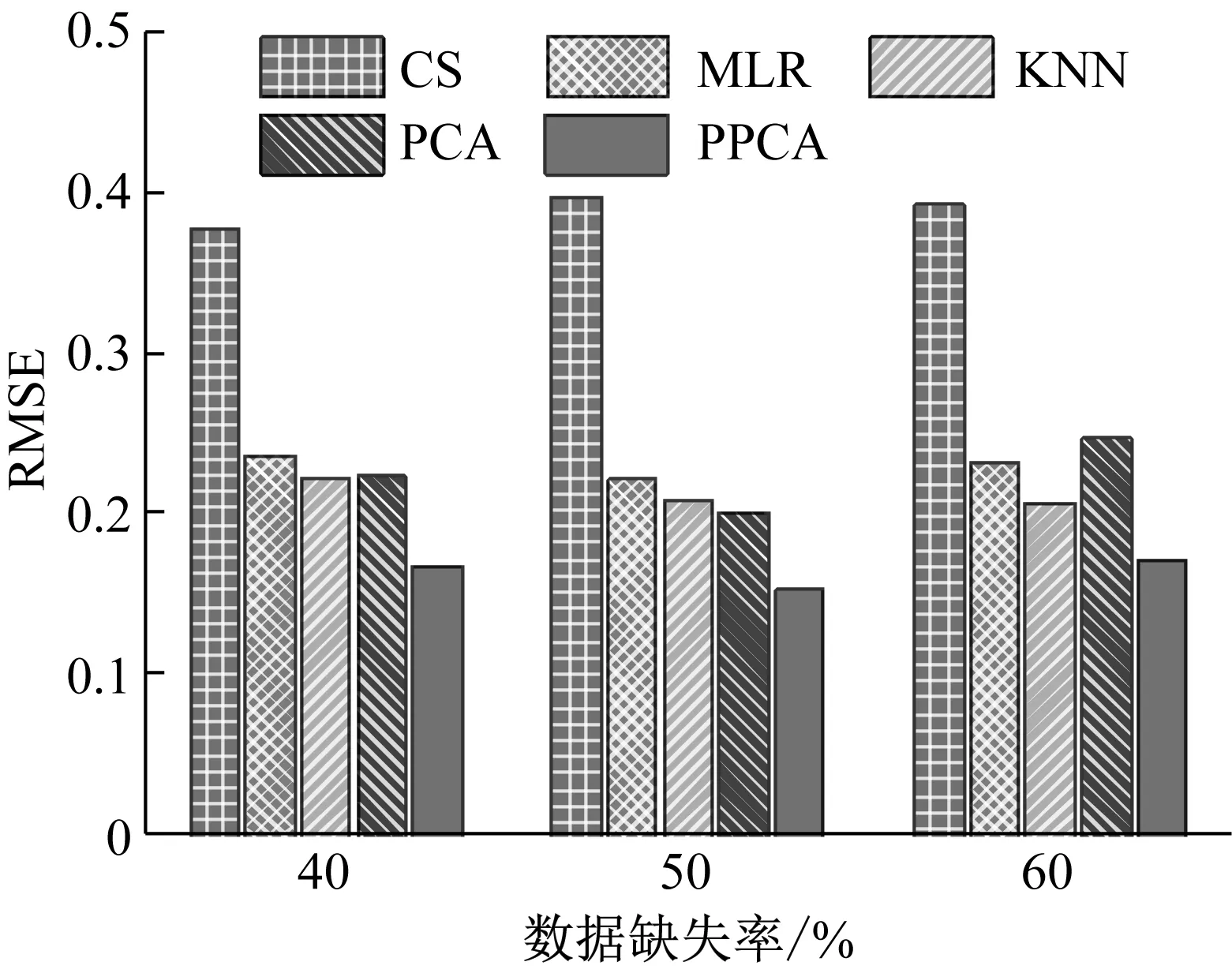
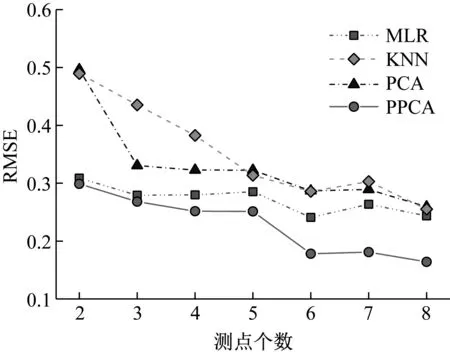
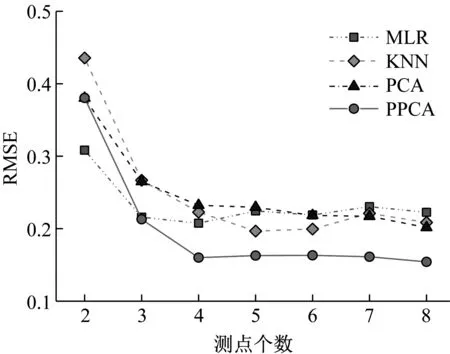
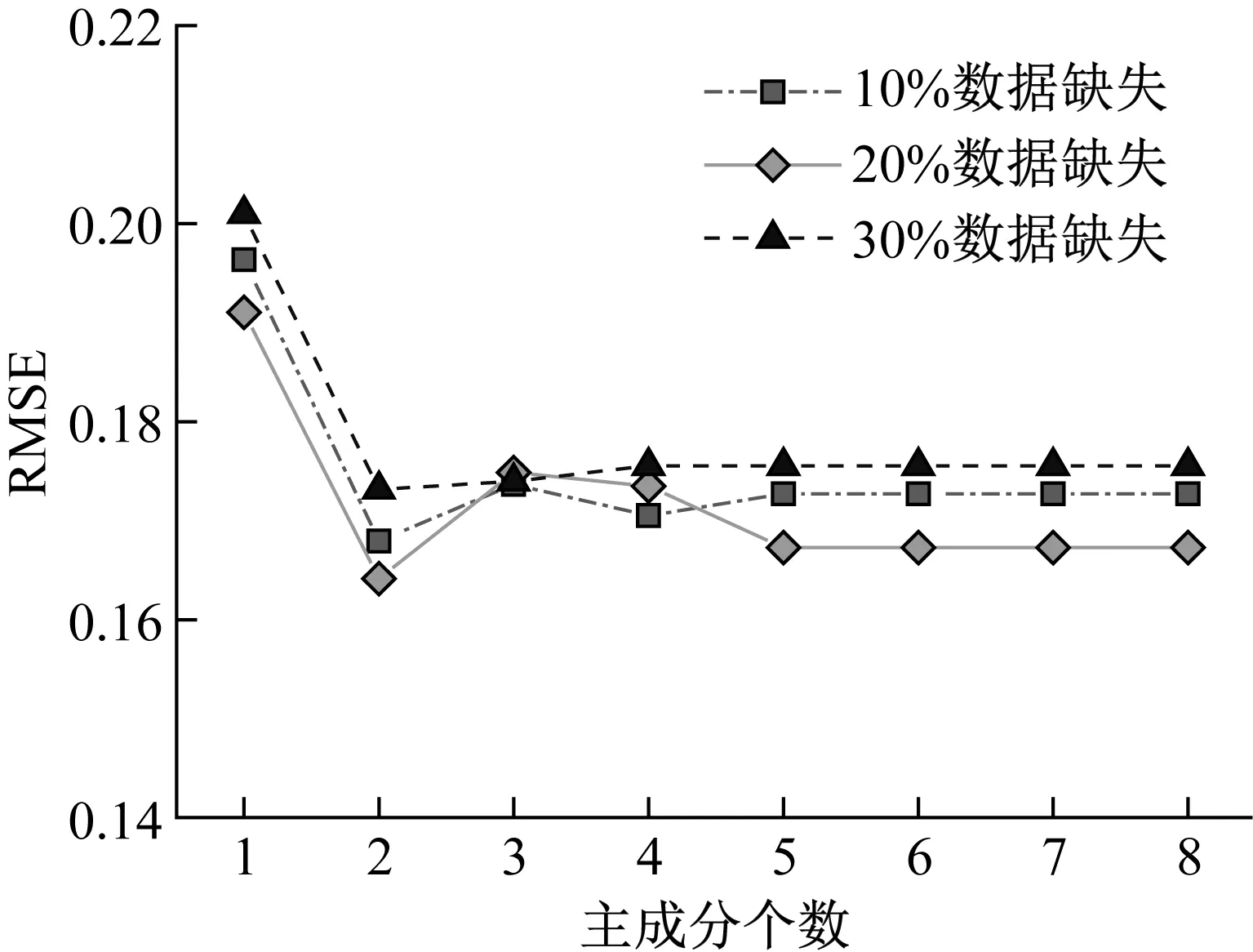
主成分分析(PCA)[13]能够将高维相关变量转化为低维互不相关的变量,广泛应用于多元数据的降维分析。对于一个d维数据向量,若其含有N个观测值ti,i∈{1,…,N},则PCA的目标是寻找q组d维(q Spj=λjpj (1) 观测向量ti在主成分轴上的投影向量可由下式得到 xi=PT(ti-μ) (2) (3) 在重构的观测向量中,仅使用了前q个主成分相关的信息,忽略了其他不重要的部分。由完整的观测数据计算得到主成分矩阵P,通过待修复数据中未缺失部分的数据计算得到投影向量,能通过式(3)对缺失数据进行修复。 在概率模型中,定义d维的观测向量ti,i∈{1,…,N}与一个q维的隐变量xi之间存在如下的线性关系 ti=Wxi+μ+εi (4) 式中:εi为残差向量;W是一个d×q维的转换矩阵,在这里由前q个主成分轴构成。通常情况下,假定隐变量xi相互独立,且服从单位方差的高斯分布,即xi~N(0,I),其中I为q维的单位矩阵。残差向量εi同样假定相互独立,在各维度数据中的噪声水平相当的情况下,可以假定残差向量服从一个各向同性方差的高斯分布,即εi~N(0,σ2I)。在给定隐变量xi的条件下,观测向量ti的条件概率分布为 ti|xi~N(Wxi+μ,σ2I) (5) 根据贝叶斯定理,在已知观测向量ti之后,可以得到隐变量的后验概率分布,也为高斯分布 xi|ti~N(M-1WT(ti-μ),σ2M-1) (6) 式中,M=WTW+σ2I。隐变量xi实际上为前q各主成分上的投影。 PPCA无法像PCA一样存在解析解,其参数可通过最大似然法求得,即寻找最优的W和σ2,使得观测向量ti的似然函数值最大。由式(5)可知,ti的似然函数涉及到隐变量xi,且其自身包含一部分缺失数据,采用最大似然法得到的结果是隐式的。因此,通常需要采用最大期望(EM)算法用来同时估计主成分轴、误差水平和缺失数据。 EM算法是通过迭代进行极大似然估计的优化算法,非常适用于包含隐变量或缺失数据的参数估计。EM算法的迭代循环由E-step(Expectation step)和M-step(Maximization step)组成。在E-step,根据现有的模型参数对缺失数据和隐变量进行后验估计,然后代入对数似然函数,得到仅与模型参数相关的新的对数似然函数。在M-step,重新估计最优的模型参数,使得新的对数似然函数值最大。 (7) 其中,联合概率密度p(ti,xi)可以通过条件概率公式求得。 (8) (9) 在M-step,重新估计使对数函数最大的模型参数W和σ2 (10) (11) 式中:N为观测向量个数;d为观测向量维度。在EM算法中,E-step和M-step不断迭代,直到模型参数收敛。 采用EM算法估计PPCA模型参数和修复缺失数据的具体步骤如下: (1) 初始化模型参数W及σ2和将缺失数据设为0,根据式(9)求得初始隐变量的后验期望; (2) E-step:根据式(8)和上一个循环步的模型参数和隐变量,估计缺失数据; (3) E-step:根据修复后的观测数据和式(9)计算隐含变量xi的后验估计〈xi〉; (4) M-step:根据式(10)和(11) 重新估计模型参数W和σ2; (5) 重复步骤(2)~(4),直到模型参数收敛。 武夷山旋转观众席位于福建省武夷山市武夷山景区,是大型户外实景演出“印象大红袍”的重要组成部分。如图1所示,该观众席主体结构通过132个导轮支承于四环钢轨道上。通过液压马达驱动,该结构可做360°旋转,最大旋转速度可达到1.2°/s。演出期间,该观众席结构可承载超过2 000名观众,并在旋转中提供360°的演出视角及自然实景景观。观众席主结构为钢网架结构,最高处为10.88 m,直径为46.6 m,质量为520 t。 为保障武夷山旋转观众席结构的运营安全,该结构安装了结构健康监测系统(如图2所示),该系统为浙江大学空间结构研究中心自主研发的长期无线监测系统[15]。无线监测系统非常适用于旋转结构,解决了旋转结构布线困难的问题。该系统已成功应用于多个大跨度空间结构的健康监测,如国家体育场“鸟巢”[16]、杭州奥体中心体育场、杭州东站等[17]。监测数据通过无线节点传输到本地基站,之后将会通过无线网络上传到监测云数据库,并同步在云数据库网站和浙江大学监测中心进行展示。 旋转观众席主结构上总共布置有55个振弦式传感器,其中34个传感器安装于立柱构件上,12个安装于环梁构件上,9个安装于斜杆上。系统每天自动采集8次应变和温度数据,采集间隔为3小时。每天的21:00时刻属于活动表演时刻,结构正承受观众荷载。 选取结构某径向桁架的一端作为子结构来进行研究(如图3所示),8个测点的应力监测数据作为观测数据(如图4所示),每个测点共100个数据点,用于演示数据修复方法。图5所示为相应的温度荷载变化。 (a) 旋转观众席总体构造 (b) 旋转观众席 (a) 无线传感器节点 (c) 无线监测系统示意图2 旋转观众席无线监测系统Fig.2 The wireless monitoring system of revolving auditorium 图3 相关测点布置Fig.3 Layout of relative strain sensors 假设所有测点均存在20%缺失,缺失方式随机,此时所有测点数据均未缺失的完整数据是很少的。PCA只能基于完整数据计算主成分矩阵,因此可能会因完整样本不足而导致误差较大。相比之下,PPCA对完整数据的数量没有要求。为确定后续分析中所采用的主成分数量,选取所有8个主成分建立PPCA模型,各主成分占比如图6所示。从图中可看出,前两个主成分占比超过了95%,为此后续分析选取前2个主成分进行数据重构。 PPCA和PCA均用于完整监测数据和缺失数据,建立主成分矩阵,得到前两个成分上的投影。其中,第一主成分的投影与温度荷载有着较强的相关性,图7为第一主成分的投影与温度的关系,从图中可看出,对于完整数据,PPCA和PCA结果基本相同,第一主成分的投影与温度荷载的相关系数均为0.923。基于20%数据缺失的数据,PPCA方法对应的相关性依然较高,相关系数为0.921;PCA方法对应的相关性有一定减弱,相关系数降为0.896。图8为两种方法对应的第二主成分上的投影。当无数据缺失时,两种方法的投影在有观众荷载作用时均有一个大的负值,表示了观众荷载的出现,其幅值与观众荷载的大小有关。当有数据缺失时,PPCA方法依然能够反映观众荷载,且与完整数据的结果基本相同,而PCA方法则不再能较好的反映观众荷载。以上结果表明,PPCA方法依然能够较准确的得到主成分矩阵,从而能够较准确的修复缺失数据;PCA方法得到的主成分矩阵则存在一定偏差,从而影响缺失数据修复的准确性。 图4 结构应力响应监测数据Fig.4 Measured stress data 图5 结构的温度荷载序列Fig.5 Temperature variations of the structure 图6 主成分占比Fig.6 Percentages of the eigenvalues (a) 完整数据 (b) 20%随机数据缺失图7 第一主成分上的投影与温度的关系Fig.7 Correlation between projections on the first PC andtemperature (a) 完整数据 (b) 20%随机数据缺失图8 第二主成分上的投影Fig.8 Projections on second PC PPCA方法和PCA方法用于对缺失数据修复,这里仅给出测点1和2的结果。PPCA除给出了缺失数据的修复值外,还给出了置信区间。由图9(a)可知,PPCA的修复结果比PCA更接近于数据真实值。为了考察PPCA方法和PCA方法处理连续数据缺失情况的效果,假设数据缺失为连续缺失。PPCA方法和PCA方法数据修复结果如图9(b)所示,同样可以看出PPCA方法的数据修复效果优于PCA方法。 (a) 随机数据缺失(所有测点) (b) 连续数据缺失(测点1和2)图9 测点1和测点2数据插补结果Fig.9 Data recovery results for sensors 1 and 2 为了更全面考察PPCA方法用于缺失数据修复的效果,选取多元线性回归法(MLR)、K最近邻法(KNN)和压缩传感方法(CS)用作对比对象。对于神经网络和贝叶斯多任务学习方法,由于本文涉及的监测数据中的完整数据较少,模型训练效果不理想,因此不用来对比。其中压缩传感方法将未缺失的数据看成是随机采样的样本来修复缺失数据。多元线性回归法基于各测点数据间的线性回归关系,利用未缺失的测点对缺失测点数据进行修复。K最近邻法将每一次采样得到的各测点数据看作多维坐标,在所有监测序列中选取与缺失点欧拉距离最近的K个样本,将这K个样本对应缺失测点的值的平均作为缺失数据的修复结果[18]。为了量化五种数据修复方法(PPCA、PCA、MLR、KNN、CS)的效果,采用数据修复均方根误差(RMSE) (12) (a) 所有测点随机数据缺失 (b) 测点1和2连续数据缺失图10 五种修复方法的数据修复均方根误差(RMSE)Fig.10 RMSE of the recovered data by five recovery methods 图11所示分别为随机缺失和连续缺失工况下,选取不同数量的测点进行分析时,四种方法的数据缺失均方根误差比较。由于压缩传感方法只采用了待修复测点本身的数据,而没有参考其他测点的数据,在这里不再对其讨论不同测点数量的影响。从图中可看出,四种方法的修复均方根误差基本都随着选取测点的增多而减小,且PPCA的修复效果在大部分情况下都是最优的,仅仅在连续数据缺失工况选取2个测点进行分析时不如多元线性回归方法。 (a) 所有测点随机数据缺失 (b) 测点1和2连续数据缺失图11 选取不同数量测点分析时四种方法的修复RMSE 接着考察主成分个数对PPCA方法修复效果的影响。图12为不同主成分个数下的数据修复均方根误差。从图中可看出,对于三种数据缺失率工况,2个主成分对应的数据修复误差均最小。这是因为前2个主成分反映了各测点间的隐含关系,其余主成分则代表了观测误差,选取次要的主成分会引入误差,从而影响了数据修复的效果。 图12 选取的主成分个数对数据修复误差的影响Fig.12 RMSE of recovered data using different numbers of PCs 本文引入了概率主成分分析方法对结构健康监测数据进行修复,武夷山旋转观众席结构的监测数据用来验证方法的有效性。同时,对比了PPCA、PCA、多元线性回归法、K最近邻法和压缩传感方法五种数据修复方法的效果。得到的主要结论如下: (1) 基于EM算法,PPCA方法能够在数据缺失情况下依然能较准确地估计主成分矩阵。PPCA方法的主成分投影更接近完整数据的结果,对主成分矩阵的识别更为准确,因而能得到更准确的修复结果。 (2) 在概率框架里,PPCA能够估计原始数据中的不确定性水平;PPCA除了给出缺失数据的修复值外,还给出了对应的置信区间。 (3) 与PCA、多元线性回归法、K最近邻法和压缩传感方法四种数据修复方法相比,PPCA方法在不同缺失工况和不同缺失率下的修复效果均最佳。 (4) 选取过多的主成分进行PPCA建模,会引入额外误差,降低数据修复的准确性。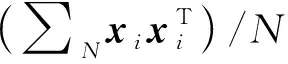
2 概率主成分分析的数据重构方法
2.1 概率主成分分析
2.2 EM算法及数据重构
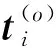
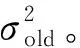
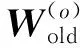
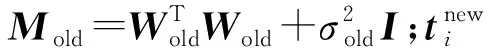
3 武夷山旋转观众席
3.1 结构简介
3.2 结构健康监测系统
4 结构健康监测数据修复
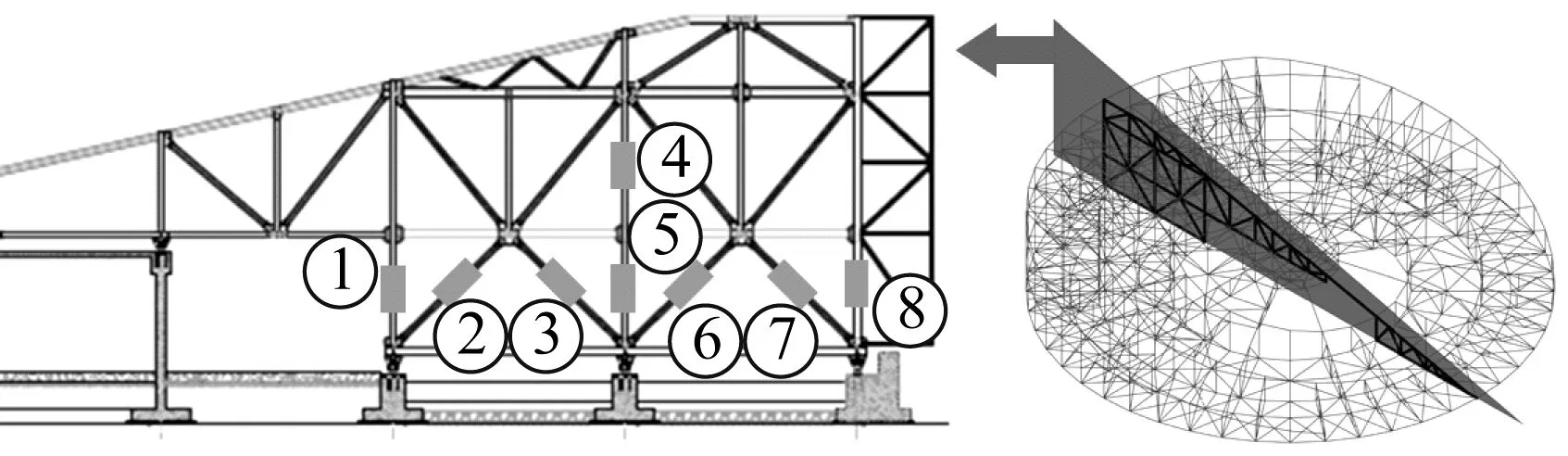
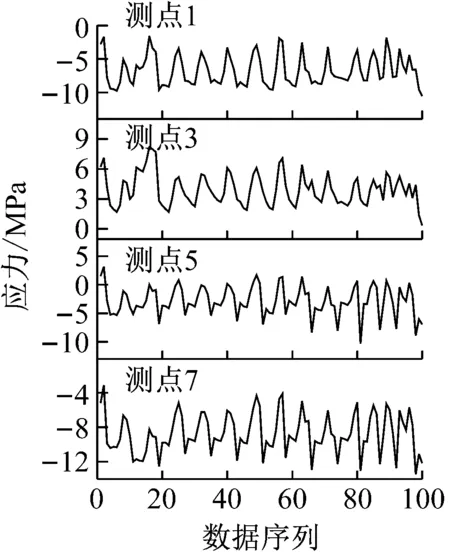
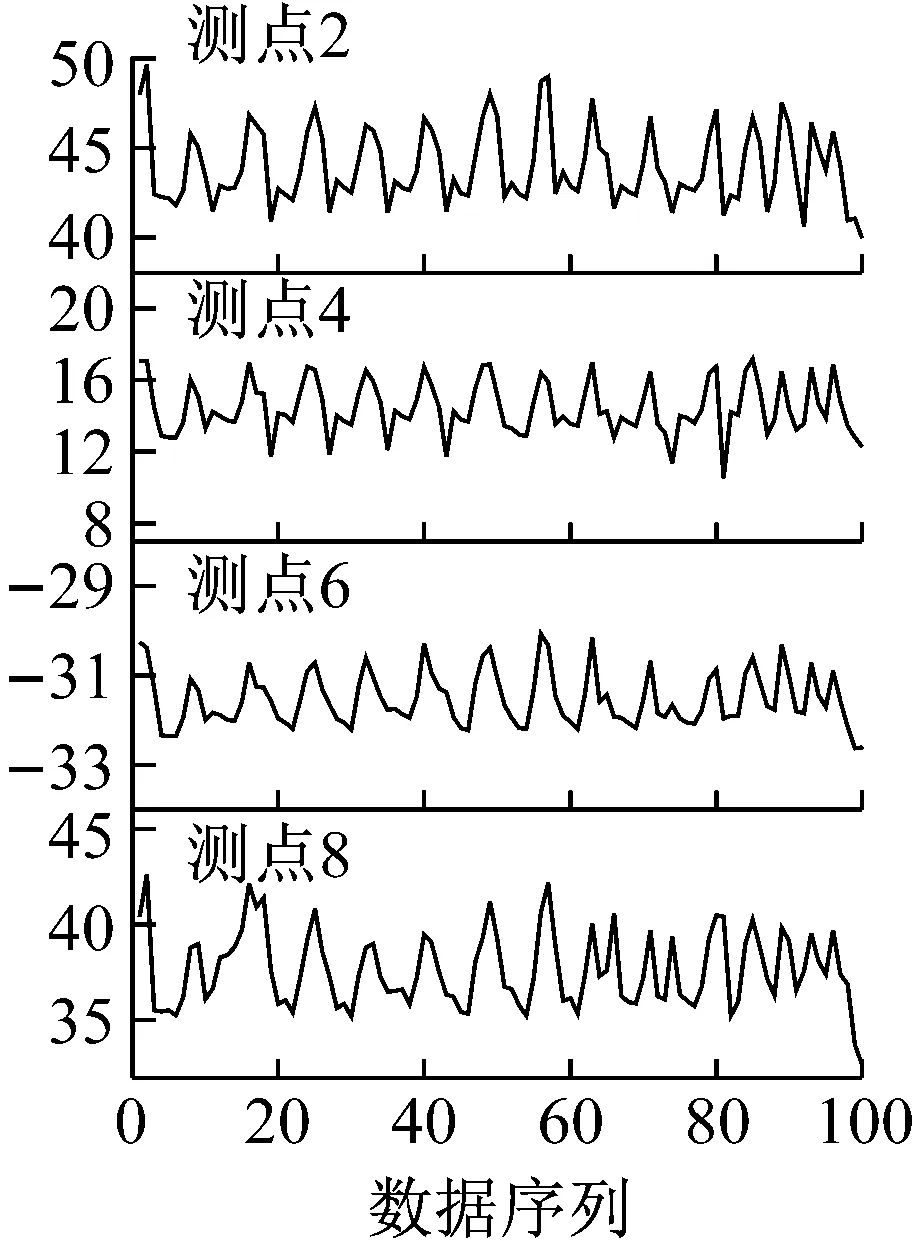
4.1 监测数据介绍




4.2 PPCA模型建立

4.3 缺失数据修复

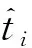
5 结 论
