基于RFOA优化GRNN的水电机组振动预测
2021-11-17王继选胡润志张少恺曹庆皎王利英
王继选, 胡润志, 管 一, 张少恺, 曹庆皎, 王利英
(河北工程大学 水利水电学院,河北 邯郸 056038)
作为水电站的核心设备,水电机组安全稳定的运行不仅可以产生巨大经济效益,同时可以确保整个厂区的安全[1-3]。研究表明,机组振动信号能够反映机组的故障信息。水电机组在运行过程中受到多种因素共同作用,其中主要影响因素包括水力、机械、电磁等,因此其振动情况十分复杂,很难准确确定其振动规律。随着机组运行时间不断地累积,机组各个部位会出现不同程度损耗,随着损耗程度不断加剧,机组性能会不断下降,部分设备甚至会出现故障,严重影响水电机组安全稳定的运行[4-5]。因此,为了提高水电机组运行效率,保证水电机组的安全可靠运行,需要对水电机组振动趋势预测进行相关研究,为维护人员提前发现水电机组故障并及时检修进而保证水电机组运行的综合效益提供保障。
由于水电机组振动具有非平稳、非线性特点,传统的预测理论难以实现对水电机组振动趋势预测。神经网络以其强大的自学习和自适应能力、并行分布处理能力以及对多维复杂非线性关系的建模能力而受到研究者的广泛青睐[6-9]。神经网络建模在水电机组振动趋势预测领域已被广泛应用。Wu等[10]使用将灰色关联分析(GRA)和模糊支持向量回归(FSVR)相结合的预测方法应用于水电机组的振动预测,通过对比实验,验证了该方法的准确性。贾春雷等[11]建立了水电机组 BP 神经网络预测模型对水电机组振动趋势进行了预测,预测结果验证了该模型的可行性。与BP神经网络相比,广义回归神经网络(GRNN)结构简单,参数设置单一。在处理函数逼近能力和学习速度等方面更具优势,在非线性问题处理中被广泛使用。但其spread(平滑因子)的取值直接影响 GRNN 的预测结果。为了提高该模型预测精度,研究者提出采用优化算法对 GRNN 的平滑因子进行优化。田源等[12]利用果蝇算法(FOA)对GRNN模型的平滑因子进行优化,并将优化后的模型用于水电机组振动的趋势预测中,通过对比测试结果,验证FOA算法可以有效提高算法预测精度。但是果蝇优化算法也存在部分缺陷,具体包括:收敛速度慢、寻优精度不高、易得到局部最优解等问题。戈涛等[13]提出一种新型改进果蝇算法,通过步长递减和随机策略,增强了算法的稳定性,提高了算法运算效率。但是该改进果蝇算法的稳定性和运算效率没有达到最佳,可进做一步改进。
针对上述模型结构相对复杂;预测精度不够高;运算速度和效率不能达到最佳等问题,本文提出一种改进的FOA算法优化GRNN模型的方法。通过将果蝇算法搜索步长和气味浓度判定公式进行改进,进一步利用改进后的算法对 GRNN 的平滑因子进行优化处理。将优化后的平滑因子代入GRNN模型用于水电机组振动趋势预测,预测结果表明,相较于其他两种预测模型,RFOA-GRNN模型在水电机组振动预测时具有更高的预测精度和模型稳定性,对维护人员提前发现水电机组故障并及时检修进而保证水电机组安全稳定的运行具有重要意义。
1 广义回归神经网络GRNN
广义回归神经网络模型(generalized regression neural network,GRNN)在1991年提出。GRNN包括输入层、模式层、求和层和输出层[14-16]。结构如图1所示。输入训练样本为X=[X1,X2…Xn]T,输出样本为Y=[Y1,Y2…Yk]T,n和k均为实数,其中n代表输入训练样本向量维度,k代表输出样本向量维度。
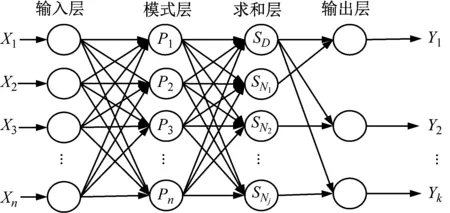
图1 广义回归神经网络结构图
从图1所示,输入层将信息传至模式层,其传递函数如式(1)所示。
(1)
式中:X为GRNN网络输入参数;Xi为第i个神经元所对应训练样本,(其中i为1,2,…,n);σ为平滑因子。
输出层Yj由求和层中分子分子层神经元SNj与分母层神经元SD相除得到,其传递函数如式(2)所示。
(2)
由式(1)可知,当平滑因子σ取值较大时,Pi趋于1,输出的结果近似等于所有样本数据的平均值,反之,当平滑因子取值接近 0 时,Pi会趋于无穷,此时输出层产生的预测值则会更加接近训练样本。如果输入的数据未包含在样本内时,所得到的预测结果与实际值误差可能会很大,可能会出现过拟合现象。由上述结论,可知使用GRNN模型进行水电机组振动预测时,为了提高预测精度,需要寻找一个最佳平滑因子σ。作为一种常用优化算法,FOA的优点是算法简单,参数少,但FOA算法存在收敛所需时间长、寻优精度不高、易得到局部最优解等问题。因此,本文引入一种改进的FOA算法去确定GRNN模型的最优平滑因子。
2 改进FOA优化GRNN模型
2.1 果蝇优化算法
果蝇优化算法是一种模拟果蝇觅食行为,寻求全局优化的新算法。果蝇本身在嗅觉和视觉上远远优于其他物种,因此它能收集漂浮在空气中的各种气味[17]。果蝇往食物所在地点飞去时,可以用敏锐的视觉找到食物和同伴聚集的地点,并朝此方向飞行。
2.2 改进的果蝇算法
FOA算法中,果蝇算法进行迭代寻优时,搜索步为固定值。由此会产生两个问题:①当设置搜索步长太大,算法全局寻优能力强,但是会降低收敛精度,导致收敛时错过最优解;当设置搜索步长过小,会增加收敛时间,且算法全局寻优能力减弱,易陷入局部最优解;②果蝇气味浓度判定值恒为正值,无法对负值区域进行搜索,造成果蝇算法全局寻优能力降低[18-19]。针对以上所述问题,本文对FOA算法做出如下改进。
改进FOA算法寻优过程可分为7个步骤,具体如下:
步骤1初始化参数
初始化果蝇群体大小Z,设置最大迭代次数M,果蝇随机生成位置(Xaxis,Yaxis)。
Xaxis=10·Rand()
Yaxis=10·Rand()
(3)
式中,Rand()为0~1之间的随机数。
步骤2对FOA算法搜索步长进行改进,采用动态递减步长的策略。
Xi=Xaxis+L·Rand()
(4)
Yi=Yaxis+L·Rand()
(5)
式中:(Xi,Yi)为果蝇在空间中迭代搜寻轨迹;L·Rand()为果蝇随机搜索空间距离;Rand()为0~1之间的随机数。
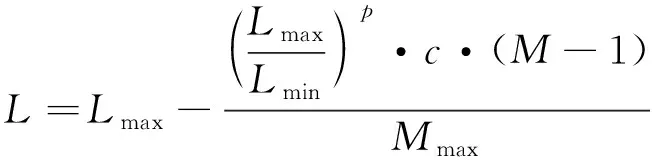
(6)
式中:L为搜索半径;Lmax为最大搜索半径;Lmin为最小搜索半径;M为当前寻优次数;Mmax为最大迭代寻优次数;p为步长调节因子;c为权重因子。此方法解决了固定搜索半径存在的问题,使算法在寻优前期有较大的搜索半径,可加快算法的收敛速度,提高算法全局寻优能力,避免算法在早期取得局部最优解。随着迭代次数的增加,搜索半径减小,算法局部寻优能力增加,算法的收敛精度提高。
步骤3改进果蝇算法气味浓度判定公式
(7)
Δ=Disti*[0.5+rand()]
(8)
式中:Disti表示果蝇个体迭代寻优时与原点之间的距离;Si表示果蝇气味浓度判定值;Δ表示跳脱因子;sgn()表示一个阶跃函数;Rand() 为0~1的随机数。给Si增加一个Δ,可使FOA算法迭代寻优过程中,能够成功跳出局部极值的状态,进而更易取得全局最优解。同时使用阶跃函数,当果蝇个体在二维坐标的二、四象限迭代寻优时,Si可取负值。通过式(8)可以实现FOA算法对负值空间的全面搜索,增强了果蝇优化算法的空间搜索能力,极大降低了算法陷入局部最优的几率。
步骤4将式(8)的Si代入函数F(Si),计算出果蝇的气味浓度值。
Smelli=Function(Si)
(9)
式中,Smelli为果蝇群体中各个体的气味浓度值;Function(Si)为气味浓度判定函数。
步骤5寻找最佳气味浓度值,当需要求解最大值时,取群体中最高气味浓度的果蝇,反之,取最低气味浓度的果蝇。
[bestSmell bestindex]=min(Smell)
(10)
式中:min(Smell)表示最低气味浓度果蝇个体;bestSmell表示最低气味浓度值;bestindex表示该果蝇在二维空间中的位置。
步骤6保留最佳气味浓度值及该值的坐标,此时果蝇群体中其他果蝇会向此方向飞行。
Smellbest=bestSmell
Xaxis=X(bestindex)
Yaxis=Y(bestindex)
(11)
式中:Smellbest表示保留最佳气味浓度值;(Xaxis,Yaxis)表示对应果蝇位置坐标。
步骤7重复执行步骤2~5,迭代寻优;判断当前迭代次数是否达到最大迭代次数;若达到,则输出最优结果;否则继续循环执行步骤2~步骤5,直至达到最大迭代次数。
2.3 改进果蝇算法寻优性能测试
为了验证本文提出的改进果蝇(RFOA)算法的寻优性能,本文选取了8个标准基函数对FOA,递减步长果蝇优化算法(DSFOA)以及RFOA算法进行性能测试,测试函数如表1所示。测试结果如表2所示。
由表2的测试结果可得,无论是求解峰值为单峰还是多峰的函数,本文所提出的RFOA算法迭代寻优所得到的测试函数的平均值和标准偏差均小于其他两种优化算法所得的结果。由此可得出RFOA算法的稳定性及寻优精度更佳。验证了RFOA算法的有效性。
2.4 RFOA优化GRNN的算法
RFOA优化GRNN的思路是,将果蝇与初始位置之间的距离倒数Si作为平滑因子,将样本数据分为两组[20],即一组数据用于预测模型训练,一组数据用于结果测试,这样可避免网络训练过度。求输出样本的均方根误差(RMSE)作为气味浓度判定函数,函数的值为气味浓度值;然后调换训练集和测试集,进行交叉训练,进一步提高算法的精度,同样求其气味浓度值。通过不断循环执行,直到得到最小的气味浓度值或达到最大迭代次数时,结束执行。此时得到最佳气味浓度值为最优平滑因子。
RFOA优化GRNN的预测流程图如图2所示,其详细步骤如下:
步骤1收集水电机组振动数据并提取主要变量,对数

表1 测试函数

表2 测试结果
据归一化处理,同时将数据分为训练样本分为测试样本;
步骤2设置种群大小Z和最大迭代次数Mmax,设置果蝇随机生成位置(Xaxis,Yaxis);
步骤3计算果蝇到初始位置距离(D),以1/D作为气味浓度判定值(S),将S作为平滑因子σ;
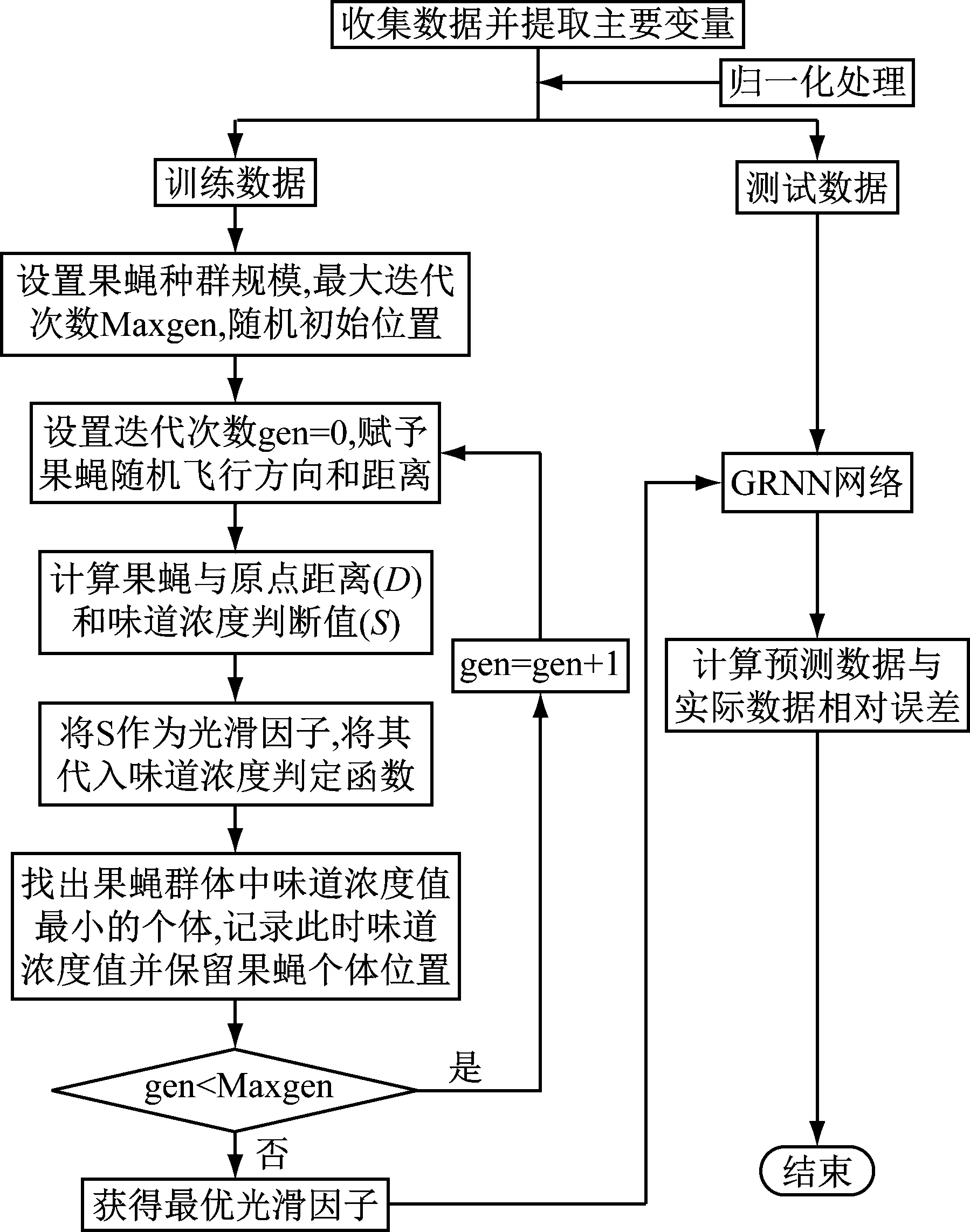
图2 RFOA优化GRNN的预测流程图Fig.2 Prediction flow chart of RFOA optimized GRNN
步骤4将RFOA-GRNN振动测试数据的均方根误差(RMSE)作为气味浓度判断函数,将平滑因子代入函数,计算出该果蝇个体的气味浓度值;
(12)
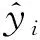
步骤5通过不断迭代,找出果蝇群体中气味浓度值最小的个体(即 RMSE 值最小),记录此时最优气味浓度值,保留此果蝇位置坐标;
步骤6判断当前迭代次数是否达到最大迭代次数;若达到,则输出最优平滑因子;否则继续循环执行步骤3~步骤5直至达到最大迭代次数;
步骤7将优化得到的最优平滑因子输入GRNN网络,对水电机组振动数据进行预测,计算相对误差。
3 实例验证与结果分析
实例水电机组振动信号选自凌津滩水电厂8号水电机组水导振动严重超标产生的振动信号,依据国家标准规定,灯泡贯流式水电机组水导轴承的振动限定值为120 μm,而本文研究的对象水导轴承振动值超过了300 μm,超过了标准限值2.5倍。为了确保水电机组运行时的安全与稳定,防止水导轴承振动严重超标对电厂正常运行产生安全隐患。电厂立项对8号机组水导轴承振动超标问题进行专题研究项目结合离线稳定性和协联试验数据、在线监测系统历史数据和现场检修测量数据,分析影响水导轴承振动的机械因素、电气因素、水力因素,通过振幅计算各因素对其振动的具体贡献率,确定水力因素是引起水导轴承振动超标的主要因素,贡献率达到68%,水导轴承振动幅值与过机流量、水头呈正相关关系;其次为机械因素,机械因素对水导水平、垂直振动的贡献率分别为33.25%、59.94%;电气因素对降低水导轴承振动有利,其对水导轴承水平、垂直振动的贡献率为-1.88%、-28.34%。
通过具体分析,引起水导轴承振动超标的水力因素主要为:协联关系、桨叶开口不均匀、桨叶与转轮室间隙,机械因素主要为水轮机侧的动不平衡。
本文研究对象为该水电机组水导-X向摆度的历史振动数据,选取机组水导轴承振动严重超标时段的100组振动数据进行预测分析,选取80组振动数据作为训练样本,剩下为测试样本。
由于水电机组振动是非线性的,其工作现场环境相对复杂,使得从水电站采集的原始振动数据会受到不同程度的干扰,所以这些数据样本中不可避免的存在一些误差样本。若直接使用这些原始数据样本,会对预测模型测试精度造成影响,也可能降低预测模型收敛能力。所以在使用这些原始数据样本进行分析之前,要进行数据归一化处理,如式(13)所示。
(13)
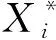
水电机组水导轴承振动严重超标时段水导-X向摆度的历史数据图如图3所示。
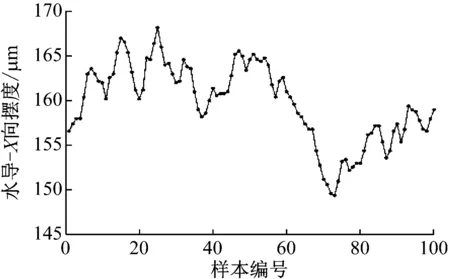
图3 水导-X向摆度历史数据图Fig.3 Historical data of water conductivity-X direction swing
图3中横坐标表示水导振动严重超标的某一时间段内连续监测的100组振动数据。
振动模型参数设置如下:种群大小Z=30;迭代次数Mmax=100;最大搜索半径Lmax=5;最小搜索半径Lmin=0.1;步长调节因子p=0.5;权重因子c=0.7。
如图4所示为三种模型RMSE收敛过程。可以得到FOA算法优化GRNN平滑因子,经过100次迭代运算,从第3代开始收敛,到第37代结束收敛,对应最小的均方根误差RMSE的值为0.216 2,此时最优平滑因子值为0.099;DSFOA算法优化过程从第2代开始收敛到第35代结束收敛,得到对应最小的均方根误差RMSE的值为0.213 8,此时最优平滑因子值为0.045;而本文提出的RFOA算法优化过程从第2代开始收敛到第28代结束收敛,得到对应最小的均方根误差RMSE的值为0.210 2,此时最优平滑因子值为0.027。
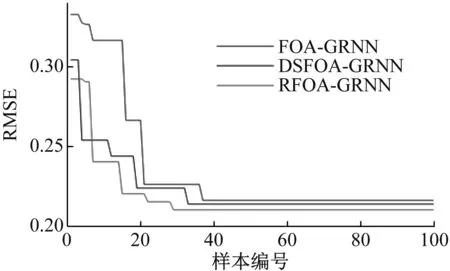
图4 三种模型迭代收敛曲线Fig.4 RMSE convergence process of three models
由此可得到RFOA-GRNN相比FOA-GRNN和DSFOA-GRNN,收敛速度更快,且精度更高。稳定性更好。此时将测试样本代入三种振动预测模型中,将得到的最优平滑因子也分别代入各模型,得到的预测结果与实际值的相对误差如表3、图5所示。
由图5可以得到,RFOA-GRNN方法的预测结果输出曲线对比其他两种方法更接近实际预测结果输出曲线。可得本文提出RFOA-GRNN方法的预测结果输出曲线可以很好的拟合水电机组振动数据曲线,预测结果误差更小,精度更高。这是由于RFOA-GRNN模型的平滑因子小于其他两模型平滑因子,从而使得此模型预测输出值更接近测试样本的实际输出值。

表3 3种模型对振动数据预测结果及相对误差
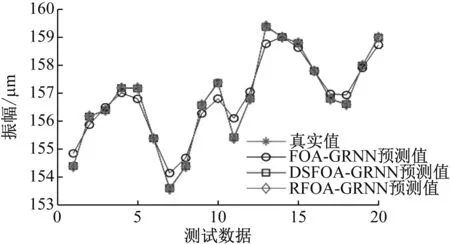
图5 三种模型预测数据与实际数据结果对比
由表3和图6可以得到,FOA-GRNN模型预测的相对误差保持在[-0.5,0.4]%之内。取绝对值后最大相对误差为0.460 2%。DSFOA-GRNN模型预测的相对误差保持在[-0.03,0.03]%之内。取绝对值后最大相对误差为0.027 9%。RFOA-GRNN模型预测的相对误差保持在[-0.000 2,0.000 2]%之内。取绝对值后最大相对误差为0.000 2%。可以发现RFOA-GRNN方法预测结果的最大相对误差比FOA-GRNN和DSFOA-GRNN方法分别减少了99.96%和99.28%。对比三种模型可以得到,本文提出的RFOA模型预测精度最高,可以很好地实现水电机组振动趋势的预测。
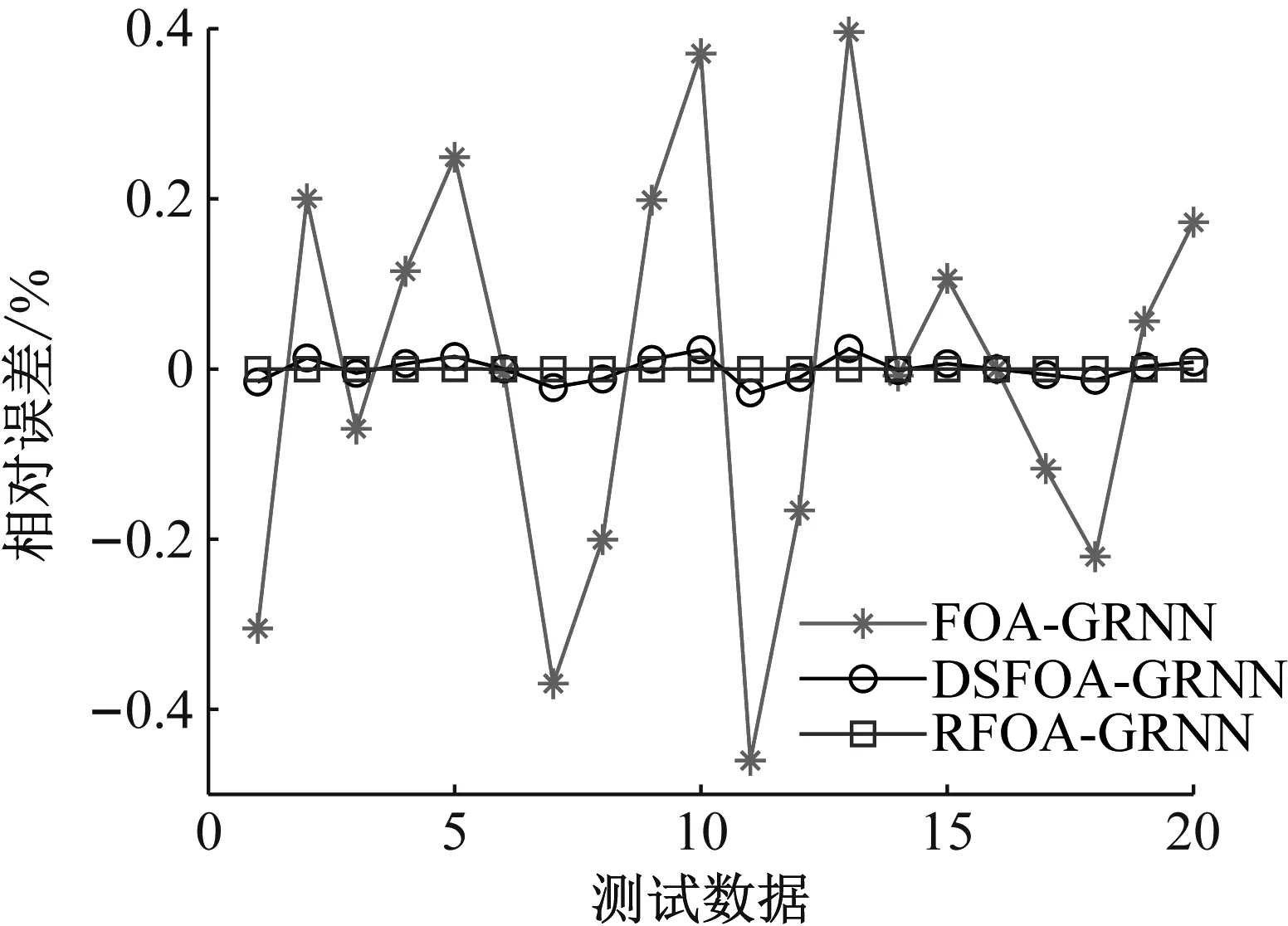
图6 三种模型预测振动数据相对误差对比
4 结 论
为了确保水电机组振动预测结果更准确,保障水电机组安全稳定的运行,本文提出了一种改进的FOA优化GRNN模型的方法,基于工程实例分析得到如下结论:
(1) 对FOA算法采用动态递减步长的策略并优化改进气味浓度判定值,在果蝇优化算法基础上增加了跳脱因子Δ并使用阶跃函数,扩大了果蝇寻优范围,解决了算法易陷入局部最优解的问题。选取测试函数对FOA,DSFOA以及RFOA算法进行测试,得出RFOA算法的稳定性更强,寻优精度更高。验证了RFOA算法的有效性。
(2) 利用FOA,DSFOA,RFOA三种优化算法优化GRNN的平滑因子并建立振动预测模型,将振动预测模型用于水电机组振动趋势预测中,与 FOA-GRNN 和DSFOA-GRNN两种模型的预测结果对比,RFOA-GRNN模型预测能力更强,预测精度更高;同时该模型结构简单、便于操作、运行高效,可以很好的应用于水电机组状态趋势预测研究中,为维护人员提前发现水电机组故障并及时检修进而保证水电机组安全稳定的运行提供保障。
