ANSMD方法及其在齿轮故障诊断中的应用
2021-11-17潘海洋蒋婉婉郑近德潘紫微
潘海洋, 蒋婉婉, 郑近德, 潘紫微
(1.安徽工业大学 液压振动与控制教育部工程研究中心,安徽 马鞍山 243002;2.安徽工业大学 机械工程学院,安徽 马鞍山 243002)
齿轮是旋转机械设备最易发生故障的部件,它的运行状态将影响整个机械设备的健康运转。齿轮传动过程中所产生的振动信号通常具有非平稳非线性,传统的非平稳信号分析和处理方法包括小波变换[1]、短时傅里叶方法[2]等,但上述方法都有各自的局限性。其中,短时傅里叶分析是在时域中加窗,能够将非平稳复杂信号分解为若干短时平稳信号的叠加。小波变换相对于短时傅里叶方法,其对非平稳信号分析更加有效,分解精度更高,因此在不同领域中的得到了广泛的应用[3-6]。但是,小波变换需要预先设定小波基和分量层数,这在一定程度上制约了小波分析的进一步应用。
针对传统非线性处理方法的不足,经验模态分解[7-8](empirical mode decomposition, EMD)、局部特征尺度分解[9](local characteristic-sale decomposition,LCD)和变分模态分解(variational mode decomposition,VMD)[10]等方法被相继提出。EMD能自适应地将调幅调频信号分解为若干个内禀模态函数(intrinsic mode function, IMF)之和,每个IMF对应着原始信号的局部时间尺度特征。EMD方法在机械故障诊断、图像处理等多个领域得到广泛应用[11-13],然而,但其在分解过程中会发生过包络、欠包络、频率混淆和包络极值会使数据序列的两端发散(如端点效应)等问题。LCD作为EMD的一种演化方法,其能将一个复杂信号分解为若干相互独立的内禀尺度分量(intrinsic scale component,ISC)之和。LCD算法可以同时提供非平稳信号在时域和频域的局部信息,避免了EMD方法的频率混淆,同时LCD具有分解能力强、抑制包络问题等特点,且在机械故障诊断领域[14-15]取得了良好的应用效果,但其仍然存在一些固有的缺陷,如端点效应,严重影响了信号处理的效果。VMD不同于EMD和LCD方法,其本质是一种非递归自适应的多分量信号分解方法,以得到信号具有最小带宽为约束条件,能够将复杂的非平稳信号分解得到若干IMF之和,但是,VMD需要预先设定初始中心频率、二次惩罚项参数和分解模态个数等。
针对EMD和LCD等方法的不足,论文借鉴VMD的思想,提出了自适应非线性稀疏模态分解方法(adaptive nonlinear sparse mode decomposition, ANSMD) ,通过将奇异局部线性算子约束到信号分解中,自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的局部窄带分量,以局部窄带分量作为基函数进行迭代,从而逼近原始信号来完成信号的分解,进而得到具有完整时频分布的稀疏分量(sparse component,SC)。
综上所述,论文结合奇异局部线性算子,提出了ANSMD方法,并将其与EMD、LCD和VMD等信号分解方法进行对比,仿真与实测数据分析结果表明,ANSMD方法在抑制模态混叠、鲁棒性等方面具有明显的优势。
1 ANSMD方法
ANSMD方法通过将信号分解转化为非线性约束优化问题,将一个复杂非平稳信号自适应的分解为若干个稀疏分量SC之和,再将每个稀疏分量信号作为基本信号进行解调,从而逼近原始信号。其步骤如下:
设V(t)为窄带信号,从L2(μ)到L2(μ)的线性算子S称为局部线性算子,如果∀t∈μ,存在t的领域Bt,使得
S(V)(t)=S(V|Bt)(t),(∀V∈L2(μ))
(1)
式中,V|Bt表示V在Bt上的限制。从局部线性算子的定义上看,一个局部线性算子配套一个相关的领域簇Bt。如果同一个线性算子配以不同的领域簇,那么它就是不同的局部线性算子。
所谓一个局部窄带信号在局部线性算子的作用下“消失”,就是说,局部窄带信号V(t)在局部线性算子S的作用下等于零,即对窄带信号V(t)而言,在任意一时间点t的领域,有S(V(t))=0,则称S的零空间内包含窄带信号V(t)。若算子S将信号V(t)多次处理,S中包含V(t)的成分将被不断提取,则该信号可表示为
(2)
R为存在V中的分量信号,U为残余无用信号。假设有窄带信号R(t),S是局部奇异线性算子,时间t有S(R(t))=0,即R(t)被局部线性算子S映射到了零空间里。这时,S(V(t))=U(t),U(t)是经过局部奇异线性算子S映射之后原始信号V(t)的剩余分量。同时,U(t)可以进一步表示为
(3)
式中:D是一个U为主对角线的对角矩阵;λ为Lagrange系数。
在算法的运用中,如果算子S为微分算子时,很难一次迭代把Ri提取完全,因此,引入泄露因子来解决上述问题,式(3)将变为
(4)
式中:γ为泄露因子;λ1为Lagrange系数。最后一项用来对算子S中的参数进行归整化处理。
为了求解上述方程,选择以下微分算子
(5)
(6)
但是,式(5)的微分算子不适用于某些特殊信号模型,只对调频信号具有明显的效果,而对复杂的调幅调频信号很难完成有效分解。因此,拟根据质-弹-阻振动运动,采用二阶微分算子
(7)
在算子SV的作用下使分解的分量η为零,即:
SV×η=0
(8)
假设分解分量为η=a(t)cos[w(t)t+b],则得到:
(9)
令φ(t)=w(t)t+b,求解式(9)得
-2a′(t)φ′(t)-a(t)φ″(t)-a(t)φ′(t)P=0
(10)
a″(t)-a(t)φ′(t)2+a′(t)P+a(t)Q=0
(11)
假设φ(t)是局部线性函数,即对任意一点t,存在t的一个邻域,使得φ″(t)=0。
求解式(10)和(11)可得
(12)
(13)
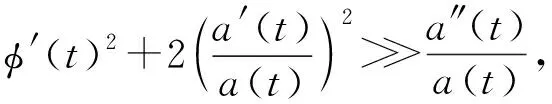
(14)
将式(12)和(14)代入式(7),因此式(7)变为
(15)
也可以表示为
SV=D2+PD+Q
(16)
(17)
D1和D2分别为一阶和二阶微分算子。这里,γ为极小数,设置为γ=0.001。λ1和λ2通常设置为区间[0.1,1]中的值。终止条件设置为‖U(t+1)-U(t)‖<ε‖S‖,其中ε=0.000 1。
因此,通过最小化公式(17)来得到第一个稀疏分量SC,将余量再次进行上述步骤得到第二个分量。ANSMD应将一个复杂信号分解为K个稀疏分量SC之和,通过对每个SC解调得到其幅值和瞬时频率,从而获得原始信号的完整时频分布。
综上,ANSMD算法流程如图1所示。
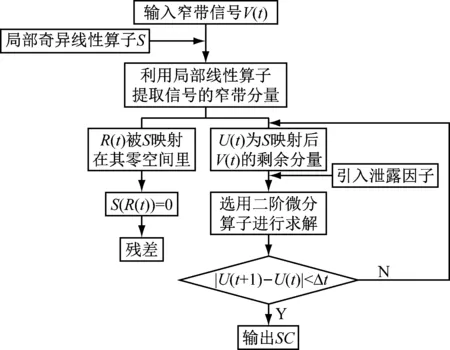
图1 ANSMD方法流程图Fig.1 The flow chart of ANSMD method
2 仿真信号分析
为了验证ANSMD方法的有效性,不失一般地,首先考察式(18)所示的混合信号s(t),即
(18)
s(t)由调幅调频分量、余弦分量和噪声分量组成。噪声分量是信噪比为5 dB的白噪声,加在有用信号上得到噪声信号s(t),信号的信噪比可以定义如下
(19)
式中,σx和σn分别是有用信号和噪声分量的标准差。
为了验证ANSMD方法的有效性,分别选取常用的EMD、LCD和VMD方法进行对比。由于四种方法的原理不同,自适应分解出的分量个数也不同,分解结果如图3~图6所示。图3是VMD的分解结果,VMD模态个数为3,惩罚参数为1 500,将噪声信号分解为3层,从图3可以看出,VMD分解第一个分量出现了模态混叠现象,与原始分量误差较大。图4是LCD的分解结果,LCD采用三次样条插值的方法来获取光滑的单分量信号,对于平稳信号会具有较好的效果,但是当信号表现出非平稳特性时,该方法在分解过程中容易产生模态混淆现象。从图4可以看出,原仿真信号被强制分解为若干个虚假分量,导致信号波形失真,与原始分量误差较大。图5是EMD的分解结果,EMD方法分解的第三个和第四个分量出现了明显的模态混叠,EMD方法采用极值点包络的方法来获取分量信号,由于极值点分布的原因,导致分解的分量严重失真,噪声鲁棒性较差。图6是ANSMD的分解结果,从图6可以看出,ANSMD分解的分量是平滑的,没有出现模态混叠现象,与实际分量相比误差较小。因此,ANSMD方法可以将含噪仿真信号进行有效分离,其具有良好的噪声鲁棒性。ANSMD采用约束优化进行分解,以得到调幅调频信号的瞬时频率具有物理意义且逼近原始信号为约束条件,得到的分量误差最小,与理想结果非常接近。

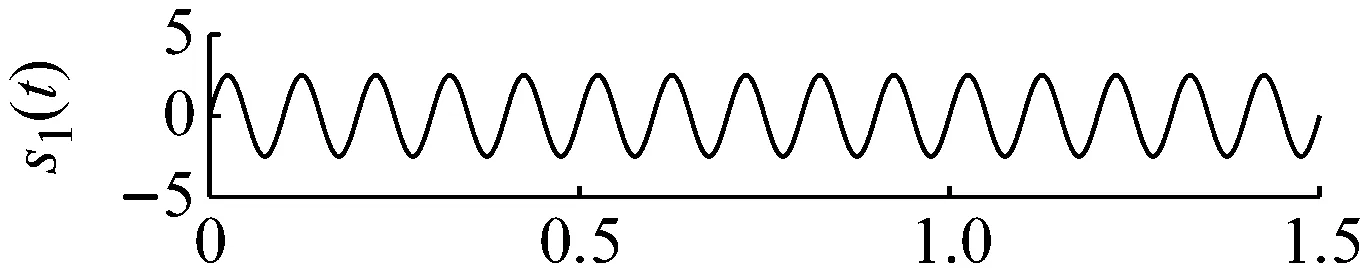
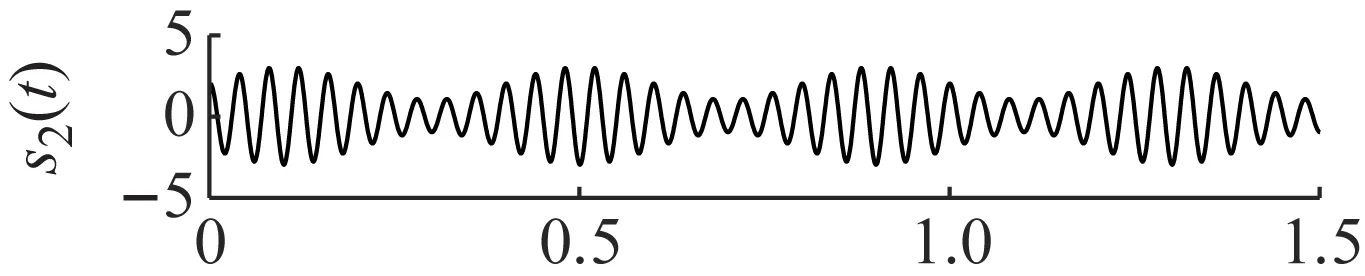
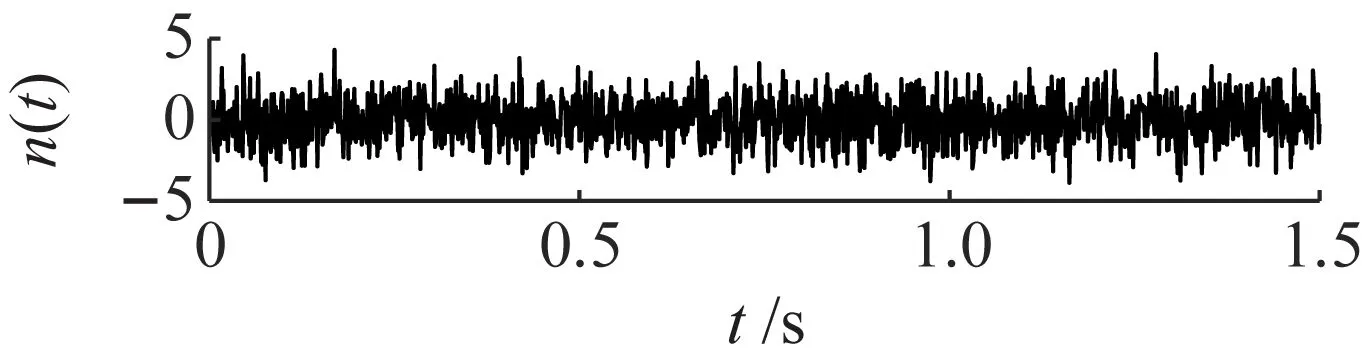
图2 仿真信号及其分量的时域波形Fig.2 Time-domain waveforms of simulated signals andits components
为了更直观地表现出ANSMD方法的优越性,将ANSMD方法、VMD方法、EMD方法和LCD方法分解仿真信号的分量残差进行了对比分析。如图7所示。从图7可以看出,ANSMD方法分解分量与原始信号分量残差较小,VMD方法、EMD方法和LCD方法与原始信号分量残差较大。因此,证明了ANSMD方法是一种更有效、更可行的信号分解方法。
3 试验分析
为了验证本文所提方法的可行性,将其运用于齿轮模拟故障试验台的实测信号分析。试验数据来自湖南大学齿轮模拟故障试验台,如图8所示,选择37齿的主动齿轮作为试验对象(主动齿轮和从动齿轮均为37齿)。为了模拟齿轮齿裂故障,采用激光切割方法在驱动齿轮的一个齿的齿根上切割了一条宽度为0.15 mm、深度为0.10 mm的裂纹。另外,齿轮转速为420 r/min,经计算,故障频率为fr=7 Hz,试验的采样频率为1 024 Hz。实测信号时域波形如图9所示。但由于拾取的振动信号中包含比较大的背景噪声,仅从时域波形就无法观察到裂纹齿轮故障的周期性调幅特性。同时,分析裂纹齿轮故障信号的包络谱,裂纹齿轮故障频率为7 Hz,如图10所示。然而,齿轮裂纹故障频率受噪声的干扰较大,导致故障特征频率不明显。因此,采用频谱图法提取边频带,如图11(a)分析裂纹齿轮故障信号的频谱图,为了更清晰的将裂纹故障边频带表示出来,将图11(a)频谱图的局部放大图表示出来,如图11(b)所示。裂纹齿轮啮合频率fm为259 Hz,但啮合频率不够明显。因此有必要采用信号分解的方法来提取和凸显故障特征信息。

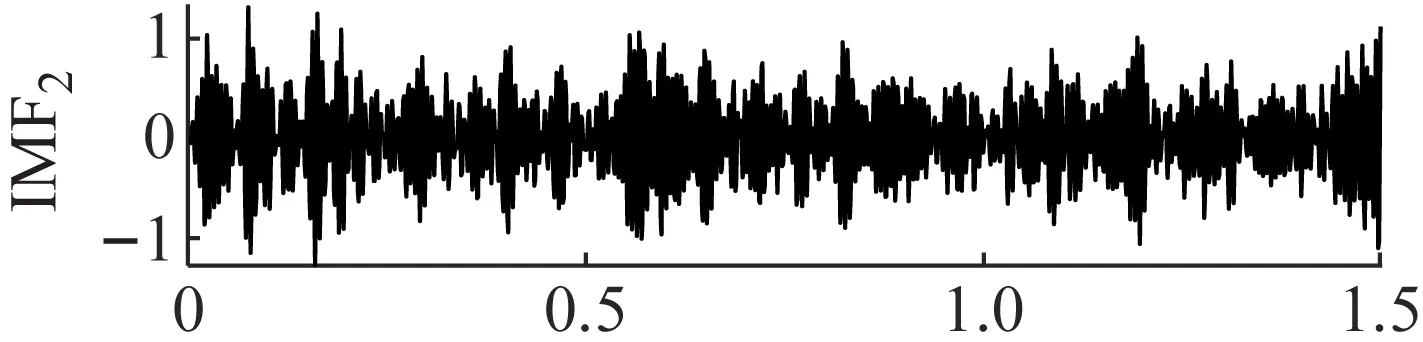

图3 VMD分解结果Fig.3 The decomposition results of VMD
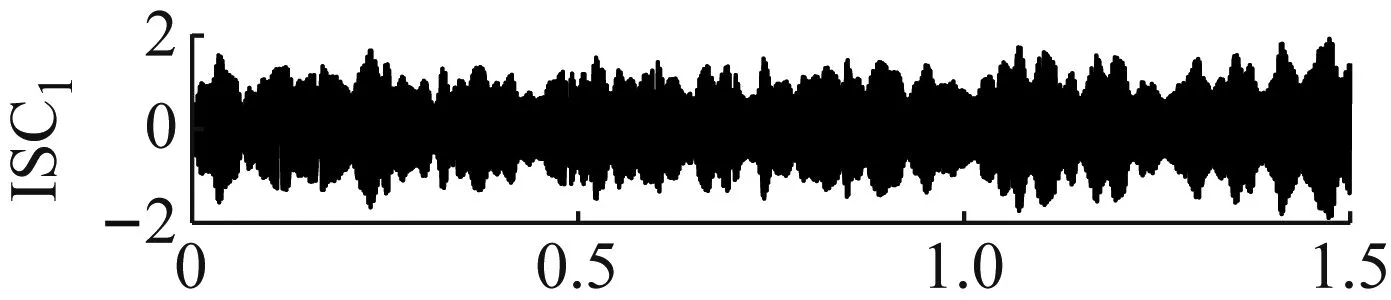



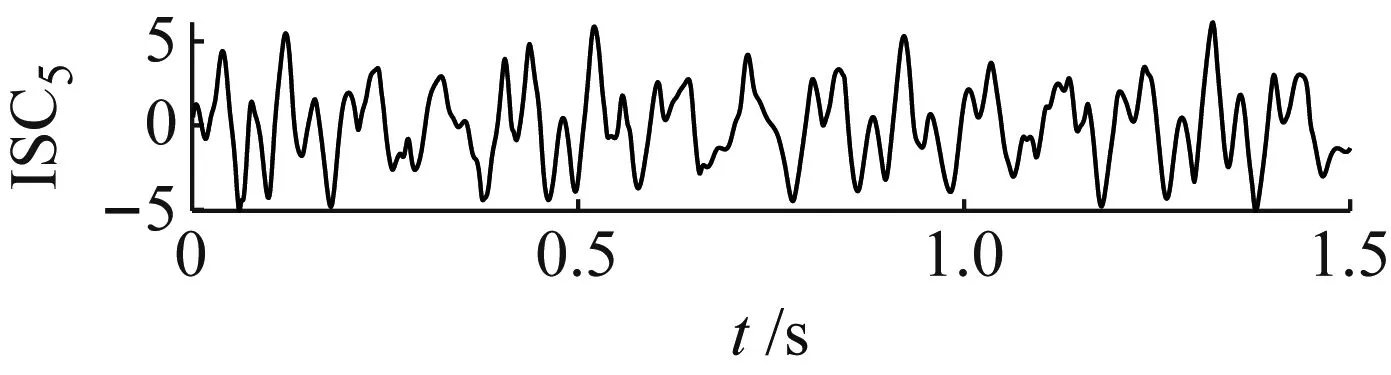
图4 LCD分解结果Fig.4 The decomposition results of LCD

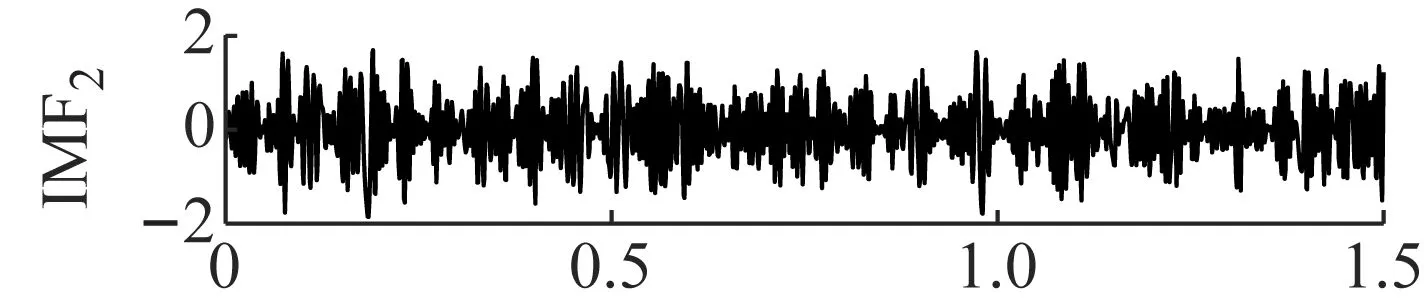

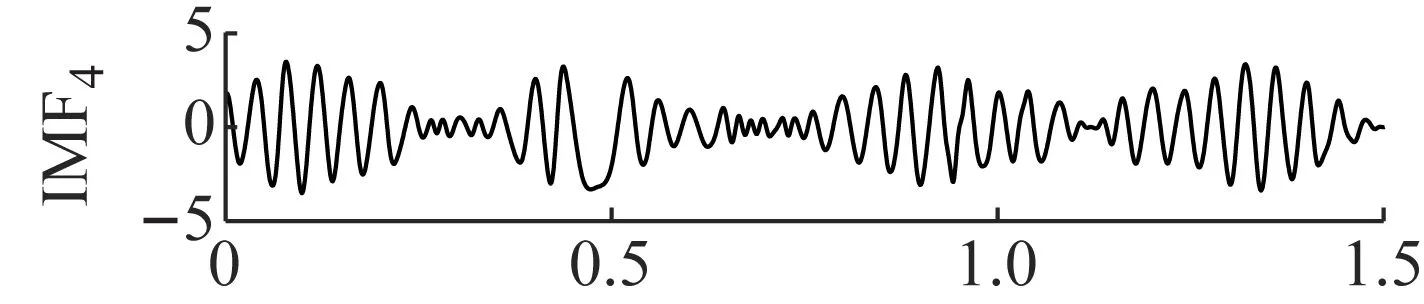
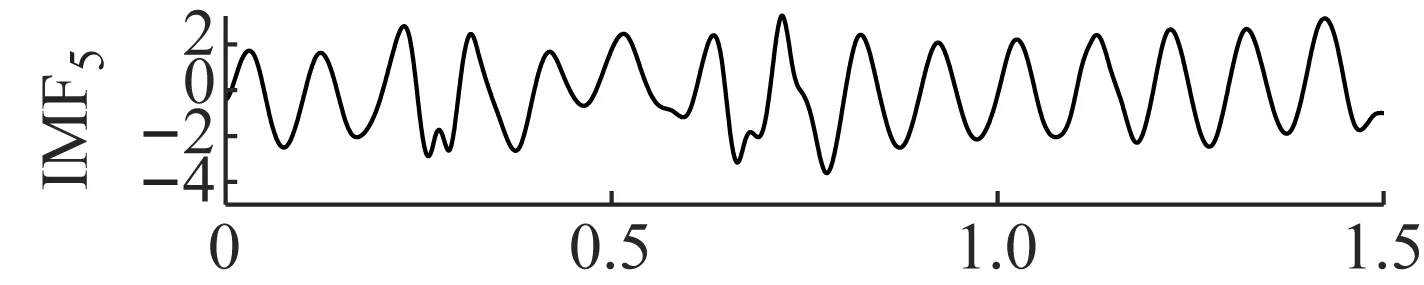
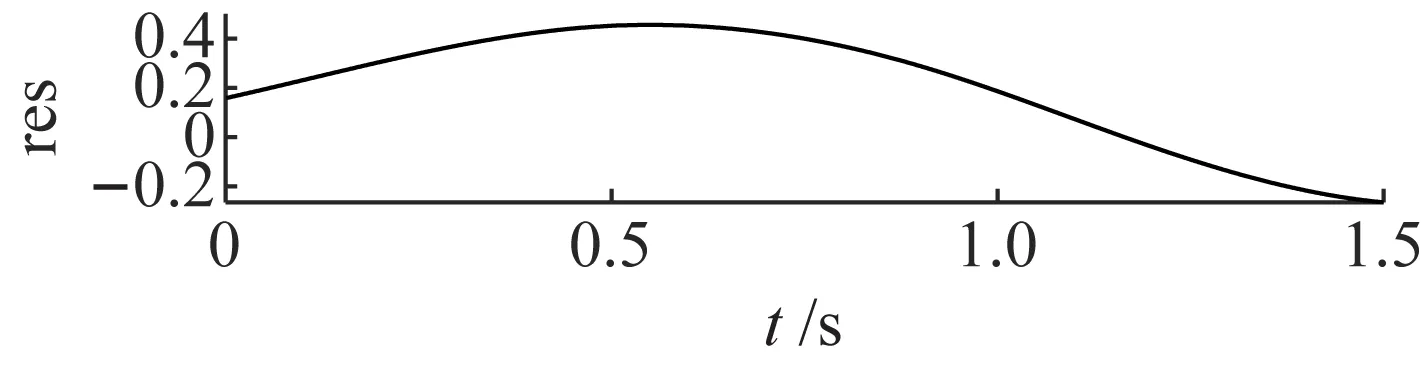
图5 EMD分解结果Fig.5 The decomposition results of EMD
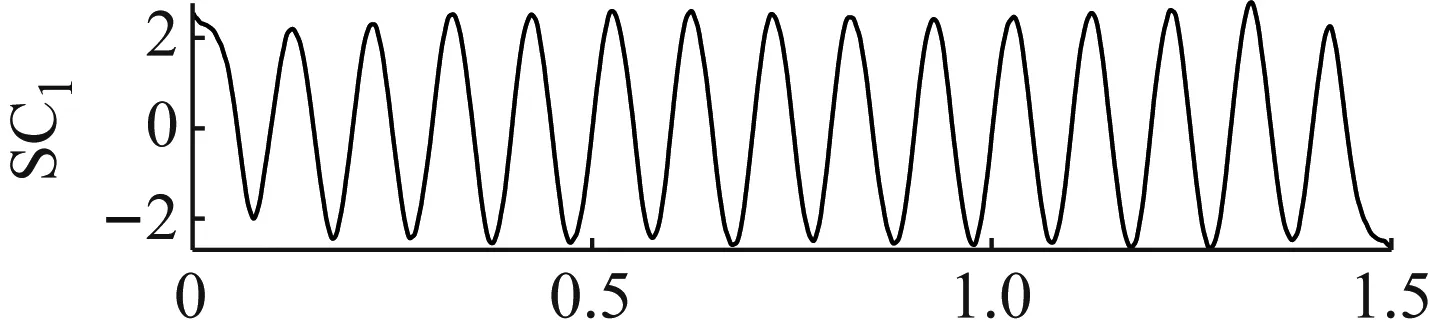


图6 ANSMD分解结果Fig.6 The decomposition results of ANSMD
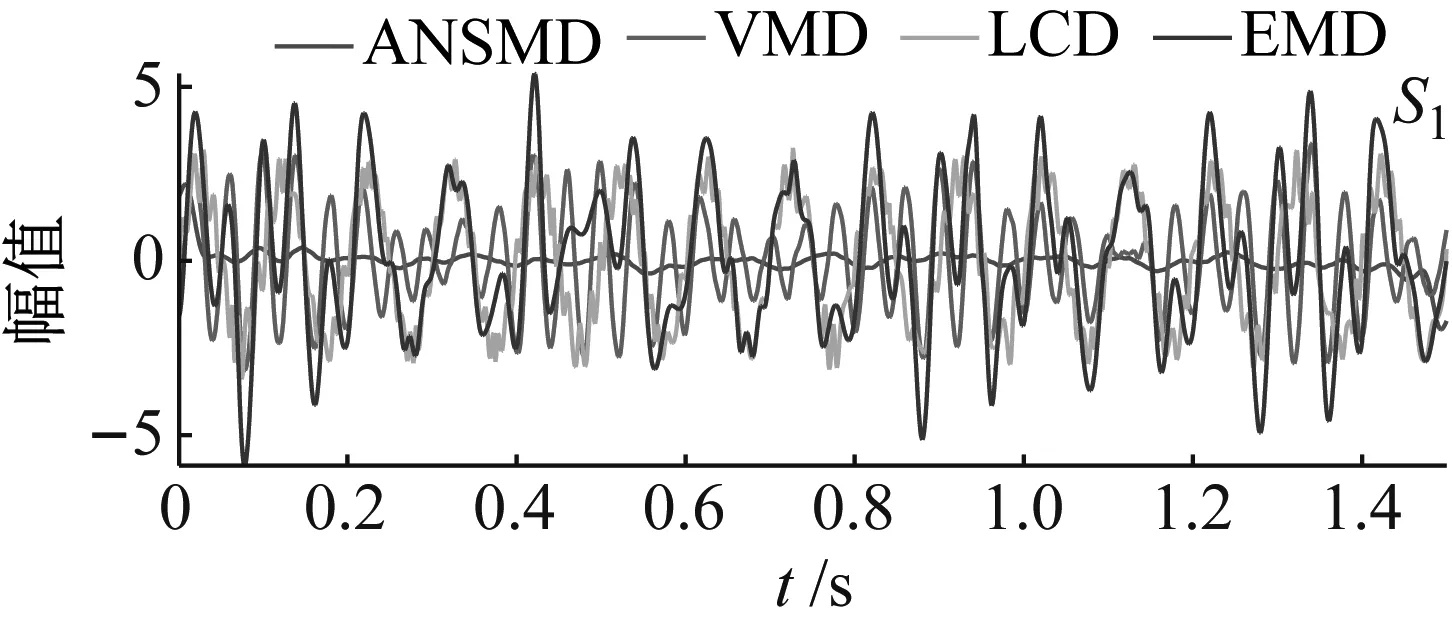
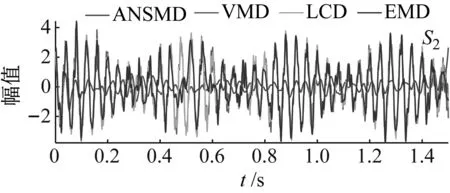
图7 各方法信号残差对比Fig.7 Comparison of signal residuals of various methods
为了验证所提ANSMD方法对齿轮故障振动信号分解的优越性,将ANSMD方法与EMD方法、LCD方法和VMD方法进行了对比分析。采用ANSMD方法对故障信号进行分解,分解结果如图12所示。从图12可以看出,所得到的分量具有一定的调制特性和冲击分量,但仅从时域波形不能确定齿轮是否存在故障。进一步作出各分量的包络谱,如图13所示,从包络谱图中可以观察到,在故障频率处峰值比较明显,而且各阶倍频幅值突出,因此,所提出方法提取的频带包含丰富的齿轮故障特征信息,可以明显地将齿轮故障特征信息进行提取和凸显。

1-直流电机;2-速度调节器;3-联轴器;4-滚动轴承;5-滚动轴承;6-齿轮;7-齿轮;8-滚动轴承;9-振动加速度传感器;10-光电转速传感器;11-滚动轴承。图8 齿轮模拟故障试验台Fig.8 Gear simulation failure test bench
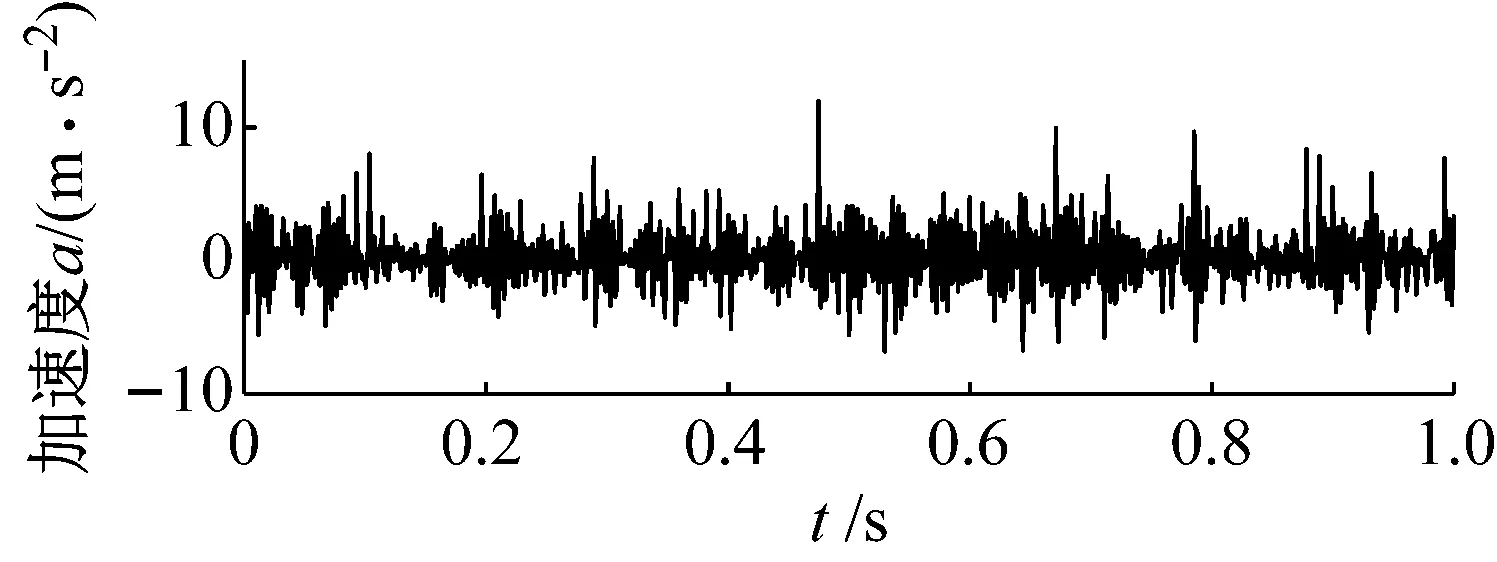
图9 实测信号时域波形Fig.9 Time-domain waveform of measured signal

图10 实测信号包络谱Fig.10 The envelope spectrum of measured signal
采用VMD方法对裂纹齿轮信号进行分解分析,分解结果如图14所示(VMD模态个数为3,惩罚参数为1 500,将齿轮信号分解为3层)。同时,分别对三个分量作出其包络谱,如图15所示。从图15可以看出,VMD分解的第二个分量的包络谱中包含了齿轮故障特征频率、转频二倍频和转频三倍频,可以诊断出该齿轮存在故障,但是相比较于ANSMD方法,其干扰成分较多。
LCD方法作为对比方法也被用来验证ANSMD方法的优越性。将同一故障信号用LCD方法进行分解,分解结果如图16所示。从图16可以看出,所得到的分量都具有明显的冲击和调幅特性。LCD方法分解后的包络谱如图17所示,从图17可以看出,所得分量的包络谱没有凸显出齿轮故障特征频率,LCD方法在进行信号分解时,通过三次样条插值的方法来分解,在分解过程中会遗漏部分的状态信息,导致得到的模型失真。因此,与LCD方法相比,ANSMD方法具有明显的优势。
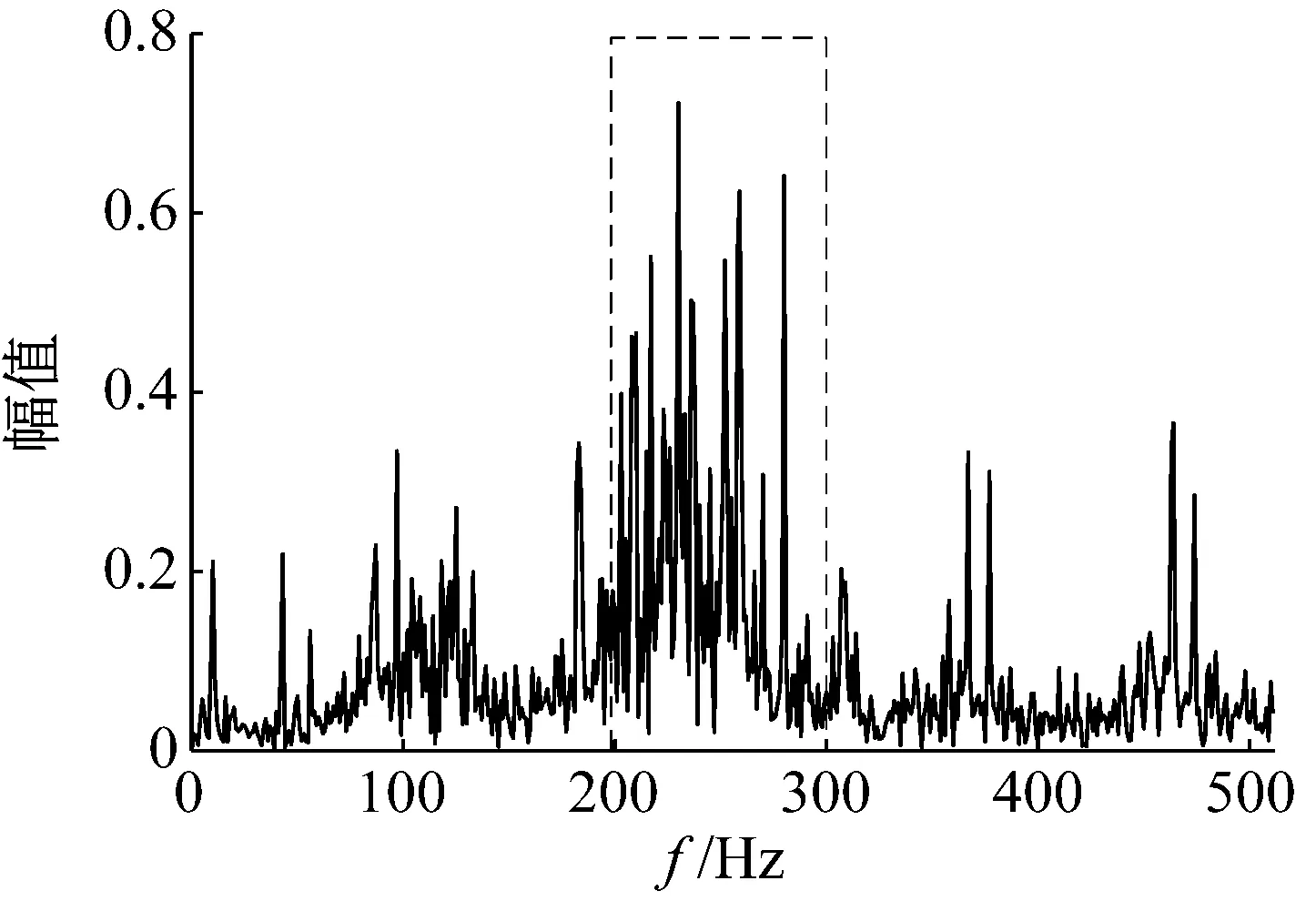

图11 实测信号频谱图Fig.11 Spectrum of the measured signal
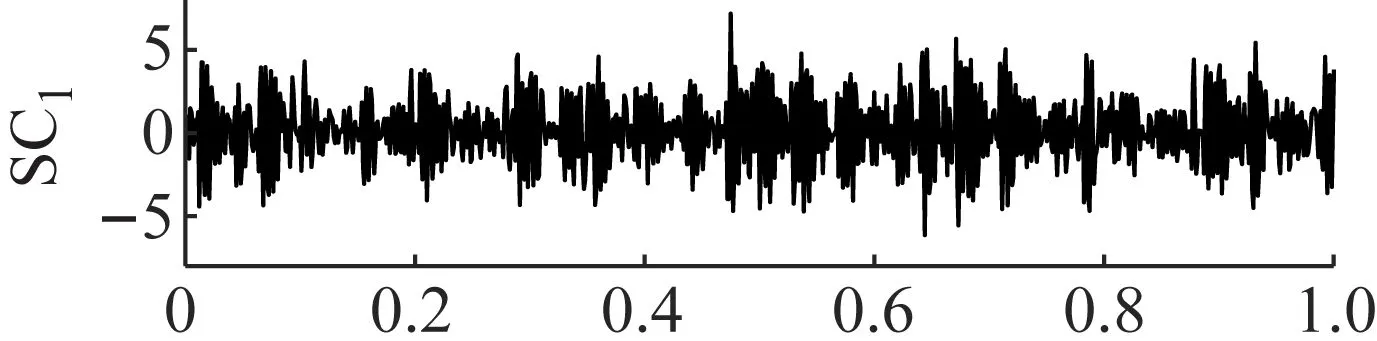
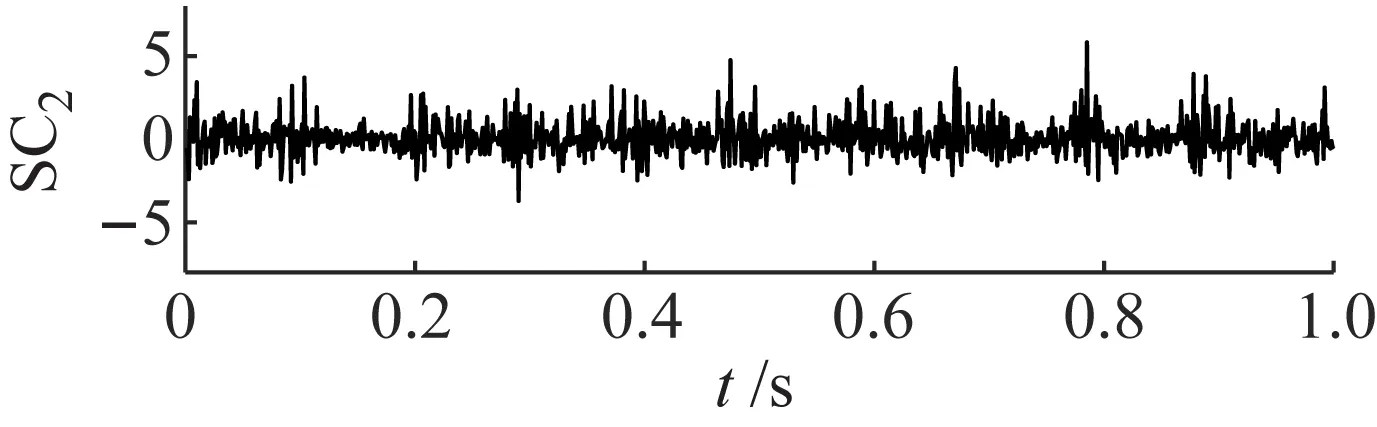
图12 ANSMD的分解结果Fig.12 The decomposition results of ANSMD
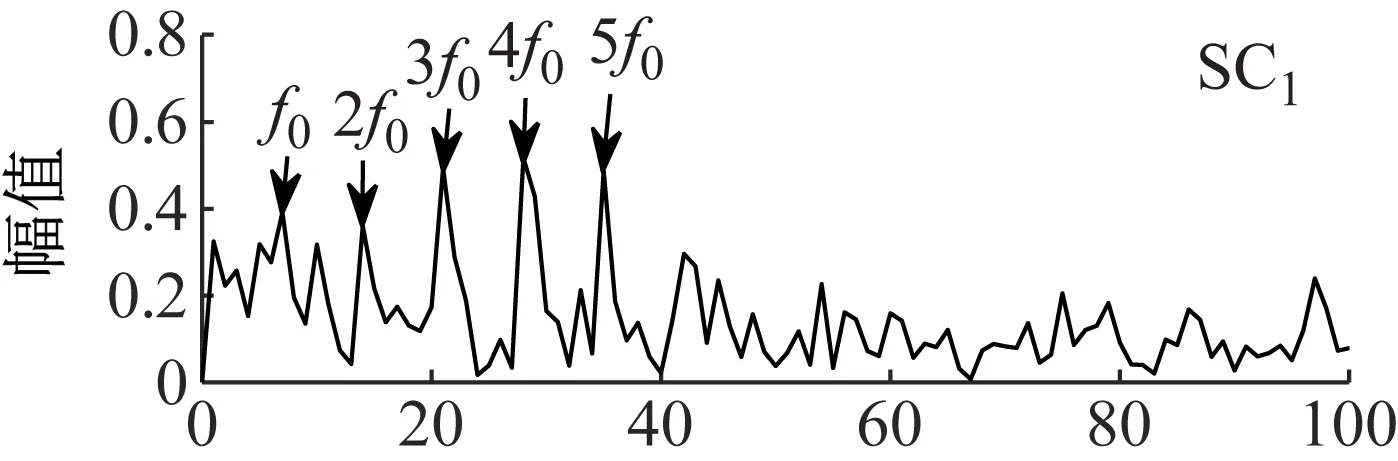
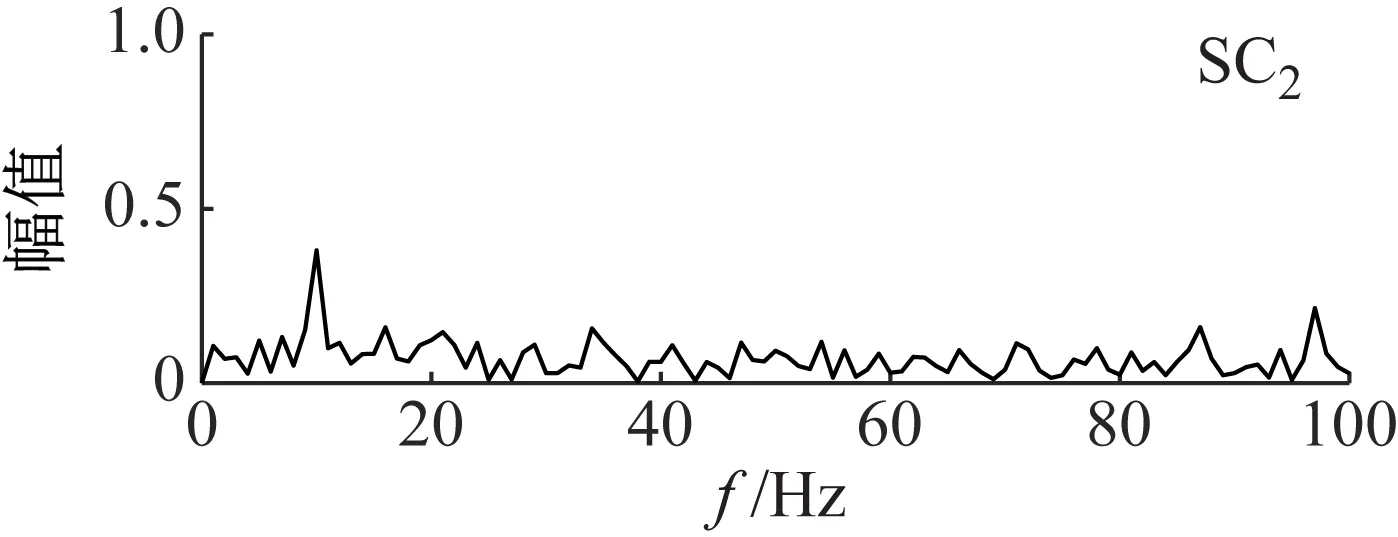
图13 ANSMD分量的包络谱Fig.13 The component envelope spectrum of ANSMD
进一步采用EMD方法进行分解,EMD的分解结果如图18所示,拟对前5个分量进行包络谱分析,如图19所示。从包络谱图中可以看出,分解得到的第一个分量的包络谱中包含了故障特征频率,第二个分量和第三个分量的包络谱中没有明显的故障特征频率,第四个分量和第五个分量的包络谱中更加没有明显的谱线。因此不能判断故障信号的状态信息。
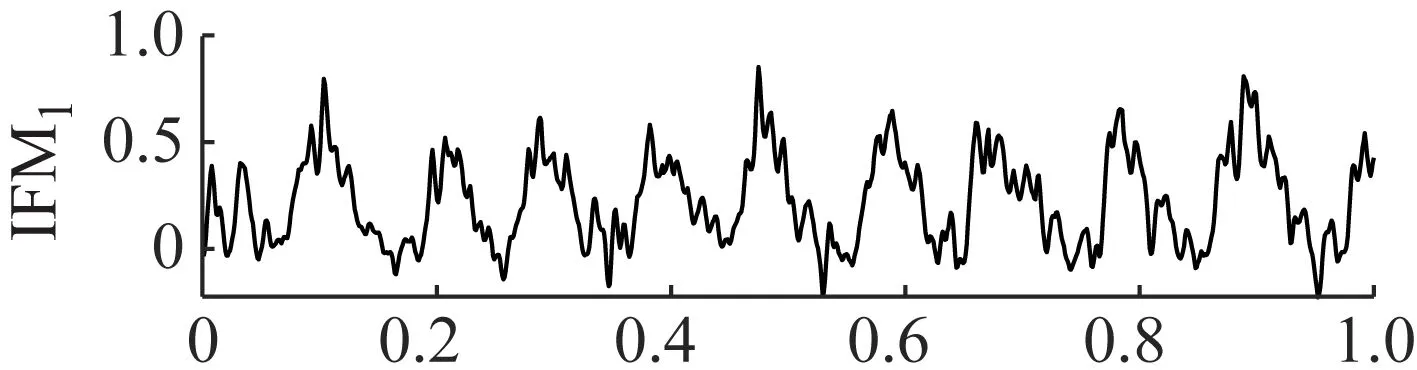

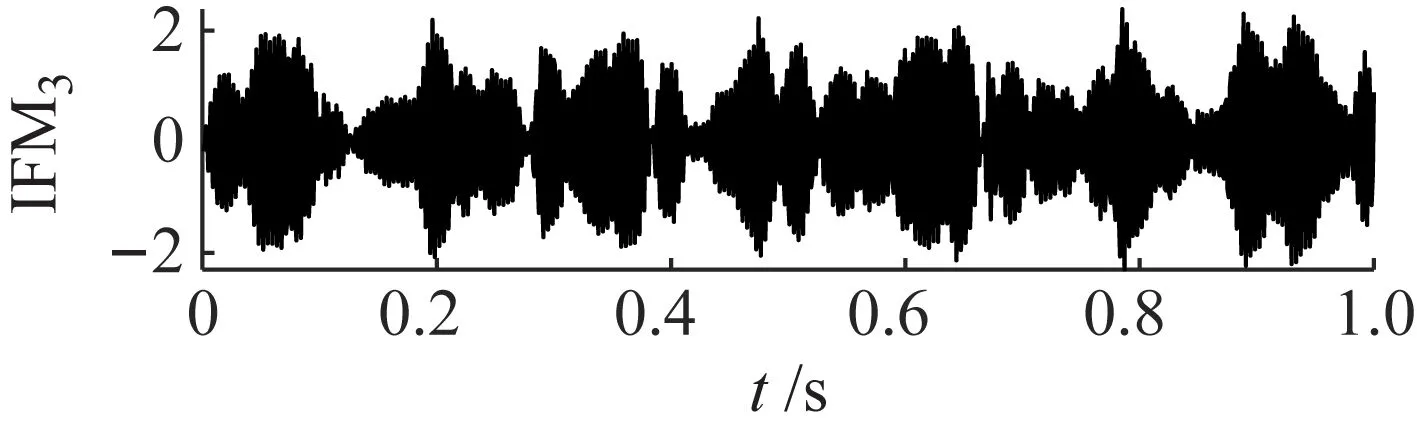
图14 VMD的分解结果Fig.14 The decomposition results of VMD
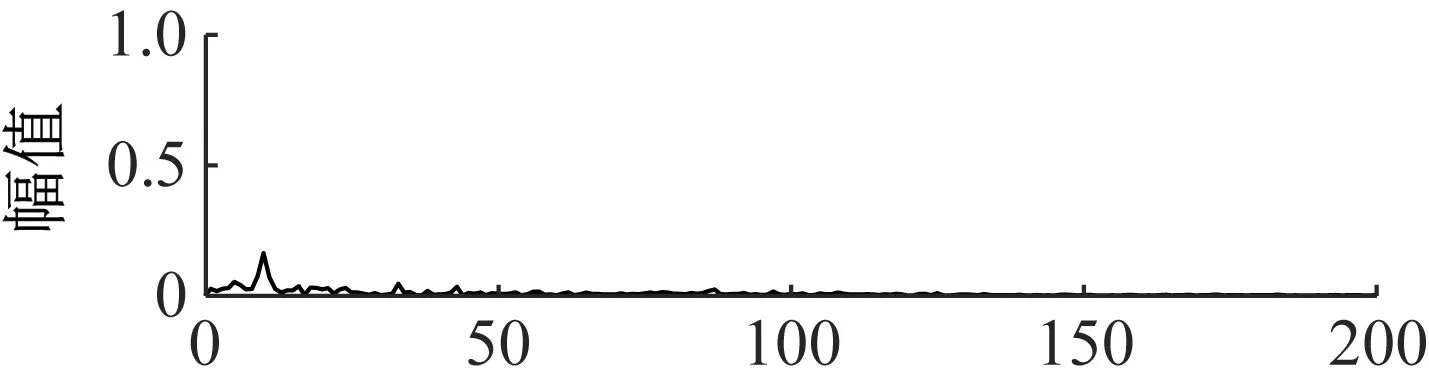


图15 VMD分量的包络谱Fig.15 The component envelope spectrum of VMD
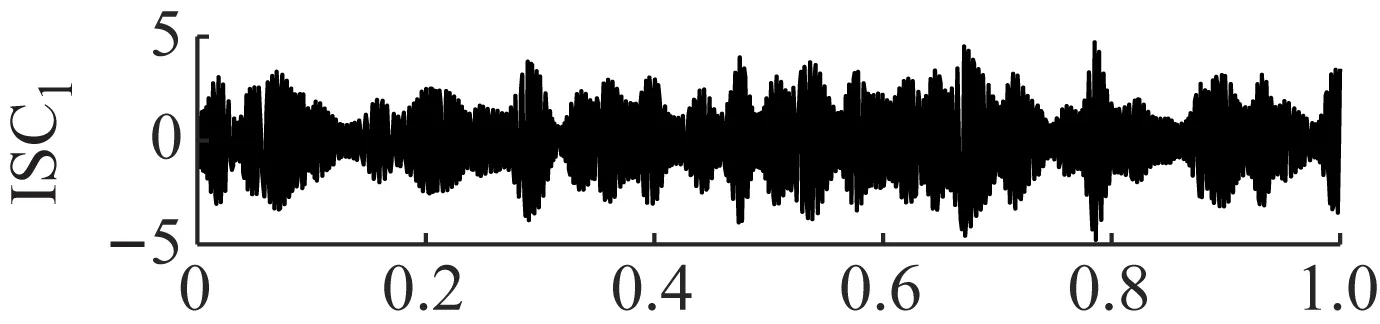

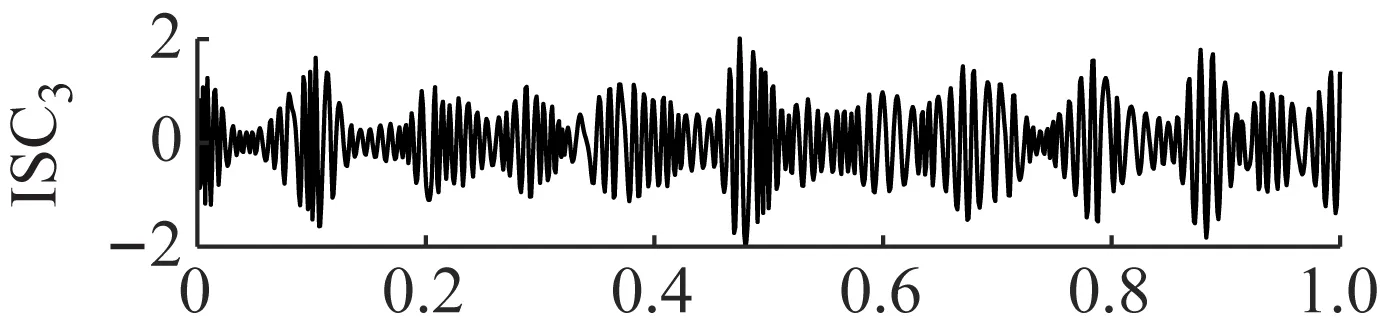
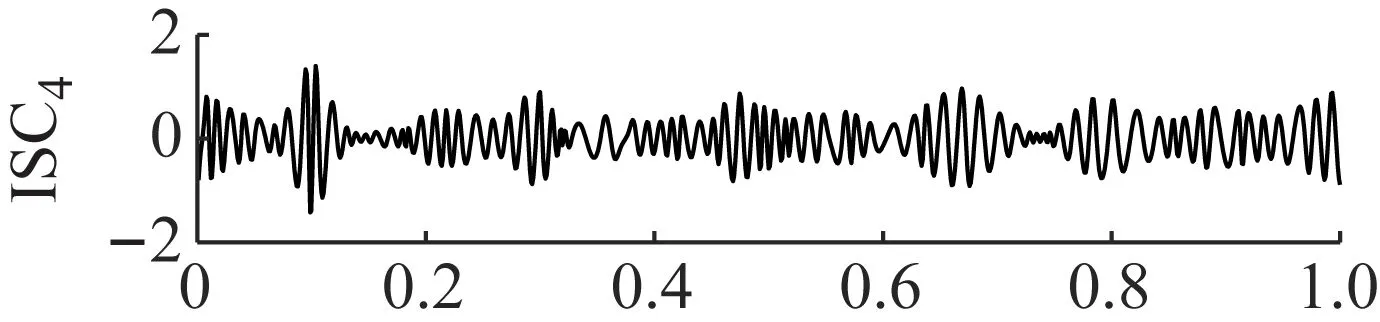
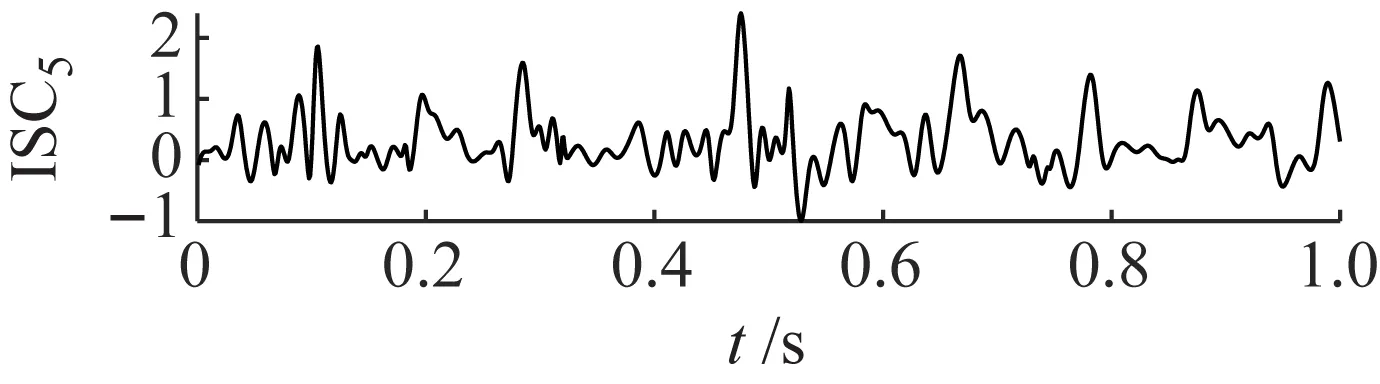
图16 LCD的分解结果Fig.16 The decomposition results of LCD
综上所述,相比较于EMD、LCD和VMD方法,ANSMD分解得到的包络谱更为明显,能准确反映齿轮裂纹故障信息,故障特征频率及其倍频更加明显。结果表明,所提ANSMD方法可以有效性地完成齿轮的故障诊断。
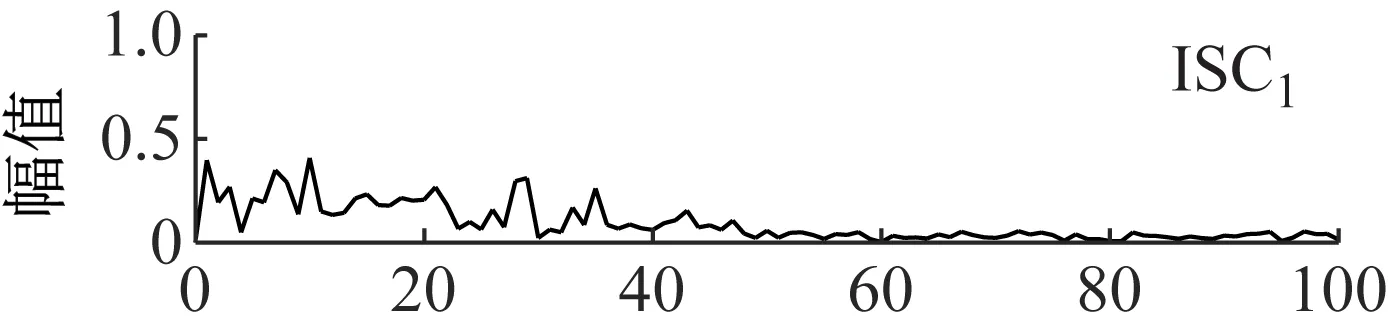

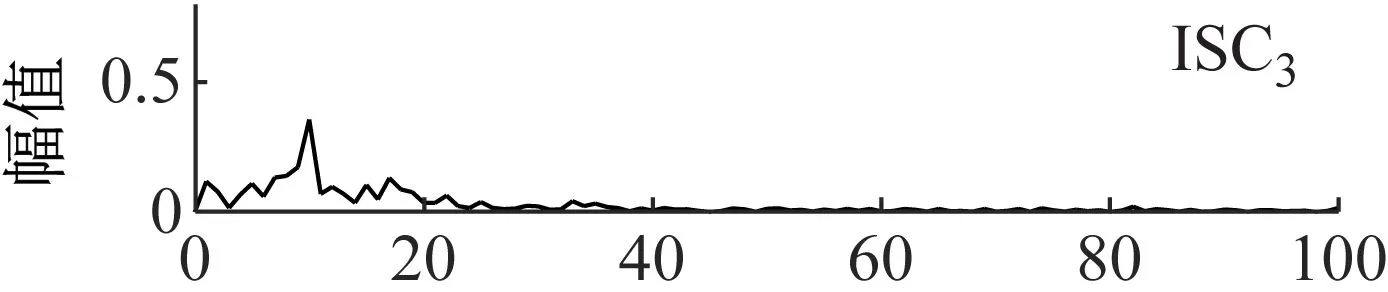


图17 LCD分量的包络谱Fig.17 The component envelope spectrum of LCD
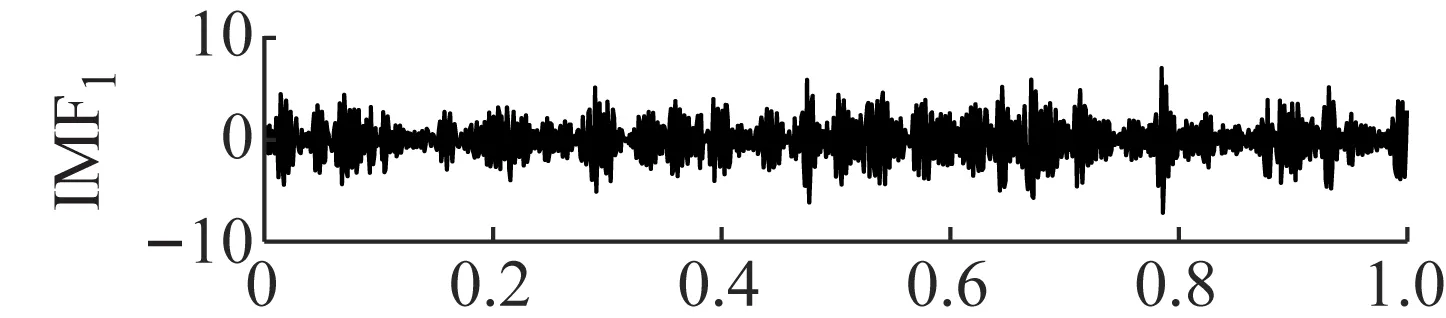

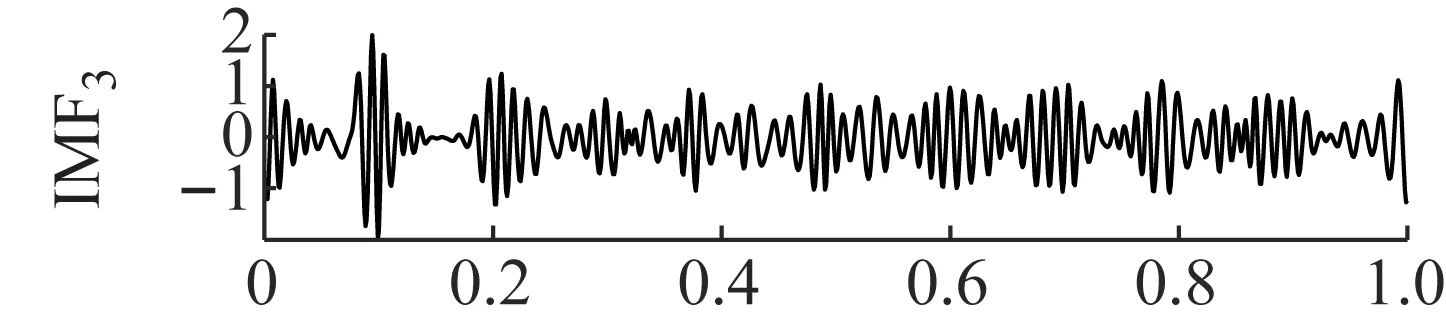
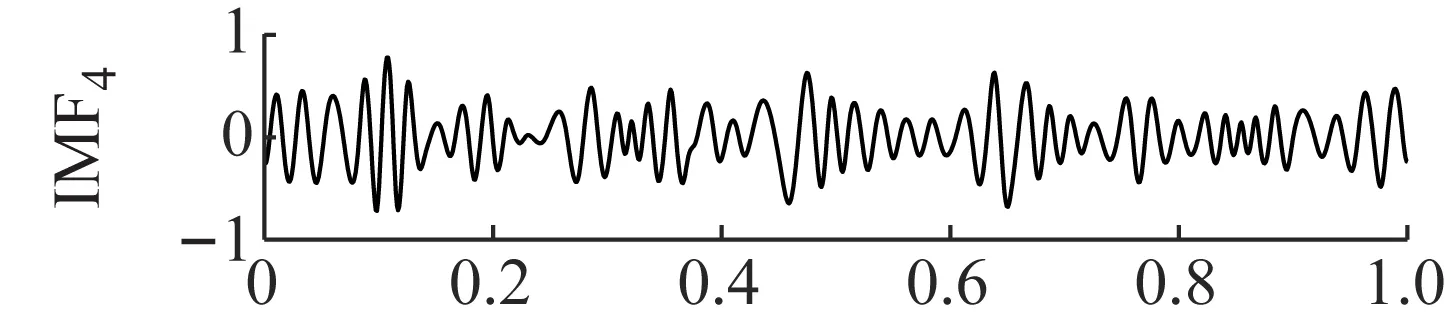

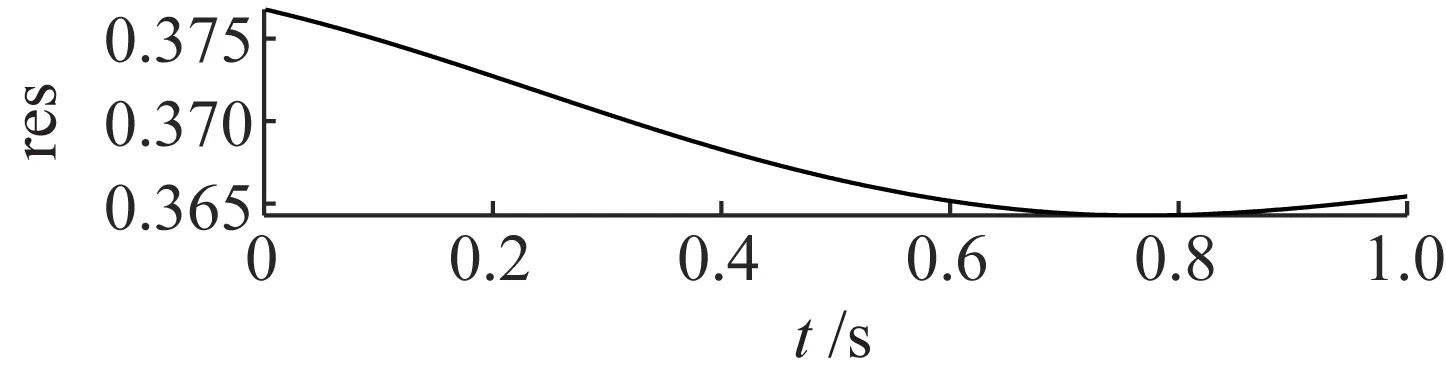
图18 EMD的分解结果Fig.18 The decomposition results of EMD
4 结 论
(1) 提出了自适应非线性稀疏模态分解方法ANSMD ,将ANSMD与EMD、LCD和VMD等方法进行了对比,仿真信号结果表明,ANSMD在抑制模态混叠、鲁棒性等方面更加突出。
(2) 将ANSMD应用于齿轮齿裂的故障诊断,通过对试验数据的分析,结果表明,所提方法能有效提取和凸显故障冲击成分,故障特征频率及其倍频更加明显。
因此,尽管所提的故障诊断方法能够有效的诊断齿轮故障,与EMD、LCD、VMD三种现有方法相比具有一定的优越性,但是所提方法仍有不足,如参数初始化问题和运算速度等方面还需要进一步的研究和完善。

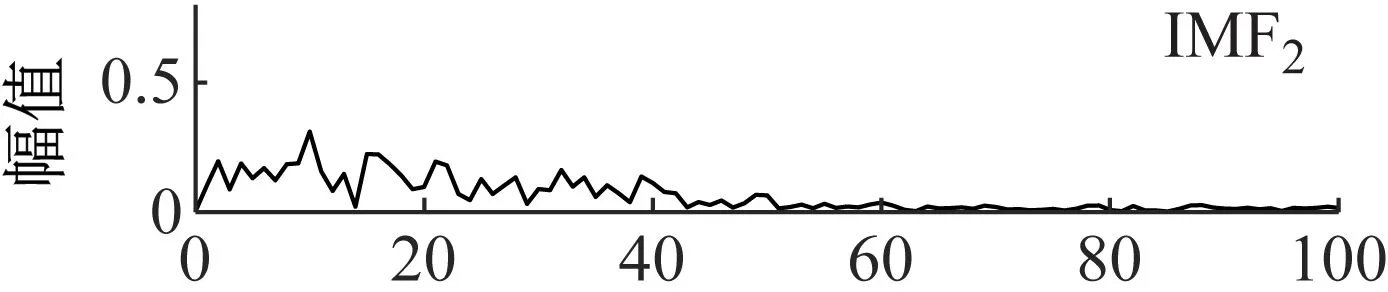
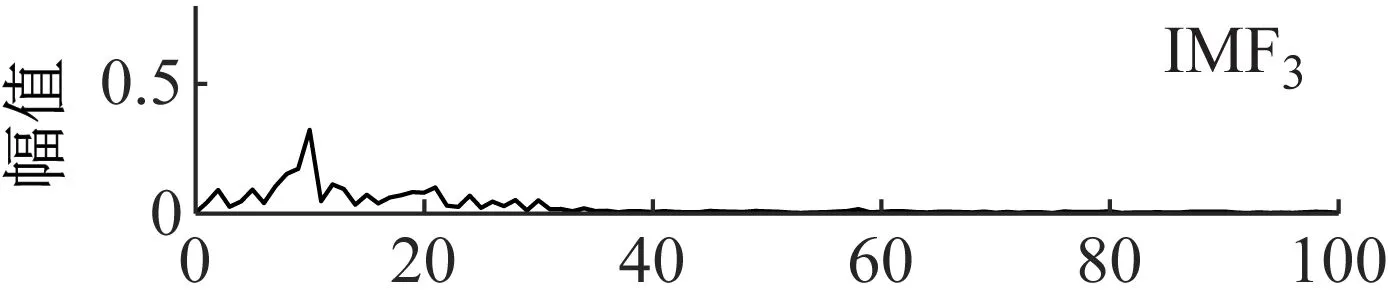
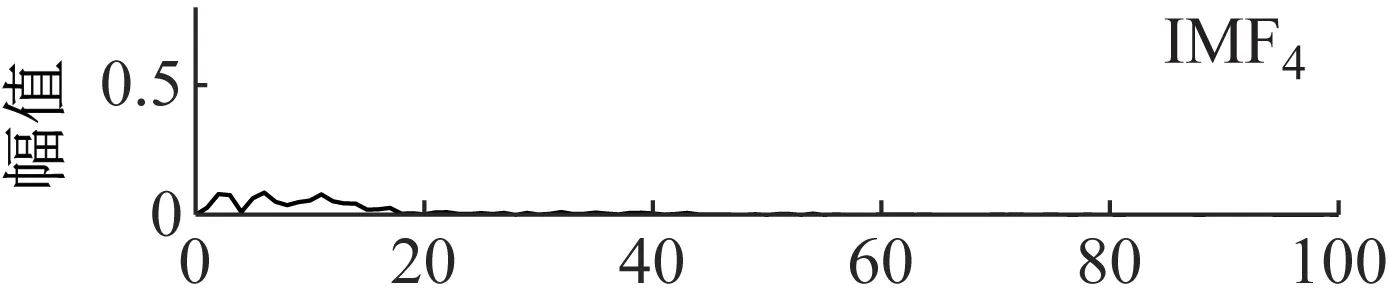

图19 EMD分量的包络谱Fig.19 The component envelope spectrum of EMD
