基于广义子集模拟和自适应Kriging模型的非线性随机动力系统的时变可靠性分析
2021-11-17唐和生郭雪媛薛松涛
唐和生, 郭雪媛, 薛松涛
(1. 同济大学 结构防灾减灾工程系, 上海 200092; 2. 同济大学 土木工程防灾国家重点实验室, 上海 200092)
工程结构的可靠性是指结构系统在规定的时间间隔内完成其预定功能的概率,近年来受到国内外学者的广泛关注。结构系统在服役期内会受到地震等具有强随机性的动力作用,同时结构系统自身材料特性与几何参数也存在固有不确定性。由于两种不确定性的来源及表征形式的不同,并且在非线性系统中叠加原理不再成立,经典的随机振动理论难以推广到非线性动力系统中,因此非线性随机动力系统在非平稳随机激励下的时变可靠性分析仍然面临巨大挑战。
根据首次超越破坏准则的基本理论,现有时变可靠性研究方法主要分为基于跨越率的方法和基于极值的方法。基于跨越率的方法的核心是计算特定时间间隔内,随机过程超过给定阈值的“跨越事件”发生次数的期望与失效概率的关系。这一概念最早由Rice[1]提出,随后利用关注响应量的各种统计数据,基于跨越事件发生服从Poisson过程假设的解析方法得到进一步发展。近年来,Andrieu-Renuad等[2]引入一阶可靠度方法(FORM),将跨越率的计算转换为并联的静态问题提出一种PHI2方法,实现了跨越率的高效求解。Hu等[3]针对跨越事件相互独立假设的不足,提出一种具有较高精度的联合跨越率方法求解时变可靠性问题。张德权等[4]提出了一种考虑认知不确定的PHI2方法,得到结构在设计周期内的时变可靠性区间。虽然基于跨越率与FORM相结合的方法的准确性已得到提高,然而在实际工程中,动力系统的时变可靠性分析是一个高维的隐式问题,这一类方法并不适用。目前针对动力系统,主要采用发展成熟的功率谱密度函数方法[5-6]。然而这类方法往往需要通过等效线性化方法才能推广到非线性系统中[7],因此存在较大误差。
基于极值的方法的关键在于识别极限状态函数的极值,对极值的不确定性进行量化获得极值分布,这类方法不受系统是否为线性的约束。在极值概率分布已知的情况下,时变可靠性问题可以转化为一个时不变问题。在实际应用中,获取极限状态极值的概率特性通常是十分困难的,特别是对于复杂的工程应用,Monte Carlo模拟(MCS)在计算上非常昂贵。为了解决计算效率问题,Wang等[8]提出了一种嵌套极值响应曲面(NERS)方法,在可靠性分析中消除了随机过程,构造了一种时间响应曲面,用于评价极限状态函数的极值响应。其他基于代理模型的方法也被广泛研究[9-10],然而绝大多数代理模型都存在维数诅咒且不适用于极限状态函数与随机过程存在双向嵌套关系的动力系统。概率密度演化方法[11-12]也被用来近似极值分布,该方法的计算精度较高,但对多变量情形,样本点数量较多导致计算耗时。数值模拟方法的目的是通过一些改进的采样技术,如重要性采样[13]和子集模拟[14]来估计时变可靠性。Hu等[15]提出一种针对极值分布的抽样方法,把时变可靠度问题转换为时不变问题进行求解,大大提高了计算效率。然而遗憾的是,即使是高效的计算方法,为得到离散时间区间内的累积失效概率,极限状态函数改变,需要对每一区间进行重复运行,造成效率的明显下降。本文采用Li等[16]提出的广义子集模拟方法(generalized subset simulation, GSS),实现仅通过单次运行得到所有时间区间内的累积失效概率,解决非平稳随机激励造成的高维输入不确定性。
传统的非线性动力系统的时变可靠性研究往往将两种不确定分离,即分别考虑随机系统在确定地震激励下的可靠性问题和确定性系统在随机激励下的可靠性问题,难以实现两者的统一处理。基于全概率定理的方法可以同时考虑系统的随机性与外部随机激励,从多角度处理不确定性来源对可靠性的影响,分析过程清晰且可以将广泛研究的Kriging代理模型应用于构建系统随机参数与累积失效概率之间的非线性关系。考虑到计算资源有限性,构建代理模型的一个关键问题就是如何通过更“好”地选取样本点来提高代理模型的精度。为此,采用Echard等[17]提出的一种结合Kriging(adaptive Kriging, AK)和原始MCS(Monte Carlo simulation, MCS)的主动学习可靠性方法(AK-MCS),主动地训练代理模型精确逼近重要区域的累积失效概率。
为解决非线性随机动力系统的时变可靠性分析中系统参数不确定性与非平稳随机激励造成的计算成本难以承受的问题,本文提出一种基于广义子集模拟和自适应Kriging模型的非线性随机动力系统时变可靠性分析的GSS-AK-MCS方法。该方法采用全概率定理对两种不确定性来源融合,将基于极值的时变可靠性分析与自适应代理模型方法相结合,显著改善不确定传播分析的计算效率,并且通过两个数值算例对所提出方法的有效性进行探讨。
1 随机动力系统时变可靠性中的全概率定理
非线性随机动力系统受到非平稳随机地震激励时的运动方程
(1)

(2)
式中:Pf(0,T)为累积失效概率;FE表示失效事件;P(FE/x)为X一次样本下的条件累积失效概率;fX(x)表示随机变量X的联合概率密度函数,且Ω为其支撑集。考虑系统失效由单一响应随机过程Y控制,对于随机变量的一次样本实现,动力系统参数确定,由累积失效概率定义
P(FE/x)=Pr(∃t∈[0,T],Y(x,t)>b)
(3)
一般来说,式(2)中的精确数值积分难以计算,因此建立条件累积失效概率P(FE/x)在随机变量空间内的代理模型,并在代理模型基础上通过Monte Carlo方法直接计算双随机时变可靠性。特别地,在处理非正态和相关的输入随机变量时,采用全概率定理不需要额外的假设从而保证了计算结果的准确性。
2 累积失效概率的广义子集模拟算法
2.1 累积失效概率的极值理论表达
动力系统的失效定义为系统的某一与位移或速度响应相关的量(例如,绝对位移、相对位移、控制点的应力或应变)超过给定阈值b(确定性的常量)。这种基于时变失效概率的可靠性评估问题也被称为首次超越问题,根据结构或系统的动力反应的临界值,考虑双侧界限的动力系统时变可靠性问题(随机过程的绝对值超过给定阈值)。
传统的Poisson过程法基于任意两次跨越事件与其发生的时间统计独立,服从(无记忆)Poisson过程假设。然而对于低阈值水平和/或窄带过程,Poisson过程法得到的是累积失效概率的保守值,将低估时变可靠性。为克服Poisson过程法的限制,Vanmarcke认为交叉事件是成群出现的且各群之间相互独立,在双态Markov过程假设的基础上提出了一种累积失效概率的改进估计。这类基于跨越率的方法对于高度非线性的动力系统求解技术难度大,不仅精度低而且计算成本极高。
基于极值的方法关注于工程系统在特定时间内的极值性能,在时变可靠性分析中,定义响应在时间段[0,T]内的极值变量
(4)
式中,θ为随机激励基本变量的一次样本。极值法将动力系统的时变可靠性问题转换为对应等效极值分布的求解,则累积失效概率可表达为
Pf(0,T)=P(ye(T)>b)
(5)
针对工程中常见的非平稳随机过程,Priestley提出一种演变谱过程模型,表示为
(6)
式中:A(t,ω)是t与ω的确定性调制函数;Z(ω)是一个正交增量过程。如果用A(t)代替A(t,ω),则非均匀调制演变谱退化为工程中常用的均匀调制演变谱。由非平稳随机过程的演变谱表示理论,导出了非平稳随机过程模拟的一个谱表示方法,其样本函数是由余弦级数公式计算产生的
(7)
式中:Δω=ωu/N,ωu表示计算截止频率,超过ωu所对应功率谱能量可忽略不计;θk为在[0,2π]区间上均匀分布、相互独立的随机相位角。因此非平稳随机过程激励可转换为一组随机变量θ=[θ1,…,θk]表示,时变可靠性问题被转化为与时间无关的一个隐式非线性高维可靠性问题。
2.2 广义子集模拟算法
基于抽样的方法由于与维数无关且未对极限状态函数做任何假设,目前是解决高维可靠性问题的唯一可行方法。针对高维小失效概率情况,MCS需要大量的计算样本才能获得较准确的失效概率,而子集模拟方法对于此类问题非常有效。然而时变可靠性分析需要对不同时间段内可靠性评估或当极限状态函数阈值发生改变时,子集模拟方法需要进行反复计算,大大增加了计算成本。因此采用Li等提出的GSS,进一步推导基于极值的累积失效概率计算公式,解决时变可靠性分析这一多失效模式问题。
首先对原始子集模拟进行简要介绍。子集模拟方法的基本思想是通过自适应地引入m层嵌套的中间事件,满足FE1⟺FE2⟺…⟺FEm=FE,将小失效概率转换成一系列相对较大的失效概率的乘积。中间事件与目标失效事件FE的表达相似,定义为FEi={ye>bi,i=1, …m}(b=bm>…>b2>b1)。其中,m为中间事件的总数。因此原始子集模拟的目标失效概率可表示为
P(FE)=P(FEm|FEm-1)P(FEm-1)=…=
(8)
在随机动力系统的时变可靠性分析中,多时间点的累积失效概率计算是一个多极限状态问题,原始的子集模拟方法需要重复计算。为克服这一局限性,采用改进后的GSS算法定义多个失效事件的并联事件驱动随机样本的生成,高效求解多时间点的累积失效概率。
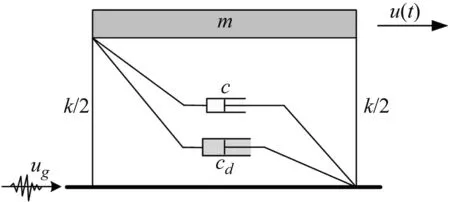
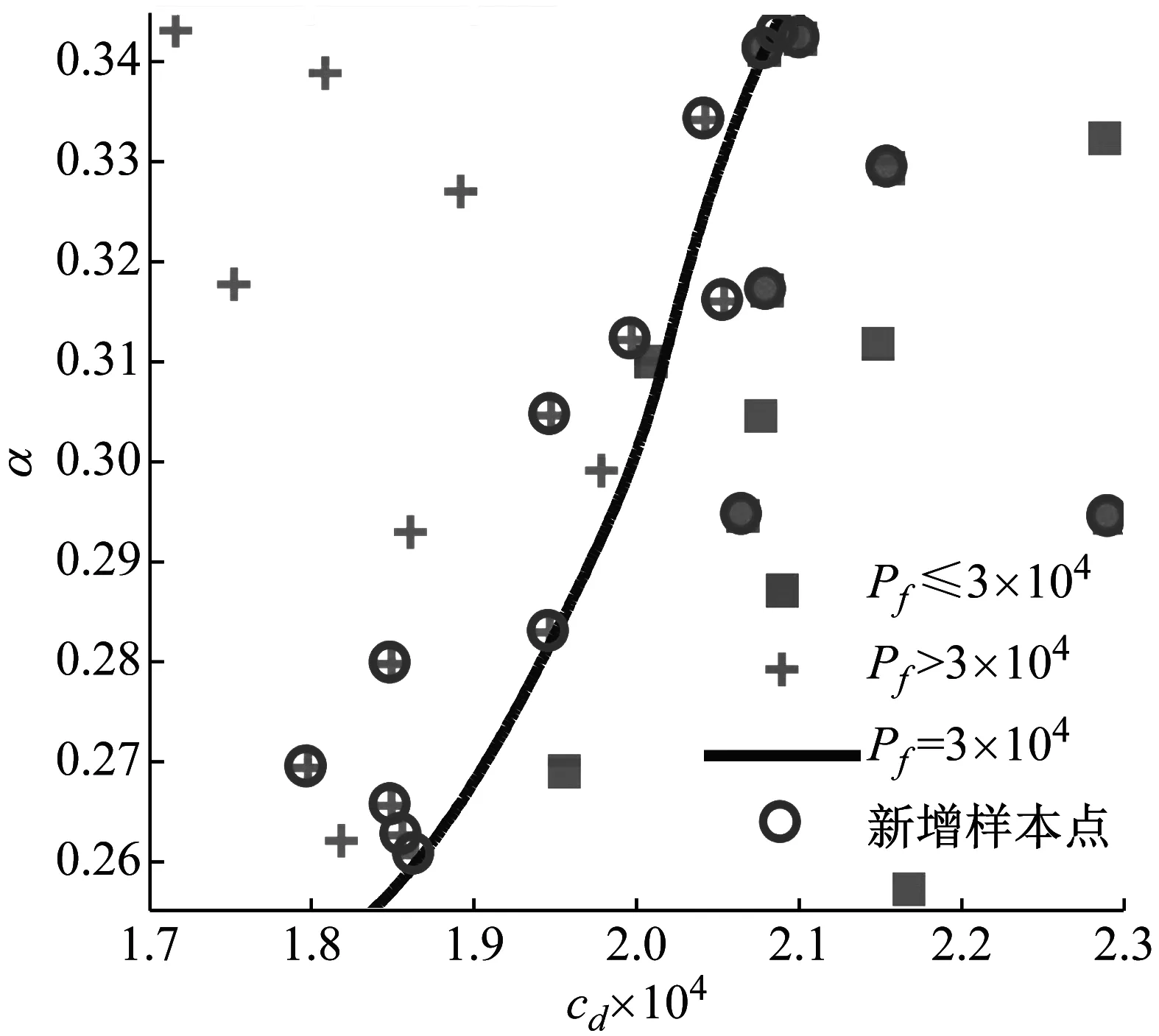
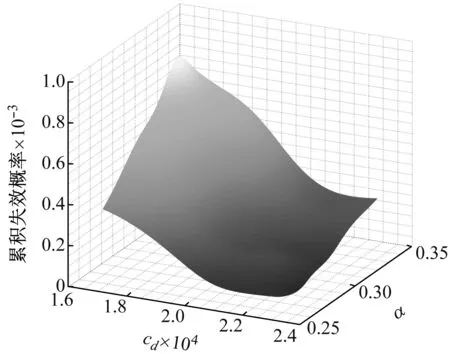
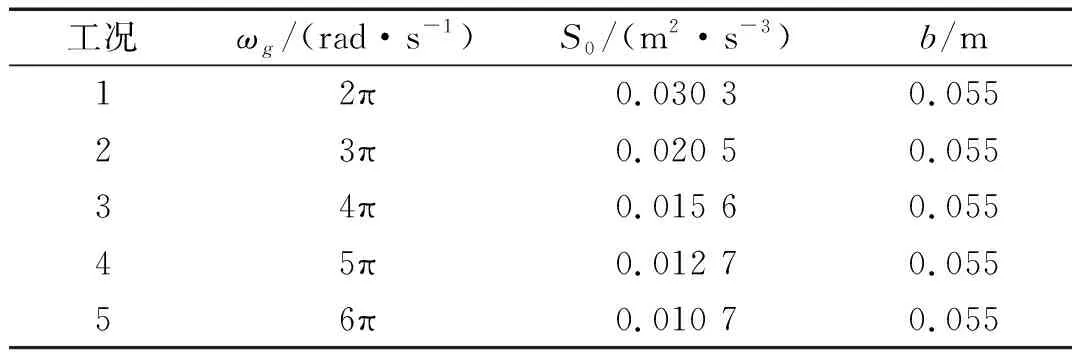
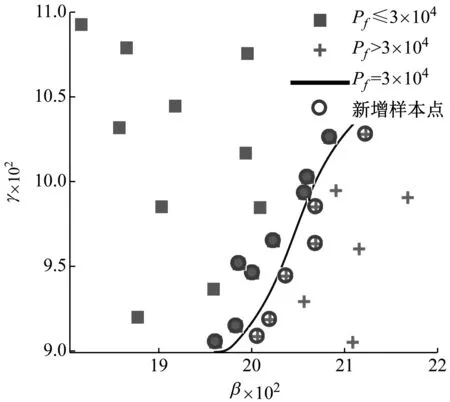
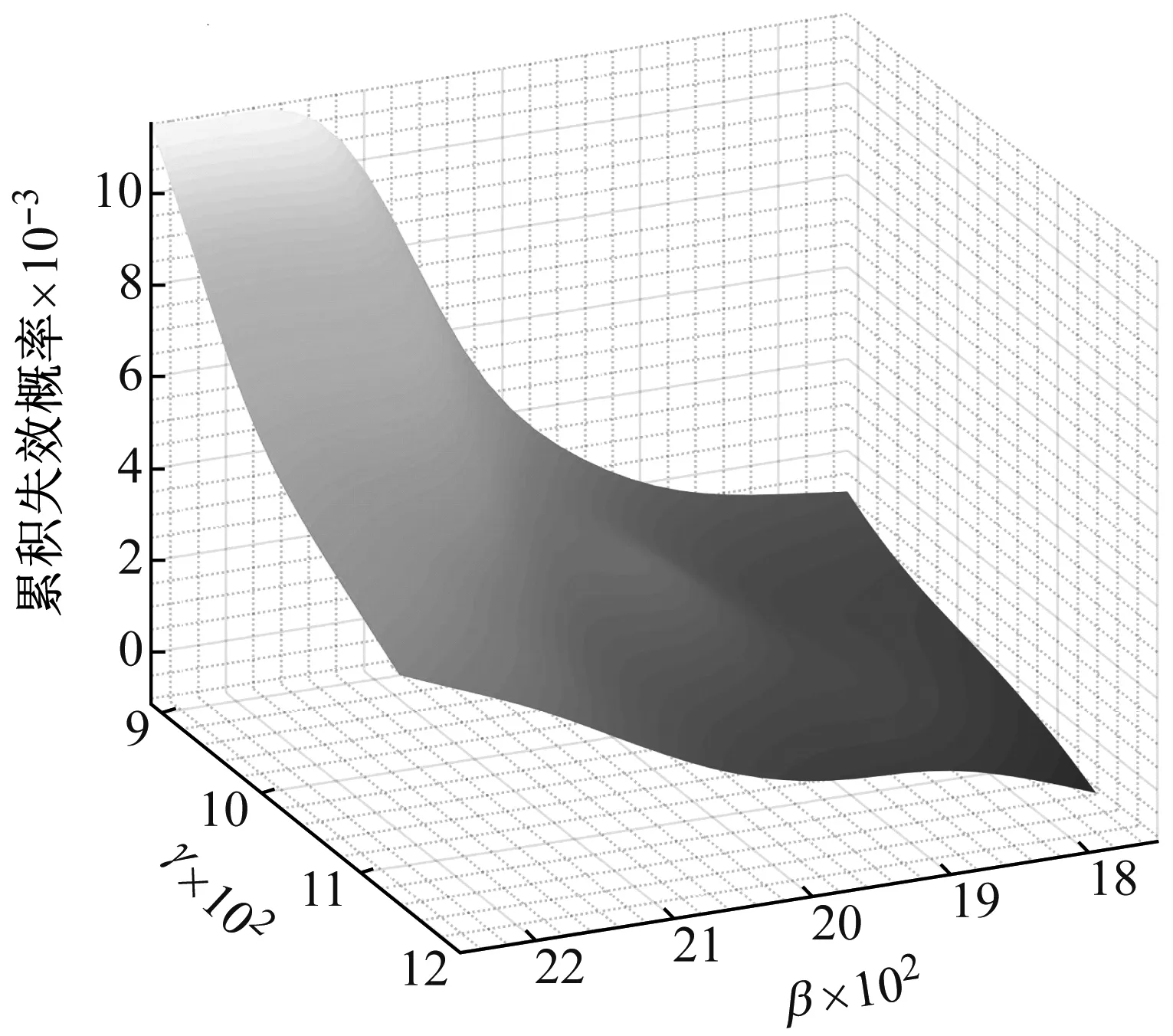
基于极值的GSS算法中,将时间段[0,T]离散化,时变可靠性的关注时间点依次为[T1,…,Tnt],由首次超越破坏的定义,其相对应的累积失效概率呈随时间递增,即P(FE1) (9) 式中,下标i表示第i个关注时间点。所有统一中间事件同样满足嵌套关系 G1⊃G2⊃…⊃Gm=G (10) 因此与原始子集模拟方法相似,GSS算法首先根据不确定参数概率分布通过MCS产生第一层随机样本。然后采用MCMC方法不断产生各层统一中间事件相应的样本。为自适应地确定中间事件,设定所有的中间条件概率为一常数p0,通常为兼顾准确性与计算效率取值p0∈[0.1,0.3]。最终仅通过一次GSS计算得到各关注时间点Tj的累积失效概率 (11) Kriging模型作为一种半参数化的方差估计最小的随机过程插值算法,具有局部和全局的统计特征,已广泛应用于工程中的可靠性分析。由于累积失效概率计算成本高昂,而在工程应用中往往针对某一阈值规定临界失效概率,因此临界失效概率对应的随机参数样本附近区域的计算精度更为重要。采用AK-MCS方法,使代理模型不断优化,提高计算精度的同时节约计算成本。具体计算步骤如下: 步骤2采用拉丁超立方抽样产生N0个初始试验设计点xS={x(1),…,x(N0)},计算相应的失效概率归一化指标gS={g(x(1)),…,g(x(N0))},构成样本集{xS,gS}。 步骤3基于样本集应用MATLAB中的DACE工具箱构建一系列Kriging模型,时间点Ti处的代理模型为 (12) 其中h(x)为基函数向量,β为回归系数向量,Z(x)是一个均值为0服从正态分布的平稳高斯过程,其协方差由相关函数计算得到。 步骤4生成大量的MC样本S={s(1),…,s(NMC)},根据构建的代理模型计算每一样本的预测值及方差。 步骤5定义U函数作为学习函数 (13) 步骤6判断是否达到收敛条件。当达到收敛准则miniU(s(i))>2,i=1,…,NMC时,代理模型更新终止。在优化后的一系列代理模型上,运用MCS计算相应的累积失效概率及时变可靠性。 根据全概率定理,非线性随机动力系统的时变可靠性问题转化为一个双层嵌套问题。首先通过拉丁超立方抽样生成系统随机参数空间内样本点;在内层中针对高维输入不确定性,通过GSS算法计算非平稳随机激励下累积失效概率;而在外层中解决系统参数不确定性,构建一系列Kriging代理模型拟合系统随机参数与累积失效概率之间的非线性关系,并通过主动学习技术对代理模型更新;最后在更新完成的Kriging模型基础上,基于全概率定理求解随机系统的时变可靠性。本文所提出的非线性随机动力系统的时变可靠性分析方法流程如图1所示。 图1 随机动力系统的时变可靠性分析流程图Fig.1 Flowchart of time-variant reliability analysis forstochastic dynamic systems 以设有黏滞阻尼器的单自由度消能减震结构系统(如图2)为例,研究GSS-AK-MCS方法在非线性动力系统时变可靠性分析中的效率和精度。 图2 单自由度消能减震结构系统计算模型Fig.2 Analytical model of the SDOF-VD structural system 该系统在地震激励作用下的运动方程为 (14) (15) 式中:cd为阻尼系数;α为速度指数;sgn(·)为符号函数。系统不确定参数cd与α均服从正态分布,结合小概率事件发生规律一般遵从“3σ”法则,各随机变量分布及代理建模范围如表1所示。 表1 非线性系统随机变量 结构所受非平稳随机激励的调制函数为 (16) 式中,T=20 s,ta=2.5 s,tb=10 s,β=0.1,计算步长Δt=0.02 s,功率谱密度函数取Kanai-Tajimi模型 (17) GSS-AK-MCS方法中在随机变量[μ-3σ,μ+3σ]范围内,采用拉丁超立方抽样均匀抽取16个初始样本点,构建初始Kriging模型。通过AK-MCS方法更新代理模型,新增样本点为20个。作为比较GSS-Kriging-MCS方法选取随机参数变量样本点总数相同为36个。以T=20 s时为例,两种方法样本点分布及累积失效概率计算结果分别见图3、4与表2。由上述结果可以得到如下结论:① 与传统Kriging代理模型相比,GSS-AK-MCS方法采用的自适应代理模型更新技术可以使样本更集中分布于关键区域;② 在随机变量样本数量相同的情况下,GSS-AK-MCS方法实现了在计算成本相同时提高计算精度。 图3 b=0.055 m时GSS-Kriging-MCS样本点设计Fig.3 Design of sample points of the GSS-Kriging-MCS forb=0.055 m 图4 b=0.055 m时GSS-AK-MCS样本点设计Fig.4 Design of sample points of the GSS-AK-MCS forb=0.055 m 表2 单自由度消能减震结构系统累积失效概率Tab.2 Cumulative probability of failure for the SDOF structure system 为进一步研究GSS-AK-MCS方法在不同频谱特征非平稳随机激励下的性能,对表3所示各计算工况采用本文所提出方法与MCS方法结果进行对比。各工况对Kanai-Tajimi模型中的地基土卓越圆频率ωg和基岩扰动白噪声强度S0的设计,满足非平稳随机激励所包含总能量相同。以工况3为例,在T=20 s时采用GSS-AK-MCS方法构建的累积失效概率代理模型如图5。GSS-AK-MCS方法中随机变量样本点共36个,平均每个样本点通过GSS方法进行28 325次时程分析,为MCS方法时程分析次数的(36×28 325)/(104×106)≈0.010%,具有相当高的计算效率。 图5 b=0.055 m时累积失效概率代理模型Fig.5 Surrogate model of cumulative probability of failurefor b=0.055 m 基于已构建的一系列代理模型,得到各工况累积失效概率随持时的变化曲线如图6所示。对各计算工况,以MCS方法结果作为累积失效概率的准确值,MCS方法计算结果在图6中由实线表示。对以上结果进行分析可以得出,本文所提出的GSS-AK-MCS方法基于时变可靠性的极值理论,无需引入对首次超越事件发生次数的假设,在不同频谱特征的非平稳随机激励情况下,均保持良好的精度;自适应代理模型的技术的引入大大降低了非线性随机动力系统时变可靠性分析的计算成本。 表3 计算工况 图6 累积失效概率计算结果Fig.6 Results for cumulative probability of failure 为验证本文所提出方法的有效性,本算例采用基于Bouc-Wen模型的五层非线性剪切框架。该非线性剪切框架的结构参数为:每层质量mi=50 kg,线性刚度ki=1.5×105N/m,阻尼系数ci=1 000 N·s/m,i=1,2,…,5。假设非线性滞回分量符合Bouc-Wen模型,结构在地震作用下的运动方程为 (18) 式中:α为屈服后与屈服前的水平刚度之比;Δu=ui-ui-1为层间位移;β、γ和n为Bouc-Wen模型无量纲滞回参数。在本算例中,结构非线性参数α=0.5,n=1.25,不确定参数β与γ均服从正态分布,各随机变量分布及代理建模范围见表4。结构所受非平稳随机激励与上一算例相同。 表4 Bouc-Wen模型随机变量 表5 T=20 s非线性框架累积失效概率 图7和图8表明本文提出的自适应代理模型方法给予预测条件累积失效概率在临界失效概率的邻近区域内的样本点更高的权重,提高代理模型在关键区域的预测精度。通过构建累积失效概率的代理模型响应面,代替非线性结构在非平稳随机过程激励下响应的复杂时程分析求解。表5中的对比分析验证了与传统Kriging代理模型和MCS方法相比,GSS-AK-MCS方法具有良好的计算精度并且显著提高了时变可靠性分析的计算效率。 图7 b=0.04 m时GSS-AK-MCS样本点设计Fig.7 Design of sample points of the GSS-AK-MCS forb=0.04 m 图8 b=0.04 m时累积失效概率代理模型Fig.8 Surrogate model of cumulative probability of failurefor b=0.04 m 本文提出了非线性随机动力系统时变可靠性的GSS-AK-MCS方法,推导了累积失效概率的计算公式并构建了累积失效概率的代理模型,以一个装配非线性黏滞阻尼器的单自由度系统和一多自由度非线性剪切框架为例验证了所提出方法的有效性,主要结论如下: (1) 基于全概率定理可将非线性随机系统的时变可靠性分析中两种来源的不确定性分别处理。采用GSS方法解决随机激励的高维不确定性,通过Kriging代理模型拟合累积失效概率与系统随机参数的非线性关系,避免了理论推导的繁琐和困难。 (2) 本文所提出的GSS-AK-MCS方法作为一种本质为数值模拟的方法,对于小失效概率问题的可靠性求解,与传统的MCS方法相比具有相当高的计算效率,并且可以通过一次计算解决时变可靠性中多时间点造成的多失效模式问题。 (3) GSS-AK-MCS方法在不同频谱特征的非平稳随机激励情况下均具有良好的计算精度,且由于自适应代理模型更新技术的引入,在不增加计算成本的条件下提高系统随机参数重要区域的可靠性精度。因此,本文所提出的GSS-AK-MCS方法为同时考虑系统参数不确定性和随机地震动作用的非线性动力系统时变可靠性分析提供了准确高效的计算方法,在工程中复杂随机结构的时变可靠性分析中具有广阔应用前景。
3 基于AK-MCS算法的时变可靠性分析
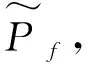
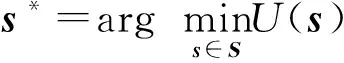

4 算例分析
4.1 附加非线性黏滞阻尼器的单自由度消能减震结构
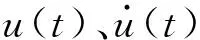
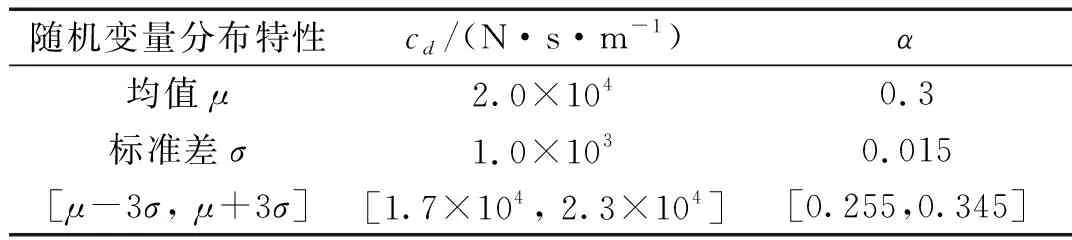


4.2 非线性多自由度剪切框架
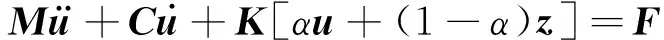



5 结 论
