非黏滞阻尼系统频响函数灵敏度分析的改进计算方法

史俊磊， 张 磊， 丁 喆

(1. 武汉科技大学 冶金装备及其控制教育部重点实验室， 武汉 430081；2. 武汉科技大学 机械传动与制造工程湖北省重点实验室， 武汉 430081)

灵敏度分析可以定量地确定系统参数改变对系统动态特性的影响，在结构优化、模型修正和参数识别等领域有着广泛应用[1-2]。黏性阻尼模型由于其模型简单和计算方便的优点已被广泛研究和应用[3]，但随着各类智能材料和高阻尼复合材料的发展，原有的黏性阻尼模型假设已不能准确地描述该类结构系统的阻尼特性。卷积型非黏滞阻尼模型由于假设阻尼力与质点速度的时间历程相关，其数学表达式为阻尼核函数与质点速度的卷积,因而能够准确地描述黏弹性阻尼材料的迟滞效应。目前，非黏滞阻尼系统的研究主要针对其特征值分析、时域响应分析和参数识别等[4-7]方面，其灵敏度分析也主要集中在特征灵敏度分析和时域响应灵敏度分析[8-9]，而非黏滞阻尼系统频响函数(frequency response function, FRF)灵敏度的研究相对较为缺乏。

FRF灵敏度分析可以评估系统参数对FRF的影响程度。一般来说，结构系统灵敏度的计算方法分为三类：有限差分法[10]、直接微分法和伴随变量法[11]。其中，有限差分法理论简单，但在某些情况下计算效率较低。当设计变量数目大于约束数目时，伴随变量法具有更高的计算效率，反之则直接微分法的计算效率较高。针对FRF灵敏度分析，Lin[12]提出了一种加权FRF灵敏度法，该方法即使在模型误差较大的情况下，仍具有良好的收敛性能。Qu[13]基于幂级数展开和模态叠加法提出无阻尼系统FRF的模态加速法以及FRF灵敏度的双模态加速法，减小该系统FRF及其灵敏度的模态截断误差。Wu等[14]基于Sturm定理得到参与FRF灵敏度计算的模态数目，并利用激励频率收敛幂级数的部分和近似被截断高阶模态影响，进而推导出无阻尼系统的FRF灵敏度表达式。Wu等[15]根据Sherman-Morrison公式，提出了一种仅利用初始FRF和参数摄动来计算灵敏度的方法，该方法避免了重复有限元分析，提高了计算效率。Erik等[16]针对黏滞阻尼系统，提出了一种高计算效率和高精度计算传递函数灵敏度的方法。Shadan等[17]利用灵敏度方法，将FRF变化与结构参数变化关联，提出了一个灵敏度方程来减小FRF数据不完全性的不利影响。Xiao等[18]针对非经典阻尼系统，在仅使用感兴趣频率范围内模态的情况下推导出FRF灵敏度的表达式，该方法在不涉及状态空间方程的基础上修正模态截断误差。Zhu等[19]考虑多重扰动对系统动刚度矩阵的影响，采用Sherman-Morrison-Woodbury和有限差分法对系统FRF灵敏度进行了求解。上述FRF灵敏度求解方法均建立在无阻尼或黏性阻尼模型的基础上，无法直接应用于非黏滞阻尼模型系统。因此亟需提出一种适用于非黏滞阻尼系统FRF灵敏度的计算方法。

本文研究具有卷积型非黏滞阻尼模型结构系统FRF灵敏度问题。非黏滞阻尼系统的特征值求解复杂，尤其对于大型结构系统，特征值分析过程非常耗时。为提高计算效率，通常只利用有限数目的低阶模态近似求解其动力响应和灵敏度。但忽略高阶模态不可避免地引入模态截断误差，对非黏滞阻尼系统动力响应和灵敏度的计算精度影响尤为显著。因此必须提出一种适用于非黏滞阻尼结构系统FRF灵敏度求解的改进方法，使其能够补偿高阶截断模态的影响，进而提高系统FRF灵敏度计算的精度。解决该问题的难点和关键在于建立非黏滞阻尼系统模态和系统矩阵间的关系。为消除非黏滞阻尼系统FRF灵敏度的模态截断误差，本文利用Neumann级数展开定理建立结构系统模态与系统矩阵间的关系，考虑其第一项和前两项近似，将系统高阶模态对FRF灵敏度的贡献用系统矩阵和低阶模态进行表达，推导非黏滞阻尼系统FRF灵敏度一阶近似法和二阶近似方法的表达式。通过数值算例验证了所提出方法的有效性和准确性。结果表明，与传统方法相比，本文所提出的改进计算方法兼顾了计算精度和效率，更适用于非黏滞阻尼结构系统FRF灵敏度的求解。

1 理论背景

卷积型非黏滞阻尼模型的阻尼力与质点速度的时间历程相关，数学表达式为质点速度与某一阻尼核函数的卷积

(1)

g(t)=Cnvg(t)

(2)

式中：t为时间；τ为迟滞时间变量；Fd(t)∈N为阻尼力向量；N为速度向量；Cnv∈N×N为非黏滞阻尼系数矩阵；N为系统的自由度；g(t)为阻尼核函数。式(1)所表示的卷积型非黏滞阻尼模型适用于线性系统，它不仅考虑了当前速度的影响，还考虑了非局部时间的速度影响，更加准确地描述了黏弹性阻尼材料的迟滞效应[20]。

理论上，任何使系统能量耗散函数非负的表达式都可作为卷积型非黏滞阻尼模型的核函数。因此阻尼核函数不唯一，通过选取不同阻尼核函数可适应不同黏弹性材料的阻尼特性，常用的阻尼核函数模型有：Biot阻尼模型[21]、指数阻尼模型和Golla-Hughes-McTavish(GHM)阻尼模型等。特别地，当选取的核函数满足g(t-τ)=Cδ(t-τ)(C∈N×N是黏性阻尼矩阵，δ(t)为狄拉克函数)时，卷积型非黏滞阻尼模型将退化为传统的黏性阻尼模型。因此，黏性阻尼模型可看作该非黏滞阻尼模型的一种特殊形式。

含卷积型非黏滞阻尼的N自由度系统时域运动方程可表示为

(3)

其初始条件为

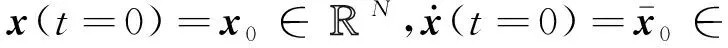
(4)

式中：M和K∈N×N分别是质量矩阵和刚度矩阵；f(t)∈N是外激励向量；x(t)和N分别是位移和加速度向量。

对式(3)进行拉普拉斯变换得

D(s)X(s)=F(s)

(5)

(6)

式中：λj和φj分别为第j阶特征值和特征向量；m为非黏滞阻尼系统的特征值数目m由两部分组成

m=2N+P，P>0

(7)

式中：2N为弹性模态数目，弹性模态是以复共轭对的形式出现；P为非黏性模态数目，非黏性模态的形式为实数。由式(7)可知，虽然系统有N自由度，但其特征解的个数大于2N。这是非黏滞阻尼系统和黏性阻尼系统的一个重要区别，也是导致非黏滞阻尼系统特征值求解耗时的原因之一。

2 非黏滞阻尼系统FRF灵敏度的求解方法

本章将根据上述非黏滞阻尼系统的运动方程，推导出传统求解非黏滞阻尼系统FRF灵敏度的表达式。

2.1 直接频响法

由式(5)可知

X(s)=D-1(s)F(s)=H(s)F(s)

(8)

其中，H(s)为系统FRF，它可表示为

H(s)=D-1(s)=(s2M+sG(s)+K)-1

(9)

该方法称为直接频响法(direct frequency response method, DFRM)，将式(9)关于设计变量p求导得到系统FRF灵敏度的表达式

(10)

2.2 模态叠加法

传统求解系统FRF灵敏度的方法除了DFRM外还有模态叠加法(modal superposition method，MSM)。MSM是在系统特征方程求出系统模态的基础上，利用留数定理推导出系统FRF矩阵H(s)。当系统全部模态参与计算时，MSM可以获得精确解，但其计算效率较低，并且在某些情况下，无法求出系统全部模态。因此，通常只考虑低阶模态，忽略高阶模态对FRF的影响

(11)

(12)

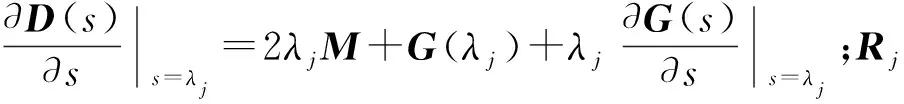
H(s)H(s)-1=I

(13)

式中，I为单位矩阵。同时对式(13)两边关于设计变量p求导，并考虑H(s)=D(s)-1得到

(14)

将式(11)代入式(14)得到系统FRF灵敏度表达式

(15)

由式(15)可知，MSM计算出FRF灵敏度的表达式中存在两个模态截断项。因此，模态截断对系统FRF灵敏度分析的影响较大。由模态截断引起的模态截断误差可以定量地表示为

(16)

当L≪m时，MSM计算出的FRF灵敏度表达式不仅不准确，且在某些特殊情况下，计算结果是错误的。为保证系统FRF灵敏度的计算精度，MSM需要保留较高阶模态，但相应的计算效率降低。因此，需要提出一种兼顾计算精度和效率的非黏滞阻尼系统FRF灵敏度的计算方法。

3 非黏滞阻尼系统FRF灵敏度的改进计算方法

在本章将提出两种考虑高阶模态影响的FRF灵敏度的改进计算方法。

3.1 非黏滞阻尼系统模态与系统矩阵关系

本小节介绍一种利用Neumann级数展开定理建立的非黏滞阻尼系统模态与系统矩阵间的关系[22]。

Neumann级数展开定理的表达式为

(I+A)-1=I-A+A2-A3+A4-…

(17)

将式(11)表示为矩阵和向量相乘的形式，并考虑所有阶模态得

H(s)=-UΘ-1Λ-1(I-sΛ-1)-1UT

(18)

其中I∈m×m，Λ=diag[λ1,λ2,…,λm]，U=[φ1,φ2,…,φm]和Θ=diag[θ1,θ2,…,θm]。利用Neumann级数展开定理将式(I-sΛ-1)-1展开得

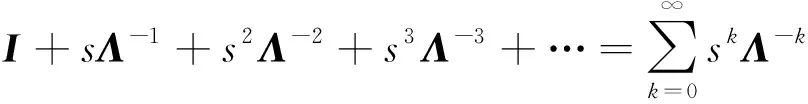
(19)

将式(19)代入式(18)，可以得到

H(s)=-UΘ-1Λ-1UT-sUΘ-1Λ-2UT-

s2UΘ-1Λ-3UT-s3UΘ-1Λ-4UT-…=

(20)

由式(9)可知，FRF还可表示为

H(s)=D-1(s)=(s2M+sG(s)+K)-1=

[I+sK-1(G(s)+sM)]-1K-1

(21)

其中I∈N×N，根据Neumann级数展开定理将[I+sK-1(G(s)+sM)]-1展开并代入到式(21)可以得到

H(s)=K-1-sK-1(G(s)+sM)K-1+[sK-1(G(s)+sM)]2K-1-[sK-1(G(s)+sM)]3K-1+…

(22)

将式(22)展开，并按s的次数由低到高排列可以得到

H(s)=K-1-sK-1G(s)K-1+s2K-1G(s)K-1G(s)K-1-s2K-1MK-1+…=K-1-sK-1G(s)K-1+s2K-1[G(s)K-1G(s)-M]K-1+…=

(23)

其中：

(24)

因此，非黏滞阻尼系统矩阵与模态间关系

-UΘ-1Λ-k-1UT=Γk

(25)

由式(25)可知，由于阻尼核函数G(s)与频率相关，当k≥2时，所有展开项都会受前项的影响，故其不能再进一步近似等效。因此，考虑非黏滞阻尼系统矩阵与模态间的前两项近似，并引出其关系

-UΘ-1Λ-1UT=K-1

(26)

-UΘ-1Λ-1UT-UΘ-1Λ-2UT=K-1-K-1G0K-1

(27)

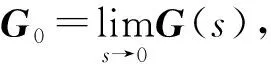
3.2 FRF灵敏度改进计算方法

在上述关系的基础上，本小节将推导考虑高阶模态影响的系统FRF灵敏度的表达式。将式(18)分为可用的低阶模态和被截断的高阶模态两部分

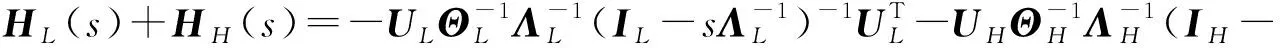
(28)

式中，H表示被截断的高阶模态数目。利用Neumann级数展开将式(28)右侧的第一项展开并取前两阶近似得

(29)

联立式(26)～(29)将被截断的高阶模态用系统低阶模态和系统矩阵表示为

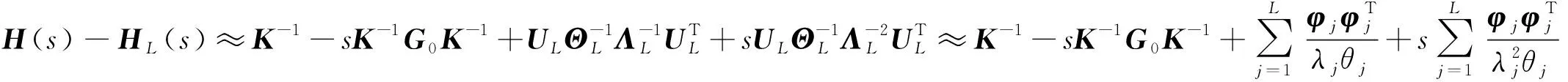
(30)

由于高阶模态对系统FRF的影响是利用非黏滞阻尼系统模态与系统矩阵关系的前两项近似表达，因此称该方法为二阶近似法(second-order approximation method, SAM)。联立式(11)和(30)得到考虑高阶模态影响的系统FRF表达式

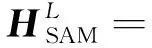
(31)

通过合并同类项，式(31)可进一步化简为

(32)

将式(32)代入式(14)得到利用SAM方法计算的非黏滞阻尼系统FRF灵敏度表达式

(33)

SAM计算得到频响函数对应的模态截断误差为

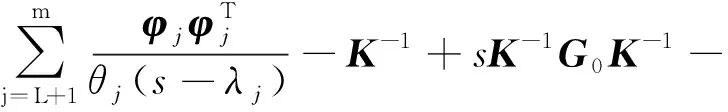
(34)

其中，下标H-SAM表示利用SAM计算出系统频响函数，其频响函数灵敏度的模态截断误差为

(35)

其中，下标Hp-SAM表示利用SAM计算出系统频响函数关于p的灵敏度，如果用非黏滞阻尼系统模态与系统矩阵关系第一项近似FRF高阶模态的贡献量可以得到

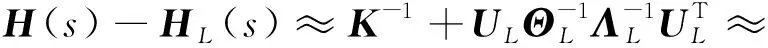
(36)

联立式(11)和(34)并化简可以得到一阶近似法(first-order approximation method，FAM)的表达式

(37)

将式(35)代入式(14)得到由FAM计算出的非黏滞阻尼系统FRF灵敏度表达式

(38)

FAM计算得到频响函数对应的模态截断误差为

(39)

其中，下标H-FAM表示利用FAM计算出系统频响函数，其频响函数灵敏度的模态截断误差为

(40)

其中，下标Hp-FAM表示利用FAM计算出系统频响函数关于p的灵敏度，与MSM相比，FAM和SAM方法考虑高阶模态对非黏滞阻尼系统FRF灵敏度的影响，但计算更加复杂。为了更清晰地表达FAM和SAM的计算流程并便于编程，其算法流程图如图1所示。

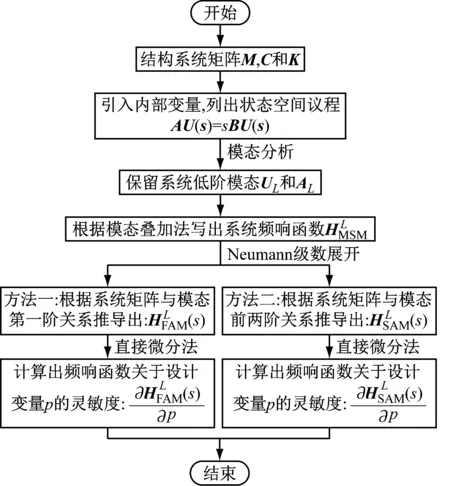
图1 FAM和SAM算法流程图Fig.1 Algorithm flow chart of FAM and SAM

4 例子与结论

4.1 质量-弹簧系统

在本节，通过如图2所示的含非黏滞阻尼模型的N自由度系统(N可以根据需要进行调整)验证本文提出的非黏滞阻尼系统FRF灵敏度的FAM和SAM的有效性，并将其与DFRM和MSM进行对比，讨论四种方法的计算精度和效率。

本例选取双指数阻尼核函数，含该阻尼模型的N自由度运动方程表达式为

(41)

式中：c为非黏滞阻尼参数；μ1和μ2均为松弛参数。

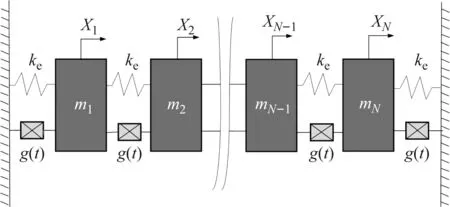
图2 含非黏滞阻尼器的N自由度系统Fig.2 N DOF non-viscously damped system

4.1.1 计算精度

本小节选取自由度数目N=4，系统参数：m1=100 kg，m2=200 kg，m3=300 kg,m4=400 kg和ke=50 000 N/m。非黏滞阻尼模型的参数为：c=50 Ns/m，μ1=50 s-1和μ2=70 s-1。

通过求解状态空间方程的特征方程可以得到系统的特征值，该系统的特征值如表1所示。可以注意到，本例中的特征值个数为16，其中弹性模态的个数为8，非黏性模态的个数P=r×q=4×2=8(其中r为阻尼系数矩阵的秩，q为频域内阻尼核函数分母的最高次幂)。由表1可知，弹性模态的形式为复数，其实部表示系统的衰减系数，虚部表示系统的阻尼振动频率。由于弹性模态的实部与非黏性模态均是负数，所以该系统是稳定的。

表1 四自由度非黏滞阻尼系统的特征解

为了验证本文提出方法的有效性和准确性，首先选取非黏滞阻尼参数c为设计变量。分别利用DFRM，MSM，FAM和SAM计算该四自由度非黏滞阻尼系统在0～40 rad/s范围内FRF灵敏度。其中，将DFRM计算得到的FRF灵敏度的结果视为参考值。为了方便起见，图中只展示系统FRF灵敏度矩阵中第一对角元素H11。H11表示输出和输入均为1号自由度时得到的系统FRF。本节中各方法所使用的频率步长均为0.2 rad/s。

图3为三种方法选取全部弹性模态计算的FRF灵敏度相对误差的结果。其中，DFRM计算的实际频响函数灵敏度也展示在图3中。本文中，频响函数灵敏度相对误差ER的计算公式为

(42)

从图3可以看出，MSM，FAM和SAM计算出的FRF灵敏度在选取频率范围内误差均在允许范围内。FAM和SAM的振幅相对误差明显小于MSM的振幅相对误差。SAM的相位相对误差明显小于FAM的相位相对误差。因此，在所比较的三种FRF灵敏度计算方法中，SAM计算精度最高。

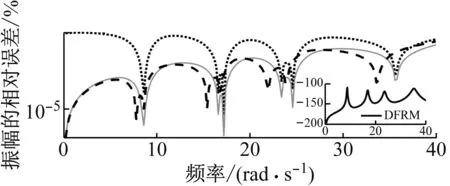
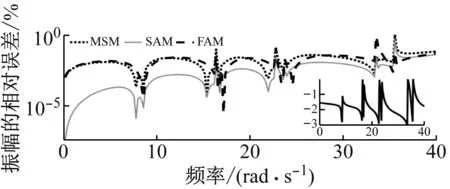
图3 全部弹性模态近似频响函数灵敏度的相对误差Fig.3 The relative error of FRF sensitivity matrixapproximated in terms of all elastic modes.

为分析模态截断误差对三种方法计算精度的影响，选取第一对(前两阶)弹性模态参与计算FRF的灵敏度，这就意味着系统的模态从第三阶开始被截断，其结果如图4所示。可以看出，当频率小于10 rad/s时，MSM的计算结果与参考值仍存在较明显的误差，而FAM和SAM的计算结果相较更接近参考值。当频率大于10 rad/s时，三种方法的FRF灵敏度结果均与参考值存在显著差异。

图4 第一对弹性模态近似频响函数灵敏度Fig.4 The sensitivity of FRF matrix approximated in terms ofthe first pair elastic modes.

图5是三种方法选取前两对弹性模态计算出的FRF灵敏度的结果。与图4结果类似，FAM和SAM的计算精度仍高于相同情形下MSM得到的结果。由于选取的最高阶模态频率为16.71 rad/s，因此FAM和SAM的计算结果在该频率以内的计算结果与参考值一致，而MSM计算的灵敏度存在较为明显的误差。

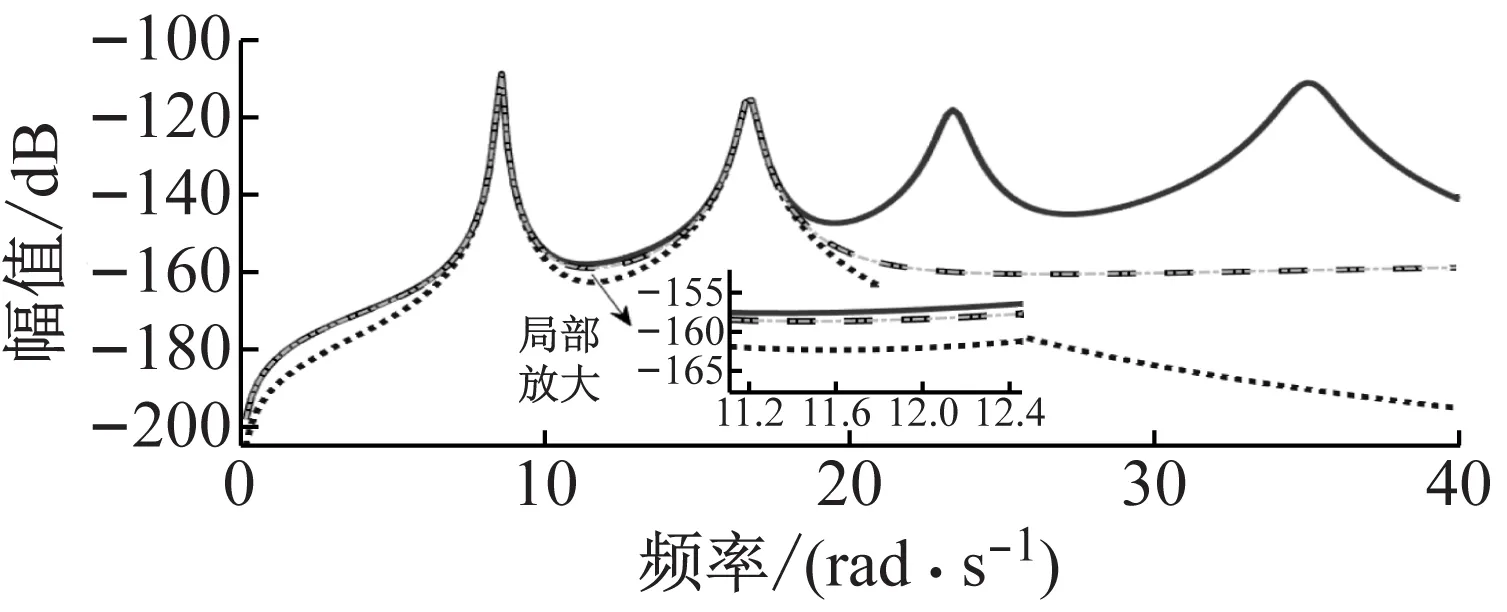
图5 前两对弹性模态近似频响函数灵敏度Fig.5 The sensitivity of FRF matrix approximated in terms ofthe first two pair elastic modes.

进一步增加参与计算FRF灵敏度的模态数目，考虑前三对弹性模态的各方法计算结果如图6所示。可以看出，相较于仅考虑第一对和前两对的灵敏度计算结果，三种方法的FRF灵敏度计算结果均有所提高。通过对比图4～图6可以看出，当利用本文提出的FAM和SAM计算非黏滞阻尼系统FRF灵敏度时，若希望得到一定频率范围内的准确结果，则需要该频率范围内的所有弹性模态参与计算。

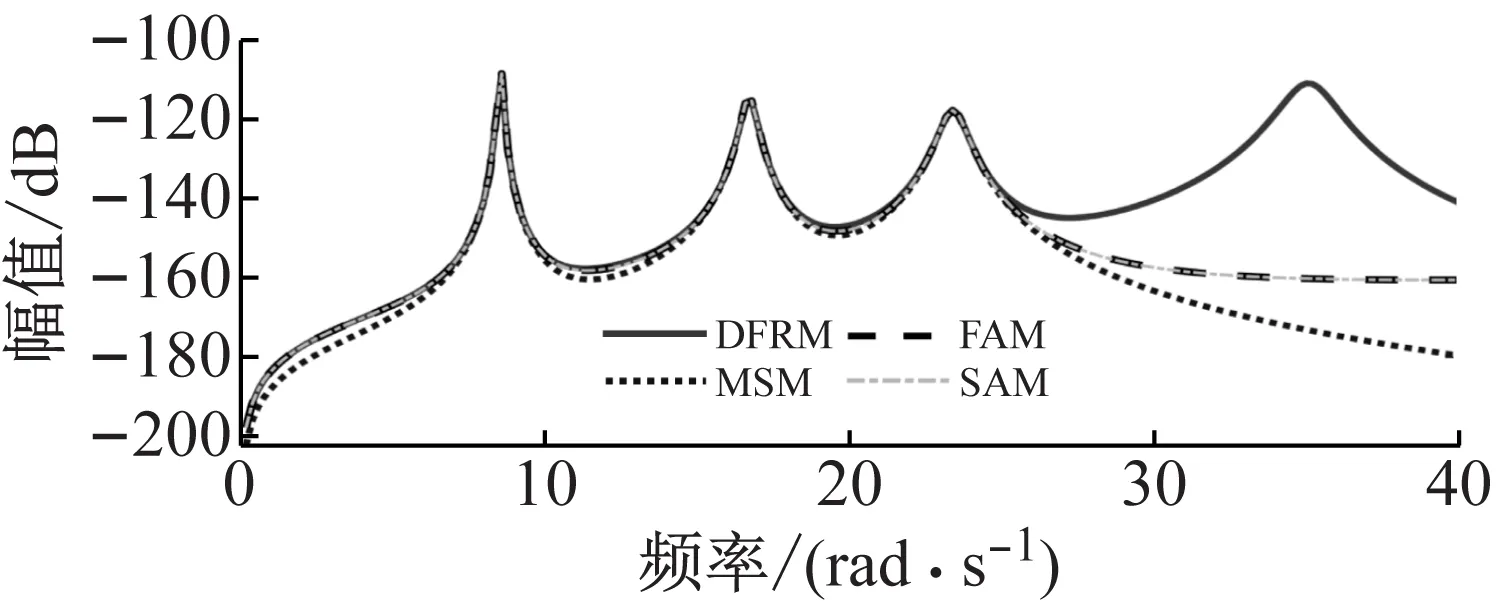
图6 前三对弹性模态近似频响函数灵敏度Fig.6 The sensitivity of FRF matrix approximated in terms ofthe first three pair elastic modes

为了更加直观地展示三种方法的准确性，图7为三种方法选取前三对弹性模态计算出FRF灵敏度的相对误差。可以看出，各方法的幅值相对误差高于相应的相位误差。当选取相同阶模态时，FAM和SAM的FRF灵敏度计算结果几乎相同，但均明显高于MSM的结果。图8给出SAM选取不同阶模态计算出FRF灵敏度相对误差。可以看出，增加参与计算的模态数目可大幅降低其FRF灵敏度的相对误差。结果表明，相较于传统的MSM方法，由于本文所提出的FAM和SAM方法考虑了非黏滞阻尼系统高阶模态截断误差的影响，因此能够大幅提高非黏滞阻尼系统FRF灵敏度的求解精度。

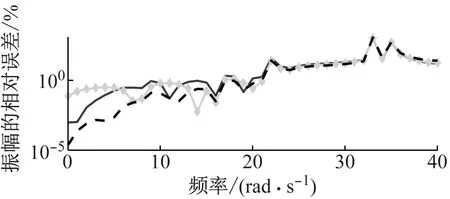
图7 选取前三对弹性模态计算出频响函数灵敏度的相对误差

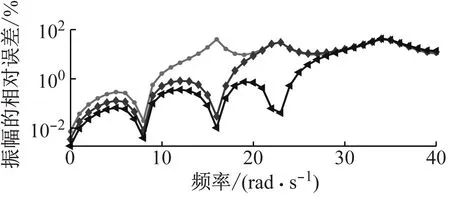
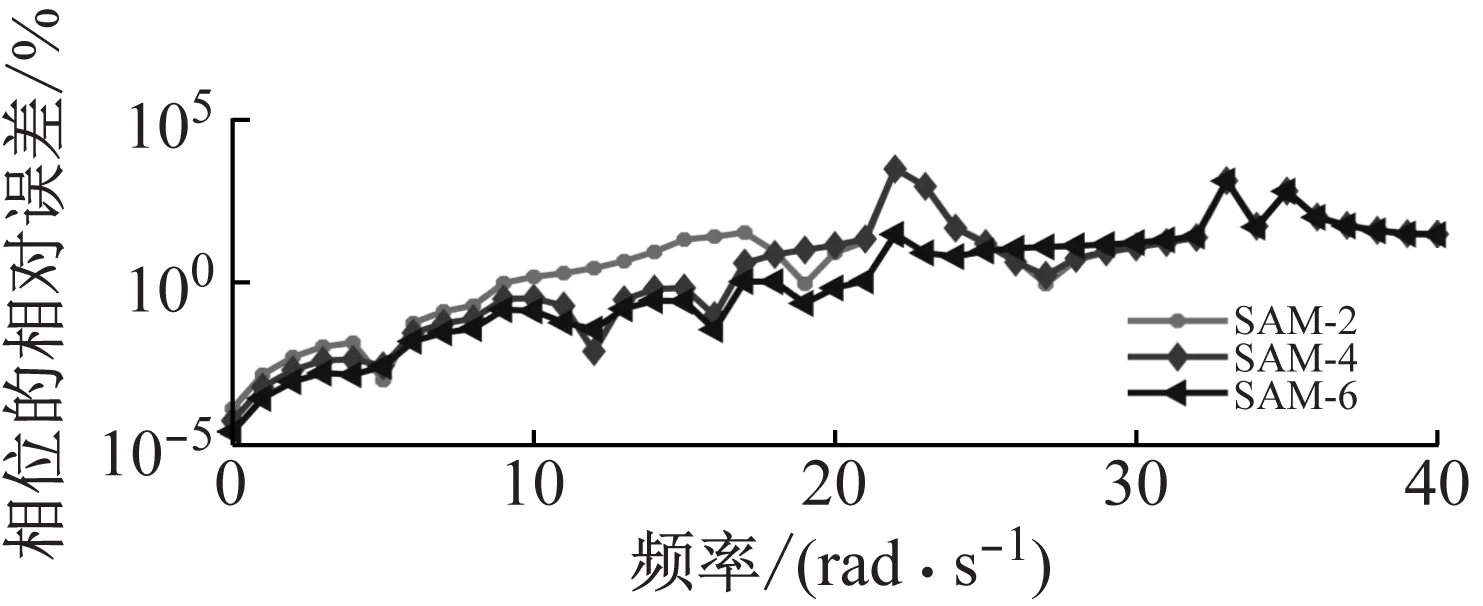
图8 SAM使用不同阶弹性模态计算FRF灵敏度相对误差

4.1.2 计算效率

为了比较DFRM，MSM，FAM和SAM的计算效率， 本小节通过图2所示的N自由度非黏滞阻尼系统，比较四种方法求解该系统频响函数H11灵敏度所消耗的时间。假定频率范围为0～5 rad/s，频率步长为0.1 rad/s，选取系统自由度N的变化范围0～1 500。

图9表示使用不同计算方法的FRF灵敏度计算时间随自由度增加的变化曲线。可以看出，当自由度小于600时，四种方法的计算时间相差不大。但随着自由度数目继续增加，DFRM的计算时间增加迅速，而FAM和SAM的计算时间增长相对平稳。这是因为在每个外激励频率下DFRM要对系统动刚度矩阵求逆，而系统自由度增加必然会引起系统动刚度矩阵维数的增加，系统动刚度矩阵求逆消耗的时间就越长。而FAM和SAM避免了矩阵求逆，仅在MSM的基础上考虑高阶模态对系统频响函数灵敏度的影响。因此，对于大自由度系统，FAM和SAM相较于DFRM在计算效率上具有明显的优势，且FAM的效率稍高于SAM。这是因为FAM和SAM分别考虑利用系统矩阵与模态关系的第一项和前两项近似高阶模态对系统频响函数灵敏度的影响。

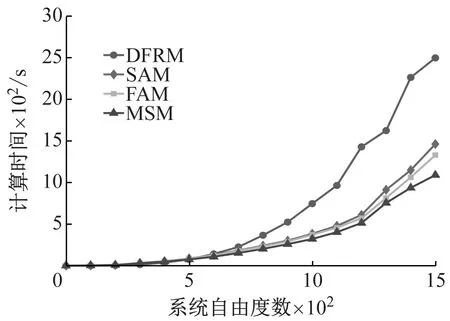
图9 四种方法计算时间随自由度数目变化图Fig.9 Computational time of different DOF with four methods

4.2 轴向振动杆

本节考虑一个具有双指数阻尼的固定-自由轴向振动杆。如图10所示，该轴向振动杆可根据需求划分为N+1个单元。轴向振动杆单元的单元刚度矩阵和单元质量矩阵如下

(43)

式中：ρ表示密度；A为杆的横截面积；E表示材料的杨氏模量；le=L/N为单元杆的长度。各参数分别为A=6.25×10-4m2，E=2.1×1011N/m2,ρ=7.8×103kg/m3，杆的总长L=4 m。整体质量矩阵M和整体刚度矩阵K可以根据经典的有限元方法组装得到。

假设轴向振动杆含双指数阻尼模型的表达式为

Cnv=μ1e-μ1(t)Cnv1+μ2e-μ2(t)Cnv2

(44)

其中，松弛因子μ1和μ2为

(45)

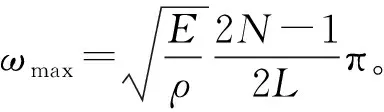
Cnv1=αM,Cnv2=βK

(46)

其中

(47)

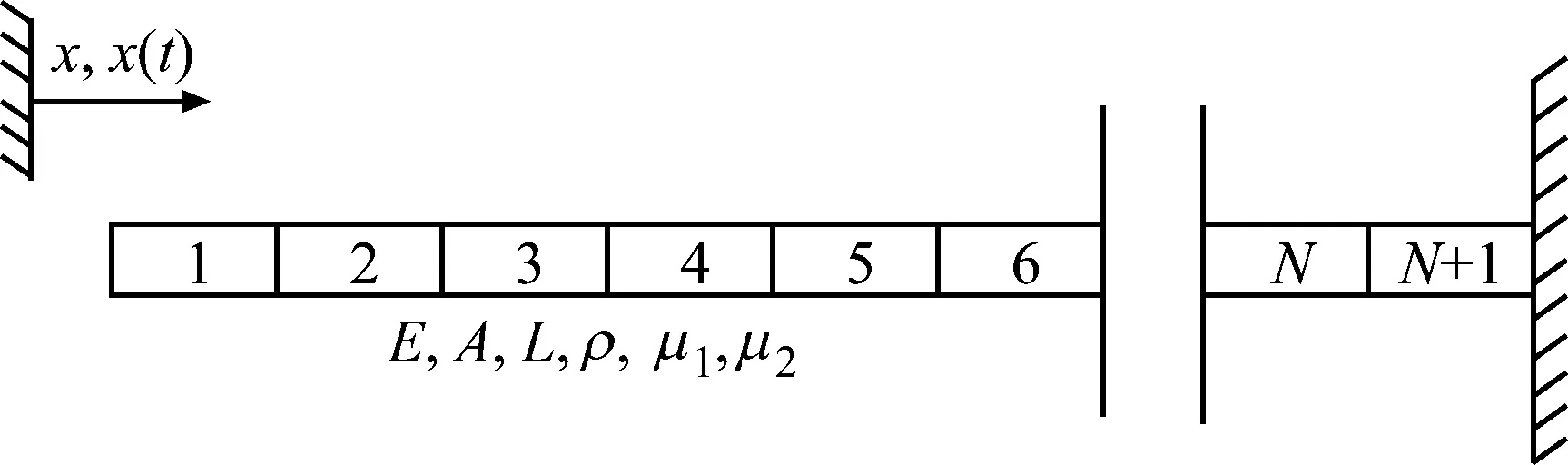
图10 含双指数阻尼模型的轴向振动杆示意图Fig.10 Axially vibrating rod with double-exponentialdamping model

4.2.1 计算精度

为了讨论不同方法的计算精度，本节将该轴向振动杆划分为80个单元，即N=80。分别使用DFRM、MSM、FAM和SAM计算该轴向振动杆自由端的频响函数H11关于ρ的灵敏度分析，选取的频率范围为：0～10 000 rad/s，选取的频率步长为10 rad/s。本算例仍然以DFRM计算出的频响函数灵敏度为参考值。

图11给出使用前两对弹性模态计算出系统频响函数灵敏度，各方法相对于DFRM的相对误差如图12所示。在所选频率范围内，FAM和SAM计算出频响函数灵敏度的精度优于相同情况下MSM的计算精度。对于FAM和SAM，二者幅值的相对误差相差无几，而SAM的相位相对误差明显比FAM的相位相对误差小。因此，就计算精度而言，SAM的计算精度高于FAM计算精度。这与质量-弹簧系统算例得到的结论相同。

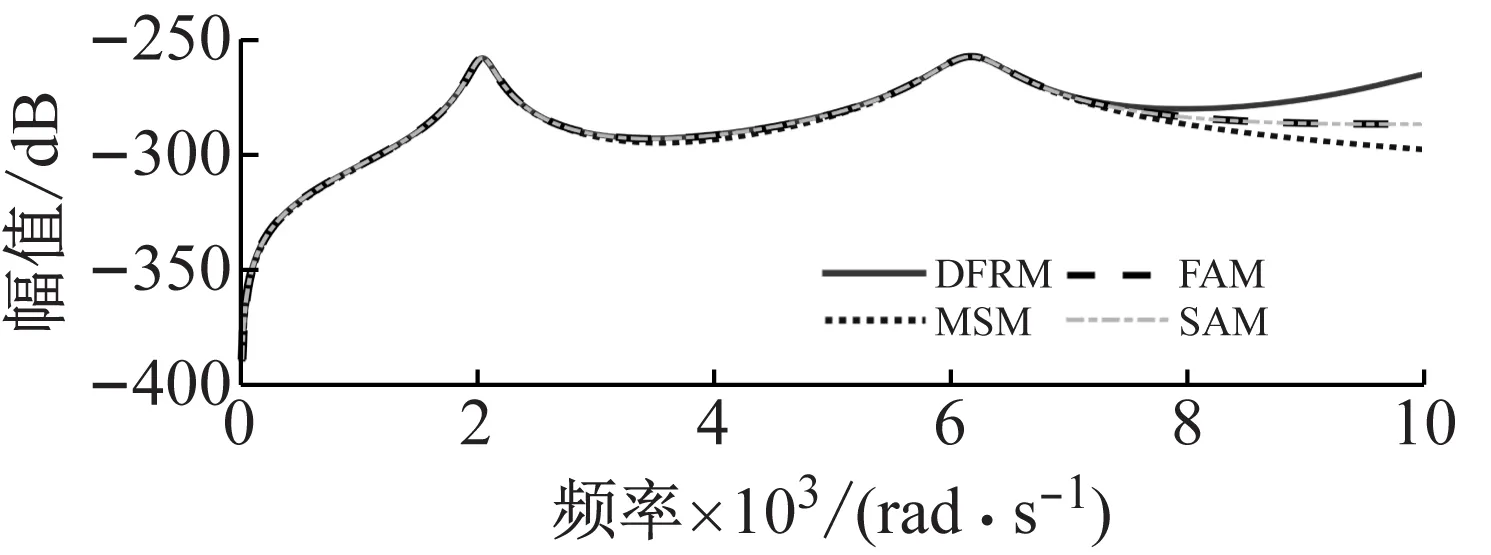
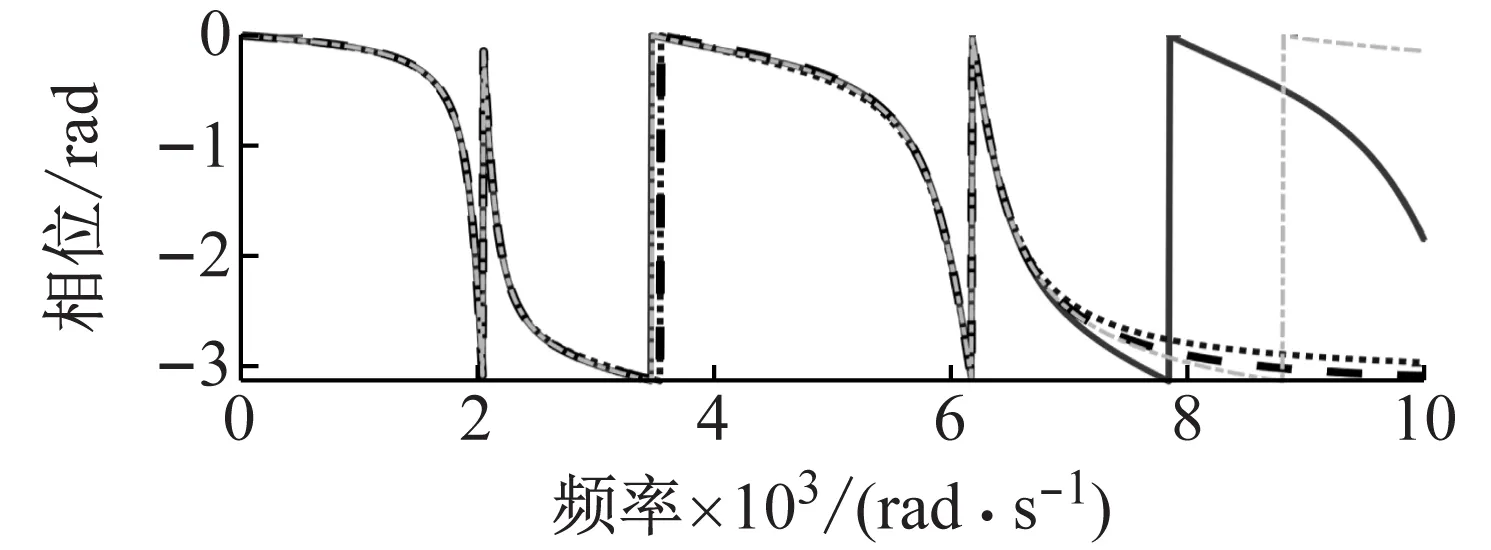
图11 前两对弹性模态近似频响函数灵敏度

4.2.2 计算效率

本小节通过改变轴向振动杆的自由度讨论DFRM、MSM、FAM和SAM的计算效率。将轴向振动杆自由度划分为N=0～800，自由度间隔为80。假定频率范围为0～10 000 rad/s，频率步长为100 rad/s。图13是四种方法计算效率对比图。可以看出，FAM和SAM的计算效率明显优于DFRM，而FAM的计算效率高于SAM。各方法的计算效率排序与质量-弹簧系统算例得到的结论相同。

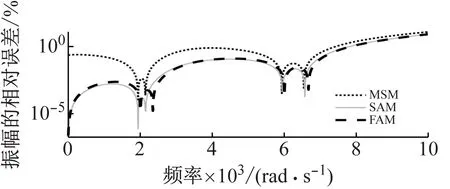
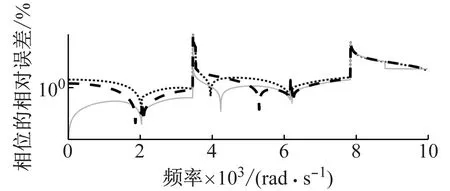
图12 前两对弹性模态近似频响函数灵敏度的相对误差Fig.12 The relative error of FRF sensitivity approximated in terms

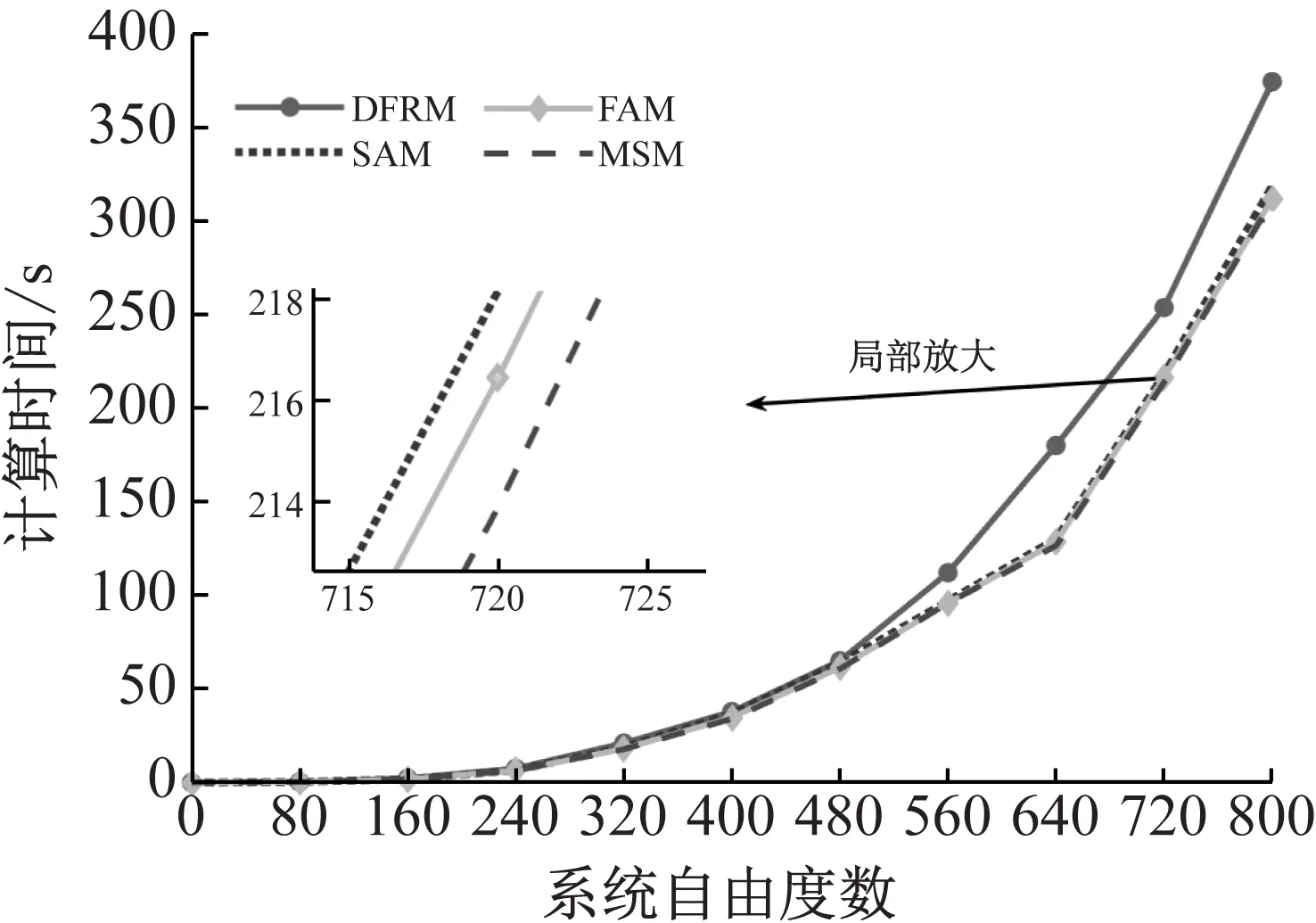
图13 不同方法计算时间随自由度数目变化图Fig.13 Computational time of different DOF with different methods

5 结 论

本文提出了具有卷积型非黏滞阻尼模型结构系统频响函数灵敏度的改进计算方法。利用复模态叠加法和直接微分法推导出了非黏滞阻尼系统频响函数灵敏度表达式。但若只用有限数目的低阶模态求解其频响函数灵敏度会引入模态截断误差，在某些情形下会严重影响非黏滞阻尼系统频响函数灵敏度的求解精度。解决该问题的关键在于建立的系统模态和系统矩阵间的关系。本文利用Neumann级数展开定理，将系统高阶模态对系统频响函数灵敏度的贡献用系统矩阵和低阶模态进行表达，进而推导出了两种考虑高阶模态影响的系统频响函数灵敏度的改进计算方法：一阶近似法和二阶近似法。通过数值算例验证两种方法的有效性和准确性，结果表明：

(1) 一阶近似法和二阶近似法能得到满意的系统频响函数灵敏度计算结果，因此本文提出的两种改进计算方法可有效地求解非黏滞阻尼系统频响函数灵敏度。

(2) 一阶近似法和二阶近似法由于考虑了高阶模态对系统频响函数灵敏度的影响，因此其计算精度优于模态叠加法；从计算效率角度看，改进的一阶近似法和二阶近似法避免了矩阵求逆，因此其计算效率高于直接频响法。综上，本文提出的两种改进计算方法兼顾了计算精度和效率，是求解多自由度非黏滞阻尼系统频响函数灵敏度问题的理想选择。

(3) 由于一阶近似法和二阶近似法分别考虑利用系统矩阵与模态关系的第一项和前两项近似高阶模态对系统频响函数灵敏度的影响，因此二阶近似法比一阶近似法的计算精度更高，而计算效率却低于一阶近似法。综合考虑计算精度和效率，建议根据需要选取不同计算方法：当需要较高计算精度时，选取二阶近似法；当需要较高计算效率时，选取一阶近似法。