石墨烯复合材料胶接制备失效数值仿真研究

2021-11-17战瑞瑞李红丽

计算机仿真 2021年3期

姜松，战瑞瑞，李红丽，刘畅

(北华大学理学院，吉林吉林 132013)

1 引言

2004年由英国曼彻斯特大学安德烈·盖姆(Andre Geim)和康斯坦丁·诺沃消洛夫(Konstantin Novoselov)教授发现石墨烯材料以来[1]，经过十余年的发展，石墨烯复合材料现已广泛应用于航空航天、冶金机械、仪器仪表、石油化工等高科技产品附加值的装备制造中。复合材料集成两种或多种材料的优点，对原有的单相材料进行积极的改善，大幅提升了材料的应用范围，为降低成本更广泛的应用石墨烯复合材料，石墨烯复合材料的制备技术成为亟待解决的问题[2]。在解决石墨烯复合材料制备过程中，利用胶接制备方式，确定制备失效数值的准确性尤为重要。在实际生产中，针对不同的石墨烯复合材料，需采用不同的基体、水凝胶、制备设备、制备环境，这给建立一个统一的，石墨烯复合材料胶接制备失效数值仿真，带来了较大的难度。

就现有的研究来看，进行胶接制备失效数值仿真的方法，主要包括基于内聚模型(聚合物)的失效数值仿真、基于原子间结合力模型的失效数值仿真、基于模糊算法的失效数值仿真。其中基于内聚模型(聚合物)的失效数值仿真，顾名思义是对聚合物交胶接制备失效进行分析，针对聚合的失效数值分析，该方法具有较高的准确性，应用于石墨烯复合材料时，不适用于金属基的石墨烯复合材料，存在分析准确性较低的不足[3]。基于原子间结合力模型的失效数值仿真，是依托原子间结合力的计算，对胶接失效数值进行仿真，对依托于原子间结合力的胶接技术十分有效，但不适用于与范德华键结合。基于模糊算法的失效数值仿真，是根据模糊算法，对胶接制备失效数值进行计算，此方法受模糊集合影响较大，分析过程重复率较小，但分析误差较大[4]。上述三种方法，分别具有各自的优势，但当应用于石墨烯复合材料胶接制备失数值仿真时，均存在失效分析准确率较低的不足，为此提出了石墨烯复合材料胶接制备失效数值仿真研究。通过确定界面结合力、最薄弱位置、环境参数、胶接应力，对胶接失效数值进行求解，可大幅提升分析准确率。

2 石墨烯复合材料胶接制备测定失效数值设计

2.1 构建测定石墨烯复合材料胶接制备失效框架

为了对现有胶接制备的失效数值进行有效测定，针对石墨烯复合材料胶接分析过程中，存在的问题进行解决。以石墨烯复合材料胶接制备特征为基础，进行石墨烯复合材料胶接制备测定失效数值的设计。石墨烯复合材料形成机理如图1所示。

图1 石墨烯复合材料形成机理

针对石墨烯复合材料胶接制备失效数值的测定，首先应对石墨烯复合材料与胶接材料产生的界面进行分析，其界面结合强度直接影响石墨烯复合材料胶接制备失效情况，是影响石墨烯复合材料胶接制备失效的最主要因素。

由于石墨烯复合材料胶接制备失效的位置，并非石墨烯复合材料与胶接材料界面结合力最强位置，而是在缺陷位置、弯角位置、结合不牢固位置产生失效[5]，为此确定界面结合力后，应对胶接最薄弱位置受力情况进行分析，求出最薄弱位置的界面胶接结合力。

影响石墨烯复合材料胶接制备失效的主要因素还有，外界环境的影响、胶接应力的影响(胶接工艺)，外界环境的影响主要表现于外力的分布情况以及环境温度的变化情况[6]。胶接应力主要体现在，石墨烯复合材料的表面处理、胶接接头的设计、胶接工艺的选择，以及胶接材料的选择四部分。最后通过胶接制备失效关系，对石墨烯复合材料胶接制备失效数值进行求解。

其胶接制备失效关系如式(1)所示

f×g=S×h-y

(1)

式中，f代表石墨烯复合材料胶接最薄弱位置；g代表石墨烯复合材料与胶接材料界面结合力；S代表石墨烯复合材料胶接制备失效值；h代表石墨烯复合材料制备环境影响参数；y代表胶接应力。

根据式(1)，求出胶接制备失效数值，其可用式(2)表示

(2)

基于式(1)、式(2)，实现构建石墨烯基复合材料胶接制备失效数值的测定框架。

2.2 石墨烯复合材料胶接界面结合力

胶接结合力的计算是测定石墨烯复合材料胶接制备是否失效的关键数值，胶接结合力计算主要分为两种情况，即双原子(离子)间结合力计算以及范德华键(或氢键)结合力计算。

为方便对胶接结合力的计算，将石墨烯与其它材料抽象为8个节点，胶接面抽象为中平面，对节点1、2、3、…、8进行分析，节点位置可采用原子位置进行代替，也可采用固定位置进行代替，得出石墨烯复合材料胶接制备抽象图如图2所示。

若胶接结合为双原子(离子)间结合型，则进行双原子(离子)间结合力计算，在双原子(离子)间结合力计算过程中首先确定x方向与y方向的受力情况，其中

X方向受力为：FAx+Fsinβ=0

Y方向受力为：FAy-Wg+Fcosβ=0

其中，W代表原子间受库仑力情况；β代表抽象点间夹角；F代表外作用力；FAx、FAy代表上下层级间相互作用力。

根据x方向与y方向受力计算，求出原子间胶接结合力，如下式(3)表示[7-8]

(3)

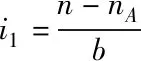
范德华键结合力计算中，与原子间计算程序相类似，但方法不同，在确定x方向与y方向受力情况后，根据范德华键力计算公式，求出胶接界面结合力。如式(4)所示

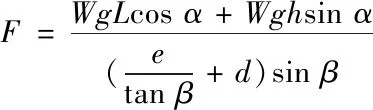
(4)

式中，e代表自然常数，约等于2.71828，其它字母含义与上式相同，由于石墨烯与其它材料采用胶接的方式进行连接，形成石墨烯复合材料。

2.3 胶接滑移线场应力

胶接应力场的计算主要是根据石墨烯复合材料胶接工艺进行确定，石墨烯与胶接材料所产生的应力，对石墨烯复合材料制备失效起到促进作用。石墨烯复合材料胶接制备过程中，属于异种材料的胶合，胶合界面原子序列不稳定，受到石墨烯以及其它材料影响较大。

将原子与原子间未产生有效连接的原子空位，定义为空间位错。石墨烯复合材料胶接界面空间位错越多，则代表石墨烯复合材料胶接制备失效可能性越大。为了对空间位错进行求解，首先对空间位错形成的滑移线场进行计算，确定胶接应力，其胶接滑移线场应力可用式(5)表示

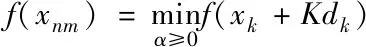
(5)

式中，f(xnm)代表胶接滑移线场应力的二次可微实函数，nm为位错线空间位置，nm∈R2。在xk代表空间位错的Hesse矩阵，可利用∇2f(xk)正定求解，空间位错信息Gk=∇2f(xk)，胶接效率gk=∇f(xk)，则石墨烯复合材料失效数值可写成式(6)所示

(6)

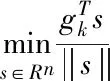
3 仿真分析

通过上述过程实现石墨烯复合材料胶接制备失效数值的测定，但是其是否能够解决现有方法存在的问题还需要进一步进行验证。采用石墨烯专用炉进行实验。实验环境如图3所示。

图3 实验环境

同时，为了对提出方法的性能进行验证，设计仿真对比实验，采用现有三种使用较为广泛的方法与提出方法进行对比研究与分析。

3.1 延展性失效分析准确率对比

延展性失效分析准确率是验证石墨烯复合材料胶接制备过程中被迫延展性操作，所带来的失效准确性。由于在制备过程中想要获取固定的石墨烯复合材料形状，石墨烯基体会经过延展拉伸处理，是石墨烯复合材料制备过程中最常见的加工手段。为此验证石墨烯复合材料胶接制备延展性失效分析是十分必要的。

根据仿真过程，利用本文提出的胶接制备失效数值仿真方法以及其它三种广泛使用的胶接失效数值仿真方法进行实验统计，得出实验结果，与仿真真实失效数值进行对比，绘制延展性失效分析试验结果对比情况图，如图2所示。

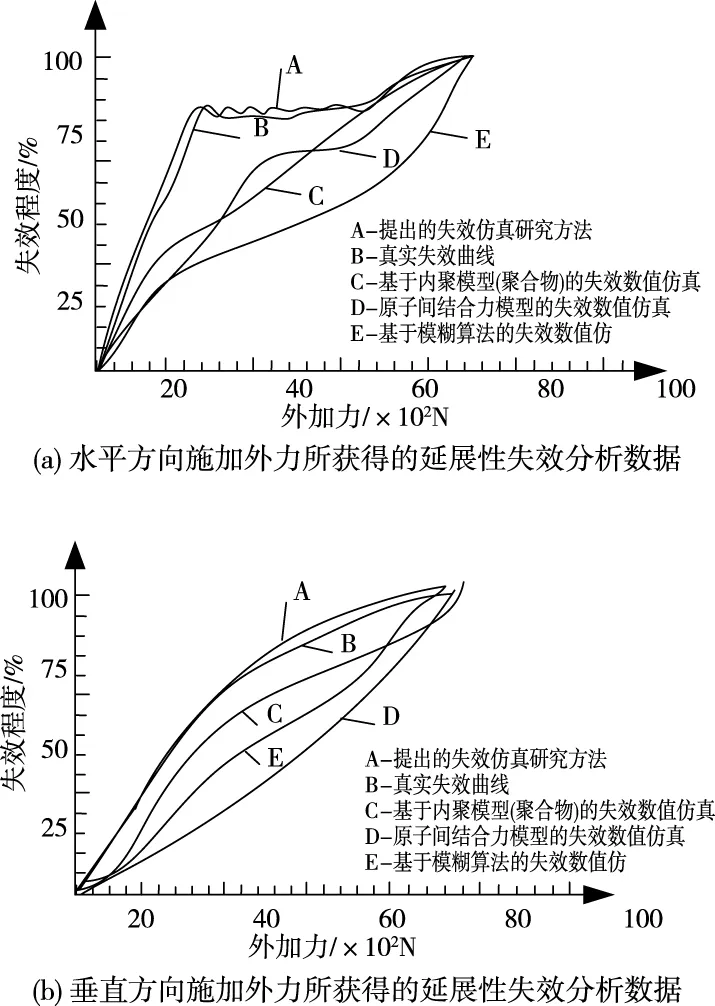
图4 延展性失效分析试验结果对比情况图

分析延展性失效实验结果对比图4(a)，可以得出提出的失效仿真研究方法，与仿真真实失效数值高度重合，在不同施加外力情况下，能够仿真真实失效程度。而其它广泛使用的三种方法，存在失效过程分析精度较低的现象，特别是基于模糊算法的失效数值仿真。经重合度计算提出的失效数值仿真研究方法，水平施加外力延展性失效分析准确率为95.72%。其它三种失效数值仿真方法。水平施加外力延展性失效分析平均准确性为63.22%。

分析延展性失效实验结果对比图4(b)，可以得出，提出的失效仿真研究方法与真实结果具有较高的重合性。经重合度计算提出的失效数值仿真研究方法，垂直施加外力延展性失效分析准确率为94.14%。其它三种失效数值仿真方法。水平施加外力延展性失效分析平均准确性为57.42%。

3.2 脆性失效分析准确率对比

与延展性失效分析准确率对比相类似，脆性失效分析准确率对比，是通过控制温度场、施加外力的变化情况，进行脆性失效分析，与仿真真实失效数值进行对比。与延展性失效分析准确率对比不同，脆性失效分析采用一端固定，一端施加垂直方向外力，施加外力包括作用力与反作用力。

实验过程中，首先控制温度场变化，在0℃下进行不同施加力的对比，随后降温，在-20℃、-40℃下进行不同施加力的对比。

根据实验过程，与仿真真实失效数值进行对比，得出不同方法在不同变量下的脆性失效分析结果对比情况表，如表1所示。

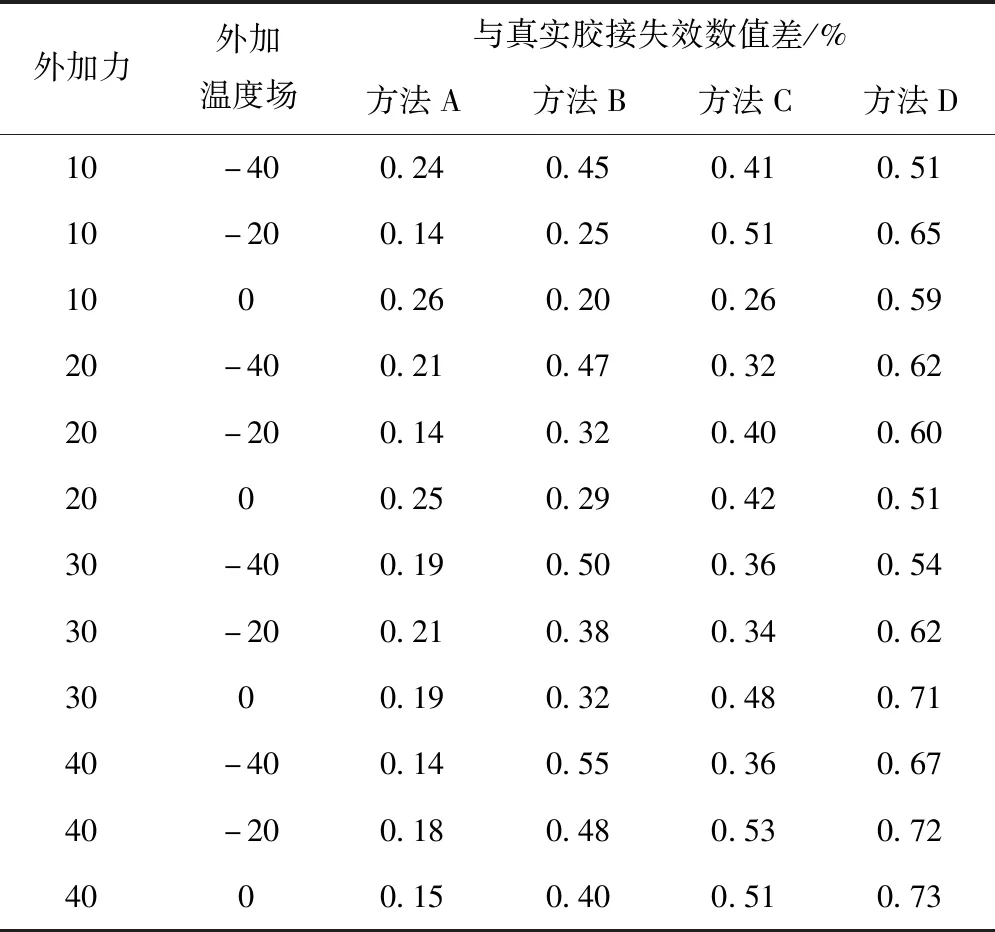
表1 脆性失效分析结果对比情况表

上表中，方法a代表本文提出的石墨烯复合材料胶接制备失效数值仿真，方法b代表基于内聚模型(聚合物)的失效数值仿真，方法c代表基于原子间结合力模型的失效数值仿真，方法d代表基于模糊算法的失效数值仿真，施加外力单位为×102N，外加温度场单位为℃。

根据实验得出的脆性失效分析结果对比表，对不同仿真方法实验结果进行相对平均偏差计算，验证在不同变量影响下，不同仿真方法的相对偏差。经计算得出方法a相对平均偏差为18.41%，其它三种方法平均偏差为23.64%、19.28%、9.84%。其中基于模糊算法的失效数值仿真方法偏差最低，但根据实验结果求出脆性失效分析准确率时，基于模糊算法的失效数值仿真，失效分析准确率为最低。经统计计算，提出的失效仿真方法脆性失效分析准确率为80.33%，其它三种方法脆性失效分析准确率分别为61.58%、58.08%、37.75%。

根据三次实验结果，进行加权分析，得出提出的石墨烯复合材料胶接制备失效数值仿真具有较高的有效性。