功率预测的改进自适应变步长光伏MPPT算法
2021-11-17袁臣虎刘晓明杜永恒
袁臣虎,王 坤,刘晓明,杜永恒
(1.天津工业大学电气工程与自动化学院,天津 300387;2.天津工业大学机械工程博士后科研流动站,天津 300387)
1 引言
随着社会的发展,人类对能源的需求不断加剧,从而导致了化石能源的日益枯竭,与此同时环境的污染日益加剧,太阳能光伏发电作为现代清洁能源的代表在此背景下应运而生。光伏电池的外特性易受环境影响,表现出了非线性的特点,光伏电池只有工作在最大功率输出点时,才能最大限度的利用太阳能,使发电效率达到最大化,因此对光伏发电最大功率点追踪(Maximum Power Point Tracking,MPPT)技术的研究具有重要意义。目前国内外学者提出了多种MPPT算法,其中广泛应用的主要有恒定电压法、比例系数电压法、变步长扰动观察法、变步长电导增量法、功率预测法、自适应神经网络控制算法、粒子群控制算法等[1]-[4]。
文献[5]提出了比例系数电压法,该方法是由恒定电压法改进而来,克服了环境与自身结温变化时对系统的干扰,但该方法在光照发生变化时会使光伏电池偏离最大功率点造成能源损失;文献[6]提出了自适应变步长扰动观察法,该方法根据当前工作点与最大功率点的位置关系调整步长大小,克服了传统扰动观察法跟踪速度与稳态精度无法兼顾的矛盾,但该方法在光照突变时容易对最大功率点产生误判现象,使工作点偏移,最终导致MPPT失败,此外,该方法的步长系数需要根据光伏电池板的性能与所处环境进行手动调整,没有实现真正意义上自适应变步长;文献[7]提出了功率预测法,该方法通过检测扰动时刻功率值来预测下一时刻功率值,从而有效的避免由于光照变化引起的误判现象,但该算法对功率的预测是基于光照均匀变化的基础上,当光照强度非均匀变化时仍然存在误判现象。针对以上的缺点和不足,本文提出了一种基于改进功率预测的自适应变步长扰动观察MPPT算法。首先该算法采用0.8倍开路电压[8]进行启动,算法启动后引入光照变化率的概念,利用光照变化率将光照变化进行线性化处理,有效的避免了光照强度非均匀变化条件下的误判问题。同时针对传统定步长扰动观察法的动态性能与稳态性能之间的矛盾问题,利用反正切函数对扰动系数进行归一化处理,提出了真正意义上的自适应变步长扰动观察法,提高了系统的动稳态性能。
2 光伏电池等效电路模型与输出特性分析
图1为光伏电池等效电路模型[9],其中,Iph为光伏电池内部光生电流,正比于光伏电池受光面积和太阳入射光的辐照度,ID为光伏电池内部暗电流,IL为光伏输出负载电流,UD为等效二极管的端电压,Uoc为光伏电池的开路电压,Rsh为光伏电池内部等效旁路电阻,Rs光伏电池内部等效串联电阻。
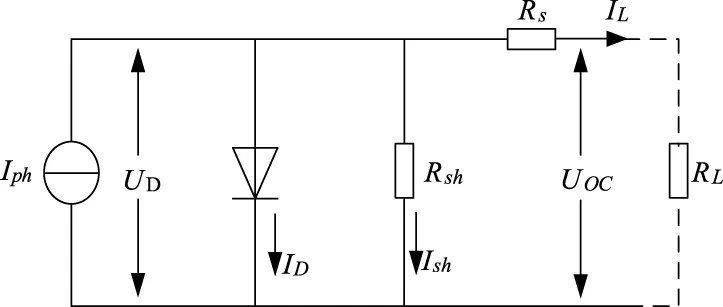
图1 光伏电池等效电路模型
根据光伏电池等效电路模型,考虑二极管P-N结的特性方程可得出光伏电池的等效数学模型如式(1)-(6)所示
IL=Iph-ID-Ish
(1)
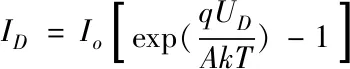
(2)

(3)
UD=UOC+ILRS
(4)

(5)

(6)
式中:Io为光伏电池内部等效二极管的P-N结反向饱和电流;Isc为光伏电池内部的短路电流;k为玻尔兹曼常数,k=1.38×10-18erg/K;A为光伏电池内部P-N结曲线常数;q为电子电荷,q=1.6×10-19C;T为光伏电池所处环境的绝对温度。本文采用如表1所示参数的光伏电池,在环境温度为25℃,光照强度分别为1000 W/m2,800 W/m2,600 W/m2,400W/m2条件下,I-U特性曲线如图2所示,在温度不变的情况下,光照强度的改变主要影响短路电流的大小,光照越强短路电流越大,对开路电压影响不大;P-U特性曲线如图3所示,光照强度越强,输出功率越大,最大功率点处所对应的电压基本不变,数值上约等于开路电压的0.8倍。

表1 光伏电池参数

图2 光伏电池I-U特性曲线
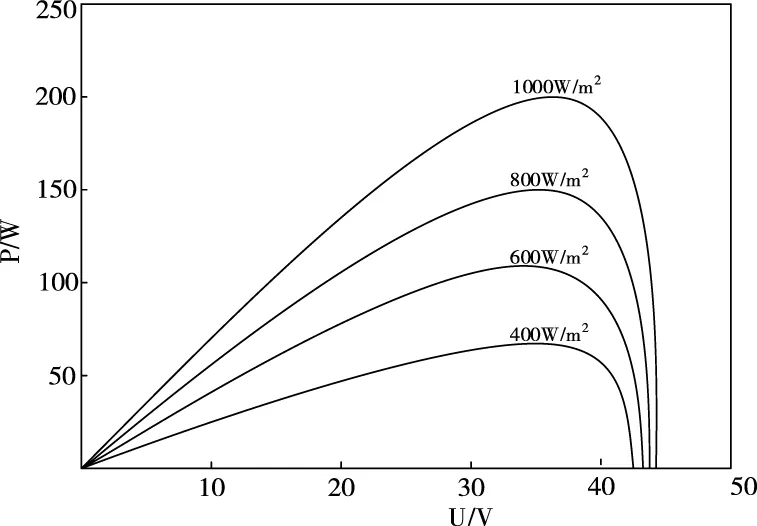
图3 光伏电池P-U特性曲线
3 扰动观察MPPT算法
3.1 扰动观察法基本思想
扰动观察法是太阳能光伏发电系统MPPT应用最普遍的方法之一,基本思想是假定光照不变情况下周期性地给光伏电池输出电压施加定步长扰动ΔU,检测扰动前后的功率变化ΔP,决定下一步的扰动方向。其电压扰动数学表达式如式(7)所示
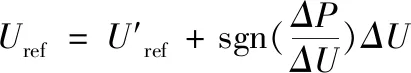
(7)
式中U'ref为光伏电池施加扰动前工作电压,Uref为光伏电池施加扰动后的工作电压。若功率变化ΔP与扰动电压ΔU同号则给予正向电压扰动,若ΔP与ΔU异号则给予反向电压扰动。
3.2 扰动观察法存在的问题
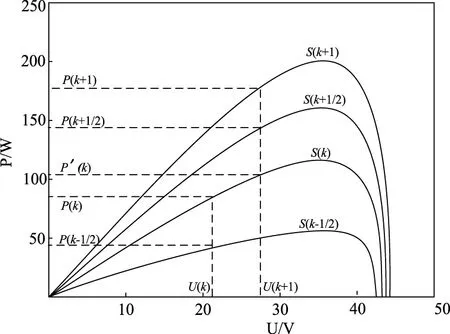
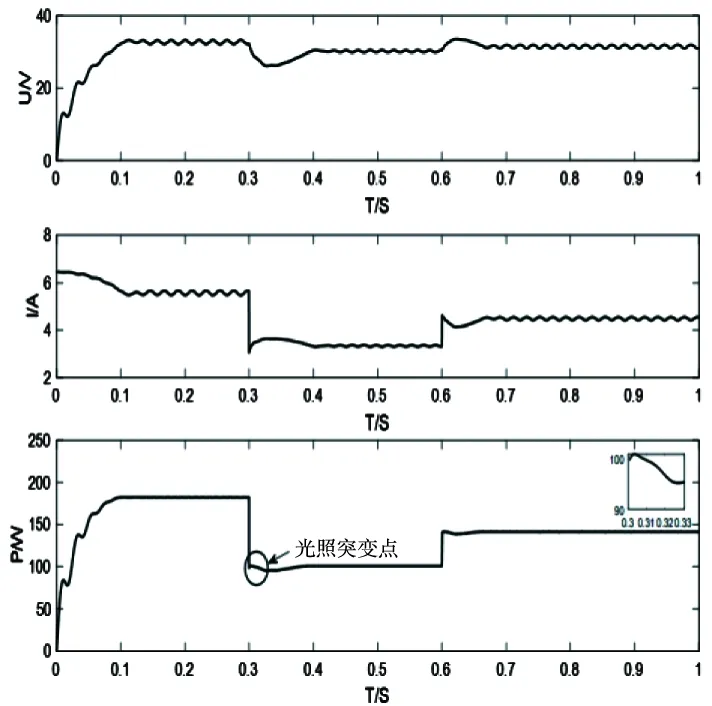
扰动观察法要求扰动前后光照不变即光伏电池工作点始终处在同一光照强度P-U特性曲线上,但由图3可知,在光照变化时,光伏电池的工作点并不落在单一的特性曲线上,而是由不同光照特性曲线上的工作点组成,因而会产生dP误判现象。在图4中,设光伏电池的工作点在最大功率点左侧,此时光伏电池的工作电压为Ua,对应输出功率为Pa,给予正向电压扰动,输出电压变为Ub,此时输出功率变为Pb,若光照不变,应有Pb>Pa,则下一步应继续给予正向扰动;但是若此时光照强度降低,则P-U特性曲线由S1变为S2,电压Ub对应的输出功率变为Pc,此时Pc 图4 扰动观察法的误判现象 针对扰动观察法存在的误判问题文献[10]提出通过功率预测算法解决。该算法以图5所示光照均匀变化时光照与功率的近似线性转移特性(电池参数如表1所示)为基础。 图5 光伏电池Lux-P转移特性曲线 其算法流程如下: 1)在图6所示的光照均匀变化时的P-U特性曲线图中设在采样周期kT~(k+1)T中光照强度变化均匀,从S(k)变为S(k+1); 2)检测kT时刻的输出电压值U(k)、功率值P(k); 3)在(k+1/2)T时刻再检测一次当前电压U(k)所对应的功率值P(k+1/2),可计算出P'(k),P'(k)=2P(k+1/2)-P(k),此时对输出电压进行扰动,得出(k+1)T时刻输出电压U(k+1); 4)在(k+1)T时刻对输出电压U(k+1)对应的功率值进行检测得出P(k+1),由图6可看出P(k+1)与P'(k)两功率均处在同一功率曲线上,即可得dP=P(k+1)-P'(k)。 由以上分析可知:功率预测法可以解决光照均匀变化情况下扰动观察法的dP误判问题。但在实际应用中不能保证在采样周期内光照强度一定是均匀变化的,即存在P'(k)≠2P(k+1/2)-P(k)的情况,则dP误判问题没有解决。 图6 功率预测算法 针对功率预测法无法解决光照非均匀变化时的dP误判问题,本文提出了引入光照变化率β,其定义如式(8)所示。 (8) 在图7中,dP0=P(k)-P(k-1/2)是电压U(k)对应的功率变化量,dP1=P(k+1)-P(k+1/2)是电压U(k+1)对应的功率变化量,且都是由于光照变化引起的,进一步可知 P(k+1/2)-P′(k)= (9) 将式(8)带入式(9)可得到 (10) 此时P(k)与P'(k)位于同一P-U特性曲线上,可得出dP为 dP=P′(k)-P(k)= (11) 即解决了扰动观察法在光照非均匀变化条件下的误判问题。 图7 改进的功率预测算法 为了解决在MPPT过程中步长因子无法自动适应动态变化,进而无法兼顾MPPT的动态性能与稳态性能的问题,本文结合dP/dU在MPP附近时的特性即当光伏电池工作在最大功率点两侧并且向最大功率点靠近时|dP/dU|-U特性曲线单调递减,且在最大功率点处|dP/dU|=0,如图8所示,提出将步长因子运用反正切函数归一化处理。具体过程如下:根据光伏电池dP/dU在MPP附近时的特性,电压扰动数学表达式可写为式(12) (12) 式中,U'ref为扰动前光伏电池的工作电压,Uref为扰动后光伏电池的工作电压,α为步长因子,经反正切函数归一化为式(13) (13) 式中 (14) Ustep_max为定步长允许的最大步长,|dP/dU|max可以由式(15)得出 (15) 式(15)中m为常数,可取0.98。 图8 光伏电池I-U、P-U、|dP/dU|-U特性曲线 图9为α-|dP/dU|特性曲线。 图9 α-|dP/dU|特性曲线 由α-|dP/dU|特性曲线可知,运用归一化思想,步长因子α的值域归一化到[0,A),在MPPT过程中步长因子可根据当前工作点的位置实时调节,动态性能得以提高;此外,由于将步长因子的最大值限定到A以内,避免了由于步长过大出现的扰动振荡现象,稳态性能也得以有效提高。 将改进的功率预测算法与自适应变步长扰动观察法相结合即得到一种基于改进功率预测的自适应变步长扰动观察MPPT算法,该算法流程如下: 1)采样电压U(k),调整占空比使U(k)=Ustart,Ustart=0.8Uoc,保持参考电压不变,以恒定电压方式启动算法; 2)算法启动后,通过改进的功率预测算法经式(11)计算出dP,根据dP/dU的符号判断下一步的扰动方向; 3)利用改进的变步长算法,经反正切函数归一化后由式(12)计算出α,若此时的工作点离最大功率点较远时,则α值较大,采用大步长追踪,当靠近MPPT时,α值逐渐减小,步长随之减小,直至追踪到MPP时,α值变为0。 图10 改进的MPPT算法运行流程图 通过仿真分析比较了大步长因子扰动观察法、小步长因子扰动观察法、改进功率预测的自适应变步长扰动观察法3种情况。本文在MATLAB环境下搭建光伏电池板模型,设定温度为25℃,初始光照1000W/m2,采用东宇公司生产的单晶硅太阳能光伏电池为研究对象,其参数如表1所示。为了验证本文提出算法在光照突变时仍然快速准确的追踪到新的最大功率点,仿真的光照变化方式选择了阶跃式变化,初始光照强度为1000W/m2,其它仿真条件不变,0.3s时光照变为600W/m2,0.6s时变为800W/m2,如图11所示。 图11 阶跃式光照变化示意图 图12为0.3V步长时扰动观察法在进行MPPT时的波形。由图可见,算法启动后在0.05s时追踪到最大功率点,在光照发生突变时经0.02s重新追踪到新的最大功率点,追踪速度相对较快,但追踪到最大功率点后一直在最大功率点处左右振荡,并且由放大窗口可明显看出在光照突变时产生了明显的误判现象。 图12 0.3V步长扰动观察法波形图 图13为0.1V步长时扰动观察法在进行MPPT时的波形。由图可见,算法在启动后0.1s时追踪到最大功率点,由放大窗口可看出在发生光照突变时经0.03s重新追踪到新的最大功率点,追踪速度明显降低,但追踪到最大功率点后功率纹波明显降低,可见定步长扰动观察法无法兼顾系统的稳态性能与动态性能。 图13 0.1V步长扰动观察法波形图 图14为本文提出的算法在进行MPPT时的波形。由图可见,本算法采用了0.8倍开路电压法启动,在0.01s时追踪到MPP,节省了启动过程的追踪时间,提高了追踪速度;由放大窗可看出,在光照发生突变时,经0.01s重新追踪到新的最大功率点,并且避免了光照突变时的误判现象;系统在追踪到MPP后,稳定在MPP附近,存在极少的纹波,提高了系统的稳定性。可见基于改进功率预测的自适应变步长算法在动态跟踪速度和稳态跟踪精度上都有较大优势。 本文通过对光伏电池输出特性分析,建立数学模型,分析了传统MPPT算法的原理与不足,在此基础上提出了改进功率预测的自适应变步长MPPT算法,引入光照变化率,将非均匀光照变化线性化处理,解决了扰动观察法在光照非线性变化时存在的dP误判问题;结合定电压启动,将步长因子运用反正切函数归一化处理,实现了MPPT过程中步长因子的自动适应动态变化。仿真表明,运用定电压启动方式,缩短了算法的启动时间;改进的功率预测算法避免了光照突变时的误判现象;运用反正切函数将步长因子归一化处理,兼顾了MPPT的动态性能与稳态性能,MPPT的动稳态性能良好。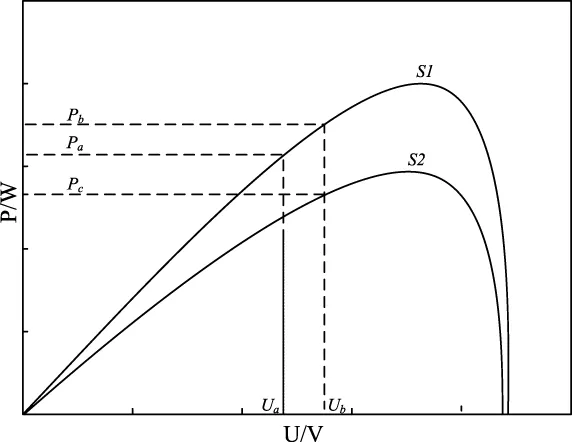
4 基于改进功率预测的自适应变步长扰动观察MPPT算法
4.1 误判问题的功率预测法分析


4.2 改进的功率预测算法




4.3 自适应变步长扰动观察MPPT算法


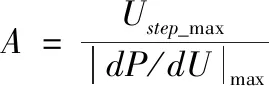



4.4 基于改进功率预测的自适应变步长扰动观察MPPT算法流程

5 改进MPPT算法仿真验证


6 结论
