交通枢纽换乘系统有效承载力仿真研究

陈 伟，李宗平

(1.西南交通大学交通运输与物流学院，四川 成都 611756；2.西南交通大学综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学综合运输四川省重点实验室，四川 成都 611756)

1 引言

随着国民经济的持续快速发展、城市化水平的不断提高，我国轨道交通正处于大发展、大建设阶段，交通枢纽作为大客流集散地，其换乘系统有效承载力研究也逐渐成为规划建设和运营管理的焦点。一旦交通枢纽换乘系统发生拥堵，不但会影响换乘效率导致客流无法有效疏解，甚至会导致乘客之间发生推搡、踩踏等冲突事件，对乘客的人身安全产生危害。因此，开展交通枢纽换乘系统有效承载力研究具有重要意义。

陈春安[1]构建北京西站枢纽内部换乘系统运能匹配系统动力学模型，对换乘系统瓶颈提出改善措施建议。薛霏[2]利用系统动力学建立轨道交通车站客流的演变模型及演变算法，通过实例与仿真软件legion的仿真结果进行对比验证该客流演变算法的可信性。马语佳[3]利用Anylogic软件对成都地铁换站乘效率进行评价，找出效率较为低下的车站并给出相关建议。陈建宇[4]运用Anylogic软件对成都北站进行仿真研究，指出了换乘空间布局和设施设备能力上的不足，提出了优化方案并验证了方案的可行性。李文新[5]通过改进社会力模型，对成都某城市综合客运枢纽内不同换乘场景下的旅客换乘进行仿真研究。

综上可以发现，已有研究成果大多集中在行人活动规律微观层面，较少考虑换乘系统各种元素及其之间复杂的关系和系统动态变化的规律。由于高铁设施设备的服务能力远大于地铁设施设备服务能力，因此本文重点研究高铁换乘地铁客流。考虑乘客对服务水平的耐受性要求，结合枢纽车站携带大件行李乘客较多的客流特征，建立客流流动系统动力学模型，并利用Vensim进行仿真，计算车站现有换乘设施设备配置数量与布局结构下的换乘系统客流有效承载力，从而为交通枢纽换乘系统规划建设和运营管理提出合理的建议和依据。

2 有效承载力定义及计算方法

2.1 有效承载力定义及耐受性分析

承载能力本意是指“某个区域在一定时期内，在确保资源合理开发利用和生态环境良性循环的条件下，资源环境能够承载的人口数量”。结合该词条，对轨道交通车站有效承载力进行如下定义：可通过计算在一定的基础设施、固定设备、移动设备、人力投入和运输组织水平下，车站区域服务水平持续维持在乘客耐受阈值以内，车站在单位时间内(小时(h)，天(d))的车站办理旅客数。

当乘客在出行过程的耐受感知逼近自身可以承受的极限，生理和心理都会处于崩溃的边缘，带来的出行体验也是极差的。为了评估乘客对客流密度的耐受性，在调查问卷中使用了实景图像，对各交通设施出现的不同乘客密度状况进行记录，选取相应的车站设施场景图，并进行编号。乘客在接受问卷调查时，选取最贴合本次出行的场景图组合，并分别进行耐受性评价。对调查结果进行非线性拟合得到乘客耐受性与客流密度的关系

β=f(ρ)

(1)

式中，β代表当前区域客流密度(人/m2)，β代表耐受评价值。在数据预处理中，本文发现乘客的耐受感知值一般都位于低于极限值(βc⟸P(β≤βc)=0.8)的某个区间范围内。在交通行为理论研究中，大多数交通行为阈值都设置在其行为样本总量的70%～80%之间[6]。本文结合人体功效学定义，取耐受感知值得累积分布的0.8处(即相应样本值累积分布的80%处)为耐受阈值βc⟸P(β≤βc)=0.8

βc⟸P(β≤βc)=0.8

(2)

将式(2)代入式(1)，可以得到通道内乘客耐受感知阈值处的乘客密度为1.21人/m2，同理可以求得站台和楼梯区域内耐受感知阈值处的乘客密度为1.83人/m2和1.77人/m2。

在得出乘客密度耐受阈值后，利用“密度-速度”关系式可以求出相应的乘客移动速度值。采用文献[7]对中国轨道交通乘客进行调查分析得到的行人“ρ-v”关系进行计算，如通道区域内乘客的“速度-密度”关系式为

v=-0.1183ρ3+0.6388ρ2-1.3428ρ+1.5869

(3)

将代入式(3)即可求得通道区域内乘客耐受阈值处的速度取值为0.69 m/s，同理求得楼梯区域内乘客耐受阈值处的上行速度为0.49 m/s，下行速度为0.58 m/s。

2.2 有效承载力计算方法

本文主要针对交通枢纽换乘系统付费区内的轨道交通设施设备有效承载力进行建模计算，因此影响客流有效承载力的因素包括乘客、列车、站台、楼梯、站厅、闸机、通道等。运用系统动力学方法构建交通枢纽换乘系统模型，以推演客流在交通枢纽内的分布及其动态变化过程。基于该模型，结合乘客耐受阈值计算结果，对交通枢纽换乘系统现状进行仿真，并通过逐步递增客流量，监测各关键设施设备负荷度的变化情况和是否达到耐受阈值，以明确目前交通枢纽换乘系统产生客流瓶颈位置及有效承载力大小。由此，本文运用系统动力学模型计算交通枢纽换乘系统有效承载力的计算步骤如图1 所示。

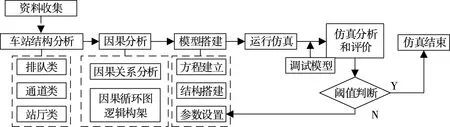
图1 交通枢纽换乘系统有效承载力计算步骤

3 系统动力学模型构建

3.1 系统动力学

系统动力学(System Dynamics，简写SD)是基于系统科学和计算机仿真，用于解决动态复杂系统问题的工具和系统思维方式，也是一门认识系统问题和解决系统问题的交叉综合学科[8]。交通枢纽换乘系统是多元素相互交融的复杂系统，系统内的乘客群体之间也存在着相互影响、相互渗透的交互作用，因而交通枢纽换乘系统客流管理问题是一个复杂的系统工程问题，其本身也是一个复杂系统[9]。为了认识该系统中的各种元素及其之间复杂的关系和系统动态变化的规律，为交通枢纽换乘系统客流管理提供决策依据，本文引入系统动力学的方法来计算交通枢纽换乘系统的有效承载力。

3.2 承载客流的因果循环逻辑构架

通过对交通枢纽换乘系统承载客流的因果分析，对因果循环图中几个关键变量进行因果连接架构分析，以树形图显示变量与工作变量的因果关系，更直观地获取每个变量之间的关系，便于系统动力学的定性分析。交通枢纽地铁站通常为换乘地铁站，其站厅及站台客流原因树构架分别如图2和图3所示。

3.3 系统动力学建模

基于上述因果逻辑图建立系统动力学方程，这里以成都东站客运枢纽作为仿真研究分析对象。成都东站的高铁出站检票口与成都地铁2 号线和 7 号线站厅位于同一平面，旅客出站后通过换乘通道即可换乘成都地铁2号线和7 号线，不需要重复安检，换乘距离小，换乘效率高。7号线站台换乘2号线站台，可以通过7号线内环方向车头处通过换乘楼梯上到2号线站台，或上至共用站厅后下到2号线站台；2号线换乘7号线，需要先到达共用站厅，再从站厅到7号线站台。以车站的通行楼梯扶梯、换乘通道、进出闸机、站厅和站台等为模型构件，建立系统动力学方程，其中站厅和两个站台方程如下

图2 地铁换乘站站厅客流原因树

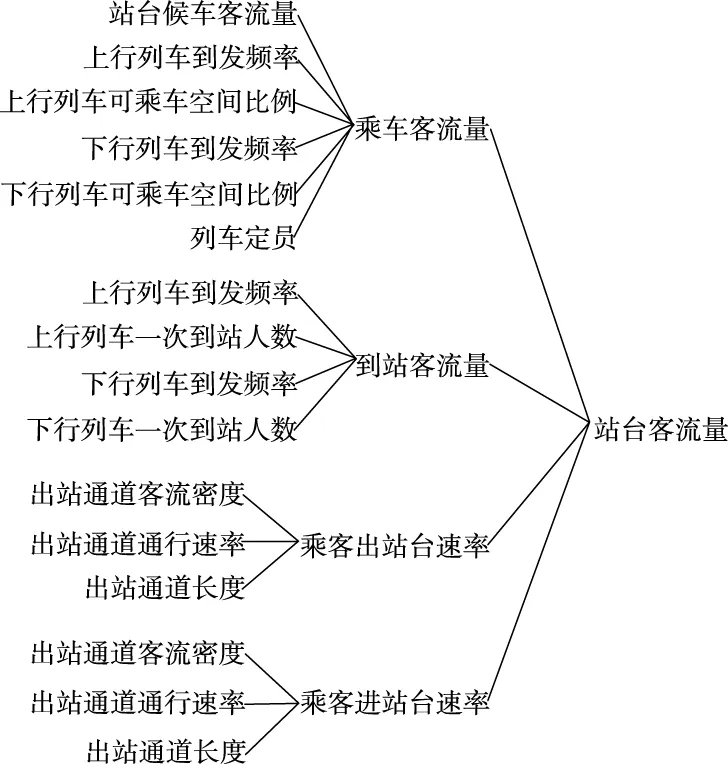
图3 地铁换乘站站台客流原因树

Flow2fout(t)-Flow2lout(t)-Flow7fout(t)-Flow7lout(t)]dt

(4)

(5)

(6)

式中，各参数的意义如表1所示。

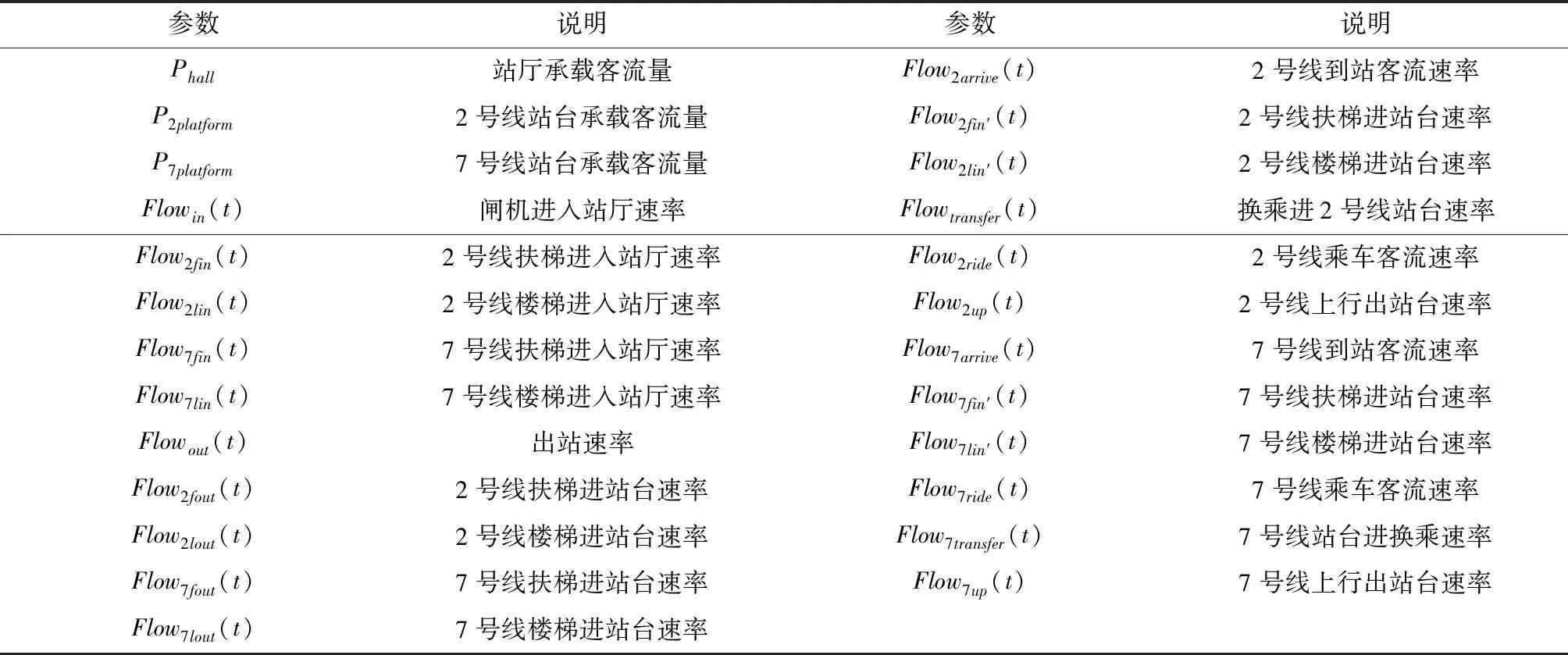
表1 参数意义说明

系统动力学流图是系统动力学的基本变量和表示符号的有机组合。根据交通枢纽换乘系统内部各因素之间的关系设计系统流图，其目的主要在于反映系统各因果关系中所没能反映出来的不同变量的特性和特点，使系统内部的作用机制更加清晰明了，然后通过流图中关系的进一步量化，实现交通枢纽换乘系统的客流运动仿真目的。建立交通枢纽换乘系统通行客流流动模型，如图4所示。模型展示了交通枢纽换乘系统客流承载区域、进站流线、出站流线、换乘流线、乘车过程等环节和影响要素。

图4 交通枢纽换乘系统存量流量图

4 仿真及分析

4.1 主要参数设置

4.1.1 自动检票机通行能力

自动检票机通行能力与乘客的类型特征紧密相关，主要表现为乘客是否携带大件行李及对设备的熟悉程度。自动检票机通行能力计算方法为

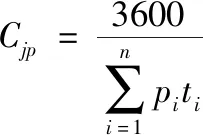
(7)

式中，Cjp代表检票机通行能力(人/h)，pi代表第i类乘客比例，ti代表第i类乘客通过自动检票机所需时间(s)。

对成都东客站旅客通过自动检票的票种、对车站熟悉情况及携带行李情况对乘客分为六类进行统计分析。乘客构成比例如表2所示。

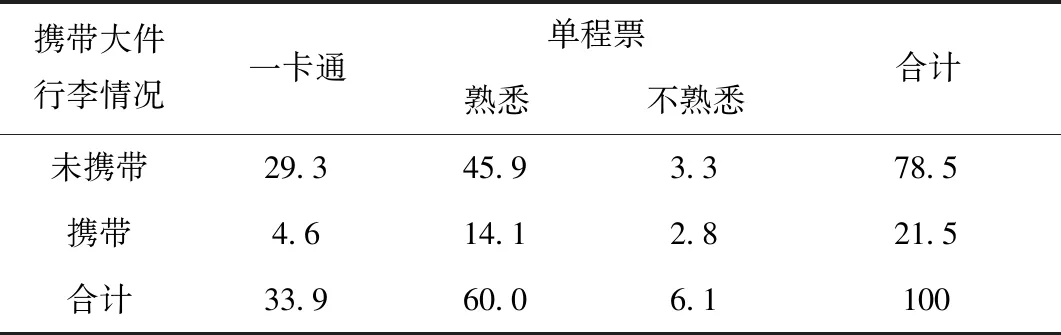
表2 乘客构成比例(%)

表3 不同类型乘客通过闸机所需时间(s)

将统计结果带入式(7)，得到考虑车站乘客特征的每台自动检票机通行能力为1330人/h。

4.1.2 楼梯通行能力

对于枢纽车站，楼梯与扶梯并行设置，旅客通常会优先选择扶梯，楼梯能力通常会比较富余。楼梯通行能力计算方法为

Cl=J·ω·(1-k)·(1-λ)

(8)

式中，Cl代表楼梯通行能力(人/h)，J代表单位时间单位楼梯宽度通行人数(人/m·h)，ω代表楼梯宽度(m)，k代表双向通行楼梯行人冲突折减系数，λ代表携带大件行李折减系数。将调查数据代入式(8)，得到考虑车站乘客特征的1.18米宽楼梯的最大通行能力为2944人/h。

4.1.3 扶梯通行能力

对于枢纽车站，携带大件行李的乘客比例较高，需要对扶梯通行能力进行折减。扶梯通行能力计算方法为

Cf=αd1Cf1+(1-α)d2Cf2

(9)

式中，Cf代表扶梯通行能力(人/h)，α代表是不携带大件行李乘客比例，d1、d2分别代表不携带、携带大件行李时的通行能力折减系数，Cf1、Cf2分别代表不携带、携带大件行李时理论通行能力(人/h)。将调查数据代入式(8)，得到考虑车站乘客特征的1米宽扶梯的最大通行能力为7624人/h。

4.2 仿真结果分析

在设定好车站设施设备的参数及客流输入输出条件之后，模型可以输出设定时间步长及范围内的客流变化情况，输出结果以动态曲线及数据表的形式给出。本实例给出60分钟内，该车站内的客流变化情况计算结果，并对模型运算结果进行统计分析。如图5，显示车站乘车人数的变化曲线，并给出相关影响因素的变化曲线。如图6，显示车站出站人数及影响因素变化曲线。则该站在60分钟内，有效承载乘车、出站人数分别约为21096人、5365人。

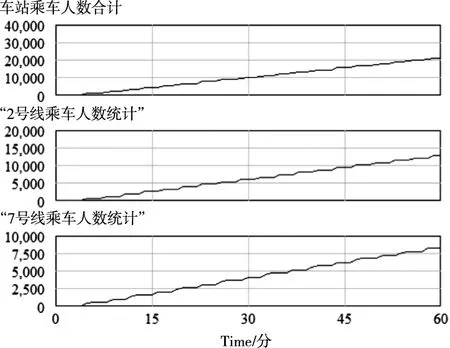
图5 车站乘车人数及影响因素变化曲线

图6 车站出站人数及影响因素变化曲线

根据远期2030年预测值[10]，成都东客站一天进站人数为14.55万人，一天内最高峰小时客流占全天进站客流的最高数值0.14，即最高小时进站人数为2.037万人/h，与模型计算出来的数值是比较吻合的，说明模型是合理且准确的。

5 结论

本文结合交通枢纽换乘系统客流特征，对设施设备能力进行修正，运用系统动力学方法建立车站模型并仿真，采用乘客耐受感知的阈值结果作为判断依据，通过逐步递增客流量，监测各关键设施设备负荷度的变化情况和是否达到耐受阈值，计算出车站客流有效承载力。模型计算值与预测值吻合度高，说明模型是合理且准确的，可以为城市轨道交通规划和应急管理提供重要参考。