基于海月水母的微小卫星结构力学特性分析

李军瑶，谷 松，陈善博

(1. 中国科学院长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100039；3. 长光卫星技术有限公司，吉林 长春 130033)

1 引言

微小卫星的界定是通过质量来定义的[1]，是指质量在10千克到100千克区间内的卫星。每一颗微小卫星能通过合并分布式卫星系统[2]和地面无线传感器网络[3]完成空间任务。对微小卫星来说，结构是卫星的基础，是卫星设计的前提。目前，微小卫星结构的研究和开发都是基于劳动密集型或高单位成本的定制制造上的[4]，研发周期长、成本高，结构占整个卫星质量比重较大，难以适应材料和微电子飞速发展的今日，故而考虑通过仿生来弥补此缺陷。

任何一种生物其自身结构的合理性、稳定性和对外部环境的适应性，都是传统产品设计所不具备的[5]，故而把研究生物作为向生物体系索取技术设计的手段[6]可以快速高效的解决很多问题。

国外研究人员对卫星结构设计和分析进行了大量的研究工作。Naoko[7]等人通过有孔虫的生物模型中，提出了一种空间系统的多面体模块结构和相应的几何装配规则。成功部署的JAXA发射工程测试卫星(ETS-VIII)和射电天文卫星(ASTRO-G)同样基于这种多面体模块化结构思想。

在自然界中，深海浮游生物与卫星有许多相似之处。首先，在深海环境中浮力与重力相互抵消和卫星几乎不受重力在力学条件上相似。其次，浮游生物从深海到浅海重力缓释过程与卫星从地面发射到外太空也有异曲同工之处。最后，就形态而言，浮游生物运动形态和卫星太阳能帆板展开上从自由边界的角度看是一样的。因此，浮生生物的形态具有参考价值。

浮游生物中，海月水母呈钟形，内部空间空阔且比表面积较大，半封闭造型有利于节省物料降低质量，形态多变，可重复设计性强。是以期望通过研究海月水母的自然形态，提取其数学模型，设计出适用于卫星的可重复性轻巧构型以满足卫星结构轻量化日益增长的需求。

2 形态仿生设计

形态仿生设计是以自然中的素材为基础，通过研究自然形态的特征、特点，通过对自然形态的整体或局部运用提炼、夸张、减弱、变化、归纳等手法，使造型脱离自然形态，最终应用到产品设计当中。

2.1 海月水母形态数学模型

海月水母体味圆盘状，无色透明，直径为10-40cm，身体水的含量达98%，水母体由外伞、内伞、口腕和胃囊四部分组成[8]。海月水母构型具有质量轻、体积小的优点[9]。仅考虑水母外形，以它外伞作为研究对象，建立数学模型。

为了建立海月水母的基本构型，将海月水母的腔体近似建模为一个不完全椭球体，在三维正交系中，设：

1) 椭球面短轴截面为圆形，半径为r；

2)h为椭球面长轴长度；

3) 夹角为θ；

图1是海月水母简化后的生长模型，根据生长模型可以得到数学表达式

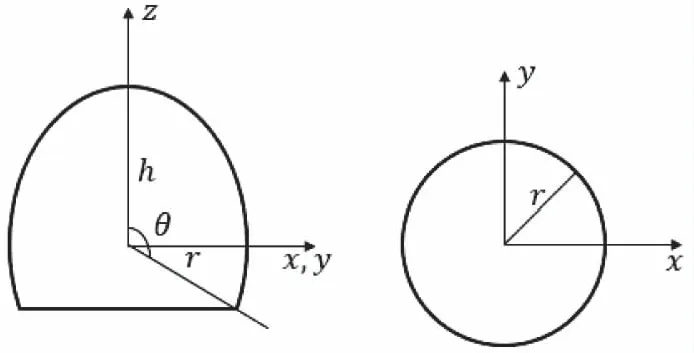
图1 海月水母生长模型图

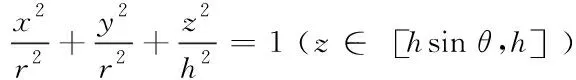
(1)

为验证数学模型的合理性，设置合理参数，对比生长模型和实物。图2为模型结果和海月水母实物图片对比。以下为参数设置：

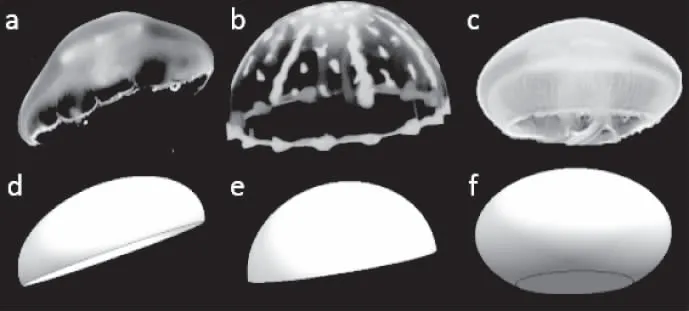
图2 海月水母(上)和数学模型(下)对比图

1)d中θ=95°，h=400，r=800；

2)e中θ=90°，h=600，r=800；

3)f中θ=130°，h=400，r=800；

数学模型实现了与水母外形相似的生长形式，可用此模型进行下一步研究。

2.2 仿生卫星构型设计

卫星的尺寸大小受火箭整流罩的限制，虽然空间有限，但这并不意味着无限制的压缩卫星体积。相反，在满足要求的情况下，根据整流罩形状和大小及卫星安装位置，设计出质量更轻的卫星结构才是构型任务的首要目的。

根据某卫星载荷尺寸和所有配套单机安装需要，合理布局并选取足够的包络空间，用此仿生模型完成构型，最终取θ=90°，h=840，r=300。构型结果如图3所示，质量分配见表1。

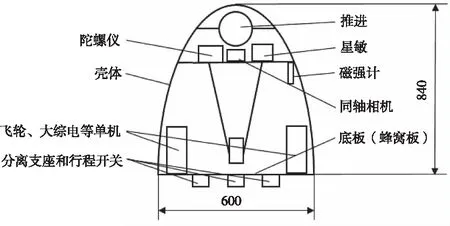
图3 卫星构型简图

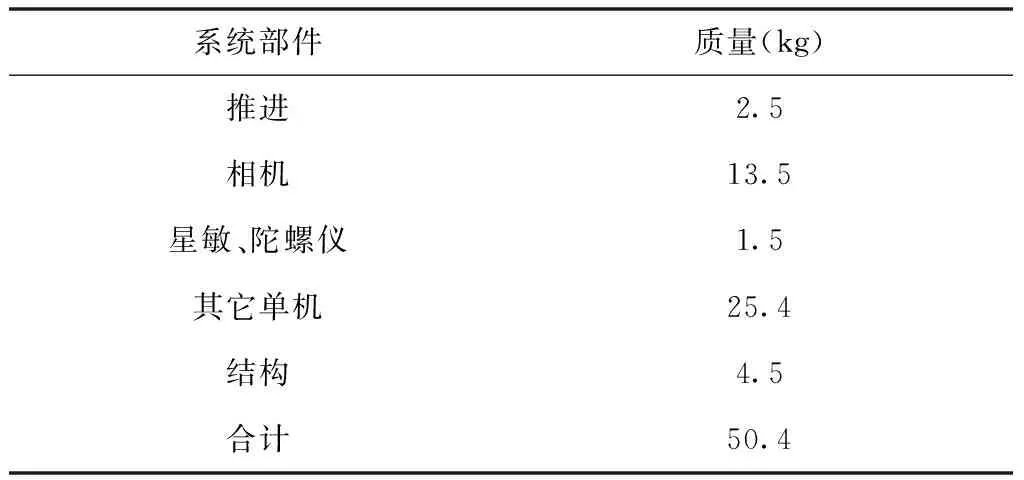
表1 卫星质量分配

卫星帆板使用扇形薄膜式柔性太阳翼[10]。相机和推进系统通过三个埋件与主结构相连，星敏和陀螺仪安装在相机背板上。为充分验证构型的力学特性，模型未经任何优化和减振处理。由表1可知，结构质量占比8.93%。

3 结构力学分析基本原理

系统的力学分析主要包括静力学分析和动力学分析。静力学分析主要是观察卫星在过载状态下结构的可靠性；动力学分析则是观察系统的稳定性，包括两个方面内容：一是系统自身的模态特性，主要是指结构的固有频率和模态振型，另一个是结构动态响应特性，指的是系统对外界激励作用下的响应状况，可用位移、速度、加速度和应力应变等物理量衡量。

3.1 结构有限元静态分析理论

卫星静力分析主要是是分析其过载状态下应力集中状况。过载分析属于线弹性系统的应力分析。线性结构的等效方程为

[K]{u}={F}

(2)

解上述方程，得到各点位移矢量{u}。根据位移插值函数，由弹性力学中给出的应变和位移及应变与应力关系，得出单元节点的应变和应力表达式为

{εel}=[B]{u}-{εth}

(3)

{σ}=[D]{εel}

(4)

求解可得最大应力和最大位移，由此可计算出安全裕度。

3.2 系统的模态分析

模态分析特性反映系统自身结构特点和动力学特性。无阻尼的系统自由振动的运动方程为

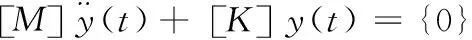
(5)

用于求解系统固有频率和模态振型的特征方程为

K-ω2M∅=0

(6)

系统的n个自振频率ωi(i=1，2……n)，以及对应自由振型∅i(i=i=1，2……n)由此可得，系统的固有模态矩阵为∅=[∅1，∅2，∅3]，表达系统模态特性的固有频率和振型得以求解。

3.3 系统的动态响应特性

当系统受到的外部激励随着时间变化时，可用振型叠加法[11]求解。令

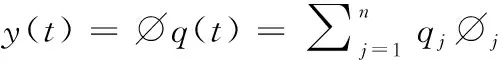
(7)

式中，∅j为第阶阻尼自振振型；qj为振型坐标，代表每一个振型所占比例大小。

用∅T左乘(7)式各项，得系统的广义运动方程

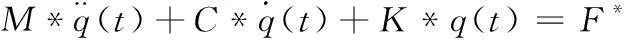
(8)

上式可分解为n个独立的单自由度的运动方程

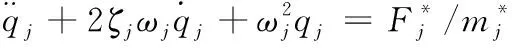
(9)

求解每一个自由度的解即可得到系统的位移、速度、加速度等物理量，依据此衡量系统对外界激励的响应特性。

3.3.1 简谐振动响应

简谐振动也成正弦振动，指运动的规律按正弦函数随时间变化的周期振动，反映结构对外界激励响应的情况可用频率传递特性表达。

简谐激励的动力学方程为

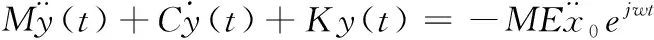
(10)

系统的广义方程为

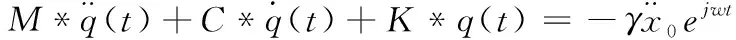
(11)

γ=∅TME

(12)

系统的频率响应矩阵为

H(ω)=(K-ω2M+iωC)-1

(13)

简谐振动方程的稳态解为

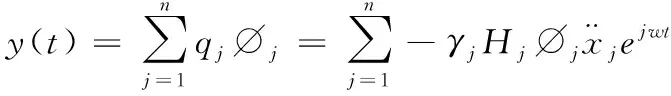
(14)

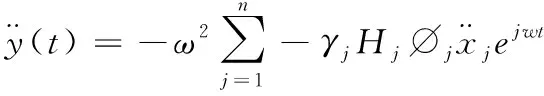
(15)

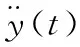
3.3.2 随机振动响应

随机振动指在振动的某一时刻，瞬时值不可知，随机振动响应是不确定问题，虚拟激励法(34)可以吧随机激励近似转化为简谐激励来进行求解，把随机问题转变成确定性问题。动力学方程为

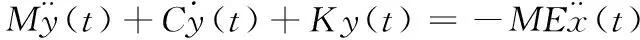
(16)

利用虚拟激励法求得简谐振动方程的稳态解为

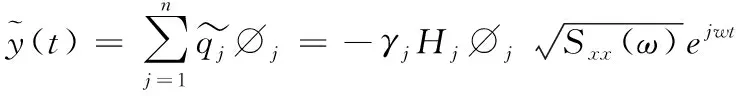
(17)

实际响应的自功率谱密度为

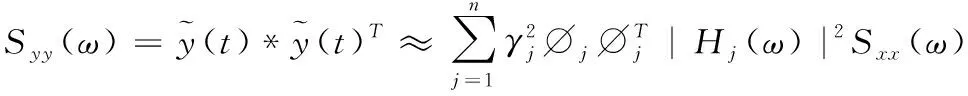
(18)

对上式积分并开方可得加速度响应的均方值RMS

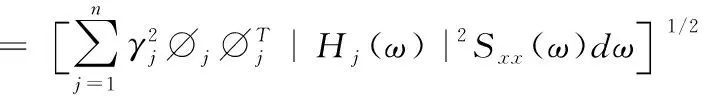
(19)

卫星的随机振动响应分析实际就是观察其响应的自功率谱密度。

4 计算机仿真

卫星有效载荷为同轴光学相机，结构形式为椭球薄壳结构。薄壳材料选用型号为T700的碳纤维复合材料，底板采用蜂窝夹层板，蜂窝板芯为正六边形铝芯格。利用PATRAN对该卫星进行过载、模态特性、简谐振动响应和随机振动响应分析。有限元模型如图4(a)所示。

该卫星的有限元模型主要利用2D单元建立，主要研究相机、推进的响应状况，其余单机和结构采用集中质量点模拟，螺栓连接等使用Rigids建立MPC单元表示。图3中结构尺寸和选用的材料特性见表2和表3。

表2 结构尺寸

表3 材料机械特性

4.1 过载分析

曲线结构比直线结构更稳定，但承载能力更弱，所以要对卫星结构的强度进行考核。根据运载所给条件：

1) 卫星最大轴向过载为：10g；

2) 卫星最大横向(X向或Y向)过载为：2g；

参考美国NASA-STD-5001标准中对卫星结构各类材料的部件推进的用于设计的安全系数，取安全系数值1.5。在计算过程中，考虑运载过程中，三个方向的过载作用状况难以预测，因此在组合最大过载工况作用下，模型受到的过载环境比实际情况要更严重，计算结果偏于安全，具有参考价值。按照材料对结构分类处理，最终结果如表4。

表4 过载分析结果

计算所得该系统的安全系数大于设计参考值1.5，结构应力水平低于材料的强度极限，结构强度满足设计要求。

4.2 模态分析

提取有限元模型的模态，其中3阶和4阶为局部模态，不具有参考价值。主要固有频率见表5，整星振型见图4(b)。

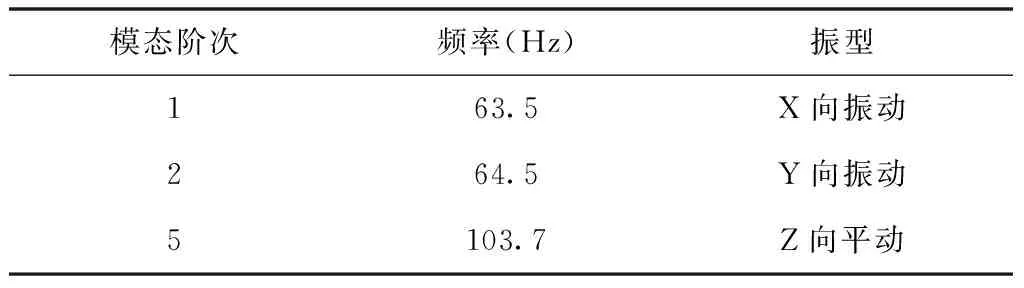
表5 卫星主要固有频率

卫星结构最低自振频率最低为63.5Hz，高于火箭给予的横向大于25Hz和纵向大于50Hz的要求，主体结构刚度均匀，满足设计要求。

4.3 简谐振动响应特性分析

卫星有效载荷为同轴相机，安装在壳体中间，推进系统在壳体上方，其它单机则主要集中在底部支撑板。采样点在相机、推进系统和大综电上选择。卫星受到的外部激励为加速度激励，作用在底部安装节点上，频率范围为5Hz-100Hz，幅度为0.8g。简谐振动分析还需考虑阻尼作用，整星结构阻尼比取0.03。三个方向的安装点输入简谐激励和采样点输出的加速度响应曲线如图5和图6。

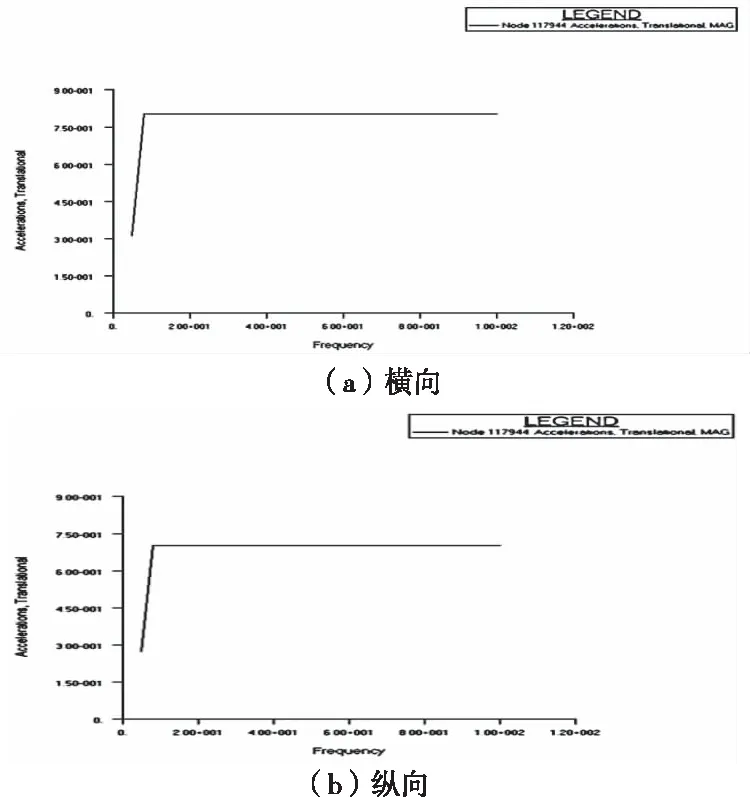
图5 简谐激励加速度曲线图

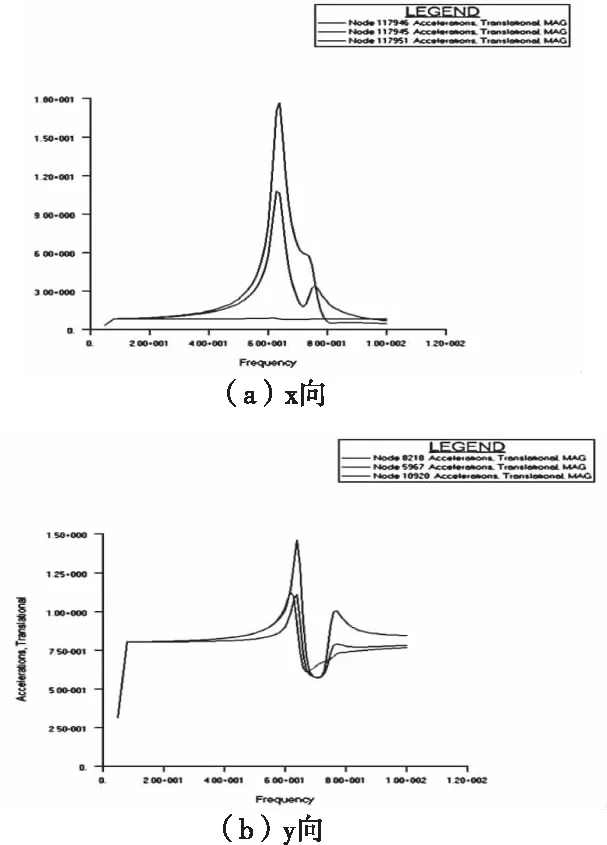
图6 简谐激励下采样点的加速度响应曲线图

从图6可看出推进峰值最高，其次是相机，大综电则几乎不受影响。X、Y和Z三个方向的简谐振动响应最大点均位于上端推进系统中，简谐振动响应加速度值分别为17.6g、15.0g和10.7g，峰值偏大。X和Y向峰值出现在65Hz附近，Z向模态大于100Hz，是以Z向无峰值，与模态计算结果相符。安装在底板的单机响应良好，满足设计要求，安装在中部的相机和上端的推进系统响应偏大，总体效果符合预期。

结合模态分析，推断出造成简谐响应过大的原因是系统约束过少且没有减振措施造成的，因此可通过增加约束、使用减振措施和提高局部刚度的方法来降低正弦响应峰值，以此保证各单机的正常工作。

4.4 随机振动响应特性

随机振动频率为5Hz-2000Hz，频率计算步长为10Hz，整星结构阻尼比取0.03，采样点与简谐分析中所取点一致。总均方根为7.9g。三个方向的输入随机激励和采样点输出的加速度响应曲线如图7所示。

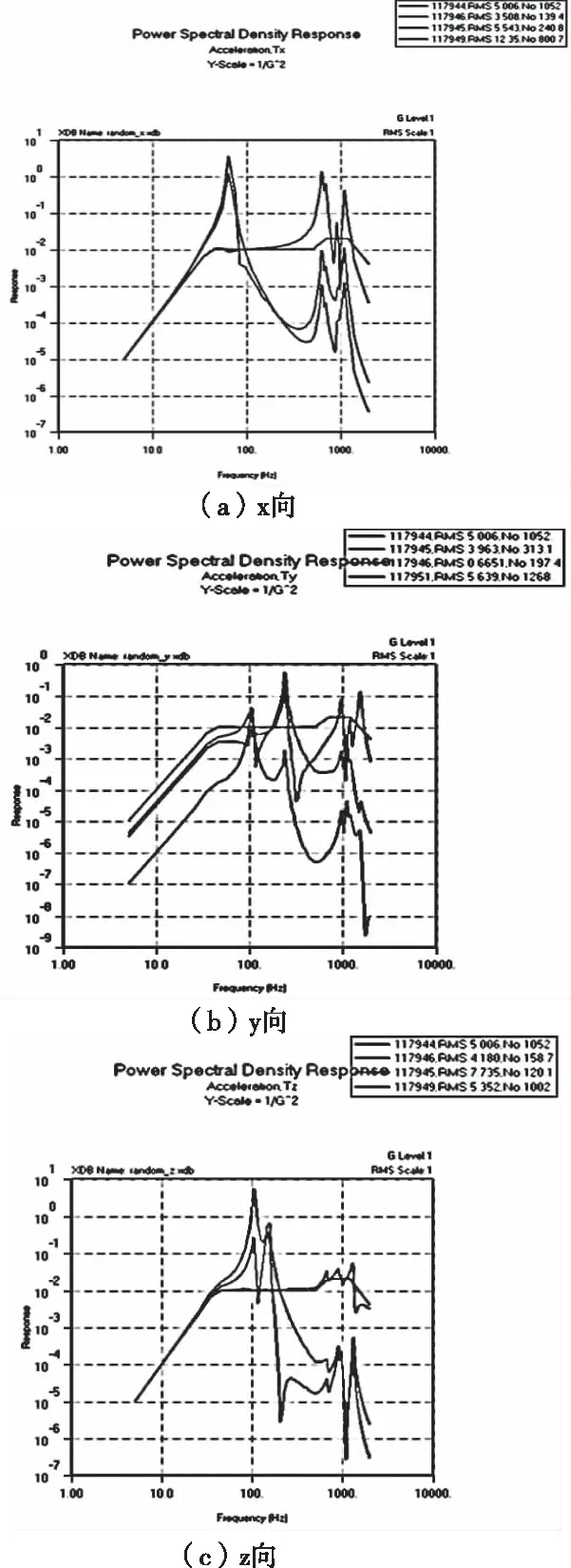
图7 PSD响应曲线图

整星结构在X、Y和Z三个方向随机振动最大响应为3.62g， 0.81g， 5.41g，均发生在推进系统处。整体结构对随机振动响应情况良好，满足随机振动响应设计要求。

5 结论

针对微小卫星良好稳定性和通用设计原则，考虑其边界条件和工作环境，提出了一种仿生构型，即通过仿照海月水母形态来设计卫星，构型形状为椭球薄壳状。

构型充分利用了其内部空间和有效载荷壳体力学性能，一体化程度较高，结构质量占比8.93%，低于一般卫星结构设计中质量占比，整星基频为63.5Hz，满足设计需求。

模型仅为验证其可行性，设计较刚，因此结构还有很大的优化空间。可通过对整体优化布局和结构拓扑优化等手段实现进一步降低结构质量从而降低质量占比。