指挥控制系统效能评估指标值灰色预测模型
2021-11-17余宏峰李琳琳
余宏峰,李琳琳,肖 彬,金 明
(火箭军工程大学作战保障学院,陕西 西安 710025)
1 引言
预测性评估是指通过对评估对象的多个评估指标时间序列数据进行预测建模得到预测结果,将其运用于评估过程,实现对未来一段时间的状态进行评估的一种新的评估方法,目前预测性评估已广泛运用于医疗卫生、航天航空、金融和军事等各个领域[1-3]。传统评估方法与预测性评估方法流程对比如图1所示。

图1 传统效能评估方法流程图(左)与效能预测性评估方法流程图(右)对比
信息化战争下对指挥控制系统灵活性和敏捷性要求越来越高[4-5],开展指挥控制系统效能预测性评估是提高评估结论准确性和系统敏捷性的重要手段,对系统总体效能的提升具有决定性作用,而评估指标值的预测结果作为预测性评估过程的数据输入,对评估结果准确与否起着至关重要的作用。
信息化条件下指挥控制系统的信息复杂性不断增长,其效能评估指标值呈现出混合数据类型的状态,针对该问题目前有不同角度的处理方法[6-8],对比这些处理方法后,本文综合考虑效能评估指标值的特点,保留数据的完整性和不确定性,同时为了简化计算和降低算法复杂度,采用将混合类型数据序列转化成区间数序列的方法进行混合数据的处理。
指挥控制系统效能评估指标值序列的样本量较小,且统一数据类型后的区间数本身具有一定的不确定性,而灰色预测模型是对“小样本、贫信息”的不确定性问题进行预测的一种有效工具,目前很多专家学者已经将灰色预测模型应用到区间数序列预测。文献[9]将区间数序列的区间中点及半径分别看作实数序列,分别建立中点序列和半径序列的预测模型,通过中点和半径的预测值还原区间数序列的上界和下界,实现区间数序列的预测;在文献[10]中,区间数表征可修部件的失效率与修复率,构建灰色状态转移矩阵,建立基于灰色生灭过程可修部件备件需求预测模型;但以上方法均采用最小二乘法对参数进行估计,基于最小误差绝对值最小的假设会造成参数与估值的偏离和平均误差较大的问题,同时以上方法未考虑到区间数的整体性,会对预测的效果造成不良影响。
针对预测模型的以上不足,本文提出一种基于最近数据优先累积法的GM(1,1)指挥控制系统效能评估指标值预测模型。该模型考虑两参数区间数的整体性,从通过发展系数和灰作用度的实际意义出发,为了解决最小二乘法作为参数估计方法的不足,通过累积法进行参数估计,并结合指挥控制系统动态性的要求,使用新陈代谢思想对模型进行完善。
2 基于区间数的混合型数据统一
2.1 区间数的定义与运算关系
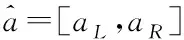
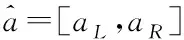
2.2 混合数据统一转换方法
由于战场环境复杂,指挥控制系统效能评估的各个指标值来源复杂多样,导致数据异构,类型复杂。本文提出的方法主要针对指挥控制系统效能评估指标值为实数、区间数、三参数区间数、语言描述和直觉模糊数等四种类型的数据,下面为具体的转换方法。
1)实数。实数即为精确数,例如指标作战筹划效率的指标值为0.87即为一个实数。

3)语言描述。语言描述是指例如“好、一般、较差”之类的定性描述,对于语言描述r,r∈R,由于r难于使用数值去度量,所以需要语言描述集合才能有对比,进而进行量化。R是一种预先定义好的语言描述集,即R={Ri|i=0,1,…,(T/2)-1,T/2,…,T},其中Ri表示R中第i+1个语言描述,T为偶数,R中包含T+1个语言描述。例如,当T=6时,此时R={R0,R1,…,R6},依次对应着“非常差,差,较差,中,较好,好,非常好”这七个语言描述。将语言描述转换成区间数的公式为:
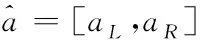
=[max{(i-0.5)/T,0},min{(i+0.5)/T,1}]
(1)
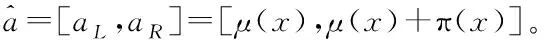
3 基于改进累积法的区间GM(1,1)预测模型
3.1 新陈代谢思想和最近数据优先累积法
3.1.1 新陈代谢思想
新陈代谢原指机体与环境之间的物质和能量交换以及生物体内物质和能量的自我更新过程[13],现将其运用到效能评估指标值的预测过程中。指挥控制系统作为一个动态系统,在预测了从现在时刻起往后的多个时刻指标值的同时,又产生了新的数据,为了提高效能评估指标值的中长期预测精度,引入新陈代谢思想,将新的数据x(0)(n+1)置入序列,同时剔除数据x(0)(1),再用序列X(0)={x(0)(2),x(0)(3),…,x(0)(n+1)}建立模型,对其进行预测,实现预测结果的实时更新。
3.1.2 最近数据优先累积法
在信息化战场的大背景下,战场数据瞬息万变,新产生的数据比旧的数据对战场走势的预测更为重要,应该有着更高的权重,但从传统累积法存在越早的数据累加次数越多的情况,也就是意味着给陈旧的数据赋予了更高的权重,这有悖于实际情况,从而提出最近数据优先累积法,给新产生的数据赋予更高的权重。
设原始序列为X={x(1),x(2),…,x(n)},定义各阶最近数据优先累积和为[14]

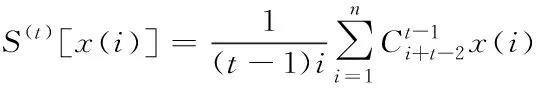
(2)
称为t阶最近数据优先累积和。
特殊地,对于长度为n的全1序列,称为S(t)[1]为t阶最近数据优先累积和,其计算式为

(3)
3.2 基于改进累积法的GM(1,1)预测模型的建模步骤
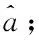
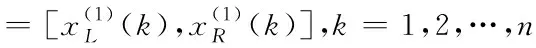
(4)
2)由区间数的一次累加生成序列计算邻值生成序列,得到白化背景值
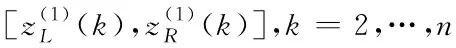
(5)

(6)
由式(2)对中点序列的定义型方程(6)两边作一阶、二阶最近数据优先累积和,得
由式(2),代入相关变量,得一阶、二阶最近数据优先累积法方程组
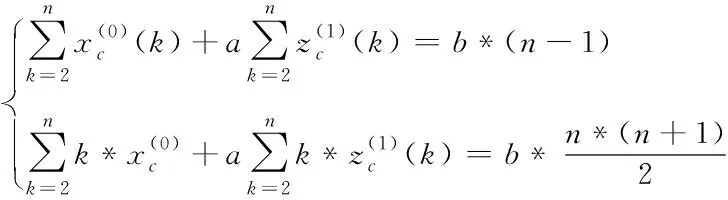
(7)
如果记a=(a,b)T
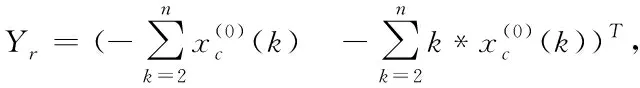
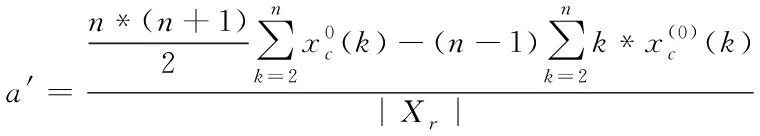
(8)
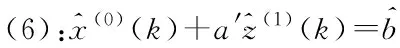
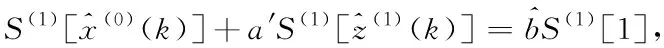

(9)
由式(9)化简得到
(10)
5)根据文献[15]中为改进借用白化响应式来表示灰度响应式对结果造成误差的情况,推导出GM(1,1)模型预测的内涵型公式为
(11)
得出预测结果序列为
6)模型预测的误差计算和预测精度的计算。区间数的相对误差计算公式为
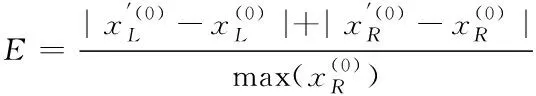
(12)
指标值的预测平均相对误差是指指标在多个时刻的相对误差的均值,公式为:

(13)
式中,Ei为指标值在i时刻的预测相对误差,n为总时刻数。
7)利用新陈代谢思想对预测序列进行更新,实现预测的动态性。
4 实例分析
指挥控制系统是指采用以计算机为核心的技术设备与指挥人员相结合、对部队和武器实施指挥与控制的“人-机”相融合、实现“全域实时动态”的高效指挥系统。效能评估是对完成作战任务能力的度量,指标体系是效能评估的关键,在结合课题组研究成果和现阶段指挥控制系统发展特点与部队实际,构建了指挥控制系统效能评估指标体系,如图2所示。
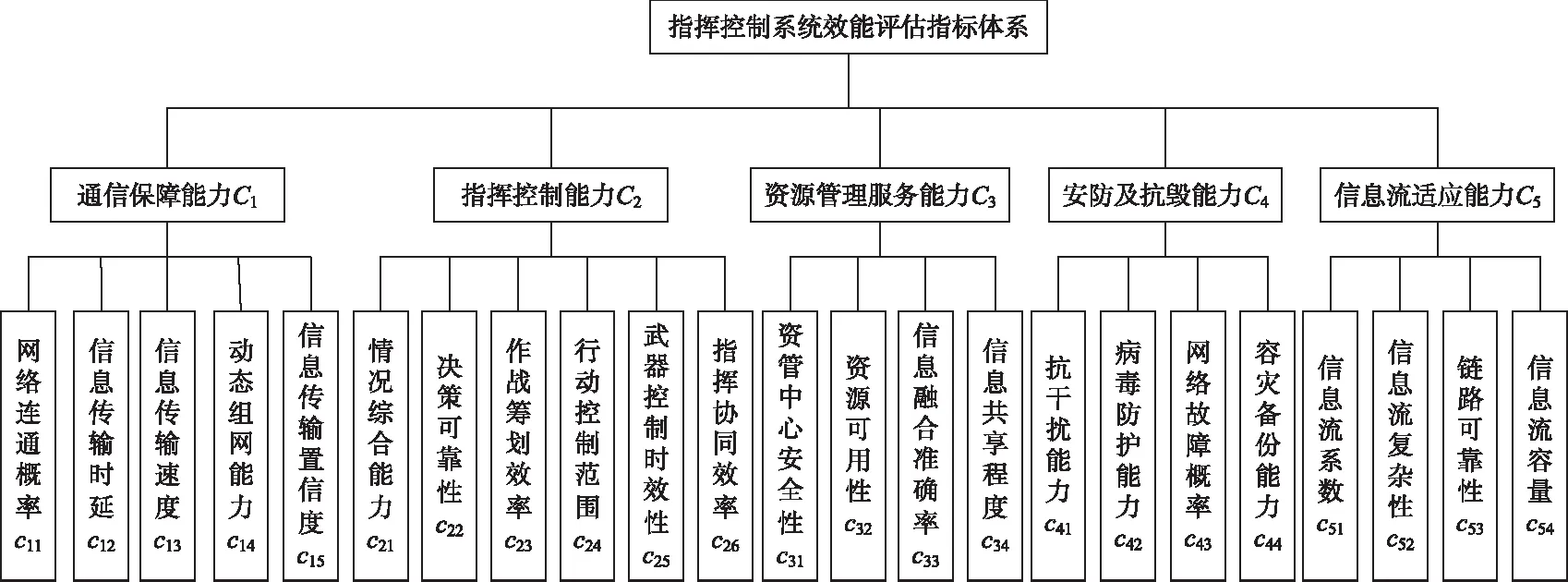
图2 指挥控制系统效能评估指标体系
本实例以某部队装备试验过程中间隔1小时的12个连续时刻指挥控制系统效能评估指标值为例,运用本文提出的基于新数据优先累积法的区间数GM(1,1)预测模型进行指标值预测的实例分析。由于篇幅受限,计算过程以通信保障能力C1的评估数据为例,其指标包括c11网络连通概率、c12信息传输时延(单位毫秒)、c13信息传输速度(光缆传输,最大速率155Mb/s)、c14动态组网能力和c15信息传输置信度,其中c11、c12、c13和c15为定量指标,指标c11用区间数表示,指标c12用三参数区间数表示,指标c13和c15分别用精确数和直觉模糊数表示,c14为定性指标,用7级语义变量(很差,差,较差,一般,较好,好,很好)表示,指标初始数据信息如表1所示。
使用第2.2节基于区间数的混合型数据统一方法将指标初始数据信息进行统一,其结果如表1所示,其中c1i行表示指标c1i的原始值,c1i′行表示指标c1i原始值转换后的值。

表1 指标数据信息统一后结果
为了验证本文所提方法的有效性,对前10个指标值数据进行拟合建模,将第11和12个数据用于模型的预测效果分析。以指标c11为例,预测步骤如下:
原始数据序列为
{[0.831,0.850],[0.826,0.841],…,[0.802,0.828]};
1)由式(4),对原始序列做一次累加生成,得
{[0.831,0.850],[1.657,1.961],…,[8.136,8.350]};
2)由式(5),生成白化背景值序列,得
{[1.244,1.2710],[2.066,2.109],…,[7.344,7.530]};
3)由中点公式计算得出中点序列,得
{0.841,0.834,…,0.802};
4)由式(8)和(10),计算得出发展系数a和灰作用度b的估值分别为
a′=0.0103,′=[b′L,b′R]=[0.8346,0.8579]
5)由式(11)得到
{[0.813,0.850],[0.822,0.845],…,[0.797,0.819],[0.789,0.811]};
以此类推,指标c11-c15应用拓展基于累积法GM(1,1)预测模型对指标值进行预测的结果如表2所示。
6)根据式(12),计算出相对误差并填入表2。

表2 指标数据信息预测结果及相对误差
根据式(13),得到各指标平均绝对误差为:Ec1={Ec11,Ec12,…,Ec15}={0.005,0.002,0.017,0.084,0.004}。
7)当各指标时刻13的指标值采集到了以后,把各指标在时刻1的指标值抛弃,使用时刻2到时刻13的指标值进行新一轮的指标值预测,且可将指标的预测值用于指挥控制系统预测性效能评估,满足指挥控制系统效能评估的动态性要求。
使用文献[9]基于中点与半径的区间数预测方法对本实例的指标值进行预测,预测结果如表3所示。

表3 文献[9]方法对指标在时刻11和12的预测结果
根据表2和表3的数据、平均绝对误差和对比文献[9]的方法,分析可知:c11网络连通概率随着时间推移逐渐变小,可能是由于战损的原因,网络节点被破坏,网络连通概率降低,而c13信息传输速度在逐渐变小的趋势在时刻10突然变大,可能是由于连通节点被抢修成功或作战距离拉近的缘故;从预测结果的平均绝对误差来看,指标c13和指标c14的误差较大,指标c13是由于在时刻10的跳变,导致序列趋势性不明显和波动较大,从而对预测精度造成了比较大的影响;指标c14是定性指标,在转化成区间数的过程是一个离散到连续的过程,转化后数据间跳跃性比较大,导致预测结果的误差比较大。对比文献[9]的在时刻11和12的预测结果,可以发现,本文方法除了指标c13的预测结果不如文献[9]的方法以外,其余指标的预测精度均优于文献[9]的方法,原因是指标在时刻10的指标值突然变化,导致趋势发生变化,从而在指标的预测精度上优于本文方法。
依次将一级指标指挥控制能力C2、资源管理服务能力C3、安防及抗毁能力C4和信息流适用能力C5等下的所以二级指标cij分别运用基于新数据优先累积法的区间数GM(1,1)预测模型和文献[9]的模型进行指标值预测,得出的各指标平均绝对误差如表4。
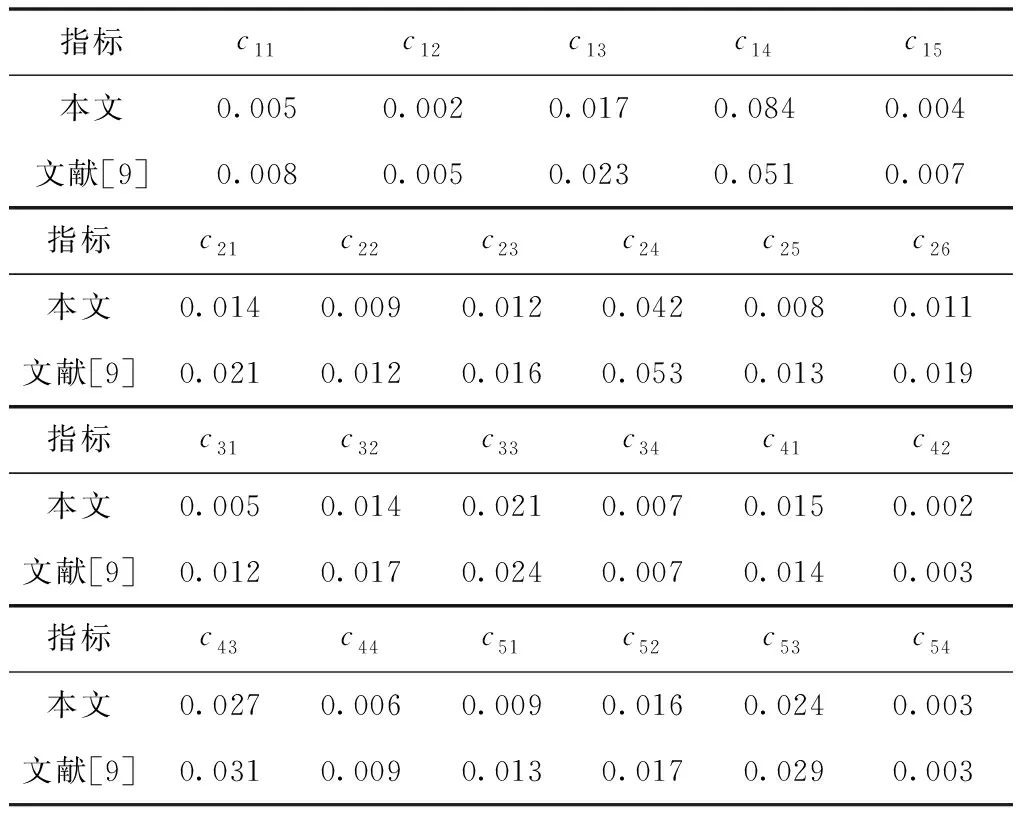
表4 运用本文方法和文献[9]方法的各指标值预测平均绝对误差
从表4的预测相对误差的结果发现,基于新数据优先累积法的区间数GM(1,1)预测模型的预测误差比较小,预测效果佳,对比文献[9]中的区间数经典方法,预测误差普遍比其小,体现了本文方法的有效性。
5 结束语
首先分析指挥控制系统效能评估指标值的特点,将混合类型的数据均转化成区间数,便于数据的处理;分析了传统GM(1,1)预测模型使用最小二乘法进行参数估计的不足,最后采用不进行假设的累积法进行参数估计,并对普通累积法的累加顺序进行调整,以适应新时刻数据比旧数据对预测更重要的原则,同时改进GM(1,1)预测模型将其预测序列类型从精确数序列预测拓展到区间数序列,再结合新陈代谢思想对预测模型的动态性进行完善。通过指标数据预测实例和与其它区间数序列预测方法进行比较验证了该模型的有效性。可将预测的指标值结果用于指挥控制系统效能评估中,实现对未来时刻的效能进行预测性评估,增加战场应对突发事件的反应时间,提高打赢战争的能力。
