多视角深度图配准算法下破损古建筑三维重建

阮競芸，厉 犇

(厦门大学嘉庚学院，福建 漳州 363105)

1 引言

近些年，人们对古迹保护越来越重视。但是经过岁月的侵蚀，大部分古迹都在不同程度上发生了风化、腐蚀甚至人为破坏等情况。如何对已破坏古建筑进行重建，并确保重建后的高还原度成为了古建筑修复领域的主要研究问题。由于三维重建技术不断发展成熟，其也被广泛地应用于古建筑还原重建领域中。

王令文[1]等人提出结合点云数据与建筑信息模型(Building Information Modeling，BIM)的古建筑三维重建与信息化管理方法。该方法使用四面体剖分算法建立三角网模型，随后以点云作为参考目标给出实体模型，并根据实际的模型信息特点，以实现信息化管理。通过实验证明该方法具有一定的有效性，且构建的信息管理部分能够在不同阶段对建筑的几何信息进行持续管理。但是该方法受外界噪声或环境等因素的干扰较大，具有一定的局限性；徐照[2]等人提出基于点云的建筑物表面损伤三维重建与属性提取方法，通过Kinect采集实际场景和信息，利用点云库(Point Cloud Library，PCL)对采集后的数据格式转化，将数据坐标系转变为与各个构建相对应的坐标系以确定建筑的损伤位置，随后采用Meshlab切割点云提取主要破损区域信息，最后在地理信息系统(Geographic Information System，GIS)环境内将处理后数据转为深度图像，实现对损伤部位信息的提取与重建。该方法的还原精度较高，最终的三维图像呈现效果较好，但是由于该方法所涉及的算法较多，导致操作较为复杂，且重建的效率较低。

针对上述问题，本文以图像配准为基本原则，提出一种多视角深度图配准算法下破损古建筑三维重建。图像配准就是通过将不同时间，不同条件下(照度、天候以及摄像机位置和角度等)获得两幅或两幅以上的图像进行匹配和叠加的过程。因此，本文通过相机坐标系的标定获得相对于标准坐标系各个摄像机的具体坐标，降低外界干扰，随后以上述摄像机标定为基础，给出图像配准方法，并凭借多视角三维拼接确定坐标系旋转平移前后的局部空间坐标变换关系，该过程中的关键部分即是确定旋转前坐标系、旋转后坐标系以及摄像机坐标系。三维拼接后通过求解平移向量、缩放因子以及最优旋转矩阵，快速完成破损古建筑的三维重建。

2 基于多视角深度图配准的三维重建

2.1 多视角深度图像摄像机标定

摄像机标定为三维重建的第一步，主要作用是确定摄像机像素位置与真实三维场景位置间的关系。假设Q(X，Y，Z)表示世界坐标中的一点，q(x，y，f)表示图像上一点，其中f表示焦距。若O表示摄像机光心，则可以通过平移和选择将世界坐标转换为相机坐标，在如图1所示的相机坐标内，Q的坐标系可以表示为[R|T]Q。

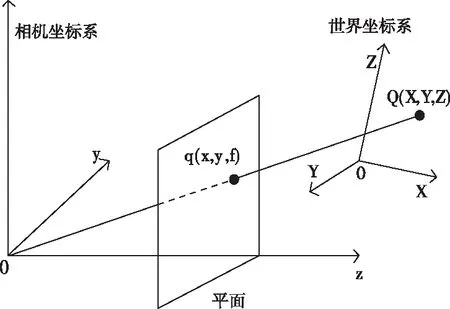
图1 摄像头成像模型

因此，Q与q之间的关系可以表示为

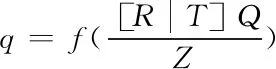
(1)

由于最后呈现出的画面是以像素的方式进行表现的，引入像素坐标m(u，v)，则像素对应的相机坐标可以表示为(dx，dy)。在实际操作过程中，像素的坐标中心可能不会与中心光轴完全重合，故引入A=(cx，cy)表示像素中心的偏移，由此可推导出下式

(2)

当通过多个摄像头进行拍摄时，在实际操作过程中摄像头做不到完全对齐，因此导致成像平面不能做到完全平行，甚至可能导致两个不同摄像头的成像平面发生交错[3]。因此通过下式对摄像头进行旋转平移变换。

(3)

式(3)中，qc1、qc2分别表示2个不同摄像机坐标，R、T表示旋转和平移矩阵[4]。将该原理应用于多个摄像头中，若多个摄像机均以某个摄像机为参照，就可以获得与之相应的旋转矩阵，从而获得各个摄像机的具体坐标。

2.2 图像配准

以上述摄像机标定为基础，给出图像配准方法，多视角三维拼接的主要就是在于确定坐标系旋转平移前后的局部空间坐标变换关系。其中主要涉及3种坐标系分别为：旋转前坐标系、旋转后坐标系以及摄像机坐标系[5]。旋转前的平面坐标为XZ，旋转轴为Y轴。建立旋转坐标系OtXtYtZt。假设旋转一定角度后坐标系为Ot1Xt1Yt1Zt1，相机坐标为OcXcYcZc。随后对转轴进行标定，转轴标定指的是确定被测物体绕转轴在相机坐标系内的具体位置。为简化标定过程，本文采用棋盘角点信息标定法。具体流程如下：将棋盘标定板放置在旋转台上，以某一摄像机坐标为参考，从而获得标定板角点的位置。棋盘角点的运动轨迹如图2所示。

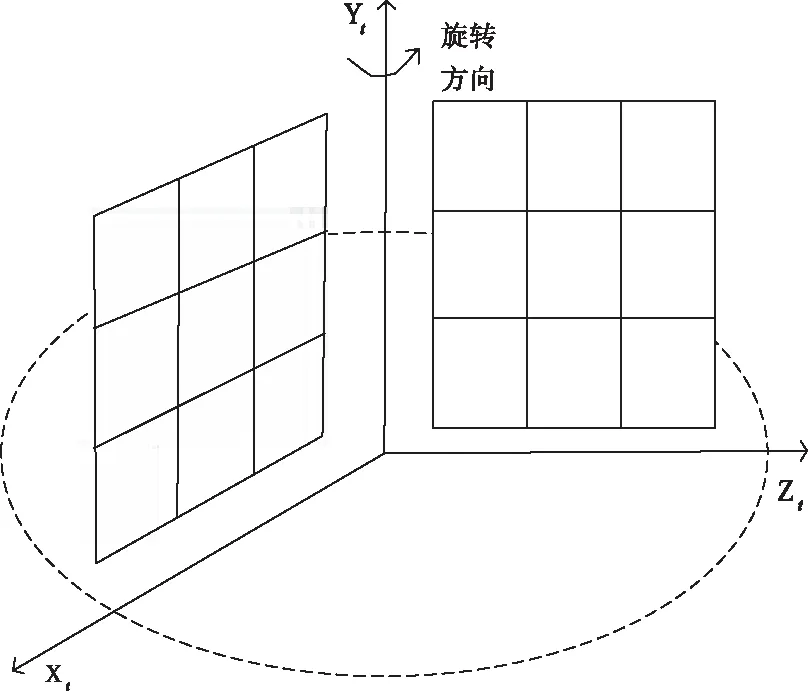
图2 角点运动轨迹

角点通过旋转而形成的平面方程如下

Ax+By+Cz+d=0

(4)

可将式(4)进一步改写为

(5)

式(5)中，n表示平面法向，(x，y，z)表示标定板的角点坐标。

理论上讲，当任意角点旋转位置的置数目为3时，即可求出由标定板角点所形成圆的法向，也就是转轴方向。但是为确保准确性，在实际操作过程中可以通过对多个角点进行求解确保在噪声干扰下的转轴方向的鲁棒性[6]。在对转轴上点的求解过程中，可以通过拟合圆心的方法进行，但是由于角点坐标是在三维空间内的，拟合出圆较为困难，因此为能够使算法实现，将摄像机坐标系条件下的转轴法向n旋转至转台坐标系下，旋转的具体方法如下：

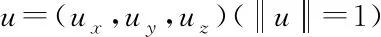
R=Icosθ+sinθ[u]×+(1-cosθ)u⊗u

(6)

式(6)中

(7)

(8)

利用式(6)将摄像机坐标系的转轴法向n转换至转台坐标系[7]，此时旋转轴可以表示为

(9)

旋转角度可以表示为

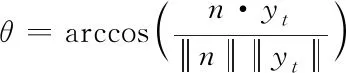
(10)

通过式(6)将角点坐标转换为旋转轴坐标系中时，角点所在平面和XZ平面互相平行。角点对XZ平面进行投影弧，即可通过最小二乘法完成圆心拟合[8]，获得圆心坐标，可将其转为摄像机坐标系下位置Xp=[xp，yp，zp]。

通过上述方法获得旋转轴位于摄像机坐标系的具体位置，为进一步求得摄像机和转台坐标系间的关系，首先建立两种坐标系统，随后根据二者坐标系间的联系，确定二者间关系。相机坐标系统可以表示为：

(11)

在设定转台坐标系统的过程中，需保证旋转轴始终为Y，X、Z轴可以根据实际情况自由选择。为了方便操作，将XZ平面和转轴之间的交点当作转台坐标系统的原点。则XZ平面方程可以表示为：Y=0，转轴的参数方程可以表示为

(12)

式(12)中，转轴法向n=(nx，ny，nz)，t表示转轴参数[9]。旋转轴上的一点坐标为Xp=[xp，yp，zp]。

(13)

对两个坐标系进行对齐处理。最后即可获得两个坐标系间的关系如下

R1=RxRy

(14)

2.3 破损古建筑三维重建

在获得两个坐标系间关系后，分别取建筑破损部分在两个坐标系中的一点，将两点进行融合即可实现三维重建全过程。融合的过程分为两个部分，一是确定坐标系中一致对应的点集，二为求解变换矩阵，完成两个矩阵点集的融合。

分别使用P1、P2代表两个坐标系统，统计古建筑的照片D中破损部分在P1、P2中对应点的数目，具体实现方法为，对于D中每幅图像K，读取其在两个坐标系统中的对应点，定义为Pk1、Pk2。随后计算出P1、P2投影在K上的像素位置，并对三维点在公共平面内的投影点位坐标进行记录，其计算公式为

xi=PXi

(15)

式(15)中，Xi表示三维点坐标，P表示与图像K相对应的摄像机矩阵，xi表示Xi投影至K上的二维点坐标。

将P1、P2投影至图像K的结果记为K1、K2。通过式(15)计算所得的投影像素点坐标不是整数[10]，因此需要对图像内的每个像素点进行进行坐标取整，取整后将两张图像中的像素点坐标位置进行对比分析，并记录出坐标值相互重合的像素点，将重合像素点组成一个点集A，则这个集合内的点为匹配点。由此即可获得整体与局部点之间的一致点对。

为实现对应点集内所有点的坐标准确对齐，需要寻找出一个相似变换T，由于两个坐标系统的对应点是已知的，因此使用具有显式解的方式对T进行求解。变换T是由三个参数组合而成，分别为平移向量L、缩放因子s、最优旋转矩阵R′，由此即可将求解问题转换成最小化目标函数[11]如下：

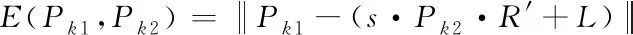
(16)

随后通过以下方法求解相应变换。

1)求解平移向量L

首先通过下式计算出P1、P2的几何中心：

(17)

式(17)中，O表示几何中心，N表示点的数目，随后通过所得的O1、O2即可计算出平移向量L如下

L=O1-O2

(18)

在实际操作过程中，采用了坐标归一化法，将两个坐标系统的中心点平移至原点O，因此式(16)还可以转换成如下形式

L=(O1-O2)+(O-O1)

(19)

2)求解最优旋转矩阵R′

在不考虑缩放因子的条件下，式(18)可进一步简化为：

(20)

为使系统坐标能够在选择变换的过程中确保结构不变，选择矩阵应该满足det(R)=1的约束条件。通过OPP算法求解出最优旋转矩阵R′如下

R′=U·VT

(21)

式(21)中，U、V分别表示特征向量矩阵。

3)求解缩放因子s

可以根据式(22)直接求得缩放因子。

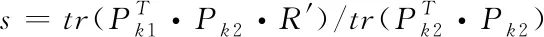
(22)

式(22)中，tr(·)表示矩阵迹[12]，通过上述方法完成缩放、平移和旋转变换后，通过下式将坐标系统P2中的点云转换至P1坐标系统下：

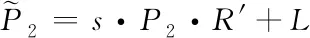
(23)

综上，即完成了两个坐标系统点云的融合，实现了破损古建筑的三维重建。

3 仿真研究

为验证多视角深度图配准算法下破损古建筑三维重建方法的有效性，设计如下仿真分析。为使实验结果更为直观，在Visual C++环境下，以用图像工具库OpenGL为图像处理平台，从重建效果和定量分析两个角度完成性能验证。为避免实验结果的单一性，将文献[1]方法、文献[2]方法作为对比，与本文方法共同完成性能验证。

图3为两个不同视角下的破损古建筑的数据图像，图4中(a)、(b)、(c)分别表示文献[1]方法、文献[2]方法以及本文方法的重建结果。

图3 不同视角下数据图像

图4 不同方法重建效果对比图

根据图4可以看出，由于本文使用棋盘坐标定位配准，能够准确地剔除环境干扰，且准确地恢复了原始图像的破损部分，且三维重建后的图像呈现效果更清晰。

在此基础上，进一步对不同方法展开定量分析，结果如表1所示。

表1 不同算法的定量分析结果

表1中的数据避免，与其它两种方法相比，本文方法给出的各项相关数值与真实值最为接近，且说明其实际还原度较好，具有较高的实际应用价值。

4 结束语

为还原破损古建筑的真实情况，本文在多视角深度图配准算法下提出了一种破损古建筑三维重建。方法主要通过棋盘角点信息标定法完成空间坐标和相机坐标之间关系，随后通过点云融合完成三维重建，实验证明该方法具有一定的有效性，但是还在以下方面存在不足：

1)在进行图像配准的过程中，没有考虑受干扰情况下的测量误差。由于实际数据较多且其中可能还包含杂点和噪点等因素影响，因此在配准之前需要对数据进行预处理。

2)本文方法针对的是包含像素信息的深度图像，存在局限性，可以考虑通过其它途径对深度图进行图像化处理，因此下一步将会在不考虑像素信息的条件下对本文算法进行完善，使其的适用性更强，能够广泛地应用至更多领域内。