基于测距交会的海面物体高精度定位仿真
2021-11-17姚国伟肖泽龙
王 华,王 倩,姚国伟,肖泽龙
(1. 中国运载火箭技术研究院,北京 100076;2. 南京理工大学电光学院,江苏 南京 210094)
1 引言
传统主动雷达主要通过获取目标的距离、角度信息来解算目标位置,当前,雷达测得的目标距离信息已经达到了较高的精度,然而,雷达的测角精度受到多方面制约而提升缓慢,使得单雷达实现远距离目标定位时随着距离不断增大,测角误差引起的目标定位误差也不断增大[1]。为解决这个突出难题,提出了多雷达协同定位的方法,目前通常采用双站测向交叉定位方法或者三站交会定位方法[2-3],双站测向交叉定位方法针对远距离目标时精度提高不明显,而三站交会定位方法的系统组成复杂,协同难度较大。本文针对海面应用场景,提出了基于测距交会的海面物体高精度定位方法,利用两架无人机携带两部主动雷达获取目标的精确距离信息,实现对海面物体的高精度定位。仿真结果显示,所提方法具有系统构成简单,计算量小、定位精度高等优点。
2 距离交会定位模型
以WGS-84大地坐标系(O-XYZ)作为基准坐标系,其定义为:以地球质心为原点,Z轴指向BIH1984.0定义的协议地球极方向,X轴指向BIH1984.0的启始子午面和赤道的交点,Y轴与X轴和Z轴构成右手系[4]。
由于针对的是海面物体的定位,因此假设物体海拔高度为零,这一假设限定了物体位于地球椭球面上,再加上由双雷达为球心、距离为半径的两个球面构成三个定位球面。三个定位球面的交点就是物体所在的位置。

图1 定位原理图
假设两部雷达中的第一部雷达(或无人机)的大地直角坐标系坐标为A(x1,y1,z1),第二部雷达(或无人机)大地直角坐标系坐标为B(x2,y2,z2),海面物体的大地直角坐标系坐标为T(x,y,z)。则两雷达到物体的距离为
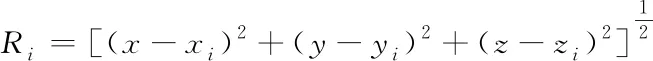
(1)
式中,i=1,2。
采用WGS-84地球椭球模型[5-6],海面物体T(x,y,z)满足

(2)
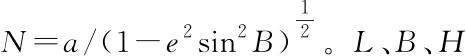
L、B、H、N都与物体位置T(x,y,z)有关。将式(2)中消去L、B得到如下椭球方程
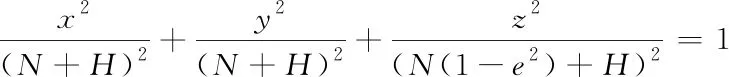
(3)
联立(1)式和(3)式可得如下方程组

(4)
解式(4)可以得出关于物体位置T(x,y,z)。
3 模型解算
式(4)所确定的测距定位模型是一组非线性方程组,直接求解析解比较困难,牛顿迭代法是解非线性方程组的有效方法[7-8],因此本文采用牛顿迭代法求解。
根据式(4)可定义:

(5)
令F(x)=[f1,f2,f3]T,则定位模型为F(x)=0。根据牛顿迭代格式,对式(5)求导得到Jaccobi矩阵
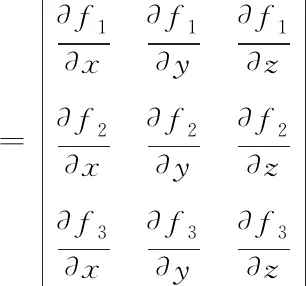
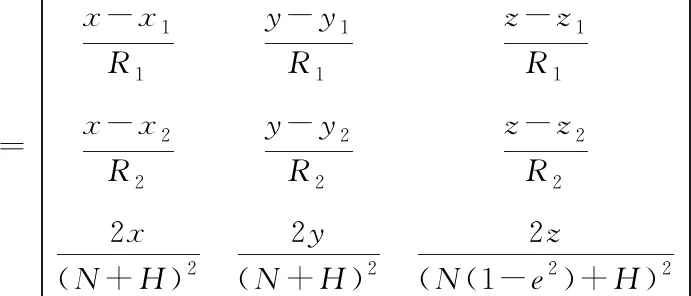
(6)
得到迭代格式如下式所示
x(k+1)=x(k)-[F′(x(k))]-1F(x(k))
(7)
使用牛顿迭代法求解非线性方程组的流程图如图2所示。
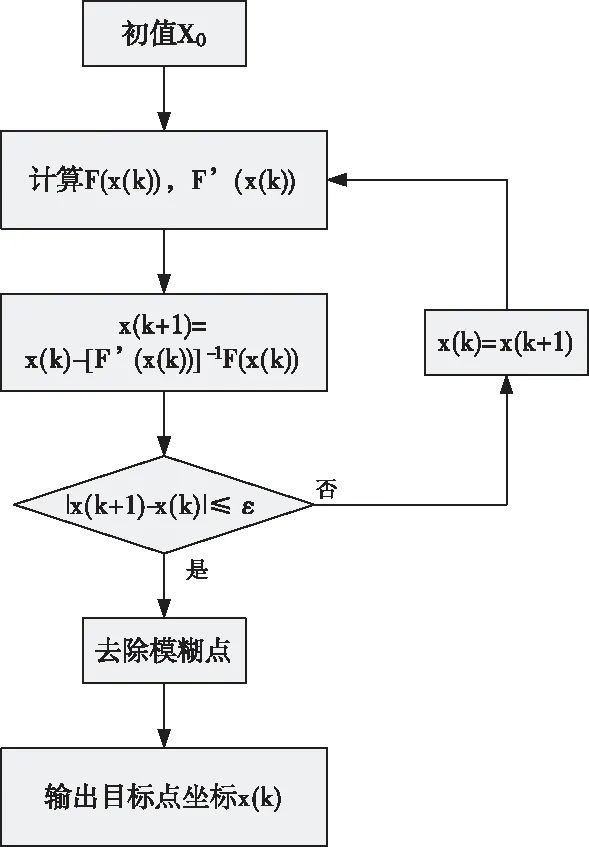
图2 迭代求解非线性方程组流程图
主要步骤简述如下:
step1:设置其中一架无人机位置的海面投影点作为迭代初值x0;
step2:将前一次物体位置x(k)(xk,yk,zk)代入定位方程(5),求出在该点的函数值F(x(k));
step3:将前一次求得的物体位置坐标x(k)(xk,yk,zk) (迭代初始初值解算结果x0(x0,y0,z0))代入(6)式中,求出F’(x(k));
step4:当F’(x(k))非奇异时,将坐标x(k)(xk,yk,zk)和F’(x(k))、F(x(k))代入迭代式(7),求出物体位置x(k+1)(xk+1,yk+1,zk+1);定义dk=|x(k+1)-x(k)|,当dk≤ε时停止迭代;
step5:滤除模糊点。step4计算出两个目标疑似位置P1(x1,y1,z1)、P2(x2,y2,z2),P1和P2对称于两架无人机位置的连线。根据无人机1的位置PU1(xU1,yU1,zU1)和其携带的主动雷达测量的目标距离L1、方位角α1、俯仰角β1,可计算出目标位置PF(xF,yF,zF)

(8)
再计算P1、PF的欧式距离D1和P2、PF的欧式距离D2,若D1 对公式(4)求微分得 (9) 整理(9)式可得 (10) 整理成矩阵形式如下式所示 AdX=dR+BdS+CdH (11) 式中 其中dh为海浪引入的物体高度误差,dr是气象引入的测距误差,dR为雷达测距误差,dr+dR表示总的测距误差,dx,dy,dz是平台位置误差。 假设机载平台的位置误差相互独立,雷达测距信息相互独立,则物体定位协方差矩阵为 pdX=E[dXdXT] (12) 为了评估双雷达测距交会的定位精度,引入定位精度几何稀释(GDOP)作为评价标准[9],它描述测距交会法在仿真计算范围内各点的定位精度。通过对GDOP的计算,可以衡量不同测量子集定位物体的性能[10]。其表达式为 (13) 针对基于测距交会的海面物体定位精度仿真条件设置如下:无人机A携带主动雷达位于(120°,0°,10000m)(经度,纬度,高度),无人机B携带主动雷达位于(120.5°,0°,10000m)。仿真目标区域为:经度范围[118°,122.5°],纬度范围[-5°,5°],目标为海面物体,海拔高度取0m。雷达测距精度为20m,平台位置精度为10m,海浪高度1m。针对基于测距交会的海面物体高精度定位精度GDOP图如图3(a)、(b)所示。 图3 定位精度GDOP图 从图3中可以看出,GDOP等高线对称分布在以两部主动雷达所处位置连线的两侧,原因是定位模型(4)属于二次方程组,当其非奇异时有两组解,即存在模糊解,这是由于在仿真计算GDOP过程中未设置雷达探测目标的角度信息,在定位解算过程中经过滤除模糊点步骤后可以得到唯一解。 此外,图中还反映出当双雷达位置与目标位置构成一个等腰三角形时,定位精度相对较高。在此前提下,双雷达与目标相对位置可用目标角(目标角即为目标与两部雷达连线间的夹角)描述,目标角与定位精度关系如图4所示。从图4中反映出当目标角介于80°~90°之间时,定位精度最高。 图4 目标角与定位精度关系图 在图中经度120.06° ~ 120.44°、纬度±0.15°~±0.37°的区域内(图中矩形区域),本方法实现的定位精度优于35m,而同区域内单雷达(按当前雷达的一般水平:测距精度20m、测角精度0.3°,雷达位置与图示位置相同)的定位精度最大值超过了338m,最小值也达到107m,因此双主动雷达测距交会定位方法的定位精度比单雷达定位精度提高2~9倍,目标距离主动雷达越远,定位精度提高越明显。 通过精度表达式推导过程可知,影响海面物体定位精度的主要因素包括主动雷达测距误差、气象引入的测距误差、无人机平台定位误差、海浪高度等。在精度仿真中将气象引入的测距误差合并到主动雷达测距误差中作为一项误差源,下面分别对上述影响因素进行仿真分析。 为了便于后续的比较分析,三项误差源变化时均遵循2倍的关系而保持其它误差值不变。由于在作战运用中,常常关注某定位精度的区域的分布情况,因此,在仿真分析中选定定位精度优于40m的区域进行比较分析。仿真条件设置与定位精度的仿真条件相同。 a)主动雷达测距误差对定位精度的影响 设定雷达测距误差为σR1=σR2=20m和σR1=σR2=10m两种情况进行仿真对比。不同测距误差影响的GDOP比较图如图5所示。 图5 雷达基线对定位精度的影响对比图 b)平台定位误差对定位精度的影响 雷达平台定位误差同样是影响物体定位精度的因素之一。分别设定平台定位误差小于10m和5m两种情况,对应的各方向雷达位置误差为σx1=σy1=σz1=σx2=σy2=σz2=5.77m、σx1=σy1=σz1=σx2=σy2=σz2=2.9m。不同平台定位误差影响的GDOP比较图如图6所示。 图6 平台位置误差对定位精度的影响对比图 c)海浪对定位精度的影响 海浪高度分别为1m和2m时,对应的GDOP分布如图7所示。 图7 海浪对定位精度的影响对比图 通过上节对GDOP的仿真,可以得到定位精度优于40m的等高线区域范围,统计结果如表1所示。 表1 误差源变化2倍时40m精度区域变化率 从表1可看出,误差值同样变化为2倍的条件下(主动雷达测距误差分别为20m和10m,平台位置误差分别为10m和5m,海浪高度分别为2m和1m),其40m等高线覆盖区域的变化率依次为4.32、1.10和1.00,充分说明此三项误差因素中,主动雷达测距误差对物体定位误差的影响最大,平台位置误差次之,海浪高度影响最小。 针对海面物体的高精度定位问题,本文建立了基于测距交会的高精度定位模型,介绍了定位模型的求解方法,并根据定位模型推导出定位精度表达式,对影响定位精度的三类主要影响因素进行了仿真分析,结果显示,利用双雷达测距交会定位方法定位精度比单雷达定位精度有较大幅度的提高,且当目标与两部雷达之间形成的目标角介于80°~90°之间时,定位精度最高。在保持目标角不变的前提下,主动雷达测距误差对物体定位误差的影响最大,平台位置误差次之,海浪高度影响最小。此仿真分析结果为后续工程化应用和系统精度优化提供了重要借鉴。4 精度仿真分析
4.1 精度表达式
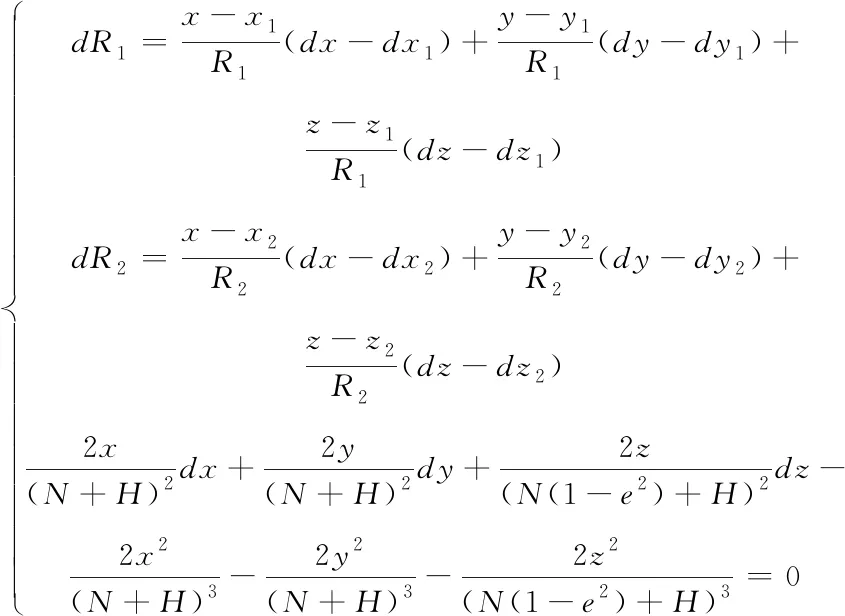

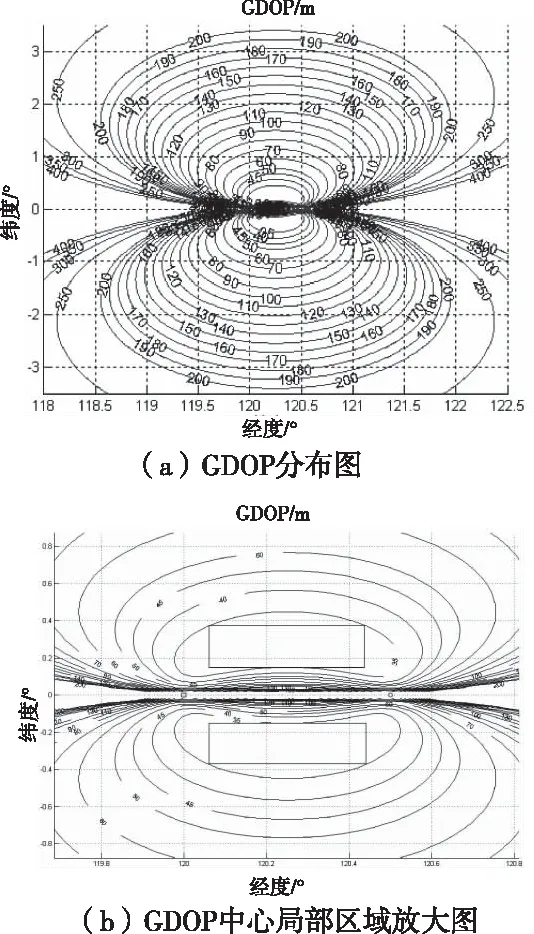
4.2 定位精度仿真

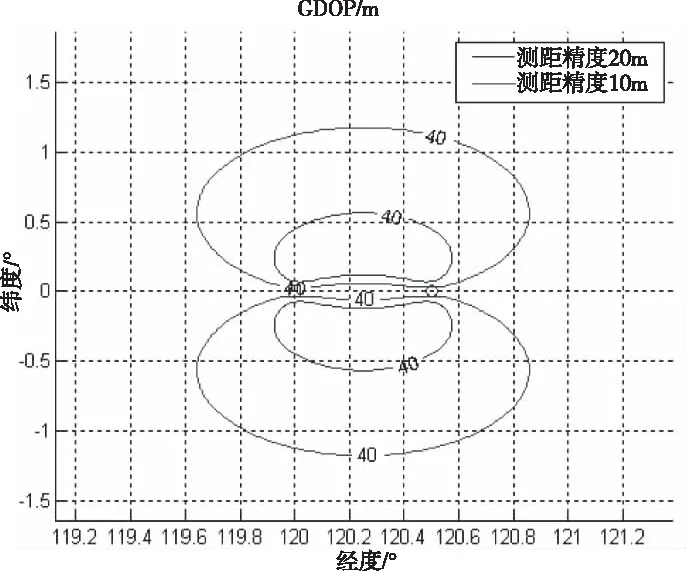
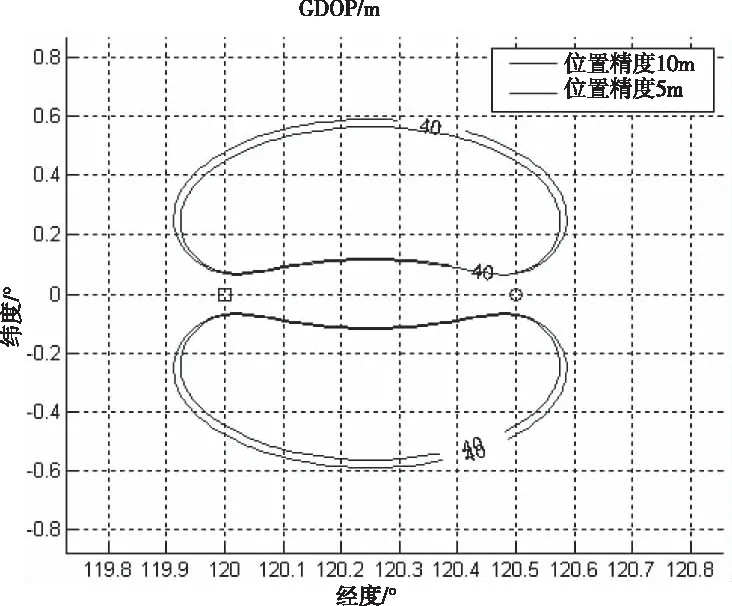
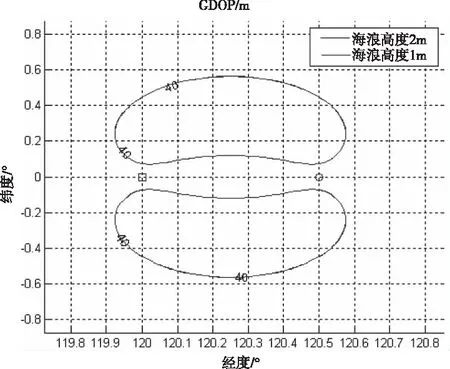
4.3 定位精度影响因素仿真分析
4.4 仿真结果定量分析
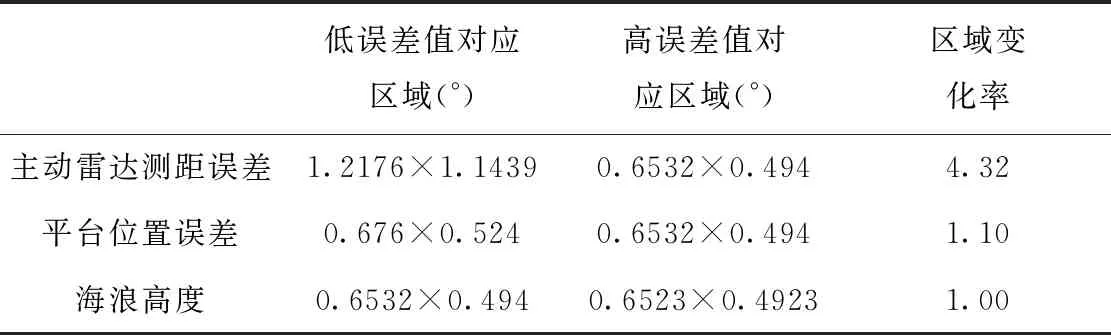
5 结论
