基于Dubins曲线的一致性编队集结控制

王锦锦，祁圣君，钟 海，粟建波

(中国飞行试验研究院飞机所，陕西 西安710089)

1 引言

无人机编队飞行因其覆盖范围广、适应能力强、作战效率高等优点，受到了世界各国的广泛关注，成为航空领域的研究热点之一。多架无人机要实现编队飞行，首先要在空中指定区域内组成链路通信，形成指定队形构型，完成集结。因此，如何安全有效地实现无人机编队集结是编队控制中首要解决的问题。

无人机编队集结的具体要求为多架无人机在建立链路通信的前提下，从初始任意状态按照给定的约束条件实现指定队形构型的过程。因此，可以将编队集结问题简化为带时间约束的多无人机航迹规划问题。

多无人机航迹规划要求设计满足编队约束条件的航路曲线，使无人机能够安全到达相应集结点。几何规划法是常用的航迹规划方法之一，目的是在起点和终点之间规划出满足约束条件的一段或者多段平滑曲线，常用的几何规划法[1]有Clothid曲线、Bezier曲线、PH曲线、Dubins曲线等。其中，Dubins曲线结构简单、路径易于解算，被广泛应用于无人机路径规划中。

信息一致性理论[2]的研究最早起源于管理科学和统计科学，后被广泛应用于分布式计算和信息融合领域。作为新兴智能化控制策略，近年来一致性理论算法被广泛应用于多智能体控制系统，在提高系统控制精度、增强鲁棒性等方面均具有突出优势，也为无人机编队飞行控制提供了新思路。

本文针对无人机编队系统进行集结控制研究，结合Dubins曲线和一致性理论，安全有效地实现多无人机编队集结控制。

2 问题描述

本文研究的一致性编队集结控制要求所有无人机在保证安全的前提下，在同一时间内，完成从初始位姿到带有终端约束的指定队形的构建。其中，终端约束包括队形约束、速度约束、姿态角约束等。因此，可将本文的集结控制问题分为集结路径规划和飞行轨迹控制两大问题。针对这两大问题，本文提出一种基于Dubins曲线的一致性集结控制算法，如图1所示。

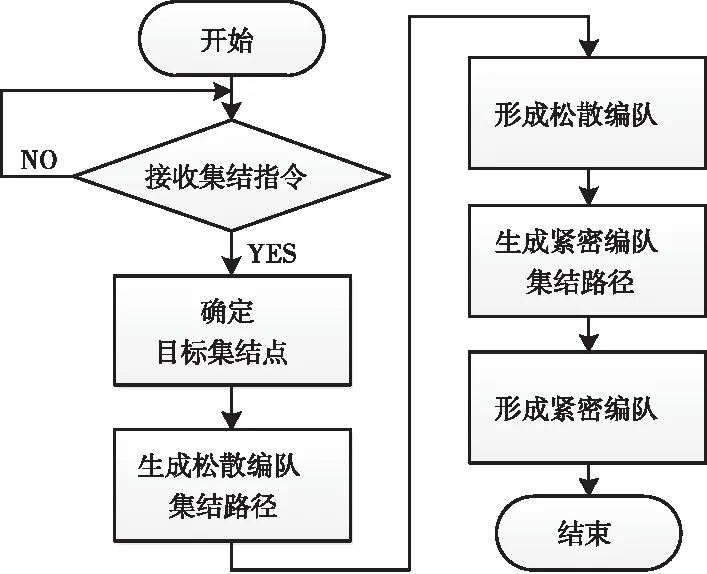
图1 一致性编队集结流程图

具体流程为：集结前首先通过地面站发送集结指令给各无人机，当各机接收到集结指令后，反馈确认信息给地面站，如果未接收到集结指令，地面站应重新发送指令；如果确认无误，则对各机进行统一编号，以方便集结；确认集结指令后，首先根据各机初始位姿信息及松散编队终端约束信息生成并分配目标集结点，以避免空间路径重叠发生碰撞；然后针对各无人机生成不同的Dubins集结路径，并结合一致性控制协议，形成松散编队；最后利用一致性控制协议实现精确航迹控制，调节机间距离，压缩队形，形成紧密编队，完成一致性集结控制。

3 编队队形描述

为准确描述编队各无人机的位置关系，本文针对N机编队提出一种l-l-l队形描述法，用于描述N机编队的三维队形。

该方法通过设置编队参考点，根据各无人机与编队参考点在三轴方向上的距离来进行队形描述，将其写成矩阵的形式，可以得到N机编队的队形描述矩阵Fd

(1)

图2 队形描述法示意图

4 一致性控制协议

对于无人机编队系统，一致性控制协议[3]表示无人机之间的信息传递规则，在该协议的作用下所有无人机的状态或输出最终趋于一致。

考虑N机编队以给定的通信拓扑结构进行信息交互，结合无人机飞行控制理论，给出编队系统中无人机Ui的一致性控制协议

(2)

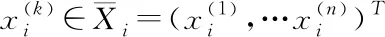
该一致性控制协议的具体含义为：将所有与无人机Ui进行通信的编队无人机的相关状态按照给定的控制协议进行反馈，并乘以一致性项系数Kk，给到Ui的相关控制输入端，最终可以实现编队无人机相关状态的一致性稳定。

5 一致性编队集结控制

5.1 形成松散编队

5.1.1 确定目标集结点

对于N机编队，当各无人机确认集结指令后，首先将所有无人机编号为U1，U2，…UN，然后根据各机位置关系和松散编队终端约束信息生成并分配目标集结点M1，M2，…MN，一个无人机对应一个目标集结点，以避免空间路径重叠发生碰撞。

(3)

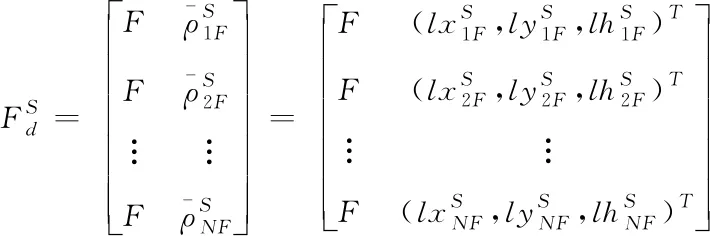
(4)

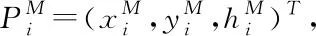
(5)

至此即可得到目标集结点M1，M2，…MN的位置坐标，考虑距离代价和三维空间位置关系，将其合理分配给各无人机。

5.1.2 基于Dubins曲线的集结路径规划

如图3所示的四机编队系统，生成松散编队要求控制各无人机在保证安全的前提下，合理规划集结路径[4]，使得各无人机在一定时间误差内到达虚线内所示的目标集结点处，根据给定的终端约束条件完成指定松散编队队形的构建。

图3 形成松散编队示意图

为形成松散编队，本文引入Dubins曲线，合理规划二维平面内的集结路径，并解决终端约束问题。

Dubins曲线的主要思想[5]为：针对空间中不同方向向量的两个点，在恒定速度和限定曲率的前提下，利用几何方法寻找从两点之间的最短可行路径。同一平面内的任意两点之间的最短路径为两点之间的直线段，当需要满足一定的曲率情况下，两点之间的最短路径为圆弧。

图4 CLC型Dubins路径示意图

步骤一：确定起始圆和终止圆

(6)

(7)

本文采用距离判断的方法，选择圆心距离最小的两个圆分别作为Dubins曲线的起始圆和终止圆，继而确定直线段AiBj的类型(内切线或外切线)和位置坐标。

步骤二：确定切线

1) 内切线的求解

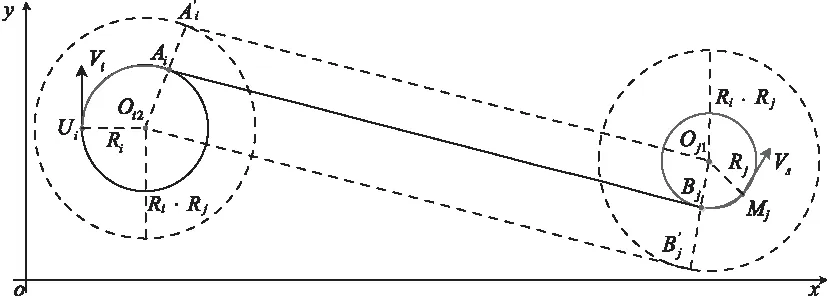
图5 内切线的求解

2) 外切线的求解

图6 外切线的求解

步骤三：确定Dubins路径

根据切点Ai，Bj的位置坐标、起始圆半径Ri、终止圆半径Rj确定Ui的Dubins集结路径长度li：

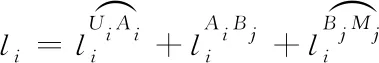
(8)

2.3.3 形成松散编队的轨迹控制

为保证各无人机到达目标集结点的时间差距在一定范围内，本文采取轨迹控制和速度控制相结合的方法，并根据无人机飞行包线要求合理选择各机飞行速度

(9)

其中Td表示预设到达目标集结点的时间，满足

(10)

对于生成松散编队的轨迹控制，本文提出一种定点集结和伴航集结相结合的控制策略，该过程可以分为以下两个阶段：

第一阶段为定点集结：

编队各无人机以给定的飞行速度，按照生成的Dubins集结路径自主飞向各自对应的目标集结点。

定点集结阶段分为弧线段和直线段，弧线段采用基于PID控制方法的协调转弯飞行控制律

(11)

Δδia=KPφ·(φi-φig)+Kp·pi

(12)

(13)

直线段采用基于PID控制方法的航向控制律

ψig=arctan[(yBj-yAi)/(xBj-xAi)]

(14)

φig=KPψ·(ψig-ψi)+Kr·r

(15)

Δδia=KPφ·(φi-φig)+Kp·pi

(16)

(17)

第二阶段为伴航集结：

先到达目标集结点的无人机先进入编队航线自主飞行，当所有无人机均通过目标集结点并进入航线后，引入一致性控制协议，实现位置以及速度的一致性，根据松散编队队形约束调整机间距离，形成松散编队。

1)垂直航迹通道中，通过调整俯仰角来实现队形在垂直方向上的稳定，其控制律结构为

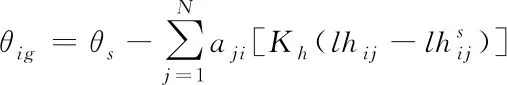
(18)

Δδie=(KPθ+KIθ/s)·(θi-θig)+Kq·qi

(19)

2)侧向航迹通道中，通过调整偏航角来实现队形在侧向上的稳定，其控制律结构为

(20)

φig=KPψ·(ψig-ψi)+Kr·ri

(21)

Δδia=KPφ·(φi-φig)+Kp·pi

(22)

3) 在前向航迹通道中，通过调整速度来实现队形在前向上的稳定，其控制律结构为

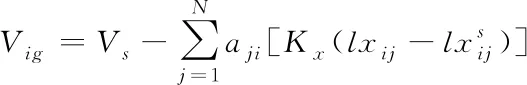
(23)

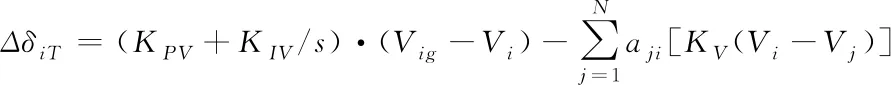
(24)

5.2 形成紧密编队

如图7所示，一致性集结过程的最后一步是由松散编队压缩队形，形成紧密编队[7]。

图7 形成紧密编队示意图

本文采用精准航迹一致性控制律来压缩队形以生成紧密编队，并实现位置、姿态以及速度的一致性稳定，实现完整的一致性编队集结。

1) 垂直航迹通道中

(25)

Δδie=(KPθ+KIθ/s)·(θi-θig)+Kq·qi

(26)

2) 侧向航迹通道中

(27)

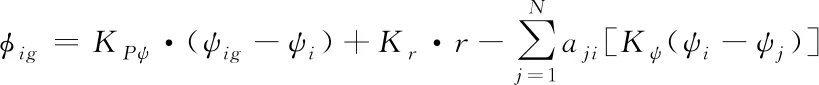
(28)

(29)

3) 前向航迹通道中

(30)

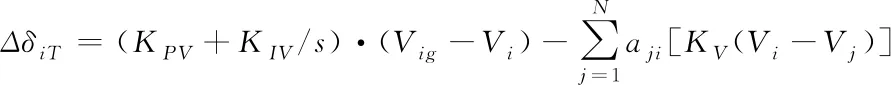
(31)

6 仿真验证

本文考虑构建四架同型号无人机组成的编队，给出确认集结指令时无人机U1，U2，U3，U4的位姿信息如表1所示。

表1 无人机位姿信息

给出松散编队终端约束信息

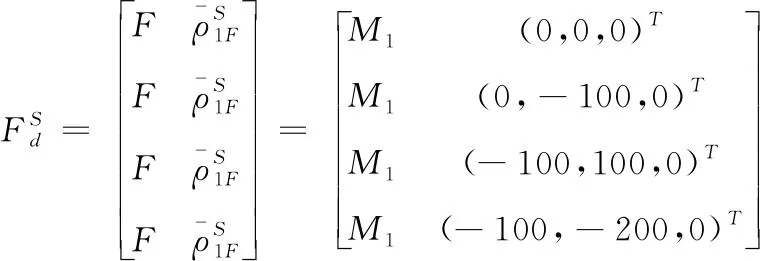
(32)

{Vs，θs，ψs}={28m/s，1.58°，0°}

(33)

紧密编队终端约束信息

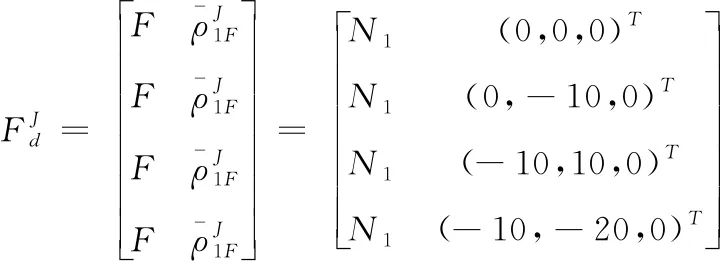
(34)

{VJ，θJ，ψJ}={28m/s，1.58°，0°}

(35)

根据本文提出的基于Dubins曲线的编队一致性集结控制算法，进行Matlab数字仿真验证，得到仿真结果如图8～10所示。

图8 集结控制三维仿真曲线

其中，图8为四机编队集结控制三维仿真曲线；

图9分别为水平二维仿真曲线和高度仿真曲线；图10为飞行状态仿真曲线，包括飞行速度、俯仰角、滚转角和偏航角。

图9 集结控制二维仿真曲线

图10 队无人机飞行状态仿真曲线

由以上仿真结果可知，在基于Dubins曲线的一致性编队集结控制算法的作用下，编队内四个无人机可以从初始位置安全有效地组建松散编队和紧密编队，完成整个集结过程，控制精度较好，满足设计要求。

7 结束语

本文针对无人机编队系统的集结控制问题，提出一种基于Dubins曲线的一致性编队集结控制算法：首先根据初始信息和约束条件确定并分配目标集结点；然后根据松散编队的终端约束信息，利用几何法求解无人机的Dubins集结路径，根据定点集结和伴航集结相结合的控制策略，结合一致性控制协议，控制所有无人机形成松散编队；最后采用精准航迹一致性控制律，调整机间距离，压缩队形，控制所有无人机形成紧密编队，实现完整的一致性编队集结。

仿真结果表明，该算法能够在保证安全的前提下满足集结的要求，实现多架无人机安全有效地完成指定编队队形的构建。