文理合一，证算并举

雷小华

2021年是广东省新高考文理合卷的第一年，立体几何大题与往年相比，分值不变，题序后移至二十. 试题以三棱锥为载体，先要对空间位置关系进行定性论证，后要利用二面角进行体积的定量计算. 考查数形结合、直观想象及运算三大能力. 紧抓基础与核心，融合往年文理考查热点，虽平淡常规，却细思巧构，寓意深远. 仔细品味，意味深长，概括如下：

推证乐章，取自“五音”;基础不牢，地动山摇;建系与否，高效为标;文理合一，证算并举.

以上仅个人观点，为抛砖引玉而已. 下面对试题略作分析.

一、试题与简解

【试题】（2021年新高考全国Ⅰ卷数学第20题，12分）

如图1，在三棱锥A-BCD中，平面ABD⊥平面BCD，AB=AD，O是BD的中点.

（1）证明：OA⊥CD;

（2）若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD的体积.

【简解】（1）∵ AB=AD，O为BD中点，

∴ AO⊥BD，

∵ AO？奂面ABD，面ABD⊥面BCD，面ABD∩面BCD=BD，

∴ AO⊥面BCD，

∵ CD？奂面BCD，

∴ AO⊥CD.

（2）解法一，几何法：

过点E作EF⊥BD交BD于F，再过点F作FG⊥BC交BC于G，连接EG，如图2. 设AO=m.

由（1）可得EF⊥面BCD，故AO∥EF.

根据三垂线定理可知：∠EGF即为二面角E-BC-D的平面角，故∠EGF=45°，

∵ DE=2EA，

∴ EF=m，OF=.

∵△ OCD是边长为1的等边三角形，O为BD中点，

∴ BC⊥CD，BC=.

故GF∥CD.

由=得，GF=.

在Rt△EFG中，∠EGF=45°，故m=，即m=1.

∴ S△BCD=×CD×BC=×1×=，

三棱锥A-BCD的体积VA-BCD=·S△BCD·AO=.

解法二，坐标法：

以O为坐标原点，OD为y轴，OA为z轴，在平面BCD内过C且垂直OD的直线为x轴，建立空间直角坐标系O-xyz，如图3. 设AO=m. 则C（，，0），D（0，1，0），B（0，-1，0），A（0，0，m），E（0，，m），

故=（0，-，-m），=（，，0），

设平面EBC的法向量为=（x1，y1，z1），则

·=-y1-mz1=0，·=x1+y1=0，即2y1+mz1=0，x1+y1=0，令y1=-1，∴ z1=，x1=，∴ =（，-1，）.

由于平面BCD的法向量为=（0，0，m），

故cos〈，〉==，解得m=1，∴OA=1，

∴S△BCD=×CD×BC=×1×=，

三棱錐A-BCD的体积VA-BCD=·S△BCD·AO=.

二、试题分析

（一）解答分析

解答前要先思考以下问题：

在第（1）问中，

①试题给出面面垂（平面ABD⊥平面BCD），你将怎样用好这一条件？会想到什么？

②有解题思路后，能把推理论证的过程完整表达出来吗？

③第（1）问的证明能用坐标法来证吗？

第（2）中，

①题目给的二面角E-BC-D的大小为45°，将如何使用？

②已知条件△OCD是边长为1的等边三角形，你对这一条件能生成的结果有感觉吗？有什么结论产生？

③选择什么方法做第（2）问？是几何法？还是坐标法？

（二）解答点睛

1. 推证乐章，取自“五音”

题目首先给你一个面与面垂直的条件，你能否熟练想到面面垂的性质定理？接下来如何用好这一定理？若要回答好这些问题，关键在基础！即平行、垂直的判定定理与性质定理这一基础知识（本文戏称“五音”）. 另外，值得特别提醒的是，不光要会，而且要全面熟练地掌握！否则，本题解答时将犯“会而不全”的错误，导致丢分！比如：在得出AO⊥面BCD之前，若①AO⊥BD，②AO？奂面ABD，③面ABD⊥面BCD，④面ABD∩面BCD=BD这四个必须满足的条件没有写全而被高考阅卷人扣分.

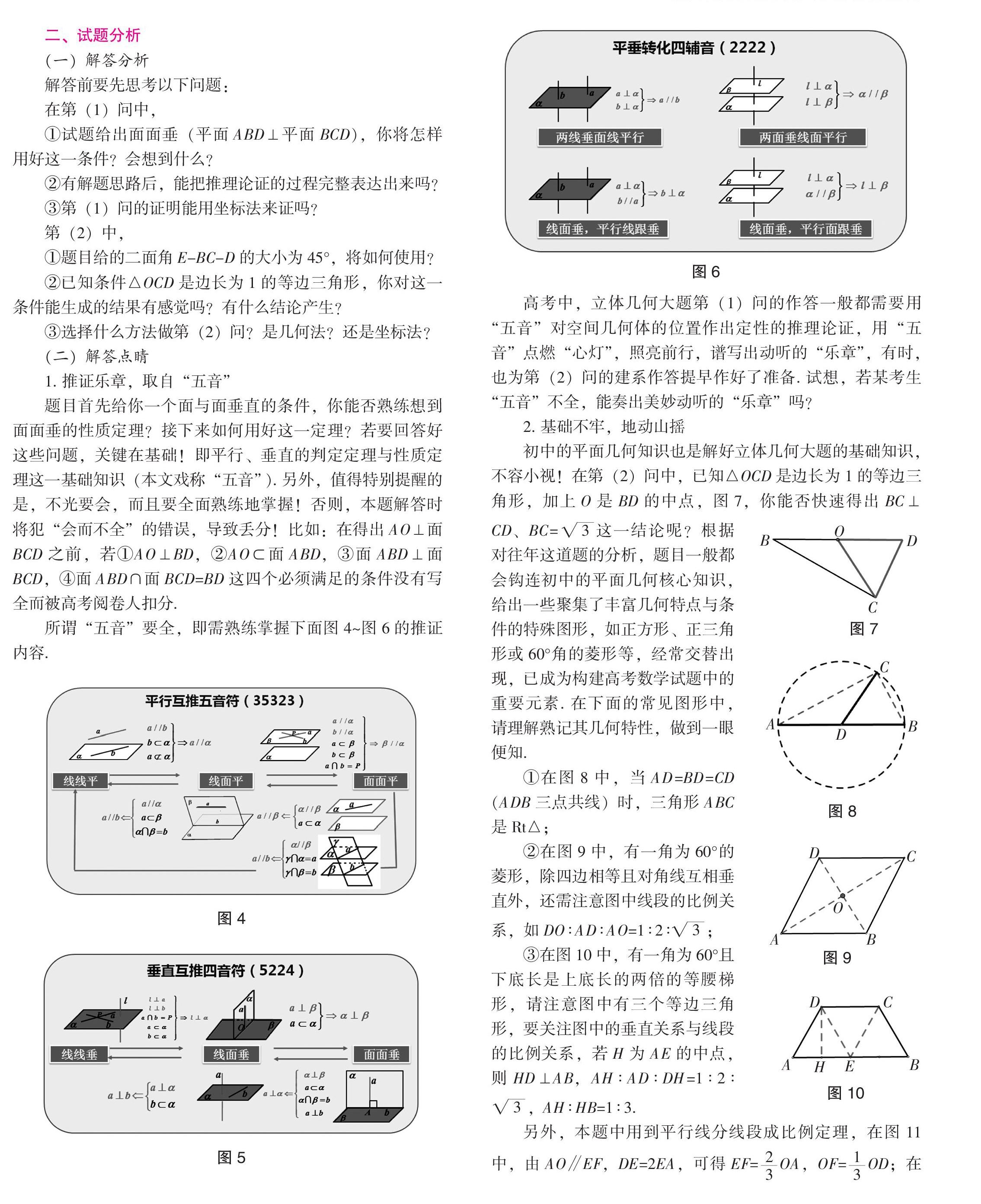
所谓“五音”要全，即需熟练掌握下面图4～图6的推证内容.

高考中，立体几何大题第（1）问的作答一般都需要用“五音”对空间几何体的位置作出定性的推理论证，用“五音”点燃“心灯”，照亮前行，谱写出动听的“乐章”，有时，也为第（2）问的建系作答提早作好了准备. 试想，若某考生“五音”不全，能奏出美妙动听的“乐章”吗？

2. 基础不牢，地动山摇

初中的平面几何知识也是解好立体几何大题的基础知识，不容小视！在第（2）问中，已知△OCD是边长为1的等边三角形，加上O是BD的中点，图7，你能否快速得出BC⊥CD、BC=这一结论呢？根据对往年这道题的分析，题目一般都会钩连初中的平面几何核心知识，给出一些聚集了丰富几何特点与条件的特殊图形，如正方形、正三角形或60°角的菱形等，经常交替出现，已成为构建高考数学试题中的重要元素. 在下面的常见图形中，请理解熟记其几何特性，做到一眼便知.

①在图8中，当AD=BD=CD（ADB三点共线）时，三角形ABC是Rt△;

②在图9中，有一角为60°的菱形，除四边相等且对角线互相垂直外，还需注意图中线段的比例关系，如DO ∶ AD ∶ AO=1 ∶ 2 ∶;

③在图10中，有一角为60°且下底长是上底长的两倍的等腰梯形，请注意图中有三个等边三角形，要关注图中的垂直关系与线段的比例关系，若H为AE的中点，则HD⊥AB，AH ∶ AD ∶ DH=1 ∶ 2 ∶，AH ∶ HB=1 ∶ 3.

另外，本题中用到平行线分线段成比例定理，在图11中，由AO∥EF，DE=2EA，可得EF=OA，OF=OD;在图11中，由GF∥CD，FD=2OF，OB=OD=CD=1，则FG=.

再者，理解记住一些常见的结论.

如图12，菱形ABCD中以BD为折痕把三角形ABD折起的过程中，一个明显结论是：BD⊥AC、BD⊥A1C、BD⊥A2C……

又如，课本必修2P79B组第2题正方体ABCD-A1B1C1D1中，如图13，有以下常用结论：

①DB1⊥平面A1BC1，DB1⊥平面ACD1;

②H为三角形A1BC1的中心，且HB1三等分DB1;

③ 平面A1BC1∥平面ACD1，且距离为DB1的;

④ 三棱锥B1-A1BC1的体积=·.

3. 建系与否，高效为标

当你权衡了几何法与坐标法的优劣，舍去几何法，选用坐标法来解答立体几何问题时，为方便施展，建好空间直角坐标系将是重要的第一步.

建系时首先需对底面与侧面有清楚的认识，考虑坐标系如何最大程度依附好指定的空间图形，形成最直接、最明显的位置与数（度）量关系，产生二维与三维、局部与整体相互联系的便利通道，这样才能突破建系难点.下面选取一些建系惯例，以供参考.

（1）含60°角的菱形，如图14.

（2）正方形、矩形、直角三角形，如图15.

（3）梯形（由三个正三角形拼成），如图16.

在本题中，较好的建系方法是，以点O为原点，在平面BCD内过点O作BD的垂线为橫轴，以OD方向为纵轴，OA方向为竖轴，建立空间直角坐标系O-xyz. 如图17.

第二步，写对所需点的坐标. 在本题中，写对点C的坐标是难点，也是关键一步，此步一错，后续皆错！

一般地，难写的点可体中取面单独画图分析. 如图18，点C（，，0）的坐标就一目了然. 另外，求平面的法向量时，若某点的坐标不易写出，看是否能绕过不写，而从图形中通过向量运算求出所需向量，效果也很好. 比如，在图三中，若你感觉求点E的坐标有困难时，可绕过不写，而考虑求出，即=+=（0，m，m），这样，同样为求该平面的法向量提供了有利条件.

当做好一些基础性的准备工作后，下面就看你是否熟记了空间三（个）角公式了. 请看下表.

第（2）问到底用什么办法更省时省力，高效作答，就今年这道题来说，前面用的几何法既省时又省力，显然好过坐标法.

若选择用几何法处理三（个）角问题时，一般需遵循“作、指、证、算” 这四个步骤，熟练于心，不可或缺. 在这里，重点介绍用三垂线定理作锐二面角的平面角的开头第一步“作”字诀.

如图19中，左图是二面角的平面角的定义图，右图是用三垂线定理作二面角的平面角的效果图. 步骤如下：

①选取半平面？琢内（非公共棱）一点P，作另一半平面？茁的垂线PH，垂足为H;

②过点H作公共棱l的垂线HG，垂足为G;

③连接PG.

根据二面角的平面角定义，可证∠PGH即为二面角的平面角.这时，解好此Rt△PHG就可以知道二面角的大小了.

例如，图20中，AB⊥平面BCD，BC⊥CD，AB=BC=CD，试问二面角C—AD—B的大小是多少？

若用几何法处理，第一步“作”很重要，操作如下：取BD的中点E，易知CE⊥平面ABD，作EF⊥AD交AD于F，连接FC，则二面角C—AD—B的平面角？兹就是图中∠CFE的大小，可求得？兹=60°. 其證明与计算请自己完成.

当然，还有其它方法如面积射影法等，在这里就不作详细介绍，仅把结论陈述如下.

如图20中，PC⊥平面ABC，三角形ABC是三角形PAB在面ABC上的射影三角形，设二面角P—AB—C的大小为？兹，则cos？兹=，请对结论进行思考并作证明.

对于偏爱几何法作答的考生，建议切实掌握常见的“三角”（线线角、线面角、面面角）的定义及相应的作图方法，其中利用三垂线定理（或逆定理）作二面角的平面角尤其要熟练掌握. 在解答过程中把“作、指、证、算”这四步必要过程写清楚，确保胜券在握.

平时练习中，建议两法都要练，两法都过硬. 这样，在临场发挥中才能左右逢源，择优而行.

三、文理合一，证算并举

今年是立体几何文理合卷的第一年，试题应有一定的导向定调功能. 从试题考查目标来看，把过去文科的体积运算与理科的角度运算加以融合，保留了文理共同的推理证明. 在第（2）问的处理办法中，既可以用偏重推理论证的几何法作答，又可以用爱好运算的坐标法求解. 或许，这种设计将是未来高考立体几何大题的走向？

『例1（变式一）』

如图21，在三棱锥A-BCD中，OA⊥CD，AB=AD，O是BD的中点.

（1）证明：平面ABD平面BCD;

（2）若三棱锥A-BCD的体积为，且△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，求二面角E-BC-D的大小.

【简解】（1）∵AB=AD，O为BD中点，

∴ AO⊥BD，

∵ OA⊥CD，BD∩CD=D，BD？奂面BCD，CD？奂面BCD，

∴ AO⊥面BCD，

∵ AO？奂面ABD，

∴ 面ABD⊥面BCD

（2）解法一，几何法：

过点E作EF⊥BD交BD于F，再过点F作FG⊥BC交BC于G，连接EG，如图22. 设AO=m.

由（1）可得EF⊥面BCD，故AO∥EF.

根据三垂线定理可知：∠EGF即为二面角E-BC-D的平面角，

∵ DE=2EA，

∴ EF=m，OF=.

∵ △OCD是边长为1的等边三角形，O是BD中点，

∴ BC⊥CD，BC=.

∴ S△BCD =×CD×BC=×1×=.

∵ VA-BCD =·S△BCD· AO=，

故m=.

由GF∥CD得=，故GF=，

在Rt△EFG中，tan∠EGF==，

∴ ∠EGF=60°.

即二面角E-BC-D的大小60°.

解法二，坐标法：

以O为坐标原点，OD为y轴，OA为z轴，过O且垂直OD的直线为x轴，建立空间直角坐标系O-xyz，如图23. 同解法一可得AO=.

则C（，，0），D（0，1，0），B（0，-1，0），A（0，0，），E（0，，），

故=（0，-，-），=（，，0），

设平面EBC的法向量为=（x1，y1，z1），则

· =-y1-z1=0，· =x1+y1=0，即2y1+z1=0，x1+y1=0，令y1=-，∴ =（3，-，2）.

由于平面BCD的法向量为 =（0，0，1），设二面角E-BC-D的大小为？兹，则？兹=〈 ，〉.

故cos？兹=cos〈 ，〉==，∴？兹=60°，即所求二面角E-BC-D的大小为60°.

『例2（新情景）』

如图24，棱长都相等的正四棱锥P-ABCD中，E为底面ABCD的中心，F为侧面PAD的重心.

（1）證明：EF⊥平面PAD;

（2）若此棱锥的侧面积与体积的比值为，点G在棱PC上，求直线BG与平面PAD所成角的正弦值的取值范围.

【解析】（1）（方法一）：

如图25，连接PF并延长交AD于H，连接EH，连接PE.

∵ 正四棱锥棱P-ABCD长都相等，F为侧面PAD的重心，

∴ PE⊥平面ABCD，H为AD的中点，

∴ PH⊥AD，HE⊥AD，

∵ HE∩PH=H，PH？奂平面PEH，HE？奂平面PEH，

∴  AD⊥平面PEH，

∵ EF？奂平面PEH，

∴ AD⊥EF.

设棱长为2m，则在Rt△PEH中，FH=，HE=m，

cos∠EHF==，

故在△EFH中，由余弦定理可得：

EF==，

∵ FH2+EF 2=（m）+（m）=m2=EH2，

故EF⊥PH.

∵ AD∩PH=H，AD？奂平面PAD，PH？奂平面PAD，

∴ EF⊥平面PAD.

（方法二）：

如图26，以E为原点，以AB中点、CD中点所在的直线为x轴，以BC中点、AD中点所在的直线为y轴，以EP所在的直线为z轴，建立空间直角坐标系E-xyz. 设棱长为2m，则PE=m.

∴ A（m，-m，0），D（-m，-m，0），P（0，0，m），由三角形重心公式得F（0，-m，m），

∵ =（-2m，0，0），=（-m，m，m）， =（0，-m，m），

且·=（-2m，0，0）·（0，-m，m）=0，·=（-m，m，m）·（0，-m，m）=0，

故⊥，⊥，即AD⊥EF，AP⊥EF，又AD∩AP =A，

∴ EF⊥平面PAD.

（2）（方法一）：设此棱锥的棱长为2m，则PE=m.

∵ 侧面积与体积的比值为，

故==，解得m=1，∴ PE=.

以E为原点，以AB中点、CD中点所在的直线为x轴，以BC中点、AD中点所在的直线为y轴，以EP所在的直线为z轴，建立空间直角坐标系E-xyz，如图27.

∴ B（1，1，0），设G（-？姿，？姿，（1-？姿））（0≤？姿≤1），直线BG与平面PAD所成角为？兹.

则=（-？姿-1，？姿-1，（1-？姿）），由（1）知：=（0，-，）为平面PAD的法向量，

故sin？兹=cos〈，〉

==·.

令f（？姿）=（0≤？姿≤1），则

f ′（？姿）=<0，故f（？姿）在[0，1]上单调递减，故f（？姿）∈[0，1]，所以sin？兹∈[0，].

（方法二）：如图28，连接DB，由（1）中方法一知：EF=，

故点B到平面ADP的距离为dB-ADP=2EF=.

当点G与点P重合时，设直线PB与平面PAD所成角为？兹1，则sin？兹1==;

当点G与点C重合时，BG∥平面PAD，线面角的正弦值为0.

因点G由点P移至点C时，直线PB与平面PAD所成角由大变小，直至变为0. 故sin？兹∈[0，].

『练习（好题重做，江门市2021年一模试题）』

如图29，四边形ABCD为菱形，四边形BDEF为平行四边形，FA=FC，AB=2，∠DAB=60°.

（1）求证：AC⊥BF;

（2）若FB=FD，且二面角E-AF-B为135°，求多面体ABCDEF的体积.

【答案】（1）略;（2）2.

通过以上分析可以看出，对具体的空间事物的情境认知并进行分析问题与解决问题的能力，在高考中主要通过立体几何这道大题来考查. 在高三进行完一轮复习后，重点应抓住平行与垂直的推理论证及三角一积的计算求解，练就熟知解题思路，把握关键图形，透析位数（位置与数量）关系，选择高效方法，准确快速作答. 总而言之，那就是夯基熟五音三角，择法奏证算乐章.

责任编辑 徐国坚