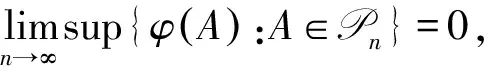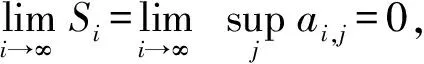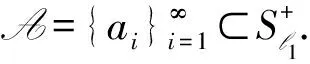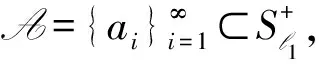半范数pA的特征
2021-11-16施慧华
施慧华
(华侨大学 数学科学学院,福建 泉州 362021)
1 pA的特征
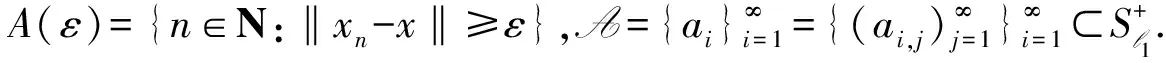

对于定义1中的序列A={ai},文献[9]定义了l∞上的连续半范数pA,即
并利用次微分证明了A-收敛等价于一族有限可加测度收敛.
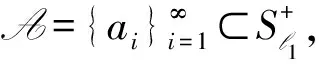
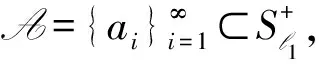
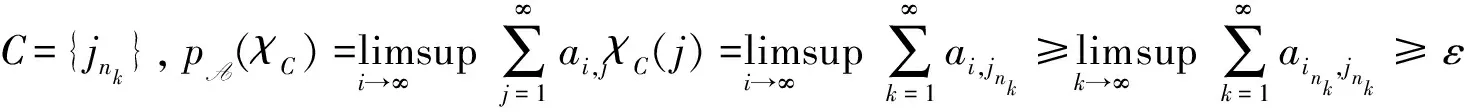
必要性.设pA(χB)=α>0.当β=0时,取C为B的任一单点子集,当β=α,取C=B.证明当0<β<α时的情况.记B={j1,j2,…,jk,…}⊆N,则
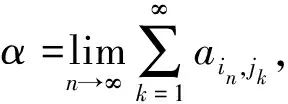
构造以下3个满足需要的数列.
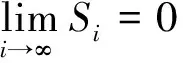
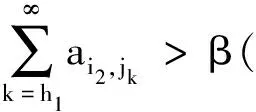
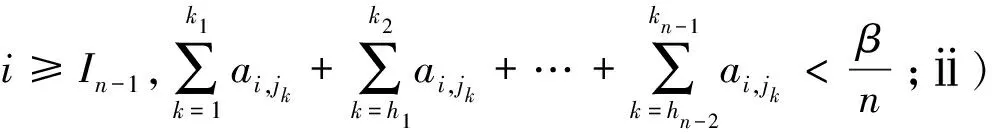
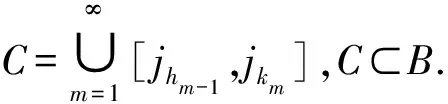
当in≤i 结合定理2及性质1,有以下推论. I⊂2N称为N的一个理想,如果I满足1)可遗传性:任意B∈I,则由A⊂B,可得A∈I;2)有限并的封闭性:任意A,B∈I,A∪B∈I.称Banach空间X中的序列{xn}I-收敛于x,若对任意ε>0,{n∈N:‖xn-x‖≥ε}∈I,当I为非平凡的真理想,即I≠Ø,且N∉I时,可得x的唯一性.若I包含所有单点集,称I是容许的.I-收敛由文献[12]提出,特别地,当I=Ifin={A⊂N:A#<∞}时,I-收敛即为收敛. 若记IA={A⊂N:pA(χA)=0},则根据pA的次可加性可知,IA是真理想.对B⊂N,由性质1可知,pA(χB)=max{〈x*,χB〉:x*∈∂pA(e)},记φA(B)=pA(χB),结合pA的非负性、单调不减和次可加性,可得φA是2N上的一个次测度(详细讨论参见文献[13-15]). 定义2[14]次测度φ是强无原子的,对于任意ε>0,存在N的有限分划{A1,…,Ak}满足φ(Ai)<ε(i=1,2,…,k). 定义3[14]理想I⊂2N称为是无原子的,若存在N的一列加细的有限分划{Pn},对任意Z⊂N,若存在单减序列{An},满足An∈Pn(∀n∈N),且(ZAn)#<∞,则有Z∈I. 文献[11]定义的BW和FinBW可以推广至Banach空间中. 定义4ⅰ)称理想I满足BW,若对任意有界序列{xn}⊂X,存在M∉I,则{xn}n∈M是I-收敛的; ⅱ)称理想I满足FinBW,若对任意有界序列{xn}⊂X,存在M∉I,则{xn}n∈M是收敛的. 显然,对容许的理想I,I满足FinBW时,必满足BW,反之,不成立,但对定义的IA有以下结论. 定理3若IA是容许的理想,则IA满足FinBW,当且仅当IA满足BW. ⅰ)B∈IA.这是由于B∩[1,jk]⊂C1∪C2∪…∪Ck,从而当ik≤i ⅱ)(MB)#=∞.如若不然,(MB)#<∞,则有MB∈IA,又B⊂M,B∈IA,故M=(MB)∪B∈IA,矛盾. 结合MB∉IA和{xn}n∈MB收敛于x,可知IA满足FinBW. 定理4[11]若φ为强无原子的次测度,则理想Z(φ)={A⊂N:φ(A)=0}不满足BW. 定理5[11]理想I不满足FinBW,当且仅当I是无原子的. 对IA,结合定理3,4,5,则有定理6. 即B∉IA,矛盾.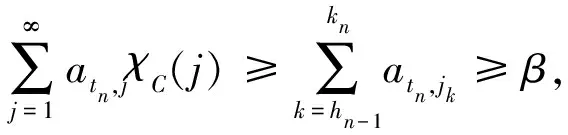
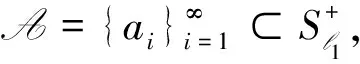
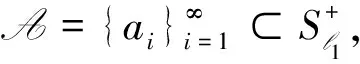
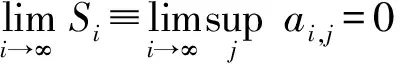
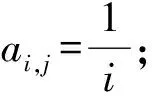
2 强无原子次测度与无原子理想