考虑下垫面复杂性的行人风环境评估
2021-11-16邓建勋李司冉张祥敏胡海涛钱长照陈昌萍
邓建勋,李司冉,,张祥敏,胡海涛,钱长照,陈昌萍,
(1.厦门大学 建筑与土木工程学院,福建 厦门 361005;2.厦门理工学院 风灾害与风工程福建省重点实验室,福建 厦门 361024)
随着我国城市的快速发展,下垫面的复杂程度越来越高,建筑物和地形的改变易引发行人风环境的不舒适问题.目前,风洞试验被广泛应用于行人风环境的研究中,陈德江等[1]利用风洞试验研究某高层建筑周边群体建筑群的风环境,结果表明,建筑风环境满足舒适性条件;马文勇等[2]利用风洞试验对群体建筑周边风环境进行研究,发现群体建筑的夹缝与角区的风速值较大;关吉平等[3]通过风洞试验研究群体建筑风环境的干扰效应,得到高层建筑建成后尾流区对周边风环境的影响结果;唐春朝等[4]利用风洞试验研究高耸建筑对周边小区风环境的影响,发现高耸建筑的建设降低了小区风环境的舒适度.然而,目前风洞试验研究城市风环境选取的研究范围较小,地表特征均为城市平坦区域,忽略了城市地形对风环境的影响.同时,试验得到的风环境变化规律需要进行进一步评价分析,学者们主要采用超越阈值概率法进行评估.陈勇等[5]对超越阈值概率的风环境评价标准作出统一划分;李朝等[6]综合考虑阵风效应,利用超越阈值概率法对复杂建筑的行人舒适度和危险度作出评价;文献[7-10]利用超越阈值概率法,评价研究区域的行人风环境舒适度.在前期对气象数据的处理中,研究者默认采用双参数Weibull分布对超越阈值概率进行计算,并没有考虑双参数Weibull分布与实际风速概率分布的拟合程度.
针对目前研究的不足,本文以福建省厦门市某桥址区为研究对象,建立较大范围的地形和城市建筑物叠加的风洞试验模型,对桥址区风环境变化作出精确判断;利用极大似然估计法估算三参数Weibull分布的位置参数[11-14],并对气象数据进行拟合;引入带有位置参数的三参数超越阈值概率计算公式,对人行桥桥面的行人风环境进行评估.
1 复杂下垫面风洞试验
1.1 试验模型及风洞概况
采用风洞试验研究福建省厦门市某桥址区风环境.建立地形-建筑物耦合模型,模型以桥址为中心,选取2.5 km直径范围内的地形及建筑物制作几何模型,地形区域内有两座山,海拔分别为212,139 m.模型缩尺比为1∶600,阻塞率均小于5%.试验模型,如图1(a)所示.试验在厦门理工学院XMUT-WT风洞实验室低速试验段进行,数据采集采用移测架和TFI眼镜蛇三维脉动风速仪相结合的方式;试验风场采用B类风场和均匀场作为来流条件.B类风场采用尖劈和粗糙元调试,如图1(b)所示.模拟的平均风速剖面和湍流度剖面,如图2所示.图2中:h为风洞试验边界层高度;v为平均风速;I为湍流度.

(a)试验模型 (b)风场调试
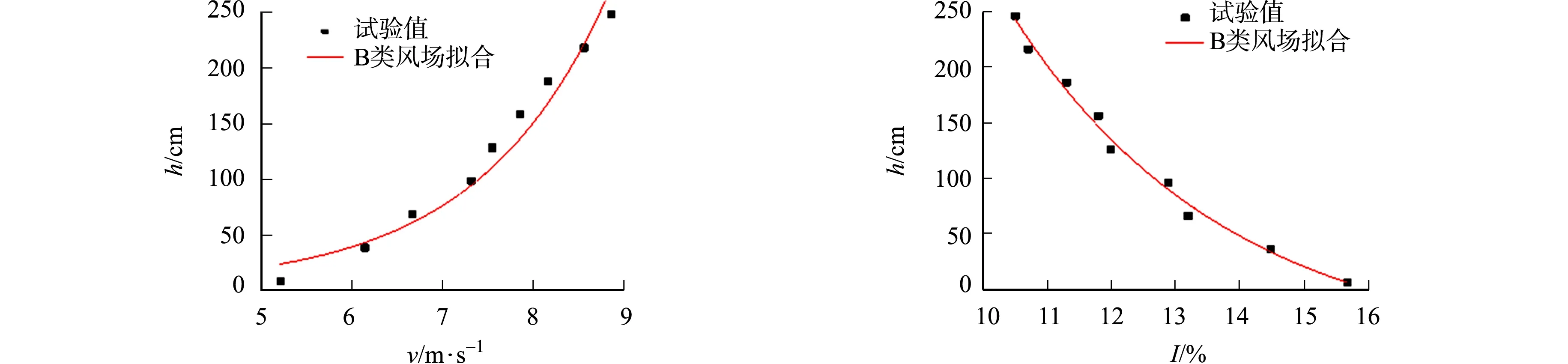
(a)平均风速 (b)湍流度
1.2 计算工况及测点布置
该人行桥梁为曲线悬索桥,曲线桥全长为216.7 m,桥轴线长为202.2 m,桥梁轴线与水平(东西方向)成38°,桥面高度距离地面34.52 m.结合两座山体位置及建筑物排布影响,以正北为第1个工况,角度间隔45°为1个工况,共设置8个工况.
桥址位置,如图3(a)所示,在桥面设置9个监测位置.同时,对桥址所处的城市街道及山体布置测点,监测街道风环境变化,监测位置,如图3(b)所示.

(a)桥址位置 (b)山体、城市街道监测位置
1.3 试验结果及分析
Ri=vi/v0.
(1)
城市街道是城市内部的通风廊道,容易形成街道峡谷风.均匀场和紊流场下,桥面行人高度处与街道同高度处的风速比散点分布图,如图4所示.图4中:Ru,Rf分别为均匀场和紊流场的风速比.
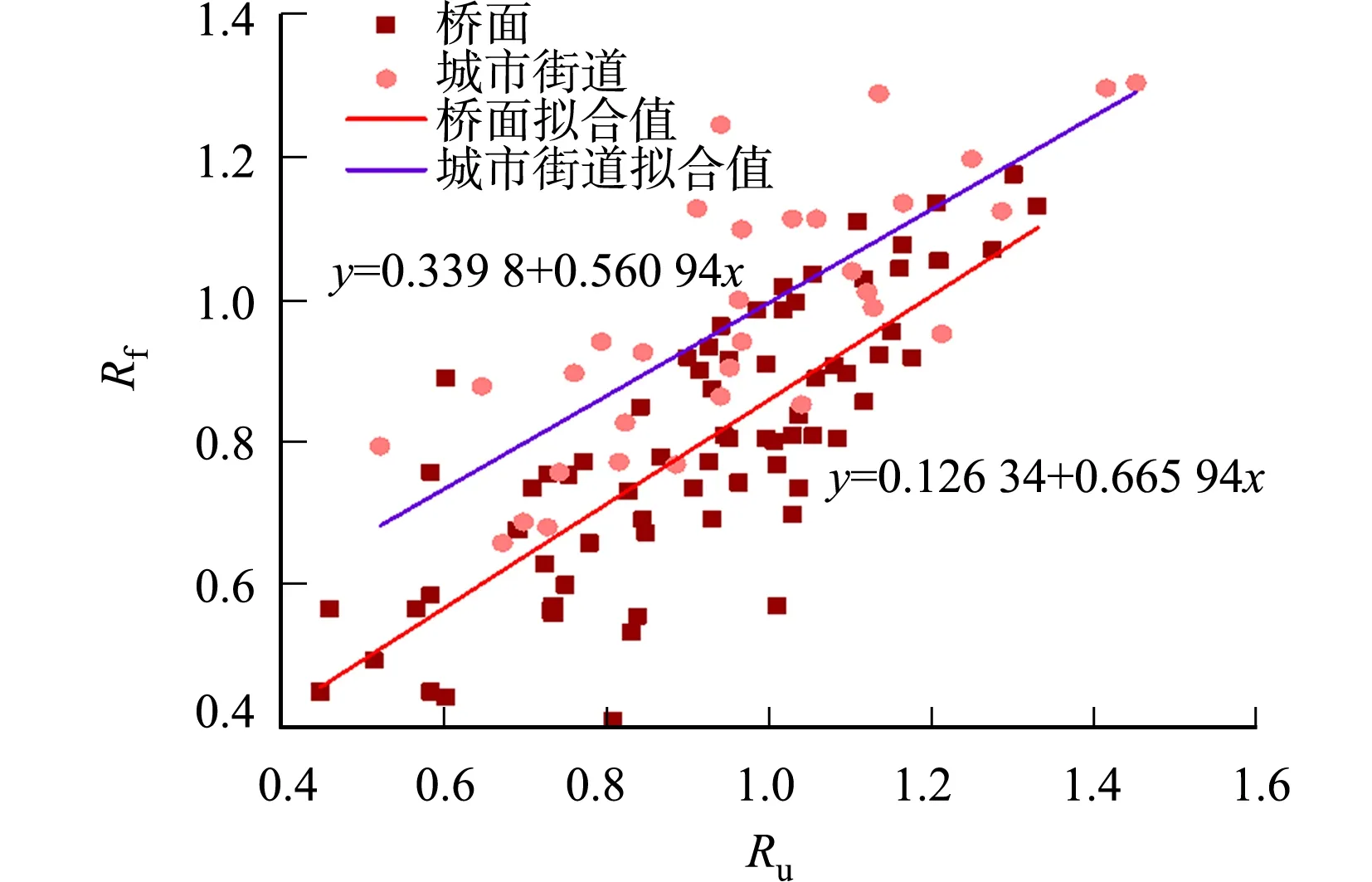
图4 风速比散点分布图
由图4可知:均匀场和紊流场风速比变化基本一致,线性拟合斜率在0.56~0.66之间,证明了风洞试验数据的真实可靠性;而桥面行人高度处风速比拟合线段在城市街道同高度处风速比拟合线段下方分布,说明该桥址区在部分风向下不是风速放大区域,主要原因是城市建筑物及山体对风速的阻挡效应.
为了了解不同工况下桥面行人高度处风速比的变化,选取受城市冠层影响较大的0°和180°工况及受山体影响的90°和270°工况进行分析,结果如图5所示.由图5可知:0°和180°工况下,桥面行人高度处风速比最大值为1.18,最小值为0.43,受城市下垫面阻挡效应影响,桥面行人高度处风速比整体较小,风速比大于1的情况是受街道峡谷风影响;90°和270°工况受山体影响下,桥面行人高度处风速比基本均小于1.桥址的起点和终点均在山脚位置,山脚处为平均风速的减速区域.
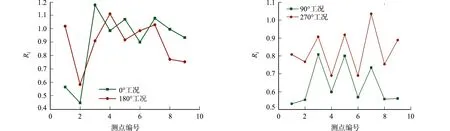
(a)0°和180°工况 (b)90°和270°工况
1.3.2 复杂下垫面影响下的平均风速剖面 桥址区风速剖面受下垫面地表特征影响,风速变化情况不同.不同工况的平均风速剖面,如图6所示.图6中:H/Hr为无量纲化高度;v/vr为无量纲化平均风速.
由图6可知:0°和180°工况的平均风速剖面与来流风速剖面有较大差异,0°工况由于城市主要街道入口与来流夹角较小,桥址区前方没有建筑物的遮挡而形成街道峡谷风,使平均风速增大,而180°工况由于地表建筑物的拖曳作用,在无量纲高度为0.35下风速减小,当无量纲高度大于0.35时,风速剖面重现出指数率剖面;90°和270°工况下,平均风速均小于来流风速,说明山体遮挡作用下桥址区为平均风速的减速区域.

(a)0°工况 (b)180°工况
山体典型位置的平均风速剖面变化,如图7所示.图7中:s为测点到山体边缘的距离.两座山体背风面及迎风面山脚处均为平均风速的减速区域.当不同山体前后排列时,山脚处的平均风速减速效果不同.海拔较高、坡度较陡的山体正对来流时,山顶风速的急剧增大,导致270°工况下山脚处的平均风速均大于90°工况下山脚处的平均风速.
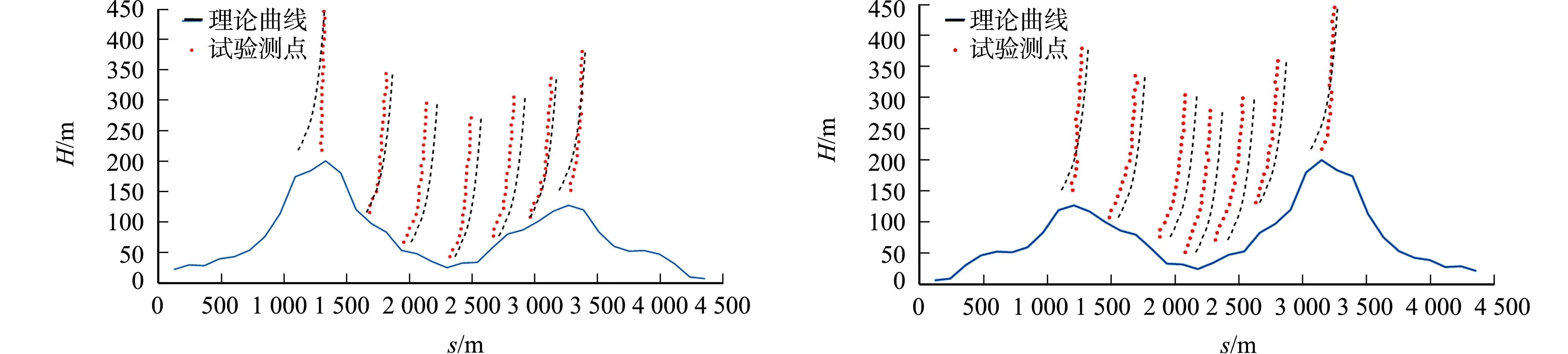
(a)270°工况 (b)90°工况
为了量化平均风速剖面与入流风速剖面的变化,利用最小二乘法拟合不同风向角(θ)下的风速剖面指数(λ),结果如表1所示.由表1可知:在地形和建筑物影响下,风速剖面指数均不满足规范要求,该桥址区地表粗糙度类型更接近C类地表;0°,90°,180°和270°工况的风速剖面指数变化最为明显,0°和180°工况的风速剖面指数增大分别受街道峡谷风和地表建筑物拖曳作用的影响,90°和270°工况的风速剖面指数变化是受山体影响.
按照国家疾病ICD-10分类标准进行死因调查及填写,育龄期死亡妇女具体资料采取EXCEL表格实施汇总和统计。

表1 不同风向角下的风速剖面指数
1.3.3 复杂下垫面影响下的湍流度 湍流度反映脉动风对行人风环境的影响.对桥址区湍流度进行监测,不同风向角的湍流度剖面,如图8所示.
由图8可知:0°和180°工况下,当无量纲高度小于0.6时,其湍流度均大于来流风场的湍流度,原因是试验模型改变了地表粗糙度,增大了湍流度;180°工况下出现湍流剪切区域,考虑为建筑群较大且较密集,导致高湍流度的出现;山体影响下,90°和270°工况下,桥址区均为湍流的放大区域.
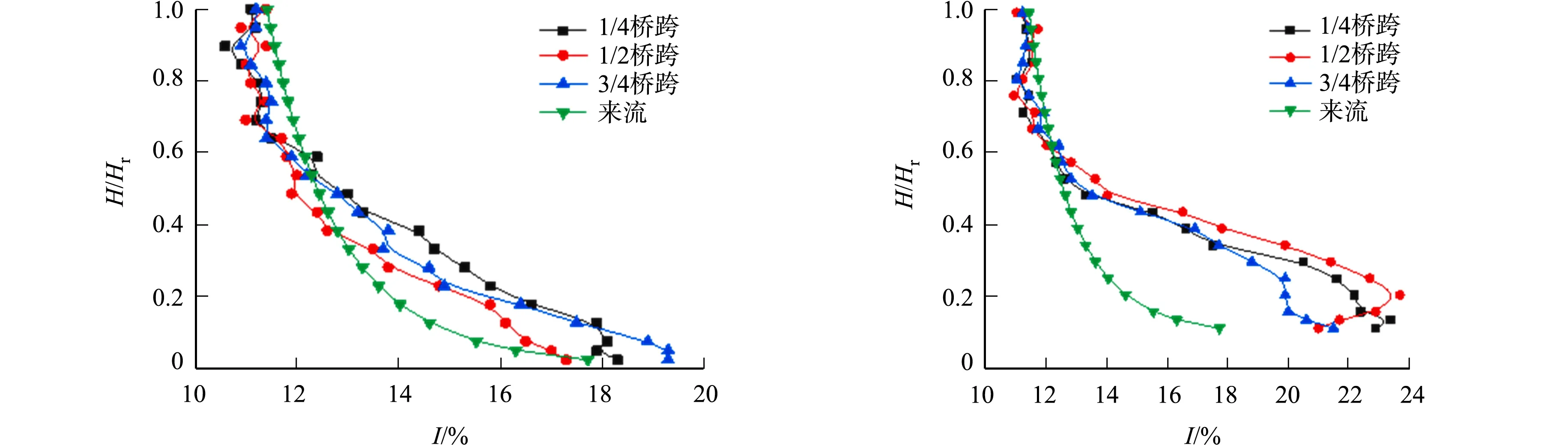
(a)0°工况 (b)180°工况
不同风向角下的湍流度剖面指数(α),如表2所示.由表2可知:受地形和建筑物影响,湍流度剖面指数均大于规范规定的B类地表粗糙度指数;山体影响下的湍流度变化最为明显,因此,在研究人行桥桥址风环境变化时,必须考虑地表粗糙的影响.

表2 不同风向角下的湍流度剖面指数
2 三参数超越阈值概率评估
2.1 人行桥风环境评价指标
基于不同的行人风环境评价标准,根据行人步行活动状态进行行人高度风环境评价标准统计,如表3所示.表3中:vTHR为风速阈值;Pexc为超越阈值概率.行人的步行状态可分为漫步、正常行走、目的性行走3类.对桥面行人高度风环境的评价也从3类步行状态展开.

表3 行人高度风环境评价标准
利用超越阈值概率法评估桥面人行高度风环境,若满足Pexc≤Pcom,Pcom为相应标准中规定的概率值,则认为该区域的行人风环境满足舒适度要求.
基于超越阈值概率的风环境评价方法需要满足2个条件:研究区域的风场分布规律和当地常年风向风速统计数据.根据不同风向的风速概率分布确定超越阈值概率计算的相关参数.研究区域的风速概率分布采用Weibull分布拟合,确定尺度参数和形状参数以计算Pexc,计算式为
(2)
式(2)中:cθ和kθ分别为Weibull分布的尺度参数和形状参数;Aθ为该风向角出现的频率.
2.2 超越阈值概率的参数估计优化
利用Weibull分布对厦门市59134气象站点2011年1月至2020年9月逐小时风向风速数据进行拟合.Weibull参数估计结果,如表4所示.表4中:vmean为气象平均风速;γθ为位置参数.
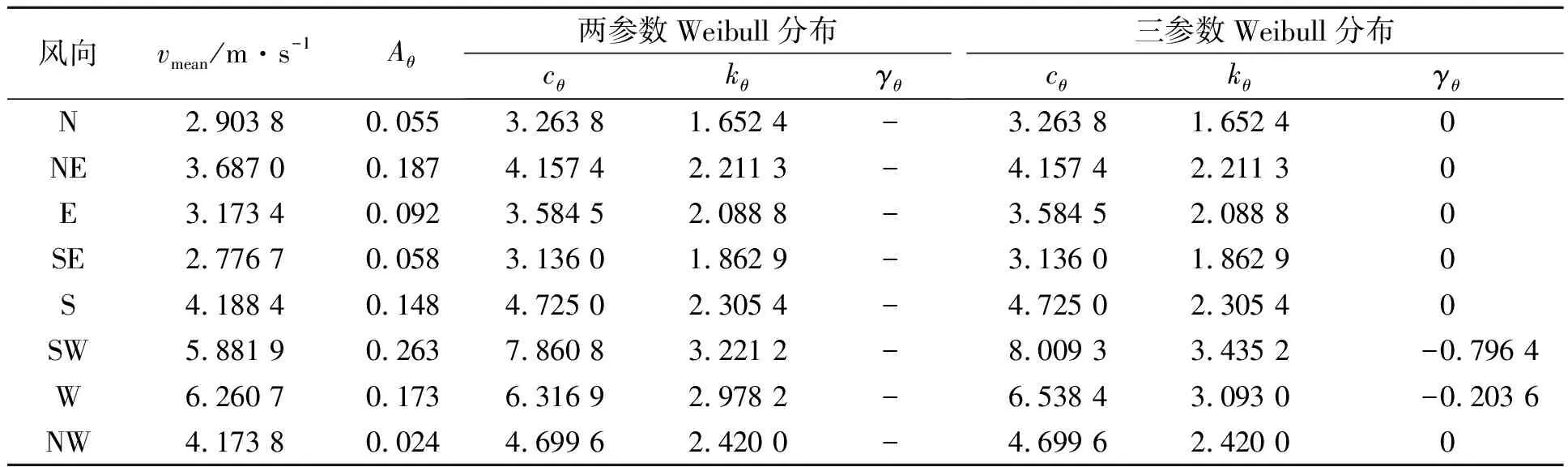
表4 Weibull参数估计结果
由表4可知:采用两参数和三参数Weibull分布拟合时,SW和W风向下的尺度参数和位置参数不同,其余风向下的尺度参数和位置参数均相同.
位置参数的作用是使拟合函数左右平移,因此,位置参数会影响不同风速的拟合程度.选取SW风向对不同平均风速的实际概率分布与两参数Weibull、三参数Weibull拟合概率分布进行对比,结果如表5所示.由表5可知:利用三参数Weibull拟合概率分布值与实际下垫面影响得到的风速概率分布更接近,三参数Weibull拟合误差比两参数拟合误差小38.74%.因此,对SW和W风向的概率分布采用三参数Weibull拟合,以增加行人风环境评估的准确性.
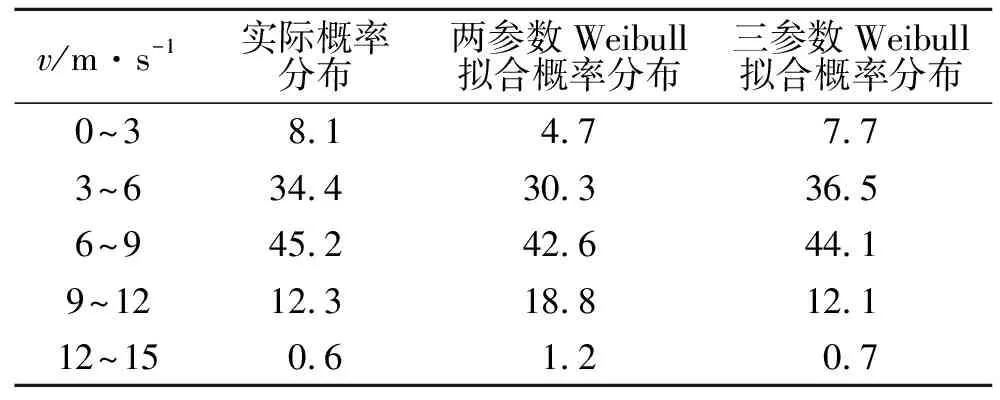
表5 概率分布对比
根据该现象引入三参数计算的超越阈值概率Pexc计算公式[18],即
(3)
2.3 不同步行状态下的评价结果
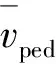
(4)
桥址区风速阈值vTHR与气象站点风速vO,i,THR之间的关系式为
(5)
将式(5)代入式(2),(3)中,得到该区域全风向风速超越阈值概率,即
(6)
针对行人在桥面不同的步行状态,不同评价标准对满足舒适度超越阈值概率的临界值不同,因此,引入超越阈值概率的相对系数p,即
p=Pexc,i/Pcom.
(7)
式(7)中:Pexc,i为测点i的全风向超越阈值概率.
将不同评价标准下的各测点全风向超越阈值概率进行统一,其相对系数,如表6所示.表6中:p1~p9分别为测点1~9的全风向超越阈值概率的相对系数.由表6可知:Isyumov and Davenport标准对行人舒适度的要求最严格,其余标准的下桥面行人风环境均满足舒适度要求;位于桥面起点和终点附近处的测点1,2,8,9的超越阈值概率相对系数较小,这是由于山体地形对风速的阻挡降低了风速比的大小,提高了桥面两端位置处的舒适度;跨中位置处的超越阈值概率约为桥址两端超越阈值概率的两倍,主要原因是跨中位置受街道风加速效应明显,因此,在桥面跨中位置需要防范街道峡谷风给行人带来的不舒适感.
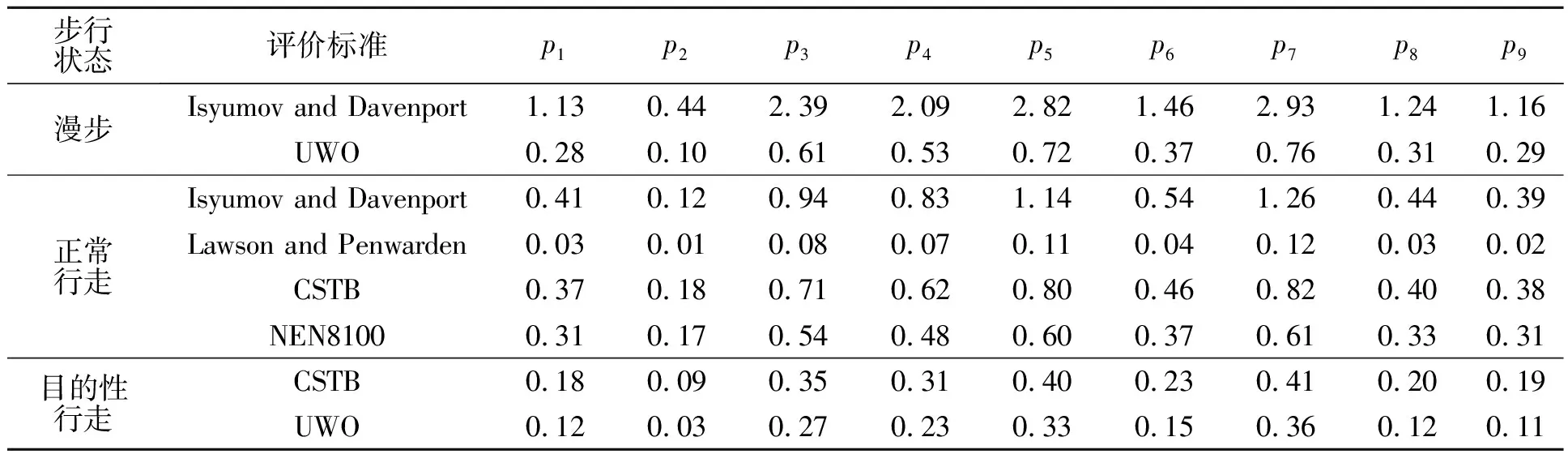
表6 各测点全风向超越阈值概率的相对系数
3 结论
利用风洞试验研究复杂下垫面影响的桥址区行人风环境,并利用三参数超越阈值概率对行人舒适度进行评价,得到以下3个结论.
1)下垫面改变了桥址区的地表类型,试验得到的风速和湍流度剖面指数均大于规范规定的C类地表值;行人风速比受不同下垫面影响,表现出街道峡谷风加速、建筑物拖曳作用和山体减速效应明显.
2)三参数Weibull分布拟合结果与真实下垫面中气象站点得到的风速概率分布相接近,相比两参数Weibull分布,其拟合误差减小了38.74%.
3)城市下垫面中山体的遮挡效应导致风速减小,增加了行人在山脚处的步行舒适度;受城市街道风加速效应影响,桥面跨中处超越阈值概率约为桥址起点和终点值的两倍.在实际工程建设中,需要防范桥面跨中处可能引发的行人风环境不舒适感,可以通过在桥面跨中位置设计挡风屏障降低行人风环境不舒适感.
