稀疏低秩协同正则优化及航空轴承故障诊断
2021-11-16张晗王兴田毅林建波杜朝辉
张晗, 王兴, 田毅, 林建波, 杜朝辉
(1.长安大学工程机械学院, 710064, 西安; 2.长安大学道路施工技术与装备教育部重点实验室, 710064, 西安; 3.西北工业大学航海学院, 710072, 西安)
航空发动机是飞机的“心脏”,高速、高温、重载和强扰动等极端恶劣环境导致其关键零部件的性能不可避免地发生衰退,带来高昂的全生命周期维护费用,甚至导致灾难性事故的发生[1]。主轴轴承作为传动系统关键零部件,极易发生疲劳、磨损、腐蚀、打滑和滑蹭损伤等故障,而一旦发生故障,轻则导致转子振动增大,重则导致发动机转子抱死、空中停车甚至机毁人亡的严重事故[2]。因此,及时有效地诊断航空高速轴承早期微弱故障,对于降低发动机全生命周期维护成本,避免灾难性事故的发生具有重要意义[3]。
航空轴承早期微弱故障特征辨识一直是国内外学者研究的热点。2015年,法国航空发动机制造商赛峰公司面向全球发起发动机轴承故障诊断的竞赛,诊断专家Antoni等参与竞赛并对竞赛情况进行了综述,指出航空发动机轴承故障诊断是最具挑战性的任务之一[4]。在国内,南京航空航天大学、西北工业大学、重庆大学、中国民航大学等学者对发动机轴承动力学行为建模以及故障诊断方法进行了深入研究[5-8]。研究结果表明,航空轴承相比于传统的地面旋转机械轴承,其振动测点安装受限,通常安装于远离轴承的承力机匣上,使得故障动态响应受到复杂传递路径调制。另一方面,由于发动机结构复杂,机匣上传感器感知的信号成分多样,不仅包含微弱的轴承故障特征,还包含高低压转子旋转振动频率、叶片的激振频率、附件机匣中各传动部件的共振频率、流体动力噪声、燃烧室燃烧噪声等。因此,从整机振动信号中辨识轴承故障特征信息,犹如大海捞针,如何从测试信号中抑制多源噪声的干扰、提取微弱故障特征是航空轴承故障诊断的关键[9]。
通过探索故障特征的固有本征模式,构造有效的先验正则约束,为微弱特征辨识问题提供了有效手段。近年来,基于稀疏先验的特征辨识技术受到了国内外学者的广泛研究。稀疏特征辨识技术的核心思想是构造与故障特征结构相匹配的先验正则和稀疏表示字典,建立特征的稀疏分解模型,进而通过优化迭代算法实现特征的提取。在稀疏先验正则研究方面:2016年,Zhang等建立了特征敏感性指标和稀疏系数衰减率的桥梁,构建了加权稀疏正则模型[10];2019年,Zhao等揭示了轴承故障特征的组内组间稀疏先验,并提出了自适应增强组稀疏模型,实现了轴承冲击特征的可靠辨识[11];2019年,Wang S等提出了广义极小极大凹函数正则消噪算法,以克服经典稀疏正则消噪算法对稀疏系数幅值造成损失及稀疏约束能力减弱问题[12]。在稀疏字典构建方面:2019年,Sun等构造了等角紧框架约束下的参数化Laplacian小波字典,以解决较高冗余度字典的病态问题[13];2021年,Jiang等提出利用编辑倒谱构建冲击特征的稀疏表示字典,可自适应从数据中获得字典原子的物理参数信息[14]。然而,这些模型多建立在高斯白噪声的统计假设之上,而航空发动机振动信号由于干扰源众多,干扰信号不再满足高斯白统计假设。针对这一问题:2018年,Cai等提出基于广义极小极大凹函数的形态成分分析模型,分别构造离散余弦字典和短时傅里叶字典实现谐波成分和冲击特征的解耦[15];2018年,Yang等基于故障响应机理以及相关滤波法,分别构造平稳信号调制字典和冲击调制字典[16];2020年,Qin等提出基于傅里叶字典的改进正交匹配追踪算法,首先滤除谐波,然后通过一维K-SVD字典学习提取瞬态冲击故障特征[17]。综上所述可知,目前基于稀疏先验的特征辨识技术从波形的差异性角度出发,致力于寻求故障特征信息的稀疏表示空间,然而由于故障特征信息和谐波干扰信号在时域内具有固有的耦合相关特性,使得在时域内构造出的特征稀疏表征字典往往对干扰信息也具有较强的稀疏表征能力,降低了故障特征的辨识精度。
近年来,相关学者探索了故障特征的二维结构化先验。2017年,Du等分析了轴承故障特征的空间相似性,揭示了故障特征在特定二维空间的低秩特性,并随后分别提出了基于核范数的加权低秩优化算法以及低秩驱动的稀疏解卷辨识算法[18-19];2018年,Xin等构造了冲击故障特征的稀疏正则约束和低秩正则约束[20];2020年,陈礼顺等利用低秩分解算法实现了航空锥齿轮的故障诊断[21];2020年,Zhang等揭示了航空高速轴承混叠变异的隐冲击模式,并提出了聚类低秩优化算法[22];2020年,Wang B等揭示了故障特征二维时频矩阵的周期组稀疏先验和低秩先验,提出了周期稀疏低秩矩阵估计算法[23];2020年,Yu等提出基于稳健主成分分析的瞬态特征辨识算法,利用特征矩阵的F范数和核范数来协同描述特征矩阵的低秩先验[24]。然而,低秩矩阵辨识的核心是主成分分析,该方法仅在干扰信息具有高斯白统计特性时有效,难以实现强谐波干扰下的特征辨识。
针对这些问题,本文通过分析非高斯噪声干扰信号和特征信号在不同变换空间的固有本征模式,揭示了谐波干扰信号在傅里叶变换域的稀疏先验以及轴承故障特征在特定二维空间的低秩先验,进而提出稀疏低秩协同正则优化模型,并开发了基于块坐标优化框架的模型求解算法,实现了轴承故障特征、谐波干扰信号以及噪声信号的解耦。仿真算例和航空轴承故障实验分析验证了算法的有效性。相比于目前的特征辨识算法,本文提出的模型联合了稀疏分解和低秩分解的优势,不再从波形的差异性角度出发,而是考虑故障信号和干扰信号在不同空间维度的结构差异性,将两类信号分别在两个完全不耦合的空间进行表示和正则,解决了目前稀疏分解算法难以构造高度不耦合字典的瓶颈问题,提高了故障特征的辨识精度。
1 先验正则
航空轴承故障动态响应通常受到强噪声、强谐波的干扰。因此,可对传感器采集的信号建立数学模型
y=x+h+n
(1)
式中:y∈m×1为观测信号;x∈m×1为一维向量形式的轴承局部故障特征信号;h∈m×1为强谐波干扰信号,该干扰信号来源于发动机转子、风扇叶片、附件机匣齿轮传动链等运动部件;n∈m×1为噪声干扰信号。从y中提取特征信息x是一个高度病态欠定问题,稀疏正则理论通过构造匹配的正则化约束来缩小解空间,可有效地消除其病态欠定性。本节将重点分析特征信号x和谐波干扰信号h在不同变换空间中的固有本征模式,进而构造匹配的正则化约束。
首先,为了增强特征信息的显著性,分析其在二维低秩空间中的分布模式,设计低秩先验正则约束。根据轴承故障动力学理论,轴承局部故障动态响应特征x可建模为
(2)
式中:g(t)表示系统的单位脉冲响应;fc为轴承故障特征频率;Ω=2πξfd为衰减系数,其中ξ为系统相对阻尼系数;fd为系统的固有频率;φ(i)表示第i个冲击响应的初相位。
由于特征向量x具有准周期特性,每一个故障周期内的局部振荡波形具有高度的相似性,因此构造分块算子R:m×1→M×S,其中M为分块算子窗长,S为信号子块数,分块算子如图1所示。
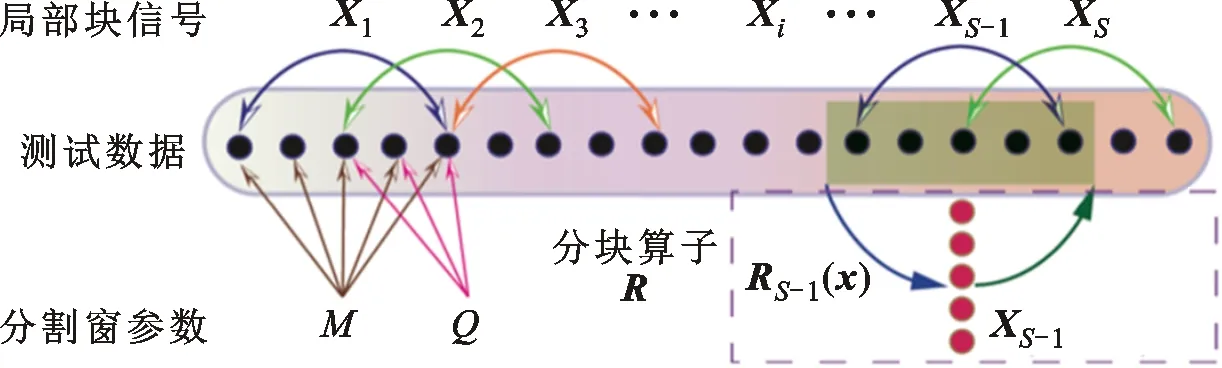
图1 分块算子Fig.1 Partition operator
分块算子可将一维的特征向量x转换为二维的特征矩阵
X=R(x)
(3)
式中X=[X1,X2,…,XS]∈M×S,Xi∈M×1代表矩阵X的第i列。分块算子窗长M设置为
(4)
式中:fs/fc为一个故障周期的采样点数;Q为分块算子的重叠长度,用于消除分块算子端点处的不连续性问题。
利用分块算子R对测试信号各个子成分做相同的处理,则一维的观测信号模型式(1)可转换为
Y=X+H+N
(5)
由于分块算子的长度和故障特征信号x的故障周期采样点数相匹配,而与干扰信号h和n的周期不匹配,所以特征矩阵X中的列向量具有高度的相似性,同时矩阵H和矩阵N中的列向量不具备相似性。从矩阵分析理论的角度,列相似的矩阵为低秩矩阵,因此特征矩阵X为低秩矩阵,而干扰矩阵H和N为非低秩矩阵,进而可通过奇异值分解(SVD)技术把潜在的相似特征投影到主子空间
(6)
式中:U=[u1,u2,…,uM]∈M×M是左奇异正交矩阵;V=[v1,v2,…,vS]∈S×S为右奇异正交矩阵;Σ=diag(σ1,σ2,…,σM)是奇异值矩阵,{σi}为奇异值序列,满足σ1≥σ2≥…≥σM≥0,该序列的大部分元素为0,具有稀疏特性。同时,矩阵H和N由于不具备低秩特性,其奇异值分解后,奇异值序列呈现出稠密的均匀分布模式。两类信号的秩分布模式和差异性如图2所示,图中a为信号幅值。可以看出,特征信号的奇异值主要集中在序列的初始阶段,因而可通过设计算子保留初始的大奇异值来增强特征信息。

图2 观测信号各成分奇异值分布模式Fig.2 Singular value distribution of each component of observation signal
基于秩分布的差异性,采用核范数来表征故障特征矩阵X的低秩先验
rank(X)≈‖X‖*
(7)
式中‖X‖*为矩阵X的凸核范数,定义为
(8)
核范数‖X‖*本质上是奇异值序列的1范数,刻画了特征矩阵X的奇异值序列具有的稀疏分布结构,最小化该核范数可有效提取观测信号中的低秩信息。
另一方面,为了抑制强干扰信号,基于其频谱结构的高度稀疏特性,设计谱稀疏先验正则。发动机转子、风扇叶片旋转产生强谐波干扰,可建模为多阶次线谱叠加信号
(9)
式中:{fi}为旋转部件的基频分量;l为高阶谐波干扰频率的阶数。假设D为正交傅里叶变换字典,则线谱信号h经傅里叶字典变换后,傅里叶系数为可表示为
(10)

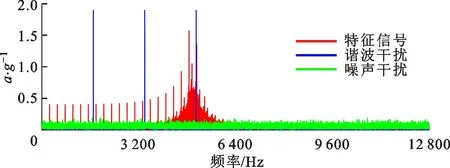
图3 观测信号各成分在频域内的稀疏分布结构 Fig.3 Sparsity structure of each signal component in frequency domain
由此,建立谐波干扰信号在一维正交傅里叶变换空间的稀疏先验正则
(11)
2 模型及算法
2.1 稀疏低秩协同正则模型
基于特征信号在二维空间的核范数正则约束和谐波干扰信号在一维傅里叶变换域内的凸稀疏正则约束,本文提出了如下的稀疏低秩协同正则模型
(12)
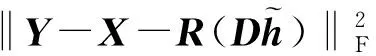
2.2 优化求解器
在广义块坐标优化求解框架下,本小节推导模型式(12)的优化求解算法,即为本文提出的稀疏低秩协同优化算法CSLA。

(13)
基于块坐标框架,模型式(13)的增广拉格朗日函数可表示为
(14)
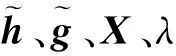

(15)
该优化问题本质上是一个平滑的最小二乘问题。因此,可获得闭式解
(RD)T(Y-X(k))]
(16)
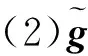
(17)
(18)
式中prox(·)表示临近点函数,且对于任何向量和阈值参数τ,具有
prox(υi;τ)=sgn(ti)⊙max(|υi|-τ,0), ∀i
(19)
其中⊙表示向量或矩阵逐点运算操作。
(3)X子问题可以抽象为
(20)
式中核范数‖X‖*是凸可微的,因此该式可看做是该核范数的临近点算子,其闭式解为
(21)
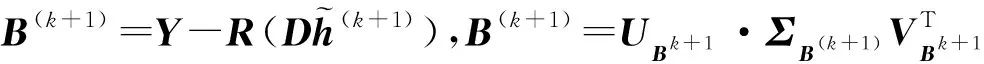
(4)拉格朗日乘子λ更新可以抽象为
(22)
最后,对这4个子问题重复迭代直至算法收敛或达到最大迭代数K,迭代收敛准则为
(23)
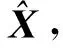
(24)
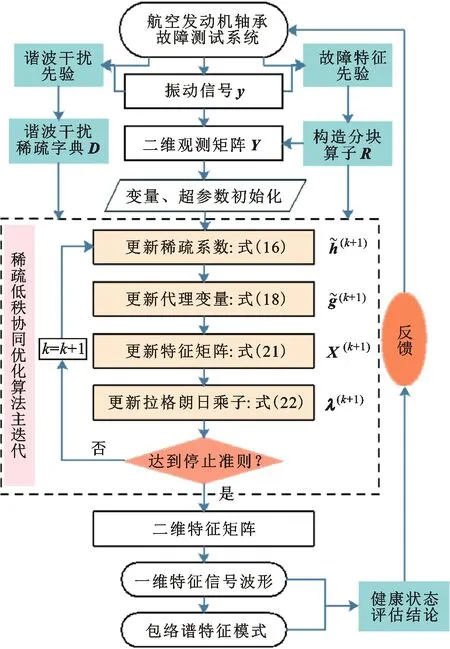
图4 稀疏低秩协同优化算法流程Fig.4 Flowchart of the proposed collaborative sparse low-rank algorithm
3 仿真分析
本节通过数值仿真实验来评估提出算法的有效性。基于信号生成模型式(2)(9),同时考虑到系统测试信号中不可避免的白噪声干扰n(t),仿真信号可表述为
y(t)=x(t)+c1h(t)+c2n(t)
(25)
式中c1、c2为常数,用于调节3类信号之间的相对能量比。
仿真信号采样频率为25 600 Hz,采样时间为1 s,轴承故障特征频率为512 Hz,系统固有频率fd为5 000 Hz,衰减系数Ω=2 000,谐波干扰信号基频为f1=900 Hz,最高阶数为l=3,谐波干扰系数c1=1,噪声干扰系数c2=1,噪声方差σ=0.5g2。仿真信号的信噪比为-4.739 dB,信干比为-13.159 dB。

(a)时域波形

(b)局部细化时域波形

(c)包络谱图5 仿真信号及其谱分析Fig.5 Simulation signals and its corresponding spectrums
仿真信号时域波形及其谱分析如图5所示。理论上,局部细化时域波形图5b应包含10个完整的冲击周期,实际上从图中可以发现,冲击特征完全被干扰信号所淹没。同时,包络谱图5c中幅值较高的频率成分fh和fh,2分别为谐波干扰的基频和二倍频,故障特征频率fc及其各阶倍频(fc,2、fc,3)均较为微弱,难以可靠地辨识。
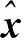
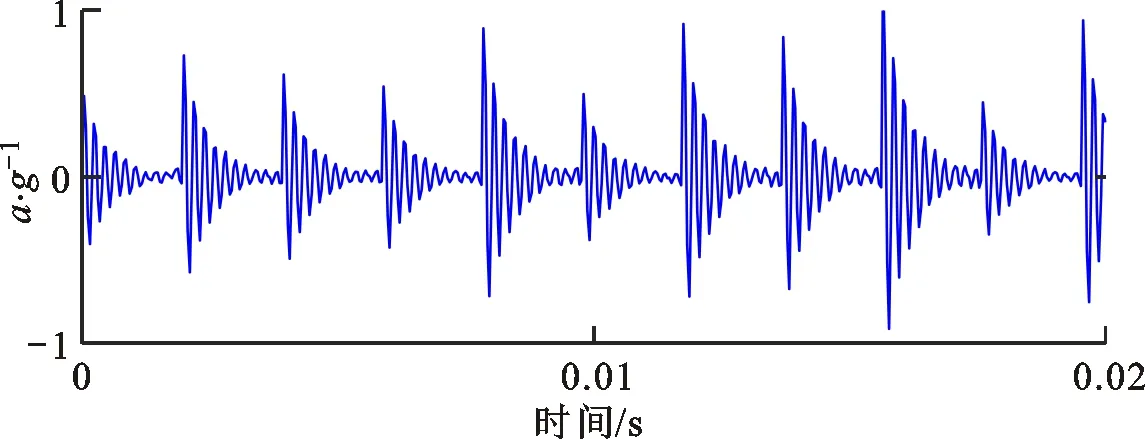
(a)局部时域波形
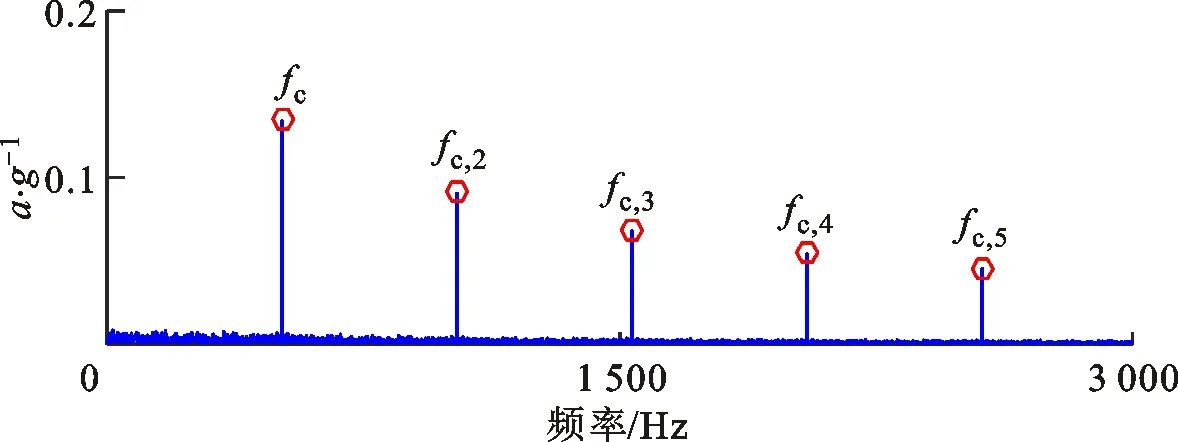
(b)包络谱图6 仿真信号的稀疏低秩协同优化算法分析结果 Fig.6 Extracted feature information from simulation signals by proposed CSLA

(a)局部时域波形
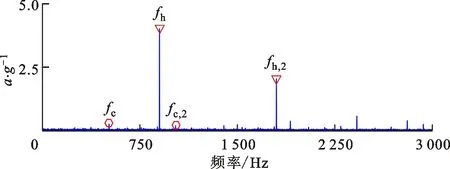
(b)包络谱图7 自适应增强组稀疏正则算法对仿真信号的分析结果Fig.7 Extracted feature information from simulation signals by AdaESPGL
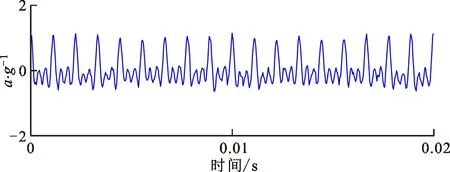
(a)局部时域波形
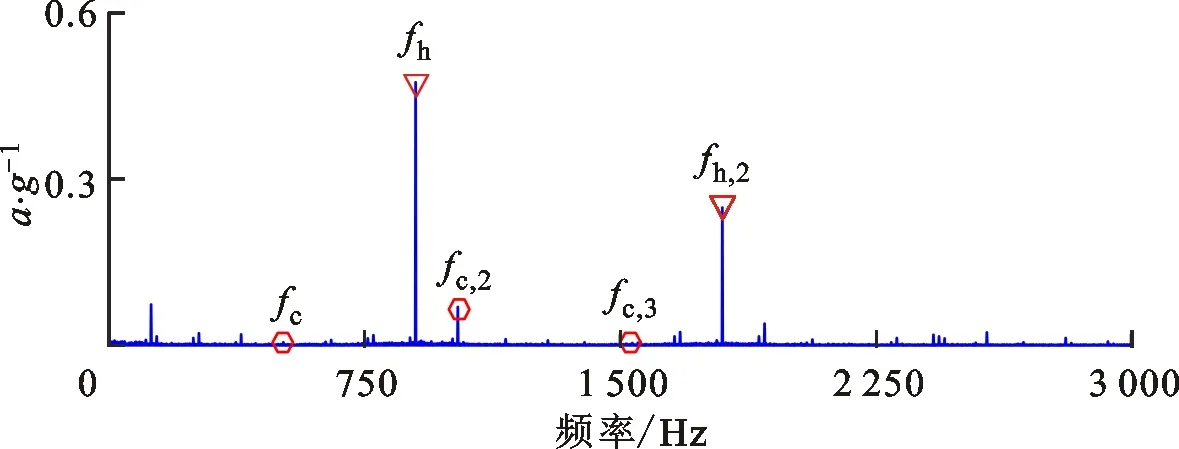
(b)包络谱图8 加权低秩正则算法对仿真信号的分析结果Fig.8 Extracted feature information from simulation signals by WLR
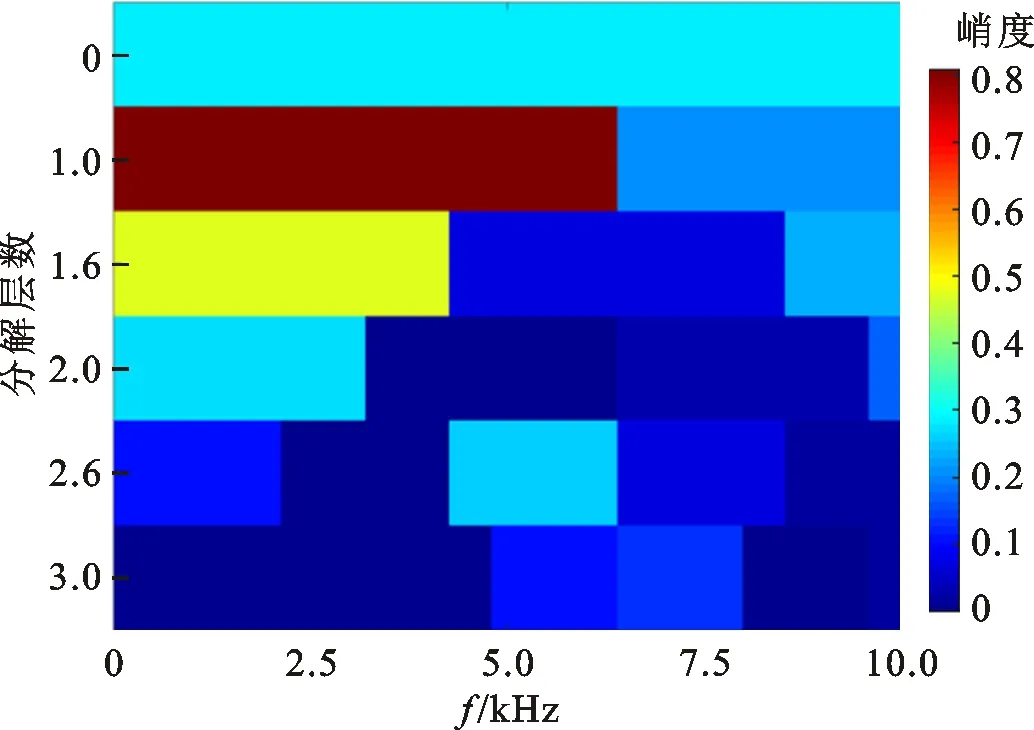
(a)谱峭度
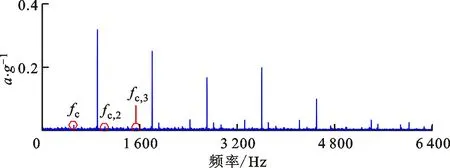
(b)谱峭度滤波信号包络谱图9 谱峭度滤波算法对仿真信号的分析结果 Fig.9 Extracted feature information from simulation signals by SK
为了进一步验证提出的稀疏低秩协同优化算法的有效性,采用3种经典算法进行对比分析,分别为自适应增强组稀疏正则算法(AdaESPGL)、加权低秩正则算法(WLR)以及谱峭度滤波算法(SK)。其中:自适应增强组稀疏算法的参数采用文献[11]推荐的参数设置;加权低秩算法的正则参数λ采用遍历方式自适应选择,遍历指标为重构信号包络谱的特征显著度水平;谱峭度滤波算法分解层数设置为3。3种算法的分析结果如图7~9所示。由图7可知,自适应周期组稀疏算法提取的特征信号中混叠有大量干扰信号,无法辨识准周期冲击特征;由图8a可知,局部细化时域波形中难以识别周期性的故障冲击模式,由图8b可知,加权低秩算法提取的特征信号包络谱中仅可识别出故障特征频率的二阶倍频;由图9可知,特征信号最大峭度为0.8,带宽为6 400 Hz,中心频率为3 200 Hz,由于带宽较大,该频带内干扰较为严重,因此在谱峭度滤波信号的包络谱中难以识别故障信息。
4 航空轴承故障诊断应用
为了充分验证提出算法对航空轴承故障特征的辨识能力,通过一组航空轴承故障试验和一组航空轴承全寿命实验来进行分析评估。同时,分别采用3类典型的故障特征检测算法进行对比分析,分别为:基于稀疏正则优化的自适应增强周期组稀疏算法,基于低秩正则优化模型方面的加权低秩算法,故障诊断中经典的谱峭度滤波算法。
4.1 案例1
轴承试验机采用某燃气涡轮研究院的某型号中等尺寸轴承试验器。该试验器结构简图及传感器布置如图10所示。测试轴承选用某型号航空发动机专用轴承,其主要尺寸参数如表1所示。
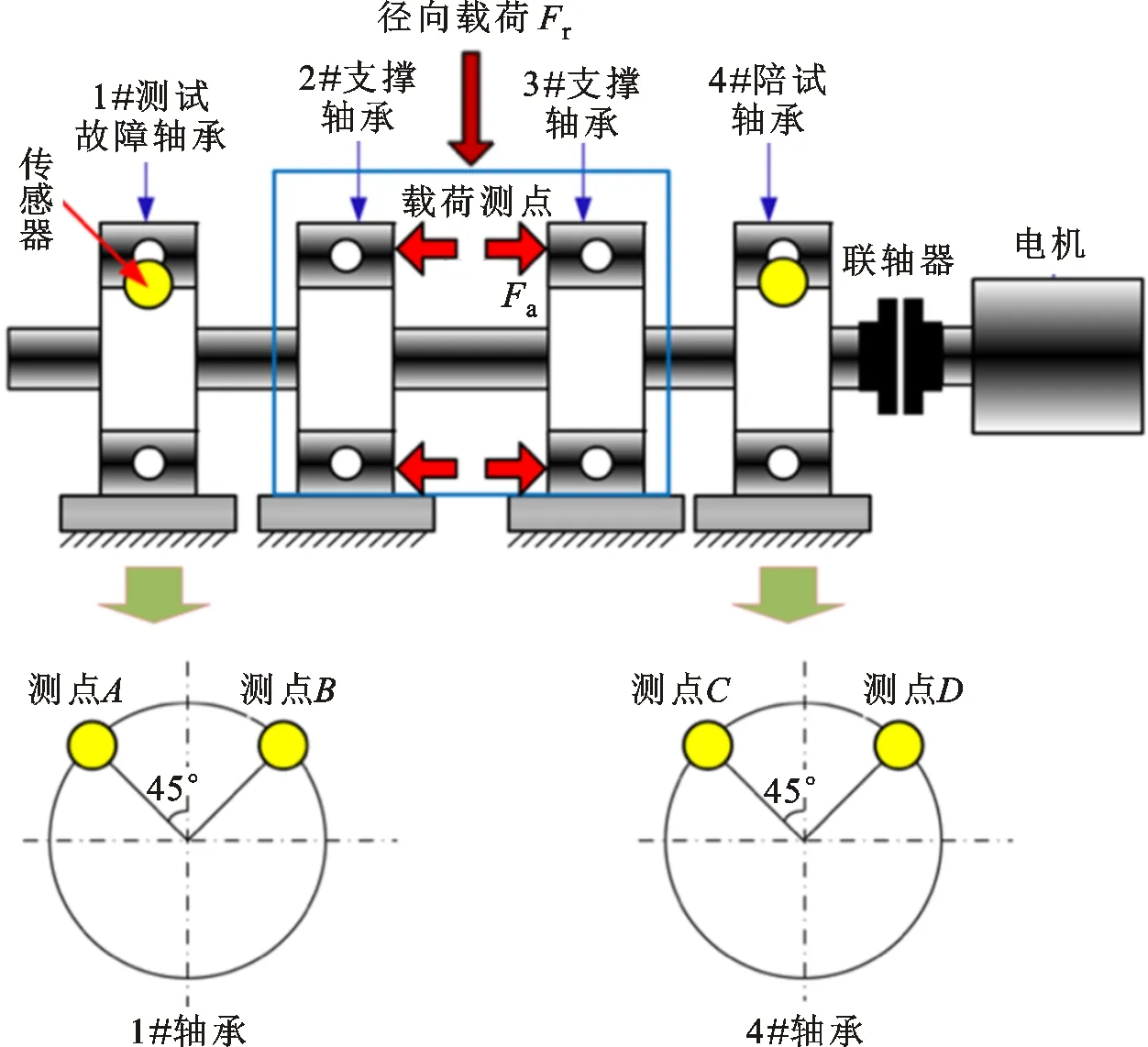
图10 航空轴承试验机主体结构及传感器测点布置Fig.10 Configuration of high-speed aero-engine bearing experiment and transducer setting
为了模拟航空轴承早期剥落故障,利用电动研磨笔在实验轴承的外圈表面预制剥落面积为1.0 mm2、剥落长度为1.128 mm的局部故障,实验轴承及其局部故障照片如图11所示。实验运行中,轴承径向加载350 N,轴向加载1 000 N,振动传感器分别安装在1#测试轴承和4#陪试轴承的轴承座上,试验器高速轴承运行转速为18 000 r/min,转频fr为300 Hz。振动信号利用数据采集仪记录,采样频率为50 kHz。振动信号的时域波形及其谱分析结果如图12所示。由图12b可以看出,实际细化波形较为杂乱,无任何明显的冲击特征,然而依据故障机理分析,在细化时域波形中应呈现出10个完整的故障周期波形;由图12c可以看出,频率成分复杂,无明显的特征频率;由图12d可以看出,外圈故障特征频率fBPFO及其倍频成分较为微弱,难以进行可靠的故障模式辨识。

表1 1#测试轴承相关参数

(a)实验轴承 (b)轴承外圈局部剥落图11 实验轴承及其局部故障照片Fig.11 Test bearing and its local spalling fault
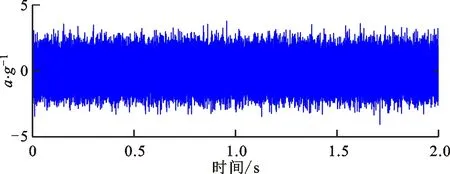
(a)时域波形
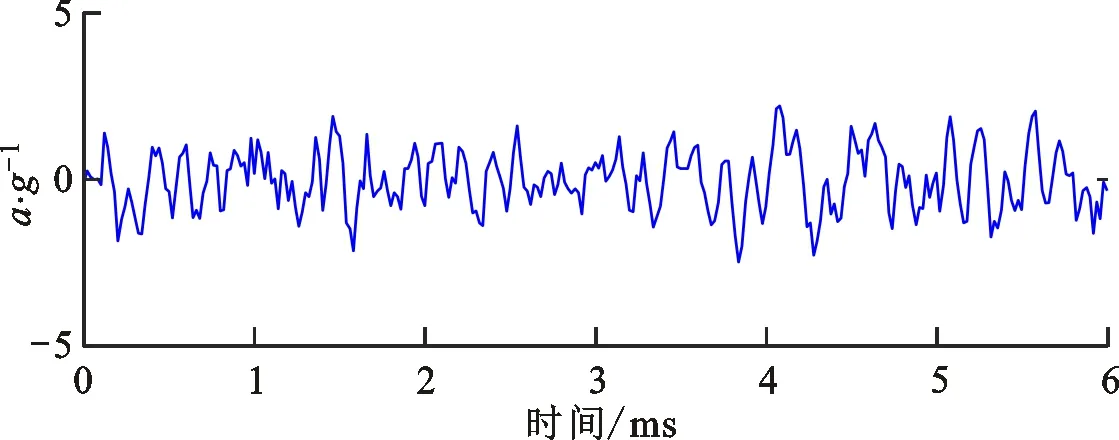
(b)局部时域波形
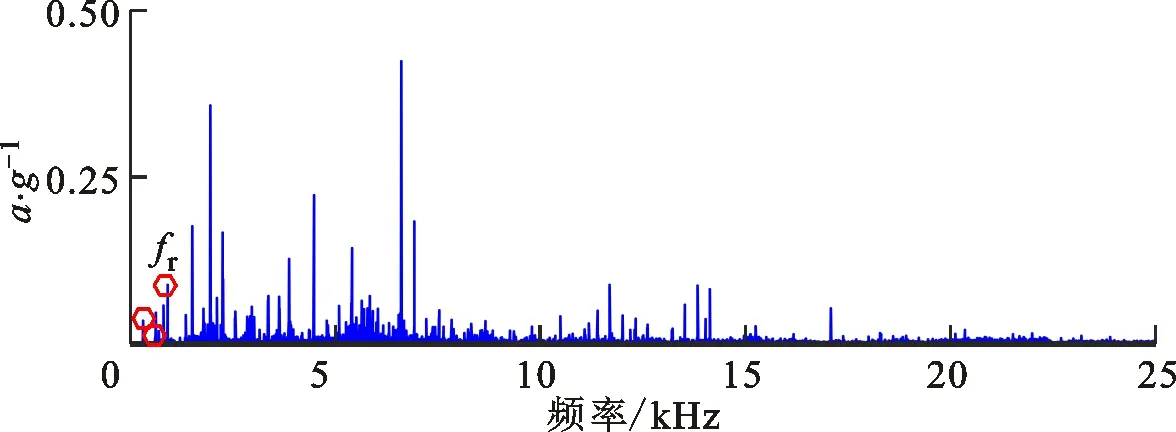
(c)频谱
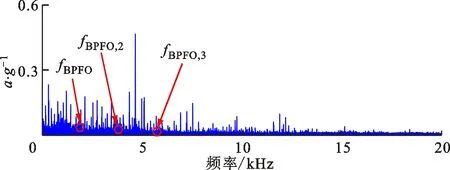
(d)包络谱图12 航空轴承测试信号及其谱分析Fig.12 Collected vibration signal and its spectrum
用本文提出的CSLA算法对测试信号进行分析,结果如图13所示。对比图12c和图13a可知,稀疏低秩算法重构信号频谱有效地提取了冲击特征频带,滤除了该频带外的强大干扰线谱;对比图12d和图13b可知,重构信号包络谱中可清晰地辨识故障特征频率及其高阶倍频,有效地预示了预制的局部剥落故障。

(a)频谱
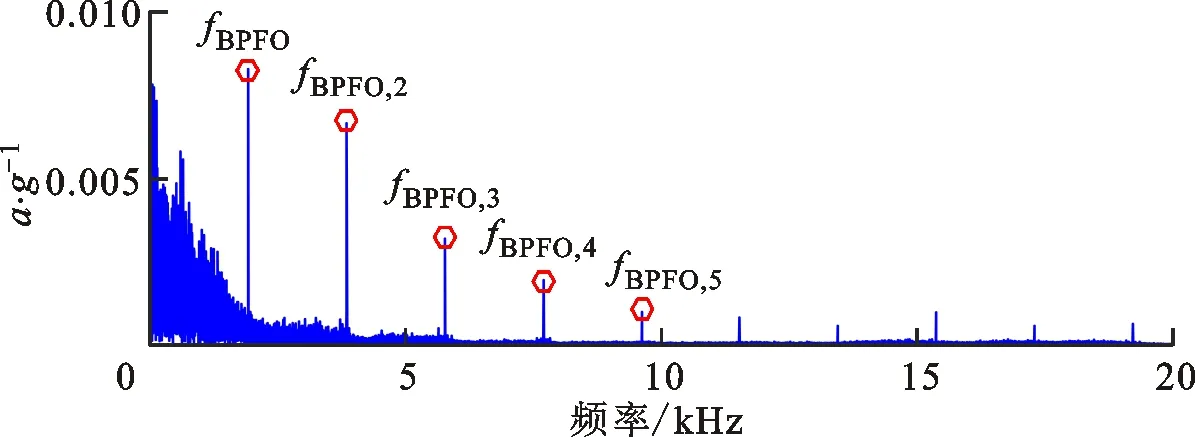
(b)包络谱图13 案例1中稀疏低秩协同优化算法对测试信号的分解结果Fig.13 Extracted feature information via CSLA
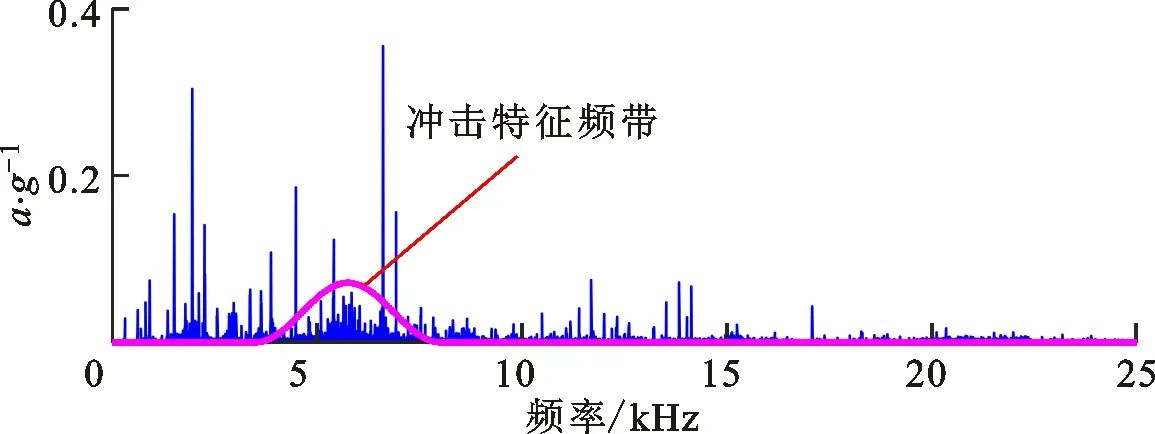
(a)频谱
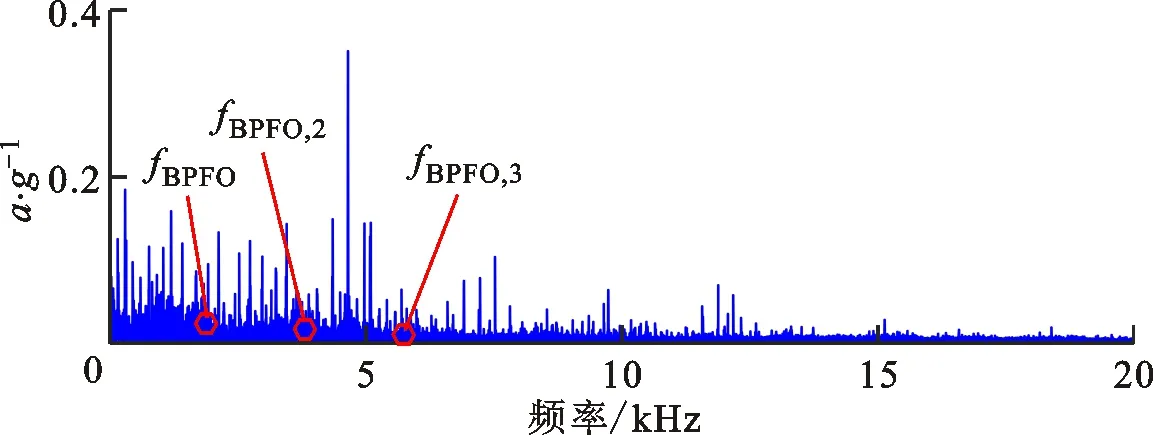
(b)包络谱图14 案例1中自适应周期组稀疏算法对测试信号的分解结果Fig.14 Extracted feature information via AdaESPGL
(a)频谱
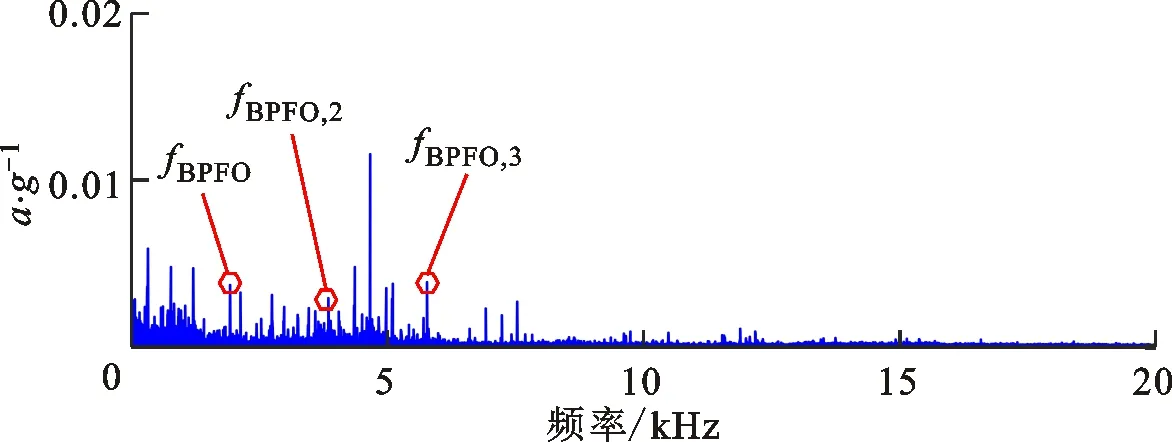
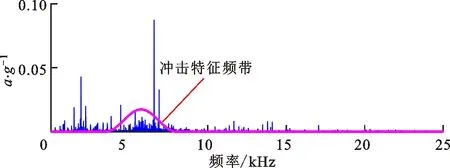
(b)包络谱图15 案例1中加权低秩算法对测试信号的分解结果Fig.15 Extracted feature information via WLR

(a)谱峭度
为了进一步验证算法的有效性,采用3类对比算法分析测试信号,结果如图14~16所示。对比图14a和图15a可知,在自适应增强周期组稀疏算法和加权低秩算法提取的特征频谱中,冲击特征频带均较为微弱,被大量离散线谱噪声所干扰,且从包络谱图14b和图15b中均无法有效识别故障特征及其各阶倍频信息。由图16a可知,信号分解层数为4,特征信号最大峭度为0.2,带宽为12 500 Hz,中心频率为6 250 Hz,由于带宽较大,该频带内干扰较为严重,因此滤波信号包络谱图16b中故障特征频率成分微弱,难以识别。
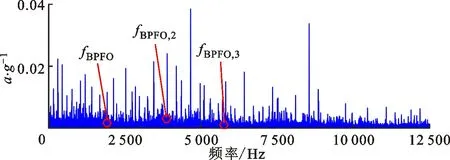
(b)谱峭度滤波信号包络谱图16 案例1中谱峭度算法对测试信号的分解结果Fig.16 Extracted feature information via SK
4.2 案例2

图17 航空轴承试验机主体外观Fig.17 Main configuration of experimental rig
本小节通过分析航空发动机轴承全寿命实验测试数据验证算法有效性。图17所示为航空轴承疲劳寿命试验机主体结构简图。测试轴承型号及参数如表2所示。加速疲劳寿命试验按照行业标准JB/T 50013—2000的要求进行。实验转速为6 000 r/min。图18为测试轴承全寿命周期振动信号的均方根趋势。有效值快速升高后,停机检查发现测试轴承内圈出现面积为3 mm2的局部剥落,如图19所示。

表2 全寿命实验中测试轴承相关参数
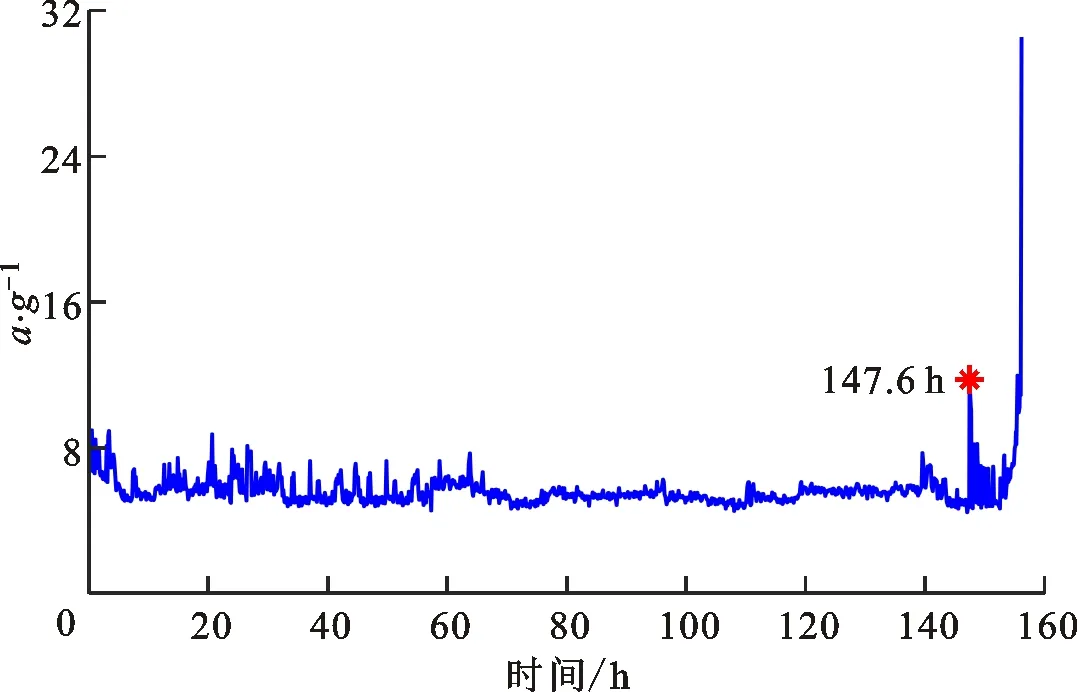
图18 测试轴承全寿命周期振动信号均方根趋势 Fig.18 Root-mean-square of vibration signal in run-to-failure experiment

图19 测试轴承内圈局部剥落Fig.19 Spalling fatigue on inner race of test bearing
轴承早期微弱故障特征的识别是保障航空发动机运行安全的关键基础,因此选用故障初期147.6 h的振动信号进行分析,相比于失效时的振动有效值,该时刻的有效值并未发生明显变化,故障特征较为微弱[25]。图20为该时刻测试信号的时域波形及其谱分析结果。由图20b可以看出,细化时域波形具有10个完整的故障周期,然而其波形较为杂乱,难以确认冲击特征波形;由图20c可以看出,频率成分复杂,无明显的内圈故障特征频率fBPFI结构,且包络谱中故障特征频率及其倍频成分较为微弱,无法有效地预示轴承的健康状态。
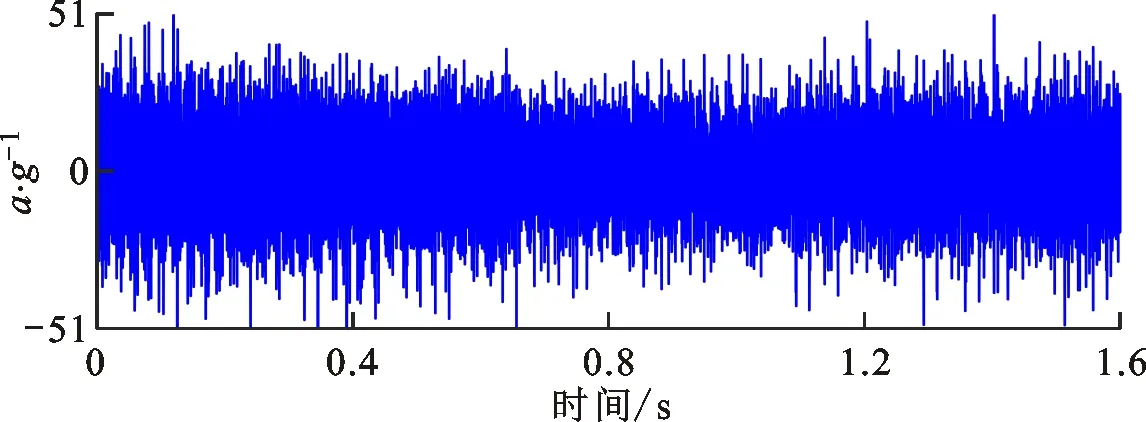
(a)时域波形
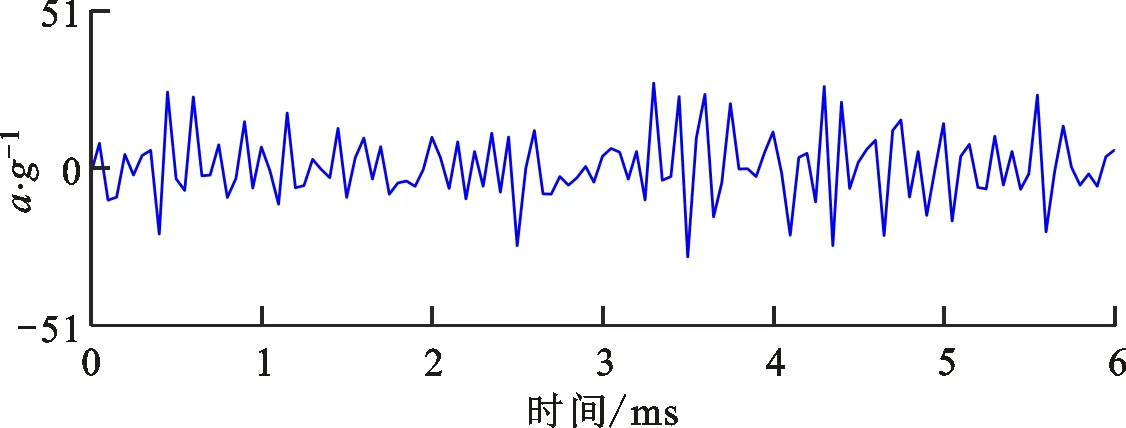
(b)局部时域波形
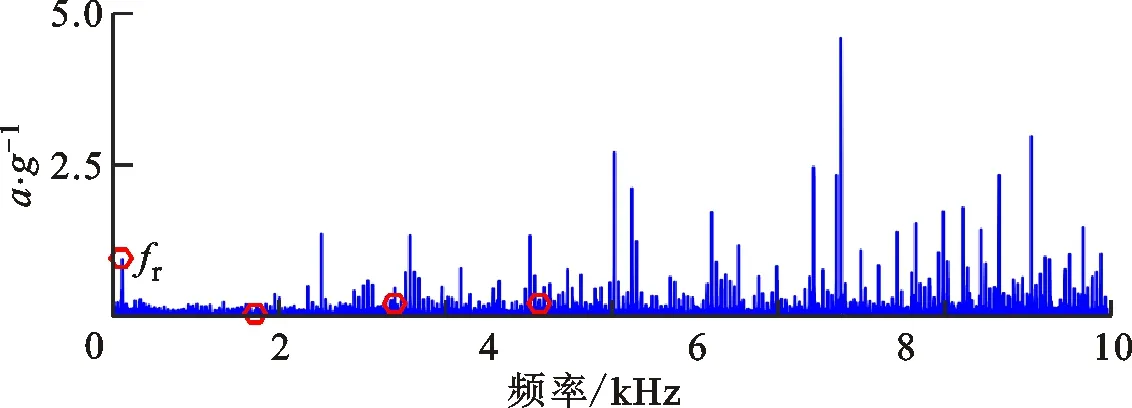
(c)频谱
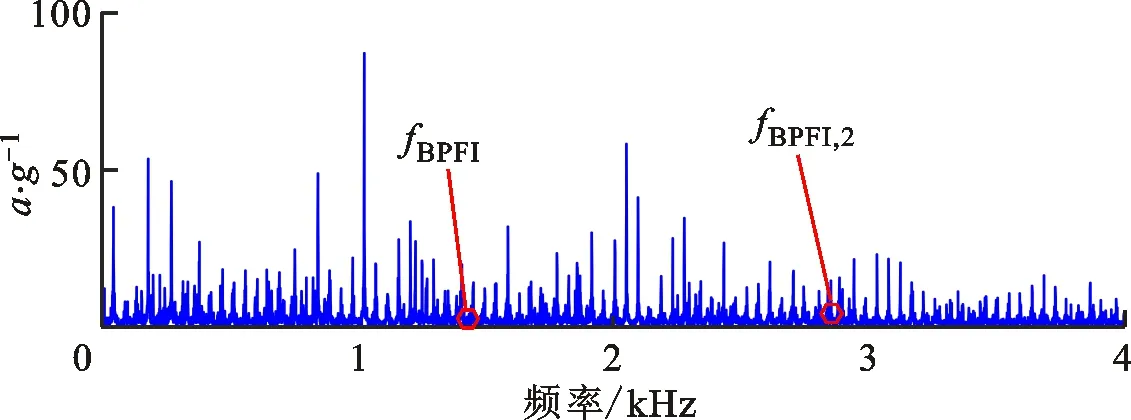
(d)包络谱图20 高速轴承内圈早期故障测试信号及其谱分析Fig.20 Vibration signal and its spectrum of test bearing with early fault on inner race

(a)频谱
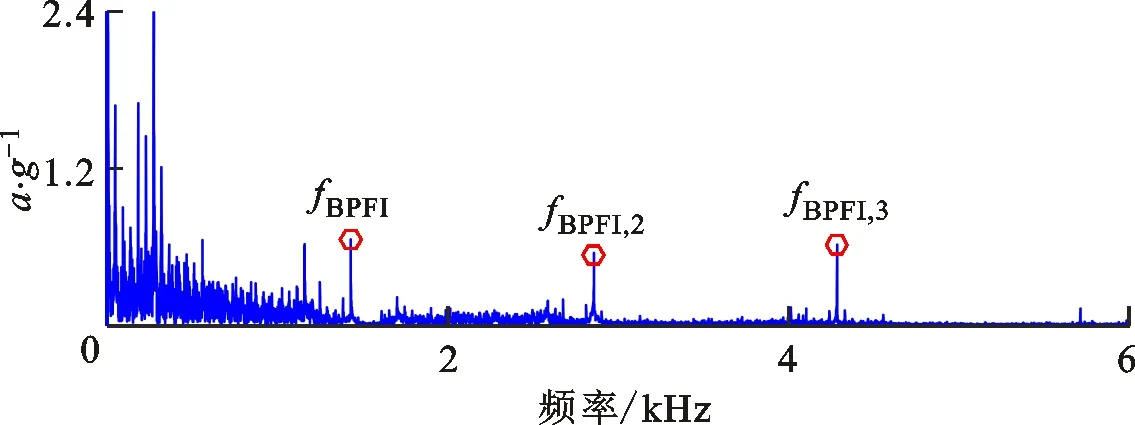
(b)包络谱图21 案例2中稀疏低秩协同优化算法对测试信号的分解结果Fig.21 Feature signal extracted by proposed CSLA
用本文提出的CSLA算法对测试信号进行分析,结果如图21所示。可以看出,相比于测试信号频谱图20c,由图21a中能可靠地发现冲击特征频带,且在包络谱图21b中故障特征频率及其各阶倍频成分均较为显著,验证了提出稀疏低秩协同优化算法对航空轴承早期微弱故障特征识别的有效性。
3类对比算法的分析结果分别如图22~24所示。由图24可以看出,特征信号最大峭度为1,带宽为5 000 Hz,中心频率为7 250 Hz。综合图22~24可知,由于测试信号成分复杂,存在大量的离散线谱成分干扰,因此稀疏正则模型及加权低秩正则模型均无法有效辨识故障特征信息。谱峭度算法获得滤波信号的频带较宽,难以获取完整的准周期冲击模式,因此从滤波信号包络谱中无法识别故障特征频率。

(a)频谱
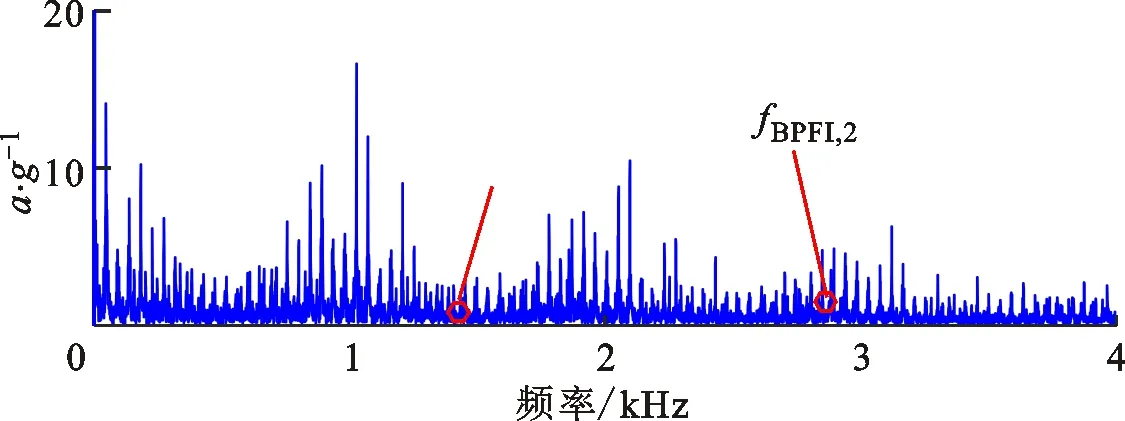
(b)包络谱图22 案例2中自适应周期组稀疏算法对测试信号的分解结果Fig.22 Feature signal extracted by AdaESPGL
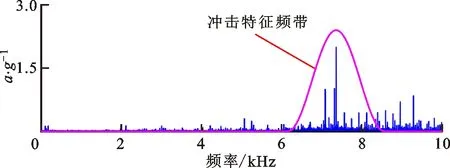
(a)频谱
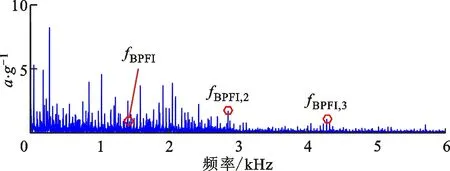
(b)包络谱图23 案例2中加权低秩算法对测试信号的分解结果Fig.23 Feature signal extracted by WLR

(a)谱峭度

(b)谱峭度滤波信号包络谱图24 案例2中谱峭度算法对测试信号的分解结果Fig.24 Feature signal extracted by SK
5 结 论
航空轴承故障的早期诊断和预警,是保障发动机运行安全的关键技术之一。航空发动机振动观测信号成分复杂,强谐波干扰是制约经典冲击特征辨识算法的关键问题。本文针对这些问题,联合空域低秩先验和谱域稀疏先验,提出了稀疏低秩协同优化模型,开发了模型的交替方向优化求解算法,实现了冲击成分的高精度识别。仿真分析和高速轴承实验验证了算法的有效性。本文结论如下:
(1)航空轴承故障观测信号由微弱的冲击成分、强大的谐波干扰以及白噪声分量耦合而成,其中冲击特征在合适的二维变换空间具有低秩属性,谐波干扰信号在一维傅里叶变换域具有稀疏属性;
(2)通过协同一维傅里叶变换域稀疏正则和二维空间特征矩阵的低秩正则,构造了稀疏低秩协同正则模型,基于块坐标优化求解框架,开发了稀疏低秩正则模型的交替方向优化求解算法,实现了冲击特征信号的准确识别;
(3)仿真分析表明,当信号中含有幅值较大的耦合谐波干扰时,提出的稀低秩协同优化算法可以同时增强冲击特征并抑制干扰信号,而经典的稀疏正则模型和低秩正则模型均难以克服显著的特征干扰耦合问题;
(4)航空高速轴承故障实验以及全寿命实验早期故障数据的分析结果表明,提出的协同算法具有可靠的微弱故障特征辨识能力。
