水下航行器仿生侧线探测阵列优化布置模型及评估方法

2021-11-16李怡昕胡桥刘钰杨倩

西安交通大学学报 2021年11期

李怡昕, 胡桥,2,3, 刘钰, 杨倩

(1.西安交通大学机械工程学院, 710049, 西安; 2.西安交通大学机械制造系统工程国家重点实验室, 710049, 西安; 3.西安交通大学陕西省智能机器人重点实验室, 710049, 西安)

自然界中鱼类在水中的生存依赖于对水中环境信息的感知,视觉系统与侧线感知系统是鱼类最主要的两个感受器官。深水中环境接近黑暗,压力不断增大。经过长期的自然选择,鱼类进化出除视觉系统以外的感受器官——侧线感知系统,辅助它们在复杂的水下环境、深海等无光源区域正常游动、捕食及躲避障碍物[1],同时也弥补了视觉功能在黑暗环境中无法作用的缺点。

鱼类的侧线感知系统为水下航行器人工侧线系统的设计提供了灵感,目前对人工侧线传感器阵列布局的研究中,主要以水下机器人的头部及侧面的等距分布为主。2005年,Guestrin等提出了一种互信息准则来选择传感器位置,以最大限度地减少感知位置的不确定性[2];2014年,巴斯大学的Chambers等模拟侧线系统设计了一个安装有多个压力传感器的三维机器鱼鱼头,研究仿生侧线系统对于圆柱绕流形成的卡门涡街的水动力特性压力信号的探测[3];2017年,佛罗里达大学的Mohseni团队设计了一种用于自主水下航行器的分布式压力传感系统,能够探测流场环境的改变情况[4];同年,该团队对其侧线传感系统进行改进,通过传感器模块化设计及其规则布局,对周围环境水动力信息及障碍墙壁位置进行探测与捕捉[5-6];2018年,Yanagitsuru等针对不同头部宽度上分布的压力传感器对周围水环境流量参数及压力变化梯度的探测进行了研究,结果显示水动力信息在不同头部分布形式下是相似的,且最前端的流量参数灵敏度与压力波动最大[7];2020年,Verma等基于概率理论利用信息增益对仿生侧线传感器阵列进行布局优化,实现了目标物位置的估计,但缺少进一步的传感器阵列数量及冗余度的优化评估,缺乏对传感器布置的实际指导意义[8]。

对于仿生侧线传感器分布的优化方法,密歇根州立大学的Ahrari团队进行了许多相关研究:2015年,针对偶极子定位问题对传感器的形状及阵列位置进行优化,明确了不同传感器数量对定位精度的影响关系[9];2016年,为了提高对目标的跟踪定位精度,采用协方差矩阵自适应进化策略确定扩展卡尔曼滤波的最优参数,结果表明当不确定性较高且传感器数量达到一定数目时,定位精度不再增加[10];2017年,采用双层优化的方法优化包括侧线的形状及位置的人工侧线参数,同时也考虑了3种不同不确定性的情况,说明了不确定性对优化设计的影响[11];同年,该团队又研究了三维空间中偶极子定位的仿生侧线系统优化设计,在传感器同方向同平面的常规布置基础上,提出了偏移策略与角度策略,优化传感器的布置位置、方向及角度,提高偶极子的定位精度[12]。国防科技大学的季明江团队在2017年用8个压力传感器制作了一条仿生侧线系统机器鱼样机,并采用无导数法、拟牛顿法和遗传算法共3种算法对其传感性能进行评估[13];2018年,采用直线型侧线系统,发现当传感器阵列距离为阵列长度一半时,使用多信号分类方法能够定位两个较近的非相干偶极子源位置[14];同年,该团队设计了一个由9个压力传感器组成的十字形仿生侧线传感器阵列,发现减小传感器的数据采样间隔和增加传感器数量都能够提高定位精度[15];2019年,该团队研究了传感器数、间距及阵列长度对探测准确性的影响,结果表明侧线传感器阵列越长、越密集,其有效定位区域越大[16]。北京大学的谢广明团队基于自然界盒子鱼的侧线系统分布特点和侧线神经丘工作原理,设计了一种在头部与两侧分布有9个压力传感器的自主机器鱼侧线系统[17],基于该仿生侧线阵列,机器鱼能够感知周围水环境的压力分布信息,并实现信息反馈,自主并高效地运动[18-19];2017年,基于盒子鱼仿生侧线系统,该团队对感知探测邻近机器鱼涡流尾迹进行了研究,通过对反卡门涡街涡流尾迹水动力特性的实验探测研究,可以有效地估计邻近机器鱼的运动振荡频率、振幅、偏移量及两条机器鱼间的相对位置[20]。

通过这些研究现状可以发现,将鱼类侧线系统应用到水下航行器中,形成人工侧线系统探测阵列,可以很好地反映水下航行器周围环境水流流速及水压特点,也可以对周围目标物进行运动信息估计及位置探测。但是,这些研究都没有对侧线系统传感器阵列进行合理地优化分布,仅是将传感器阵列均匀的分布在水下航行器两侧及前端,缺少对传感器布置位置及数量的优化,缺乏对传感器阵列优化分布系统化的数学模型及理论指导,影响了对目标物位置探测的准确度。因此,需要对传感器分布方式的优劣性进行判断,并通过数学理论指导,得到传感器阵列优化布置方案。

本文针对水下航行器仿生侧线探测系统传感器阵列优化布置的问题,提出了一种结合贝叶斯概率模型及顺序启发式算法的传感器阵列优化布置方法。通过将实际问题转化为数学模型,结合流场仿真分析,采用顺序启发式算法及冗余度约减计算,对传感器阵列布局进行优化与评估。结果表明:与传统方法相比,提出的阵列优化布置模型及评估方法得到的非目标位置的干扰区域探测概率减小到1%以下,有效提高了目标物位置的探测概率,证明了阵列优化方法的可行性与有效性。

1 阵列优化布置方法

本文基于对水下航行器探测目标物的二维流场仿真,利用贝叶斯概率模型及顺序启发式算法,结合几何特征筛选方法与相关性计算,达到对目标位置的准确探测。针对水下航行器仿生侧线传感器优化布局问题,对运动目标物形成的流场环境下的水下航行器周围流场分布情况进行水动力仿真分析,采集流场仿真分析得到的压力值数据,获得每个观测点在拟定流场环境下的压力测量值,将这些压力值带入基于贝叶斯定理的顺序启发算法中,得到表示信息熵变化的目标函数值。通过比较目标函数值,确定水下航行器侧线传感器优化布置方案,通过计算相关性冗余度,对阵列优化分布传感器数量进行评价,依据阵列优化布置参数设计水下航行器侧线传感器优化阵列。通过阵列对比与后验概率表征的方法,结合仿真实验验证传感器优化阵列在水下航行器探测目标物问题上的准确性与有效性。总体方案流程如图1所示。

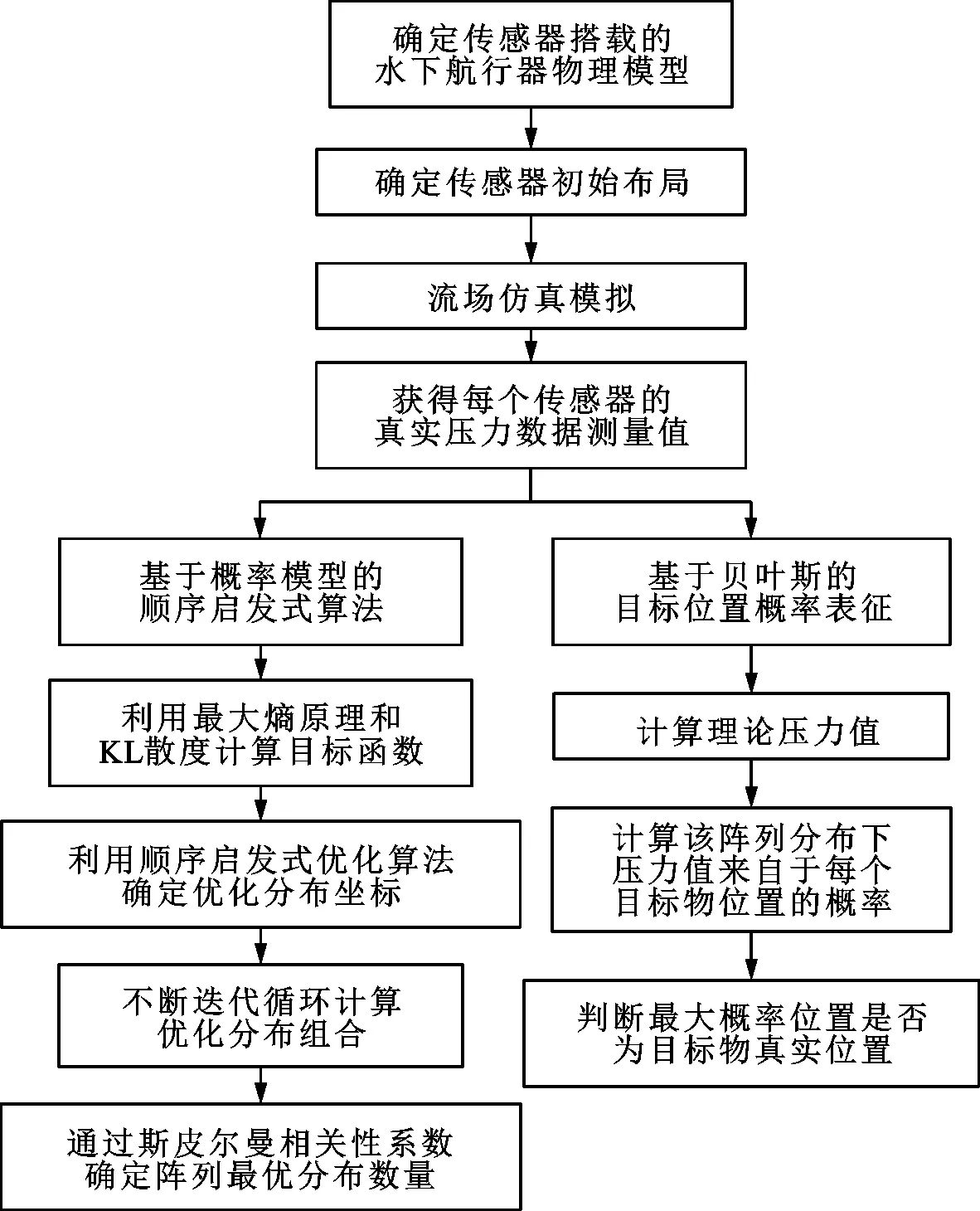
图1 传感器阵列优化布局总体方案流程Fig.1 Flow chart of sensor array placement optimization strategy

1.1 仿生侧线探测阵列优化布置模型

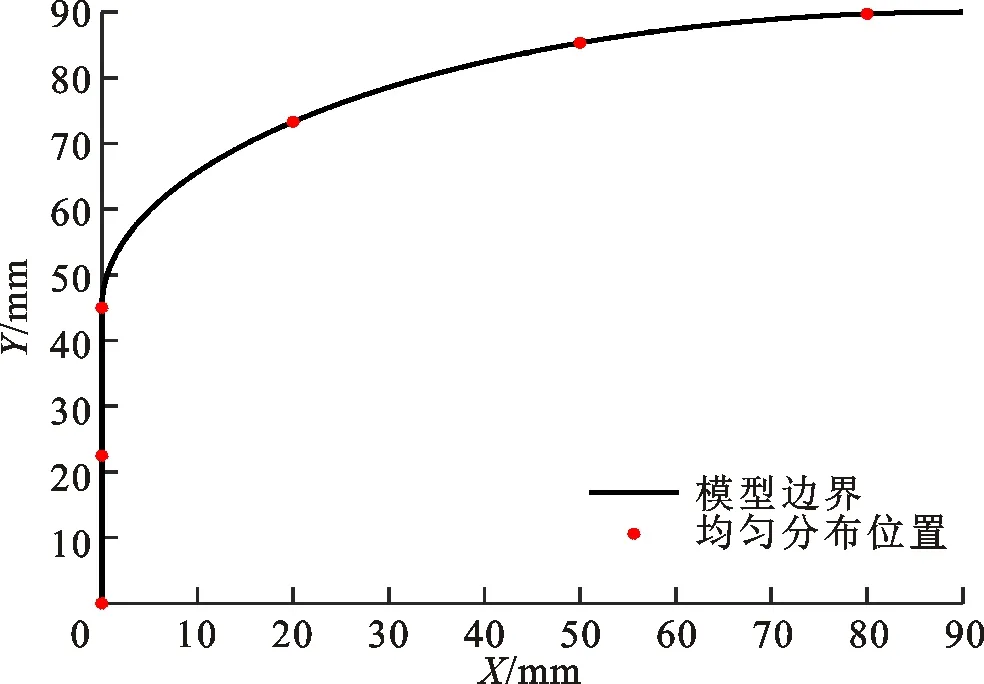
1.1.1 物理模型建立进行传感器阵列布局优化之前,需要对侧线系统载体及目标物运动区域等物理模型及参数进行设定。考虑到仿真分析、优化算法结果与后续实验研究的可行性,本文选用标准尺寸的水下航行器作为侧线载体进行仿真及优化分析。其中,头部端面直径为90 mm,尾部端面直径为180 mm,根据标准规格水下航行器尺寸参数,得到曲面处曲线方程[21]

(1)

式中X和Y分别为水下航行器曲面处曲线的横坐标和纵坐标。

根据标准水下航行器尺寸规格,设计水下航行器侧线系统载体,曲面部分长度为90 mm,后端面部分长度为110 mm,总体长度为200 mm。水下航行器尺寸及三维结构模型如图2所示。

确定好水下航行器的结构尺寸后,需要确定初始传感器布局位置点,即水动力流场仿真中的压力值观测点。将水下航行器二维截面的边界分为顶面、侧面与底面共3个部分,其中:侧面每间隔2 mm设置一个观测点,共45个观测点位,观测点沿y轴正方向依次编号为91～135;顶面与底面x方向每间隔2 mm设置一个观测点,各设有45个观测点位,顶面观测点沿x轴正方向依次编号为1～45,底面观测点沿x轴正方向依次编号为46～90;再加上3部分连接点处的观测点位,顶面与侧面连接处观测点编号为136,底面与侧面连接处观测点编号为137,总计137个初始观测点位置。具体分布情况如图3所示。

图2 水下航行器尺寸及结构模型Fig.2 Size and structure model of underwater vehicle

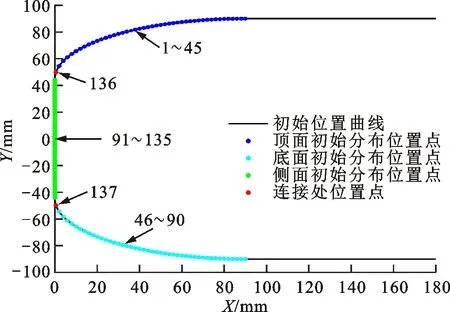
图3 传感器初始分布示意Fig.3 Initial sensor distribution

基于水下航行器的设计尺寸,拟定探测目标物运动形式、运动区域尺寸等参数。规定水动力仿真分析目标物运动区域尺寸为Lx×Ly,水下航行器前端面中心点位于该流场区域的(x2,0)处(规定原点位于目标运动区域与水下航行器之间)。采用振动偶极子作为目标物进行位置探测工作,偶极子目标物ri位置区域尺寸为Lx×Ly。与水下航行器距离最近的目标位置点位于(x1,0)处,目标物间隔横纵坐标为(Δx,Δy)。每个位置为一个偶极子目标物振动位置点,共设置30个目标物振动位置点。目标位置点编号方式如下:当目标位置点横坐标分别为x1、x1-Δx、x1-2Δx、x1-3Δx和x1-4Δx时,位置点分别沿y轴正方向依次为编号1～6、7～12、13～18、19～24和25～30。设置对偶极子目标物直径为d、振动速度为v(v=Acos(2πft)),传感器位置面局sj位于水下航行器一侧。具体流场区域尺寸及位置如图4所示。

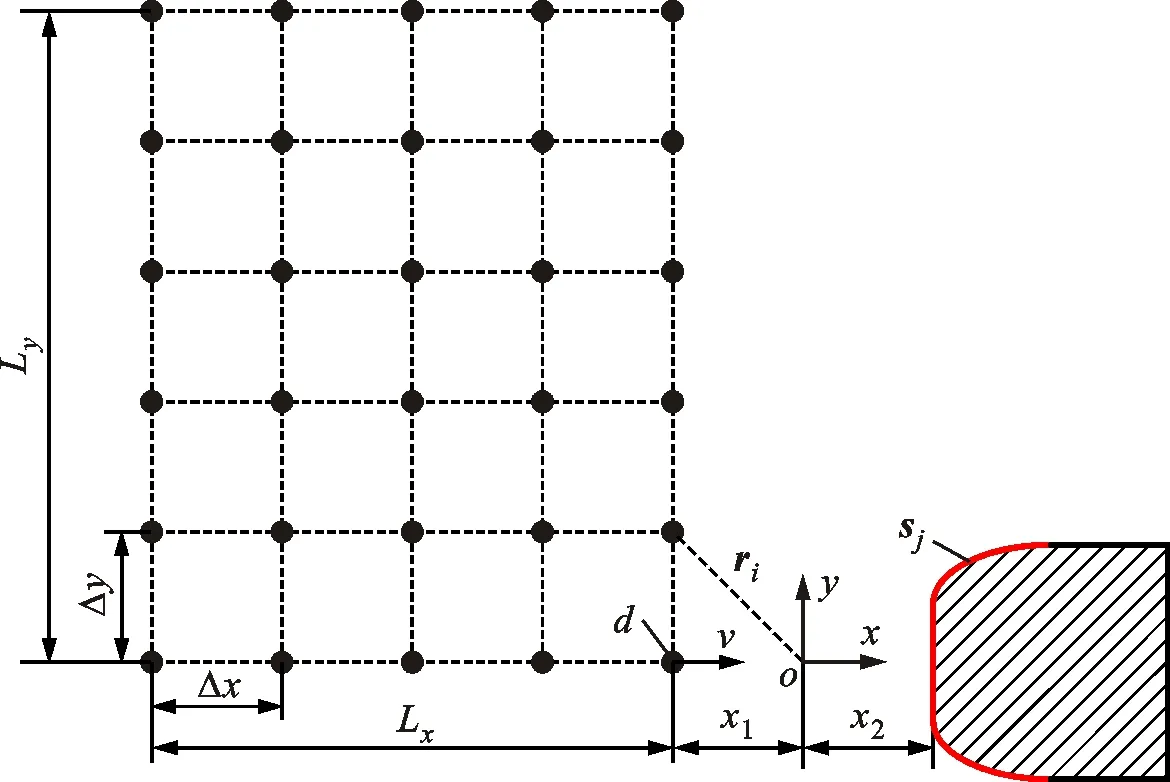
图4 流场区域尺寸及位置示意Fig.4 Size and location of flow field area

1.1.2 流场仿真分析基于1.1.1小节水下航行器传感器位置布局、流场区域尺寸及目标物运动区域尺寸的参数设置,在FLUENT流体仿真软件中进行流场环境仿真,通过建立流场模型、确定计算域、划分计算网格、设置求解参数、迭代计算与后处理等步骤,完成对该流场环境下水动力模型的仿真。在图3中传感器位置编号1、10、100处设置压力观测点1～3。当目标物在位置1处振荡时,3个不同压力观测点的测量值如图5所示。可以看出,对于偶极子目标物ri产生的流场,压力测量值与测量时间呈周期性变化关系。

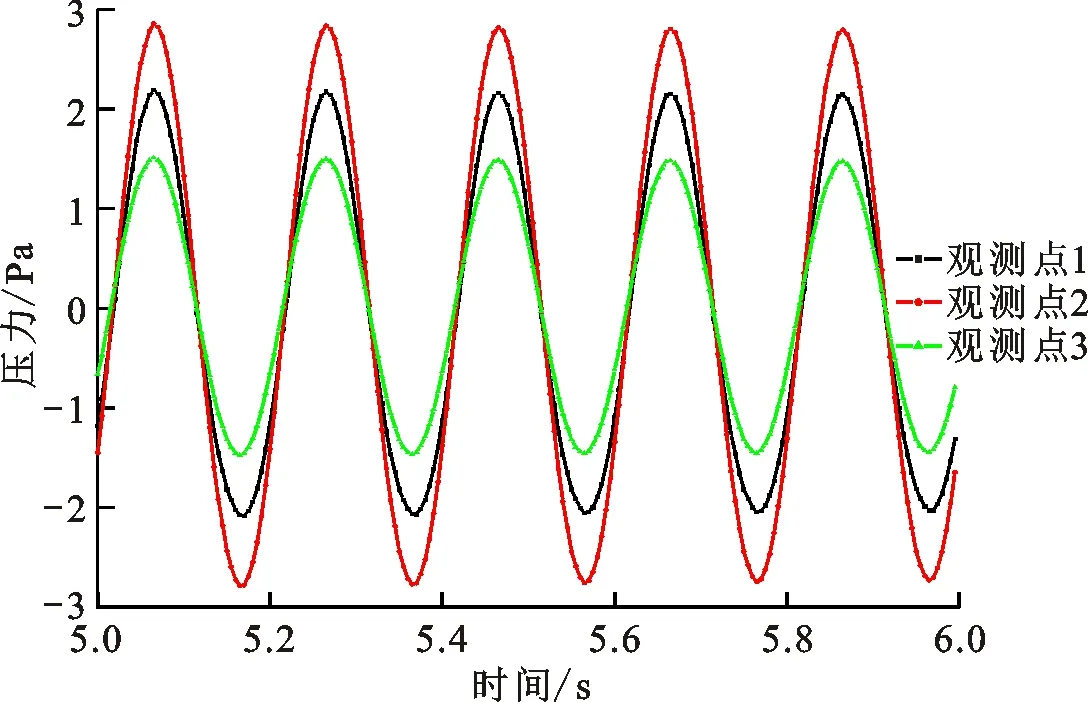
图5 压力观测点压力值变化曲线Fig.5 Pressure variation curves of pressure observation points

1.1.3 优化算法设计

(1)贝叶斯定理的应用。完成1.1.1小节物理模型建立及1.1.2小节流场仿真等工作后,需要对阵列优化算法进行设计。对水中目标物位置探测的准确程度是评价一组传感器阵列位置分布优劣程度的重要指标之一,根据传感器侧线阵列对水中目标物探测的工作特点,对应贝叶斯概率模型,将目标探测工作与概率事件一一对应。贝叶斯定理用来描述两个条件概率之间的关系,如P(A|B)和P(B|A)分别代表事件A在事件B发生条件下的发生概率和事件B在事件A发生条件下的发生概率。根据定理可得到贝叶斯公式[22]

(2)

对于水下航行器侧线阵列目标物探测工作,假定当前偶极子目标物ri位置为(xi,yi),探测偶极子目标物位置为事件A,事件A的不确定性由概率分布规律来量化,概率分布规律根据分布在水下航行器的侧线传感器阵列捕获到的压力数据信息进行更新。只要分布在水下航行器上的侧线阵列能够探测到偶极子目标物ri振动对周围流体的扰动所产生的水压数据信号,就可以检测到振动偶极子的位置,即可通过该数据对事件进行判断,判断某一未知压力信号是由偶极子目标物ri的振动所造成的。因此,传感器优化分布问题可以转化为寻找一种传感器侧线阵列分布形式,对目标物的位置做出最准确的估计与判断。

假设侧线传感器分布在水下航行器的一侧,s(s∈Rn)表示传感器位置布局,F(rs;s)表示传感器位置布局s对于r处产生的偶极子振荡流场的预测压力值,该预测值通过基于Navier-Stokes方程下的流场仿真计算获得。假定事件A的先验概率为已知,记作p(r),在当获得传感器的测量值y后,根据贝叶斯定理有后验概率分布p(r|y,s)与相对应的先验概率分布p(r)和似然概率p(y|r,s)的乘积成正比[18],可以确定后验概率分布p(r|y,s)

p(r|y,s)∝p(r)p(y|r,s)

(3)

式中似然概率函数p(y|r,s)表示给定一传感器位置布局s后,该布局下所测得的压力测量值y来自于r处干扰源振动的概率。由于真实压力测量值与理论压力测量值存在一定的误差,假设预测误差ε(s)为真实测量值y与理论测量值(即预测测量值)F(rs;s)之间的差,即

y=F(rs;s)+ε(s)

(4)

最大熵原理提供了一种选择随机变量统计特性时最符合客观情况的分布准则,选择具有最大熵的分布作为随机变量的分布是一种有效的处理方法。又有当均值与协方差矩阵一定时,随机变量符合正态分布时具有最大熵。假定预测误差ε(s)符合该定义,并且ε(s)服从均值为0且协方差矩阵Σ(s)一定的多元高斯分布N(0,Σ(s))。根据预测误差公式,得到真实压力测量值的似然函数p(y|r,s)服从均值为F(rs;s)、协方差矩阵一定的多元高斯分布,表达式为

(5)

(2)确立优化目标函数。最优传感器布局的问题转化为已经确定的某一传感器位置布局s是否能对目标物位置r进行最准确的估计,即传感器位置布局s下得到的测量值对于估计干扰源位置r最有效。为了用数学方式对该信息量进行描述,引入信息理论中KL散度,即相对熵的概念。相对熵(或信息散度)是用于衡量两个概率分布之间差异的非对称性,可以衡量两个随机分布之间的距离。当两个随机分布相同时,它们的相对熵为0,当两个随机分布的差别增大时,它们的相对熵也会增大[19]。现在重新考虑事件A——寻找偶极子目标物运动位置位于目标区域中的坐标,已知事件A先验分布为p(r),得到压力测量值后的后验分布为p(r|y,s)。后验概率p(r|y,s)中传感器布局位置s是作为条件给定的,当选定的传感器布局方式s越好时,压力传感器测得的信息量则越多,那么先验概率分布p(r)与后验概率分布p(r|y,s)的差别越大,即相对熵越大。因此,表示事件A的先验分布与后验分布的信息增益的效用函数由两者间的相对熵定义为

(6)

式中Ω为偶极子目标物的积分域。

在传感器布局优化阶段,压力传感器测量值y无法通过实验得到,通过误差模型式(4)来确定给定固定干扰源位置r及传感器位置布局s下的传感器测量值y。事件A的先验分布与后验分布间的信息增益由两者间的相对熵来表示,通过将此信息增益效用函数最大化来确定传感器最优分布方式s。传感器布局的优劣情况可由式(6)来反映,表示某一传感器位置布局在获得测量值y后的信息增益变化。为了表示该布局下所有传感器的相对熵,对式(6)进行改进,计算所有可能的压力传感器测量值的相对熵期望值为效用函数,并通过最大化该效用函数来确定传感器的最佳布局方式。通过计算每个布局下的效用函数值确定优化后的传感器分布方式,改进后的函数定义为

(7)

式中Ψ为传感器测量值y的积分域。

从式(7)可以看出,除了先验分布p(r)为已知,p(r|y,s)与p(y|s)均为未知参数,因此需要用到贝叶斯概率公式对目标函数进行转化。根据贝叶斯定理,结合该问题可以得到事件A和事件B分别对应偶极子目标物运动位置与压力传感器测量值两个事件,式(2)可以写作

(8)

将式(7)中部分函数进行变换

(9)

p(y|r,s)p(r)

(10)

目标函数式(7)转化为

U(s)=

(11)

式(11)为利用贝叶斯定理转化后的目标函数,其中先验概率p(r)为已知,似然函数p(y|r,s)可通过多元高斯函数进行数学表达(式(5)),只有概率分布p(y|s)为未知参数。已知压力传感器测量值y的概率分布为p(y|r,s),对干扰源位置变量r积分即可得到p(y|s)

(12)

基于式(12),将目标函数中的未知量转化为已知量,并用数学表达式进行定义

(13)

式中:Nrs为目标物位置数;Ny为初始阵列分布传感器数。

(3)计算优化阵列布局。目标函数式(13)已获得,传感器优化布局模型理论推导完成,将传感器初始分布坐标点导入计算,即可得到相应的优化布局。通过最大化式(13)中的目标函数,得到最优传感器布局方式,然而最优传感器布置问题的特点是存在相对较多的多个局部最优解,而将各种传感器数量组合下的局部最优解分别进行计算是不科学、低效率的,使用应用广泛的遗传算法等优化算法,需要给定具体优化参数,会导致超参数的结果,因此需要寻找一种更有效的算法进行传感器分布优化。

假设存在一固定数量N0的传感器分布组合并已知优化前的传感器初始分布位置点,选用顺序启发式传感器布局算法是一种更有效更加整体化的传感器分布优化方法。通过在分布模型一侧放置若干个传感器,传感器数量逐渐增加的同时保证信息熵变化为最大,一次选择一个传感器分布位置点来确定传感器优化总体布局。具体而言:首先在具有传感器初始布局的条件下,选择一个信息熵降幅最大的传感器位置点,即目标函数值最大的位置点,作为第一个传感器的最佳位置S1;在给定第一个传感器的最佳位置的基础上,通过S1与第二个传感器的位置S2组合所获得的信息熵变化量进行计算,变化量最大即目标函数最大的传感器组合为前两个传感器的最佳位置,得到传感器最优分布组合(S1,S2),该方法即为顺序启发式传感器阵列优化布置算法;以相同的方式继续计算,当获得i-1个传感器最优位置分布点的分布组合时,选择使i个传感器位置组合获得的信息熵变化量最小的第i个点作为最优传感器的分布位置点,即获得i个传感器的最优分布组合(S1,S2,…,Si);对于最多N0个传感器,不断重复循环上述过程即可。对于从1到N0的所有传感器,只有当i个传感器的最优传感器位置是i+1个传感器的最优传感器位置的子集时,顺序传感器布局算法才会给出最优的传感器配置。不断重复以上步骤,完成传感器阵列优化布置计算,得到传感器优化布局方案。顺序启发式传感器阵列布置优化算法流程如图6所示。

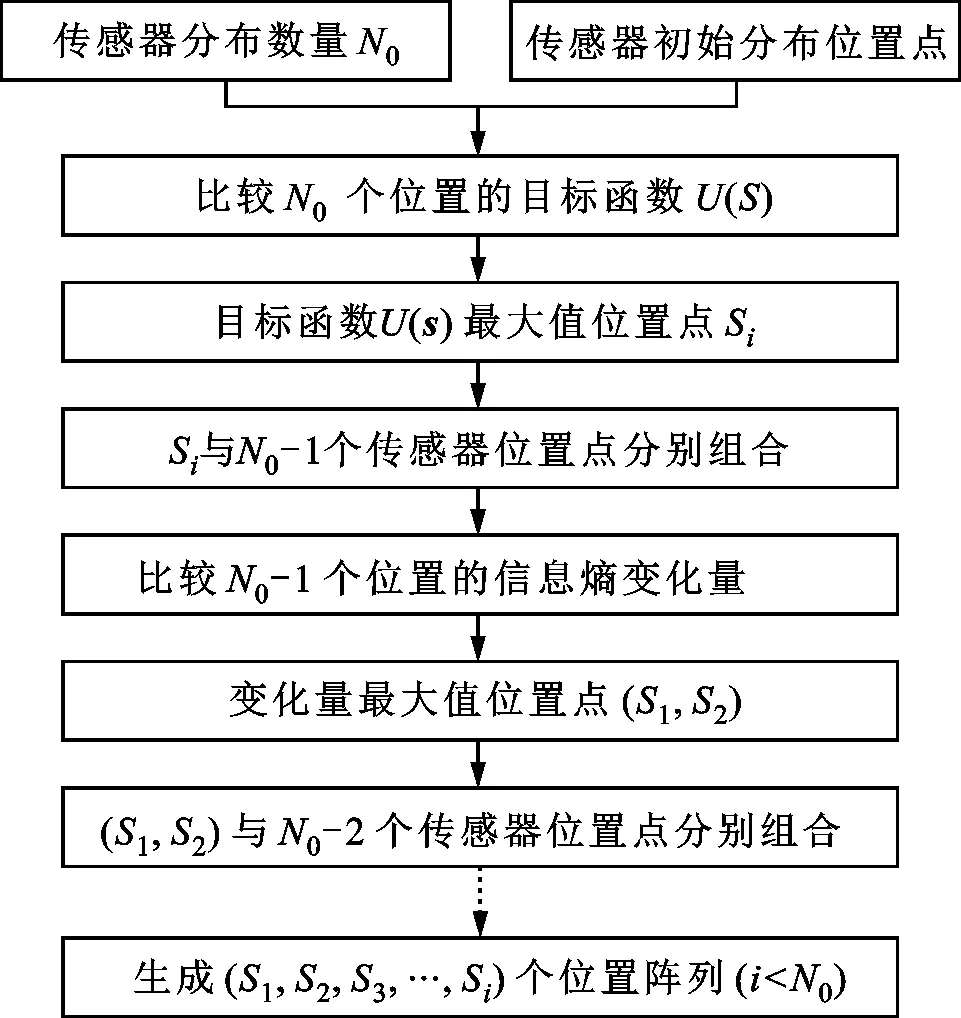
图6 顺序启发式阵列布置优化算法流程Fig.6 Flow chart of sequential heuristic array layout optimization algorithm

1.2 仿生侧线探测阵列优化评估方法

通过传感器阵列优化目标函数U(s)对优化布局进行初步计算后,考虑到水下航行器传感器布局的实际成本、经济效益及实际要求,需要针对已完成的传感器优化阵列进行相关性计算冗余度约减,对优化函数进行进一步评估,用最少的传感器准确地表征目标物的运动位置。

将传感器数量增加前后的两种布局分别表示为sj与sj+1,为了评估这两种布局下,对位置r处目标物位置探测的信息冗余度,引入斯皮尔曼相关性的概念,斯皮尔曼相关性系数R也称为等级相关系数或斯皮尔曼秩相关系数,利用单调方程评价两个统计变量的相关性[23]。当数据中没有重复值并且两个变量完全单调相关时,对应的斯皮尔曼相关性系数为1或-1。R根据原始样本数据的排序位置进行求解,数学表达式为

(14)

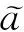
为了计算优化阵列分布之间的相关性,计算每个传感器位置分局sj(j=1,2,…,m)下,目标物位置在r时,对应的似然概率分布p(y|r,s),用于表征定位目标物位置的准确性。因此,各个分布sj间的相关性为

(15)

式中:i=2,3,…,Nrs;p(y|r(i),sj)表示在传感器位置布局sj下的压力测量y来自于r(i)的概率。

考虑到数据特征点较多,存在大量的冗余或不相关数据,影响斯皮尔曼相关性系数的计算,需要对特征样本进行有效的评估及选择。在样本集中,如果当前特征差异不大,那么这个特征对区分样本贡献不大,必须在构造特征过程中将其去掉,即选择有用特征摒弃无用特征。通过特征距离评估方法,对无明显变化的后验概率进行约减。计算各个特征在不同传感器阵列分布下的特征距离,距离越大的特征表示其对于计算相关性越有用,而距离越小的特征则认为特征值比较接近或者相同,对相关性计算没有作用。特征距离V计算公式[24]为

(16)

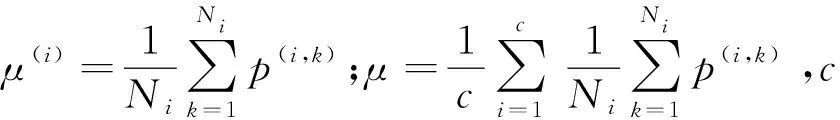
计算各传感器位置布局sj对每一个目标物位置ri的似然概率,计算每个目标物位置ri所有的似然概率间的特征距离V。对特征距离进行归一化后,根据特征距离V的分布特点,选择特征距离的阈值。选择特征距离阈值以上的特征位置点进行相关性计算。

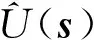
(17)

式中n为优化阵列传感器数,n=2,3,…,Nrs。

2 仿真实验及分析

2.1 优化阵列布局结果

将1.1.3小节优化算法流程写成程序文件,包括计算目标函数主程序、初始布局处理子程序、协方差矩阵计算子程序等,对初始布局下的传感器阵列优化进行计算。对图5通过流体仿真采集到的压力观测值变化曲线进行特征提取,获得阵列布局优化流程所需要的各传感器压力数据测量值,即理论压力值。计算傅里叶变换后的基频幅值,与水下航行器中传感器初始布局相结合,作为顺序启发式传感器布局优化算法的数据输入。

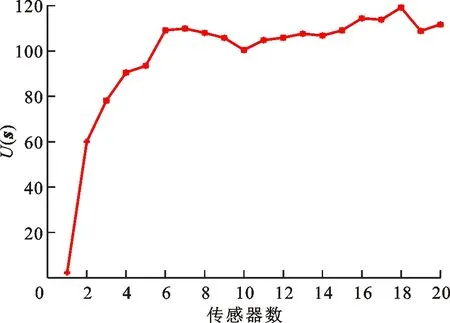
图7 目标函数变化曲线Fig.7 Variation curve of objective function

基于贝叶斯定理的顺序启发传感器布局优化方法,采用137个传感器观测点作为初始传感器分布点,计算不同传感器数下的目标函数U(s),结果如图7所示。可以看出,随着传感器数的增加,目标函数呈现出先上升后趋于不变的趋势,表明后续传感器的增加对目标位置信息量的获取没有意义,即增加传感器数量不会增加侧线阵列对目标位置探测的准确度。随后根据阵列优化分布位置点,初步生成阵列优化分布传感器数量为20个,有s=[28,26,23,21,18,42,3,38,31,17,32,29,45,22,2,13,44,27,34,30],式中数字为测点编号。阵列优化布局结果如图8所示。可以看出,传感器集中分布在水下航行器的曲线一侧,前端直线一侧传感器分布较少。

接着计算每一个目标位置在所有传感器位置布局下的似然概率,并求各概率之间的特征距离V。对特征距离进行归一化后,根据特征距离评估值分布特点,选择特征距离的阈值为0.5。特征距离与样本特征之间的关系如图9所示,可以看出,第1、3、4、5、12、13、14、15、16个目标位置特征点的特征距离评估值较高。

图9 特征距离评估值变化曲线Fig.9 Variation curve of evaluation value of characteristic distance

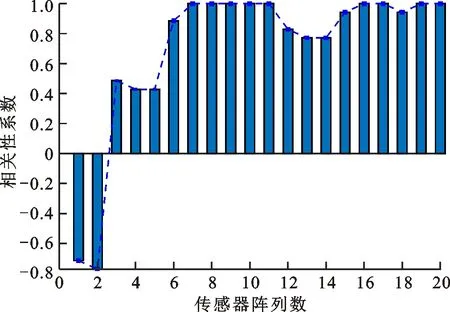
图10 特征选择后的相关性系数变化Fig.10 Change of correlation coefficient after feature selection

选择特征距离阈值以上的特征位置点进行相关性计算,结果如图10所示。可以看出:随着传感器数量的增加,两相邻布局之间的相关性系数呈变化趋势;当传感器数量增加时,若相关性系数变大,则传感器阵列对目标物位置探测的信息冗余度提高,增加传感器是没必要的;当传感器数量增加时,若相关性系数变小,则传感器阵列对目标物位置探测的信息冗余度降低,即提供了有助于目标物位置确定的有用信息,增加传感器是必要的。

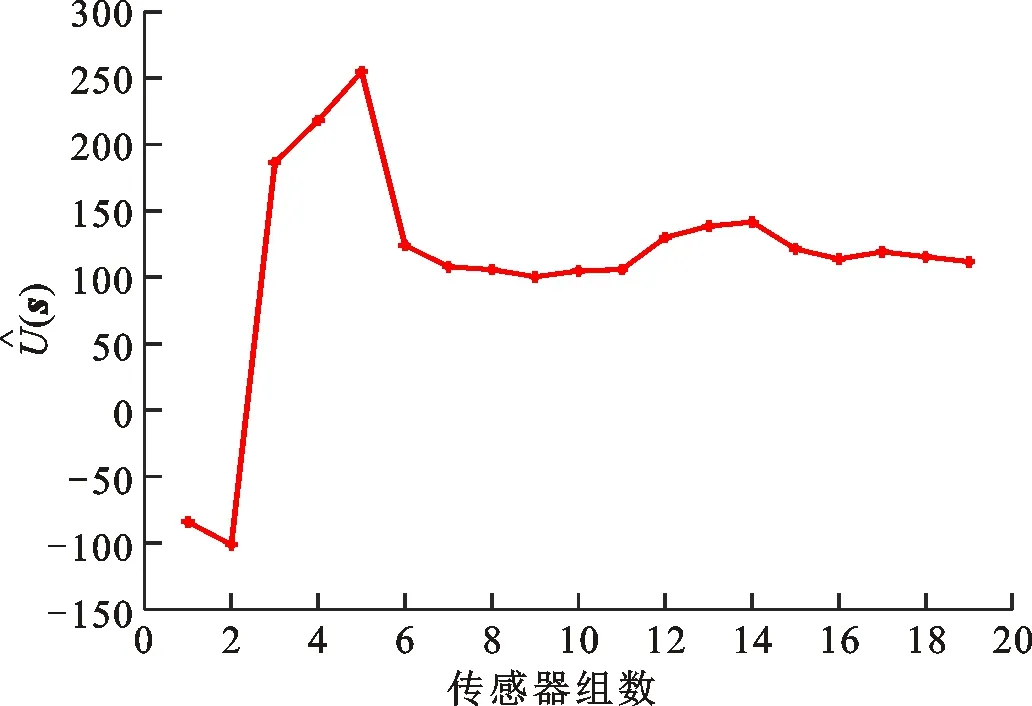
图11 评价函数变化曲线Fig.11 Variation curve of evaluation function

2.2 目标探测概率表征

依据2.1小节中对水下传感器优化阵列的计算结果、传感器数量及传感器分布位置sbest,已经确定水下航行器传感器最优分布方案,下面对优化阵列的有效性及准确性进行证明。传感器优化布局验证采用基于概率的传感器布局验证方法,计算在该优化阵列分布sbest下,探测各目标物位置点的后验概率函数值,用概率表征探测到的目标物位置,反馈目标物位置坐标点,具体步骤如下:

(1)按照初始阵列布局在水下航行器上布置传感器;

(2)某一位置目标物进行拟定运动,采集运动过程中流场压力值随时间的变化情况;

(3)将压力信号进行特征提取得到各传感器接收到的压力信号,利用贝叶斯概率模型计算压力来自所有目标物可能位置的概率;

(4)将各目标物位置的概率与真实目标物位置比较,确定最大概率是否对应真实目标物位置,若是,则认为该传感器布局可以对目标物位置进行评估及探测。

水下航行器传感器阵列布局验证流程如图12所示。

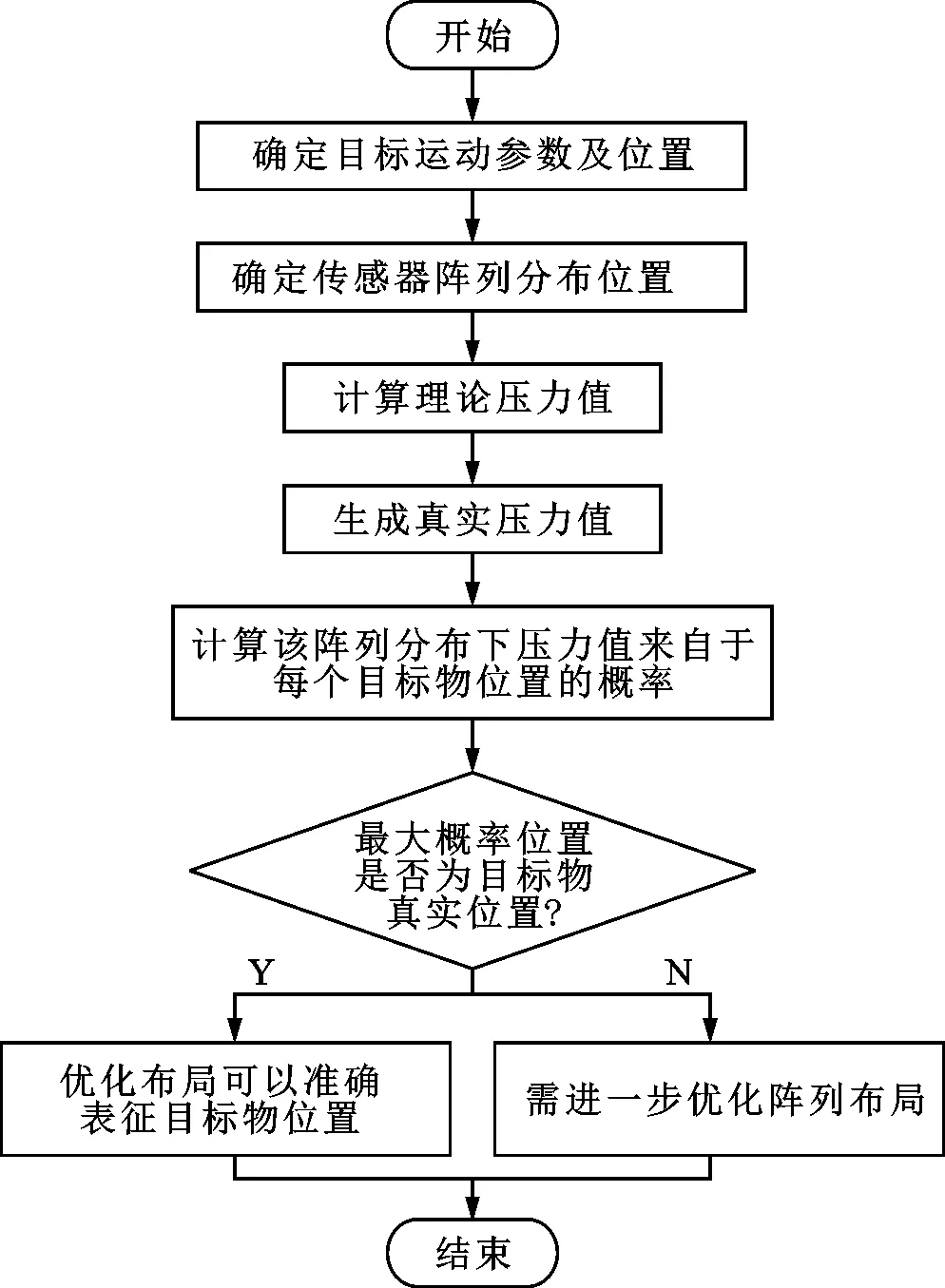
图12 概率表征流程Fig.12 Flow chart of probability representation

(a)优化阵列布局方案

(b)均匀阵列布局方案

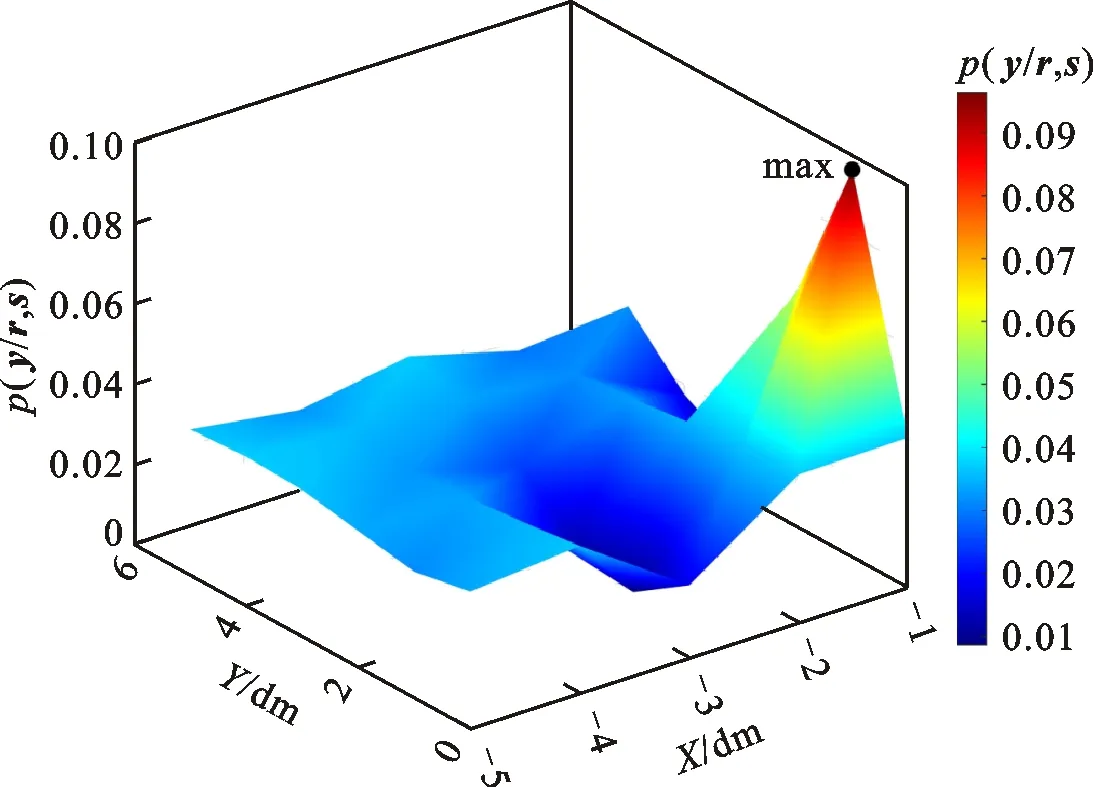
(c)优化布局阵列探测位置编号2处的目标物概率

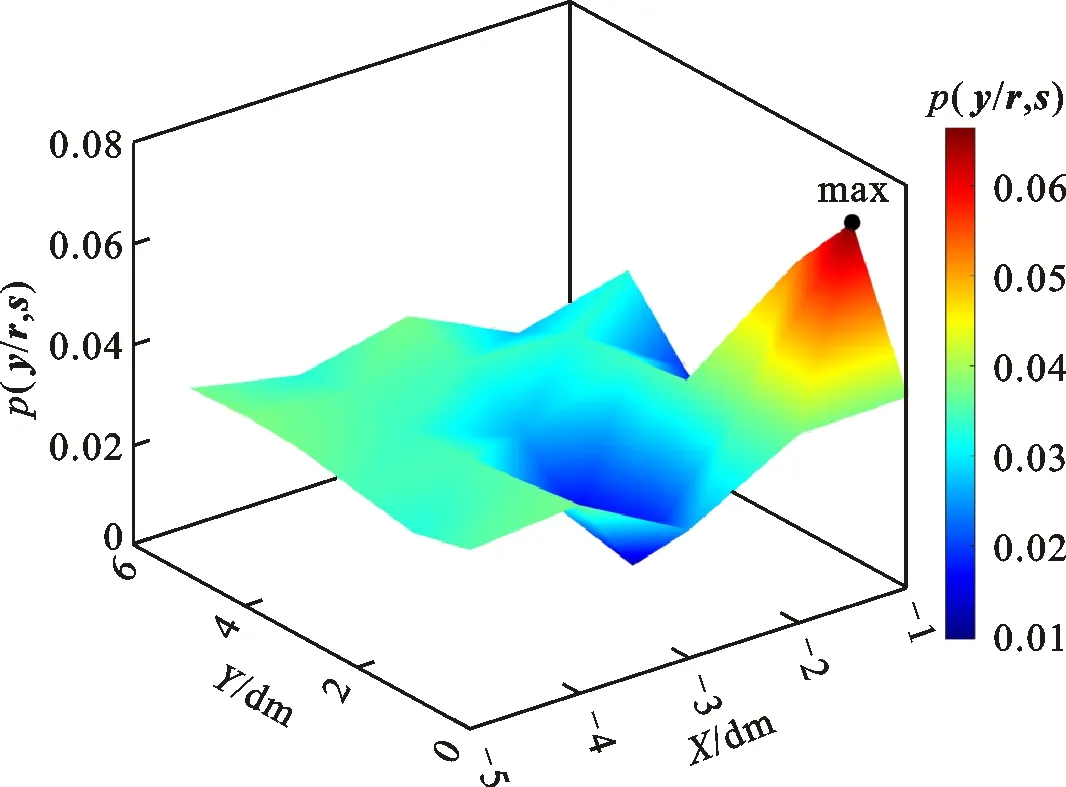
(d)均匀布局阵列探测位置编号2处的目标物概率

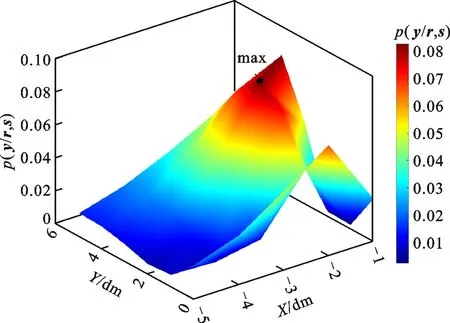
(e)优化布局阵列探测位置编号9处的目标物概率

(f)均匀布局阵列探测位置编号9处的目标物概率图13 优化阵列与均匀阵列布局及其探测的目标物位置概率Fig.13 Optimized array and uniform array layout scheme and probabilistic representation of detecting target position

通过优化阵列分布sbest与均匀分布snormal分别对探测某一位置目标物概率的表述,对比两种阵列探测目标物位置的优劣性,达到对传感器阵列优化分布检验的目的。两种阵列分布形式及相对应的探测目标物位置概率表征如图13所示。图13d中,均匀阵列探测导致概率分布辨识度不高,干扰区域概率较高,接近5%;图13c中,优化阵列探测的目标位置概率峰值更加明显,且干扰区域概率减小到1%以下。同样地,对比图13e与图13f,前者目标位置辨识度更高,干扰区域概率降低。对于探测远近两个目标物的位置,传感器优化阵列都优于传统均匀布置阵列。

从图13可以看出,在传感器数量一致的前提下,阵列优化布局方案sbest=[28,26,23,21,18,42]探测位置编号2处与位置编号9处的目标物概率均比传统均匀布局方案snormal=[10,25,40,113,125,136]探测位置编号2处与位置编号9处的目标物概率高,且各个探测区域位置的区别程度也更加明显,直接证明了优化布局方案在探测目标物位置上的优势及准确性与可行性。