基于光纤传感技术的泥石流冲击力测量系统与反演方法

夏曼玉，张少杰，杨红娟，杨超平

(1. 中国科学院、水利部成都山地灾害与环境研究所 中国科学院山地灾害与地表过程重点实验室,四川 成都 610041; 2. 中国科学院大学, 北京 100049)

0 引 言

泥石流冲击力是泥石流防治工程设计中最重要的参数之一[1]。泥石流冲击力主要分为浆体动压力和石块撞击力。其中，浆体动压力(P)分为流体静力学模型(P=αρcgh)[2]和流体动力学模型(P=kρcu2)[3]，参数α和k需要借助冲击力测量数据拟合确定。目前对泥石流冲击力的测量方法主要有野外测量和室内水槽实验。水槽实验易控易测，且精度高，故而成为泥石流浆体动压力研究的主要手段。例如，Scheidl等采用水槽实验分析了泥石流的冲击模型，证明了流体动力学模型比流体静力学模型更合理[4]；Yang等通过开展水槽实验提出了基于冲击力测量的泥石流内部流速分析方法[5]；Tang等结合材料变形特性和流体动力学参数，修正了泥石流冲击力计算模型，并利用水槽实验的实测数据对修正模型进行了校验[6]。

水槽实验一般采用压电式压力传感器测量泥石流冲击力[4-7]。压力传感器按照一定的排列方式和间距布设在钢梁的迎水面，再将钢梁以垂直于床面的方式布置在水槽末端[5]。当泥石流与压力传感器接触后，便可探测和采集泥石流的冲击力。这种传统测量模式下的电信号易受电线阻抗效应的影响，且未考虑测量系统的变形对测量结果的影响[6]。光纤布拉格光栅(Fiber Bragg Grating，FBG)克服了传统泥石流监测传感器的缺点，具有抗腐蚀、耐高温、灵敏度高、抗电磁干扰、安装方便等优点，可以在地质条件复杂、天气剧烈变化等恶劣环境下长期稳定工作。光纤布拉格光栅已经广泛应用在结构健康监测等工程领域[8-11]，并在地质灾害方面得以逐步推广应用[12-15]。近年来，各种基于光纤布拉格光栅的泥石流探测设备被开发出来[16-21],但目前尚未有将光纤传感技术应用在泥石流水槽冲击力测量的相关报道。

为了克服压电式压力传感器测量模式在泥石流冲击力研究中存在的问题，进一步提升实验测量数据的可靠性，本文设计了基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统；依据泥石流的宾汉体特性和悬臂梁受冲击形成的力-光耦合效应，构建泥石流冲击力反演公式，并通过水槽实验对泥石流冲击力公式进行校验，为水槽实验中的泥石流冲击力测量和反演提供支撑。

1 基于光纤传感技术的测量系统

1.1 测量系统设计与光纤布拉格光栅力-光转化机制

在测量泥石流冲击力时，承载传感器的梁会产生弯曲变形，对冲击力测量结果造成一定的影响。以往的冲击力研究没有考虑到冲击变形对测量结果的影响，本研究以此为出发点，将材料的冲击变形考虑在内，结合光纤布拉格光栅的测量优势，设计了基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统。如图1所示，基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统包括L型悬臂梁和固定其上的光纤布拉格光栅应变传感器。悬臂梁材料选择适用于野外环境且可承受较高冲击荷载的301钢板，材料的弹性模量(E)为2.0×1011Pa。与冲击力计算相关的参数主要是梁的宽度和厚度。在保证梁不会被破坏的同时，将梁的宽度设计得尽量小，即钢板的宽度小于水槽宽度(46 cm)的1/10，以减少对泥石流流动的影响，同时考虑到粘贴光纤布拉格光栅的施胶宽度(不小于1 cm)，将钢板的宽度设置为2.000 cm；钢板的厚度主要和光纤波长信号相关，通过对不同厚度的悬臂梁进行水槽冲击预实验，最终将钢板的厚度设置为0.095 cm，此时结构仍在弹性阶段，并且光纤波长信号变化明显。综上所述，将钢板的尺寸设置为25.000 cm×2.000 cm×0.095 cm，在距离一端5.000 cm处将钢板弯折90°，形成L型悬臂梁。在下半部分按照螺栓的尺寸打孔，便于固定在水槽底部；将L型测量系统固定于水槽底部，利用其上半部分的弯曲变形测量得到作用其上的泥石流冲击力。

图1 基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统示意图

如图2所示，泥石流的冲击力会导致L型悬臂梁弯曲，光纤布拉格光栅应变传感器的中心波长会发生变化。该应变传感器对应变和温度的变化敏感，其中心波长偏移量与温度、应变之间均具有良好的线性关系。在进行水槽实验时，泥石流冲击的持续时间较短，可以忽略温度变化的影响，中心波长偏移量仅对应变敏感。根据中心波长的最大偏移量可以求解该应变传感器的峰值应变。其表达式为

图2 悬臂梁受泥石流冲击示意图

(1)

式中：a为光纤布拉格光栅应变传感器应变一次项系数，由该应变传感器型号确定；λ0为应变光栅初始中心波长；λ为应变光栅测量中心波长，由该应变传感器测量记录，本文取波长曲线最高点的值；ε为悬臂梁应变，本文取峰值应变。

悬臂梁于测点处的峰值应变还可根据材料的本构关系求得。其表达式为

(2)

式中：E为结构材料的弹性模量；σ为悬臂梁的应力。

悬臂梁的应力和弯矩之间有如下关系

(3)

将式(1)～(3)进行整理，可得

(4)

式(4)将光纤布拉格光栅中心波长偏移量与悬臂梁变形建立联系，为该测量系统应用于泥石流冲击力测量提供了理论基础。在已知悬臂梁材料参数和光纤布拉格光栅应变系数的情况下，仅测点处的弯矩是未知变量，其计算方法将在冲击力反演模型中进一步推导得出。

1.2 冲击力反演模型

目前，计算泥石流浆体动压力比较常用的公式[3,22-24]为

P=kρcu2

(5)

式中:ρc为泥石流密度；u为泥石流流速；k为泥石流冲击力系数，多为实验拟合得到；P为泥石流冲击力，本文特指浆体动压力。

式(5)表明,在泥石流密度一定的情况下，泥石流冲击力与流速的二次方呈线性关系。同时，泥石流流速随着流深的增加而增大，至流体表面达到最大流速。假设泥石流为宾汉体，则泥石流的垂向流速分布可通过式(6)～(8)推导得出。

宾汉体的应力-应变关系满足

(6)

式中：h为流深；z为计算位置处与床面之间的距离；θ为床面倾角；ρ为流体密度；g为重力加速度；η为流体刚度系数；τy为屈服应力；τ为流体切应力。

边界条件为

(7)

式中：us为表面流速。

进而可以推导出宾汉体的垂向流速分布为

(8)

式中：hc为流核厚度，可通过残留泥深估算[25]，即泥深曲线最终趋于平缓段的数值。

将式(8)代入式(5)中，可建立冲击力与流深的直接联系，从而得出冲击力的垂向分布公式。其表达式为

(9)

根据材料力学的相关知识，悬臂梁受到分布力作用时，可以求得测点处的弯矩。其表达式为

(10)

式中：h1为测点(应变传感器所在处)泥石流流深，本文测点位置固定。

利用相同的水槽实验工况开展预实验，各组实验的残余泥深均大于0.02 m。为了保证每一次冲击高度都超过测点位置，兼顾光纤布拉格光栅粘贴需要留出大于0.01 m的高度，选择将测点高度设置为0.02 m；h取泥石流最大流深，即泥深曲线最高点的数值。

结合式(9)、(10)，可得测点处弯矩的表达式[式(11)]。将式(11)代入式(4)中，可得泥石流冲击力系数表达式[式(12)]；再将式(12)代入式(5)中，可以得到表面处泥石流冲击力(最大冲击力)的计算公式[式(13)]。式(11)中，he为h与hc的差值。

为了求解冲击力计算公式中的未知参数，同时验证本文提出的泥石流冲击力测量方法的准确性，有必要开展水槽冲击实验。

(11)

(12)

(13)

2 水槽实验

2.1 实验装置

实验装置主要包括泥石流模拟系统和数据采集系统两部分。其中，泥石流模拟系统分为物源区、流通区及回收区，可模拟泥石流的运动过程；数据采集系统包括泥位、应变测量仪器和记录泥石流运动形态特征的高清摄像机。

2.1.1 泥石流模拟系统

泥石流模拟系统包括料斗、水槽和尾料池。其中，水槽长600 cm、宽46 cm、高40 cm，底部为钢板，两侧为透明玻璃。水槽坡度固定为12°，水槽上部与料斗相连，料斗设置有控制物料启动的闸门，水槽末端下方为尾料池，可将每次实验的样本进行回收利用。水槽的整体框架用钢管搭建，同时起到支撑和稳定作用。水槽实验装置如图3所示。

图3 水槽实验装置

2.1.2 数据采集系统

数据采集系统包括激光距离传感器、高清摄像机和基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统。水槽实验模型如图4所示，激光距离传感器的量程为0.05～500.00 m，精度为1.0 mm，采样频率为15 Hz，安装在冲击力测量系统的前上方，用于测量泥石流的流深变化。两台高清摄像机录像频率为每秒25帧，分别放置在水槽的末端和旁侧，在水槽的侧边利用白色防水胶带进行位置标记，通过影像解析测定流体的表面流速，即实验中通过泥石流表面乒乓球位置的变化确定泥石流的表面流速。

图4 水槽实验模型

基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统沿着水槽流向布置。为测得流体稳定状态下的冲击情况，将该测量系统安装在距离水槽末端60 cm处，即距离料斗9/10处，此时泥石流的运动已处于稳定状态。其中，光纤布拉格光栅解调仪的波长范围为1 528～1 568 nm，波长分辨率为0.1×10-12m，测量精度为±0.5×10-12m，采样频率为100 Hz，应变一次项系数a=0.001 nm·με-1，悬臂梁迎水面尺寸为20 cm×2 cm，横截面尺寸为2.000 cm×0.095 cm，即b=2.000 cm，c=0.095 cm。

2.2 实验材料

实验材料取自云南省昆明市东川区蒋家沟泥石流下游的原始堆积体。受到水槽尺寸的限制，同时为了减小颗粒组成差异对实验的影响，实验前筛去粒径大于20 mm的固体颗粒，仅取用粒径小于或等于20 mm的部分作为实验材料。为了解实验材料的颗粒组成情况，取3组样品进行颗粒分析。实验材料颗粒级配曲线如图5所示。

图5 实验材料颗粒级配曲线

2.3 实验工况

以泥石流密度为变量，开展了不同泥石流密度的水槽冲击实验。蒋家沟泥石流以黏性泥石流为主，同时考虑到如果泥石流密度过大会在该水槽中无法启动。本实验在黏性泥石流的密度范围(1.8～2.4 g·cm-3)中选取了3种密度(1.8、1.9、2.0 g·cm-3)，共开展了7组水槽实验，每组实验用料0.2 m3。实验过程为：将充分浸泡好的物料放置于料斗中，利用搅拌机将物料充分搅拌，快速拉开料斗的闸门，流体冲击布置于水槽末端的冲击力测量系统，最后回收至下方的尾料池中。实验过程中，利用数据采集系统对冲击过程的各项数据进行记录。为了记录到完整的泥石流冲击数据，数据采集系统在拉开料斗闸门之前启动。

2.4 实验结果

利用数据采集系统可获得每组实验的最大流速、最大泥深和光纤布拉格光栅波长最大偏移量的实测数据。实验结果可见表1和图6、7。为了去除冲击过程中的噪声，对泥深数据采用相邻平均法进行平滑；同时为了去除颗粒碰撞引起的光纤布拉格光栅波长测量的尖峰，对数据进行了低通滤波，综合分析各组的功率谱，截止频率选取0.4 Hz。

表1 水槽实验结果

图6、7显示了不同密度下实验数据处理前后的泥深和光纤布拉格光栅中心波长变化过程。由于光纤布拉格光栅中心波长偏移量与应变之间具有良好的线性关系，所以悬臂梁应变与光纤布拉格光栅中心波长呈现同样的变化规律。在同一实验工况下，泥深均呈现了先增大后减小的规律，光纤布拉格光栅中心波长偏移量同样呈现相同的变化趋势。对比不同实验工况结果发现，光纤布拉格光栅中心波长最大偏移量随着密度的增加而增大，即悬臂梁的最大应变与密度成正相关关系。根据冲击特征，可将冲击过程分为3个阶段：第一阶段为启动阶段，泥深迅速增加，流速增大，对钢板的冲击逐渐增大至最大；第二阶段为减缓阶段，在冲击达到峰值后，由于泥石流方量有限，并且运动过程中沿程损失，流速减缓，泥深减小，对钢板的冲击力逐渐减小；第三阶段为稳定阶段，泥石流极缓慢运动至停止流动，在水槽底部形成一定厚度的残留层。由于激光距离传感器和冲击力测量系统安装存在一定的距离，所以泥深曲线和光纤布拉格光栅中心波长变化曲线时间不同步，但总体变化趋势相同。

图6 不同密度下泥深变化

将数据采集系统得到的相关数据代入式(12)和(13)中，可得出每组实验的冲击力系数，进而求出各组的冲击力，计算结果见表2。

表2 冲击力计算结果

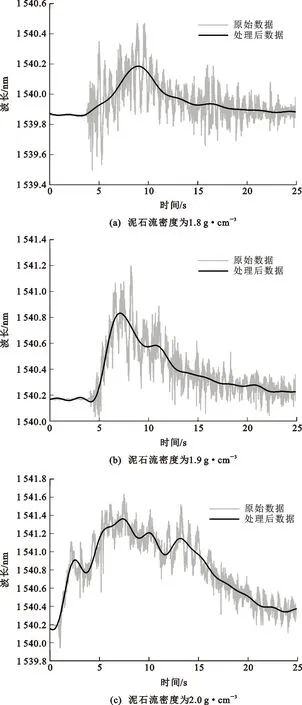
图7 不同密度下光纤布拉格光栅中心波长变化

根据7组水槽实验得出冲击力峰值为30.75～74.06 kPa。将同一密度的冲击力进行平均，得出密度1.8、1.9、2.0 g·cm-3的平均冲击力峰值分别为35.38、59.52、49.77 kPa，由于实验条件设置(如水槽尺寸、坡度、实验材料颗粒级配、方量、浆体密度等)的不同，以及后期提取泥石流浆体曲线方法的差异，水槽实验得出的泥石流浆体动压力有所不同，但多处在kPa量级。例如，利用蒋家沟泥石流堆积体作为物源，唐金波等开展水槽实验，对冲击力信号进行小波降噪处理，得出泥石流浆体动压力为12.72～18.64 kPa[23]；曾超等利用清水和小于2 mm颗粒配置的浆体(浆体密度为1.4～2.2 g·cm-3)开展水槽实验，得出泥石流浆体动压力为11.5～28.3 kPa[26]，与本实验得出的冲击力峰值相比偏小，这主要与实验设备、实验材料颗粒级配以及数据处理等方面的差异有关。

本研究中冲击力系数为0.92～1.95，均大于均质流体的动压力系数(0.5)，这与泥石流为非均质流体有关。章书成等根据1975年在蒋家沟所测得的泥石流冲击力系数约为3.0[24]；Zhang对蒋家沟测量得到的大约70组冲击力数据进行分析，得出蒋家沟泥石流冲击力系数为3.0～5.0[27]。本研究中的冲击力系数均小于以上由野外测量分析得到的结果，这是因为以上研究中考虑的是整个泥石流体，而在本研究中去掉了石块的影响，仅考虑泥石流浆体的影响。

3 结 语

(1)基于宾汉体假设推导出泥石流冲击力沿流深的变化规律，同时考虑到冲击变形对冲击力的影响，本次研究设计出基于光纤布拉格光栅的悬臂梁式泥石流冲击力测量系统。依据测量系统的变形特征和泥石流的流体特性，构建了基于宾汉体的冲击力反演公式；通过对水槽实验收集到的数据分析得知，数据之间呈现较好的规律性，光纤布拉格光栅中心波长最大偏移量随着密度的增加而增大；同一密度下光纤布拉格光栅中心波长变化与泥石流冲击过程相符，这与泥石流的冲击特性相吻合，从而验证了冲击力反演模型和测量系统之间具有良好的适应性。

(2)根据水槽实验得出泥石流冲击力峰值为30.75～74.06 kPa，这与前人利用蒋家沟泥石流堆积体开展水槽实验得出的泥石流冲击力同属一个量级，从而证明了测量系统的可靠性。同时，冲击力系数为0.92～1.95。一方面，冲击力系数均大于均质流体的动压力系数(0.5)；另一方面，该值低于蒋家沟泥石流的野外测量经验值(3.0)，这是因为该经验值考虑的是整个泥石流体，而在本研究中去掉了石块的影响，仅考虑泥石流浆体的影响。以上研究结果证明了本文提出的测量系统在充分克服传统压电式压力传感器自身缺陷的基础上，具有极高的测量稳定性、可靠性，可为水槽冲击力的测量以及冲击力反演提供有效支撑。

(3)本文提出的冲击力测量系统与水槽实验的冲击特性之间具有较强的关联性，为了进一步将该测量系统进行推广，今后有必要补充相关实验。例如，借助砝码的应力-应变标定实验；包含清水组和浆体组的对照实验；采取多测点测量的方式校验泥石流冲击力垂向分布特征，进一步提高测量系统精度的实验等。