“化学反应工程”中动力学参数确定方法探索

齐 济，周 泉，张 伟

(大连民族大学 生命科学学院，辽宁大连 116605)

2017年2月18日,教育部在复旦大学召开了高等工程教育发展战略研讨会，正式提出“新工科”的概念，随后各高校的新工科探索实践陆续开展。2019年5月，教育部提出要从五个方面推动新工科建设，第五项即“大学教学组织创新再深化”。新工科建设的快速推进[1]，使高等院校面临新旧工科的双重挑战，在新工科的浪潮中，旧工科不进则退，获得国际专业认证[2]、教育部专业认证[3]成为各大学工科专业的努力方向。“化学反应工程”是化工专业的核心课程，目前课程改革主要包括四方面：一是设备操作通过多媒体(仿真)动画生动化[4-7]；二是计算内容通过计算机和软件科学化简易化[8-10]；三是实验辅助理论内容[11-13]；四是设计、实习和竞赛辅助理论内容[14-16]。所有改革都是以课程内容为核心，以培养符合时代要求的应用型人才为目的而展开的。“化学反应工程”中动力学参数的确定，是动力学中很重要的部分，动力学参数确定后，才能得出实用的反应速率方程，对反应器的体积进行设计计算，从而实现反应时间和生产周期的精确设计。动力学参数的传统确定方法是通过数据处理后进行反复绘图试验估出，本文在传统积分法和微分法的基础上，通过简单易得的Excel绘图，实现最小二乘法拟合，通过相关系数分析，对参数确定方法的适用范围进行了分析与讨论。

1 动力学参数的概念

“化学反应工程”中的动力学参数，是指速率方程中所包含的参数，如吸附平衡常数、反应速率常数以及反应级数。平衡常数和反应速率常数均是温度的函数，可以用阿伦尼乌斯方程表示，方程中的活化能、指前因子和吸附热也属于动力学参数。动力学参数的数学模型有两种：双曲线型和幂函数型。双曲线型需要确定反应速率常数和吸附平衡常数；幂函数型需要确定反应级数和反应速率常数。这些动力学参数确定后，其他参数均能随之确定。动力学参数的确定方法是在实验数据的基础上进行估值，有两种方法：积分法和微分法。化学反应工程要解决的重要问题是反应速率方程的确定，而反应级数的确定是确定反应速率方程的先决条件。

2 反应级数的估值方法

以恒容反应速率方程为幂函数为例，反应速率方程如式(1)。

(1)

(2)

微分法估计反应级数，先对式(1)两边取自然对数得式(3)，以lnCA为横坐标，以lnrA为纵坐标绘图,斜率为反应级数。

lnrA=αlnCA+lnk。

(3)

3 实验数据的选择

以李绍芬《化学反应工程》(第三版)例2.2中的实验数据为例，醋酸和丁醇在等温条件下进行酯化反应如式(4)。

CH3COOH+C4H9OHCH3COOC4H9+H2O。

(4)

醋酸的初始浓度CA0为0.233 2 kmol·m-3,丁醇的初始浓度为1.16 kmol·m-3,测得反应时间t和醋酸转化量CA0-CA的数据见表1。

表1 反应时间与醋酸转化量实验数据

4 结果与讨论

4.1 积分法估值

将表1中的实验数据通过Excel函数进行换算，结果见表2。

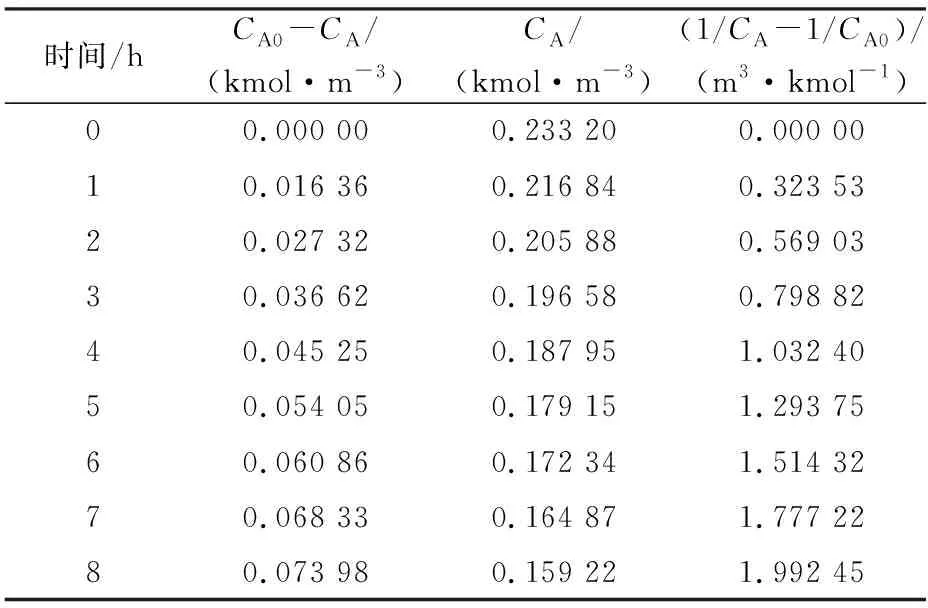
表2 积分法实验数据处理

图与t关系图

故反应级数为2的假设在实验范围内成立,根据直线斜率得反应速率常数k为0.254，得出反应速率方程如式(5)。

(5)

4.2 微分法估值

将表1中的实验数据通过Excel函数计算完成换算，处理后的结果见表3。

表3 微分法实验数据处理

以lnCA为横坐标，lnrA为纵坐标，Excel绘图如图2。

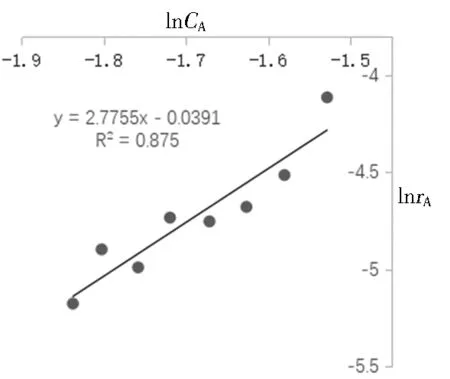
图2 lnrA与lnCA的关系图

得到的直线相关系数只有0.875，由斜率可估出反应级数为2.775 5级,由截距可估出反应速率常数k为0.962，反应速率与浓度的关系式如式6。

rA=0.962CA2.7755。

(6)

4.3 分析与讨论

基于表1的实验数据，运用积分法，首先需要假设反应级数，然后绘图试差，若假设不正确，需要反复绘图试验；运用微分法拟合度不高，估出的反应级数与反应速率常数与积分法差异很大，说明微分法的适用是有条件的。在学习过程中，有的同学会感到迷茫，为什么这种两边取对数画直线的方法叫微分法呢？其中并没有运用微分方程，用的是幂函数型反应速率方程。通过上述实例数据处理分析，可以让学生直观明了地理解应用微分法进行动力学参数估值，反应速率的函数模型和实验数据都是有条件的，双曲线型积分困难更适合微分法，微分法要求实验测试点必须密集，本文采用的数据为每间隔一小时测定一次，不适合微分法估值。另外，在不需要深入分析反应机理，单一因素考查反应速率的情况下，也可首先绘出关键反应组分的浓度CA与反应时间t的关系，如图3。

图3 浓度CA与反应时间t的关系

曲线通过多项式拟合的相关系数为0.999，接近1，拟合度较好。对拟合方程求导，得出恒容反应速率方程如式(7)。这种求解反应速率方程的方法，抛开了幂函数型和双曲线型反应数率数学模型的限制，不用对反应级数等动力学参数进行估值，直接拟合出反应速率方程，在实验范围内应用较方便。

(7)

5 结 语

“化学反应工程”是化工类的专业基础课，在新工科不断探索、教学改革不断深入、工程教育认证不断推进的进程中，均需要真正理解复杂工程问题的内涵，对工程问题的复杂性形成全面而准确的认识，强化培养学生在面对普遍存在的冲突场景时解决问题的能力。在解决复杂工程问题能力的培养方面，学校需要着重从课程体系、教学内容和教学模式上进行变革,其中教学内容的融会贯通、深入拓展、整合创新、学以致用是教学改革的坚实基础。