不同工况下机电复合传动装置行星齿轮系统瞬态温度场
2021-11-15庞大千曾根李训明郭磊赵富强孙占春
庞大千, 曾根, 李训明, 郭磊, 赵富强, 孙占春
(1.中国北方车辆研究所, 北京 100072; 2.车辆传动重点实验室, 北京 100072)
0 引言
行星齿轮系统由于结构紧凑、承载能力强等特点,广泛应用于高速重载情况下的机电复合传动装置。目前对于行星齿轮系统的研究大多集中于故障诊断及动态特性研究方面[1-2],而对于瞬态温度场的研究则非常匮乏。在高速重载情况下,轮齿表面会形成复杂和非均匀的温度场,齿轮的齿面接触温度也会比以往高很多。较高的齿面温度常常会导致油膜断裂,使得啮合在一起的轮齿更容易互相粘连,在旋转时将齿面剥离[3-5]。行星齿轮系统在高速重载工况下更容易形成高温环境,使得齿面有更高的几率出现损伤。
1937年,Blok[6]利用二维摩擦热通量公式,推导出了两物体相对滑动时的瞬态接触温度近似公式。同年,Blok[7]利用假设恒定速度的方式提出了齿轮瞬态接触温度的计算公式。1963年底,Blok[8]提出可以预测润滑状态及闪现温度。1974年,Tobe等[9]通过进一步改进啮合间的摩擦热分配来研究瞬时接触温度。Terauchi 等[10]使用示波器测量齿轮表面温度,以改进齿轮温度的数值分析。Wang等[11]、Patir等[12]和Townsend等[13]发展了齿轮温度场分析理论,研究了齿轮端面对流换热系数、啮合齿面摩擦热流量等边界条件,建立了齿轮有限元本体温度场,得到了齿轮啮合过程中的本体温度的大小和分布情况,研究了输入载荷、几何参数和润滑特性对齿轮温度场的影响。1993年,Anifantis等[3]建立了二维温度场有限元分折和计算模型,对加载边界条件以及热载荷在主、从动轮间的分配问题进行了研究。Tevrus[14]采用数值和实验两种方法对齿廓温度进行预测。Shi等[15]对机车牵引齿轮的温度场进行了分析。Wang 等[16]对螺旋伞齿的摩擦热产生以及瞬态热特性进行了充分研究。Li等[17]利用有限元法对齿轮偏载后的稳态温度场进行了分析。Luo等[18]利用有限元法对齿轮本体温度场的影响因素进行了分析。Zhang等[19]利用热弹流耦合方法来确定螺旋伞齿的齿面温升。Li等[20-21]通过有限元和实验的方法对含裂纹直齿轮瞬态温度场及斜齿轮瞬态温度场进行了研究。宋万良等[22]对齿轮系统固体膜润滑齿面温度进行了分析和计算。
综上所述,目前对于齿轮温度场的研究大部分停留在定轴齿轮系统阶段,行星齿轮系统的温度场研究非常匮乏。因此,本文拟对行星齿轮系统模型进行仿真实验研究,以揭示转速、扭矩以及输出功率对于行星齿轮系统齿面不同区域的影响规律,并通过试验验证本文所用方法的可靠性。本文的研究结果可为机电复合传动用行星齿轮系统的高质量设计和表面强度研究提供可靠的理论依据。
1 温度场分析的微分方程和边界条件
本文研究的传热模型为线性的,其三维热传导微分方程的一般形式为
(1)

齿轮啮合摩擦产生的热流施加在齿面上,建立齿轮的非稳态热传导微分方程如下:
(2)
因此,温度场是一个空间和时间的函数,即T=f(x,y,z,t)。根据Blok的理论[8],瞬态过程只能在啮合齿面N上观察到,是一种很薄的热层。瞬态的影响对于热层下的区域可以忽略[12]。当齿轮开始运动到足够长时间后,齿轮体温度将趋于稳定[8]。齿轮的摩擦散热和冷却散热也趋于平衡,各轮齿的温度变化完全相同,因此采用单个轮齿进行温度场研究。图1所示为单齿传热模型。图1中,S为齿侧壁,J为齿轮毂侧壁,K为J的镜像面,d为齿轮毂内壁,t1为齿根圆面,t2为齿上壁。
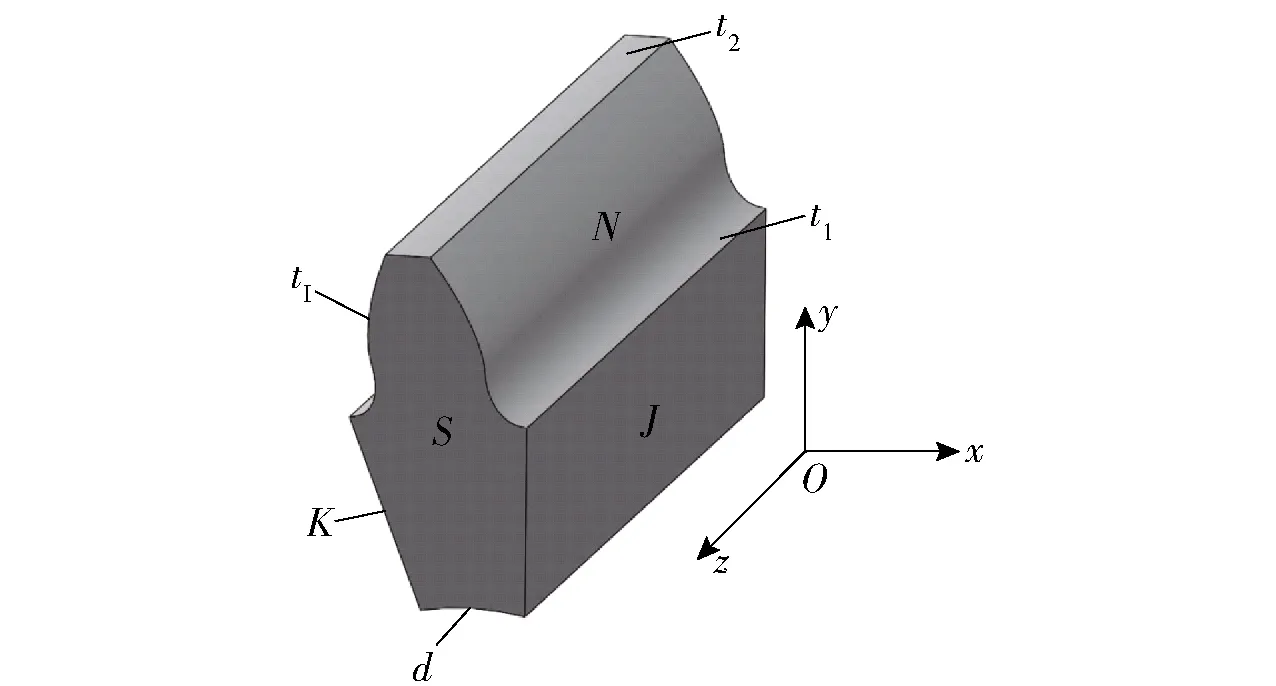
图1 单齿传热模型Fig.1 Single tooth heat transfer model
在图1的单齿导热计算区域,非稳态温度场还应该满足以下边界条件与初始条件:
1)啮合面(N区),其边界条件由(3)式给出:
(3)

2)齿轮侧,即图1中的边界S,其边界条件由(4)式给出:
(4)

3)齿顶面,即图1中的边界t2,其边界条件由(5)式决定:
(5)
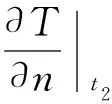
4)非啮合齿面,即图1中的边界t1,其边界条件由(6)式决定:
(6)
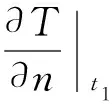
5)边界d,其边界条件由(7)式决定:
(7)
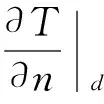
6)齿面J、K表面有导热现象,两表面的导热热值相等,其边界条件为
(8)
T|J=T|K.
(9)
7)初始条件为
T=f(x,y,z,t)|t=0 s.
(10)
2 齿轮参数及模型建立
表1所示为太阳轮、行星轮及外齿圈的参数。为了使计算结果更加准确,采用全齿轮建模(见图2(a));为了确保计算速度以及计算精度,有限元模型使用区域网格加密(见图2(b))。由于本文计算瞬态温度场,加密网格类型采用六面体,网格数量为495 980.
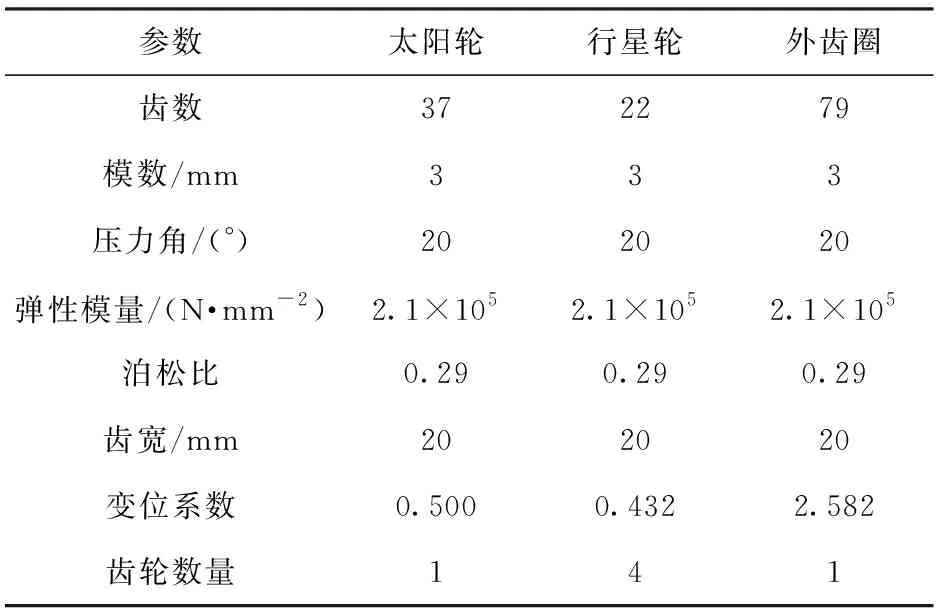
表1 行星齿轮系统参数Tab.1 Planetary gear system parameters

图2 行星齿轮系统三维模型及有限元网格Fig.2 Three-dimensional model and finite element grid diagram of planetary gear system
为了更好地说明齿面瞬态温度场的位置与设定,将齿面分为3个区域进行标注(见图3),由于齿廓面及节线处的相对滑动速度较小,本文只讨论齿根面和齿顶面的温度变化。
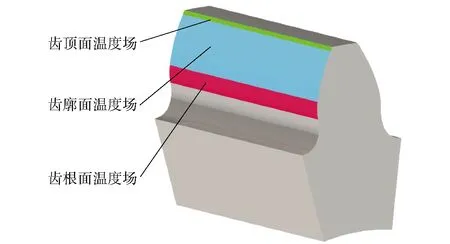
图3 齿面接触区域划分示意图Fig.3 Schematic diagram of tooth surface contact area division
3 算例及结果分析
本节将讨论不同扭矩、不同转速以及不同输出功率对行星齿轮系统齿面瞬态温度场的影响情况,并针对上齿面和齿根面温度场变化进行详细分析。根据实际运行情况,行星齿轮系统为喷油润滑模型;根据喷油润滑而言,将摩擦系数设置为0.05,由于行星轮存在公转及自转,为了表述结果和分析更加简洁,在分析行星轮温度场时以太阳轮转速作为参考。
3.1 不同转速对行星齿轮系统温度场的影响
3.1.1 不同转速对太阳轮瞬态温度场的影响
对相同扭矩、不同转速下的行星齿轮系统齿面瞬态温度场进行分析,为行星框架加载500 N·m扭矩,外齿圈固定,太阳轮转速依次设置为3 000~9 000 r/min,每1 000 r/min一个转速点,不同转速下太阳轮齿面瞬态温度场如图4所示。

图4 不同转速下太阳轮齿面瞬态温度场(扭矩500 N·m)Fig.4 Transient temperature field of sun gear tooth surface at different speeds (500 N·m)
由图4(a)可以看出,随着转速上升,齿面瞬态温度绝对值均有升高,齿顶面与齿根面温度升高幅度基本相同,而齿廓面温度升高幅度则较小。这主要是因为当进入齿廓面啮合时,齿面间相对滑动速度逐渐减小,当啮合面处于节线处时,相对滑动速度为最小,位于图4中旋转角度-2.2°位置,此时齿面瞬态温度为最低,且此处的温度随着转速的提升并没有出现较大的变化。从图4中还可以看出:齿顶面温度绝对值要大于齿根面,齿顶面、齿根面最高温度,如图5所示;随着转速增加,齿顶面与齿根面的温差逐渐增大,表明随着转速升高,齿根面与齿顶面的最高温度差将逐渐增大,当转速超过5 000 r/min后温度升高斜率将会降低,具体升高数值图如表2所示。

图5 不同转速下太阳轮齿根面与齿顶面最高温度曲线图(扭矩500 N·m)Fig.5 Maximum temperature curves of tooth root surface and tooth top surface of sun gear at different rotating speeds (500 N·m)

表2 不同转速下太阳轮齿根面和齿顶面最高温度Tab.2 Maximum temperatures of root surface and top surface of sun gear at different rotating speeds
3.1.2 不同转速对行星轮瞬态温度场的影响
对相同扭矩、不同转速下的行星齿轮系统齿面瞬态温度场进行分析,为行星框架加载500 N·m扭矩,外齿圈固定,太阳轮转速依次设置为3 000~9 000 r/min,每1 000 r/min一个转速点,不同转速下行星轮齿面瞬态温度场如图6所示。
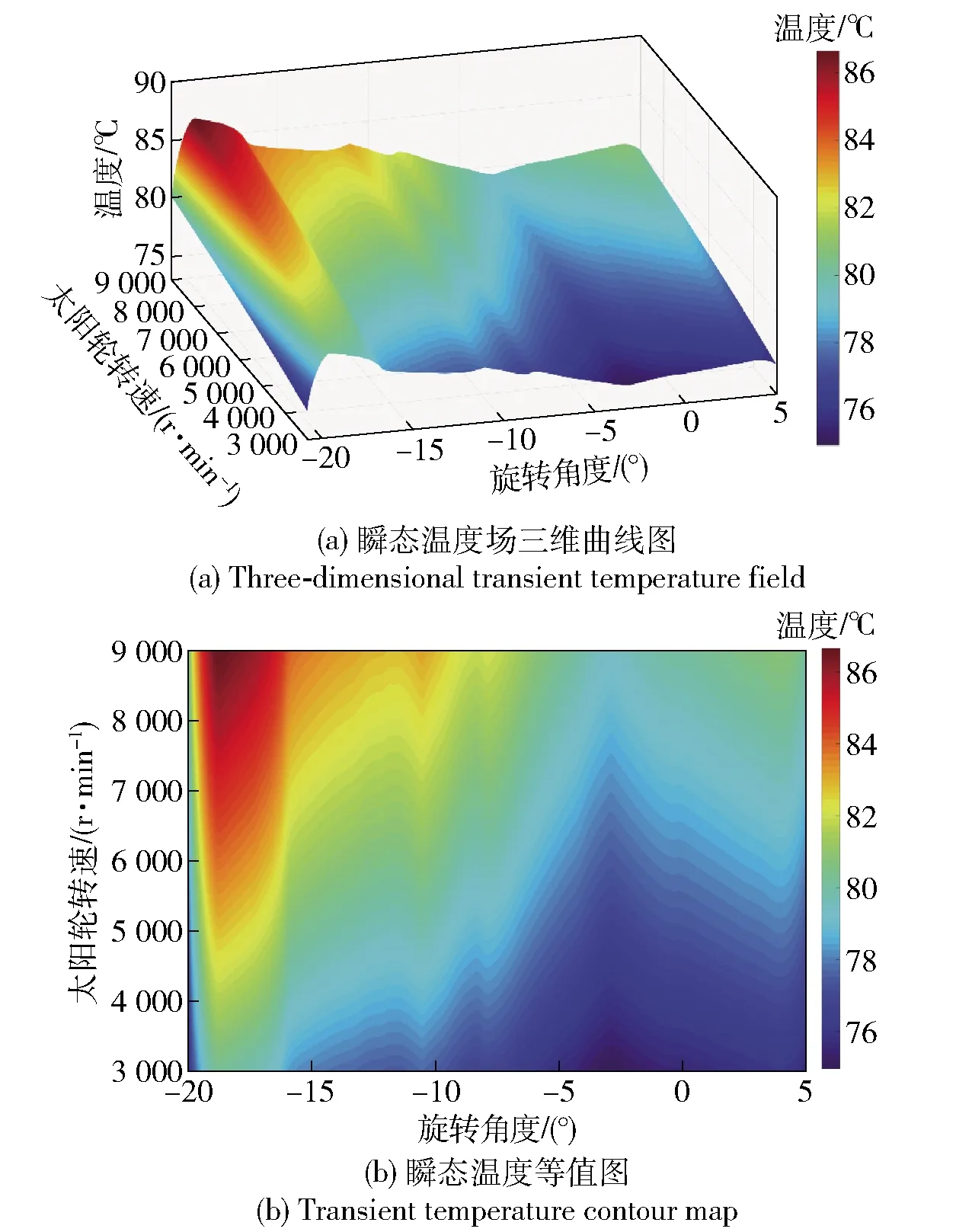
图6 不同转速下行星轮齿面瞬态温度场(扭矩500 N·m)Fig.6 Transient temperature field of planetary gear surface at different speeds (500 N·m)
由图6可知:不同转速下行星轮齿面瞬态温度随着转速升高而增大;齿根面的最高温度大幅高于齿顶面的温度,并且齿顶面最高温度的增加量很小(由于齿根部位散热较差,容易积累热量从而造成齿面胶合,此系统后续需要进行优化,从而使齿根面瞬态温度降低);行星轮齿根与齿顶面最高温度差也存在随转速升高的趋势,温差并不大,但温差绝对值要大于太阳轮(见图7)。具体温度值如表3所示。

图7 不同转速下行星轮齿根面与齿顶面最高温度曲线图(扭矩500 N·m)Fig.7 Maximum temperature curves of root surface and top surface of planetary gear at different rotating speeds(500 N·m)
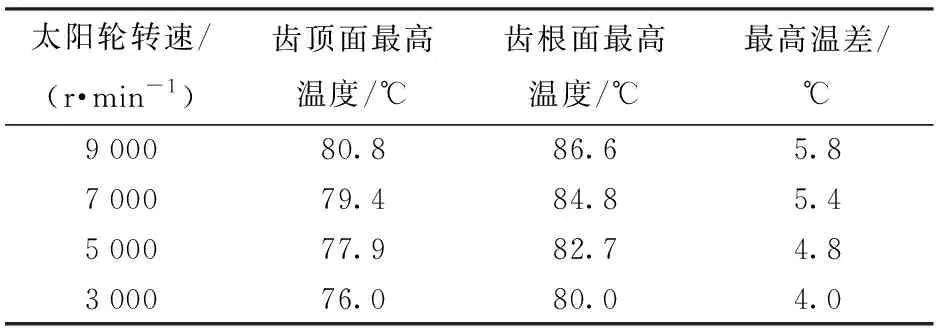
表3 不同转速下行星轮齿根面和齿顶面最高温度Tab.3 Maximum temperatures of root surface and top surfacer of planetary gear at different rotating speeds
由表3可以看到:行星轮啮合时齿根面的高温区域要大于齿顶面;齿根面与齿顶面呈现的温度区域并不像太阳轮那样具有明显的对称性,表明行星轮在齿顶面位置的产热量极低。通过对齿面行星轮齿面产热进行的分析证明了上述讨论结果(见图8),具体发热数值如图9所示。图9中,A表示齿根面最高温度位置,C表示分度圆位置,E表示齿顶面最高温度位置。
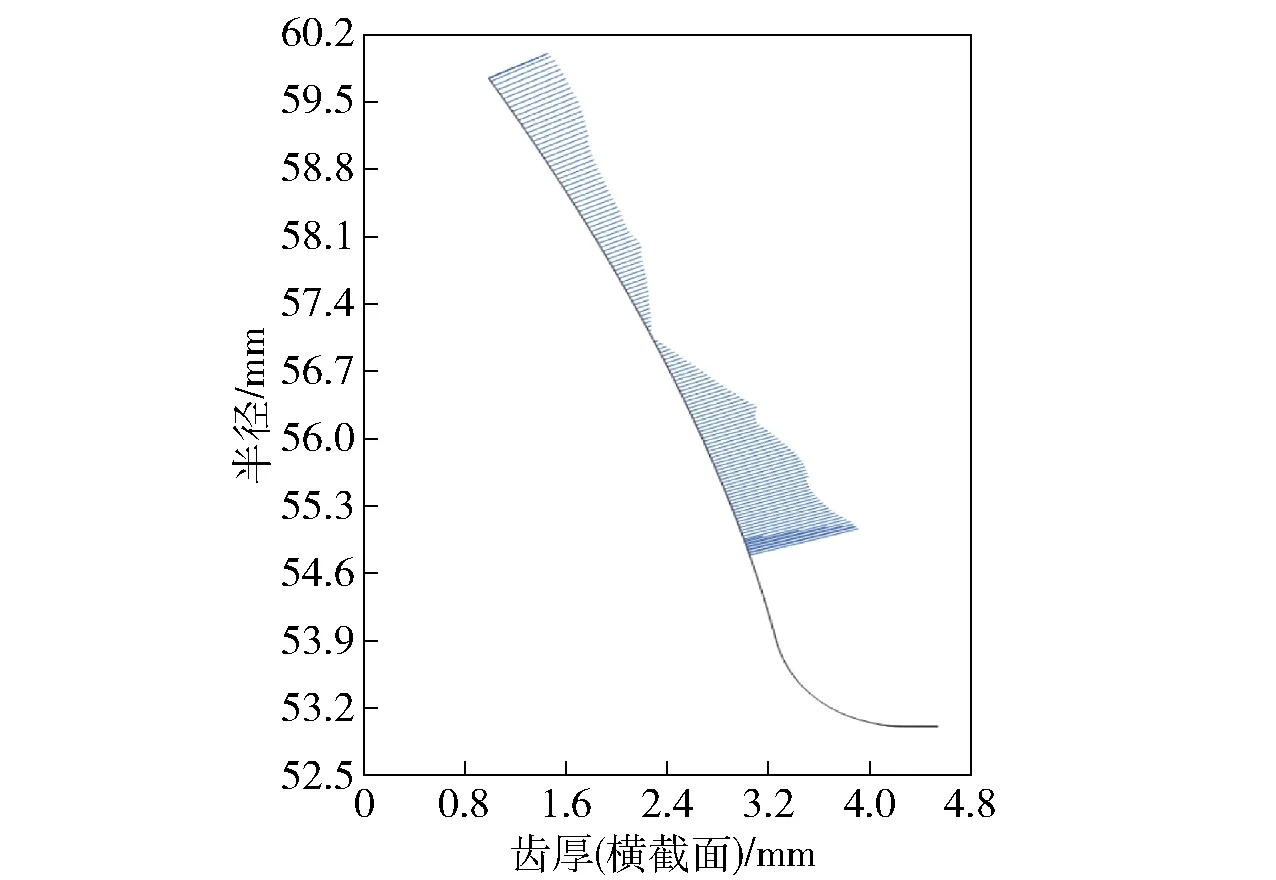
图8 行星轮齿面发热趋势(扭矩500 N·m,齿面上蓝色线长短代表眼齿廓上的发热量趋势)Fig.8 Heating trend of tooth surface of planetary gear(500 N·m,the blue lines on the tooth surface represent the trend of heating on eye tooth profile )

图9 太阳轮及行星轮齿面啮合发热曲线图(扭矩500 N·m)Fig.9 Meshing heating curves of sun gear and planetary gear surfaces (500 N·m)
3.2 不同扭矩对行星齿轮系统温度场的影响
讨论扭矩对行星齿轮系统齿面瞬态接触应力的影响情况,将太阳轮转速设置为3 000 r/min,选取扭矩300~900 N·m 7个转速点进行计算。
3.2.1 不同扭矩对太阳轮瞬态温度场的影响
如图10所示,随着扭矩增加,齿面瞬态啮合温度逐渐升高,但是齿根面升高速率要低于齿顶面升高速率,齿顶面最高温度要高于齿根面的最高温度。

图10 不同扭矩下太阳轮齿面瞬态温度场(转速3 000 r/min)Fig.10 Transient temperature field of tooth surface of sun gear under different torques (3 000 r/min)
表4所示为不同扭矩下齿顶面与齿根面最高温度值,从中可以看到随着扭矩增大,齿顶面与齿根面最高温度差值逐渐增加。表5所示为不同扭矩齿面瞬态温度平均值及升高率,从中可以看出齿面瞬态温度平均增长率值会随着载荷的增大而逐渐减小。

表4 不同扭矩下太阳轮齿根面和齿顶面最高温度Tab.4 Maximum temperatures of tooth root surface and tooth top surface of sun gear under different torques
3.2.2 不同扭矩对行星轮瞬态温度场的影响
图11所示为不同扭矩下行星轮齿面瞬态啮合温度。由图11可以看到:随着扭矩增加,齿根面瞬态温度逐渐升高,且齿根面瞬态温度大于齿顶面瞬态温度;随着载荷升高,齿顶面与齿根面的最高温度差值也有明显增大。表6所示为不同扭矩下行星轮齿根面和齿顶面最高温度。

图11 不同扭矩下行星轮齿面瞬态温度场(转速3 000 r/min)Fig.11 Transient temperature field of planetary gear surface under different torques (3 000 r/min)
由表6可以看出,随着载荷增加,行星轮齿顶面最高温度的上升率要小于齿根面最高温度上升率,造成齿顶面与齿根面最高温度差值会随着载荷的变化而改变。这是因为行星轮既进行公转也有自转,在本文所用模型中,在旋转至齿根位置时自转与公转叠加后的相对滑动速度最大,从而导致在齿根部位的瞬态温度最高,后面可以针对行星轮齿根部位进行优化。
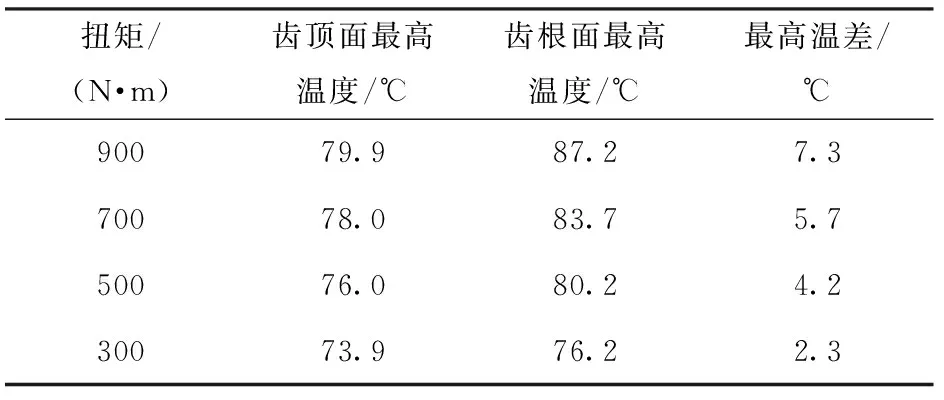
表6 不同扭矩下行星轮齿根面和齿顶面最高温度Tab.6 Maximum temperatures of tooth root surface and tooth top surface of planetary gear under different torques
3.3 恒功率条件下不同转速对行星齿轮系统温度场的影响
根据驱动电机的外特性可知,在输出功率恒定时,随着输出转速升高,输出扭矩则会降低,根据这一特性,本节研究恒定300 kW输出功率下,不同转速对行星齿轮系统齿面瞬态温度的影响。
3.3.1 恒功率下不同转速对太阳轮齿面瞬态温度的影响
图12所示为300 kW输出功率下不同转速点太阳轮齿面瞬态温度场曲线图。由图12可以看出,随着转速的增加,齿面瞬态温度逐渐降低,且降低幅度为非线性。

图12 300 kW输出功率下不同转速点的太阳轮齿面瞬态温度场Fig.12 Transient temperature field of tooth surface of sun gear at different speed points under 300 kW output power
不同转速下齿顶面及齿根面最高温度如图13所示,从中可以看到随着转速的升高,齿顶面与齿根面的最高温度逐渐降低,在5 000 r/min之前的下降率要高于5 000 r/min之后的下降率,具体数值如表7所示。由表7可见,与恒扭矩和恒转速工况不同,在恒功率情况下,随着转速升高,齿顶面最齿根面的最高温度差值会出现先升高、后降低的情况。
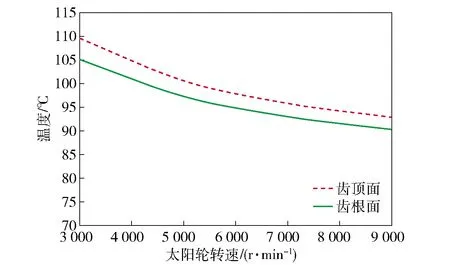
图13 太阳轮齿顶面与齿根面最高温度曲线图(功率300 kW)Fig.13 Maximum temperature curves of tooth top surface and tooth root surface of sun gear (300 kW)
值得注意的是:在300 kW恒功率下,随着转速的升高齿顶面和齿根面的最高温度有所减小,减小的绝对值约等于上一个转速点的2倍(见表7);当转速从3 000 r/min升至5 000 r/min时,温度齿顶面温度由109.6 ℃降低至100.6 ℃,降低量为9 ℃;当转速从5 000 r/min升至7 000 r/min时,温度齿顶面温度由100.6 ℃降低至95.5 ℃,降低量为4.8 ℃,该现象也出现在齿根面最高温度差值上。

表7 300 kW输出功率下不同转速点的太阳轮齿顶面及齿根面最高温度Tab.7 Maximum temperatures of top and root surfaces of sun gear at different speed points under 300 kW output power
3.3.2 恒功率下不同转速对行星轮齿面瞬态温度的影响
图14所示为300 kW输出功率下不同转速点的行星轮齿面瞬态温度场曲线图。由图14可知,恒定功率下,随着转速升高,行星轮齿根面温度场最高温度逐渐增大,而齿顶面温度场的最高温度则变化较小。齿根面温度场最高温度随转速升高也呈现了非线性降低(见表8)。由表8可见:与太阳轮不同的是,随着转速升高,齿根面与齿顶面最高温度差会出现线性减低的情况;随着转速的升高,齿顶面和齿根面的最高温度减小的绝对值约等于上一个转速点的2倍的规律同样也出现在行星轮齿面瞬态温度场上。

表8 300 kW输出功率下不同转速点的行星轮齿顶面及齿根面最高温度Tab.8 Maximum temperatures of top and root surfaces of planetary gear at different rotating speed points under 300 kW output power
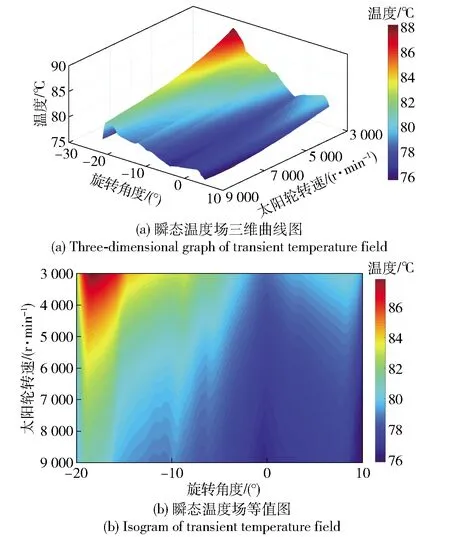
图14 300 kW输出功率下不同转速点的行星轮齿面瞬态温度场Fig.14 Transient temperature field of planetary gear face at different rotating speed points under 300 kW output power
4 试验验证
利用本文方法对试验台齿轮进行有限元瞬态温度场分析,并测量试验台齿轮箱中实际齿面温度,对比有限元分析结果与试验结果。通过与试验数据的比较,验证本文方法的正确性。
图15所示为齿轮系统试验台。试验台齿轮为一对直齿轮,表9所示为试验齿轮的参数。

表9 试验齿轮参数Tab.9 Parameters of test gears

图15 齿轮系统试验台Fig.15 Test bench of geared rotor system
为大齿轮加载1 400 r/min转速,为小齿轮加载138 N·m转矩。为确保温度数据的稳定性,速度和转矩将在3 min内提升至设定值。将驱动电机在设定值下稳定运行30 min. 30 min后关闭电机,打开齿轮箱顶盖,用红外测温仪测量大齿轮齿面温度。为了准确测量齿轮温度,重复3次试验并测量了温度。利用本文方法对试验齿轮模型加载同等工况,计算出温度场结果。
表10所示为测量值与有限元分析值对比,从中可以看出测量值与有限元计算值之间的平均误差为5.86%,因此可以认为本文方法所得的齿轮温度场结果是准确的。图16所示为实际测量过程图片以及有限元计算结果温度场云图。

表10 大齿轮试验温度与有限元计算温度对比Tab.10 Experimental and calculated temperatures of gear

图16 实际测量过程图片以及有限元计算结果温度场云图Fig.16 Actual measurement process and temperature field of finite element calculation results
5 结论
本文利用有限元法对机电复合传动装置行星齿轮系统进行仿真实验,分析了不同转速、扭矩以及恒功率下太阳轮和行星轮瞬态温度场。仿真结果揭示了不同转速、不同扭矩对行星齿轮系统太阳轮及行星轮齿面瞬态温度场的影响规律,对机电复合传动装置行星齿轮系统的优化和高质量设计提供了可靠的理论依据,并进行了试验验证。所得主要结论如下:
1)建立机电复合传动装置行星齿轮系统三维模型,同时对齿面进行区域划分,将齿面分为齿根面、齿廓面及齿顶面。
2)随着转速升高,太阳轮齿根面与齿顶面的最高温度差将逐渐增大,当转速超过5 000 r/min后温度升高斜率将会降低,不同转速下行星轮齿面瞬态温度随着转速升高而增大;齿根面的最高温度大幅高于齿顶面的温度,行星轮齿根与齿顶面最高温度差也存在随转速升高的趋势,齿根面与齿顶面呈现的温度区域并不像太阳轮那样具有明显的对称性,表明行星轮在齿顶面位置的产热量极低。
3)随着扭矩增大,太阳轮齿顶面与齿根面最高温度差值逐渐增加,齿面瞬态温度平均增长率值会随着载荷的增大而逐渐减小。随着扭矩增加,行星轮齿根面瞬态温度逐渐升高,齿根面瞬态温度大于齿顶面瞬态温度,且齿顶面与齿根面的最高温度差值也有明显增大。
4)在恒功率条件下,随着转速的增加,太阳轮齿面瞬态温度逐渐降低,且降低幅度为非线性,齿顶面与齿根面的最高温度逐渐降低,在5 000 r/min之前的下降率要高于5 000 r/min之后的下降率。随着转速的升高,太阳轮齿顶面和齿根面的最高温度有所减小,减小的绝对值约等于上一个转速点的2倍。
5)利用本文方法对试验台齿轮进行有限元瞬态温度场分析,并测量试验台齿轮箱中实际齿面温度,对比有限元分析结果与试验结果。通过与试验数据的比较,验证本文方法的正确性。
