串联式混合动力车辆发电机组协调控制策略
2021-11-15马晓军徐浩轩刘春光
马晓军, 徐浩轩, 刘春光
(陆军装甲兵学院 兵器与控制系, 北京 100072)
0 引言
串联式混合动力系统具有结构简洁、优化控制相对简单的优势,其发动机和传动装置之间可以不设置任何机械连接,通过调整发动机速度和转矩即可使其工作在最大效率区。近年来,国内外许多军用车型采用了串联式混合动力系统,作为串联式混合动力系统主动力源的发动机- 发电机组的协调控制问题也日益凸显[1-3]。混合动力车辆行驶过程中,发动机需要根据最佳燃油经济消耗跟随控制策略切换转速工作点,但过大的加载速率会限制发动机- 发电机组的转速调节能力,此时实际转速不再能跟踪目标转速,后功率链的需求功率超出发动机- 发电机组的输出能力,发动机出现超载甚至灭车的情况[4-5]。
针对这一问题,孙逢春等[6]研究了不同加载速率对发动机转速切换过程的影响,并通过仿真给出了不同转速下最大允许的加载速率,避免了发动机过载的情况。温博轩等[7]通过发动机- 发电机组间设置传动装置,提高了转速调节能力。但限制加载速率太小会减缓机组的功率响应能力,限制加载速率过大则难以避免机组转速的振荡,加载速率的限幅很难取到最优。串联式结构由于取消了机组与电机之间的机械连接,一般由发动机直接拖动发电机,增加传动装置的方法更适应于并联和混联式系统。总之,目前对该问题的研究相对较少,还没有统一的解决方案。
在机组动态调节过程中,发动机- 发电机组系统内部主要是转速调节问题[8-10],对外主要是输出到母线上的电功率响应问题[11-13]。本文从这两个问题出发,采用发动机油门开度调节输出功率、发电机控制器调节转速的机组调速方法,合理控制电磁转矩变化,避免了动态调节过程中发动机超载甚至灭车的情况。同时对整个过程的调节时间和最小能量损耗寻优,通过合理配置发电机电磁转矩变化区间,实现对直流母线的高品质供电。通过对一种串联式车载综合电力系统的硬件在环仿真,验证本文控制策略的可靠性。
1 机组失稳原理分析
发动机- 发电机组一般采用发动机控制转速,发电机通过整流装置调节电磁转矩进而控制输出功率,这种方法可以使机组快速响应负载功率需求,在发电厂和船舶机组中得到了广泛运用[14]。这些工况下机组不需要频繁调速,且发动机可以选择足够大的规格。对于车载机组:一方面,由于车内空间限制,发动机与发电机的容量相近,在车辆需要高速过弯或急加速时,车辆陡增的功率需求可能使作为阻力矩的发电机电磁转矩短时间内超过发动机输出扭矩,导致机组失稳[15-18];另一方面,由于机组输出能力以及燃油经济性与转速的耦合关系,机组需要根据行驶需求频繁切换转速点。要处理好机组功率跟随控制与机组调速的矛盾,就要首先分析机组失稳的原因。
发动机- 发电机组是高度非线性的系统,在分析其调速的稳定性时,需要将系统状态方程在稳态工作点处局部线性化处理,利用雅可比矩阵的特征根分布来判断系统在稳态工作点附近的稳定性。在建立模型时进行合理近似:低转速段发动机转速- 转矩外特性有比例关系,燃油等延时环节采用1阶惯性环节代替,发电机电磁转矩响应的时间相对发动机响应时间可以忽略。车载发电机组低转速段调速的模型如图1所示。图1中:ω为机组目标角速度;(Kps+Ki)/s为机组的转速PI控制器,Kp、Ki分别为PI控制器的比例系数和积分系数,s为拉普拉斯算子;状态量x1、x2、x3分别为油门开度、发动机输出转矩、机组实际角速度;kx1x3为机组转矩输出,k为比例系数;1/(Ts+1)为转矩输出燃油延时,T为惯性环节时间常数;P/x3为发电机反馈的阻力矩,P为机组目标加载功率;J为机组轴的转动惯量。
根据图1中的关系,将稳态工作点通过坐标变换平移至坐标原点,可得表达式为
(1)
式中:η、ω0、F分别为将稳态工作点平移到坐标原点所产生的偏移量。根据Lyapunov间接法,可得系统在稳态工作点附近的雅可比矩阵为
(2)
当机组工作在1 000 r/min的稳态工作点附近时,将表1设定数据代入矩阵,随着目标加载功率增大,特征根轨迹变化如图2所示。由图2可见:当加载功率较小时,3个特征根均位于负半平面;当目标加载功率增大到132 kW后,一对共轭特征根移动到正半平面,系统失稳。
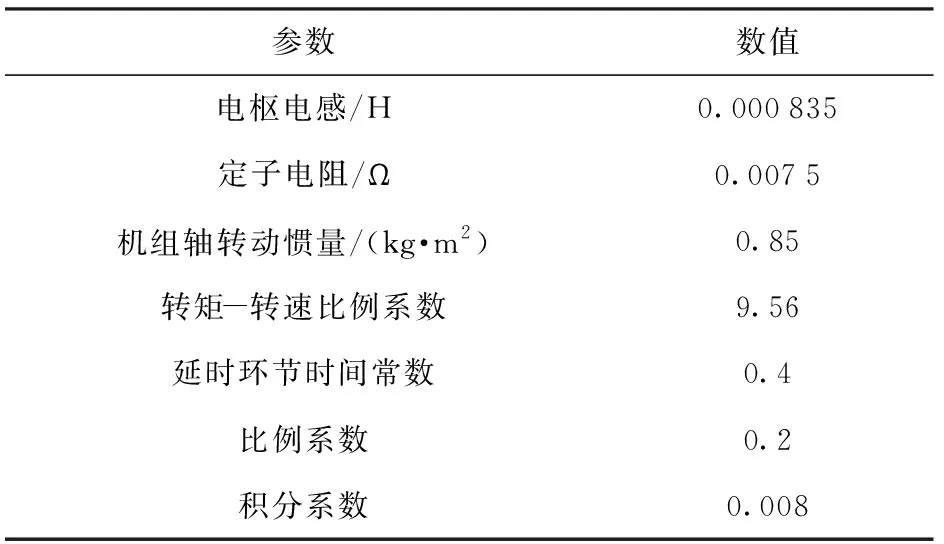
表1 发电机组设计参数Tab.1 Design parameters of generator set
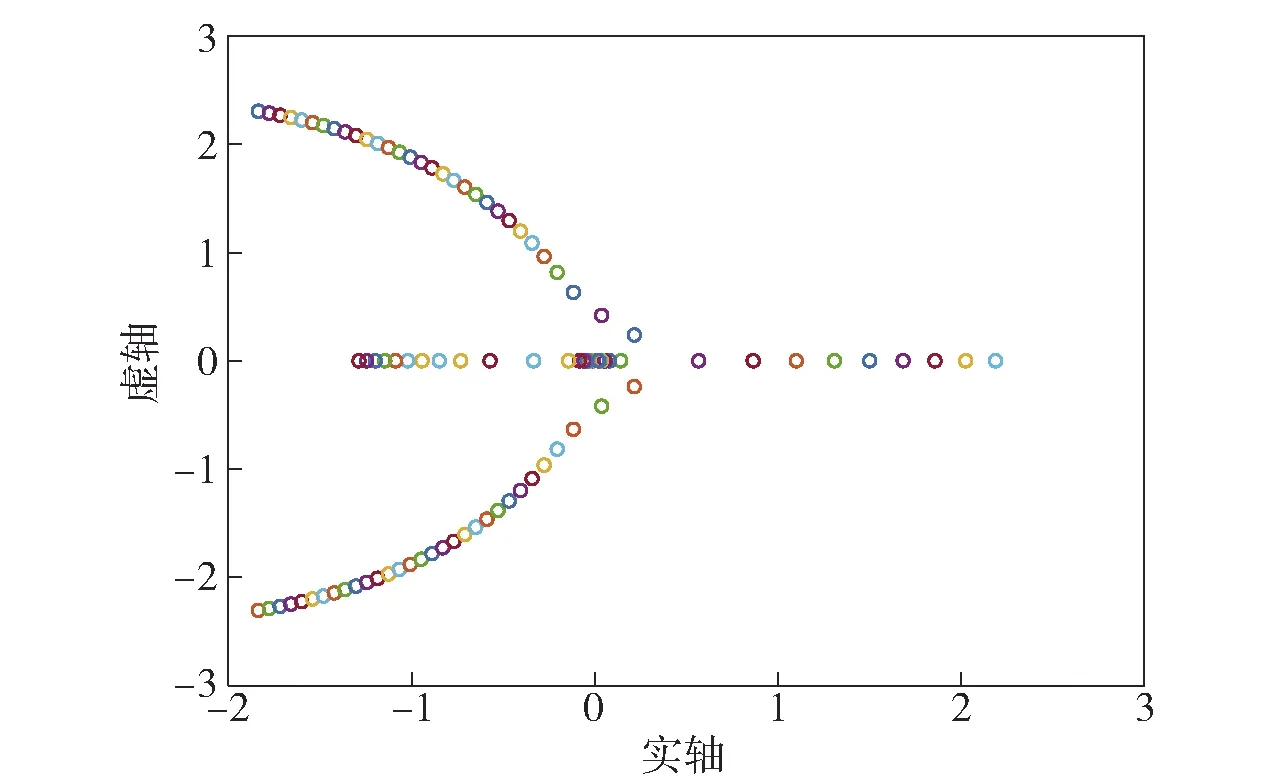
图2 特征根轨迹图Fig.2 Characteristic root locus
由(2)式可见,该模型同样可以分析机组其他参数及系统初始状态对机组稳定性的影响,除目标功率因素外,更高的转速点和更低的油门开度更有利于系统在调速过程中保持稳定。机组失稳主要还是由于发动机与发电机的响应速度相差较大,发电机快速完成功率响应后,阻碍了发动机的转速响应,而发动机输出能力受转速制约,因此最终无法完成转速调节。高转速点和低油门开度均能为发动机扭矩输出提供较高的裕度,因此更有利于机组调速稳定性。
2 新型协调控制策略设计
2.1 转速调节方法改进
通过第1节分析可知,目标加载功率与当前转速点及油门开度均对稳定性有影响。但发动机的高效区一般在接近满油门开度处取得,使机组一直保持在高转速和较低油门开度的状态,不能满足燃油经济性的要求。目前的机组协调控制策略还是以限制目标加载功率为主,一般通过限制发电机电枢电流变化率从而控制电磁转矩变化区间,即令发电机响应更慢以等待发动机响应,这种方法很难兼顾平顺调速与快速功率响应的需求。
输出到母线的电功率由发电机转速与电磁转矩决定,传统的协调控制策略由发动机调速,发电机电磁转矩响应功率需求。但电磁转矩的响应速度比发动机调节转速的速度快得多,且快速增长的电磁转矩作为阻力矩,更减缓了转速响应的速度。因此,要解决功率控制和转速控制的矛盾,必须要处理好其中的耦合量,即发电机电磁转矩的控制问题,使功率控制与转速控制中,发电机电磁转矩的变化趋势一致。
新调速控制方法将发动机- 发电机组看作一个整体进行功率- 转速闭环控制:外环为功率环,由发动机控制器调节发动机油门开度,实现机组的功率闭环控制;内环为速度环,由发电机控制器控制发电机组转速,并使发电机跟随发动机功率输出电功率。此时,发电机电磁转矩只与转速调节相关,整个机组的控制遵循优先调节转速的原则。控制原理如图3所示,机组调速模型如图4所示。
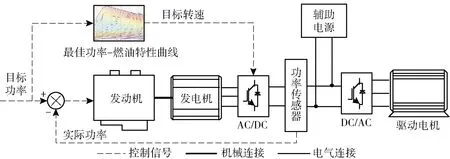
图3 机组新型协调控制策略Fig.3 The proposed coordinated control strategy

图4 发电机调速模型Fig.4 Generator set speed control model
图4中,K1/(τ1s+1)表示增益为K1、滤波时间常数τ1的电流反馈滤波环节,K2/(τ2s+1)表示存在增益K2、滞后时间常数τ2的三相脉冲宽度调制(PWM)逆变器,L为等效电感,R为定子绕组电阻,Pn为极对数,Ke为转矩系数,ωgd为发电机目标转速,iqgd为q轴目标电流,Uq为q轴目标电压,Φf为磁通量,iq为q轴实际电流,Te为发电机电磁转矩。
电流反馈滤波环节和PWM逆变器均视为小惯性环节,结合图4所示的模型可知,电流环的控制对象开环传递函数为
(3)
式中:Ti=τ1+τ2,通过小惯性环节合并而来;KR=1/R;Tm=L/R.加入PI控制器后,电流环的闭环传递函数为
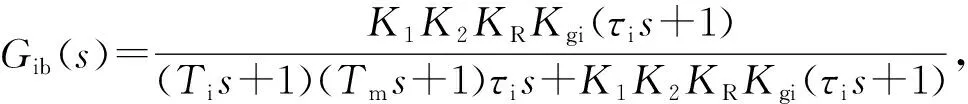
(4)
式中:Kgi、τi分别为电流环的比例系数和积分系数。电流环设计一般采取零极点对消的方式消去电流开环被控对象的时间常数,即取τi=Tm,此时(4)式上下对消零极点,得
(5)
式中:Tj=τi/(K1K2KRKgi)。由于速度环截止频率低且Ti为极小值,对(5)式进行处理,得
(6)
则其速度环控制对象可以表示为
(7)
式中:K=Ke/J.此时系统可以看作输入为给定转速、扰动为发动机输出转矩的反馈连接,其两条支路均为有限增益稳定,根据小增益定理,系统只要设计合适的PI参数,即可使机组系统在调节转速过程中保持稳定。由于发动机转矩的影响,转速调节的速度仍受当前转速点影响。
2.2 功率响应过程解析
机组采用发电机调节转速后,机组转速调节速度和抗负荷冲击能力都得到提升。但从功率响应效果来看,还需要进一步优化。对发动机而言,主要是通过转速的前馈控制,加快动态调节过程中油门开度变化;对于发电机,主要通过对转速- 电流双闭环控制的电流环调节范围限制。
功率响应的优化主要有两个目标:一是在动态调节过程中系统的耗散能量最小,主要体现为母线电压变化;二是完成动态调节的时间最短,主要体现为机组转速和功率跟踪情况。对整个动态调节过程而言,优化目标能量耗散Je和调节时间Jt分别为

(8)
Jt=tf-t0,
(9)
式中:tf为动态过程的结束时间;t0为起始时间。对于最优化问题,一般可以通过庞特里亚金最小值原理求解转速与电磁转矩的变化规律。但在本文问题中,电磁转矩Te的允许变化范围是根据转速变化的,转速同样是时变的,难以通过最小值原理求解最优控制率,采用迭代寻优则失去了讨论的一般性,因此采用转速作为中间变量求解。设动态调节过程中发动机输出转矩与电磁转矩及转速的关系为
T=h(ω),
(10)
Te=gω,
(11)
(12)
式中:g为转矩限幅系数,0≤g≤k.
(10)式为在发动机前馈控制下的转速- 转矩变化关系,为方便后续分析,可以视为多段直线对曲线的拟合,k在不同区间上取值不同。(10)式、(11)式、(12)式代入(9)式,可得
(13)
式中:ωf为动态过程的末态角速度。(13)式解出的时间关系代入(8)式,得
(14)
可见寻优目标Jt随系数g的增大单调递增,在g=0时取得最小调节时间,但Jt的最小值并不一定与Je同时取得。对Je在g上求偏导,得
(15)
由(15)式可见,系数g在分子部分被消去,不影响导数值的正负,函数Je的变化仅与目标加载功率P以及角速度调节的初始值ω0及终值ωf有关:当满足
(16)
时,Je单调递增,最小能耗同样在g=0时取得,系统同时满足调节时间最短,系统能耗最小;当满足
(17)
时,Je单调递减,Je与Jt的优化目标矛盾,减小系统能耗需要延长调节时间,最优值应该由最大允许调节时间tr限制。综上所述,电磁转矩的最优控制率应为
(18)
此控制率为理想情况,系统能力无限大时的状态。实际系统能力有限,当满足(16)式条件时可以直接由闭环控制调节,当满足(17)式条件时可以通过限制电流内环的调节范围,使电磁转矩按照(18)式规律变化。
3 仿真及结果分析
仿真实验主要验证发动机- 发电机组在抗负荷冲击、转速调节及功率调节方面的有效性。限于实验条件,在硬件在环实时仿真平台(见图5)上进行机组协调控制仿真验证。实时仿真平台由驾驶员操控舱、以实车中央控制器为核心的综合控制系统、基于系统实时仿真平台软件包RT-LAB的电机驱动系统及综合电力系统,以及基于动力学仿真软件Vortex的系统构成,各系统间采用Flexray总线通信。

图5 硬件在环仿真平台Fig.5 Hardware-in-the-loop simulation platform
图5中,综合电力系统采用一种发动机- 发电机组、蓄电池和超级电容器联合供电的串联式混合动力电传动车辆参数为依据,机组通过AC/DC连接直流母线,蓄电池通过DC/DC连接直流母线,超级电容器直接挂接在母线上。仿真选定的系统设计参数如表2所示。

表2 系统设计参数Tab.2 System design parameters
实验采用新型控制策略与当前常用的根据转速限制加载速率的传统控制策略进行比较,传统控制策略功率限幅值根据全局最优的经验设定为发动机最大输出能力的0.82倍。由于电池采用稳压或功率跟随策略在动态调节过程中输出的功率是不同的,且在小功率变化过程中蓄电池的输出使系统能量损耗不易观测,为使观测结果更加清晰,在将系统调整到相同状态后,5 s时从系统中切除蓄电池。
设计工况1为机组5 s时从100 kW加载到150 kW,转速相应从1 400 r/min调节到1 580 r/min,此时功率转速关系满足(17)式。工况2为机组5 s时从20 kW加载到250 kW,转速相应从1 090 r/min调节到1 960 r/min,此时功率转速关系满足(16)式。
图6所示为工况1机组转速与母线电压变化曲线,本次实验选取的容许调节时间tr为3 s. 由图6(a)可见,由于计算采取的发动机外特性近似以及转速滞环保护等产生的误差,新型控制策略转速调节时间约为2.7 s,略短于容许调速时间。新型控制策略在幅值较小的功率调节过程中,为保证母线电能质量,使电磁转矩保持在相对较高的状态,一定程度上牺牲了调节速度,相比传统控制策略调节更慢。由图6(b)可见,采取新型控制策略后,虽然整体调节时间稍长,但机组可以更快地响应后功率链需求,维持母线电压稳定,减小系统能量损耗。

图6 工况1机组转速与母线电压Fig.6 Speed of engine-generator set and bus voltage under Condition 1
图7所示为工况2机组转速与母线电压变化曲线。由图7可见:传统控制策略下,过大的加载速率使转速长时间无法达到目标值,虽然限幅策略避免了发动机灭车,但机组很长时间无法响应功率需求,母线电压大幅降低;采取本文控制策略后,机组优先调节转速,最终使机组调节时间与系统能量损耗均达到最优,对母线电能质量改善显著。
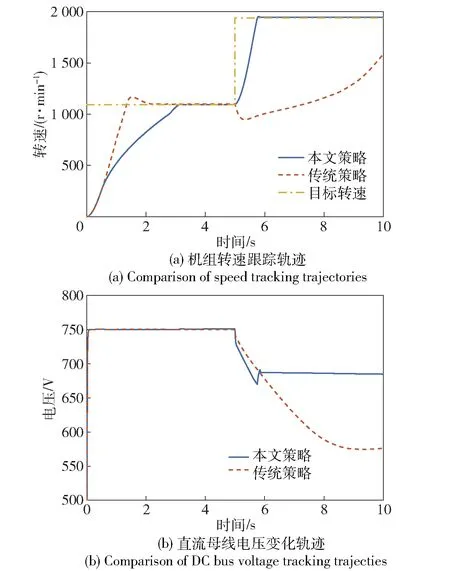
图7 工况2机组转速与母线电压Fig.7 Speed of engine-generator set and bus voltage under Condition 2
为进一步验证(18)式所给出控制规律的准确性,取(16)式、(17)式的临界状态进行实验验证,此时系统的能量损耗与系数g的取值无关,为在g的定义域内均匀取值,分别取g为0、0.3k、0.5k、0.8k. 图8所示为临界工况母线电压变化轨迹。由图8可见,虽然不同取值的g调节时间,即达到最低点的时间上有差异,但最低点均在695 V左右取得。此时g的取值不影响系统的能量损耗,结合图6、图7变化规律,证明了(18)式的准确性。
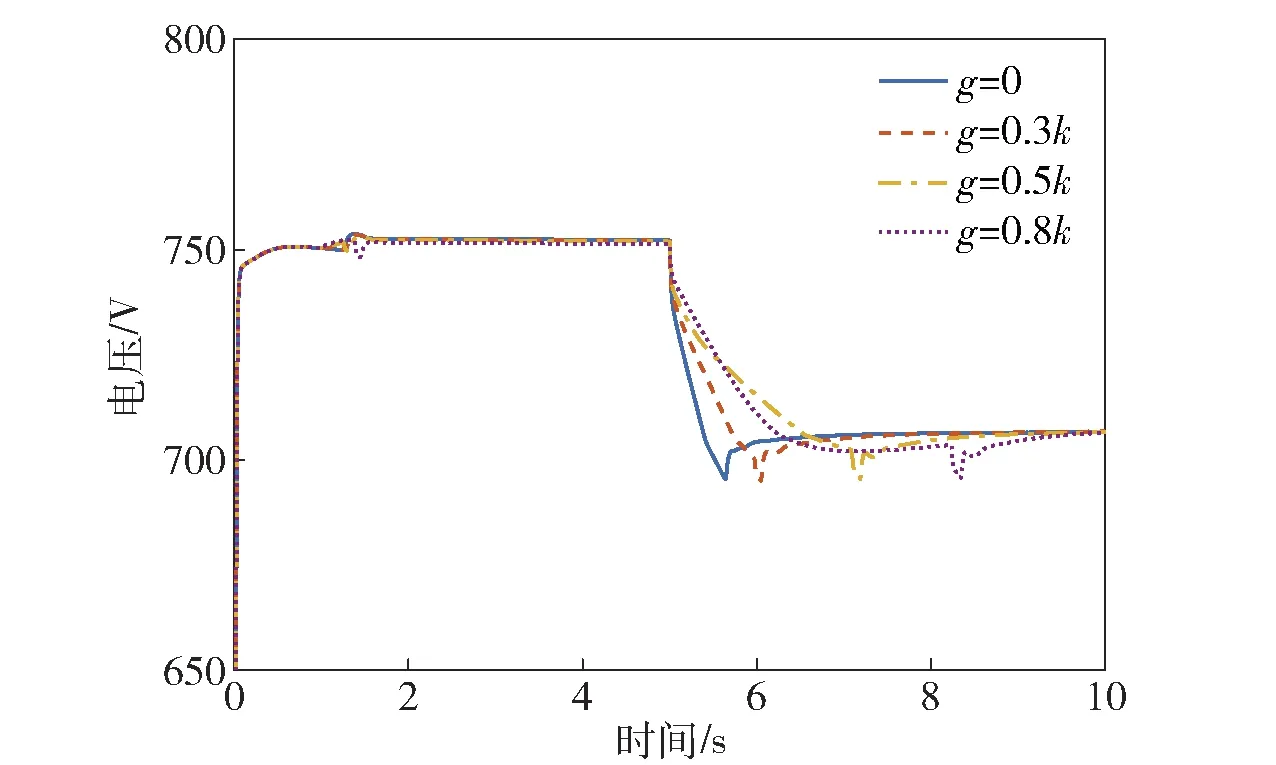
图8 临界工况母线电压变化轨迹Fig.8 DC bus voltage tracking trajectories under critical condition
4 结论
本文根据串联式混合动力系统的特点,设计了发动机- 发电机组新型控制策略。通过机组的功率- 转速闭环控制以及在此基础上的发电机电磁转矩变化范围限制,实现了机组的平顺调速和动态调节过程最小能量耗散,并通过硬件在环仿真实验验证了控制策略的可靠性,为串联式混合动力车辆的机组协调控制研究提供了新的思路。
