轮式装甲车辆电驱动轮机电耦合动力学建模与振动特性
2021-11-15刘越席军强田真张欣
刘越, 席军强, 田真, 张欣
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.中国北方车辆研究所 车辆传动重点实验室, 北京 100072)
0 引言
未来轮式装甲车辆最高行驶速度不断增加而本体车重却大幅度下降,要求传动系统能传递更大的功率和扭矩,急需解决传动范围增大与体积、质量大幅度缩小的矛盾,基于电驱动轮的轮式装甲车辆成为了适应未来新技术战争的最优解决方案[1-3]。电驱动轮主要包含轮毂电机和行星齿轮传动两部分,通常轮毂电机产生电磁振动,行星齿轮传递机构产生机械振动。一般地,电磁振动由径向力、切向力和转矩脉动等激励产生,主要由高频成分组成[4-5]。而齿轮传动机构通常有两类噪声:一类是齿轮啸叫,又叫白噪声;另一类是齿轮拍击噪声[6-7]。齿轮啸叫主要由齿轮啮合不平顺造成,而齿轮拍击噪声通常由轮毂电机的扭矩波动造成,因此轮毂电机和齿轮系统形成复杂的机电耦合振动。相比而言,齿轮啸叫的贡献更大,通常占齿轮箱振动噪音的80%以上。通常所说的齿轮箱振动分析,主要是指齿轮高频啸叫分析[8]。
电机在工作过程中,气隙中的磁场使得气隙磁密发生变化而产生径向电磁力。交变的径向力波作用于定子、转子铁心,引起铁心位移随时间的周期性变化,造成电机本体和电驱部分发生振动,振动频率是径向力波的作用频率。同时,由于电机驱动电流的谐波失真和齿槽效应,电机输出转矩会发生一定范围内的波动,即转矩波动,周期性的转矩波动会导致电驱系统发生振动,振动频率是转矩波动频率[9-12]。此外,切向力和不平衡磁力拉力也是电磁振动的激励源。由于齿轮啮合过程中,轴系变形、轮齿刚度变形、齿廓受载变化、外界扭矩变动等影响,齿轮啮合过程并不平稳。对外的表现为齿轮转动过程或快或慢,造成啮合过程中啮合位移的变化,形成时变的啮合力,最终引起齿轮箱发生振动。通常把齿轮啮合位移的变化,描述为齿轮传递误差(TE)[13-15]。因此,齿轮箱振动激励主要来自于齿轮啮合传递误差。
文献[16]针对多源驱动系统建立了多激励源的机电耦合模型,研究系统的动力同步性问题,系统动力学模型采用集中质量法,但未涉及电机转矩脉动和齿轮的啮合刚度带来的系统耦合振动问题。文献[17-18]建立了综合考虑电机控制因素和机械系统影响的模型,分析定轴式电驱动系统的扭转振动,并提出用谐波电流优化方法减少电机的输出转矩波动。文献[19]建立了包含电动机、齿轮传动系统的电传动动力学模型,研究了电动机- 齿轮传动连接刚度和阻尼以及齿轮啮合刚度对电机动力学特性的影响。
本文针对轮式装甲车辆电驱动轮这一典型机电耦合系统,综合考虑电驱动轮内部激励包含轮毂电机的电磁激励、齿轮系统的刚度激励、误差激励和啮入啮出激励、轴承动态刚度激励等,采用仿真分析软件建立电驱动轮动力学分析模型,进行轮毂电机及行星齿轮机构机电耦合动力学仿真。
1 永磁同步电机空间径向电磁力模型
研究电机径向电磁力波是研究电机振动特性的关键内容,令p为电机极对数,θ为空间角度,Qs为定子槽数,v为定子电枢反应磁动势谐波极对数,μ为转子磁动势谐波极对数。对于内转子表面式结构永磁电机,若考虑因脉宽调制等因素所产生的时间谐波分量,则给定时间t定子磁动势表达式为
(1)
式中:frv为定子磁动势谐波幅值;ω0为转子旋转的电角频率;βv为定子磁动势初始角度。
转子磁钢产生的磁动势为
(2)
式中:frμ为转子磁动势谐波幅值;βμ为转子磁动势初始角度。
具有矩形槽的气隙磁导λ(θ)可近似表示为
(3)
式中:Λ0为气隙磁导的恒定分量;λk为给定谐波磁导次数k下的谐波分量。
气隙磁密bα(θ,t)的表达式为
bα(θ,t)=[FA(θ,t)+FR(θ,t)]λ(θ).
(4)
若忽略气隙磁密的切向分量,则根据麦克斯韦张量公式,位置θ处的径向电磁力波为

(5)
式中:μ0为空气磁导率。(5)式可简化为
p(θ,t)=pA(θ,t)+pAR(θ,t)+pR(θ,t),
(6)
式中:pA(θ,t)由定子电流独立产生的部分,与定子绕组结构和电流大小有关;pAR(θ,t)为定子电流产生的磁场与永磁磁场相关作用产生,为耦合项,与定转子结构均有关;pR(θ,t)为由转子磁场独立产生的部分,与永磁体磁场有关。
2 轮毂电机及机械系统建模
2.1 轮毂电机激励获取
电磁力产生振动的原因是由于电磁径向力具有时空二向性,当径向力施加到定子槽上,引起定子振动。径向力时空二向性指的是施加到每个定子槽上的径向力不尽相同,同时径向力会随着时间的变化产生周期性的改变。通常电磁径向力产生噪声的是高频啸叫声,以及激励频率与结构固有频率接近时产生共振,从而引起辐射噪声增大。
以电机转速为600 r/min的额定工况点计算,此时电机线电流的有效值为284.3 A,电流密度为15.71 A/mm2. 电机的直流母线电压为750 V,功率因数角为39.29°. 考虑电机本体的温升影响,进行电机的电磁计算。根据所搭建电机参数化模型计算电机的电磁性能,得磁密云图、反电动势、转矩曲线和电磁力曲线如图1~图4所示。

图1 电机磁密云图Fig.1 Magnetic density map of motor

图2 电机的反电动势曲线Fig.2 Back EMF curve of motor

图3 电机输出转矩曲线Fig.3 Motor output torque curve

图4 电机输出电磁力曲线Fig.4 Electromagnetic forces of motor
建立电机的饱和参数模型和损耗模型,基于dq轴模型如图5所示,通过改变电角度γ的值,可实现电机整个工况范围的计算。图5中,vs为相电压,ΨR为定子磁链,Is为定子相电流有效值,Id为直轴d的电枢电流,Iq为交轴q电枢电流,λm为转子磁链,Ld为直轴同步电感,Lq为交轴同步电感。

图5 永磁电机的dq轴相量图Fig.5 dq axis phasor diagram of permanent magnet motor
实现电机有限元模型导入之后,进行电机电磁激励力的导入和处理。导入给行星齿轮机构的电磁激励包括径向力、切向力和转矩脉动,如图6~图8所示。根据电机的极槽数(10极48槽),确定电磁激励的谐波阶数为10阶,后续阶次均以10的整倍数进行增长。

图6 电机不同转速下径向力激励谐波Fig.6 Harmonic wave excited by radial force at different motor speeds

图7 不同电机转速下切向力激励谐波Fig.7 Harmonic wave excited by tangential force at different motor speeds

图8 不同电机转速下转矩脉动激励谐波Fig.8 Harmonic wave excited by torque ripple at different motor speeds
由图6可得,电磁径向力前5阶的谐波分量幅值较大,后续高阶次谐波分量所占比重较小,且不同转速下的相同阶次具有不尽相同的幅值。径向力激励下电机定子齿前5阶的模态振型,随着阶次的提高,定子齿的振动幅值越来越小,因此提取前5阶谐波分量的径向力激励作为行星齿轮机构的激励力精度是足够的。
2.2 基于Romax行星齿轮动力学模型建模
对行星齿轮机构建模和分析采用齿轮传动领域专业设计和分析工具Romax软件,通过轴系、齿轮、轴承等基本元件建模、材料属性定义、润滑油定义、约束定义等,完成行星机构动力学模型搭建,如图9所示。

图9 行星齿轮系统轴系模型Fig.9 Shafting model of planetary gear system
为了准确考虑电驱动轮壳体和轮辋的刚度影响,将其进行几何模型简化及划分有限元网格,并导入动力学模型中。
除壳体和轮辋以外,行星齿轮机构中行星架也需要建立有限元模型,在完成各个有限元模型的基础上,将有限元模型导入Romax中进行有限元模型的安装、节点连接、刚度缩聚等。
3 机电耦合激励下系统模态与振动分析
3.1 系统模态分析
在Romax软件中计算得到电驱动轮各阶模态,如表1所示。
电驱动轮3阶、8阶、16阶、20阶模态振型和模态能量分布如图10所示。
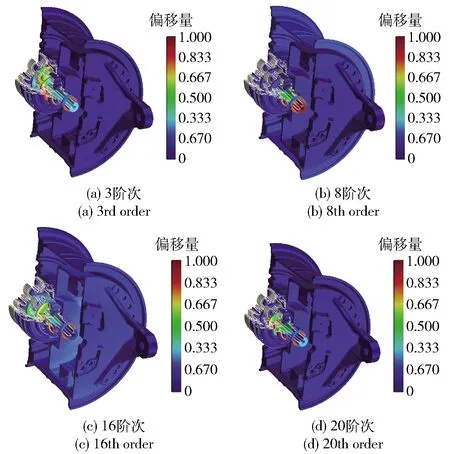
图10 系统阶次模态Fig.10 System order modals
在图10中可以看出:第1阶次工作模态频率为0.3 Hz,接近于零频,是因为电驱动轮存在一个旋转方向的刚体自由度,因此会产生1阶接近于零频的刚体模态。从电驱动轮整体的工作模态振型和模态能量分布来看,较低阶次模态振型以电驱动轮的全局模态为主,高阶次的模态振型则更多体现电驱动轮的局部模态,特别是行星齿轮机构的局部振荡。另外,前20阶次的模态出现了较多的壳体与轴系以及轴系相互之间的耦合振动状态,例如:第3阶变形模态中,电机端一排行星齿轮轴系和二排行星齿轮轴系都有不同的模态能量贡献;第8阶变形模态中,轮辋占20.7%的模态能量贡献,壳体则占1.1%的模态能量贡献;第16阶变形模态中,壳体占47.7%的模态能量贡献,轮辋占8.9%的模态能量贡献。
3.2 轴系模态与轴承振动位移分析
以电机转速9 000 r/min、输出扭矩120 N·m的高速工况为例,综合考虑电机端高速行星排的行星轮和齿圈啮合刚度和传动误差,电驱动轮电机输出轴(一排太阳轮轴)9 000 r/min内的模态如图11所示。

图11 电机输出轴全速域模态分析Fig.11 Modal analysis of input shaft in full speed domain
由图11可以看出:电机输出轴转速2 505.3 r/min和4 570.9 r/min附近的模态更容易被激起,2 505.3 r/min转速下该激励的频率为1 415 Hz,与系统的第46阶次整体模态频率一致,即在转速2 505.3 r/min下激起系统第46阶次整体模态振动;转速4 570.9 r/min下该激励的频率为2 581.6 Hz,与系统的第104阶次整体模态频率一致,该阶次激励下,轴承位移响应如图12所示。
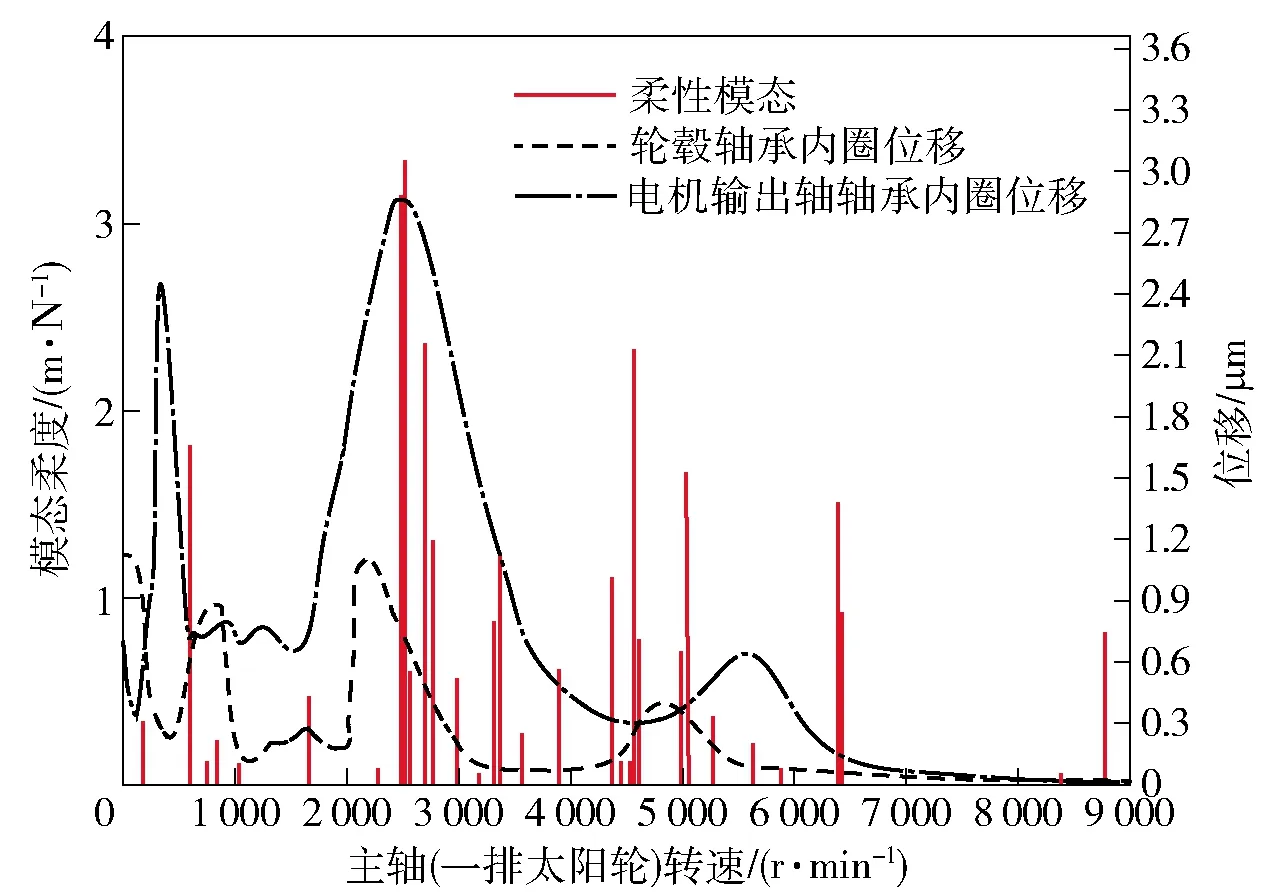
图12 轴承位移响应曲线Fig.12 Displacement response curves of hub bearing
由图12可以看出:电机输出轴转子球轴承在转速500 r/min和2 505.3 r/min附近出现最大的振动位移响应,最大达到2.7 μm. 轮毂轴承由于自身刚度较大,且远离振源,其振动位移响应相对于输入轴承位移响应要小很多;随着电机转速的攀升过程,在电机输出转速为2 505.3 r/min、4 570.9 r/min和6 392.2 r/min时,即对应于激励频率为1 415 Hz、2 581.6 Hz和3 609.46 Hz时,电驱动轮的输入、输出轴承的振动情况会有所加剧,尤其是在2 505.3 r/min和4 570.9 r/min两个转速附近,高速端支撑轴承会出现较为剧烈的轴承振动。
3.3 行星架振动加速度响应分析
表面速度平方均值能够较好体现整体振动响应等级,通过分析不同阶次激励下壳体的表面速度平方均值来获得各个阶次激励对最终振动响应的贡献,从而找出影响振动主因。以电机转速9 000 r/min、输出扭矩120 N·m工况为例,分别计算各行星排阶次激励下的行星架表面速度平方均值,如图13~图15所示。
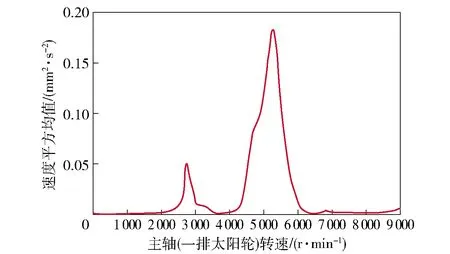
图13 一排行星架33阶次激励下表面速度平方均值Fig.13 Square mean value of surface velocity under the 33rd order excitation by the first planetary array

图14 二排行星架8阶次激励下表面速度平方均值Fig.14 Square mean value of surface velocity under the 8th order excitation by the second planetary array

图15 三排行星架2阶次激励下表面速度平方均值Fig.15 Square mean value of surface velocity under the 2nd order excitation by the third planetary array
通过行星齿轮机构3个行星架不同阶次激励下的振动响应对比,高速端行星排的激励阶次所产生的表面振动响应远大于后两排行星激励阶次下的振动响应。因此,在传动误差激励中电机端一排行星架33阶次激励是电驱动轮振动响应的主要激励,且传动误差激励所产生较大振动的区域为中速运行范围。
图16所示为电磁径向力各阶次激励的壳体表面速度平方均值响应。

图16 电磁径向力各阶次激励的壳体表面速度平方值响应Fig.16 Square mean value of shell surface excited by electromagnetic radial force
由图16可以看出:10阶次的电磁激励在高转速范围的振动响应更高,其他各阶次激励的壳体振动速度响应较小,因此电磁激励中在高转速范围内10阶次电磁激励是电磁振动响应的主要影响因素之一;50阶次激励在低转速2 000 r/min附近有较大的振动响应,即在低转速范围区域,50阶次的电磁激励是电磁振动的主要激励。因此,电磁激励主要是在高转速区域范围所产生的振动响应较大,且大于行星齿轮传动误差激励产生的振动响应。
4 结论
1)通过对比前5阶径向力谐波合成的激励与所有谐波合成的激励差别,采用曲线拟合的方式对比发现,前5阶径向力谐波基本与所有径向力谐波曲线一致,因此采用前5阶径向力谐波代替原始径向力作为电磁激励进行分析是准确的。
2)低阶模态主要是电驱动轮的全局模态,高阶模态主要是电驱动轮的局部模态,特别是行星齿轮机构的局部模态。低频激励主要激起电驱动轮的整体模态,而高频激励主要激起行星齿轮机构的局部模态变形。
3)高速端行星排的激励阶次所产生的表面振动响应远大于后两排行星激励阶次下的振动响应,是电驱动轮振动响应的主要激励。
4)通过电磁径向力各个阶次激励下壳体表面速度均方根值振动响应对比,发现10阶次的电磁激励在高转速范围的振动响应更高,占主要影响。同时50阶次激励在低转速2 000 r/min附近有较大的振动响应,因此在低转速区电磁激励的高阶次占主因,而在高转速区低阶次激励占主因。
