同轴磁齿轮极数配合规律
2021-11-15何明杰彭俊罗英露李伟业
何明杰, 彭俊, 罗英露, 李伟业
(1.中车株洲电力机车研究所有限公司, 湖南 株洲 412001; 2.襄阳中车电机技术有限公司, 湖北 襄阳 441047)
0 引言
为提升电机的功率密度和减小体积,一般需将电机转速设计得较高。通常采用减速设备来实现驱动电机和负载之间的匹配。传统的机械齿轮减速设备存在振动大、噪声高、可靠性差、结构复杂、需润滑、维护量大等问题[1],不利于其在特殊军工场合的应用。为解决以上问题,磁齿轮逐渐引起各国学者重视。磁齿轮具有非接触传动、振动小、噪声低、可靠性高、效率高和免维护等优点。磁齿轮的研究可追溯至1901年,当时世界上第一款电励磁磁齿轮被美国学者提出[2]。随后,世界上首款永磁体励磁的磁齿轮于1941年被提出来,但是由于永磁材料的限制,其转矩密度非常低[3]。1968年,基于磁场调制原理的同轴磁齿轮被美国学者提出并申请了专利,该结构极大地提升了磁齿轮的转矩密度[4]。随着永磁材料的发展,稀土永磁体获得了广泛应用,大量采用稀土永磁材料的同轴磁齿轮被各国学者争相研究[5-6]。
目前,针对磁齿轮的研究主要分为以下几类:新结构研究[7-12]、磁齿轮对比研究[13-20]、转矩波动抑制研究[21-22]、优化设计方法研究[23-28]等。
文献[7]提出了一种磁阻式磁齿轮,其内转子采用凸极结构,可在较高转速下安全运行,但该磁齿轮的转矩密度较低。文献[8]提出一种外转子和调制齿上均安装永磁体的磁阻式磁齿轮,在一定程度上提高了磁齿轮的转矩密度。文献[9]对比研究了不同结构交替极磁齿轮在输出转矩方面的差异。文献[10]提出一种采用T形调制齿的磁齿轮,该磁齿轮具有较大的聚磁效应,且可减小端部漏磁,从而提高了转矩密度。文献[11]深入研究了磁齿轮调制齿形状对输出转矩的影响。文献[12]提出一种可利用端部漏磁的新型同轴磁齿轮,在一定程度上提高了磁齿轮的输出转矩。文献[13]对比分析了传动比对磁齿轮输出转矩的影响。文献[14]对比分析了采用稀土永磁材料和铁氧体磁齿轮在输出转矩、效率、成本等方面的差异,研究结果表明采用铁氧体永磁材料磁齿轮的输出转矩相对较低,但其效率和成本均优于采用稀土永磁材料的磁齿轮。文献[15]对磁齿轮的端部效应进行了深入研究,结果表明当磁齿轮轴向长度较短,即为盘式结构时,在设计阶段需考虑端部漏磁的影响。文献[16-18]对径向磁通磁齿轮、轴向磁通磁齿轮和横向磁通磁齿轮的输出特性进行了全面对比分析。文献[19]对比分析了不同调制环形状同轴磁齿轮之间的转矩性能差异。文献[20]基于有限元法对比分析了行星磁齿轮与同轴磁齿轮的转矩输出性能,并对同轴磁齿轮进行了优化设计。为了减小磁齿轮的转矩波动,文献[21-22]提出了一种采用Halbach永磁阵列的磁齿轮。文献[23-25]分别基于差分进化算法和基因遗传算法对磁齿轮进行了优化设计,以提高磁齿轮的转矩密度、减小转矩波动。文献[26]基于磁齿轮设计理论,采用有限元法对其主要结构尺寸进行了优化设计。文献[27-28]针对永磁体表贴式磁齿轮分别提出混合解析模型和集中参数等效磁路模型,以便于磁齿轮的分析与优化设计。
尽管近几十年来国内外学者对磁齿轮进行了众多研究,但仍缺乏对磁齿轮内转子极对数、外转子极对数和调制齿数量选取原则的系统性研究。因此,本文基于气隙磁密谐波磁场,对同轴磁齿轮极对数的选取原则进行深入分析,并给出能够产生较高稳定转矩的内转子永磁体极对数、外转子永磁体极对数和调制环齿数配合规律。
1 拓扑结构
图1所示为内转子极对数5、外转子极对数19、调制齿个数24(5/19-24)的同轴磁齿轮,该结构的永磁体安置于内转子和外转子表面,又称为永磁体表贴式同轴磁齿轮。调制环位于内转子和外转子之间,其由多个导磁性能良好的调制齿组成。
本文研究的磁齿轮均以内转子作为输入轴、外转子作为输出轴,调制环保持静止,此时磁齿轮的工作原理简述如下:调制环对内转子永磁体和外转子永磁体磁动势分别进行调制,当内转子极对数、外转子极对数和调制齿个数满足一定条件后,内外转子永磁体可分别在内外气隙中产生极对数和旋转速度均相同的谐波磁场,通过二者的相互作用产生稳定的转矩。
假定内转子作为输入轴、外转子作为输出轴,调制环保持静止不动,则磁齿轮的传动比Gr可定义为
(1)
式中:ωi和ωo分别为内转子和外转子旋转角速度。
2 气隙磁场分析
2.1 磁动势和比磁导
永磁体表贴式同轴磁齿轮二维展开模型如图2所示。图2中,θo、θi分别为外转子、内转子永磁体磁极中心线距离调制齿中心线的初始位置,θ为距离坐标原点的圆周位置角。
以调磁齿中心线为坐标原点,定义内转子极对数为Ni,则内转子永磁体磁动势的电周期为2π/Ni,可得到内转子永磁体磁动势的傅里叶级数为
(2)
式中:t为内转子旋转的时间;Fim为内转子永磁体磁动势第m次谐波的傅里叶系数,m为内转子永磁体磁动势谐波次数。
同理,定义外转子极对数为No,则外转子永磁体磁动势的电周期为2π/No,外转子永磁体磁动势的傅里叶级数可表示为
(3)
式中:Fon为外转子永磁体磁动势第n次谐波的傅里叶系数,n为外转子永磁体磁动势谐波次数。
磁齿轮调制环对气隙比磁导具有调制作用,定义调制环齿数为Ns,经调制环调制后的气隙比磁导周期为2π/Ns,气隙比磁导的傅里叶级数可表示为
(4)
式中:Pδ0为气隙比磁导常数分量;Pδk为气隙比磁导k次谐波分量的傅里叶系数,k为气隙比磁导谐波次数。
2.2 气隙磁密
根据电机磁动势- 比磁导基本理论,磁齿轮内转子和外转子永磁体磁动势经调制环调制后产生的气隙磁密可由(5)式计算得到:
(5)
式中:Bδi(θ,t)为内转子永磁体产生的气隙磁密;Bδo(θ,t)为外转子永磁体产生的气隙磁密。
结合(2)式~(5)式,可得到内外转子永磁体产生的气隙磁密解析式为
(6)
(7)
内外转子永磁体磁动势谐波幅值Fim和Fon分别与谐波次数m和n呈反比,气隙比磁导谐波幅值Pδk与谐波次数k也呈反比,故随着谐波次数增加,其幅值明显减小,磁动势和气隙比磁导高次谐波对气隙磁密的影响相对较小,可忽略。因此,气隙磁密主要由永磁体磁动势基波分量、气隙比磁导常数分量和基波分量共同决定。此时,(6)式和(7)式可简化为

(8)

(9)
式中:Pδ1为气隙比磁导1次谐波分量的傅里叶系数。
2.3 谐波磁场分析
如(8)式所示,内转子永磁体磁动势和气隙比磁导相互作用后产生的气隙磁密主要由3项组成:第1项为永磁体磁动势基波分量与气隙比磁导常数分量相互作用产生的气隙磁密;第2项和第3项为气隙比磁导基波分量对永磁体磁动势基波分量调制后产生的气隙磁密。类似地,外转子永磁体磁动势和气隙比磁导相互作用后产生的气隙磁密也由3项组成:第1项为永磁体磁动势基波分量与气隙比磁导常数分量相互作用产生的气隙磁密;第2项和第3项为气隙比磁导基波分量对永磁体磁动势基波分量调制后产生的气隙磁密。
磁齿轮内转子永磁体磁动势与气隙比磁导相互作用产生的气隙磁密谐波极对数和旋转速度如表1所示;外转子永磁体磁动势与气隙比磁导相互作用产生的气隙磁密谐波极对数和旋转速度如表2所示。
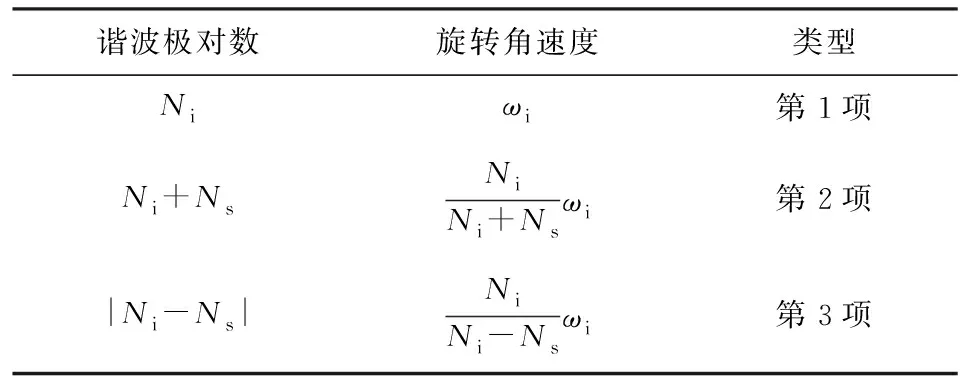
表1 内转子永磁体磁动势与气隙比磁导相互作用产生的气隙磁密谐波分析Tab.1 Air-gap flux density harmonics produced by the interaction of inner-rotor MMF and air-gap specific permeance

表2 外转子永磁磁场与气隙比磁导相互作用产生的气隙磁密谐波分析Tab.2 Air-gap flux density harmonics produced by the interaction of outer-rotor MMF and air-gap specific permeance
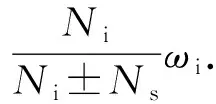
3 磁齿轮极对数选取原则分析
根据电机基本设计理论,磁齿轮能产生稳定转矩的必要条件为:内转子永磁体产生的气隙磁密和外转子永磁体产生的气隙磁密存在极对数相同、旋转角速度也相同的分量。因此,结合表1和表2可得到磁齿轮可产生稳定转矩的必要条件,如表3所示。
受转子外径尺寸的限制,磁齿轮内转子永磁体极对数一般应小于外转子永磁体极对数,故一般不采用表3中条件3、5和8所示的极对数配合。基于表3中简化后的条件可知,条件1、2、4、6、7和9可划分为3类,如表4所示。

表3 磁齿轮稳定传递转矩的条件Tab.3 Conditions for steadily transmitting torque
如表4所示,条件①表明磁齿轮内转子永磁体极对数和外转子永磁体极对数相等、内转子和外转子旋转速度相同,因此满足该条件磁齿轮的传动比为1.满足该条件的磁齿轮依靠内外转子永磁体产生的基波磁密(其极对数分别为Ni和No)的相互作用来产生转矩。此外,满足该条件磁齿轮的内外转子极对数和旋转速度与调制环齿数无关,因此该类型磁齿轮无需调制环。此时,该磁齿轮仅能无接触式传递转矩,对转矩和转速无增加或减小,其作用类似于连接轴或法兰。

表4 磁齿轮稳定传递转矩的简化条件Tab.4 Simplified conditions for steadily transmitting torque
条件②表明磁齿轮外转子永磁体极对数等于内转子永磁体极对数与2倍调制环齿数之和。满足该条件的磁齿轮由极对数为No-Ns和Ni+Ns的气隙磁密相互作用来产生转矩。此外,满足该条件磁齿轮的内外转子旋转方向相同,旋转角速度需满足(10)式,其传动比为No/Ni.
(10)
条件③表明磁齿轮外转子永磁体极对数等于内转子永磁体极对数与调制环齿数之和。对于满足该条件的磁齿轮,内气隙中的主要工作谐波极对数为Ni和No-Ns,外气隙中的主要工作谐波极对数为No和Ni+Ns.满足该条件磁齿轮的内外转子旋转方向相同,旋转角速度需满足(10)式,其传动比为No/Ni.
条件④表明磁齿轮调制环齿数等于内外转子永磁体极对数之和。对于满足该条件的磁齿轮,内气隙中的主要工作谐波极对数为Ni和Ns-No,外气隙中的主要工作谐波极对数为No和Ns-Ni.满足该条件磁齿轮的内外转子旋转方向相反,旋转角速度需满足(11)式,其传动比为-No/Ni.
(11)
对于磁齿轮而言,其内外气隙的磁密基波幅值最高,且其极对数分别为Ni和No.因此,相同条件下,满足条件①的磁齿轮可产生更高的转矩。由于气隙磁密谐波极对数越大,其幅值越小,因此满足条件②和③磁齿轮的最高转矩小于满足条件④磁齿轮的最高转矩,且满足条件②磁齿轮的最大转矩最小。
4 不同极对数磁齿轮性能对比
4.1 拓扑结构和主要设计参数
为了验证上述理论分析,并充分对比表4所述4类磁齿轮的性能差异,本文设计了4台磁齿轮M1、M2、M3和M4,其拓扑结构和主要设计参数分别如图3和表5所示。

图3 4种不同类型磁齿轮拓扑结构Fig.3 Topologies of magnetic gears

表5 4种磁齿轮主要结构参数Tab.5 Structure parameters of four magnetic gears
4.2 气隙磁密
磁齿轮M1、M2、M3和M4内气隙和外气隙中的磁密分布曲线分别如图4(a)和图4(b)所示,从中可见在磁齿轮内气隙和外气隙中均含有大量谐波磁场。由图4(c)和图4(d)可知:磁齿轮内气隙和外气隙中谐波幅值最高的磁场极对数分别为5对极和19对极;仅磁齿轮M1的气隙中含有15对极磁场谐波;对于磁齿轮M2,经齿数为7的调制环对5对极的内转子永磁磁场和19对极的外转子永磁磁场调制后,产生了极对数为2和12的偶数对极磁场谐波;对于磁齿轮M3和M4,其气隙中仅含有奇数对极谐波磁场。
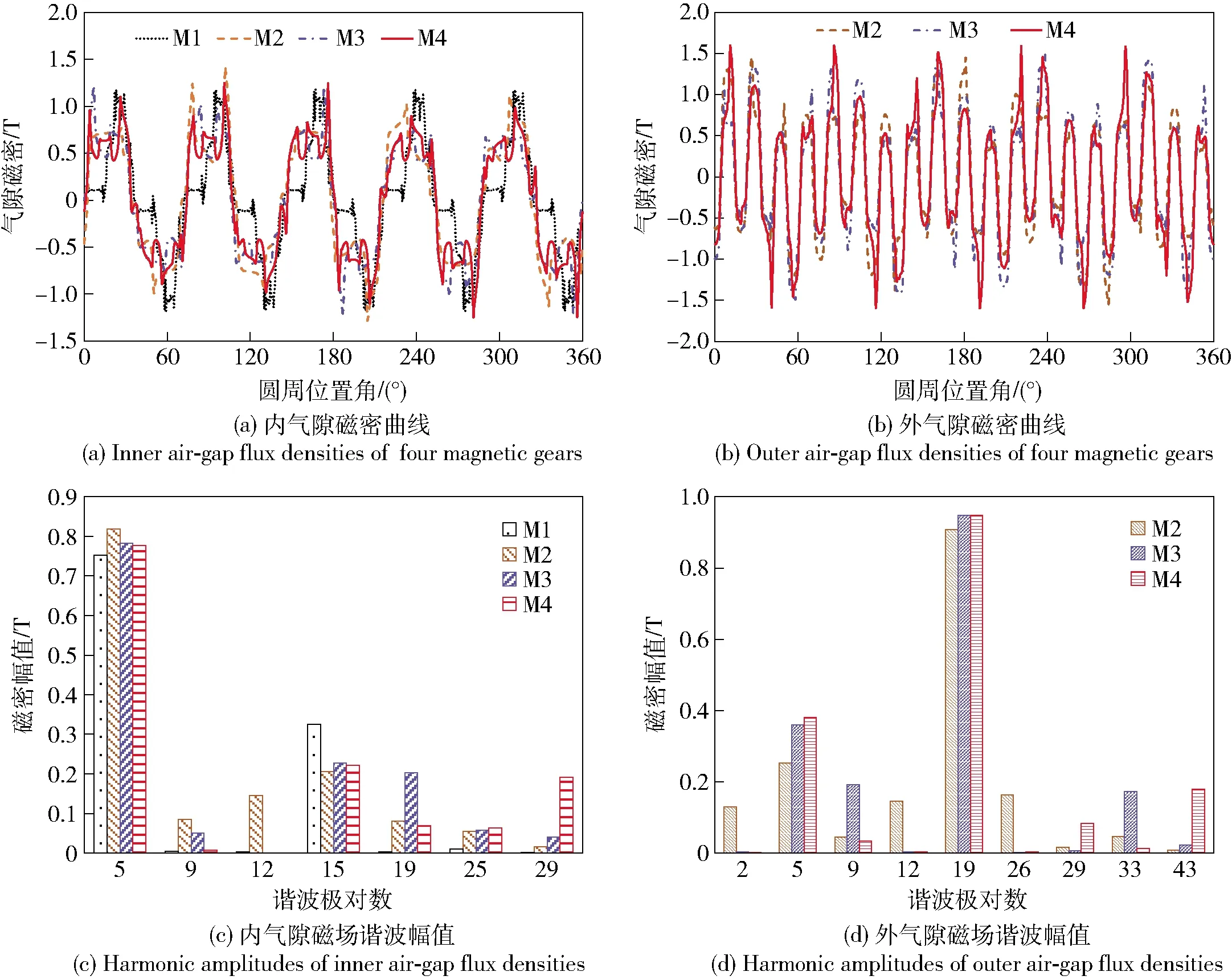
图4 磁齿轮磁密曲线和磁场谐波分析Fig.4 Air-gap flux densities of four magnetic gears
为进一步分析磁齿轮M2、M3和M4的工作谐波,本文对内转子永磁体和外转子永磁体分别单独励磁时的内外气隙磁密进行了分析,相应的分析结果分别如表6~表8所示。
由表6可见:1)对于磁齿轮M2,内转子永磁体极对数为5,其磁动势经齿数为7的调制环调制后,可在内气隙中产生出极对数为5、12、15和19的谐波,其中5、12和15对极谐波幅值较高,19对极谐波幅值相对较小;外转子永磁体极对数为19,其磁动势经齿数为7的调制环调制后,可在内气隙中产生较小幅值的12和19对极谐波,5对极和15对极谐波磁密幅值小于0.01 T,可忽略。因此,内气隙中主要工作谐波的极对数为12和19,但产生的转矩较小。2)在外气隙中,内转子永磁体磁动势经调制环调制产生的19对极谐波幅值较低。因此,尽管外转子永磁体在外气隙中产生了较高幅值的19对极谐波,但其产生的转矩相对较小。对于磁齿轮M2,由于内气隙和外气隙中幅值较高的谐波产生的转矩较小,因此磁齿轮M2的转矩较小。
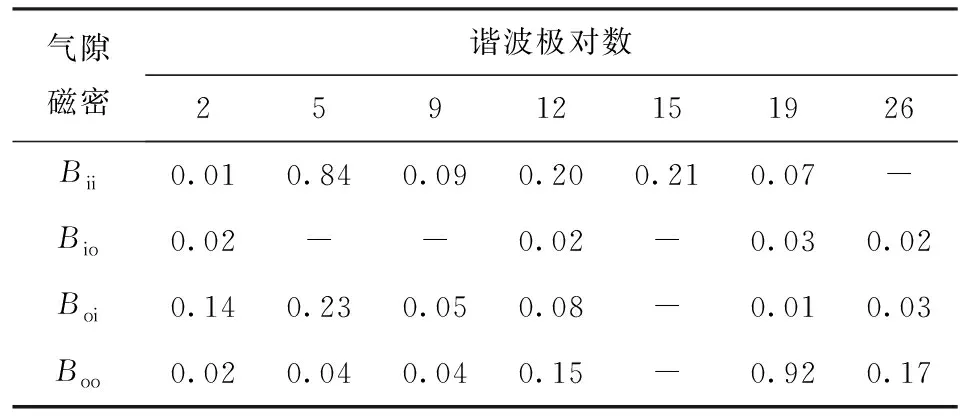
表6 磁齿轮M2气隙磁密谐波分析Tab.6 Harmonics of inner and outer air-gap flux densities for M2 T
由表7可见:1)对于磁齿轮M3,经齿数为14的调制环调制后,5对极的内转子永磁体可在内气隙中产生出幅值较高的5对极和19对极谐波;外转子永磁体极对数为19,经调制环调制后也可在内气隙中产生5对极和19对极谐波,但其幅值相对较低。因此,通过两种5对极谐波和19对极谐波的分别相互作用,可产生一定的转矩。2)在外气隙中,经齿数为14的调制环调制后,5对极的内转子永磁体可产生极对数分别为5、9、19、33和37的谐波,但极对数为19、33和37的谐波幅值相对较低。外转子永磁体极对数为19,经齿数为14的调制环调制后,可产生极对数分别为5、9、19、33和37的谐波,且极对数为5、19和33的谐波幅值相对较高。因此,5对极谐波为工作谐波,且其幅值相对较高,故磁齿轮M3可产生的转矩相对磁齿轮M2的较高。
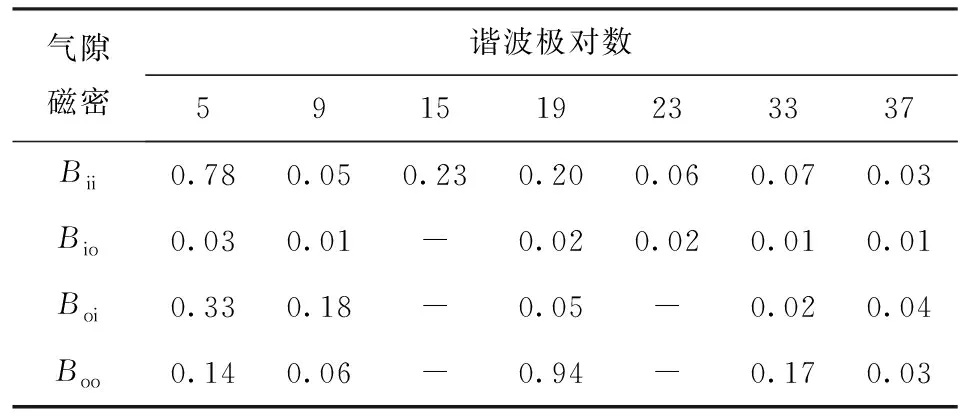
表7 磁齿轮M3气隙磁密谐波分析Tab.7 Harmonics of inner and outer air-gap flux densities for M3 T
由表8可见:1)对于磁齿轮M4,经齿数为24的调制环调制后,5对极的内转子永磁体可在内气隙中产生出幅值较高的5对极、15对极和29对极谐波。19对极的外转子永磁体磁动势经调制环调制后可在内气隙中产生极对数为5和19的谐波,且其幅值较高。因此,内气隙中5对极谐波为主要工作谐波,且产生的转矩较高。2)在外气隙中,5对极的内转子永磁体磁动势经齿数为24的调制环调制后,可产生较高的5对极和19对极谐波。外转子永磁体极对数为19,其磁动势经调制环调制后可产生基于上述分析可知:与磁齿轮M2和M3相比,磁齿轮M4内外气隙中的工作谐波幅值均较高,其具有最强的转矩输出能力;磁齿轮M2因其气隙中的工作谐波幅值较低,其产生的转矩低于磁齿轮M3和M4.
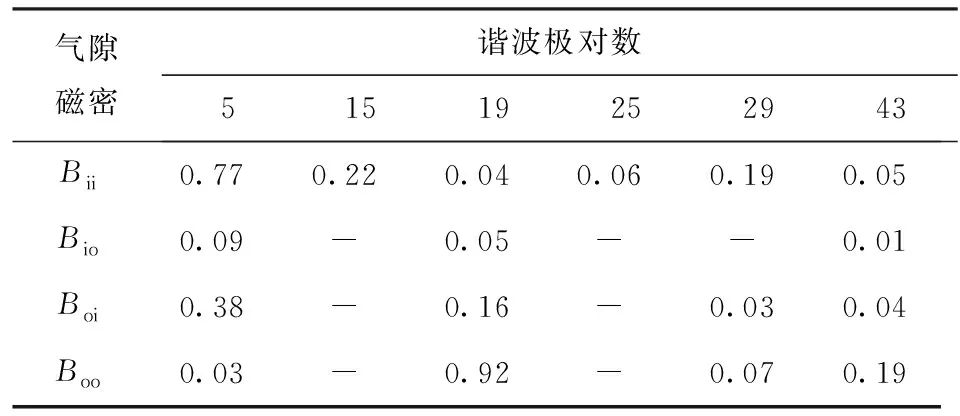
表8 磁齿轮M4气隙磁密谐波分析Tab.8 Harmonics of inner and outer air-gap flux densities for M4 T
19对极和43对极谐波,且其幅值均较高。因此,外气隙中的主要工作谐波为19对极谐波,且内外转子永磁体产生的19对极谐波幅值均较高,从而使磁齿轮M4具有较高的转矩输出能力。
4.3 转矩特性
磁齿轮M1、M2、M3和M4的转矩特性如图5所示。由图5可知:磁齿轮M1、M2、M3和M4内转子可传递的最大转矩分别为388.9 N·m、-1.7 N·m、-17.6 N·m和59 N·m;外转子可传递的最大转矩分别为388.9 N·m、6.8 N·m、67.1 N·m和224 N·m.显然,磁齿轮M1在4种磁齿轮中具有最强的转矩输出能力,但其传动比仅为1,不具有转矩放大能力,表明该磁齿轮仅能用于非接触式传递转矩,其作用与连接轴或法兰类似。磁齿轮M4具有较强的转矩输出能力和较大的传动比,而磁齿轮M2和M3的输出转矩较低,一般不采用该极对数配合的磁齿轮。

图5 M1、M2、M3和M4的转矩输出特性Fig.5 Torques output characteristics of magnetic gears M1, M2,M3 and M4
基于上述分析可知,极对数满足表4中条件①的磁齿轮具有较强的转矩传递能力,但其传动比为1,不具有转矩放大能力;若磁齿轮极对数满足表4中的条件④,则该磁齿轮的传动比为-No/Ni,且转矩传递能力也较强,但内外转子旋转方向相反;极对数满足表4中条件②和条件③的磁齿轮输出转矩较差,一般不予采用。
因此,在设计磁齿轮时,一般根据表4中的条件④对磁齿轮内转子永磁体极对数、外转子永磁体极对数和调制环齿数进行设计,以获得较强的转矩输出能力和更高的传动比。
5 样机测试
针对磁齿轮M4(内转子极对数为5,外转子极对数为19,调制环齿数为24),本文进行了样机加工制造,其主要设计参数与表5中所给参数相同。该磁齿轮结构示意图如图6(a)所示,其中内转子与高速转轴相连,外转子与低速转轴相连,调制位于内转子和外转子之间,其通过螺母与机壳相连。图6(b)~图6(e)分别为外转子、调制环、内转子和整机实物图。如图6(c)所示,该磁齿轮调制环由多个调制齿拼接而成,相邻调制齿之间通过环氧树脂材料填充。同时,为了增加调制环机械刚度,在调制环两端施加端环进行固定。磁齿轮内转子永磁体通过高强度胶进行粘贴,确保其与转子铁心紧密接触。为了进一步增强内转子的可靠性,防止磁齿轮工作过程中永磁体脱落,内转子外围利用碳纤维进行了绑扎。

图6 极对数为5/19-24的磁齿轮样机Fig.6 Prototype of magnetic gear with 5/19-24 pole pairs
为验证该磁齿轮原理的可行性,本文开展空载试验测试了内转子和外转子转速,如图7所示。试验结果表明:内转子和外转子旋转方向相反,且内外转子旋转速度满足(11)式,即内转子转速为外转子转速的-3.8倍,表明该磁齿轮的传动比为-3.8,与理论分析完全一致。若不考虑磁齿轮自身损耗,则外转子转矩为内转子转矩的3.8倍。
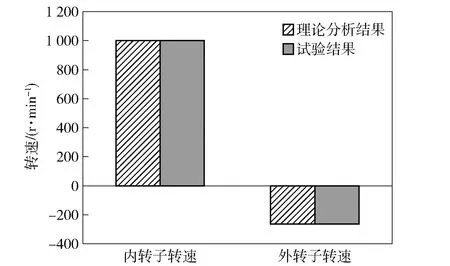
图7 磁齿轮转速Fig.7 Operation speed of the prototype
6 结论
本文基于磁动势- 比磁导理论推导了磁齿轮气隙磁密解析式,深入分析了磁齿轮内转子和外转子永磁体经调制环调制后产生的气隙磁密谐波,并研究了磁齿轮内转子永磁体极对数Ni、外转子永磁体极对数No和调制环齿数Ns的选取原则。得出主要结论如下:
1)No=Ni,且无调制环,则磁齿轮具有较强的转矩传递能力。此时内外转子旋转方向相同,传动比为1,对转矩和转速无增强或减小作用,可将其看作一种非接触式联轴器或法兰,应用于特种车辆、潜艇等特种装备的扭矩传递装置时,可极大程度减小振动和噪声。
2)No+Ni=Ns,则磁齿轮的传动比可设计的较大,具有降低转速、增强扭矩的作用,且转矩传递能力强,可将其用作特种车辆传动系统的减速装置。
3) 若No=Ni,且No+Ni=Ns,则内转子和外转子转速相同、旋转方向相反、扭矩大小相同,将其应用于直升飞机,可省去反扭矩旋翼,从而简化系统结构,具有体积小、质量轻、成本低等优点。
由此可见,磁齿轮可对转矩和转速有一定的增强和减小作用,且具有无接触、免维护、低振动、低噪声等优点,在特殊军工场合具有广泛应用前景。
