如何从距离和方向两个维度认识平移

应耀杰

“平移”是“空间与几何”领域中的重要内容，教学时可以开展以下活动帮助学生从距离、方向两个维度来理解平移。

一、在“按要求画图”中认识方向和距离

1.方向确定，平移后位置不唯一

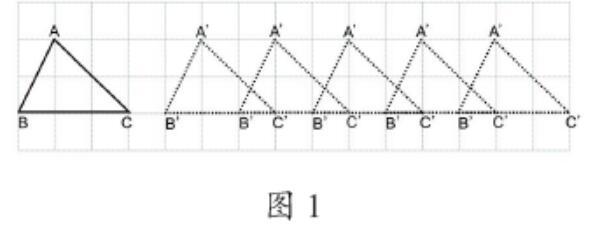
（1）画一画：三角形ABC向右移动后出现的新三角形A′B′C′。

（2）说一说：三角形ABC怎样移动可以得到三角形A′B′C′。

（3）比一比：都是向右平移，为什么大家画出来的位置会不相同？学生对比作品后发现，新得到的三角形A′B′C′虽然都在原图形的右侧，但有些近、有些远，位置不确定（如图1）。学生由此体会到只知道方向，并不能唯一确定图形平移后的位置。

2.距离确定，平移后位置不唯一

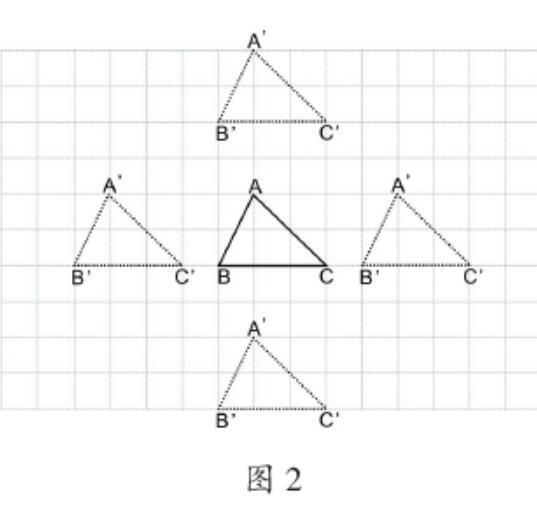
（1）画一画：三角形ABC平移4格后出現的新三角形A′B′C′。

（2）比一比：都是移动4格，为什么大家画出来的位置还是不相同？学生发现新得到的三角形A′B′C′不仅能向右移，也可以向上、下、左等方向移（如图2）。学生由此体会到只知道距离，也不能唯一确定图形平移后的位置。

3.方向、距离都确定，平移后位置唯一

（1）画一画：三角形ABC向右平移4格后出现的新三角形A′B′C′（如图3）。

（2）想一想：这次作图为什么只有唯一结果？引导学生发现，只要确定了方向和距离，就能确定图形平移后的唯一位置。

二、用“方向”与“距离”两个条件描述图形的平移运动

1.选一选

呈现图4，请学生选择哪几个图形是长方形EFOG平移后得到的。

2.分一分

小组合作，把新图形①～⑧根据长方形EFOG的移动变化分一分类。学生把图形①③⑤归为平移一类;把图形②⑦归为旋转一类;把图形④⑥⑧归为另一类。

3.说一说

观察这三组图形，说一说移动中的发现。从图形①③⑤的移动中再次体会图形的平移一定需要明确方向和距离;从学生对图形⑤不同平移过程的描述，引导学生发现平移的路径可以有很多种，可以先向左平移4格，再向下平移4格，也可以先向下平移4格，再向左平移4格。

4.改一改

小组讨论：不是平移得到的5个图形做怎样的调整，也能符合平移的要求？学生发现，通过旋转或改变图形长、宽的尺寸即可符合平移的要求。

通过开展画、比、说、悟等活动，不仅可以帮助学生从距离和方向两个维度认识平移，还能提高学生精准辨析、深度思考的能力。

（华师大宁波艺术实验学校西校区   315101）