多目标联合的上行链路功率优化算法

张延年，吴 昊，张 云

(南京交通职业技术学院 电子信息工程学院，江苏 南京 211188)

0 引言

作为前沿技术，无人机(Unmanned Aerial Vehicle,UAV)已在多个领域内广泛使用[1-2]。其中，将UAV作为飞行基站，能够有效地将设备终端连通至蜂窝网络[3-4]，提高了频谱利用率，扩大了通信覆盖范围。基于UAV的通信系统不同于传统的由静态基站组成的通信系统。不失一般性，UAV以及物联网网络(Internet of Things,IoT)中的设备均是由电池供电[5]，限制了它们的通信距离。因此，如何有效地利用它们的能量成为研究热点之一。

目前，研究人员已对UAV位置、路径规划，物联网中节点位置部署问题进行了大量研究[6-14]。文献[5]针对UAV-IoT通信场景，研究了UAV部署和上行链路功率的控制策略。文献[6]针对地-空通信链路(地面上的节点安装一架天线，UAV安装了多架天线[8])，对其上行链路的速率和进行了优化。然而，其在优化速率和过程中只考虑了地面节点的位置。

针对UAV-IoT通信系统，提出多目标联合的上行链路功率优化(Multi-objective joint Optimization of Uplink Power,MJOP)算法。MJOP算法通过从UAV水平位置、飞行高度和波束宽度三方面优化上行链路功率，进而降低了总功耗。

1 系统模型及问题描述

1.1 系统模型

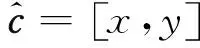
图1 系统模型Fig.1 System model

假定UAV与用户u间的信道模型为自由空间信道模型，且它们之间的链路为视距链路。此外，UAV配备的定向天线，其天线增益为G，用户配备全向天线。不失一般性，UAV天线的半功率波束宽度的方位角和仰角相等，且分别表示为2Θ，其中Θ∈(0,[π/2])[14]。参照文献[15]，在方位(θ,φ)的天线增益可近似表述为：

(1)

式中,G0≈2.284 6；θ和φ分别表示方位角和仰角；g表示天线增益。

此外，令hu表示用户与UAV间的上行信道增益：

(2)

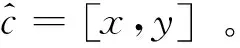
1.2 问题描述

假定总体的资源块长度为M,将其均匀划分为N个块，每个用户用一块。m1被分配给用户1，m2被分配给用户2，mN被分配给用户N。资源块总长度M=W×τmax，其中W表示系统带宽，τmax表示不同资源块之间的最大传输间隔。

依据文献[16]，用户u上能够获取的信息速率：

(3)

式中，γu=PuhuG,Vu=1-(1+γu)-2≈1，其中Pu、γu、Vu和εu分别表示传输功率、信噪比、信道色散和解码时所产生的误码率；Q-1(εu)表示关于变量εu的高斯函数。

依据式(3)，并结合文献[14]的推导可得：

(4)

将式(1)和式(2)代入式(4)可得：

(5)

为了方便进行数据处理，假定各用户所需的数据率相等，即Ru=R。

最后，可形成上行链路总功耗的优化目标函数：

(6)

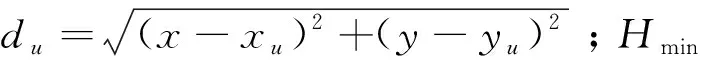
问题P(式(6))是一个多变量联合的非凸、非线性的函数 ，直接求解问题P是非常复杂的。为此，采用“分而治之”的策略求解式(6)。

2 迭代求解目标函数

如上所述，直接计算式(6)的全局最优解是非常复杂的。因此，采用基于扰动理论(Perturbation Theory,PT)的迭代方法求解[17-18]。先将式(6)拆分成2个子问题：UAV二维位置、UAV的高度H以及波束宽度Θ，再获取每个子问题的最优解。

2.1 基于UAV位置优化的子问题

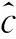
s.t.(du)2≤H2tan2Θ,∀u∈{1,2,…,N}，

(7)

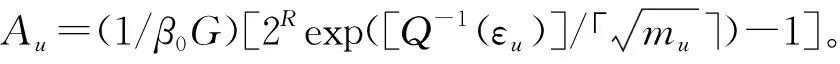
为了求解式(7)，先设置惩罚因子对约束条件进行转换：

κmmax{0,(du)2-[HtanΘ]2}2],

(8)

式中，m表示迭代次数；κm表示惩罚因子。

2.2 基于最速下降法的P1问题求解

为了能够快速求解P1问题，采用最速下降法。引用Barzilai-Borwein法设置每次迭代的步长ηn，n表示迭代指标数。

(9)

式中，

(10)

(11)

基于最速下降法的求解P1问题的过程如算法1所示。

算法1:求解P1问题的过程1.初始化阶段:c^ ηn,ξ,ζ2.设置迭代值:m=0,n=03.while|c^m-c^m-1|<ζdo4. 更新惩罚因子κm=10m-15. while|∇f～1(cn)|<ζdo6. 更新f～1(cn)和ηn7. 计算c^n+1=c^n-ηn∇f～1(cn)8. n=n+19.m=m+1

2.3 基于UAV高度H和波束宽度Θ优化的子问题

(12)

3 性能分析

3.1 实验环境

N个设备分布在于半径为100 m的圆形区域内，系统带宽为2 MHz，具体的仿真参数如表1所示。

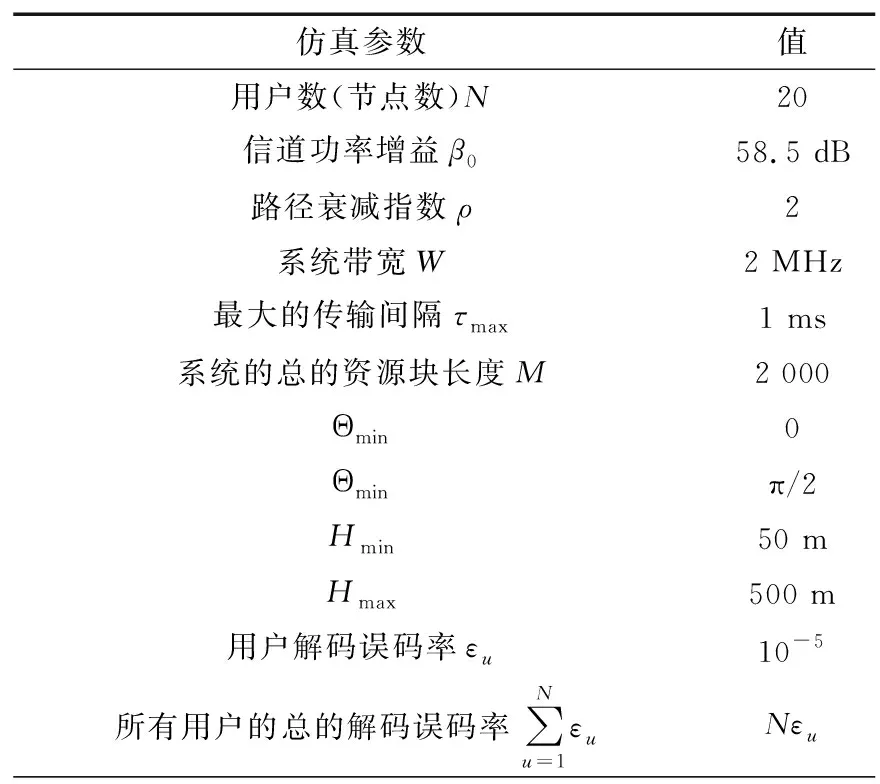
表1 仿真参数Tab.1 Simulation parameters

3.2 MJOP算法的收敛性能

首先分析MJOP算法获取最优值的收敛性能，如图2所示。图2给出传输速率(R=0.5,1.5,2.5 Mb/s)下的MJOP算法收敛情况。

图2 MJOP算法的收敛情况Fig.2 Convergence of MJOP algorithm

由图2可知，上行链路的传输速率越高，所消耗的总功率就越高，这符合逻辑。原因在于，传输速率越高，在带宽一定的情况下，单位时间内传输的数据量就越多，所消耗的功率就越大。此外，在R=0.5,1.5,2.5 Mb/s三种情况下，MJOP算法只需经过2次迭代就能收敛于总功率值。这说明，MJOP算法能够快速地求解问题的最优解。

总的用户解码误码率Nεu对MJOP算法的影响如图3所示。

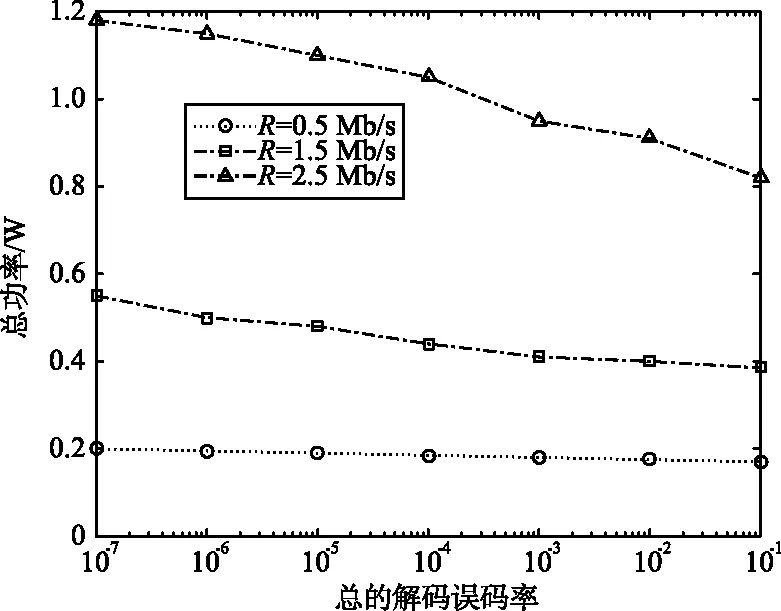
图3 总的用户解码误码率对总功率的影响Fig.3 Sum power vs overall decoding error

由图3可知，Nεu越大，所消耗的总功率越低。原因在于，Nεu越大，链路可靠性越差，所消耗的总功率就越小。为了维持链路的服务质量，可靠性越高，所消耗的总功率就越多。

3.3 对比分析

为了更好地分析MJOP算法，选择同类的2个优化策略进行对比分析：① UAV的二维位置固定，只优化UAV高度和带宽，将该策略记为FP-HB；② UAV高度和带宽固定，只优化UAV的二维位置，将该策略记为HB-OP；③ 穷搜索策略。

图4给出了MJOP、FP-HB、HB-OP和穷搜索策略的所消耗的功率。

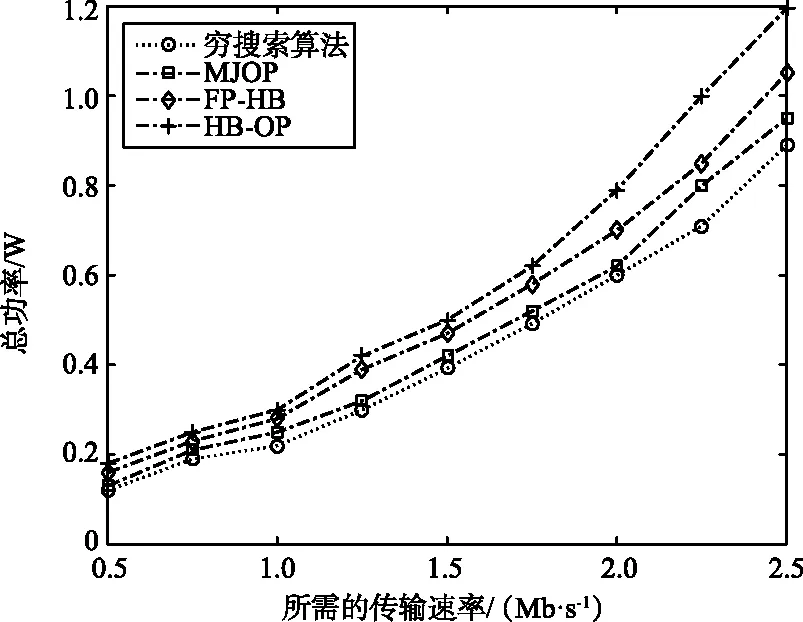
图4 各算法的总功率Fig.4 Sum power of all algorithms

由图4可知，消耗的功率随传输速率R的增加而呈线性增加。R越大，单位时间内需要传输的数据量越大，所消耗的功率必然越多。

此外，相比FP-HB和HB-OP策略，提出的MJOP算法减少了所消耗的总功率。这说明通过对UAV二维位置、高度和波束宽度Θ的多目标联合优化，能够减少总功率。相比于穷搜索策略，MJOP算法所消耗的功率仍较大。

4 结束语

为了减少UAV和物联网设备能耗，提出了基于多目标联合的上行链路功率优化算法MJOP。MJOP算法从UAV水平位置、飞行高度和波束宽度三方面减少上行链路的功耗。仿真结果表明，提出的MJOP算法有效地降低了上行链路的功耗。

本文只考虑一个UAV的场景，后期将进一步优化MJOP算法，使其适应用于多UAV通信场景。此外，值得说明的是，本文是采用了“分而治之”策略求解式(7)。为此，将式(7)拆成2个子问题，再分别求解，获取在给定约束条件下的最优解。从理论上讲，本文提出的多目标联合的上行链路功率优化算法优于每个目标独立功率优化算法(将式(7)拆成3个子问题)。后期，将比较这2类算法的性能。