基于压缩感知的Massive MIMO信道估计算法

张朝柱，施 炯

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

0 引言

在高速环境中，由于基站和用户之间存在较高的相对速度导致较高的多普勒频移，使得信道冲激响应受到干扰出现时间选择性衰落[1-3]。对OFDM系统造成非常明显的影响。正交时频空间(Orthogonal Time Frequency and Space，OTFS)调制[4]在处理时变信道有很大优势，通过基展开模型，来消除信道中时间的影响，在时延-多普勒域中进行，获得高于OFDM调制的性能增益。文献[4-5]中，Hadani R等人通过对信道在时延方向和多普勒方向的结构和稀疏特性，提出了OTFS调制技术，在时延-多普勒域上完成数据传输，证明了OTFS调制技术与OFDM调制存在相适应性。文献[6]中，为了应对高多普勒频移，以信道的基展开模型，结合时延信道具有稀疏性，提出时延-多普勒二维信道模型，基于此提出基于分布式的压缩感知算法，可以有效抑制载波间干扰，在保证性能的同时有效减少导频子载波数量。文献[7]利用Massive MIMO系统中时延维、多普勒维和角维的稀疏特性，提出了3D-OMP算法，该算法在高速场景下性能优秀。本文针对高速场景下，Massive MIMO下行信道估计中导频开销大及存在较高多普勒频移的问题，结合时延-多普勒-角域信道结构，通过压缩感知理论，在信道稀疏度未知情况下，提出了基于三维信道结构的块自适应压缩采样匹配追踪(3D-B2ACoSaMP)算法，该算法通过分别对多普勒域信道单一块长度估计，对角域维度唯一稀疏块的块位置及块长度进行估计以及对时延维常规稀疏度进行估计，有效提高信道估计性能。仿真表明,通过该算法进行信道估计具有良好的性能。

1 Massive MIMO OTFS系统模型

1.1 SISO OTFS系统模型

高速运动场景下通信是现代通信必须面对的问题。OTFS调制是替代OFDM系统以应对高速运动场景通信而提出的技术方案。OTFS技术通过信道维度转换，达到降低时间影响的目的[8-9]。OTFS系统框图如图1所示。

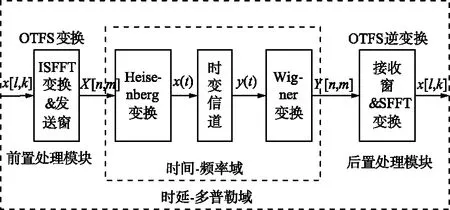
图1 OTFS系统框图Fig.1 Block diagram of OTFS system

通过文献[10]可以知道，OTFS技术和OFDM技术有良好的适应性，可以在OFDM系统基础上完成，如图2所示，通过在系统的发射和接收端增加ISFFT和SFFT变换来完成，Heisenberg变换和Wigner变换如图2所示进行替代，实现OTFS技术与当前OFDM技术的兼容[4,9,11-12]。

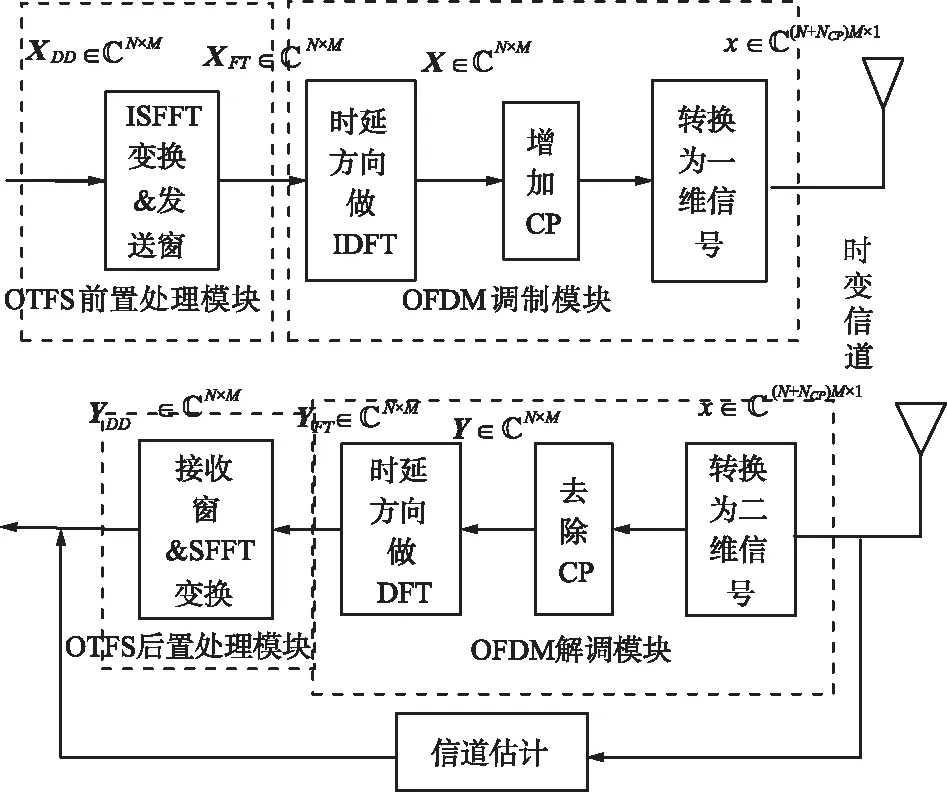
图2 SISO OTFS信道估计框图Fig.2 Block diagram of SISO OTFS channel estimation

使用正交调幅(Quadrature Amplitude Modulated，QAM)数据符号，其长度为N×M，通过将一维转为二维信号，得到延迟-多普勒域的OTFS帧XDD∈N×M，N和M分别为时延和多普勒方向的数据符号个数，其中，SFFT和ISFFT的数学表达式为[13-15]：

XDD[l,k]=SFFT(XFT[n,m])=

(1)

XFT[n,m]=ISFFT(XDD[l,k])=

(2)

假设发送窗Wtx为所有元素均为1的矩阵，则通过OTFS预处理模块得到时频域信号XFT∈N×M，表示为：

(3)

式中，FN∈N×N和M×M为离散傅里叶变换矩阵。

信号经过OFDM模块，首先通过IDFT变换获得二维信号X∈N×M：

(4)

式中，X=[x1,x2,…,xM]，xn∈N×1为一个OFDM符号，每个OFDM符号带宽为NΔf，持续时间为T；Δf为子载波间隔。

添加长度为NCP的循环前缀来去除码间干扰，随后进行维度转换获得一维发送信号x。定义其信道抽头个数为L+1，hk,l表示时变信道，zk为加性噪声，则接收信号y的第k个元素yk为：

(5)

经过OFDM解调后，通过维度转换和移除循环前缀，得到二维信号YFT：

YFT=FNX。

(6)

通过OTFS后处理模块，得到时延-多普勒域信号YDD，表示为：

YDD=XFM。

(7)

由文献[7]可知，当发送脉冲和接收脉冲在时间维上准确满足双正交性，频率维满足近似双正交性时，YDD中第(l,k)个元素表示为：

(8)

(9)

式中，l满足l=0,1,…,N-1；k满足k=0,1,…,M-1；ZDD(l,k)为时延-多普勒域加性噪声，而且满足H(l,k)=H(l+N,k+M)。

1.2 时延-多普勒-角域信道及稀疏性分析

考虑单小区Massive MIMO系统，基站天线数为Nt，将其排列成均匀线阵，相邻两天线之间的距离为半波长，假设小区内有K个单天线用户，每个用户的下行信道是相同的，可以先分析其中的一个用户情况[16]。假设信道存在Np条长度为L的主路径，分析第i条主路径的第l条子路径，定义该路径信道增益为mli，多普勒频率为vli，发射波束角度为γli，定义βli=(d/λ)sinγli，则βli∈[-1/2,1/2)，该主路径下所有子路径时延为τi，第nt个天线与用户间信道为hnt，时延-多普勒-角域信道为Hl,k,a，时延-多普勒-空域信道为Hl,k,nt：

(10)

式中，Hl,k,a可以表示为Hl,k,nt沿空域维度的离散傅里叶逆变换(IDFT)[17]，则Hl,k,a为：

(11)

(12)

在实际信道之中，只有几条主路径。研究表明，无线信道在时延域上具有稀疏性，信道能量主要集中在这些散射路径之中。假设最大路径时延为τmax，则信道Hnt在时延维有限支撑为[0:Nmax-1]，其中，Nmax≈τmaxNΔf。

定义v为用户移动速度，λ为波长，则第i条主路径的第l条子路径的多普勒频率vli为：

(13)

式中，φli表示上述子路径信号到达方向与用户移动方向的夹角，φli∈[-π/2，π/2)，所以最大多普勒频率为vmax/2=v/λ，多普勒频率vli∈[-vmax/2，vmax/2)，则时延-多普勒域信道Hnt沿多普勒方向的有限支撑为[-Mmax/2,Mmax/2-1]，其中，Mmax≈vmaxMT，T=1/Δf。现定义存在一用户乘坐在速度为250 km/h的高铁上，其中，Δf=15 kHz，载波频率为2.15 GHz，可以得到最大多普勒频率vmax/2≈498 Hz，Nmax/2≈vmaxMT/2=vmaxM/2Δf≈0.07M/2，说明在多普勒方向上，非零值大约存在7%。所以信道Hnt在多普勒方向存在唯一块，其位置在多普勒信道中间向两边扩展，随着用户移动速度的增加，多普勒维扩展也会随着增大，其块长度未知[7]。

对于角维信道稀疏性，由于主路径的角度扩展很小，时延-多普勒-角域信道沿角维呈现突发块稀疏特性[18]。定义H∈Ng×Mg×Nt为时延-多普勒-角域三维信道，其信道结构如图3所示，其中，角维的非零块的位置和块长度是未知的。

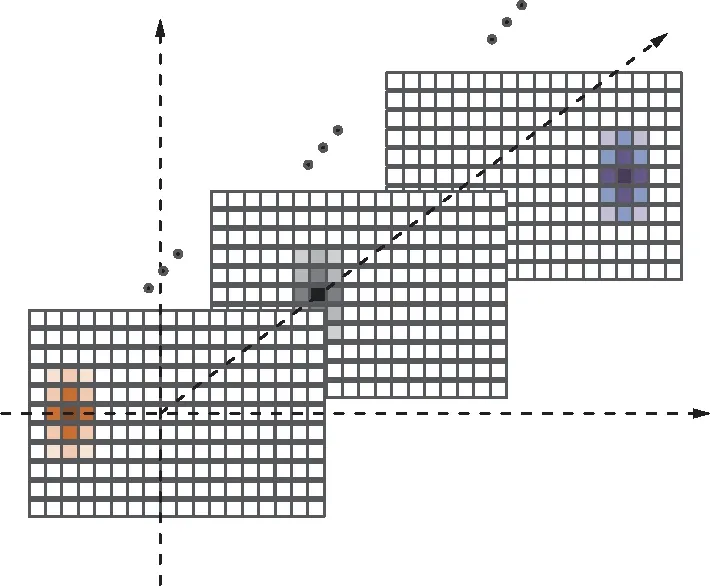
图3 时延-多普勒-角域信道稀疏结构Fig.3 Time delay-Doppler-angle domain channel sparse structure

1.3 时延-多普勒-角域信道模型

假设时延-多普勒域上，OTFS帧结构如图4所示。

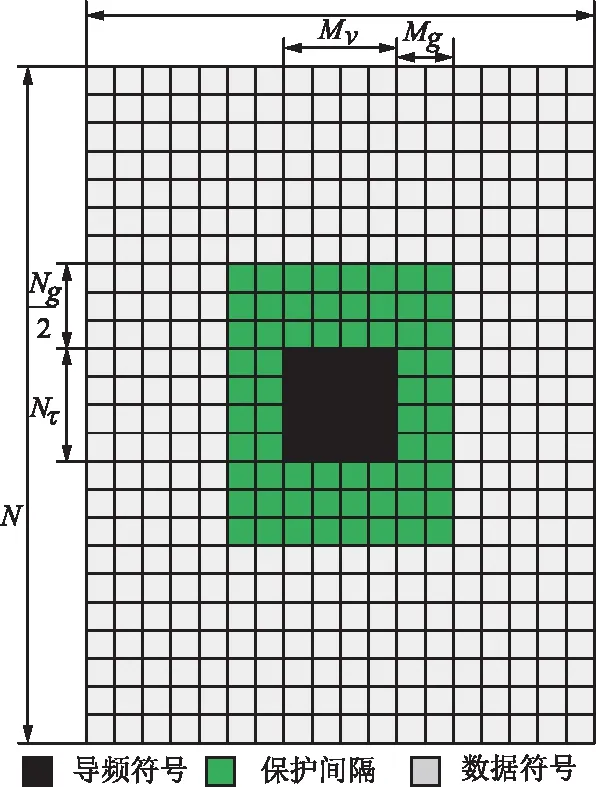
图4 OTFS帧结构Fig.4 Structure of OTFS frame

图4大小为N×M，时延方向长度为Nτ，沿多普勒方向长度为Mv，为了避免干扰，需要设置保护间隔，沿多普勒方向和沿时延方向分别为Ng和Mg/2，根据上一节时延-多普勒域信道Hnt支撑判定，保护间隔沿多普勒方向大小满足Mg/2≥Mmax/2-1，沿时延方向满足Ng≥Nmax-1。为减少导频开销，本文之中使用非正交导频，导频序列为复高斯随机序列，但导频之间是互相独立的，导频位置相同。

定义xl,k,nt为第nt个天线发送的训练导频符号，要求基站侧的天线同时发送信号，接收端获得的信号yl,k：

(14)

式中，l1=0,1,…,Ng-1；k1=-Mg/2,…,0,…,Mg/2-1；nt=0,1,…,Nt-1，将式(12)代入式(14)可得：

(15)

式中，

式(15)所得到的yl,k为接收到的导频信号矩阵Y中第(l+1,k+1+Mv/2)个元素，将导频信号矩阵Y转化为列向量形式y，则yl,k为向量y的第lNτ+k+1+Mv/2个元素，Y∈Nτ×Mv，y∈NτMv×1。同理，Hl1,k1,a为列向量hk的第lNt+a+1+Nt/2个元素，所以，式(15)可表示为：

(16)

(17)

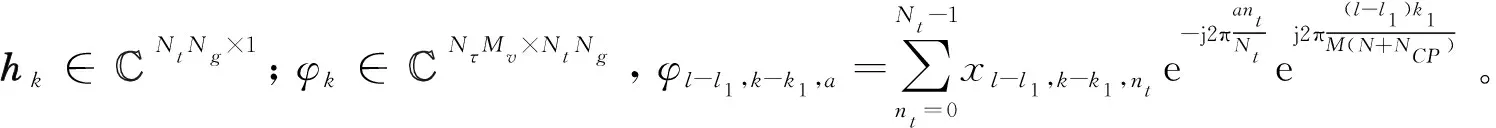
定义：

(18)

(19)

式中，Φ∈NτMv×NgMgNt，h∈NgMgNt×1。则式(17)可表示：

y=Φh+z，

(20)

得到压缩感知基础模型，Φ为测量矩阵，满足不相关性[7,19]。对此将信道估计问题转换为压缩感知信号重构问题。

2 算法设计及分析

3D-B2ACoSaMP算法主要部分为：一是创新性地通过结合角维和时延维信道，对时延维稀疏度估计以及角域维度块位置及块长度估计；二是对于多普勒域信道稀疏块位置已知，对块长度进行估计。将h和Φ进行初始分块：

(21)

(22)

3D-B2ACoSaMP算法流程：

输入：测量向量y，测量矩阵Φ，迭代次数t=1，步长S=1，分块索引λ=0；

步骤1：初始化：r0=y，索引J0=∅，Λ0=∅，支撑集Φ0=∅，块长度Nt/2λ;

步骤 2：块相关测试：

步骤 3：将列向量ut转换为二维矩阵形式et，同时更新索引Λt：

et=invec{ut}；

步骤 5：求最小二乘解

步骤 8：更新支撑集

步骤 9：更新残差

rt,v=y-Φ(ΦΩtTΦΩt)-1ΦΩtTy;

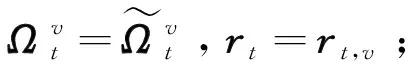
步骤11：如果‖rt‖2>‖r0‖2则重构失败，进入步骤13；如果‖rt‖2≥‖rt-1‖2，令S=S+1，支撑集、残差和估计信道均取上一次迭代结果。

步骤12：重复步骤2～11，直至满足‖rt‖2/‖r0‖2≤pth。

步骤13：更新分块索引

λ=λ+1;

步骤14：重复步骤1～13，当满足迭代停止条件或者块长度满足Nt/2λ=1。

输出：信道h，残差rk。

通过上述分析，三维信道结构之中，时延维稀疏度未知，多普勒维唯一块长度未知，角维唯一块长度和位置均未知，对此， 3D-B2ACoSaMP算法中将三维信道中时延-角域维度二维矩阵转换为一维向量模式，结合多普勒维度，将三维信道矩阵转化为二维信道模式，以方便接下来算法中信道支撑集获取。

用户移动速度在同一时间相同，对此，定义每个主路径多普勒维度的唯一块长度相同。下面将算法之中的主要步骤进行解释。步骤3～6为时延维信道估计，对于步骤3中：

et=invec{ut}，

(23)

et∈Mg×NgNt，是将步骤2得到的块相关矩阵按照图3转换成三维矩形，之后再以(Mg×Ng)为基准转换成二维矩阵，以便于简化算法中对时延稀疏度估计的复杂度，步骤4～6为时延为支撑集的获取。

步骤7中：

(24)

为多普勒维信道非零块长度的获取，根据信道矩阵之中能量集中的原则，通过设定噪声门限pth，可以排除大多数噪声路径，完成对多普勒维支撑集获取。

步骤9～10，通过残差比较，判断本次迭代获得的多普勒支撑是否优于上一次迭代获得的多普勒支撑集，最终选择最优支撑集，其步骤如图5所示。

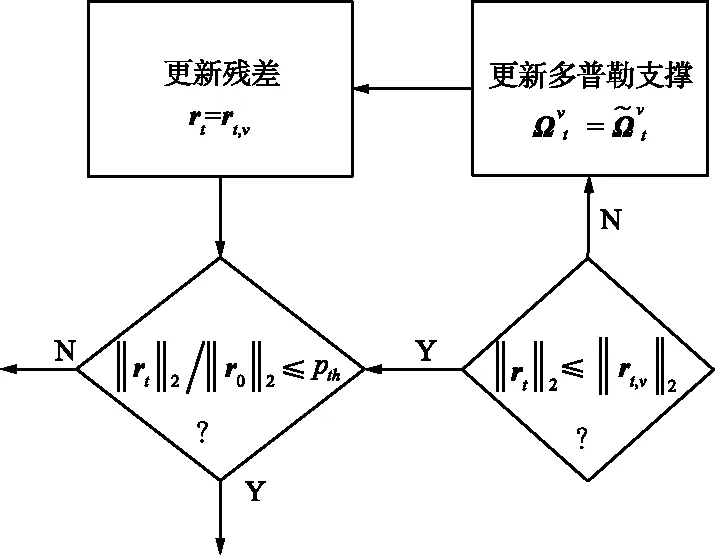
图5 3D-B2ACoSaMP算法中判断条件Fig.5 Decision conditions of 3D-B2ACoSaMP algorithm

步骤11～12为算法输出判定。其中监督条件为‖rt‖2/‖r0‖2≤pth，停止条件为‖rt‖2≤10-2pth，当满足监督条件而不满足停止条件时，进入步骤13，更新块长度，通过迭代循环来获得角维块长度和位置的判定，获得角维支撑集的获取。当监督条件和停止条件均满足时，输出信道估计结果。3D-B2ACoSaMP算法流程图如图6所示。

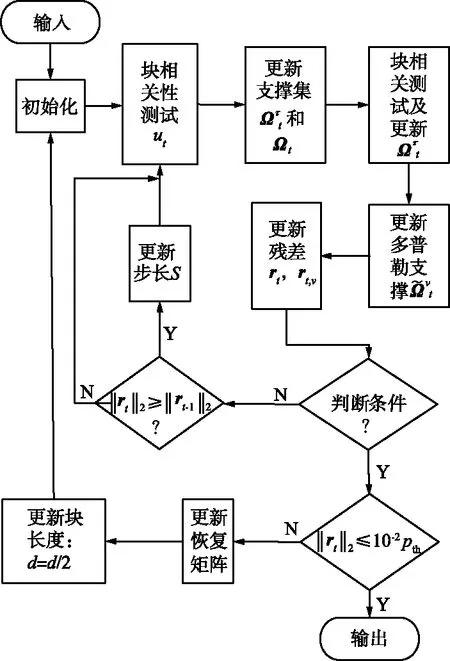
图6 3D-B2ACoSaMP算法流程Fig.6 Flow chart of 3D-B2ACoSaMP algorithm

算法主要应用了块长度和块稀疏度自适应思想。对于块稀疏度自适应，其思想来源于SAMP算法，对此不再叙述。块长度自适应，通过迭代残差来判断块长度，当重构后残差反向增大，则通过块长度减半来逐渐接近真实块长度。虽然提高了算法复杂度，但提高了其应用优势，而且通过块回溯思想，减少重构错误提高重构概率。

3 仿真分析

以Massive MIMO系统下3GPP标准空间信道模型进行建模，信道稀疏度未知，对LS算法、CoSaMP算法以及提出的3D-B2ACoSaMP算法进行仿真，仿真参数如表1所示。OTFS帧沿多普勒维度数量M定义为M=Mv，比较了LS算法、CoSaMP算法及3D-B2ACoSaMP算法在信噪比、导频数量、基站天线数量及用户移动速度等情况下的算法性能。算法性能通过归一化均方误差(NMSE)和误比特率(BER)表示。

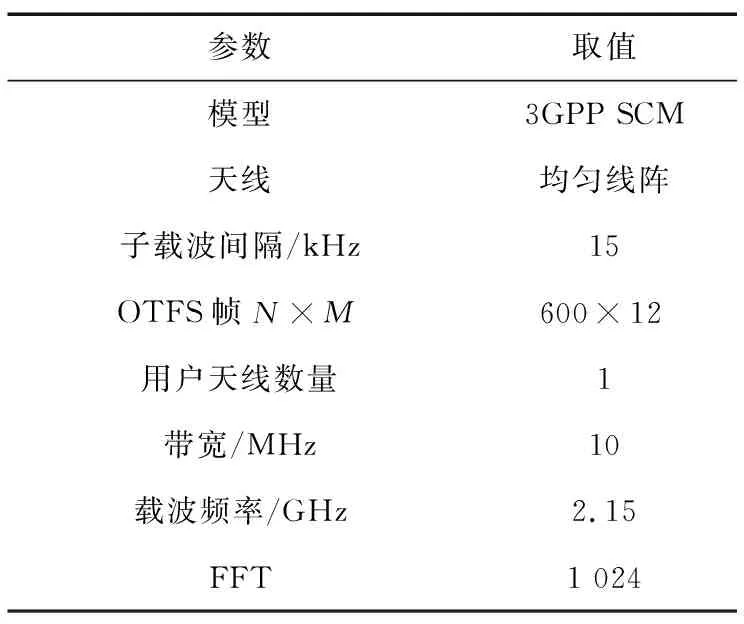
表1 仿真参数Tab.1 Simulation parameters

算法性能将通过参数NMSE进行评估，LS算法NMSE表示为：

(25)

最终结果为所有Nt根天线的平均值。根据式(20)，CoSaMP算法及3D-B2ACoSaMP算法NMSE表示为：

(26)

图7为不同SNR下LS算法、CoSaMP算法及3D-B2ACoSaMP算法性能比较。其中基站有32根天线，导频数量为240，用户以100 m/s的速度前进。LS算法性能较差，远低于基于CS的算法，这是因为导频数量较少导致的，难以实际应用。从图中可以看出，3D-B2ACoSaMP算法性能最优，和CoSaMP算法比较，每次迭代对多普勒唯一块进行估计，提高了算法精度，在SNR上约有8 dB的性能优势。

图7 不同信道估计算法性能与SNR之间的关系Fig.7 Relationship between the performance of different channel estimation algorithms and SNR

图8为导频数量对算法性能的影响。基站有32根天线，用户以100 m/s的速度前进，SNR=5 dB。LS算法性能最差，基本难以获得可以使用的CSI，3D-B2ACoSaMP信道估计算法性能最优，而且随着导频数量的增加，3D-B2ACoSaMP信道估计算法性能优势在加大，总体来说，同CoSaMP算法相比，导频占比少了约10%。

图8 不同信道估计算法性能与导频数量之间的关系Fig.8 Relationship between the performance of different channel estimation algorithms and the number of pilots

图9为不同天线数量对算法的影响。SNR=5 dB，用户以100 m/s的速度前进，导频数量为240。可以看出，LS算法性能最差，而且随着天线数量的增多，其性能快速降低。3D-B2ACoSaMP信道估计算法性能最优，算法利用了信道的三维稀疏结构，获得了比CoSaMP算法更高的性能。

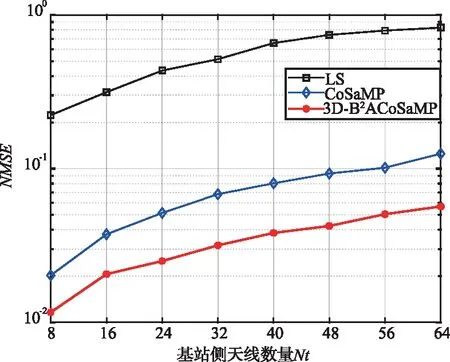
图9 不同信道估计算法性能与BS侧天线数量之间的关系Fig.9 Relationship between the performance of different channel estimation algorithms and the number of BS side antennas

图10给出了用户移动速度对算法性能的影响。设置基站有32根天线，SNR=5 dB，导频数量为240。整体来说，随着速度的增加，多普勒频移会提高，多普勒方向的信道也会随之扩展，导致算法在性能会出现下降。在同一导频开销下，本文提出的算法性能优于CoSaMP算法，远高于LS算法。

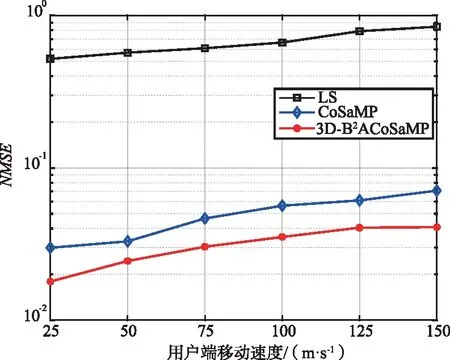
图10 不同信道估计算法性能与用户端移动速度之间的关系Fig.10 Relationship between the performance of different channel estimation algorithms and the moving speed of user terminal

图11为SNR和算法BER性能比较。基于OTFS系统，用户以100 m/s的速度前进，分别以理想状态下CSI，通过LS算法、CoSaMP算法、3D-B2ACoSaMP算法估计得到的CSI，进行信号重构，通过时延-多普勒二维反褶积方法进行信号检测，BER为性能指标，可以得到，传统LS算法获得的CSI精确度最差，3D-B2ACoSaMP算法性能优于CoSaMP算法，在低信噪比情况下CoSaMP算法及3D-B2ACoSaMP算法性能接近，而且，对于3D-B2ACoSaMP算法，在SNR低于15的时候，非常接近理想状态下BER性能曲线；在SNR大于15的时候，和理想状态下BER性能曲线较为接近，基本也处于同一量级，BER大小均在10-3～10-5之间，算法性能优秀。

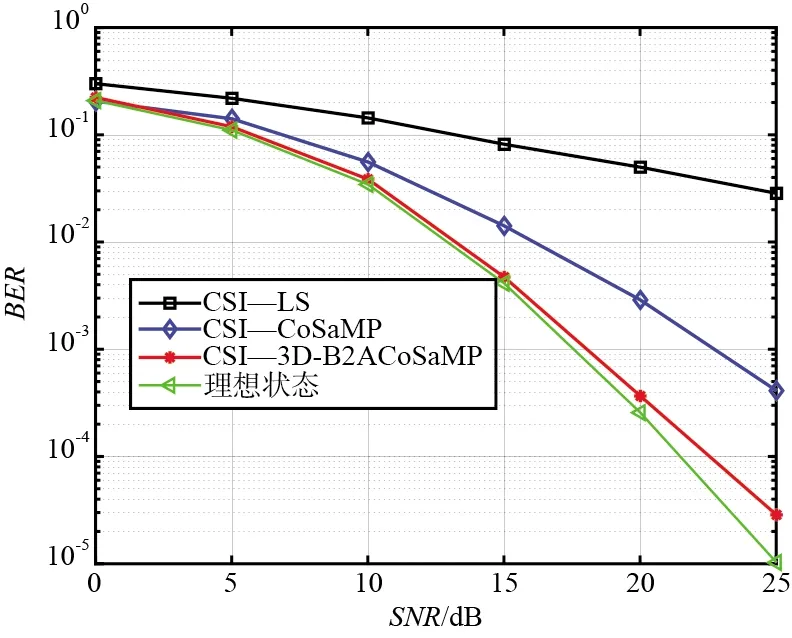
图11 信噪比和算法BER性能比较Fig.11 Comparison of SNR and algorithm BER performance

4 结束语

研究了Massive MIMO OTFS系统时延-多普勒-角域稀疏信道模型，提出了3D-B2ACoSaMP算法，通过Matlab在高速场景下进行了仿真分析，仿真结果表明LS算法性能较差，3D-B2ACoSaMP算法性能相较于CoSaMP算法在信噪比上约有8 dB的性能优势。在BER性能上，3D-B2ACoSaMP算法性能优于CoSaMP算法，接近理想状态下BER性能曲线。本文并未在毫米波频段下进行信道估计研究，而且对导频矩阵设计未进行深入研究，接下来可以研究毫米波下Massive MIMO OTFS系统信道估计以及对导频序列进行研究，来提高信道估计性能。