Detecting entanglement of quantum channels

Chaojian Li，Bang-Hai Wang，Bujiao Wu and Xiao Yuan

1 School of Computer Science and Technology，Guangdong University of Technology，Guangzhou 510006，China

2 Advanced Institute of Information Technology，Peking University，China

3 Center on Frontiers of Computing Studies，Department of Computer Science，Peking University，Beijing 100871，China

Abstract Entanglement is the crucial resource for different quantum information processing tasks.While conventional studies focus on the entanglement of bipartite or multipartite quantum states，recent works have extended the scenario to the entanglement of quantum channels，an operational quantification of the channel entanglement manipulation capability.Based on the recently proposed channel entanglement resource framework，here we study a further task of resource detection—witnessing entanglement of quantum channels.We first introduce the general framework and show how channel entanglement detection is related to the Choi state of the channel，enabling channel entanglement detection via conventional state entanglement detection methods.We also consider entanglement of multipartite quantum channels and use the stabilizer formalism to construct entanglement witnesses for circuits consisting of controlled-Z gates.We study the effectiveness of the proposed detection methods and compare their performance for several typical channels.Our work paves the way for systematic theoretical studies of channel entanglement and practical benchmarking of noisy intermediate scaled quantum devices.

Keywords: quantum entanglement，quantum channel，entanglement detection，entanglement witness

1.lntroduction

Entanglement is a key feature of quantum physics [1—3]，having wide applications in various quantum information processing tasks including quantum dense coding [4]，quantum teleportation [5]，quantum cryptography [6]，quantum computation [7]，etc.However，because almost every quantum system is noisy，how the noise affects the quantum system and whether entanglement survives under the noise is important for robust and reliable quantum information processing.It thus becomes one of the basic problems of quantum entanglement theory to check whether a quantum state is entangled or not.Entangled quantum states could be detected and analyzed by several theoretical and experimental tools.Many researchers have contributed to various separability standards and detection methods [8—16].Notable approaches in the practical analysis of entanglement include the usage of positive but not completely positive maps[8]and entanglement witnesses [9—12].

Conventional entanglement theory focuses on the nonlocal correlation of quantum states，and quantum channels are used as their manipulation tool.Recent works have shown that quantum channel itself could be regarded as the resource object [17—22] and the entanglement of channels has be studied under the framework of quantum resource theories[23—28].Analog to quantum states，quantum channels are also categorized into entangled and separable ones，with the amount of entanglement quantified via channel entanglement measures [23—25].Since a positive channel entanglement measure generally implies the existence of entanglement，it serves as a natural way to detect channel entanglement.However，a channel entanglement measure generally requires full information of the process，hence demanding a cost that is exponential to the system size.Because the channel has both inputs and outputs，the cost increases even quadratically faster than the one of states.Efficient state entanglement detection methods exist when exploiting the specific structure of the target resource and allowing a certain amount of failure，whether we could analogously detect channel entanglement remains open.

Here，we address this problem by considering general approaches for detecting channel entanglement.We first review the framework of state and channel entanglement as well as the task of entanglement detection.Then we show that detecting the channel entanglement is equivalent to detecting the entanglement of the corresponding Choi state，the output state of the channel given the maximally entangled input.We give three general channel entanglement detection strategies based on conventional state entanglement detection methods—negative partial transpose(NPT)[29]，the computable cross norm or realignment criterion (CCNR)criterion [30，31]，and entanglement witnesses.We further extend the discussion to multipartite quantum channels and show how the stabilizer formalism[32]helps in designing entanglement witnesses for circuits consisting of CZ gates.As examples，we consider noisy CNOT and SWAP channels and show the effectiveness of the propose methods.

2.Background

We first review the framework of entanglement for bipartite states and channels，and the task of entanglement detection.For a system A，we denote the corresponding Hilbert space as HAand the set of state operators as D(A) .Consider a bipartite system AB，we call the stateσABseparable when it can be expressed as [33—35]

withλi≥0，∑iλi= 1，and local statesσA，σBon quantum systems A and B，respectively.Otherwise the state is entangled.On the other hand，quantum channels are linear and completely positive and trace-preserving maps which act on quantum states [36].A quantum channel N could be written in the Kraus form [37] as

where the Kraus operators{Ki} fulfilLet NAB∈ CPTP(AB→A′B′)be a bipartite channel，it is called separable [23，25] if it can be written as

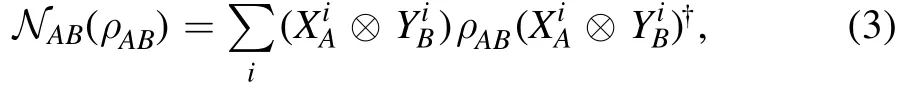
Suppose a quantum information task requires to prepare an entangled stateψABand the practically prepared state isρAB.The task of entanglement detection is to determine whetherρABis entangled.A general detection strategy corresponds to a function f，which distinguishes separable and entangled states.However，since the geometry of the set of separable states is complex，detecting the entanglement of an arbitrary state is a challenging task.A conventional entanglement detection strategy is to exploit a linear witness operator W such that Tr (WσAB) ≥0for all separable statesσABand it detects the entanglement ofρABwith Tr (WρAB)＜0[16].Here we review three general strategies of constructing the witness operator，which will be extended to detecting entanglement of quantum channels in the next section.

The first method is to exploit the positive but not completely positive map of transpose，or the NPT property of states.In particular，we always havewhen applying a partial transposeTAon a separable stateσAB，whereas we could have a negative partial transposed statewhenρABis entangled.In this case，we can find the eigenvector∣φ〉with a negative eigenvalue [38]，i.e.withλ＜0.Then，a linear witness operator can be constructed as follows [16，29]

It is easy to verify that for any state with positive partial transpose，which include separable statesσAB，we have

and for the entangled stateρAB，

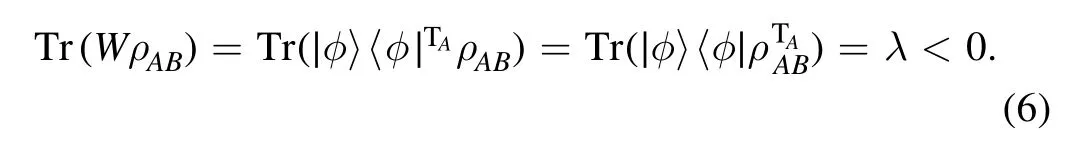
In practice，we may not know the density matrixρABand hence cannot get the eigenvectors with negative eigenvalues.Nevertheless，a realistic quantum protocol generally assumes an ideal pure stateψAB，and the partial transposed pure statecould be used as the witness operator.Indeed，any partial transposed pure state could serve as the witness operator，although to be able to detect the entanglement of a given state，the operator should be accordingly chosen.

The second method is based on a Schimidt decomposition [39] of the density operator，namely the computable CCNR.Specifically，denote the set of Hermitian operators on H as L ( H) ，which is a linear space with inner productfor anyV1，V2∈L ( H).Then for any density matrixρAB∈ D (HAB) ⊂L (HAB)，the Schmidt decomposition ofρABis

whereλk≥0，andare orthonormal bases in L ( HA) and L ( HB) ，respectively.Then we can construct the witness as follows [30，31]

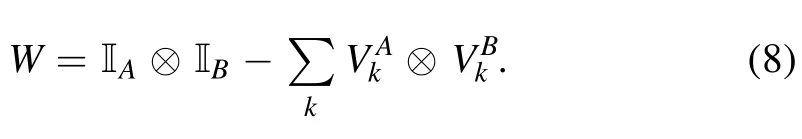
It is easy to verify that for any separable statewe have

Therefore，the stateρABis entangled whenever Tr[ρABW]＜0.Again，the witness operator W could be constructed from any state，for example based on the ideal pure stateψAB.

In the third method，we construct the witness operator W based on any observable O as

where

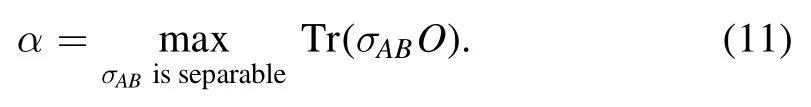
Since Tr[σABO] ≤α，we have Tr[WσAB] ≥0for all separable states.In practice，we could chooseO=ψABand the witness operator can effectively detect entanglement with white noise.

Given the witness operator，a practical scheme is to decompose the operator into local observables.This is particularly important for detecting multipartite entanglement because it is hard to measure a general multipartite observable.Efficient witnesses have been constructed for several typical classes of states including the W state and general graph states.In the next section，we show how similar strategies could be extended to efficient channel entanglement detection.

3.Channel entanglement detection

3.1.Bipartite channels

Since a quantum channel has both inputs and outputs，we first map a channel to a quantum state.In particular，consider a bipartite channel NABthat maps AB toA′B′，we consider the maximally entangled input state ΦAA⊗ΦBBwithand d being the dimension of each subsystem [23—25].The output state

is called the Choi state which is a one-to-one map between states and channels.The entanglement of the biparitite channel can be now reformulated via the entanglement of the Choi state.

Lemma 1.A bipartite channel NABis entangled if the Choi stateis entangled.

Similar results have been discussed in several works[23—25]and we refer to appendix for the proof.Based on such a connection，we can now study the entanglement of channels via its Choi state.Focusing on entanglement detection，our task now becomes to find an observable W，such thatfor all separable channels N.Following the above results for quantum states，we can similarly introduces three types of witness operators for Choi states of channels.

We will shortly show that we can realize the witness with quantum games consisting of proper input states，measurements，and payoffs.Next，we extend the discussion to the multipartite scenario.

3.2.Multipartite channel entanglement

We consider the entanglement of multipartite channels[40，41].Consider a channelΘnthat maps n systems{1 ，2，… ，n}to n systems{1 ′ ，2′，… ，n′}，it is fully separable when

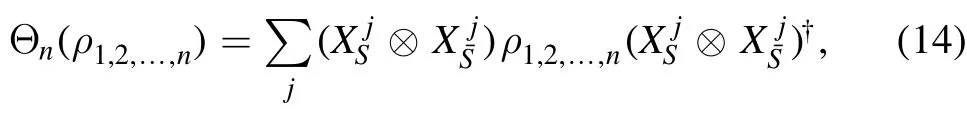
Based on the Choi state of the channel

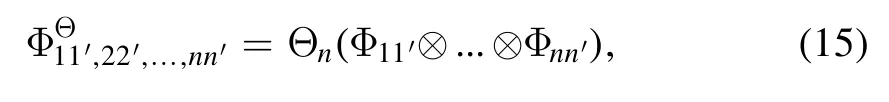
we can similarly relate the entanglement ofΘnto the entanglement of

Lemma 2.A multipartite channelΘnis(genuinely)entangled if the Choi state(genuinely) entangled.

Therefore，we could use techniques of detecting multipartite entanglement to detect channel entanglement.While the three entanglement detection methods work similarly for multipartite channels，how to make the detection to be efficient is in general a challenging task for multipartite channels.

3.3.Entanglement detection via quantum games

In the above discussion，the entanglement witness is constructed and applied with respect to the Choi state of the channel.While we could get the Choi state by inputting a maximally entangled state，we need to double the system size，making its implementation hard.Here，we show a different yet equivalent entanglement detection way via quantum games [43—46].

A quantum gameG is defined by the tuple G=({αij} ，{ρi} ，{Oj})，whereρiare input states，{Oj}is a positive observable valued measures at the output，andαij∈R are the real coefficients which define the particular game.The performance in the gameG enabled by a channel N is quantified by the payoff function

Consider the bipartite channel NABas an example，we haveaccording to the Choi—Jamiolkowski isomorphism.Then we have

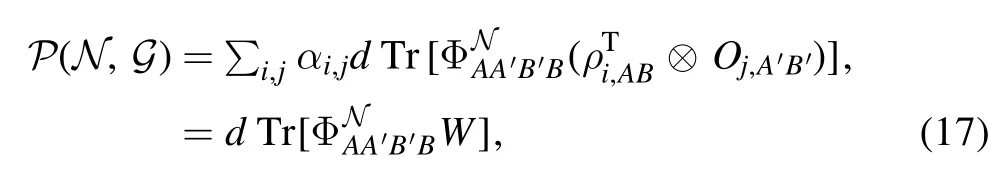
where the W operator is

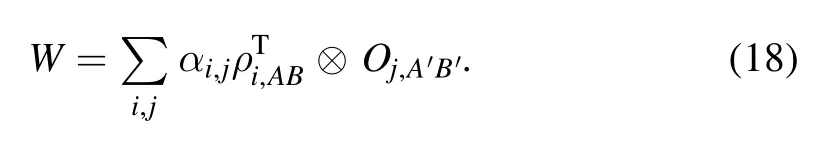
Therefore，for any witness operator W，we can decompose it as above and it corresponds to a quantum game[43].Suppose the quantum game with a witness operator W is G(W) ，then we can show that for any separable channel NABwe have

In practice，we can equivalently realize the witness via a quantum game.Instead of witnessing the entanglement of the Choi state，we can apply the channel to a set of input states，measure the output，and linearly combine the measurement outcomes.The game payoff function plays a similar role of detecting channel entanglement.

4.Example

Now we show entanglement detection for several typical channels.We also note the following fact that local unitary operations before and after the channel does not change the entanglement.

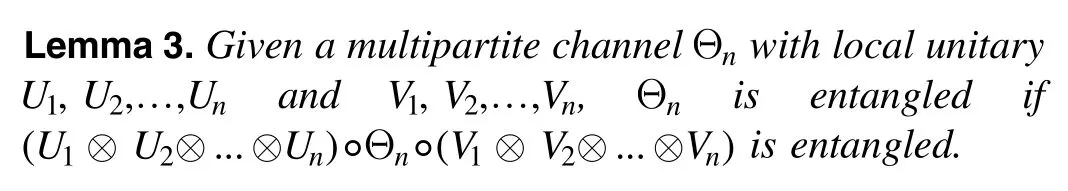
Therefore，any entanglement witness for a channel N works similarly to other channels V◦ N ◦ U that are equivalent to N under local unitary operations U andV.

4.1.Bipartite channels

We first consider bipartite channels，specifically，the CNOT and SWAP gate under local depolarizing noise，as shown in figure 1.In particular the CNOT and SWAP gates are unitary

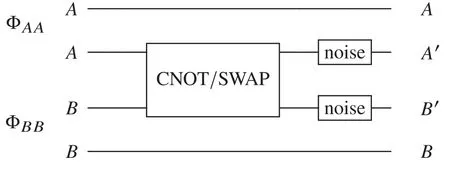
Figure 1.The CNOT or SWAP gate with local depolarizing noise.Given maximally entangled input states ΦA A = ∣Φ〉〈Φ∣AA and ΦB B = ∣Φ 〉〈Φ∣BB，the output state corresponds to the Choi state of the noise channel.The task is to detect the entanglement of the output state between the bipartition betweenAA′ and B′ B.

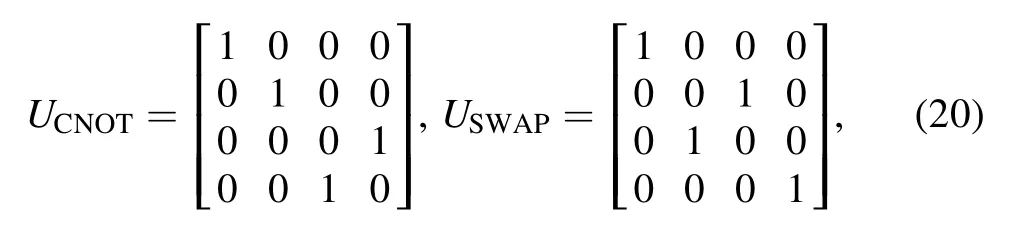
and the local depolarizing noise is

The noisy CNOT/SWAP channel is

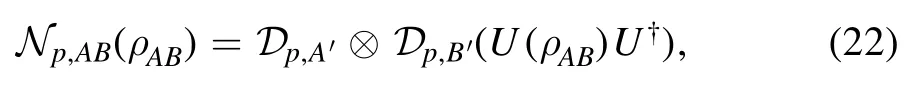
where U is eitherUCNOTorUSWAP.Here we explicitly show the three entanglement witnesses for the CNOT gate and the result works analogy for the SWAP gate.

The Choi state of the CNOT gate is

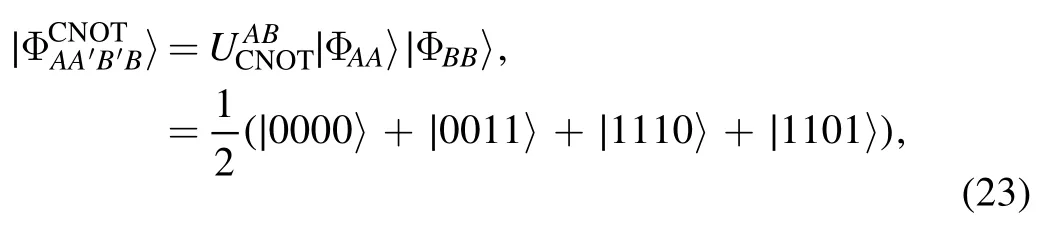
and the density matrix is

The three witness operators could then be constructed accordingly.Consider the eigenvector with a negative eigenvalue ofthe witness operators of the first method isWCNOT，1= ∣φ〉〈φ∣TAA′with

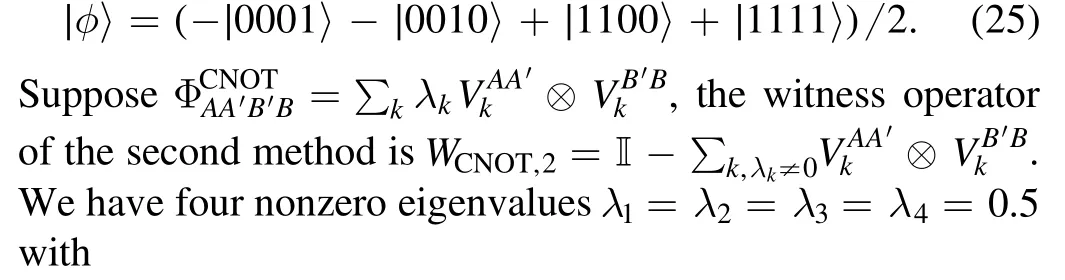
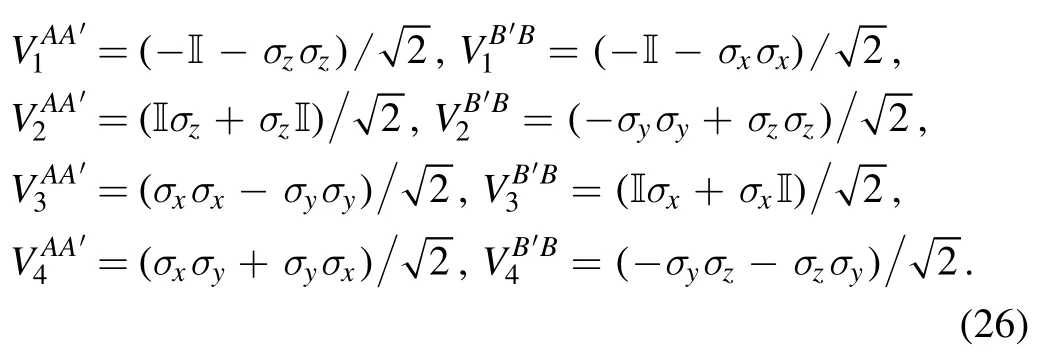
Given the witness operator，we can now construct the quantum game by decomposing the witness in the Pauli basis.In particular，we have the quantum games forWCNOT，1andWCNOT，2as shown in tables 1 and 2，respectively.We note that interestingly，even though the two witness operatorsWCNOT，2andWCNOT，3are constructed differently，we do haveWCNOT，2= 2*WCNOT，3.We note that in the quantum games forWCNOT，1andWCNOT，2，we used Pauli matrix as input states for simplicity，which is not exactly correct.Nevertheless，we can solve the problem by decomposing each Pauli matrix as a linear combination of pure states.Furthermore，there may exist better decomposition of the witness operator when we consider general input states and measurements [44，47].

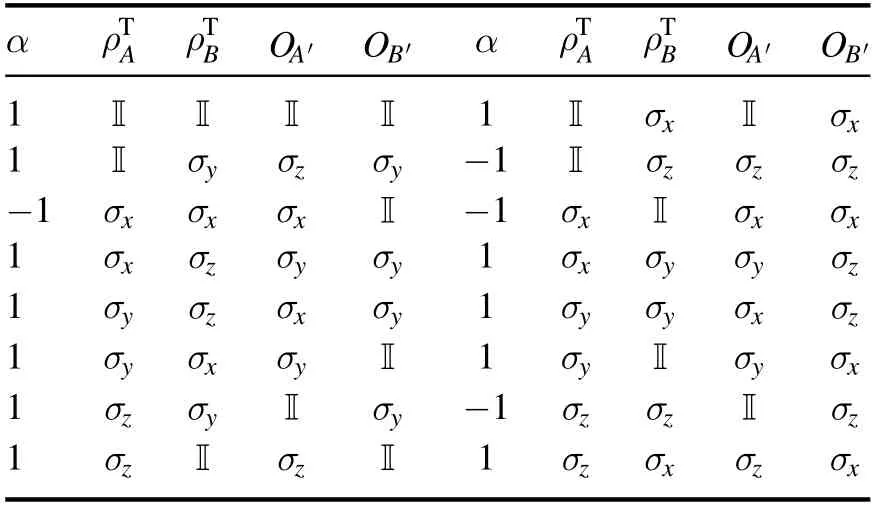
Table 1.Quantum game with WCNOT，1 for the noisy CNOT gate.

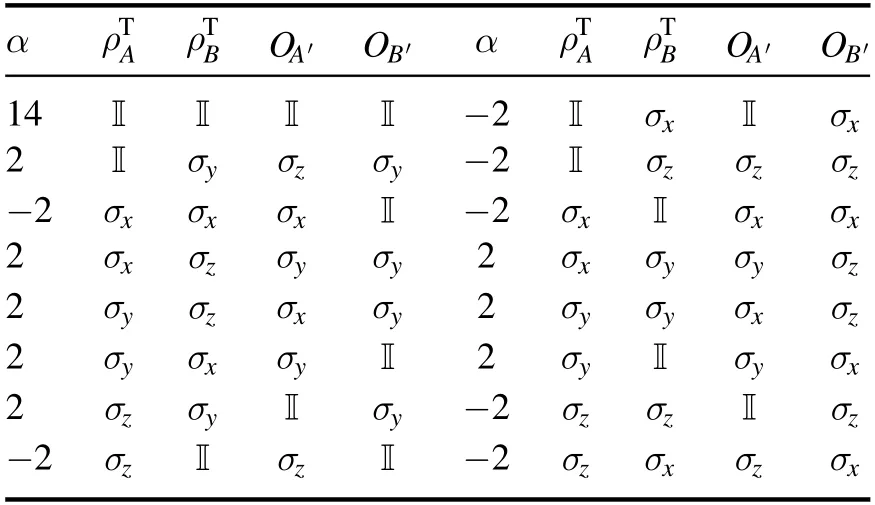
Table 2.Quantum game with WCNOT，2 for the noisy CNOT gate.

For the SWAP gate，its Choi state is

and the density matrix is

The three witness operators could then be constructed accordingly.Consider the eigenvector with a negative eigenvalue of，the witness operators of the first method is

Interestingly，for the second and third method，we again have the same witness (with different but irrelevant normalization factor).In particular，we haveWSWAP，2=6WSWAP，3withWe also convert the witness into quantum games.In particular，we have the quantum games forWSWAP，1andWSWAP，2as shown in table 3 and 4，respectively.

Table 3.Quantum game with WSWAP，1 for the noisy SWAP gate.

Table 4.Quantum game with WSWAP，2 for the noisy SWAP gate.

Consider a noisy CNOT and SWAP gate with different noise ratio，we show the three entanglement witness values in figure 2.Since the second and third methods give basically the same witness，we have normalized the witness value.For the noisy CNOT gate，the second and the third methods outperform the first method，whereas for the noisy SWAP gate，have the same effect under normalization.

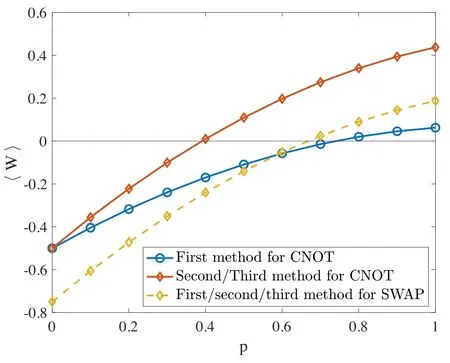
Figure 2.Entanglement witness values for the noisy CNOT and SWAP gates as a function of the noise parameter p.Since the witnesses have different normalization，we only plot different witness values under normalization.In particular，for the noisy CNOT gate，the second and third witnesses have the same value after proper normalization.For the noisy SWAP gate，they all have the same value after normalization.

4.2.Multipartite channels

Up to now，we have studied the effectiveness of the proposed detection methods and compare their performance for several typical bipiartite channels.Here we consider the entanglement of multipartite quantum channels，and use stabilizer witness to detect multipartite channels consisting of noisy CZ gates[48].We consider a special circuit with two CZ gates in figure 3(a)and the results could be similarly generalized to larger circuits with more CZ gates.Using lemma 3，the Choi state ΦAA1BB1CC1of the circuit could be mapped to a graph state∣GCZ〉(see figure 3(b))with white noise on local system[49].Therefore，we can use stabilizer witness to detect the entanglement of the graph state∣GCZ〉 to study the entanglement of the noisy CZ multipartite channel [50].The elements of the stabilizer for

Figure 3.(a)An example quantum circuit consisting of two CZ gates with local depolarizing noise.The Choi state of (a) is equivalent to(b) the graph state∣G C Z 〉up to local unitary rotation.

graph state∣GCZ〉 are products of the operators

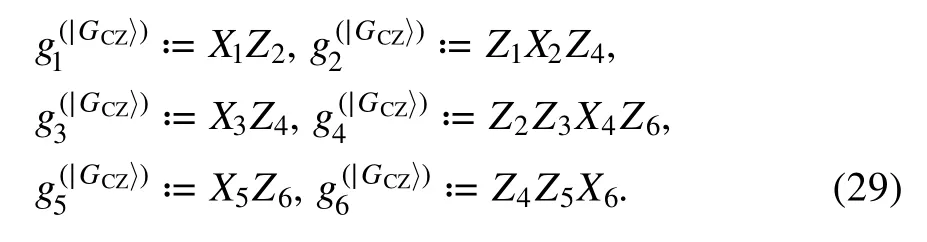
Then，we can consider the following stabilizer witness

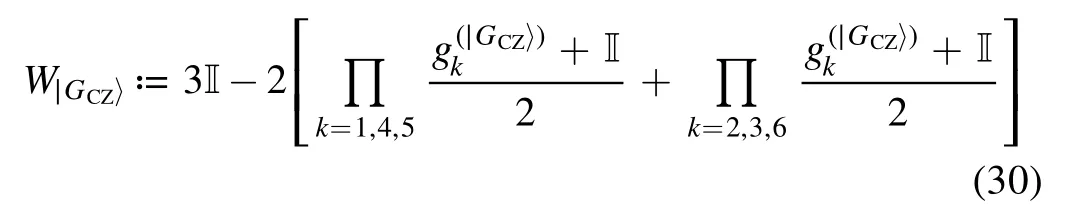
for the graph state to detect the genuine entanglement of the channel.We can similarly convert the witness into a quantum game according to section 3.3.In particular，we apply the Hadamard gate on qubit2，4，6 and map the Pauli measurements on qubit1，3，5 as input states.The entanglement of the noisy CZ multipartite channel is shown in figure 4.We can clearly observe the existence of genuine entanglement wheneverp＜ 0.2.We note that the method could be extended to quantum circuits consisting of multiple CZ gates.In the general case，we can similarly construct the stabilizer witness.

Figure 4.Stabilizer witness valueas a function about the noise parameter p.

5.Conclusion

In this work，we have studied entanglement detection of quantum channels.By relating the channel entanglement to the entanglement of the corresponding Choi state，we exploit state entanglement detection methods for witnessing channel entanglement.Using the language of quantum games，we can further convert the witness operator as a quantum game of the channel.Based on the general result，we proposed three methods to construct witnesses that allow to detect entanglement of bipartite channels and compare their performance for noisy CNOT and SWAP channels.From these results，the three methods could become convenient tools for routine performance detection of bipartite quantum channels.We also introduced the definition of mulitipartite channel entanglement，noting that Choi state of quantum channels with CZ gates correspond to graph states.We can then use graph state witnesses to detect multipartite circuits consisting of CZ gates.

Acknowledgments

We are grateful to Jinzhao Sun for helpful discussions.This work is supported by the National Natural Science Foundation of China under Grant Nos.62 072 119 and 61 672 007，and Guangdong Basic and Applied Basic Research Foundation under Grant No.2020A1515011180.

Appendix A.Proof of lemma 1

Here we prove that a bipartite channel is separable if its Choi state is separable.First，let N ∈ CPTP (A0B0→A1B1) be a bipartite channel.If N is separable，it can be expressed as

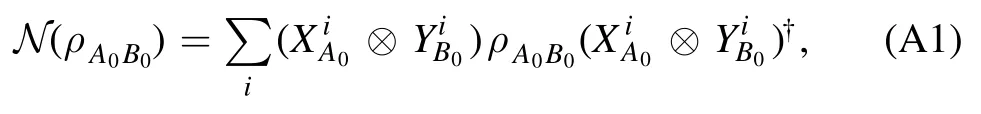
Lemma 4.For a bipartite channel N ∈ CPTP (A0B0→A1B1) ，its Choi state is separable if N is a separable channel.

Proof.If a bipartite channel N ∈ CPTP (A0B0→A1B1) is separable.Then，we have

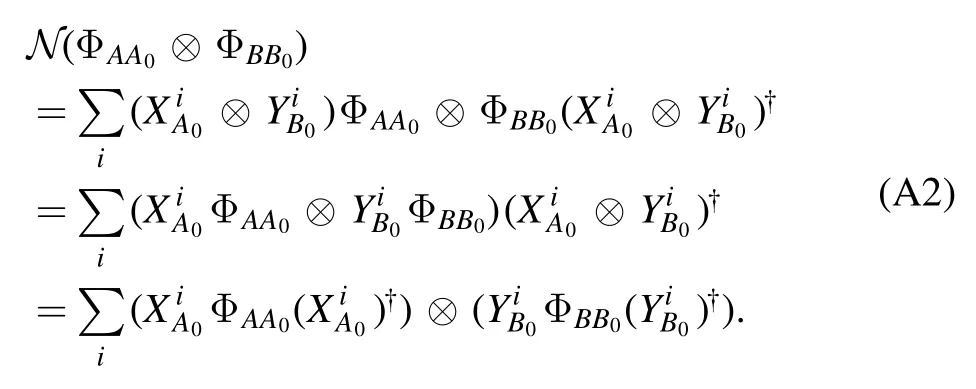
So Choi state of the bipartite channel N is separable.□

If Choi state ΦAA1BB1of a bipartite channel N is separable，it can be expressed as

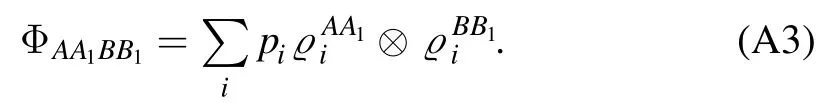
we assume thatandare pure states.Hence

Lemma 5.For a given bipartite channel N ∈ CPTP (A0B0→A1B1) .N is separable if its Choi state is separable.

Proof.We first assume that the input state is a product state，i.e.ρAB=ρA⊗ρB.According to the Choi—Jamiolkowski isomorphism，we have

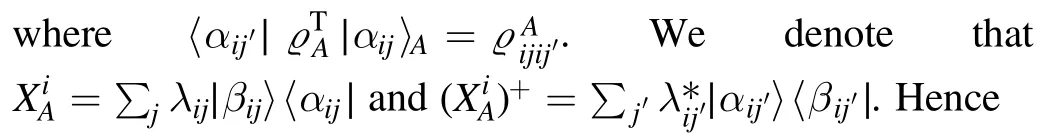
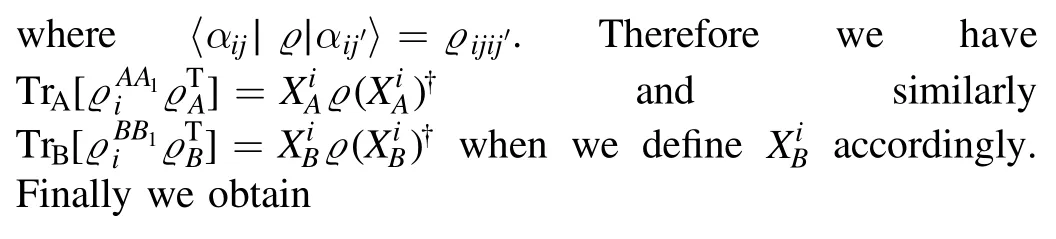
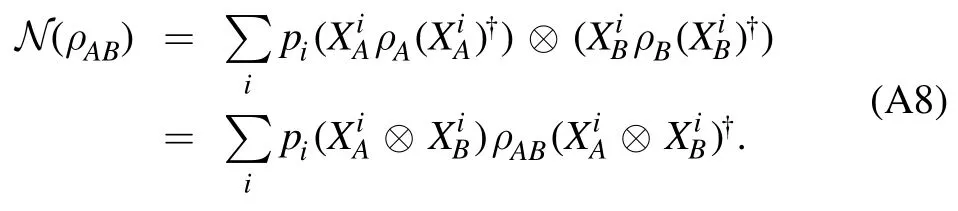
For a general input state，we can always decompose it as a linear combination of product states (possibly with negative coefficients).Together with the linearity of the above equation，it is not hard to see that it also hold for any bipartite quantum state.□

Appendix B.Sketch proof of lemma 2

The proof of lemma 2 follows naturally with the help lemma 1.First，we show that a separable multipartite channel is equivalent to a separable Choi state.In this case，we divide the parties into two partitions and regard the system as a bipartite one.Then we can exploit lemma 1 to prove the equivalence.The equivalence for genuine entanglement follow naturally.