Wormhole solutions and energy conditions in f(R，G) gravity

M Farasat Shamir，G Mustafa，Saad Waseem and Mushtaq Ahmad

1 National University of Computer and Emerging Sciences，Lahore Campus，Pakistan

2 Department of Mathematics，Shanghai University，Shanghai，200444，China

3 National University of Computer and Emerging Sciences，Chiniot-Faisalabad Campus，Pakistan

Abstract In this manuscript，the traversable wormhole solutions have been explored in modified f (R ，G)gravity by taking into consideration the model f (R ，G ) = R +γG2，where R is the Ricci curvature scalar and G is the Gauss—Bonnet term.An acceptable form of the redshift function has been incorporated which is a non-constant in nature along with the implementation of those already defined in literature，the two shape functions namely andIt is shown by studying the energy condition and through the graphical analysis that the null energy bounds for the effective energy-momentum tensor are generally violated for the presence of the ordinary matter in modified f (R ，G)gravity.Energy conditions associated with the matter content threading the wormhole geometries are evaluated and in general are found to favor the null energy conditions in the vicinity of the wormhole throat，the existence of the nonexotic wormhole geometries threaded by the matter has been confirmed under this gravity.

Keywords: f(R，G) gravity，energy conditions，wormholes，shape function

1.lntroduction

The hypothetical existence of a wormhole has been revealed due to a specific solution of the Einstein field equations which comprises a non-trivial connection of isolated points in spacetime.A wormhole could be envisioned as a channel with two ends and each end situating at diverse space-time positions in the Universe.Regardless of the theoretical presence of the wormholes，these contacts endure consistency with the general theory of relativity (GR).Huge distances such as trillions of light-years or more; small distances comprising just a few meters; different universes; or time countless points in our universe could be attached via these wormholes.The unification of the space and time to just a sole spacetime continuum，as projected in the special theory of relativity，could enable someone to go beyond space and time through a wormhole，by incorporating the suitable conditions.Even supposing that wormholes，due to the Schwarzschild solution，are not traversable in both directions，nonetheless，their existence enthused the associated investigations to perceive the idea of the traversable wormhole geometries structured by keeping the wormhole throat open due to the existence of exotic matter，while some others are acknowledged as the Lorentzian wormholes[1]，etc.

A number of very accurate independent observational data emerging from reliable resources agree that the Universe is experiencing an epoch of accelerated expansion[2].Several examples in the literature have previously explained the reasons behind this accelerated expansion extending from the miscellaneous models of dark energy to the substitute theories of gravity.Many valid questions about dark matter and dark energy，initial singularity，cosmological constant，flatness problems，etc have not been truly addressed by the GR.The GR，though，the most beautiful theory of the century，has reported nothing to these glitches which are thought to be the core cause of the accelerating expansion of the Universe.Consequently，as an alternative，modified theories of gravity have fascinated researchers with diverse cosmological tactics and aspects to expose the secrets behind the expanding phenomena.After truly acknowledging the myth of the GR theory，numerous other theories have been premeditated by building some complex Lagrangian.Namely，theories likef(R)，f(R，T)，f(R，G)，andf(G)(here R is the Ricci scalar and G is the Gauss—Bonnet term) have been formulated with the blend of curvature，topological scalars invariants，and their derivatives [3—13].These theories have spoken the purpose of solving the intricacies owing to the quantum gravity and deliver the researchers with diverse platforms through which the motives for the accelerating expansion of the Universe has been discussed.

Modifications in GR has received tremendous considerations，starting from the expansion of the Universe to the presence of wormholes and other associated concepts[14—16].Investigating the possible existence of wormhole geometries and their stability in GR requires tremendous attention.So far，a big portion of literature has been published mentioning black holes，however，the emerging center of attention seems to be towards wormholes.Morris and Thorne[17] were the pioneers in introducing the concept of traversable wormholes.Einstein and Rosen [18] suggested that if spacetime could be curved such that it produced a shortcut route then traveling to different places in space could become possible through a bridge，that was hypothesized as a wormhole.Having asymptotically flat both ends，the shape of the wormhole is like a tube，which is further classified as a static and non-static wormhole.Observing wormhole geometries still remains a huge challenge，as Wheeler [1] suggested that the size of wormholes sometimes could be too small to spot them easily.For the presence of a wormhole，a violation of the null energy conditions(NEC)is required[19].

Several efforts have been made to investigate wormhole geometries.Taking into account the energy conditions in discussing wormholes is the most crucial scenario.Energy conditions tell us about the matter that threads the wormhole[20] due to the presence of the termRαβ μα μβin the Raychaudhuri equations [21].Wormholes can exist in the presence of a hypothetical matter called an exotic matter which is responsible for the existence of wormhole geometries.In GR，it is believed that for the existence of a traversable wormhole，the violation of NEC is required.However，in modified theories of gravity，there are many studies where NEC need not be violated.Recently，Samanta and Godani [22] worked onf(R)gravity and satisfied all energy conditions at the wormhole throat.Violation of the energy conditions remains a complicated issue as Barcelo and Visser[23]predicted.It is interesting to note that Visser [24，25] developed a rich class of wormhole solutions confined to the utilization of the ordinary matter with the extraordinary matter used at the wormhole throat.

Banerjee，Jasim and Ghosh [26] worked on traversable wormholes and satisfied NEC with isotropic pressure.Inf(R)gravity，Godani and Samanta [27] worked on two shape functions and discussed energy conditions.Previously，Visser and his co-authors [28] discussed traversable wormholes and explained that by appropriately choosing wormhole geometry，the use of violating matter can be limited.General dynamic wormholes and violation of NEC was discussed by Hochberg and Visser [29].In hybrid metric-Palatini gravity，Capozziello et al [30] explained the probability for the existence of wormholes at the throat with violation of NEC.Inf(R，G)gravity，Bhatti et al[31]studied wormhole solutions and energy conditions.In Gauss—Bonnet gravity，static and symmetric wormholes and energy conditions were discussed by Maeda and Nozawa [32].Lobo worked on traversable wormholes and energy conditions and verified that NEC is violated [33].Inf(R)gravity，Mazharimousavi and Halilsoy[34] constructed wormholes with the introduction of external matter and showed that WEC is satisfied.

Inspired by the above discussions，we have focused onf(R，G)gravity and studied two different forms of shape functions for which we have plotted energy conditions.The paper is structured as follows: In addition to wormhole metrics and its conditions，a short analysis off(R，G)gravity is carried out in section 2.The derived field equations off(R，G)gravity along with two shape functionsandwhich are already defined in literature by Godani and Samanta [35] are discussed in section 3.In section 4，the energy conditions are also discussed by taking into account these two shape functions and the result of each type of shape function is analyzed and discussed in detail.In the last section，a conclusion of our work is presented.

2.Wormhole geometry in f（R，G） gravity

The coupling of the scalar curvature R with the Gauss—Bonnet term G in the form off(R，G)gravity [36] has brought a significant change.The action of modified Gauss—Bonnetf(R，G)gravity is defined as [37]:

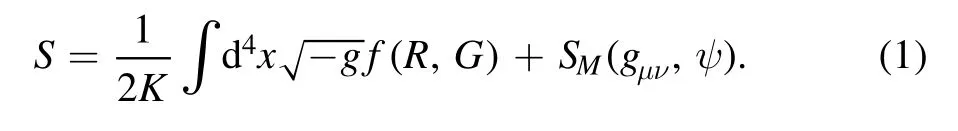
The Gauss—Bonnet term is given by:

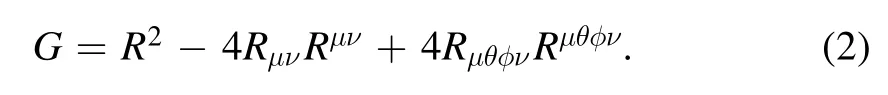
Varying equation (1) with respect to the metric tensor，gives us the following field equation:

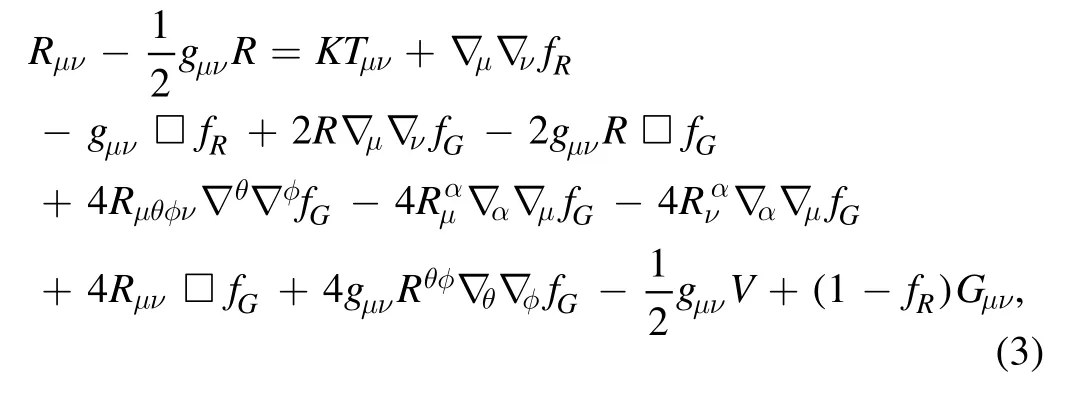
where (□) corresponds to the D’Alembert operator.

fR=andare the partial derivatives with respect to R and G，respectively.The energy-momentum tensor is defined as:

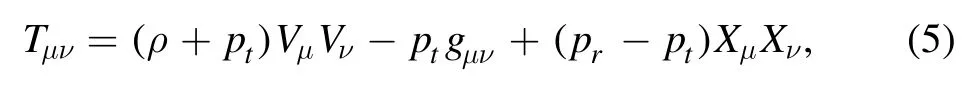
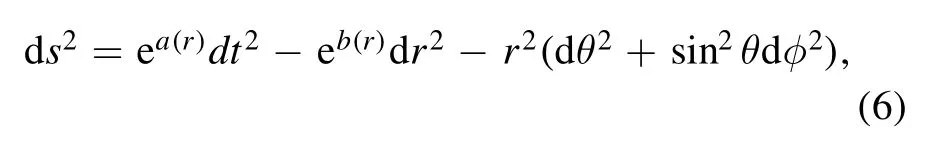
wherea(r) andb(r) are both the functions of radial coordinate r.Herea(r) indicates the redshift function.Now considerwhereβ(r)is known as the shape function of the wormhole geometry.The following conditions should be satisfied for the existence of a traversable wormhole.

· At the throatβ(ro) =roand out of the throat

· Radial coordinate r ranges fromr0≤r≤∞，where r0is the throat’s radius.

· Redshift function must be finite everywhere to ensure no horizons.

·β′(ro) ＜1(flaring out condition).

· Asymptotically flatness requires the limitas∣r∣→∞.

The curvature scalar R turns out to be:

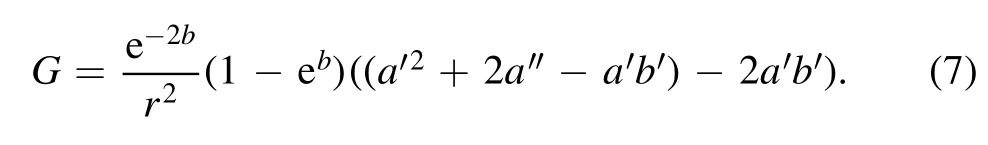
The expression for G turns out to be:

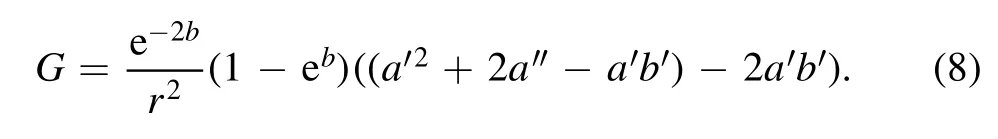
3.Field equations and energy conditions in f（R，G）gravity

By manipulating equations(2)—(6)，the following field equations are obtained:

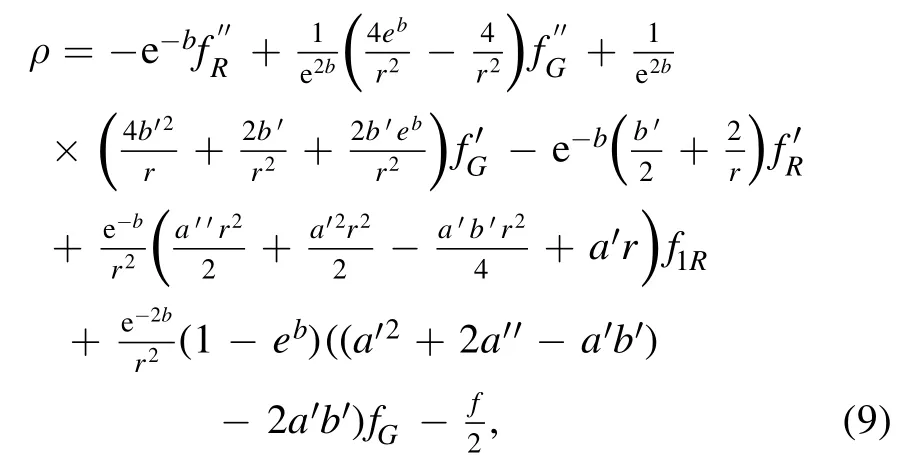
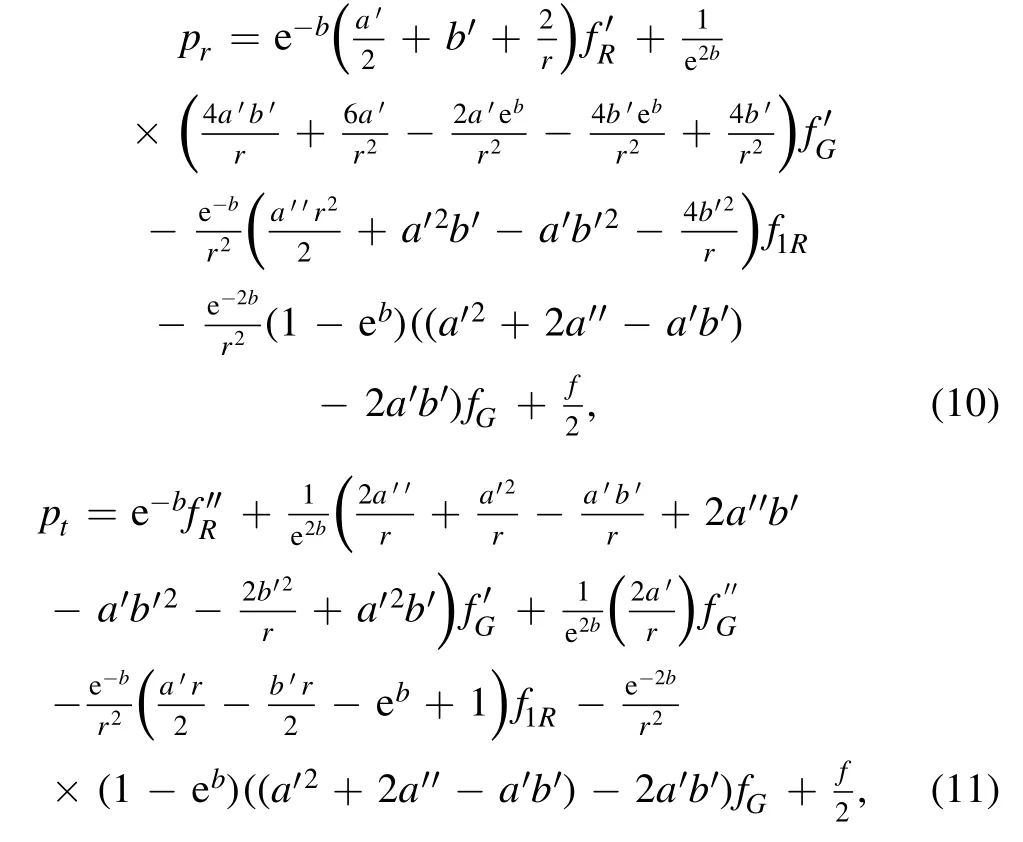
where the prime (′) here gives the derivative with respect to the radial coordinate r.In the case of wormhole discussions，the redshift function is taken as constant in different modified theories of gravity，which simplifies field equations easily，but in our case，while solving the model，our Gauss—Bonnet term vanishes if we take it as constant.So，we assume a simpler form of the redshift function[38，39]where η is an arbitrary constant.The difficulty is to simplify the terms ρ，prand ptas these include many unknowns and high-order derivatives.Thus a suitable form of function is chosen to make things easier which is as follows:

wheref1(R) =Ris a linear function of Ricci scalar andf2(G)=γG2is a power law model withγbeing an arbitrary constant.The exclusive expressions for ρ，pr，and ptconcerning the matter threading the wormholes comprise the shape function together with the functionf(G) and its radial derivatives.These functions are responsible for the matter content required for the existence of the wormhole geometries.The violation of the energy bounds remains the most fundamental and vital reason in approving wormhole geometries in the conventional GR.Nevertheless，the modified gravitational theories have exposed themselves with different character to a great extent，justifiably due to the fact that the Einstein equations are quite different to those of the modified theories of gravity.The concept of these energy conditions is believed to emerge from the existence of a termin the Raychaudhuri equations for the time-like congruences well-defined and denoted byμϱand the null geodesics byκϱ.

Consequently，we have the following important energy constraints as:

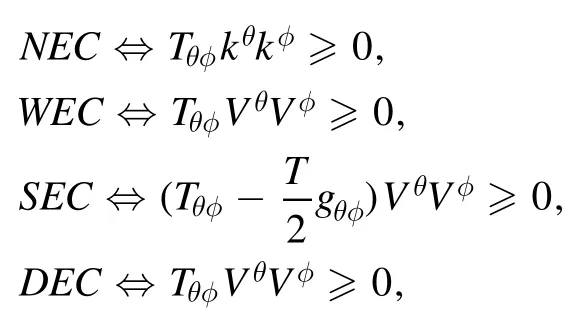
wherekθis null vector andVθis a time-like vector.For DEC，Tθ φ Vθis not space like.Energy conditions involving the energy density and pressure terms are defined as:

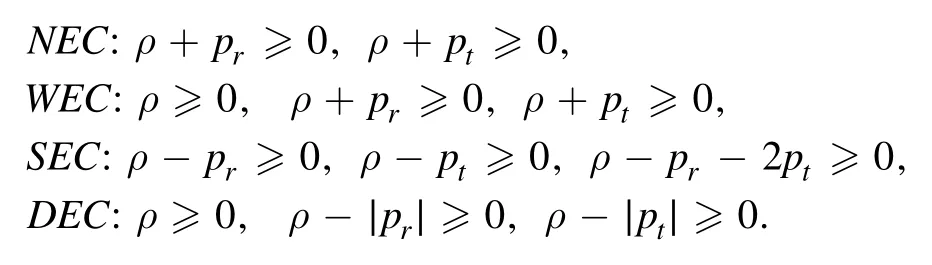
It has been stated in the literature that the energy conditions are violated near the wormhole throat [40].Energy conditions are satisfied while dealing with normal matter because it has positive energy density and positive pressure but exotic matter has negative energy which is the opposite of normal matter and the presence of exotic matter gives rise to the violation of energy conditions.In this work，we choose the particular form of the shape functions，i.e.b(r) from the literature.Two forms of shape functionb(r) are chosen，which are defined as:

The second specific shape function is defined as:

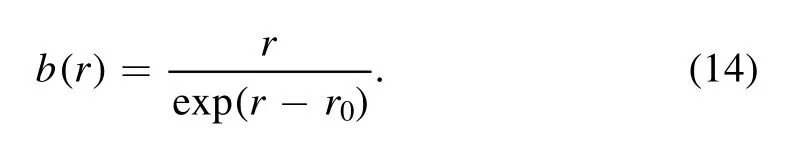
where，r0represents the wormhole throat location.For the current study，we choose it asr0=0.2.Both the considered specific shape functions satisfy the required properties for the existence of a wormhole.In addition，these shape functions satisfy the physical and cosmological implications，such as being theoretically useful as shortcuts in the wormhole spacetime and inducing closed time-like curves，possibly violating causality.In previous literature[41—45]，several such specific shape functions are defined and wormholes are studied.

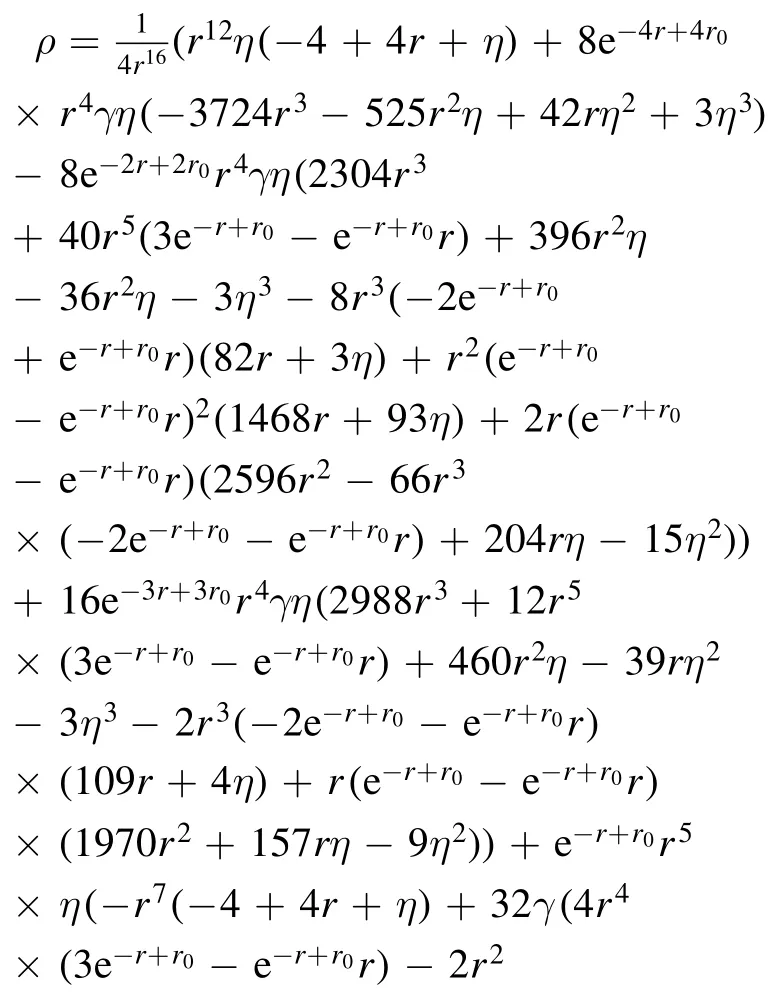
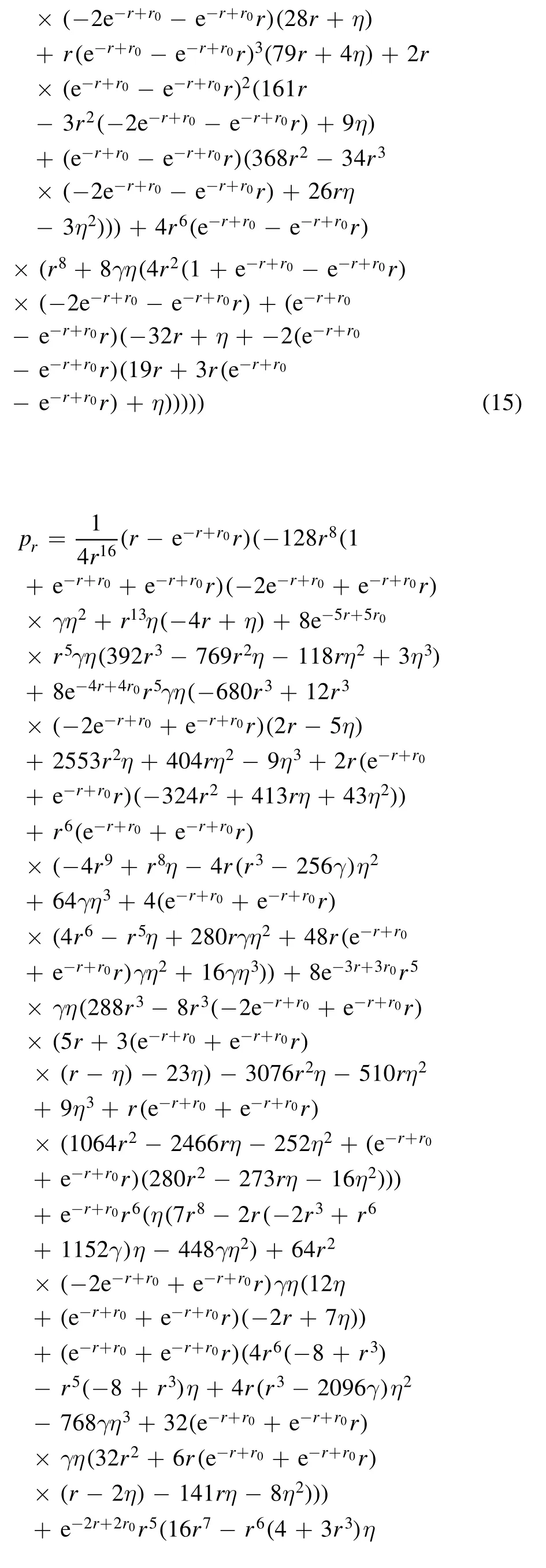
We have achieved wormhole solutions and evaluated different forms of energy density，radial and tangential pressures in connection to both expressions of the shape functionb(r).The graphical analysis for the first specific shape function is provided in figures (1，2，3).The behavior of energy conditions for second specific shape function is presented in figures(4，5，6).From the figures(1，4)the presence of exotic matter is confirmed as NEC is violated for both the models.The figures (2，5) show the graphical behavior ofρ+ptandρ-prfor both specific shape functions.The graphical behavior ofρ-ptandρ-pr-2ptis provided in figures (3，6).

4.Conclusion

The main focus of this work is to investigate wormhole solutions under the geometry off(R，G)gravity.In this paper，we have offered an exciting and useful discussion regarding the existence of wormhole geometries through the ordinary matter in modified Gauss—Bonnetf(R，G)gravity，by considering its specificf(R，G) =R+γG2model，where G is the Gauss—Bonnet scalar coupled with the Ricci scalar R.We have invested two particular forms of the shape functionb(r) together with the non-constant redshift functiona(r)into the modifiedf(R，G)field equations to developρ+prandρ+ptof the energy conditions WEC and NEC，which are decisively fundamental constituents，the role of which is very vital and decisive in establishing any possible existence of wormhole geometries in modifiedf(R，G)gravity.For the ordinary matter responsible for threading these wormhole geometries，we have employed the argument that the validity of the energy conditions is due the curvature incorporating high-order derivatives，which may be termed as the gravitational fluids，authorizing the existence of corresponding wormhole solutions.This is fundamentally unlike their counterparts in the GR.

The reason for taking non-constant redshift is because our Gauss—Bonnet term becomes zero in the case of constant redshift.The existence of wormhole geometries has been investigated by the choice of the two shape functions i.e.andunder the condition that the redshift functiona(r) and the two cases ofb(r) obey all the wormhole geometry conditions including the flaring out condition，throat condition and typical asymptotically flatness condition.The energy conditions for both the cases are discussed and plotted.The graphical behavior of ρ，ρ+pr，ρ+pt，ρ-pr，ρ-ptandρ+pr+2ptare shown in figures (1，2，3，4，5，and 6).For the exponential shape function，ρ shows positive but decreasing behavior whereas both functionsρ+prandρ+ptattained negative behavior.For the logarithmic shape function behaviour of energy conditions remain the same as for the exponential shape function.Violation of NEC in both cases confirms the presence of exotic matter，hence favoring the existence of wormhole geometries in ourf(R，G)under investigation.

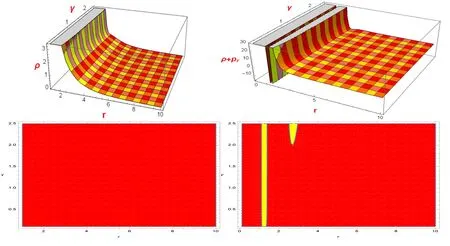
Figure 1.The development of ρ andρ + pr is shown.Here，we assumeη = 15 andr 0 = 0.2withρ ＜0 (Yellow)，ρ ＞0 (Red)，ρ + pr ＜0(Yellow)，andρ + pr ＞0(Red).

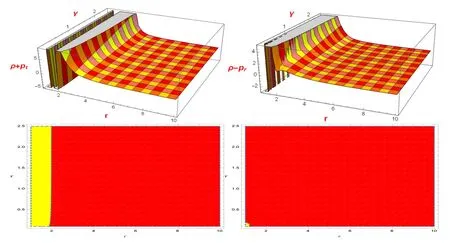
Figure 2.The development ofρ + pt andρ - pr is shown.Here，we assumeη = 15 andr 0 = 0.2withρ + pt ＜0(Yellow)，ρ + pt ＞0(Red)，ρ - pr ＜0(Yellow)，andρ - pr ＞0(Red).

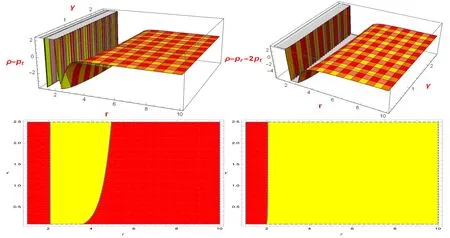
Figure 3.The development ofρ - pt andρ - pr -2pt is shown.Here，we assumeη = 15 andr0 = 0.2withρ - pt ＜0(Yellow)，ρ - pt ＞0(Red)，ρ - pr - 2pt ＜0(Yellow)，andρ - pr - 2pt ＞0(Red).

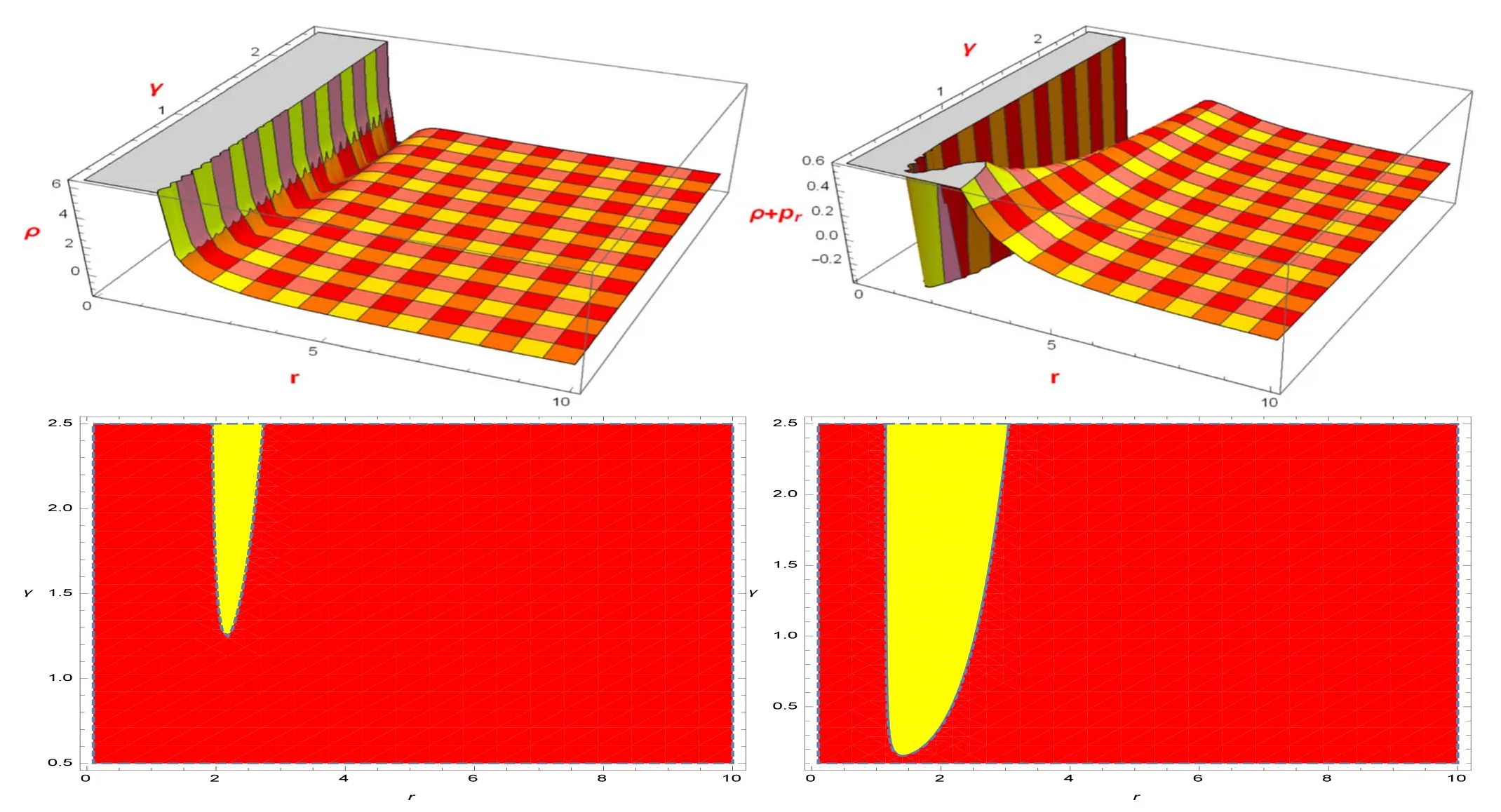
Figure 4.The development of ρ andρ + pr is shown.Here，we assumeη = 15 andr 0 = 0.2withρ ＜0 (Yellow)，ρ ＞0 (Red)，ρ + pr ＜0(Yellow)，andρ + pr ＞0(Red).

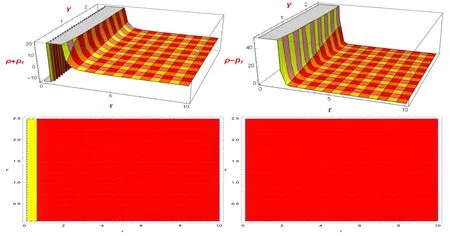
Figure 5.The development ofρ + pt andρ - pr is shown.Here，we assumeη = 15 andr 0 = 0.2withρ + pt ＜0(Yellow)，ρ + pt ＞0(Red)，ρ - pr ＜0(Yellow)，andρ - pr ＞0(Red).

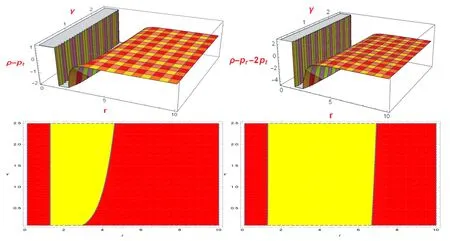
Figure 6.The development ofρ - pt andρ - pr -2pt is show，.Here，we assumeη = 15 andr 0 = 0.2withρ - pt ＜0(Yellow)，ρ - pt ＞0(Red)，ρ - pr - 2pt ＜0(Yellow)，andρ - pr - 2pt ＞0(Red).