lntrinsic ferromagnetism in CoBr2 nanolayers: a DFT + U and Monte Carlo study

A Jabar，R Masrour，G Kadim，M Hamedoun，A Hourmatallah，N Benzakour，A Rezzouk，K Bouslykhane and J Kharbach

1 Laboratory of Solid Physics，Faculty of Sciences Dhar El Mahraz，Sidi Mohamed Ben Abdellah University，BP 1796，Fez，Morocco

2 MAScIR，Institute of Nanomaterials and Nanotechnologies，Rabat，Morocco

3 Equipe de Physique du Solide，Laboratoire LIPI，Ecole Normale Supérieure，Bensouda，BP 5206，Fès，Morocco

Abstract The intrinsic ferromagnetism of CoBr2 bulk was investigated using DFT(density functional theory)combined with the full potential linear augmented plane wave method and Monte Carlo simulations.The ground state of CoBr2 exhibits ferromagnetic behavior and a semiconductor character.We used the generalized gradient approximation(GGA)and GGA + U(Hubbard correction)approximations to determinate the magnetic moment.The magnetic moment reached the experimental value and was in good agreement with the other theoretical values.The value obtained was used as an input to a Monte Carlo study to calculate the thermal magnetization and magnetic hysteresis cycles.Ferromagnetic behavior was observed and was found to be due to an positive exchange interaction.These results lead us to believe that this material could be a promising spintronic material.

Keywords: CoBr2 nanolayer，DFT，Monte Carlo，transition temperature，magnetic hysteresis cycles

1.lntroduction

Binary transition metal halides MXy (M = metal cation，X=halogen anion)provide a rich family of materials in which low dimensional magnetism can be examined，and such studies were carried out through much of the last century[1，2].Cobalt dihalides contain cobalt with the electronic configuration 3d7，which can have a high(S = 3/2)spin state.Cobalt(II)bromide crystallizes inside cadmium iodide structures with the space groupP3¯m1[3].The experimental value of the magnetic moment of Co in CoBr2is 2.8 μB[4]，and the value obtained by DFT calculations is 3 μB[5].Compressive strain stabilizes the ferromagnetic phase by decreasing the nearest dCo-Codistance and enhancing the hybridization p-d between the cobalt and bromide ions[6].However，the total magnetic moment of cobalt(II) bromide is 2.57 μB/unit cell [6].The ferromagnetic intra-chain interaction，parallel to the c-axis in bulk CoBr2，is denoted by J0(J0= 6 K)[7].Effective field theory and Monte Carlo studies have been used to study the magnetic and thermodynamic properties of a kekulene-like nanostructure[8]and a zigzag graphene nanoribbon [9].Density functional theory has been used to study the magnetoelectric coupling effect of Co(Fe)/BiFeO3[10]and the full Heusler alloy CrCoVSb[11].

The Monte Carlo method has been used to study the magnetic and thermodynamic characteristics of:a rectangular core–shell ferrimagnetic mixed-spin (3/2，2) Ising nanoribbon under the effects of a sublattice crystal field，exchange coupling，and temperature [12]，a diluted Ising nanographene monolayer under a longitudinal magnetic field [13]，the magnetic behaviors and magnetocaloric effect of a nanographene bilayer [14]，the dielectric properties of an antiferroelectric/ferroelectric BiFeO3/Co bilayer structure [15]，nanographene with a sandwich-like structure in a longitudinal magnetic field [16]，and triangular double-layer graphene nanoislands [17].

The paper is organized as follows: after this introduction，we describe the procedures of the DFT + U calculation and the Monte Carlo simulation based on the Ising model in section 2.The electronic properties，thermal magnetization，thermal susceptibility，and magnetic hysteresis cycles are presented in detail in section 3.Finally，section 4 presents our conclusions.

2.Model and methods

In order to calculate the magnetic moment of Co using DFT，it is necessary to study the electronic properties of the CoBr2compound.Full potential linearized augmented plane wave(FPLAPW) calculations [18] were performed with the lattice parameters (a = b = 3.68 Å and c = 6.12 Å)，as reported in[5].The magnetic moments are considered to lie along the(001)axis[5](see figure 1).We used the GGA and GGA + U approximations applied in Wien2k.These approximations are used to correct the magnetic moment values.The k points were based on a 12*12*6 Monkhorst-Pack scheme.The effective Coulomb-exchange interaction，Ueff，is given by (U-J)，where U and J are the Coulomb and exchange parameters.The values of U for the Co atom are cited in table 1 and J was set to 0 eV.

Table 1.Magnetic moment(μB) of Co obtained by GGA and GGA + U compared to other experimental and theoretical values.

Figure 1.The structure of CoBr2 bulk.

The Hamiltonian of the CoBr2compound is given by:

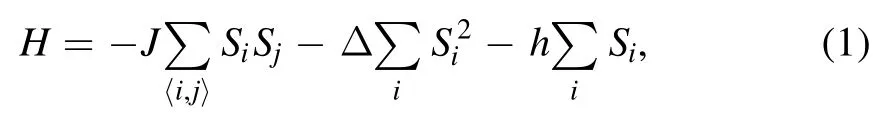
where h is the external magnetic field，JCo-Co= J is the first exchange interaction(see figure 1)，and Δ is the crystal field.Here，is the magnetic moment of Co2+.The magnetic moments obtained by ab initio calculations are given in table 1.

The CoBr2compound is assumed to reside in unit cells and the system consists of the total number of spins N = 1513 of cobalt ions.We applied a standard sampling method to simulate the Hamiltonian given by equation (1).We imposed free boundary conditions on the CoBr2compound.The configurations were generated by sequentially traversing the lattice and making single-spin flip attempts.The flips are accepted or rejected according to a heat-bath algorithm under the Metropolis approximation.Our data were generated using 100000 Monte Carlo steps per spin，discarding the first 10000 Monte Carlo simulations.

Internal energy per site E is

The magnetization of Co2+in CoBr2is

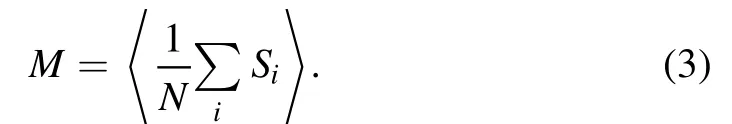
The magnetic susceptibility of Co2+in CoBr2is

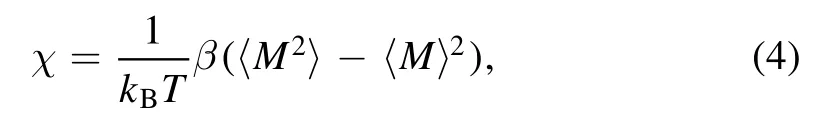
where kBis the Boltzmann constant and T is the absolute temperature.

3.Results and discussion

We have plotted the total and partial densities of states for CoBr2in figure 2.Figure 2(a)displays the total density of states(TDOS) as a function of the energy.The contribution of the spin-up electron density is greater than the contribution of the spin-down electron density，confirming that CoBr2has ferromagnetic behavior.In addition to this，the DOS shows that the conduction band(CB)has an important contribution from Co-d orbitals，whereas the valence band (VB)is dominated by Br-p，Br，and Co-d orbitals close to the Fermi level，EF.Figure 2(b)displays the PDOS of CoBr2.This DOS shows that the CB has an important contribution from Co-d orbitals，whereas the VB is dominated by Br-p，Br，and Co-d orbitals close to the Fermi level，EF.The strong contribution of the electronic density of Co-d is due to the hybridization that occurs with the Br-p states.Figure 3(a) displays the total and partial density of states for different U values.An increasing in the U-value generally leads to an increase in the contribution of the total CoBr2 DOS，and，in particular，leads to an increase in the contribution of the partial DOS of the Co-d orbital.The value gap，which is close to the Fermi level EFin the spin-up and spin-down electrons，is evidence of a semiconductor character.

Figure 2.Total (a) and partial (b) density of states for CoBr2 using the GGA-mBJ approximation.

Figure 3.(b) Magnetic moment values for different U values.

Figure 3.(a) Total partial densities of states for CoBr2 using GGA + U (U = 4，6，9，and 10 eV) approximations.

The intrinsic ferromagnetism of CoBr2was investigated via DFT combined with FP-LAPW and Monte Carlo simulations.Figure 3(b) shows the variation of the magnetic moment of Co2+as a function of different values of U.The larger the value of U，the higher the magnetic moment.The magnetic moment of Co2+is shown in table 1 as m = 2.49520 μBas obtained from GGA，and m = 2.67822 μBas obtained from GGA + U (U = 3.67).These values are comparable with that obtained by [6]，while the value m = 2.80963 μBobtained from GGA at 6 eV is comparable with experimental results [4].In addition，the value m = 2.90829 μBobtained using GGA at 10 eV is close to that of 3 μBdescribed in [5].We calculated the energy difference ΔE = EG-AFM- EFMin order to find the value of JCo-Co.Our calculations show a positive value of ΔE.This confirms that the CoBr2bulk is stable in the ferromagnetic phase (table 2).The value of the JCo-Comagnetic coupling is in good agreement with that cited in [7] (table 2).Figure 4 displays the thermal magnetization and thermal magnetic susceptibility with h = 1.0 T and Δ = 0.0 via MCs.A transition temperature，TC，of 26.85 K was obtained，which is comparable with that obtained in [5]，TC= 27 K.Figure 5 illustrates the crystal field dependence of the magnetization M of CoBr2bulk at h = 1.0 T.The magnetization decreases with increases in the temperature and the absolute value of the crystal field.Figure 6(a) shows the magnetic hysteresis cycle of CoBr2bulk for several temperatures T = 20，24，27，and 32 K，Δ = 0.0，and figure 6(b)shows the results for Δ = 0.0，-2.0，-4.0，and -7.0，T = 20 K.The saturation magnetization decreases with an increase in the temperature values and absolute value of crystal field.The magnetic coercive field，hC，and the remanent magnetization，Mr，decrease with an increase in the temperature and the absolute value of the crystal field.Paramagnetic behavior is observed at temperatures near and above the critical temperature.The effect of fluctuations of the magnetic moment in the presence of a magnetic field in our compound show very small coercivity and high saturation magnetization in the superparamagnetic regime，as shown in [19].

Table 2.Exchange interaction JCo-Co，the total energy of the magnetic-ordering configurations (G-AFM and FM)，and the difference energy (ΔE).

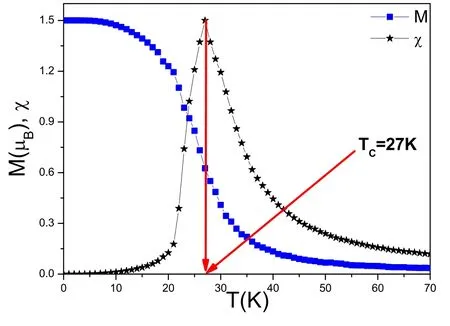
Figure 4.Temperature dependence of the magnetization M and the magnetic susceptibility of CoBr2 bulk with h = 1.0 T and Δ = 0.0.

Figure 5.Crystal field dependence of the magnetization M of CoBr2 bulk with h = 1.0 T.

Figure 6.Magnetic hysteresis cycle of CoBr2 bulk for several temperatures T = 20，24，27，and 32 K，Δ = 0.0 (a) and Δ = 0.0，-2.0，-4.0，and -7.0，T = 20 K (b).

4.Conclusions

We have studied the magnetic properties of CoBr2bulk by using the framework of DFT combined with FP-LAPW and MCs simulations.The magnetic moment of Co has been studied and compared with other theoretical results.The ground states of CoBr2have ferromagnetic behavior and a semiconductor character.The value of TCobtained is consistent with the values obtained by experiment and from other theoretical results.The system exhibits a ferromagneticparamagnetic transition in the vicinity of a critical temperature，which is a second-order transition.We found that the values of hCand Mrdecrease with increases in the temperature and the absolute value of the crystal field.