Valley-resolved transport in zigzag graphene nanoribbon junctions
2021-11-13MingLiZiLiangCaiZhiBoFengandZhengYinZhao
Ming Li Zi-Liang Cai,Zhi-Bo Feng and Zheng-Yin Zhao
College of Science,Xuchang University,Xuchang 461000,China
Abstract Applying the transfer matrix and Green’s function methods,we study the valley-resolved transport properties of zigzag graphene nanoribbon(ZGNR)junctions.The width of the left and right ZGNRs are NL and NR,and NL ≥NR.The step/dip positions of the conductance G,the intravalley transmission coefficients (TKK andTK ′K ′),and the valley polarization efficiencyP KK′correspond to the subband edges of the right/left ZGNR that are controlled by NR/NL.The intervalley transmission coefficients(TK K ′andTK ′K)exhibit peaks at most of the subband edge of the left and right ZGNRs.In the bulk gap of the right ZGNR,TK K ′=T K ′K=0,andP KK ′=±1,the valley polarization is well preserved.As NR increases,the energy region forP KK ′=±1 decreases.When NL is fixed and NR decreases,G,TKK,TK ′K ′andP KK ′exhibit more and more dips,and the peaks ofTK K ′(T K ′K) become more and more high,especially when(NL-NR)/2 is odd.These characters are quite useful for manipulating the valley dependent transport properties of carriers in ZGNR junctions by modulating NL or NR,and our results are helpful to the design of valleytronics based on ZGNR junctions.
Keywords: transfer matrix method,ZGNR junction,valley polarization,Landauer–Büttiker formula,edge state
1.lntroduction
With the progresses in fabricating stable graphene nanostructures,various electronic and optical properties of these structures,including graphene quantum dots,have been explored [1–3].Since graphene has exceptional electron and thermal transport properties,it is a promising material that can be used in advanced low-energy electronic devices [4–7].Zhang and Wu et al [8–10] investigated the resonant tunneling through S- and U-shaped graphene nanoribbons(GNRs)and graphene nanorings in between two semi-infinite zigzag GNR leads,thus tunability of the resonant tunneling is realized by only changing the geometry of the GNRs.Furthermore,a GNR junction can be formed by interconnecting two semi-infinite GNRs with different widths[11].Moreover,the conductance of GNR metal–semiconductor junctions,as the key elements in all-graphene circuits,has been studied in detail recently[12–14].Due to the energy mismatch between subbands in the left and right zigzag graphene nanoribbons(ZGNRs),a traveling carrier is scattered by the junction interface,which causes a finite junction conductance[11,15,16].
In addition to charge and spin,carriers in graphene host an extra valley degree of freedom,because there are two degenerate and inequivalent valleys (K andK′ ) at the corners of the first Brillouin zone[17–19].The valley-dependent properties in graphene have attracted a great amount of interest [7,20–25].A.Rycerz et al [21] proposed a valley filter and an electrostatically controlled valley valve based on a quantum point contact in a graphene sheet.Wu et al [25] showed that the gauge fields induced by strain can lead to valley-dependent transport phenomena in a single layer of graphene,such as the Brewster angles and the Goos–Hänchen effect.Other novel two-dimensional honeycomb lattice materials,such as silicene[26] and transition metal dichalcogenides [27] also have the valley degree of freedom.So the new field of valleytronics is born out of the manipulation of valley degree of freedom for carriers in these materials [20,28–31].
Moreover,to utilize the valley as an information carrier,the valley polarization efficiency of the transmission current is a key quantity.However,the valley degree of freedom is dependent on the momentum and highly related to the translation invariance of the crystal lattice.Therefore,for systems with interfaces,disorders as well as bias voltages,translational symmetry (TS) is broken and the momentum is not a good quantum number [32].For systems lacking TS,the valley depolarization effect can be induced even without any disorder,which must be considered in the design of valleytronic devices[33].It is therefore interesting to ask,what will the valley transport be like in a GNR junction? We wonder under such circumstances,whether the valley filter still perform high valley efficiency.What is more,modulation of the valley-resolved transport properties of ZGNR junctions by the width of the left and right ZGNRs has not been studied,which is crucial for designing valley filter with high efficiency based on ZGNR junctions.Thus in this paper,we main study ZGNR junctions.The left and right leads are composed of semi-infinite ZGNRs,and the central conduction region is marked by a box as shown in figure 1,which is different from that in [8–10,21,25].By applying the transfer matrix and Green’s function methods and analyzing the width dependent conductance channels(the edge states,the conduction subbands and valence subbands),we systematically investigate the dependence of valley-resolved transport properties of ZGNR junctions on the width of the left and right ZGNRs,and results are analyzed in detail.Step positions of G,TKK,TK′K′andPKK′are decided by NR.As NRincreases,G,TKK,TK′K′and their step numbers increase,the energy region forPKK′= ±1decreases.For a fixed NLand decreasing NR,G,TKKandTK′K′decrease,outside the bulk gap of the right ZGNR,G(TKK,TK′K′andPKK′)exhibits more and more dips,and the peak values ofTKK′(TK′K)become more and more large,especially when (NL-NR)/2 is odd.These transmission characters may be utilized to manipulate the valley degree of electrons in ZGNR junctions in the future.
The rest of the paper is organized as follows.In section 2,we briefly introduce the transfer matrix and Green’s function methods (the detailed descriptions are given in the appendix),the tight-binding model and the specific structure of ZGNR junctions.Results of numerical calculation and discussion are given in section 3.Finally,we give the conclusion in section 4.
2.Model and method
Figure 1 shows the geometry of ZGNR junctions,the left and right leads are composed of semi-infinite ZGNRs,and the central conduction region is marked by a box.Here NLand NRdenote the width of the left and right ZGNRs,and NL≥NR.The Hamiltonian for the ZGNR junction reads [34–37]

Figure 1.The geometry of ZGNR junctions.In the upper/lower panel,(NL-NR)/2 is even/odd.The central conduction region is marked by a box.
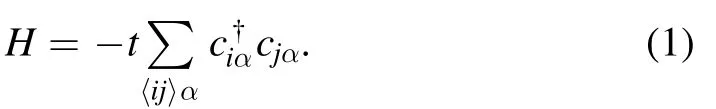
Here t=2.75 eV is the transfer energy of the nearest neighbor hopping,〈ij〉 represents the nearest neighbors.For ZGNR junctions,we assume that all edge sites at the interface are terminated by hydrogen atoms,and neglect the difference between the values of the site energy and the transfer energy for the atoms at the edge and the center [3,38,39].
Adopting the transfer matrix and Green’s function method (see the appendix for detail),the physical transmission matrix element from mode(channel)i in the left terminal to mode (channel) j in the right terminal tijis calculated [32,40–44].The valley-resolved transmission coefficients are obtained by collecting tijin two separate valleys (K andK′ ),and the transmission coefficient from valley K in the left terminal to valleyK′ in the right terminal is [32,44]

The linear conductance of the junction at zero temperature can be calculated byTK′K′) [45].To investigate the valley polarization of transmission current,the valley polarization efficient is defined as [32]

3.Results and discussion
Figure 2 shows the intravalley transmission coefficients (TKKandTK′K′)as a function of EFfor a ZGNR with NL=NR=40 and the corresponding energy band structure.Indeed,when EF>0,the step positions of TKKandTK′K′coincide with the minima of the conduction subbands,while they coincide with the maxima of the valence subbands when EF<0.Therefore,the plateau height/step positions of TKKandTK′K′are determined by the number/edges of occupied transverse subbands that are controlled by the ribbon width N.As can be seen in figures 2(a) and 2(b),TKK/TK′K′jumps from 0 to 1 at EF=0,then increases step by step with decreasing/increasing EF,andTKK/TK′K′jumps from 0 to 1 when EFcrosses the lowest conduction subband/topmost valence subband,then increases step by step with increasing/decreasing EF.In fact,this is also the case for G andPKK′,as shown in figure 3.Around EF=0,there are two conducting channels contributing to G by the edge states,but only the one atK′/Kvalley contributes to G when EF>0/EF<0,assuming the current is right-going in the device.Thus the carriers can transmit through theK′valley andTK′K′(EF) >TK K(EF)when EF>0,and through the K valley andTK′K′(EF) <TK K(EF) when EF<0 [17].If there are no edge states,the conductance is zero around EF=0 and a conductance gap will appear,since there are no conducting channels.So the energy region between the top of the first valence subband and the bottom of the first conduction subband is defined as the bulk gap region.

Figure 2.(a) TKK andTK ′K ′ versus EF and (b) the band structure for a ZGNR with N=40.

Figure 3.G,TKK,TK ′K ′andP KK ′versus EF for ZGNRs with different width N.

Figure 4.G,TKK,TK ′K ′,TK K′,andTK ′K versus EF for ZGNR junctions with NL=40 and different NR.In the left/right panels,(NL-NR)/2 is even/odd.
In figure 3,we show G,TKK,TK′K′andPKK′as a function of EFfor pure ZGNRs with different width N.G,TKK,TK′K′andPKK′show perfect quantized step-like plateaus and the step height of G is 4e2/h.For a pure ZGNR device,the intervalley transmission coefficients (TKK′andTK′K) are zero.Because the left and right ZGNRs have the same number of conductance channels,which match well at the interface,carriers are not strongly scattered and can transmit only within the same valley.Thus the valley degree of freedom for carriers can be well preserved when they transmit through a pure ZGNR.Step positions of G,TKK,TK′K′andPKK′are decided by the ribbon width N.As N increases,the energy space between subbands decreases rapidly,so G,TKK,TK′K′and their step numbers increase accordingly.In the bulk gap region of a pure ZGNR,becauseTK′K′=1for EF>0 and TKK=1 for EF<0,the full valley polarization (PKK′=±1) can be produced by the zigzag edge states.As N increases,the energy region forPKK′=±1 decreases,and the step number ofPKK′increases.The plateau height of∣PKK′∣are 1,1/3,1/5,1/7,1/9,etc,as can be derived from equation(3)and can be seen in figures 3(b) and (c),because ∣TKK-TK′K′∣ =1,and the sum of TKKandTK′K′are 1,3,5,7,9,etc.In figures 4 and 5,we show G,TKK,TKK′,TK′K,TK′K′andPKK′as a function of EFfor ZGNR junctions with NL=40 and different NR.Compared with pure ZGNRs,the conductance properties of ZGNR junctions show evident differences.Step positions of G,TKK,TK′K′andPKK′are decided by NR,their curves still show obvious plateaus when(NL-NR)/2 is even,but exhibit sharp dips.Because the left and right ZGNRs have different number of conductance channels,which mismatch at the interface,and carriers are strongly scattered,especially when (NL-NR) is large.For(NL-NR)/2 being odd,due to the stronger scattering at the mismatched interface,the conductance plateaus are destroyed to a certain degree,G exhibits sharp dips and even oscillation behavior.But in almost the whole bulk gap region of the right ZGNR,TKK′=0,PKK′=1,the full valley polarization(PKK′=±1) can still be remained.This can be ascribed to the zigzag edge states of the right ZGNR.In the bulk gap region of the right ZGNR,carriers transmit completely through theK′valley when EF>0 and through the K valley when EF<0[17],assuming the current is right-going in the device.So carriers can transmit only within the same valley,and there are no intervalley transmissions (TKK′andTK′Kare zero).Therefore,within the gap interval regime,the valley degree of freedom for carriers can be well preserved,implying that the valley polarization efficiency could be high.
When NLis fixed and NRdecreases,G,TKK,TK′K′and their step numbers decrease rapidly,they show more and more dips,the energy region forPKK′=±1 increases and the step number ofPKK′also decreases,andTKK′(TK′K) increases outside the bulk gap of the right ZGNR.In figure 5,panels(c)and (d) are the zoom in of panels (a) and (b),respectively,which clearly present the behavior ofPKK′in the high |EF|region.As shown in figures 5(a)and(c),when(NL-NR)/2 is even,∣PKK′∣shows dips outside the bulk gap of the right ZGNR,but the plateaus are basically intact.As shown in figures 5(b) and (d),when (NL-NR)/2 is odd,dips of∣PKK′∣become deeper,plateaus ofPKK′are broken seriously as NRdecreases to a certain degree.Naturally,the intervalley scattering in a pure ZGNR is vanishing.Nevertheless,in ZGNR junctions,when EFis not in the bulk gap of the right ZGNR,carriers may be transmitted from one valley to another (TKK′andTK′Kare not zero),and many deep dips appear in the profile of G,TKK,TK′K′andPKK′,especially when(NL-NR)/2 is large and odd,due to the strong scattering of carriers at the mismatched interface.Therefore,in order to strengthenTKK′(TK′K),we can increase(NL-NR)/2 and let it be odd.However,compared with the intravalley transmission coefficients (TKKandTK′K′),the intervalley transmission coefficients (TKK′andTK′K) are much smaller.Thus the intravalley transmission coefficients(TKKandTK′K′)contribute dominantly to G.So the valley dependent transport properties of carriers in ZGNR junctions can be manipulated by both NLand NR.

Figure 5.P KK ′versus EF for ZGNR junctions with NL=40 and different NR.In the left (right) panels,(NL-NR)/2 is even (odd).The enlarged area in the lower panels clearly present the behavior ofP KK ′in the high |EF| region.
Next,in order to further clarify the complex behavior of G andTK′Kin ZGNR junctions,we calculate the corresponding density of states(DOS).In figure 6,G,TK′Kand DOS(the red dot line)versus EFfor ZGNR junctions with NL=40 and NR=16,18 ,36 and 38 are shown,the DOS versus EFfor ZGNRs with NL=NR=40,16,18,36 and 38 are also shown for comparison.Obviously,for ZGNR junctions,step and dip positions of G correspond exactly to the peaks of the DOS.For ZGNRs,the DOS (the blue dash line for N=40 and the green real line for other N) peaks coincide with the edges of the subbands.Either at the subband edges of the left wider or the right narrower ZGNR,the DOS of the ZGNR junction(the red dot line)increases,and even shows peaks.G shows dips at some of the subband edges of the left wider ZGNR where there exists a DOS peak,while G exhibits steps at every subband edge of the right narrower ZGNR,andTK′Kexhibits peaks at most of the subband edges of both the left and right ZGNRs.Therefore,in ZGNR junctions,dip positions of G are determined by the width of the left wider ZGNR NL,step positions of G are determined by the width of the right narrower ZGNR NR,and peak positions ofTK′Kare determined by both NLand NR.For a fixed NLand decreasing NR,by comparing panel(a)/(b)with panel(e)/(f)in figure 6,we can see that a DOS peak(the red dot line)appears at more and more subband edges of the left wider ZGNR,thus G shows more and more dips and the peaks ofTK′Kbecome more and more high,especially when(NL-NR)/2 is odd.As(NL-NR)approaches zero,most dips of G and peaks ofTK′Kdisappear,since most of the DOS peaks (the red dot line)located at the subband edges of the left wider ZGNR disappear,especially when |EF| is not very large,as shown in figures 6(e)and(f)for NR=36 and 38,respectively.Because the energy mismatch between subbands in the left and right ZGNRs decreases,the scattering of carriers at the mismatched interface becomes weaker.The curves of TKK,TK′K′,TKK′andPKK′versus EFcan be analyzed similarly.

Figure 6.G,TK′ K and DOS(the red dot line)versus EF for ZGNR junctions with NL=40 and NR=16,18,36 and 38,the DOS versus EF for ZGNRs with NL=NR=40,16,18,36 and 38 are also shown for comparison.
4.Conclusion
In summary,the valley dependent transport properties of ZGNR junctions are studied by the transfer matrix and Green’s function method.In the bulk gap region of the right ZGNR,TKK′=TK′K=0and the valley polarizationPKK′=±1,thus the valley polarization can be well preserved.Out of the bulk gap of the right ZGNR,the plateau values of∣PKK′∣are 1/3,1/5,1/7,1/9,etc.It is found that step/dip positions of G,TKK,TK′K′andPKK′can be modulated by NR/NLand peaks positions ofTKK′andTK′Kcan be manipulated by both NLand NR.As NRincreases,G,TKK,TK′K′and their step numbers increase,the energy region forPKK′=±1 decreases.When NLis fixed and NRdecreases,outside the bulk gap of the right ZGNR,G (TKK,TK′K′andPKK′) shows more and more dips,andTKK′(TK′K) has more and more high peaks,especially when (NL-NR)/2 is odd.SoTKK′andTK′Kcan be strengthened by increasing (NL-NR)/2 and letting it be odd.However,compared with the intravalley transmission coefficients (TKKandTK′K′),the intervalley transmission coefficients (TKK′andTK′K) are much smaller.So the intravalley transmission contributes dominantly to G.Our findings may provide valuable guidance for the design and fabrication of valleytronic devices based on ZGNR junctions.
Acknowledgments
This work was supported by the Natural Science Foundation of Henan Province under Grant No.212300410388,and the“316” Project Plan of Xuchang University.
Appendix
Let us introduce the transfer matrix and Green’s function method in detail.Assuming the lead is characterized by the unit cell Hamiltonian h and nearest-neighbor hopping matrix t=Hi,i+1.Here the number of basis states in each unit cell is assumed to be M and thus h and t are M×M matrices.The wave propagation in this lead is governed by the uniform Schrödinger equation [9,41,42]
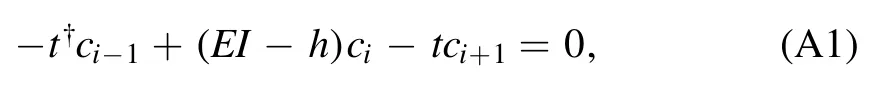
here I is the M×M identity matrix and ciis a vector of dimension M containing the wave-function coefficients on all sites and/or orbitals of the ith unit cell.Assuming the thickness of each unit cell in the lead is a,and imposing the Bloch symmetry ci=λci-1,ci+1=λ2ci-1(λ ≡eikais the Bloch factor),the above equation can be written as[9,41,42]

The above equation can be rewritten as a generalized 2M×2M eigenvalue problem [9,41]

For a given energy E and without imposing any boundary conditions,equation (A3) can be solved to yield 2M eigenmodes,which are classified into M right-going ones and M left-going ones according to the characteristics of their corresponding k(λ)[41].The eigenvalues are denoted as λ±,iwhere i=1,···,M,and the corresponding eigenvectors are u±,i,which are M×1 matrices.Here + and - correspond to the right-going and left-going waves,respectively.
The propagation matrices P±for left-going and rightgoing waves can be written as [9,40–42]

withU±=[∣u±,1〉 ,···,∣u±,M〉].The group velocity of the eigenmode i in the p lead can be calculated by [41,42]

Generally,the layered system can be divided into the semi-infinite left lead L,the central region C (unit cells 1 ≤m ≤N),and the semi-infinite right lead R.The Green’s function of the central region can be expressed as
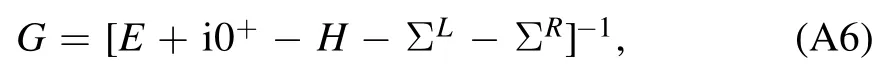
where H is the effective Hamiltonian for the central region,and ΣL,Rare self-energy corrections due to the left and right leads,which can be calculated by [41,42]
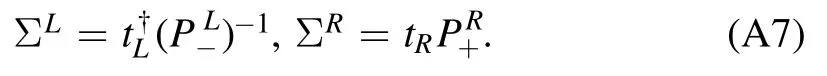
The physical transmission matrix element from the rightgoing eigenmode i in the left terminal to the right-going eigenmode j in the right terminal is computed by[32,40–44]

hereQ0= (E+ i0+)I-his the(N,1) block of G,which relates the first unit cell to the last unit cell of the central region,and aL(aR) is the thickness of the unit cell in the left (right) lead.
Thus the valley-resolved transmission coefficients are obtained by collecting tijin two separate valleys (K andK′ ),and the transmission coefficient from valley K in the left terminal to valleyK′ in the right terminal is [32,44]

ORClD iDs
杂志排行
Communications in Theoretical Physics的其它文章
- lntrinsic ferromagnetism in CoBr2 nanolayers: a DFT + U and Monte Carlo study
- The interplay of diffusion and heterogeneity in nucleation of the networked Ising model
- How polar hydroxyl groups affect surface hydrophobicity on model talc surfaces
- Wormhole solutions and energy conditions in f(R,G) gravity
- Constraint on nuclear symmetry energy imposed by f-mode oscillation of neutron stars
- Impurity effects of the Λ hyperon in the hypernuclear systems Mg and Si
