(2+1)-dimensional coupled Boussinesq equations for Rossby waves in two-layer cylindrical fluid*
2021-11-13ZheyuanYuZongguoZhangandHongweiYang
Zheyuan Yu,Zongguo Zhang and Hongwei Yang,∗∗
1 College of Mathematics and System Science,Shandong University of Science and Technology,Qingdao,266590,China
2 School of Mathematics and Statistics,Qilu University of Technology (Shandong Academy of Sciences),Jinan,250353,China
Abstract In this paper,the existence and propagation characteristics of Rossby waves in a two-layer cylindrical fluid are studied.Firstly,based on the dimensionless baroclinic quasi-geostrophic vortex equations including exogenous and dissipative,we derive new (2+1)-dimensional coupled Boussinesq equations describing wave propagation in polar coordinates by employing a multiscale analysis and perturbation method.Then,the Lie symmetries and conservation laws of the coupled Boussinesq equations are analyzed.Subsequently,by using the (G/′G)-expansion method,the exact solutions of the (2+1)-dimensional coupled Boussinesq equations are obtained.Finally,the effects of coupling term coefficients on the propagation characteristics of Rossby waves are analyzed.
Keywords: Rossby waves,(2+1)-dimensional coupled Boussinesq equations,two-layer cylindrical fluid
1.lntroduction
In many large fluid systems,such as atmospheric and oceanic systems,stratification often occurs due to temperature,particle concentration and density.The stratification of a fluid mainly comes from the non-uniform distribution of power,density and other factors in a certain dimension [1].Therefore,the characteristics,structure,function,and dynamic development process in time and space of a stratified flow are different from and much more complicated than those of a homogeneous fluid [2–4].On the one hand,the fluid in a stratified flow usually has many layers,but most of the theoretical studies on fluid systems examine single-layer fluids.On the other hand,the number of layers of a stratified flow is often limited,and current research does not involve the direction of an infinite number of layers and continuity.Therefore,the stratified flow is simplified to a two-layer fluid system for the convenience of further research [5].
As early as the 19th century,Helmholtz and Kelvin analyzed the stability of stratified flow interfaces.Shortly thereafter,Boussinesq studied the effect of density changes on a stratified flow and proposed the famous Boussinesq approximation.These theories have laid a solid foundation for the development of stratified flow research.In the 20th century,Jeffreys,Keulegan,Yi Jiaxun,Turner,Schiller and others promoted the continued development of understanding of stratified flows.In the 1970s,the first international conference on stratified flows was held in the Soviet Union,which marked a new height in the study of stratified flows [6–8].
As a result of the rotation of the Earth and the spherical effect,the ocean atmosphere produces a large,permanent fluctuation with a long history of life [9–11].This kind of wave has the characteristic of organized consistency in structure,and the isolated wave characteristic of stable large amplitude,so it is called a Rossby wave [12,13].
Rossby waves are very common in rotating fluids.Such fluctuations had been theorized in the late 19th century,but were not observed in the ocean until the late 20th century.In 1964,Long first theoretically proved the existence of Rossby waves based on the Korteweg–De Vries (KdV) equation and its solution [14].Subsequently,in 1976,Benny extended Long’s conclusion and found the relationship between Rossby wave velocity and amplitude[15].In 1978,Redekopp and Weidman proved the existence of Rossby waves in zonal flows[16].In 1984,Akylas obtained the forced KdV equation of Rossby waves [17].In 1992,Liu Shishi analyzed the influence of dimensions on Rossby waves [18].In 1995,Rodhead established the envelope Rossby wave model and studied the blocking interaction [19].In 2006,Zhao Qiang et al deduced the Petviashvili equation of Rossby waves[20].In 2020,Yang Liangui et al studied topographic Rossby waves and obtained a Gardner evolution equation [21].
The local symmetry approach is regarded as one of the most crucial methods for seeking invariant solutions.Lie point symmetry is included in the local symmetries.The process of finding exact solutions of lower-dimensional equations cannot continue without Lie symmetry transformation and the obtaining of conservation laws [22,23].Due to the limitation of the local symmetry approach,more attention has been paid to the nonlocal symmetries method.The nonlocal symmetry for a number of partial differential equations becomes the Lie point symmetry in the process localization [24,25].
In this paper,the existence and propagation characteristics of Rossby waves in a two-layer cylindrical fluid are studied.Firstly,based on the dimensionless baroclinic quasigeostrophic vortex equations including exogenous and dissipative,new (2+1)-dimensional coupled Boussinesq equations describing wave propagation in polar coordinates are established by a multiscale analysis and perturbation method [26,27].Secondly,the Lie symmetries and conservation laws of the (2+1)-dimensional coupled Boussinesq equations are analyzed by using a Lie group analysis method[28–30].Thirdly,by using the (G′/G)-expansion method[31],the exact solution of the (2+1)-dimensional coupled Boussinesq equations is obtained.Finally,the effects of coupling term coefficients on the propagation characteristics of Rossby waves are analyzed.
2.Derivation of the (2+1)-dimensional coupled Boussinesq equations
With the emergence of various global marine pollution problems,Rossby waves in two-layer fluids have attracted increasing attention.The Rossby waves in a two-layer cylindrical fluid are rarely seen in previous articles.In this paper,we study Rossby waves in polar coordinates.The dimensionless barotropic quasi-geostrophic vortex equations with exogeny and dissipation are considered as:
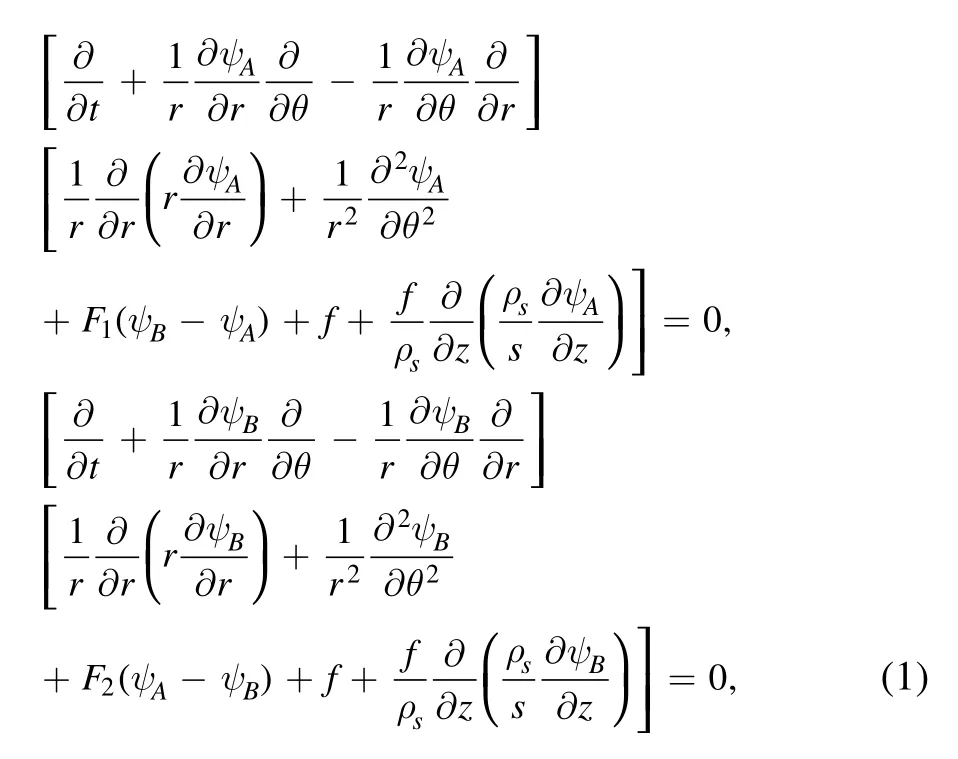


To derive the coupled Boussinesq equations,the stream functionsψAandψBare rewritten into two parts.One is the fundamental stream function,and the other is the disturbed stream function.Hence,the stream functions have the following form:

Assuming that the effect of coupling constants on Rossby waves is not strong,we can introduce the following transformations:
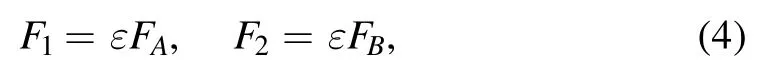
where ε is a small parameter.We also set the stretched variables as

Then,we expand the perturbation stream functions into the following form:

Substituting the stream functions (3),transformations (4),stretched variables(5),and perturbation stream functions(6)into equations(2),two polynomials about the small parameter ε can be obtained.Taking the coefficients ofε2,we have
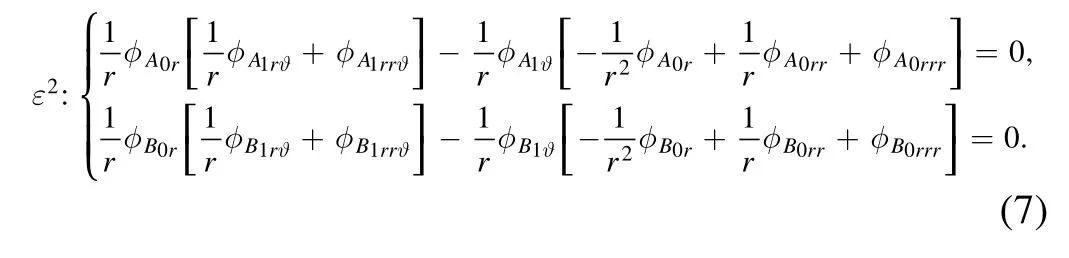
It can be observed that equations (7) can be integrated with respect to ϑ.The integration results in a set of equations that relate only to r,
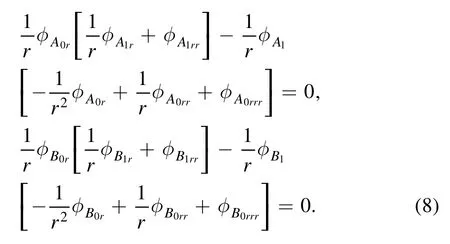
Hence,we assumeφA1andφB1have separate variable forms as

By substituting equations (9) into (8),we get

In order to get the relationship between the perturbation stream functions,we take the coefficients ofε3:
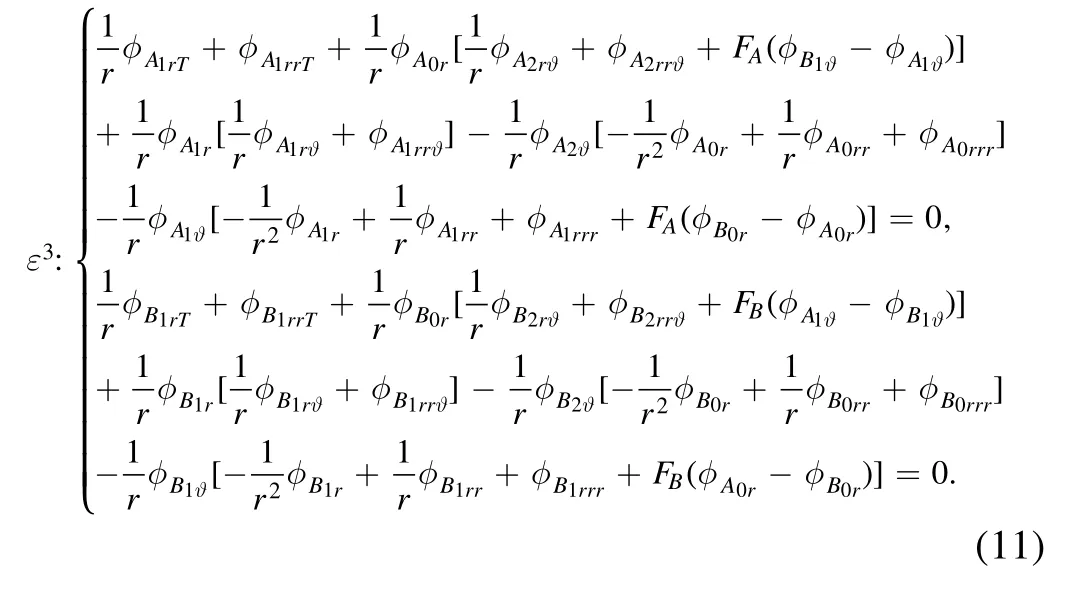
Substituting equations(9)and(10)into(11)and integrating with respect to ϑ,we get
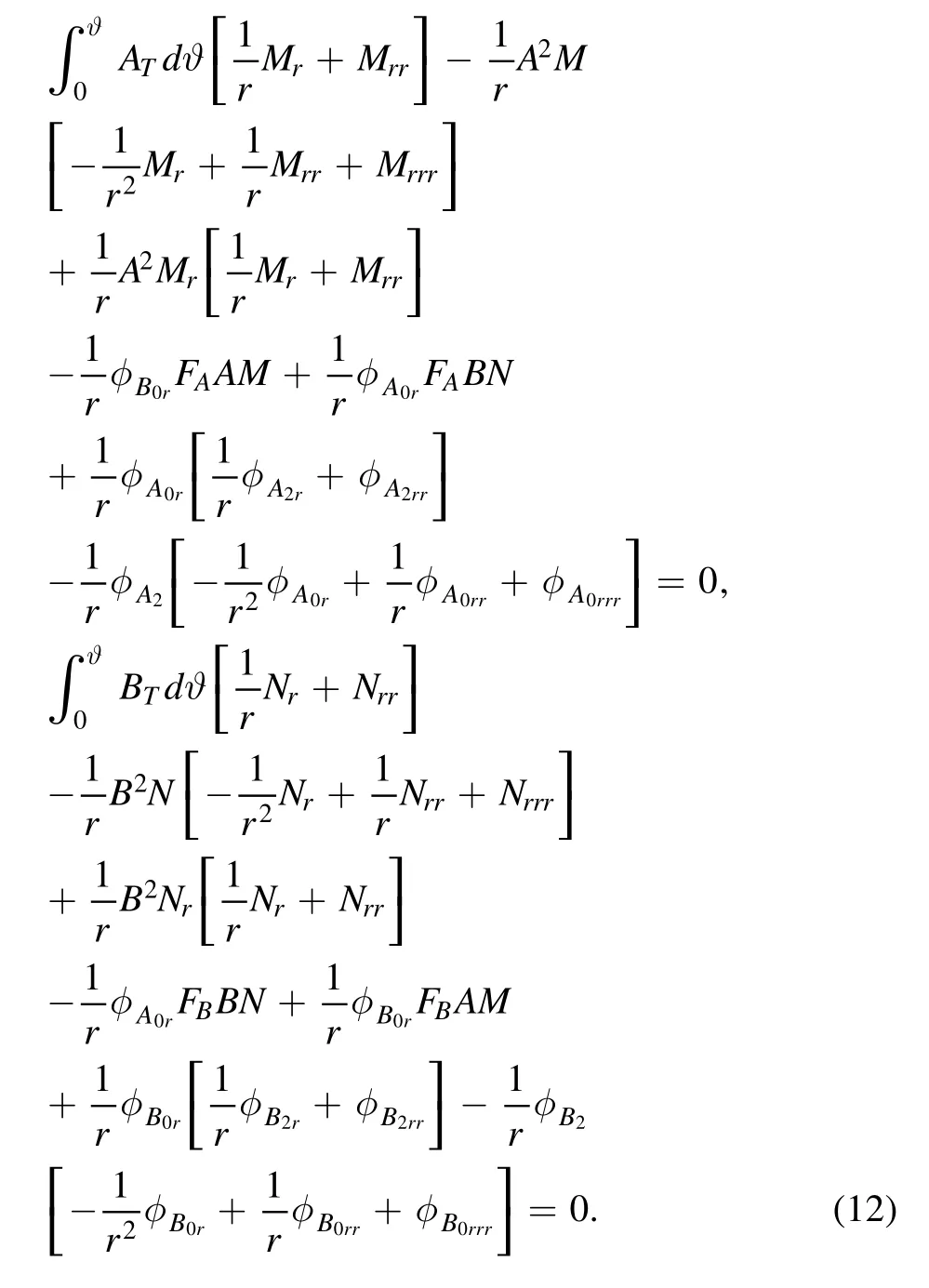
By observing equations (12) in the expression,we assume the functionsφA2andφB2have separate variable forms as
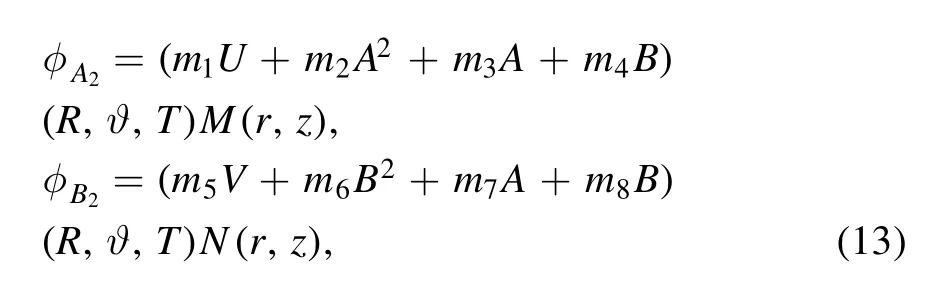

In order to compute the relationship between the stream functions,we collect the coefficients of the parameterε4:

Substituting variable separation functions (9),identities (10),and variable separation functions(13)into equations(15),we obtain a set of equations aboutφA3andφB3.Formerly,φA3andφB3would be set to zero or integrated with respect to variable ϑ fromϑ1toϑ2.However,in this article,we neither takeφA3=φB3= 0nor integrate with respect to variable ϑ fromϑ1toϑ2.
Nonetheless,it is possible to arrive at some consistent and meaningful solutions.In this paper,we give only one possible choice ofφA3andφB3as

where
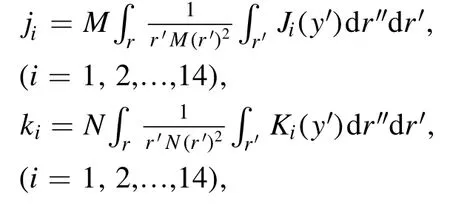
andJi(i= 1,2,… ,14),Ki(i= 1,2,… ,14) are in the appendix.
By eliminating the term containing r and integrating the equation over ϑ once,we find that A and B,which only contain R,ϑ and T,apply to the relation of the following (2+1)-dimensional coupled Boussinesq system:
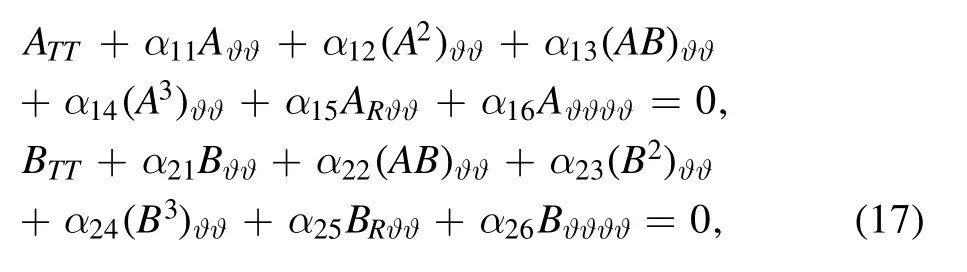
where constantsα1j(j= 1,2,… ,6) andα2j(j= 1,2,… ,6)are inJi(i= 1,2,… ,11) andKi(i= 1,2,… ,11).
Distinctly,equations (17) are the (2+1)-dimensional coupled Boussinesq equations that can describe the Rossby wave in polar coordinates.Compared to the traditional Boussinesq system,the new equations have both the nonlinear coupling term (AB)ϑϑand the high-order nonlinear terms(A3)ϑϑ,(B3)ϑϑ.Therefore,the new model has stronger coupling and nonlinearity compared with the traditional model.As can be seen,although the nonlinear terms are coupled,the strongest nonlinear terms are not coupled.
The cylindrical coordinate system is better than the rectangular coordinate system for reflecting the change in distance and direction of particles.The study of cylindrical coordinates is also an indispensable part of daily research.The Rossby waves in a two-layer cylindrical fluid have rarely been studied in previous articles.However,the new model established in this paper can describe the Rossby waves in polar coordinates.
3.Conservation laws of the (2+1)-dimensional coupled Boussinesq equations
3.1.Lie symmetry analysis
Firstly,it is assumed that the Lie point transformation of equations (17) acting on the dependent variable and independent variable is invariant,so
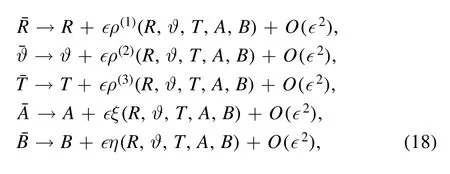
whereρ(1),ρ(2),ρ(3),ξ and η are infinitesimal functions,andξϑ,ηϑ,ξϑϑ,ηϑϑ,ξTT,ηTT,ξ Rϑϑ,η Rϑϑ,ξϑϑϑϑandηϑϑϑϑare the prolongations of infinitesimal functions.They can be written as

where DR,Dϑ,and DTare the total derivative operators as follows:

Then,we write the infinitesimal generator V as

Under the Lie point transformation,the invariance of the the(2+1)-dimensional coupled Boussinesq system(17)results in the following invariance conditions:
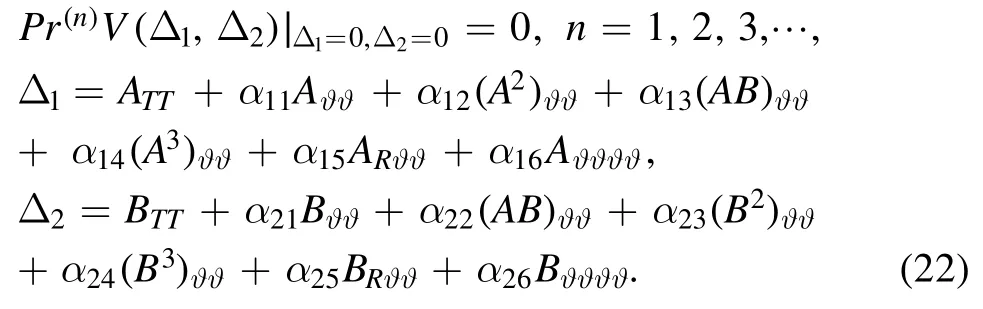
According to equations (21) and (22),the invariance criteria are as follows:
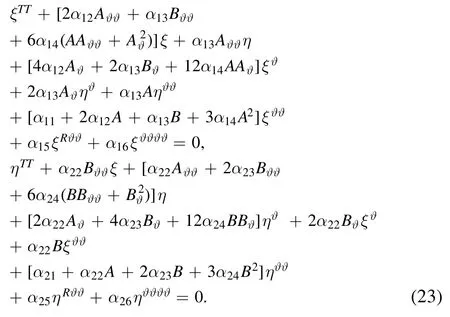
Substituting the prolongations (19) and the total derivative operators (20) into the invariance criteria (23),we have two partial differential multinomials in regard to A and B.The same terms are combined,and the coefficients of each term of the polynomial are set to zero.Whenα13=α22= 0,by computing the equations,a set of Lie algebra of point symmetries is obtained as follows:

Therefore,we can write the Lie algebra of point symmetries as
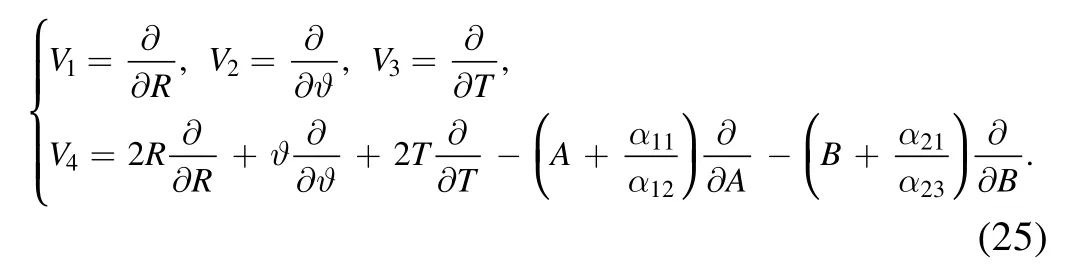
3.2.Conservation laws
A formal Lagrangian for the (2+1)-dimensional coupled Boussinesq equations can be presented as follows:
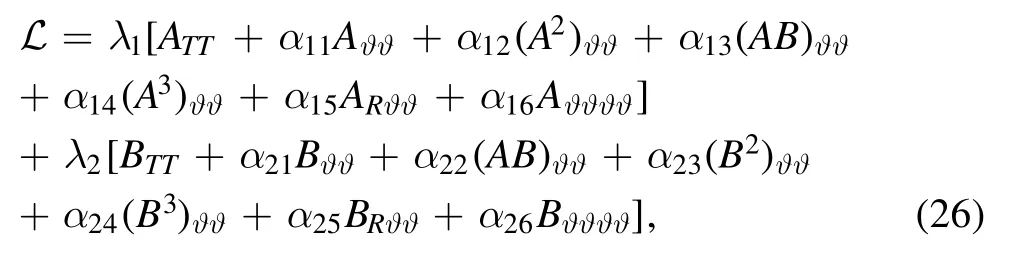
whereλ1=θ1(R,ϑ,T) andλ2=θ2(R,ϑ,T) are new functions.According to the formal Lagrangian,the functional can be written as
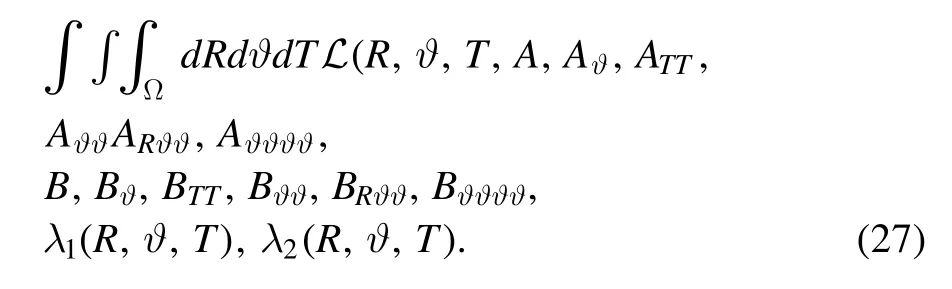
Obviously,the adjoint equations of equations(17)are the Euler–Lagrangian equations we are looking for:
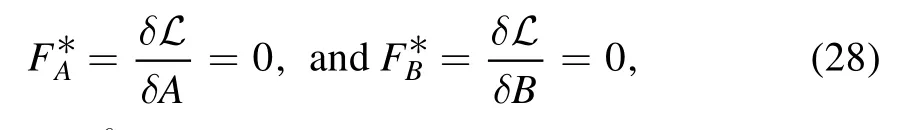

Therefore,the Euler–Lagrange equations (28) also have the following form:

In the preceding part,we obtained the Lie algebra of point symmetries of the (2+1)-dimensional coupled Boussinesq equations (17).Therefore,the Lie feature functionWi(i=1,2) can be written as
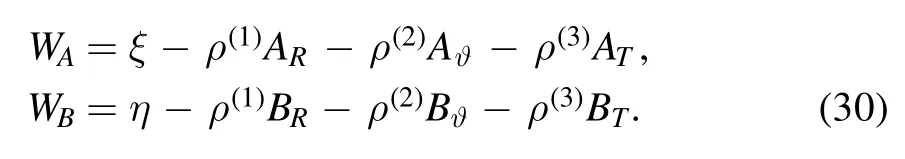
Applied to theVj(j=1,2,3,4) of the symmetry (25),we have

Therefore,the components of conserved vectors of the(2+1)-dimensional coupled Boussinesq equations (17) are defined as


wherem= 1,2,3,4.When m = 4,we can have the following components of conserved vectors:
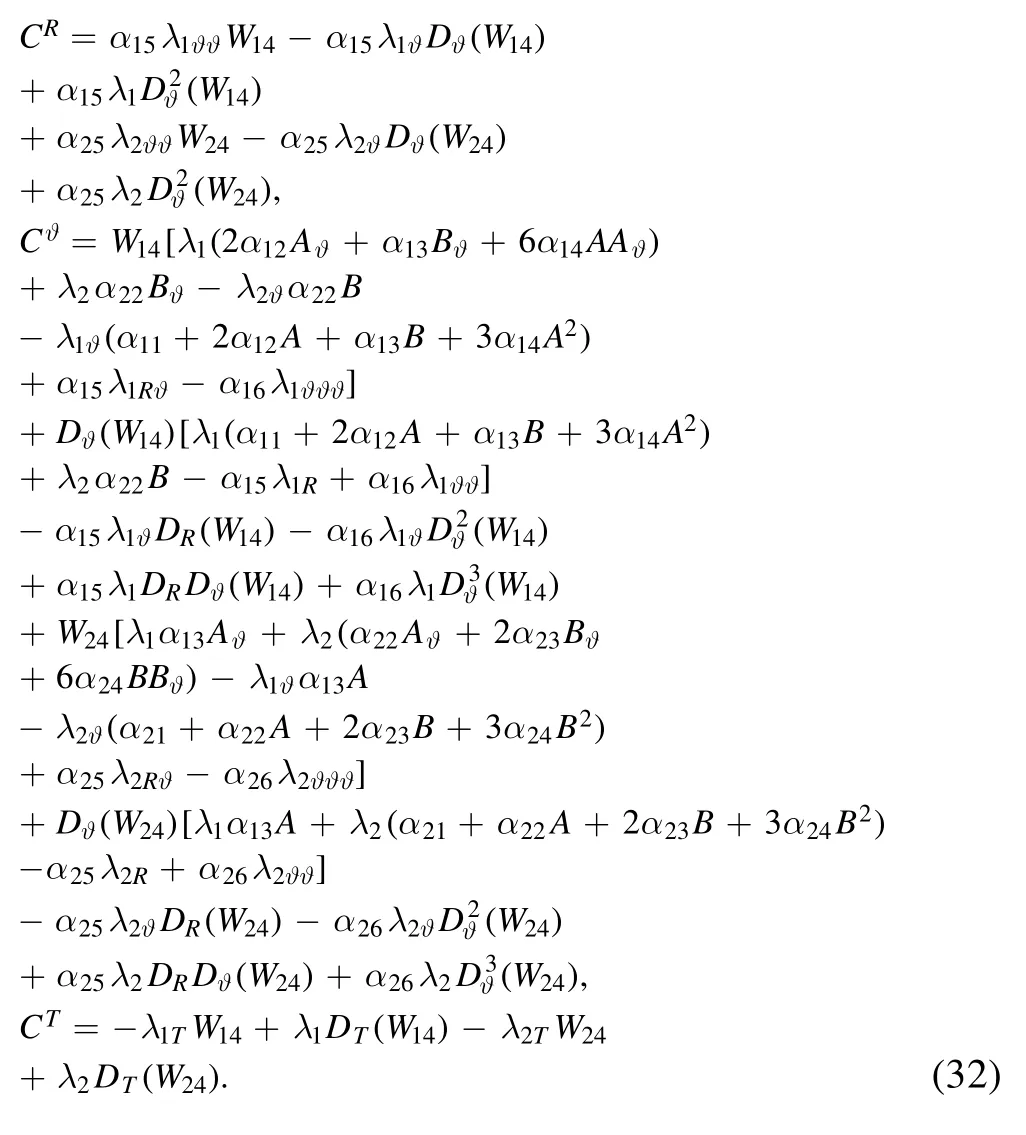
Equations(25)are the Lie algebra of point symmetries of the(2+1)-dimensional coupled Boussinesq equations,and equations (32) are the conservation laws of the (2+1)-dimensional coupled Boussinesq equations.The Lie symmetry and conservation laws have a significant impact on the property study and practical application of the equations; for example,stability analysis and construction of solutions for some special structures.
4.Exact solutions of the (2+1)-dimensional coupled Boussinesq equations
The solution of the nonlinear partial differential equations plays an important role in the application of the equations.This is mainly because the solution of the equation can describe the process and characteristics of motion more intuitively.In this section,we will use the (G′/G)-expansion method to calculate the exact solution of the (2+1)-dimensional coupled Boussinesq equations.
Firstly,the traveling wave transformations are introduced as
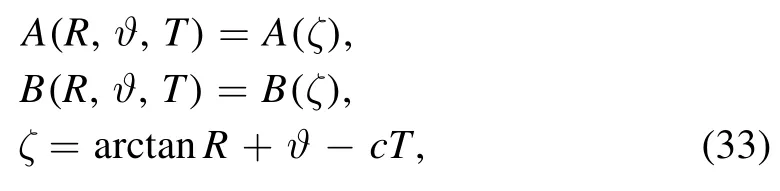
where c is the propagation velocity.The traveling wave transform (33) is substituted into the (2+1)-dimensional coupled Boussinesq equations (17),and the ordinary differential equations about A and B are simplified as:
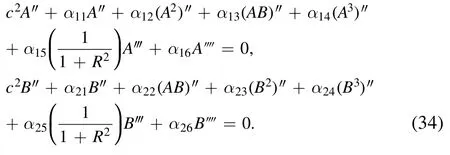
It is obvious that the ordinary differential equations (34) are integrable.Therefore,integrating equations (34) with respect to ζ twice:

In order to cancel out A3,A″ ,B3andB″ ,we give N = 1.Therefore,the (2+1)-dimensional coupled Boussinesq equations (17) have the following solution:
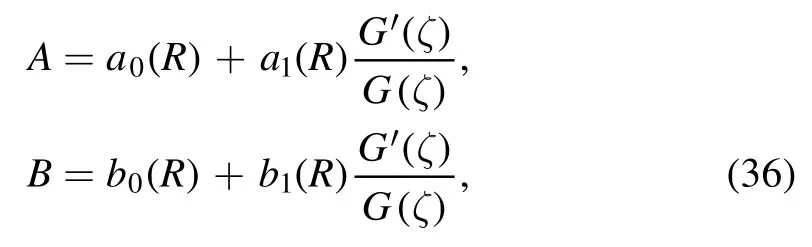
wherea0(R),a1(R),b0(R) andb1(R) are arbitrary functions that can be determined later.G(ζ) satisfies the second-order linear ordinary differential equation

whereλ(R) andμ(R) are arbitrary functions that can be determined later.The general formula forcan be expressed as

By substituting general solutions (36) and equation (37)into ordinary differential equations (35),a multinomial in regard tois constructed.Setting the coefficient of each term of the polynomial as zero,a set of equations in regard to a0,a1,b0,b1,λ and μ can be derived.By calculating the equations,the coefficient relations can be obtained as follows:

where c is an arbitrary constant.By substituting general formula (38) and equation (39) into general solutions (36),we have:
Case 1.Whenλ2-4μ>0,the hyperbolic function solutions can be written as
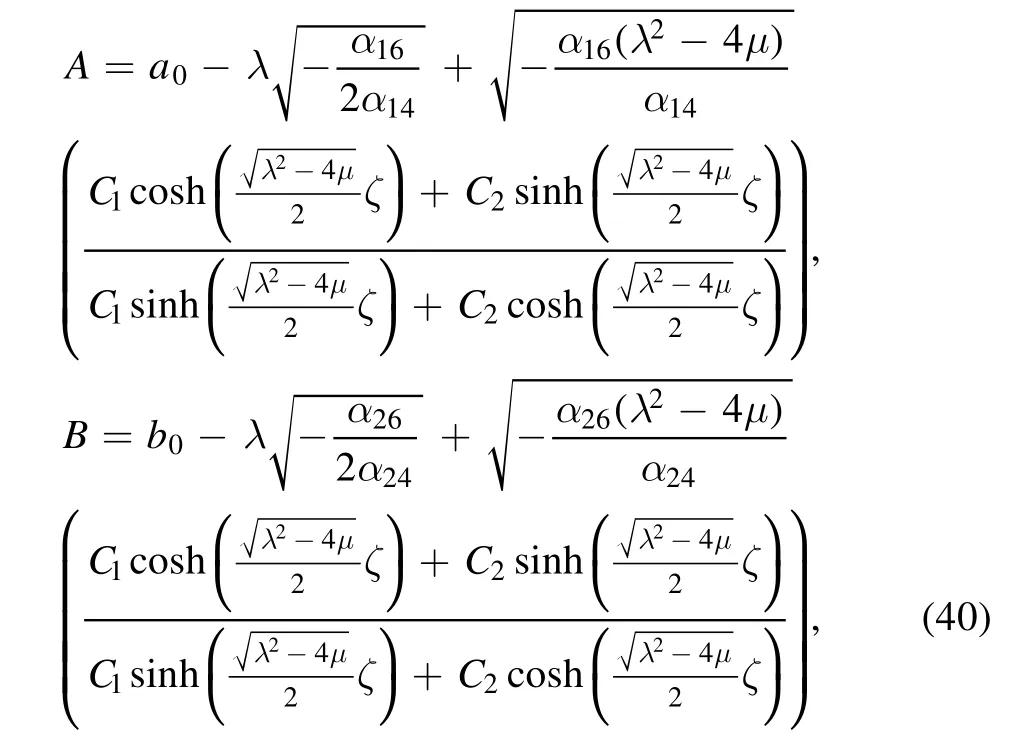
whereζ= arctanR+ϑ-cT,C1and C2are arbitrary constants.By taking the special values of C1and C2,some solutions can be obtained from equation (43),such as:
i.SettingC1=0andC2≠0,we have

ii.SettingC1≠0andC2=0,we have
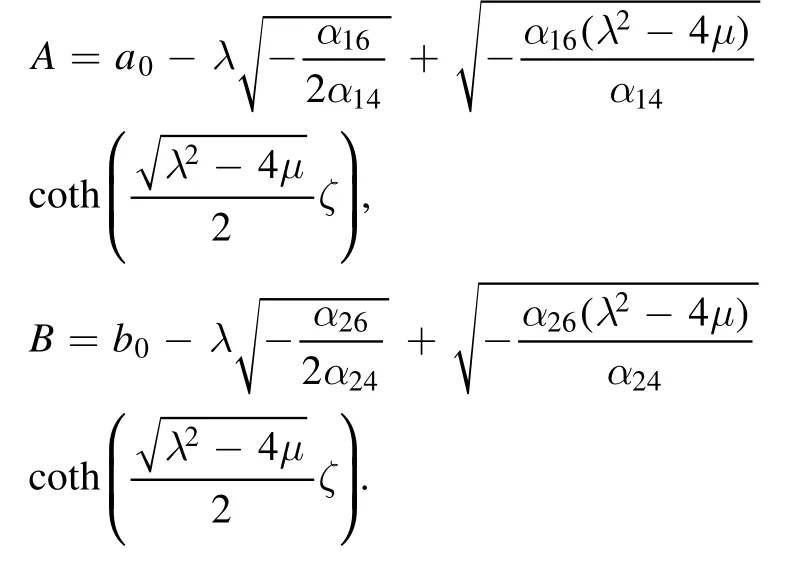
iii.SettingC1≠0andwe have


Case 2.Whenλ2-4μ<0,the trigonometric function solutions can be written as

whereζ= arctanR+ϑ-cT.
Case 3.Whenλ2-4μ=0,the rational fractional function solutions can be written as

whereζ= arctanR+ϑ-cT.
To understand the propagation characteristics of Rossby waves more intuitively,some suitable parameters were selected to draw diagrams.
Obviously,as shown in figures 1–2,the coefficients of the coupling terms will change the shape of the Rossby waves,which could be more in accordance with the physical truth.It can be seen from figure 1 that the hyperbolic function solutions are linear soliton solutions,and whenR→0,the wave height increases with increasing coefficients of the coupling terms.This can be explained by closer distances and stronger perturbations affecting the stability of the wave.However,whenR→+∞,the coupling term coefficients have no effect on the wave height.It can also be seen from figure 2 that the trigonometric function solutions are periodic soliton solutions,and whenR→0,the wave height increases with increasing coefficients of the coupling terms.

Figure 1.Plot of solution A in equations (40) when α1 4 = 1.
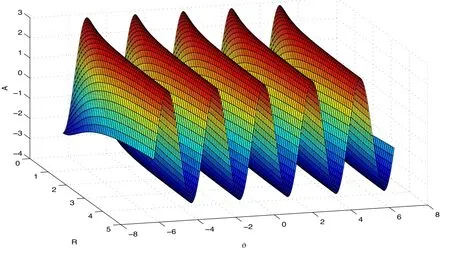
Figure 2.Plot of solution A in equations (41) when α1 4 = 1.
5.Conclusion
In this paper,the Rossby waves in a two-layer cylindrical fluid are studied.To better reflect the change in distance and direction of particles,form the dimensionless baroclinic quasi-geostrophic vortex equations include exogenous and dissipative in two-layer cylindrical fluid,new (2+1)-dimensional coupled Boussinesq equations which can describe the Rossby waves in polar coordinates are established.The new model has stronger coupling and nonlinearity compared with the traditional model.Although the nonlinear terms are coupled,the strongest nonlinear terms are not coupled.Then,Lie symmetries and conservation laws of the coupled Boussinesq equations are analyzed.Subsequently,by using the(G″/G)-expansion method,the exact solution of the (2+1)-dimensional coupled Boussinesq equations is obtained.Finally,the effects of coupling term coefficients on the wave shape characteristics are analyzed.WhenR→0,the wave height increases with increasing coefficients of coupling terms.However,whenR→+∞,the coupling term coefficients have no effect on the wave height.
Appendix
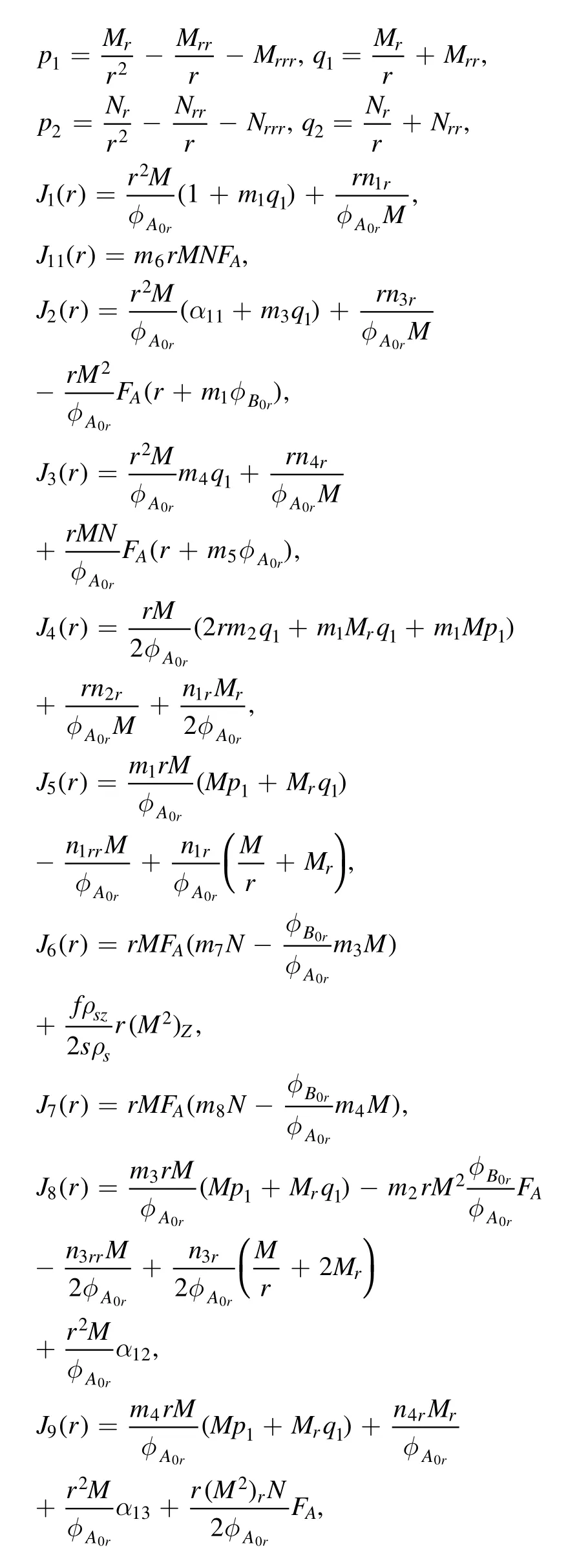


杂志排行
Communications in Theoretical Physics的其它文章
- lntrinsic ferromagnetism in CoBr2 nanolayers: a DFT + U and Monte Carlo study
- Valley-resolved transport in zigzag graphene nanoribbon junctions
- The interplay of diffusion and heterogeneity in nucleation of the networked Ising model
- How polar hydroxyl groups affect surface hydrophobicity on model talc surfaces
- Wormhole solutions and energy conditions in f(R,G) gravity
- Constraint on nuclear symmetry energy imposed by f-mode oscillation of neutron stars
